Comprehensive Assessment of Climate Change Impacts on River Water Availability for Irrigation, Wheat Crop Area Coverage, and Irrigation Canal Hydraulic Capacity of Large-Scale Irrigation Scheme in Nepal

Abstract

While atmospheric warming intensifies the global water cycle, regionalised effects of climate change on water loss, irrigation supply, and food security are highly variable. Here, we elucidate the impacts of the climate crisis on irrigation water availability and cropping area in Nepal’s largest irrigation scheme, the Sunsari Morang Irrigation Scheme (SMIS), by accounting for the hydraulic capacity of existing canal systems, and potential changes realised under future climates. To capture variability implicit in climate change projections, we invoke multiple Representative Concentration Pathways (RCPs; 4.5 and 8.5) across three time horizons (2016–2045, 2036–2065, and 2071–2100). We reveal that although climate change increases water availability to agriculture from December through March, the designed discharge of 60 m³/s would not be available in February-March for both RCPs under all three time horizons. Weed growth, silt deposition, and poor maintenance have reduced the current canal capacity from the design capacity of 60 m³/s to 53 m³/s up to 10.7 km from the canal intake (representing a 12% reduction in the discharge capacity of the canal). Canal flow is further reduced to 35 m³/s at 13.8 km from canal intake, representing a 27% reduction in flow capacity relative to the original design standards. Based on climate projections, and assuming ceteris paribus irrigation infrastructure, total wheat cropping area could increase by 12–19%, 23–27%, and 12–35% by 2016–2045, 2036–2065, and 2071–2100, respectively, due to increased water availability borne by the changing climate. The case for further investment in irrigation infrastructure via water diversion, or installation of efficient pumps at irrigation canal intakes is compelling. Such investment would catalyse a step-change in the agricultural economy that is urgently needed to sustain the Nepalese economy, and thus evoke beneficial cascading implications for global food security.

1. Introduction

Spatiotemporal variation in precipitation [1,2] and freshwater availability [3] are reducing the likelihood of water supply in irrigation systems, severely challenging how irrigation water use is prioritised [4,5,6]. Globally, the agricultural irrigation sector uses about 70% of the world’s total annual water consumption [7,8,9]. This indicates that water use in agriculture should be increasingly scrutinised as the changing climate increases volatility in rainfall and irrigation supply, particularly given that many irrigation schemes in developing nations operate at low efficiency due to a lack of maintenance and robust water management policies [8,10,11,12,13].

Seepage and operational losses in unlined irrigation canal networks have long been a continuing problem for practitioners [14], for such losses can impair system efficiency of water use to less than 50% [15]. Indeed, in many Indian and Pakistani irrigation systems, around 50% of water can be lost in seepage and evaporation during delivery from the head of the canal to the field (Sharma et al. cited in [16] and Memon et al. [17]).

Seepage losses from irrigation canals are a function of the permeability of subsoils, sediment quantity in irrigation water, depth of the local water table relative to the canal bottom, drainage distance, bed width and/or side slope, and the water depth and velocity. In India, the seepage losses from unlined canals are typically 0.026–0.61 m³/m²/day [18]. In an experimental channel in arid Saudi Arabia, Moghazi and Ismail [19] reported average seepage of 2.65, 2.16, and 0.464 m³/m²/day in canals with uncompacted earthen beds, compacted channel beds, and prefabricated bitumen jute mat, respectively. Other work has shown that seepage losses in unlined canals in permeable soils can be 20–30% of the total water supply [20]. According to Wilkinson [21], a canal having a seepage loss >0.031 m³/m²/day is considered to be a good candidate for canal lining investment in terms of both economic outlay and benefit.

Kilic and Tuylu [22] investigated water losses in the conveyance system of the Ahmetli irrigation scheme in Turkey using the inflow–outflow method. They reported that the average water loss in the main canal was 5.78 m³/m²/day, (ranging from 1.04 to 12.27 m³/m²/day). Eshetu and Alamirew [23] similarly evaluated water loss in Ethiopian irrigation canals lined with a geo-member and reported water losses of 1.08 m³/m²/day (range 1.06 to 1.11 m³/m²/day). In the earthen portion of the irrigation main canal, the average water loss was 1.55 m³/m²/day. Mohammadi et al. [24] analysed water losses in irrigation channels in Iran and reported average water losses of 1.21 m³/m²/day in the main canal. Water losses varied from 1.12 m³/m²/day to 1.38 m³/m²/day. Akkuzu [25] assessed water losses in an irrigation canal in Turkey using the inflow–outflow method and reported that the average water loss was 1.21 m³/m²/day, varying from 0.17 m³/m²/day to 3.11 m³/m²/day at different locations of the canal.

Factors affecting canal water-carrying capacity include flow obstructions due to vegetation, siltation, and reduction in canal bank height due to compaction in the filling area or surface erosion. Regular hydraulic maintenance is required for efficient water flow management. Hence, hydraulic assessment is required for efficient water flow management in irrigation systems.

Climate change has direct impacts on multiple sectors of water resources in Nepal including hydropower [26], water supply [27], and irrigation [28,29]. The irrigation water requirement is projected to decrease in both western [29] and eastern [28] irrigation schemes in Nepal due to a projected increase in rainfall.

Here, we investigated the impacts of climate change on river water, accounting for losses and system capacity for short (2016–2045), mid (2036–2065), and long-term horizons (2071–2100) using low (RCP4.5) and high (RCP8.5) socioeconomic development scenarios. Future climate data were obtained at a high spatial resolution across the Nepal Eastern Terai region. Downscaled climate data from ensembles of global circulation models (GCMs), representing the four corners of climatic extremes—cold and dry (CD), warm and dry (WD), cold and wet (CW), and warm and wet (WW) [1]—were used for each time horizon and greenhouse gas (GHG) emissions scenario in a contemporary hydraulic model for assessment. The main aims of the paper were to (1) develop a generalised, scalable methodology to assess the impacts of climate change on river water availability for irrigation, crop area under irrigation, and irrigation canal hydraulic capacity, (2) quantify climate change impacts of on river water availability for irrigation, (3) project implications of water availability on wheat cropping area, and (4) assess the current and likely future hydraulic capacity of canal systems in the Sunsari Morang Irrigation Scheme. It is hoped that the developed comprehensive assessment methodology in this research will help water professionals in other parts of the globe to conduct similar investigations for their local irrigation systems.

2. Materials and Methods

2.1. Study Area

The Sunsari Morang Irrigation Scheme, the largest irrigation scheme in Nepal, was designed by the British in the 1960s to reduce the severity of famine rather than maximise yield per hectare. Irrigation water is diverted from the Koshi River via side intakes. The Koshi River, one of the largest tributaries of the Ganges, originates in China and flows through Nepal and India (Figure 1a). The Koshi River basin is the largest river basin in Nepal with a catchment area of about 540,000 km² near Chatara in Nepal. There are no permanent water diversion structures (weirs or barrages) across the river. River water enters into the main canal through the side intake by gravity; hence canal discharge depends mainly on the river water level. The irrigation scheme is designed to irrigate 68,000 hectares of agricultural land in the south-eastern plains of Nepal. The southern plains of Nepal, which cover 23% of the total area of Nepal, also known as the Terai region, are the food basket of the country, producing around 54% of the total major cereal crop production of Nepal [30]. The Sunsari Morang Irrigation Scheme (SMIS) irrigates the Sunsari and Morang districts of eastern Nepal (Figure 1b), which contributes about 7% of the country’s major cereal crop production [30]. Hence, adequate, reliable, and timely irrigation supply in the Sunsari Morang irrigation scheme is crucial as it is the lifeblood of the millions of people in eastern Nepal.

The main canal length is 55 km. There are 25 branch (secondary) canals supplied from the main canal. These secondary canals (running North-South) then branch into distributary (sub-secondary) and tertiary canals. The total length of branch and distributary canals is about 425 km, whilst the tertiary canals add a further 410 km. In addition to the branch canals, a few direct outlets from the main canal also supply water to the command area. A schematic of the main canal and major branch canal network of the Sunsari Morang Irrigation Scheme is shown in Figure 1c. The light green lines in Figure 1c represent the main and branch canals.

Entry of silt from the river (intake) into the canal network has been a problem since the Sunsari Morang Irrigation Scheme began operation. There are no scheduled operations and maintenance plans, which is a legacy issue of the initial design objective to reduce the severity of famine rather than maximise irrigation production year on year. Being a large-scale irrigation scheme with a limited yearly operation and maintenance budget, the canal system is not well maintained. While siltation and weeds are common in the canal system, few studies have been carried out to investigate the impacts of such flow obstructions on canal flow capacity.

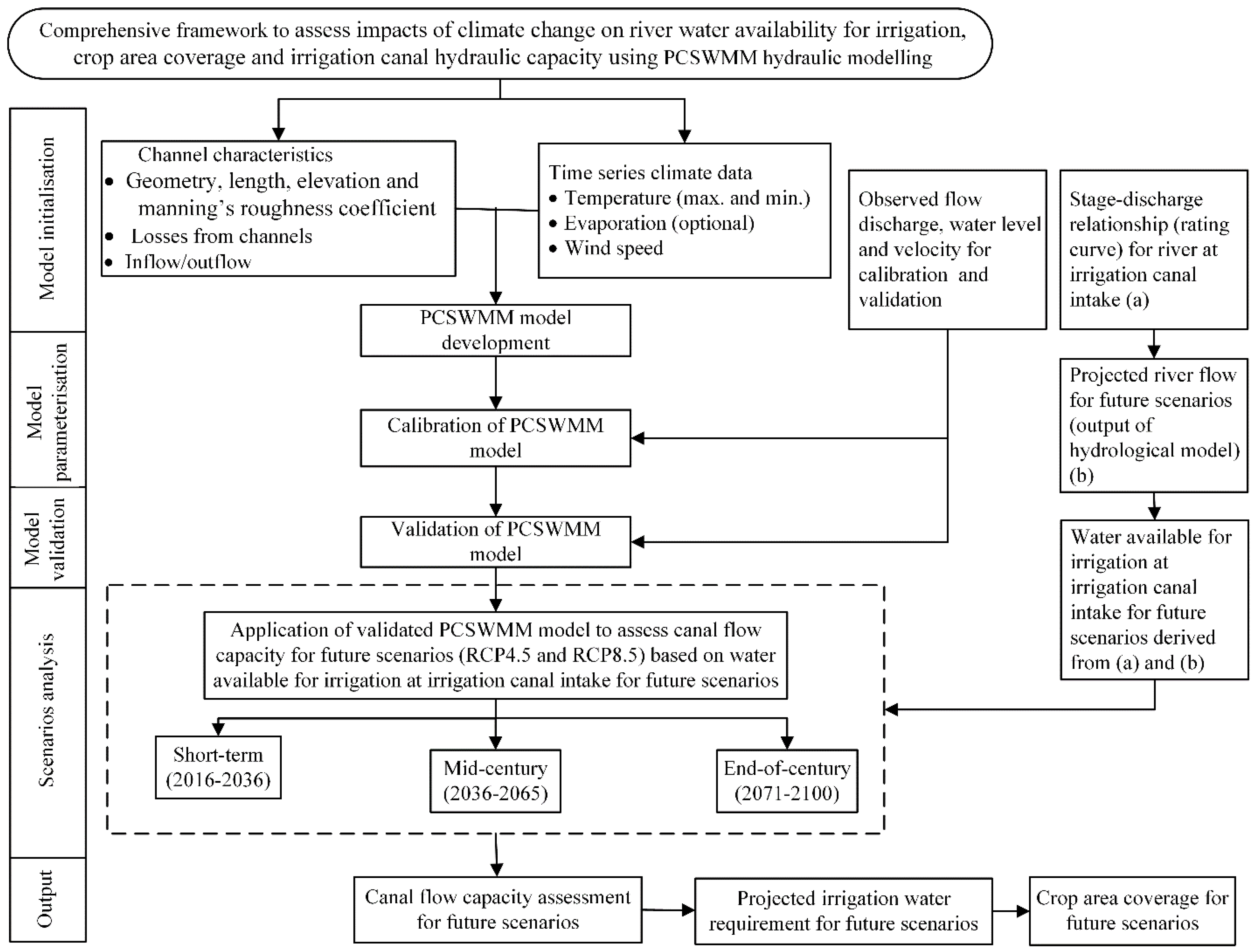
2.2. Assessment Methodology

Figure 2 shows a schematic of the methodology to assess the impacts of climate change on river water availability for irrigation, crop area coverage, and irrigation canal hydraulic capacity using a commercially available hydraulic model—the Personal Computer Storm Water Management Model (PCSWMM) (Computational Hydraulics Inc. (CHI), Guelph, ON, Canada. https://www.pcswmm.com/ (accessed on 1 March 2020)). Key steps include model initialisation, model parameterisation, model validation, scenario analysis, and output. The steps involved in the methodology are mentioned in the following sections.

2.2.1. PCSWMM Input Data Processing and Model Development (Model Initialisation)

PCSWMM input data include the size, length, elevation, and slope of the canal, inflow or outflow from the canal, Manning’s roughness coefficient of the canal, losses from the canal, and climate data (temperature, precipitation, wind speed). The observed discharge, velocity, and water depth at the main canal of the irrigation canal will be used for the PCSWMM model development.

2.2.2. Model Parameterisation

After model initialisation, the PCSWMM model is calibrated using observed discharge, flow velocity, and water depth in the main irrigation canal.

2.2.3. Model Validation

The calibrated PCSWMM model is validated using observed discharge, flow velocity, and water depth in the main irrigation canal network.

2.2.4. Scenario Analysis (Canal Capacity Assessment)

The validated PCSWMM model is applied to assess the hydraulic capacity of the canal, based on water availability for irrigation at the irrigation canal intake considering future climate change scenarios as they affect Koshi River flows. Changes in future water availability for irrigation at the irrigation canal intake are compared with the reference (base) period data. The flow capacity of the main canal is assessed with respect to future water availability for irrigation at the irrigation canal intake.

2.3. Personal Computer Storm Water Management Model (PCSWMM) Hydraulic Model

A hydraulic model is necessary for the investigation of the hydraulic capacity of irrigation canals under various water availability scenarios and canal geometric and hydraulic conditions. The Storm Water Management Model (SWMM) model has been successfully used to simulate the hydraulic characteristics of irrigation canals. Kim et al. [13], Do et al. [31], and Bang et al. [32] assessed the hydraulic performance of irrigation canals in South Korea using the Storm Water Management Model (SWMM) model. Schoenfelder et al. [33] applied SWMM to evaluate the hydraulic performance of irrigation canals in the USA. Banda and Kasitu [34] used SWMM to assess the capacity of a drainage system in South Africa. SWMM is a US EPA tool, and PCSWMM comes from CHI Canada. The PCSWMM is a commercial model while SWMM is available for free.

3. Application of Methodology for Case Study

3.1. PCSWMM Input Data and Model Initialisation

Irrigation canal geometry including cross-section, length, elevation, and slope were measured during field visits and also collected from the Sunsari Morang Irrigation Project Office. Climate data for 2016–2020 were taken from APSIM Next Generation [35].

Canal discharge measurements were carried out at different locations of the main canal using a current meter (Figure 3). The current meter used in the study was manufactured by Virtual Electronics Company, Roorkee, India (serial number: VEC-CMCT-03) and the rating curve for the current meter was calibrated by the Hydraulic Research Station, Malikpur (Pathankot), Government of Punjab, India. The canal network of the Sunsari Morang Irrigation Scheme, including the main canal and branch canals, is shown in Figure 1b. Canal discharge measurements were carried out on the main canal at distances of 5.2 km, 11.8 km, 13 km, 15 km, 22.5 km, and 25.3 km from the irrigation intake on the Koshi River. The discharge data were also used for the calculation of losses between the two measuring stations. Canal discharge measurements were taken using the current meter by placing the current cup assembly at 20, 60, and 80% depth of water level below the water surface at each segment to measure the average flow velocity of the respective segment. In all three cases, there was no outflow in the section between the two measuring stations.

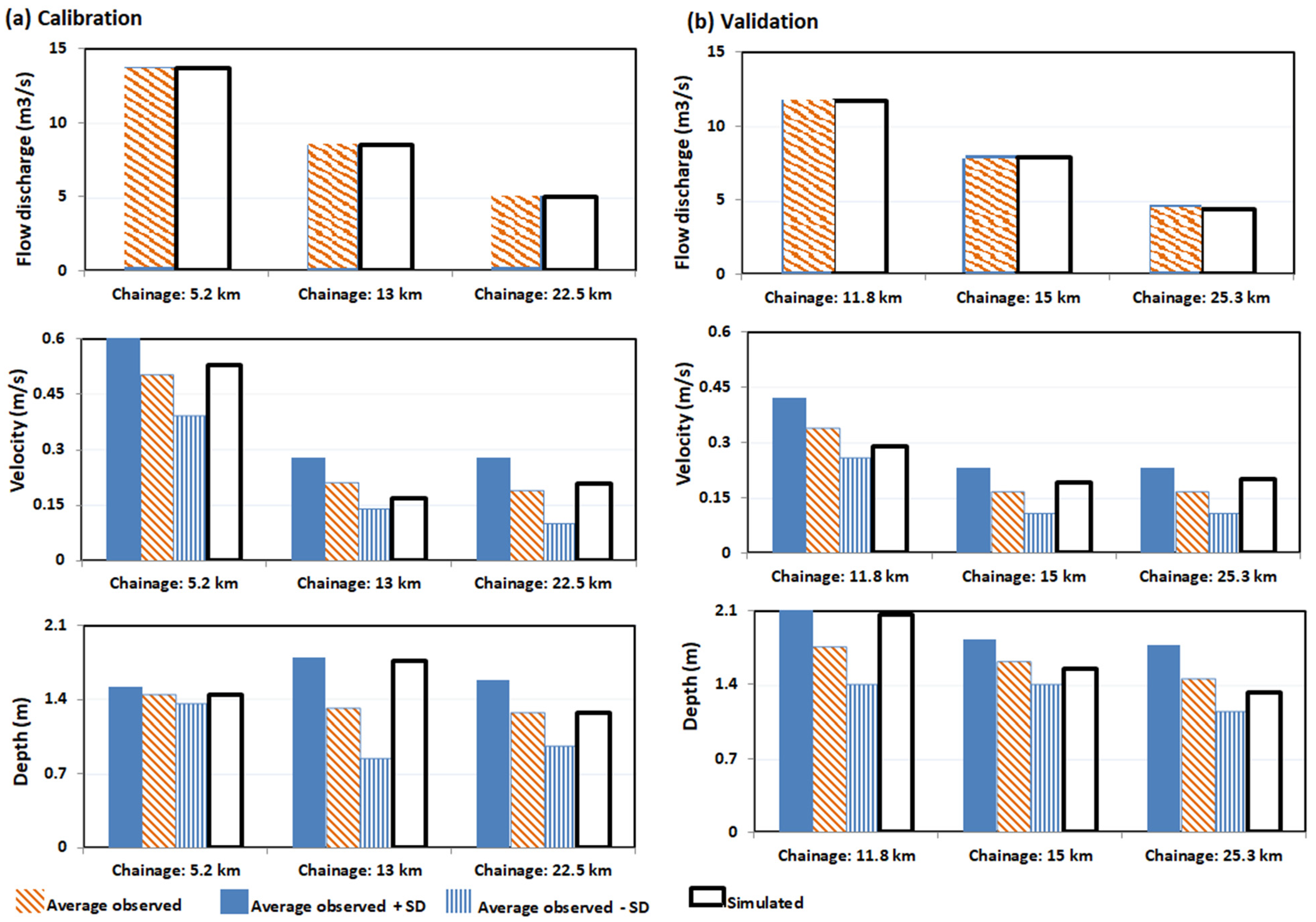
3.2. Model Parameterisation (Calibration)

After model initialisation, the PCSWMM model (version 5.0.012) was calibrated using observed discharge, flow velocity, and water depth in the main Sunsari Morang irrigation canal over the period 2018–2020. Canal discharge measurements at distances of 5.2 km, 11.8 km, and 13 km from the irrigation intake on the Koshi River were used for the calibration (Figure 1c).

First, canal discharge at the intake of the main irrigation canal was adjusted to match the simulated discharge with the observed discharge at the 5.2 km distance from the irrigation water river intake. After this, simulated velocity and simulated water depth are compared with observed values. Similar processes were carried out to calibrate measurements at the 13 km and 22.5 km distances from the irrigation intake along the main canal. The observed and simulated discharge, velocity, and water depth for the calibration period are shown in Figure 4a.

The average observed discharge, velocity, and water depth data for the calibration period at a 5.2 km distance along the main canal from the irrigation intake structure are 13.77 m³/s, 0.5 m/s, and 1.44 m, respectively, whilst the corresponding simulated discharge, velocity, and water depth data are 13.71 m³/s, 0.53 m/s, and 1.45 m, respectively. The agreement between observed and simulated values is excellent. The minimum (mean minus standard deviation) and maximum (mean plus standard deviation) standard deviation ranges for velocity are 0.39 m/s and 0.61 m/s for the calibration period based on the variation in velocity within the measured canal section. The simulated velocity for the calibration period is within the standard deviation of the mean. Likewise, the minimum and maximum standard deviation ranges for water depth are 1.36 m and 1.52 m for the calibration period, based on the variation in water depth within the measured canal section. The simulated water depth for the calibration period is within the standard deviation of the mean.

The average observed discharge, velocity, and water depth data for the calibration period at a 13 km distance from the irrigation intake structure are 8.53 m³/s, 0.21 m/s, and 1.32 m, respectively. These simulated values are close to the observed values. The simulated discharge, velocity, and water depth data for the calibration period are 8.53 m³/s, 0.17 m/s, and 1.77 m, respectively. The minimum (mean minus standard deviation) and maximum (mean plus standard deviation) ranges for velocity are 0.14 m/s and 0.28 m/s for the calibration period based on the variation in velocity within the measured canal section. The simulated velocity for the calibration period is within the standard deviation of the mean. The minimum and maximum standard deviation ranges for water depth are 0.84 m and 1.80 m for the calibration period based on the variation in water depth within the measured canal section. The simulated water depth for the calibration period is within the standard deviation of the mean.

Similarly, the average observed discharge, velocity, and water depth data for the calibration period at a 22.5 km distance from the irrigation intake structure are 5.04 m³/s, 0.19 m/s, and 1.27 m, respectively. The simulated values are close to the observed values. The simulated discharge, velocity, and water depth data for the calibration period are 5.01 m³/s, 0.21 m/s, and 1.27 m, respectively. The minimum (mean minus standard deviation) and maximum (mean plus standard deviation) ranges for velocity are 0.10 m/s and 0.28 m/s for the calibration period, based on the variation in velocity within the measured canal section. The simulated velocity for the calibration period is within the standard deviation of the mean. Likewise, the minimum and maximum standard deviation ranges for water depth are 0.96 m and 1.58 m for the calibration period based on the variation in water depth within the measured canal section. The simulated water depth for the calibration period is within the standard deviation of the mean.

The PCSWMM model’s performance for the calibration period is good as the simulated values for discharge, velocity, and water depth are close to observed values and within the standard deviation of the mean.

The calibrated PCSWMM model was validated using observed discharge, flow velocity, and water depth at the main canal of the Sunsari Morang Irrigation canal network. The observed discharge, flow velocity, and water depth at the main canal of the Sunsari Morang Irrigation Canal for the period 2018–2020 were used for the validation of the PCSWMM model.

3.3. Model Validation

Using the calibrated model based on discharge, velocity, and water depth data, the PCSWMM model was then validated using discharge, velocity, and water depth data at three canal sections that were different from those used for model calibration. These sections were located at 11.8 km, 15 km, and 25.3 km chainage distance along the main canal (Figure 1c). The observed and simulated discharge, velocity, and water depth data for the validation period are shown in Figure 4b.

The average observed discharge, velocity, and water depth data for the validation period at 11.8 km distance from the irrigation intake structure are 11.81 m³/s, 0.34 m/s, and 1.76 m, respectively. The simulated values are close to the observed values. The simulated discharge, velocity, and water depth for the validation period are 11.73 m³/s, 0.29 m/s, and 2.06 m, respectively. The minimum (mean minus standard deviation) and maximum (mean plus standard deviation) standard deviation range for velocity are 0.26 m/s and 0.42 m/s for the validation period. Likewise, the minimum and maximum standard deviation ranges for water depth are 1.41 m and 2.11 m for the validation period. The simulated velocity and water depth for the validation period are within the standard deviation of the mean.

Likewise, the average observed discharge, velocity, and water depth data for the validation period at a 15 km distance from the irrigation intake structure are 8.01 m³/s, 0.17 m/s, and 1.62 m, respectively. The simulated values are close to the observed values. The simulated discharge, velocity, and water depth for the validation period are 7.9 m³/s, 0.19 m/s, and 1.62 m, respectively. The minimum (mean minus standard deviation) and maximum (mean plus standard deviation) standard deviation ranges for velocity are 0.11 m/s and 0.23 m/s for the validation period. Likewise, the minimum and maximum standard deviation ranges for water depth are 1.41 m and 1.83 m for the validation period. The simulated velocity and water depth for the validation period are within the standard deviation of the mean.

In the same way, the average observed discharge, velocity, and water depth data for the validation period at 25.3 km distance from the irrigation intake structure are 4.65 m³/s, 0.17 m/s, and 1.46 m, respectively. The simulated values are close to the observed values. The simulated discharge, velocity, and water depth for the validation period are 4.39 m³/s, 0.20 m/s, and 1.32 m, respectively. The minimum (mean minus standard deviation) and maximum (mean plus standard deviation) standard deviation ranges for velocity are 0.11 m/s and 0.23 m/s for the validation period. Likewise, the minimum and maximum standard deviation ranges for water depth are 1.15 m and 1.77 m for the validation period. The simulated velocity and water depth for the validation period are within the standard deviation of the mean.

The PCSWMM model’s performance for the validation period is good, as the simulated values for discharge, velocity, and water depth are close to observed values and within the standard deviation of the mean.

3.4. Canal Discharge Carrying Capacity Considering Water Availability under Future Climates (Scenario Analysis)

The validated PCSWMM model was applied to assess the hydraulic capacity of the main canal of the SMIS, based on water availability (Koshi River flows) at the irrigation canal intake using projected river flows under future climate change scenarios (RCP4.5 and RCP8.5), for the short-term (2016–2045), mid-century (2036–2065), and end-of-century (2071–2100) periods. The GCMs/ensembles selected for the short-term period for the cold and dry, warm and dry, cold and wet, and warm and wet corners of climatic extreme for RCP4.5 and RCP8.5 are ACCESS1-3_r1i1p1, MPI-ESM-MR_r3i1p1, NOAA_GFDL_GFDL-ESM2G_r1i1p1, CanESM2_r2i1p1, and ACCESS1-3_r1i1p1, IPSL-CM5A-LR_r2i1p1, NOAA_GFDL_GFDL-ESM2M_r1i1p1, and CanESM2_r4i1p1, respectively. Similarly, the GCMs/ensembles selected for the mid-term period for the cold and dry, warm and dry, cold and wet, and warm and wet corners of climatic extreme for RCP4.5 and RCP8.5 are EC-EARTH_r12i1p1, MIROC5_r2i1p1, CCSM4_r2i1p1, CanESM2_r2i1p1, and ACCESS1-3_r1i1p1, MIROC-ESM-CHEM_r1i1p1, NOAA_GFDL_GFDL-ESM2G_r1i1p1, and CanESM2_r1i1p1, respectively. Likewise, the GCMs/ensembles selected for the end-of-century period for the cold and dry, warm and dry, cold and wet, and warm and wet corners of climatic extreme for RCP4.5 and RCP8.5 are EC-EARTH_r2i1p1, CSIRO-Mk3-6-0_r1i1p1, CCSM4_r2i1p1, CanESM2_r3i1p1, and EC-EARTH_r9i1p1, MIROC-ESM-CHEM_r1i1p1, NOAA_GFDL_GFDL-ESM2G_r1i1p1, and CanESM2_r3i1p1, respectively [1]. Changes in future water availability for irrigation at the irrigation canal intake were compared with the reference (base) period (1981–2010) data. The analysis will provide insights into the carrying capacity of the canal system vis a vis water availability in the Koshi River at the canal intake.

Future water availability for irrigation (at the irrigation canal intake) was based on projected Koshi River flows at the irrigation canal intake. This was carried out in the following steps:

(a)

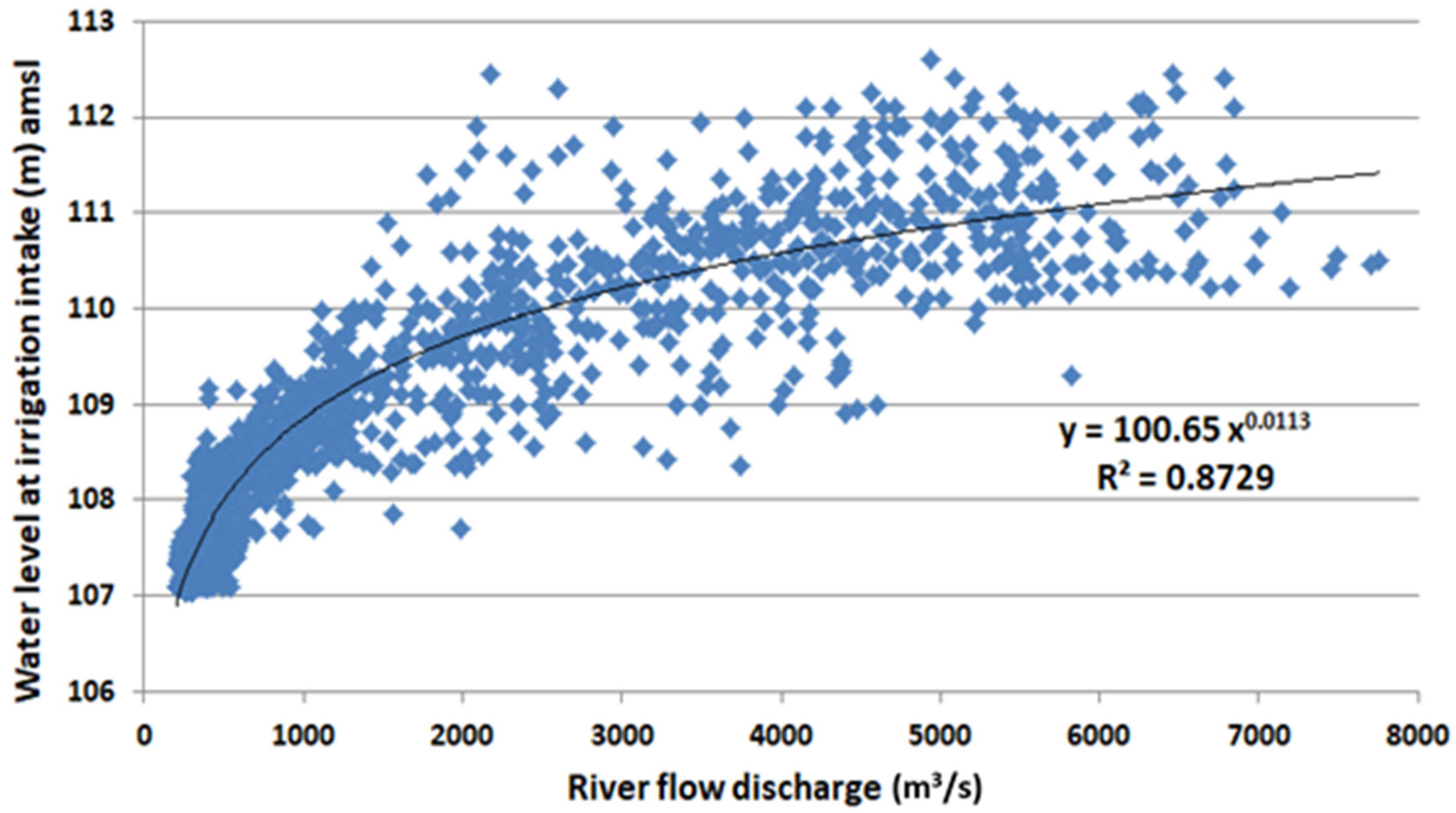
Development of a stage–discharge relationship (rating curve) for the Koshi River at irrigation canal intake.

(b)

Projected river flow for future climate scenarios, using the output of the Soil and Water Assessment Tool (SWAT) hydrological model [3].

(c)

Water availability for irrigation at the irrigation canal intake for future scenarios derived from (a) and (b) above.

Records of Koshi River water levels at the irrigation intake were obtained from the Sunsari Morang Irrigation Project Office, and the river discharge data were obtained from the Department of Hydrology and Meteorology, Nepal. Although record-keeping exists for the irrigation intake, only about six years’ worth of data are available between 1996 and 2012. Data available on the river water level at the irrigation intake were used for developing a stage–discharge relationship (rating curve) for the Koshi River (Figure 5). The elevation of the intake crest level at the entry point to the main irrigation canal is 107 m above mean sea level (AMSL). More concentrated dotted points near 107 m AMSL represent river water in the dry season. When the river water level is ≤107 m, no river water can flow into the canal. The relationship between water level elevation and river discharge developed from the plot of the data is presented in Equation (1):

$$\mathrm{W}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r} \mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{l} \mathrm{e}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(\mathrm{m}\right)=100.65\ast {river flow discharge \left({\displaystyle \frac{{\mathrm{m}}^3}{\mathrm{s}}}\right)}^{0.0113}$$

(1)

Using the rating curve in Figure 5, water level elevations for observed river discharge for the reference (base) period (1981–2010) were calculated. The minimum average monthly flows in the Koshi River at the irrigation canal intake for the three study periods were taken from the hydrological analysis reported in Kaini et al. [3]. Water level elevations for projected future minimum average monthly flows in the Koshi River at the irrigation canal intake during the dry season (December–May) were calculated using rating curve Equation (1).

Based on water level elevations at the canal intake for projected future minimum average monthly flows, water availability for irrigation at the irrigation canal intake in the future during the dry season was calculated. In the dry season, water flows into the canal from the river over a weir. The weir acts effectively as a broad-crested weir, provided the head over the crest is less than 1.5 times the width of the crest [36]. The weir crest elevation is 107 m AMSL. There are 12 rectangular intake orifices with a total width of 48 m. The opening size of each orifice bay is 4 m wide by 5 m high (Figure 6). Hence, the width of the weir at each bay is 4 m.

The average and median values of the water level (head) over the weir crest in the dry season (December–May) during 1982–2010 were 107.78 m and 107.72 m, respectively. The water level at the intake and the corresponding river discharge derived from the stage–discharge relationship in the dry season during 1982–2010 is shown in Figure 5. The maximum head over the weir crest in the dry season is about 2.6 m, which is less than 6.0 m (1.5 × 4 m). Hence, the weir always acts as a broad-crested weir in the dry season.

The discharge from a broad-crested weir was calculated by Equation (2) [36]:

$$Q=1.7 \left(L-K n H\right){ H}^{3/2}$$

(2)

where Q = discharge in m³/s, L = clear waterway length (m), K = coefficient of end contraction generally taken as 0.1, n = number of end contractions (twice the number of gated bays), and H = head over the crest (m).

Water availability for irrigation at the irrigation canal intake in future dry seasons was calculated based on water level elevations at the canal intake using the projected future minimum average monthly flows and Equation (2).

4. Results and Discussion

4.1. Average Monthly Water Availability for Irrigation at the Irrigation Canal Intake for Dry Season during 1982–2010

The study area has monsoon (June–September), post-monsoon (October–November), and dry (December–May) seasons. Average monthly water availability for irrigation at the irrigation canal intake for the dry seasons (December–May) during 1982–2010 is shown in Figure 7. The average monthly water availability for irrigation at the irrigation canal intake during 1982–2010 in December, January, February, March, April, and May were 76.69 m³/s, 41.68 m³/s, 27.87 m³/s, 29.39 m³/s, 50.50 m³/s, and 124.84 m³/s, respectively. The lowest flow into the canal was in February, followed by March. The standard deviation of the mean varies from 13.30 m³/s to 42.44 m³/s in February and 13.49 m³/s to 45.29 m³/s in March. This shows that there was a low discharge into the canal during January, February, March, and April, compared to the designed discharge of 60 m³/s.

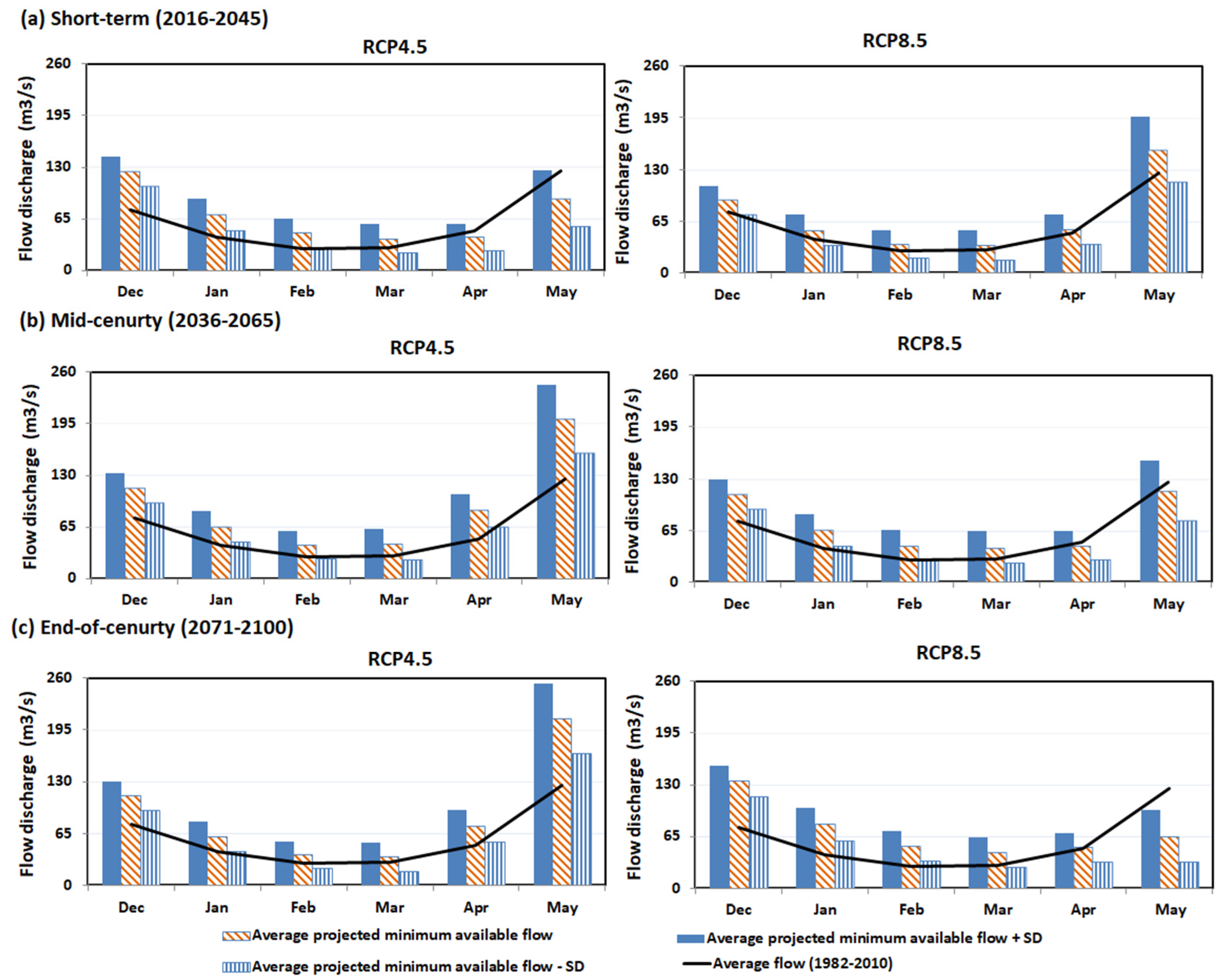
4.2. Projected Average Monthly Minimum Flow Availability for Irrigation at Canal Intake

Data pertaining to monthly or bi-monthly water availability, rather than annual or seasonal water availability, is crucial for the design and management of irrigation schemes in developing countries. In many irrigation schemes in developing countries, mechanisms allowing the diversion of water from the source into the irrigation canal operate on gravity flow and lack pumping mechanisms and impoundment structures.

Table 1. Projected average monthly minimum flow (m³/s) into the irrigation canal intake for different climate change scenarios (RCPSs) and future time periods, with reference (base) period flow for comparison.

Scenarios	Dec	Jan	Feb	Mar	Apr	May
Reference period (1982–2010)	76.69	41.68	27.87	29.39	50.50	124.84
Short-term (2016–2045)_RCP4.5	124.80	70.42	47.65	40.50	42.02	90.64
Short-term (2016–2045)_RCP8.5	92.18	54.35	36.96	35.57	55.26	155.43
Mid-century (2036–2065)_RCP4.5	114.41	65.15	42.80	43.46	85.89	200.22
Mid-century (2036–2065)_RCP8.5	110.84	66.21	46.69	44.44	46.87	115.34
End-of-century (2071–2100)_RCP4.5	112.03	60.87	37.93	35.57	73.78	209.31
End-of-century (2071–2100)_RCP8.5	134.76	80.70	53.43	45.42	51.68	65.51

shows the average monthly minimum flow into the Sunsari Morang Irrigation Scheme canal intake under future time periods and climate change scenarios. These values were derived based on the development of a stage–discharge (water height–discharge) curve for the Koshi River at the canal intake (Equation (1)), with river flows under future scenarios projected using a hydrological model [3]. Irrigation water available from flows into the canal intake is expected to increase for all future scenarios in December through March. Projected flows in April and May are less certain due to potential flow variations in water availability [3]. Table 1 shows that although there is an increase in water availability for irrigation in December, January, February, and March, the designed discharge of 60 m³/s would not be available in February and March for all future scenarios.

The projected average monthly minimum flow at the canal intake is shown in Figure 8. In December and January, the lower standard deviation of the mean for future average monthly minimum flow availability is above the mean flow for 1982–2010. In February, the lower standard deviation of the mean for future average monthly minimum flow availability for irrigation is similar to the mean flow for 1982–2010. In March through May, the lower value of the standard deviation of the mean for future average monthly minimum flow availability at the canal intake is below the mean flow for the reference (base) period.

4.3. Implications of Climate Change for Potential Irrigated Cropping Area

The irrigation water requirements for winter wheat crops at the farm level, derived from crop modelling [28], are shown in

Table 2. Irrigation water requirement (mm) for wheat crops at field level in the SMIS, derived from crop modelling.

Irrigation Water Requirement (mm) for a Wheat Crop at Field Level
Scenarios	Dec	Jan	Feb	Mar	Apr
Reference period (1982–2010)	3	44	118	198	66
Short-term (2016–2045)_RCP4.5	4	48	125	195	67
Short-term (2016–2045)_RCP8.5	4	50	130	197	58
Mid-century (2036–2065)_RCP4.5	4	49	126	198	58
Mid-century (2036–2065)_RCP8.5	5	53	127	192	50
End-of-century (2071–2100)_RCP4.5	4	55	135	196	51
End-of-century (2071–2100)_RCP8.5	4	52	125	183	29

. Table 2 was derived based on projected downscaled data for future scenarios [1] coupled with APSIM modelling [28]. Table 2 indicates that the highest future irrigation demand for wheat crops occurs in March, followed by February. Although the irrigation demand is high in March and February, the water flows into the canal intake will be less in these months as shown in Figure 8.

Conveyance losses and losses in the field should be considered for estimating the irrigation requirements for water diversion from the canal intake. The irrigation water requirements for wheat at the canal intake are shown in

Table 3. Irrigation water requirements (liter/sec/ha) for winter wheat crops at the irrigation canal intake.

Irrigation Water Requirement (L/s/ha) for Winter Wheat at the Irrigation Canal Intake
Scenarios	Dec	Jan	Feb	Mar	Apr
Reference period (1982–2010)	0.03	0.5	1.35	2.26	0.75
Short-term (2016–2045)_RCP4.5	0.05	0.55	1.43	2.23	0.77
Short-term (2016–2045)_RCP8.5	0.05	0.57	1.49	2.25	0.66
Mid-century (2036–2065)_RCP4.5	0.05	0.56	1.44	2.26	0.66
Mid-century (2036–2065)_RCP8.5	0.06	0.61	1.45	2.19	0.57
End-of-century (2071–2100)_RCP4.5	0.05	0.63	1.54	2.24	0.58
End-of-century (2071–2100)_RCP8.5	0.05	0.59	1.43	2.09	0.33

. In Nepal, average irrigation field efficiency, distribution canal efficiency, and main canal efficiency values for wheat crops are considered as 0.60, 0.75, and 0.75, respectively [37]. Considering these values of efficiencies, irrigation water diversion requirements from the intake structure for wheat at the irrigation canal intake were estimated using canal efficiencies and Table 2.

Based on the projected average monthly minimum flow availability for irrigation at the canal intake, and irrigation water requirements for wheat crops at the canal intake, the potential area coverage by wheat crop area was projected (

Table 4. Potential wheat cropping area based on minimum likely irrigation flows under future climates. All values are in thousands of hectares.

Scenarios	Dec	Jan	Feb	Mar	Apr
Reference period (1982–2010)	2556.3	83.4	20.6	13.0	67.3
Short-term (2016–2045)_RCP4.5	2496.0	128.0	33.3	18.2	54.6
Short-term (2016–2045)_RCP8.5	1843.6	95.4	24.8	15.8	83.7
Mid-century (2036–2065)_RCP4.5	2288.2	116.3	29.7	19.2	130.1
Mid-century (2036–2065)_RCP8.5	1847.3	108.5	32.2	20.3	82.2
End-of-century (2071–2100)_RCP4.5	2240.6	96.6	24.6	15.9	127.2
End-of-century (2071–2100)_RCP8.5	2695.2	136.8	37.4	21.7	156.6

). For example, the projected average monthly minimum flow availability for irrigation at the canal intake in the short-term (2016–2045) for climate change scenario RCP4.5 is 40.50 m³/s (Table 1), and the irrigation water requirements for this period is 2.23 L/sec/ha (Table 3). Hence, the potential wheat area coverage for the short-term (2016–2045), considering the RCP4.5 scenario is 18,200 hectares. The minimum area that can be covered throughout the cropping period of the wheat crop (December–April) should be taken as the potential area coverage for the wheat crop. Hence, the area that could be covered in March is considered as potential area coverage, as it describes the minimum area coverage during the month when the irrigation demand is at its maximum.

Although water available for irrigation was sufficient for irrigating 13,000 ha of wheat crops during the reference period 1982–2010, with no water deficit conditions, the average wheat area coverage during 2008–2016 was 26,000 ha. This shows that there was a water deficit in the wheat crops in the SMIS command area and farmers are still practicing protective irrigation, where irrigation is provided to protect crops from catastrophic failure without considering actual irrigation demand. Hence, productivity (kg/ha) is relatively low, which was also observed during field visits. The actual wheat yields in 2018–2019 and 2019–2020 were 1862 kg/ha and 2145 kg/ha, respectively, despite the potential yields of 4312 kg/ha and 4604 kg/ha as predicted by the APSIM crop model [28]. The Sunsari Morang Irrigation Scheme was designed without considering crop water requirement criteria; the main criteria during its design were to maximise crop area whilst avoiding severe water deficit and crop failure [38,39,40]. Similar objectives were applied in many other irrigation schemes designed during the British colonial period [4,41]. Jurriens et al. [42] argued that crop yield vulnerability design criteria have been omitted or ignored in most regions of India. This resulted in the increasing use of water over increasingly large areas of India and neighbouring countries since 1980.

Table 4 shows that the maximum wheat area that could be irrigated without crop water stress is governed by irrigation water available and crop demand in March (other months having lower irrigation demand). With existing irrigation intake, the wheat crop area could be increased by 3000–5000 ha (12–19%) in the short-term period, 6000–7000 ha (23–27%) in the mid-century period, and 3000–9000 ha (12–35%) in the end-of-century period, with no water deficit conditions. Wheat area coverage at present is 26,000 ha, demonstrating the potential to increase cropping area. We argue that a river diversion structure or implementation of a pumping mechanism at the irrigation canal intake or using the local streams or groundwater resources within the irrigation command area could increase canal inflow, and hence cropping area, providing complementary upgrades to the distribution system occur [5,41]. Rehabilitation of other existing irrigation schemes via improvements in irrigation infrastructure is common in the region [43], suggesting that our proposed upgrades should be economically viable. The increased flow of irrigation water after investment could be used for multiple uses within the irrigation command area [44] based on social, economic, and cultural practices that currently exist in this region [45].

4.4. Conveyance Losses at Canal

The water losses at different portions of the main canal are shown in

Table 5. Conveyance losses at different chainages of the main canal.

Distance from Intake	Discharge (m3/s)	Wetted Perimeter (m)	Losses (m3/m2/day)
5.2 km	13.77	21.23	1.21
11.8 km	11.81	20.92
13 km	8.53	29.72	0.77
15 km	8.01	30.58
22.6 km	5.04	20.56	0.60
25.4 km	4.65	19.73

. The canal water losses between 5.2 km and 11.8 km, 13 km and 15 km, and 22.5 km and 25.3 km distances from the irrigation canal intake were 1.2 m³/m²/day, 0.77 m³/m²/day, and 0.6 m³/m²/day, respectively, with an overall average water loss of 0.86 m³/m²/day. Our work clearly demonstrates that a key challenge in Nepalese irrigation systems lies in mitigating conveyance losses [46].

4.5. Canal Flow Capacity Assessment

Canal flow capacity in the SMIS is limited by silt deposition (from the Koshi River) and weed growth in canals. Silt deposition has been an issue since the beginning of the project. Silt deposition varies along the length of the canal. In 2018–2020, a maximum silt depth of 0.80 m was observed in the main canal. The maximum flow capacity of the main canal was assessed in the validated PCSWMM model considering full water depth in the canal. While the SMIS was designed for a flow capacity of 60 m³/s of discharge, we found that the current canal capacity is only 53 m³/s up to 10.7 km chainage from the canal intake (demonstrating a 12% reduction in discharge capacity of the canal). The canal flow capacity reduces further to 35 m³/s at 13.8 km chainage from canal intake compared with a designed discharge capacity of 48 m³/s (demonstrating a 27% reduction in canal flow capacity). Likewise, the canal flow capacity reduces to 27 m³/s at 22.1 km chainage from canal intake against the designed flow capacity of 39 m³/s. In this portion of the canal, the discharge capacity of the canal was reduced by 31%. The flow capacity of overall sections of the canal was reduced by 23% relative to design parameters. Regular maintenance of irrigation canals is challenging for Nepalese irrigation systems [46] but clearly urgently called for if water and food security of the region are to be maintained.

5. Conclusions

The implications of future climate change on water supply and demand in Nepal’s largest irrigation scheme were assessed. We revealed that climate change could benefit the region, increasing river flows that could be used by the irrigated agriculture sector. Invoking a novel approach that combined hydraulic modelling of the irrigation canal with hydrological and agronomic simulations, we reveal the following novel insights:

• Water losses along the Sunsari Morang Irrigation main canal were 1.2 m³/m²/day, 0.77 m³/m²/day, and 0.60 m³/m²/day between the chainage 5 to 25 km, while average water loss in the main canal was 0.86 m³/m²/day. Similar water losses were also reported in other regions. Average water losses in the main canal were 5.78 m³/m²/day in Turkey [22], 1.21 m³/m²/day in Turkey [25], 1.08 m³/m²/day in Ethiopia [23], and 1.21 m³/m²/day in Iran [24].
• Average monthly water flows into the Sunsari Morang canal during the dry season months (December, January, February, March, April, and May) of 1982 to 2010 were 77 m³/s, 42 m³/s, 28 m³/s, 29 m³/s, 50 m³/s, and 125 m³/s, respectively. The inflow into the canal during January, February, March, and April was substantially less than the designed canal flow capacity of 60 m³/s, suggesting that engineering interventions enabling increased inflow rates (e.g., via river barrage, pumping, etc.) could be accommodated by the existing canal.
• Whilst future climate change projections indicate an increase in river water availability for irrigation extraction in the months of December, January, February, and March, the nominal maximum designed canal discharge capacity of 60 m³/s will still not be met in February and March, for all future time periods and climate change scenarios.
• Weed growth, silt deposition, and lack of regular maintenance have reduced the canal discharge carrying capacity by 12–31% (depending on chainage distance) with an average discharge reduction of 23%. Lining, relining, or piping sections of the canal and regular maintenance (silt and weed removal) could improve flow carrying capacity.
• The current amount of water available for irrigation was sufficient for irrigating 13,000 ha of wheat during 1982–2010 with no water deficit conditions, while the average wheat cropping area supported by the scheme during 2008–2016 was 26,000 ha. This shows that farmers are still practicing protective irrigation in the Sunsari Morang Irrigation Scheme command area.
• The irrigated broadacre cropping area could be increased by 3000–5000 ha in the short-term (2016–2045), 6000–7000 ha in the mid-century (2036–2065), and 3000–9000 ha in the end-of-century (2071–2100) periods with no water deficit occurring. However, given that climate projections are for more variable weather, and more extreme events [47], it is likely that the frequencies of drought in the region may change in the future. This deserves further attention in the future.
• As with all cereal crops, wheat grain yield is most sensitive to water stress in the flowering to grain filling stages, a period that includes the peak water demand period of March. Options could be explored that tap into alternative water supplies, or allow a certain yield reduction from partial water stress, thereby allowing the total area of wheat to be expanded. An increased area but with a lower average grain yield may increase the total yield from the whole SMIS. This water stress versus yield interaction could be efficiently explored in future research.