Next Article in Journal
Comprehensive Zoning Strategies for Flood Disasters in China
Previous Article in Journal
Spatiotemporal Dynamics of Ecosystem Water Yield Services and Responses to Future Land Use Scenarios in Henan Province, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 16
Issue 17
10.3390/w16172545
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

A Review on the Optimization of Irrigation Schedules for Farmlands Based on a Simulation–Optimization Model

by
Yin Zhao
1,2,3,
Guoan Li
4,
Sien Li
2,3,*,
Yongkai Luo
1 and
Yuting Bai
1
1
Shandong Key Laboratory of Eco–Environmental Science for the Yellow River Delta, Shandong University of Aeronautics, Binzhou 256600, China
2
Center for Agricultural Water Research in China, China Agricultural University, Beijing 100083, China
3
National Field Scientific Observation and Research Station on Efficient Water Use of Oasis Agriculture in Wuwei of Gansu Province, Wuwei 733000, China
4
Bincheng Yellow River Bureau, Binzhou Yellow River Bureau, Binzhou 256600, China
*
Author to whom correspondence should be addressed.
Water 2024, 16(17), 2545; https://doi.org/10.3390/w16172545
Submission received: 15 August 2024 / Revised: 3 September 2024 / Accepted: 7 September 2024 / Published: 9 September 2024
(This article belongs to the Section Water Use and Scarcity)
Browse Figures
Versions Notes

Abstract

:
Agriculture is the most important sector that is consuming water resources. In the context of global water scarcity, how to use limited water resources to improve water use efficiency in agriculture or achieve maximum crop yield and fruit quality is of great significance for ensuring food and water security. Optimizing irrigation schedules is an effective measure to improve water use efficiency, where crop models also play an important role. However, there is little research summarizing the optimization of irrigation schedules based on crop models. This study provides a systematic review on how to optimize irrigation schedules based on crop models and simulation–optimization models. When optimizing irrigation schedules based on crop models, the selected models are usually mechanistic agro-hydrological models. Irrigation scenarios and optimization objectives are mainly focused on both crop and water aspects, such as maximizing crop yield, fruit quality, water productivity, and irrigation water productivity. Minimizing crop water consumption and total irrigation amounts serve as optimization objectives, and irrigation quantity, irrigation frequency, and irrigation interval serve as decision variables. In saline areas or low fertilizer utilization areas, the optimization objectives and decision variables also involve some indicators related to salt and nitrogen, such as the maximum desalination rate, minimum salt content, fertilizer utilization efficiency, nitrogen fertilizer productivity, nitrogen fertilizer utilization efficiency, nitrogen leaching rate, which serve as the optimization objectives, and the irrigation water salinity, or fertilization schedules serve as the decision variables. When optimizing irrigation schedules based on simulation–optimization models, the models have mainly been upgraded from water-production function to crop mechanism models. In addition, optimization algorithms have been upgraded from traditional optimization techniques to intelligent optimization algorithms. Decision-making techniques are used to make decisions on optimization results. In addition, the spatial scale for the optimization problem of irrigation schedules was developed from fields to regions, and the time scale was developed from the growth stage, beginning with months, and shortening to ten days, then to a day, and then to an hour. This study also provides a detailed introduction to widely used optimization algorithms, such as genetic algorithms, as well as decision techniques. At the same time, it is proposed that the future should focus on improving crop models and analyzing uncertainty in research on irrigation schedule optimization, which is of great significance for the precise regulation of irrigation schedules.

1. Introduction

Water resources are a key factor in promoting sustainable socioeconomic development, as well as an important strategic resource for ensuring food security and ecological health. Water scarcity is a global problem currently faced around the world, and agriculture is the most important sector that is consuming water resources. Agricultural water consumption accounts for 70% of the total water consumption globally, and water use efficiency is at a relatively low level [1]. The expected growth rate of the world population has led to a continuous increase in the demand for food, and the demand for agricultural irrigation water has also been increasing year by year [2]. Improving water use efficiency in agriculture is a key way to ensure both water resources and food security.
Optimizing irrigation schedules is an important measure to improve agricultural water use efficiency [3]. The crop irrigation schedule mainly includes the irrigation frequency, irrigation date, single irrigation quota, and total irrigation quota. A moderate water deficit could improve water use efficiency and fruit quality, while could not significantly decreasing crop yield [4,5,6]. Therefore, when water resources are insufficient and only deficit irrigation can be used, how to allocate the limited irrigation water reasonably in spaces (different regions, different crops) and time (different growth stages of crops) to achieve the highest yield or benefit, or minimize the loss of crop yield caused by this water shortage, is the core idea behind the optimization of irrigation schedules [7].
Optimization methods for irrigation schedules mainly include linear programming, nonlinear programming, and dynamic programming [8]. In addition, intelligent evolutionary algorithms such as genetic algorithms (GAs), simulated annealing (SA), and particle swarm optimization (PSO) [9,10] have also been widely applied due to the increasingly complex problems associated with the optimization and allocation of water resources. These methods simplify the evapotranspiration processes of farmlands under different irrigation schedules and their impacts on crop yield, making it difficult to objectively reflect on the yield changes under the different irrigation conditions.
The responses in crop production to irrigation schedules can be studied through a combination of field experiments and crop models. Field experiments are limited by factors such as the limited number of experimental variables and high costs, making it difficult to evaluate the crop growth and field water balance under various irrigation scenarios [11]. Crop models can overcome the influence of these limiting factors. They can serve as a tool to simulate crop growth, yield formation, and fruit quality under different field management schemes, effectively supplementing the shortcomings of field experiments in terms of manpower, time, space, economy, and resources [12].
Simulation models for crop growth can simulate the hydrological processes of farmlands and changes in crop yield under different irrigation conditions and can find the optimal solution through optimization methods [13]. The combination of both simulation models and optimization methods provides an effective way to optimize crop irrigation schedules [14,15]. The objective of this study is to (1) review how to optimize irrigation schedules based on both crop models and simulation–optimization models, (2) summarize the improvements in optimization methods for irrigation scheduling optimization, and (3) analyze the existing problems and challenges, propose future research priorities, and provide both reference and direction for further research on irrigation schedule optimization.

2. Optimization of Irrigation Schedules Based on Crop Models

The optimization of irrigation schedules based on crop models can be achieved by the combination of field experiments and crop models [16]. The specific steps involved in the optimization of irrigation schedules based on crop models are as follows: firstly, based on the field experimental data, verify the applicability of the crop models in simulating the dynamics of the soil, water, heat, salt, fertilizer, crop growth, yield, fruit quality parameters, and water consumption under both different irrigation conditions and various agricultural management measures; secondly, use the validated crop models to comprehensively evaluate the effects of the various irrigation scenarios on water consumption, crop productivity and fruit quality; and finally, determine the optimal irrigation schedules under the given objectives. The specific process of irrigation schedule optimization based on crop models is shown in Figure 1. The setting of the irrigation scenarios, the setting of the optimization objectives, and the selection of the crop models will vary with the needs of the users.

2.1. Irrigation Scenarios

The optimization of irrigation schedules based on crop models usually involves manually inputting pre-set irrigation scenarios by users to explore the crop production situation under various irrigation scenarios. Irrigation scenarios usually reach several to tens of thousands of types, typically include an irrigation quota, irrigation frequency, and irrigation time, or a combination of two or more of these factors [17,18]. Precipitation can affect the decision-making process for irrigation schedules. Researchers make decisions on irrigation schedules for different hydrological years. The hydrological year is determined by selecting years with precipitation assurance rates of 25%, 50%, and 75% as typical representative years for wet, normal, and dry years, based on the long-term sequence data of the study area [1]. It can also be determined by the drought index with the values of >0.35, −0.35~0.35, and <−0.35 for wet, normal, and dry years [17]. Multiple upper and lower irrigation limits or combinations of the two can also be set at the different stages of crop growth, while simultaneously considering different soil textures [19,20]. In addition, the sensitivity of the crops to water at each growth stage is also determined by performing deficit irrigation at the different growth stages of the crops, while conducting sufficient irrigation at other growth stages [21]. Previous studies indicated that the seedling stage of maize was not sensitive to a water deficit, and the male ear stage, silk emergence stage, grain filling stage for maize were the most susceptible to water stress, which could affect the quality and quantity of the crop yield [22].
In areas where freshwater resources are scarce and irrigation sources rely on underground brackish or saline water, crop models were used to seek a suitable level of salinity for irrigation water, or appropriate interaction measures between both irrigation quantity and irrigation water salinity [23]. In saline areas, the appropriate range between the irrigation quotas and irrigation water salinity should be adjusted with the degree of salinization (i.e., initial soil salinity) [24,25]. In addition, leaching during the nongrowth stages of crops is considered an effective measure of salt leaching. For example, Lin et al. [26] used the SHAW model to explore a strategy of combined winter and spring irrigations for salt leaching suitable for cotton growth in Xinjiang, China. At present, in addition to water scarcity, the low efficiency of fertilization in arid regions around the world is also an important issue affecting crop production and fruit quality [27,28]. Seeking suitable water and fertilizer schedules is an important way to ensure food security. Therefore, the exploration of the optimal combination of irrigation schedules and fertilization amounts by crop models is also a hot research topic [16,29].

2.2. Optimization Objectives

The optimization objectives are generally to maximize water productivity, irrigation water productivity, crop yield, and fruit quality, while minimizing crop water consumption and total irrigation amount [30,31]. In arid areas with water scarcity, users usually consider two or more objectives associated with both water and crop simultaneously, and there may be conflicting outcomes between multiple objectives. For example, as the irrigation amount is reduced, the soil water storage decreases, which intensifies soil water stress and leads to a reduction in crop yield. This indicates that the objective of maximizing the crop yield is contradictory to the objective of minimizing the irrigation amount [13]. Therefore, balancing two or more optimal objectives is a very difficult problem. Previous studies showed that, within a certain range of irrigation amounts, crop yields increased rapidly with the increase in irrigation amounts, and with further increases in irrigation amounts, the crop yield either increased slowly or decreased [32,33]. That is, when the irrigation amount exceeded a certain range, the crop yield was limited by other factors, such as the crop varieties or climate conditions, and the potential for a yield increase was small [34]. A moderate water deficit could significantly increase fruit quality parameters, such as soluble solids, sugar content, sugar acid ratio, carotenoids, and vitamin C [35,36]. For water productivity, it first stabilized at a certain value with an increase in irrigation amount and then decreased [24]. When determining the optimal irrigation schedules, the statistical analysis was usually conducted based on the simulation scenario results, such as establishing the correlation between the various objectives and decision variables, and then determining the optimal irrigation schedules [17,32,34]. However, there were also studies that coupled crop models with multi-objective optimization decision-making methods, such as the entropy method, to seek the optimal irrigation schedules [37]. The optimization results of the irrigation schedules might vary with the objectives set by the users. For example, Yu et al. [24] proposed that when the objective was to maximize water productivity, the recommended total irrigation amount was 275–300 mm for the arid region of Northwest China, with an annual average rainfall of 45.7 mm and a pan evaporation of 2500 mm. When the objective was to find a balance between water use and crop production, it was recommended to control the irrigation amount at around 300 mm. If the objective was to increase crop yield, further increases in the irrigation amount can be employed.
In saline areas, in addition to the objectives of both water and crop, the maximum desalination rate and the minimum salt content in the soil layer of the root zone can also be included as additional objectives [11]. The objective of soil salt content is usually achieved by adjusting the irrigation schedules during the crop growth periods or by leaching salt during the fallow periods [38]. Lin et al. [26] identified the optimal strategy of combined winter and spring irrigations for salt leaching in severely saline cotton fields in southern Xinjiang, China, with the objectives of achieving soil water, heat, and salt conditions that are suitable for the emergence of cotton seedlings, as well as the desalination rate and cotton emergence rate. Zeng et al. [39] proposed an optimal irrigation schedule for the Hetao Irrigation District in Inner Mongolia, China, with the objectives of increasing the soil moisture content and accelerating salt leaching. In areas with low fertilizer utilization efficiency, the nitrogen fertilizer productivity, nitrogen fertilizer utilization efficiency, and nitrogen leaching rate were usually included together with the water and crop production as the optimization objectives [16,40].

2.3. Crop Models

Crop models are powerful tools for evaluating the relationship between crop yield, fruit quality, and water use [41]. The crop models are usually strong mechanism models that consider the impact of natural environmental conditions on crop physiological growth, such as weather conditions, including solar radiation, air temperature, humidity, and wind speed, and soil environment conditions, including soil water, heat, and nutrients [42,43]. When optimizing irrigation schedules, crop models that can be used to reflect the relationship between crop yield and water use include the following: WAVES (WAter Vegetation Energy and Solute) [24], AquaCrop [34], SWAP (Soil–Water–Atmosphere–Plant) [23], HYDRUS [44], DNDC (Denitrification–Decomposition) [45], DSSAT (Decision Support System for Agrotechnology Transfer) [46], and RZWQM2 (Root Zone Water Quality model 2) [21]. They are often used for optimizing water and nitrogen schedules or regulating water and salt, because of their good performance as crop models for elucidating the salt and nitrogen transport processes in the soil and the crop growth processes under different agricultural management measures. The model features for some of these commonly used models are shown in Table 1 for the convenience of users who are involved in model selection. Crop models that can be used to reflect the relationship between the fruit quality and water use mainly include the “virtual fruit” [47], QualiTree [48], SUGAR [49], and TOM-SUGAR models [50]. They have been widely applied in crops such as grapes [51], blueberries [52], tomatoes [53], and pears [54] to simulate the dynamics of fruit sugar content, dynamics of water and carbon flux in plants, and vegetative growth under different water conditions [52,55].
Before making decisions on irrigation schedules based on crop models, it is necessary to determine a set of crop and soil parameters suitable for the study area based on experimental data, that is, localizing the model parameters. The crop models mostly have the characteristics of multiple-input parameters, along with the strong spatiotemporal variability of soil and crop parameters and the significant uncertainty of model parameters. The traditional method of “trial and error” has been used to debug these model parameters [73]. This method requires the subjective debugging of the input parameters based on the researcher’s own knowledge and understanding of the models. It is not only time-consuming and laborious, but also the simulation accuracy of the models is not very satisfactory [74]. On this basis, sensitivity analysis can be performed for the model parameters, and then only the parameters that have a significant impact on the model-output results need to be selected for calibration and validation, while the nonsensitive parameters in the model are briefly processed [75]. In addition, the calibration methods of the model parameters can also include a parameter calibration based on statistical theory, such as the least squares method [76] and the Markov Chain Monte Carlo (MCMC) method [77], as well as intelligent optimization algorithms such as the Genetic Algorithm (GA) [78], Simulated Annealing (SA) [9], and Particle Swarm Optimization (PSO) [10]. These methods have been widely applied in many agricultural simulation models, such as the WOFOST [79], DNDC [80], and AquaCrop models [81].

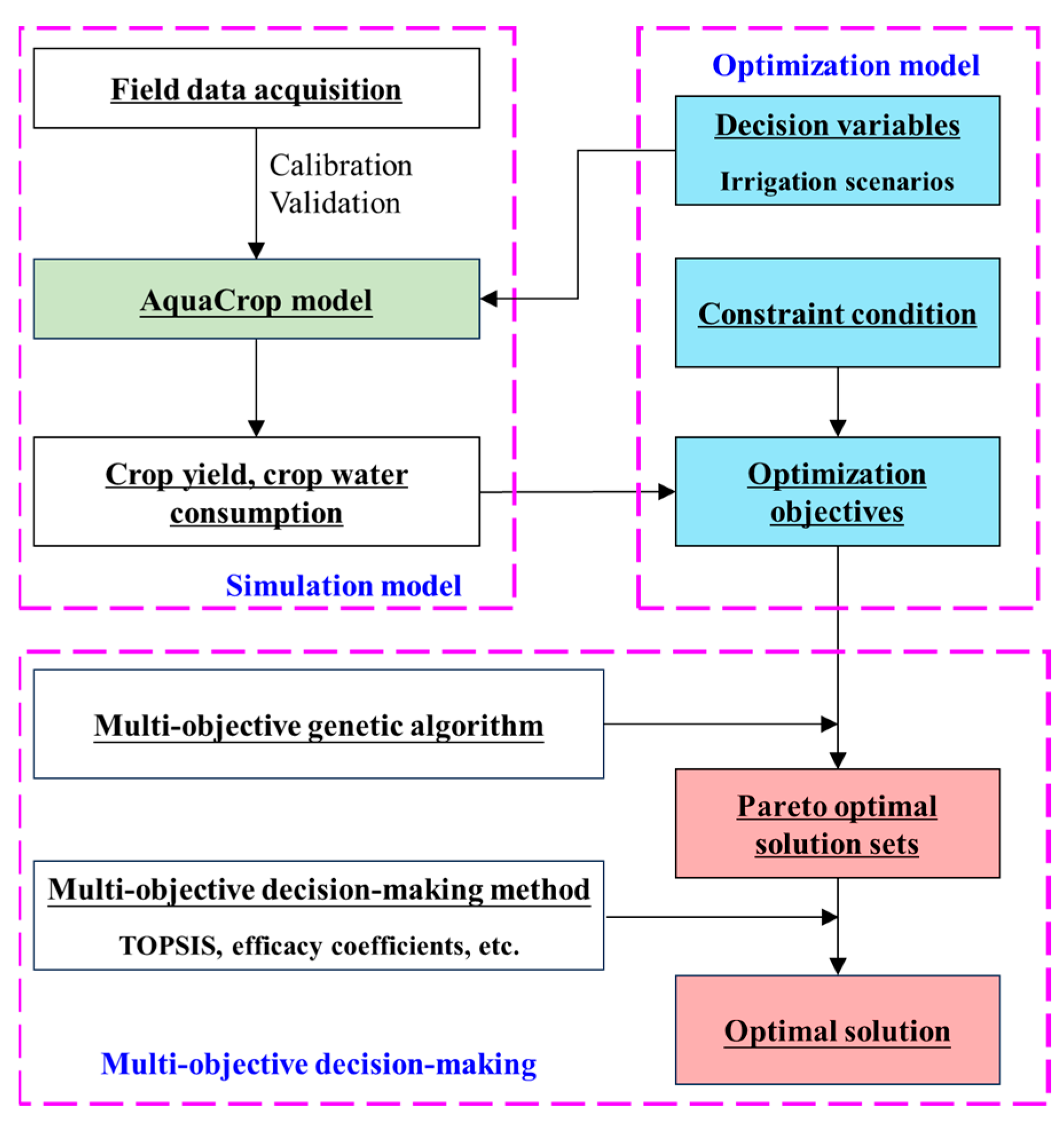
3. Optimization of Irrigation Schedules Based on Simulation–Optimization Models

The optimization of irrigation schedules based on simulation–optimization models is based on the water balance model of the farmland and the dynamic water production function model, or the crop growth model. These models can reflect the evapotranspiration process of the farmland under various irrigation schedules, and their impacts on crop yield and fruit quality. After validation of the models, they were combined with optimization techniques to obtain specific irrigation schedules.

3.1. Optimization of Irrigation Schedules Based on Water Balance–Water Production Function–Optimization Algorithm

The optimization of the irrigation schedules based on the water balance–water production function–optimization algorithm included two parts: simulation of the farmland water balance and crop yield and the optimization of irrigation schedules. The field water-balance model is a conceptual model that determines the changes in soil moisture based on the input and output of soil moisture during a certain period [1]. The calculation model of crop yield usually uses crop water-production functions, which refer to the quantitative relationship between the crop yield and water input or water consumption during crop growth and development [82]. It could reflect the ability of crops to use water to produce dry matter [82]. The specific steps of the optimization of the irrigation schedules based on water balance–water production function–optimization algorithm are as follows: at the beginning, the dynamic process of crop evapotranspiration under a certain irrigation condition was first simulated through the farmland water balance; then the relative yield was estimated using the crop water-production function and the cumulative function of water sensitivity index; and finally, optimization methods were used to determine the irrigation quota, irrigation date, and the irrigation frequency required to maximize the relative yield/benefit.
There are many factors that affect the water-production function model, mainly including the crop types, soil types, irrigation methods, irrigation water quality, climate conditions, and field management measures [83]. The water-production function model for a specific crop in a specific region needs to be determined through years of experimentation. At present, there are two main types of mature water-production function models: additive models, including the Blank [84], Stewart [85], and Singh models [86], and multiplicative models, including the Jensen [87], Minhas [88], and Rao models [89].
During the processes of irrigation schedule optimization, the Jensen model is commonly used to reveal the relationship between crop yield and water consumption. When combining the Jensen model with the optimization methods for irrigation schedule optimization, the optimization methods initially used were 0–1 linear programming [90] and simplex search method (nonlinear programming) [91]. These optimization methods were local search methods, and if the initial value selection was unreasonable, a local optimal solution could be obtained. Usually, the decision variable is set as whether to irrigate on a certain day or the irrigation date, and the maximum relative yield is used as the optimization objective. To obtain the global optimal solution, a globally searchable genetic algorithm has been proposed to determine the optimal irrigation schedules [7]. The decision variables, constraints, and optimization objectives were diverse. Usually, irrigation date and irrigation water amount were used as decision variables, and the maximum relative crop yield and the minimum total irrigation amount throughout the entire crop growth period were used as optimization objectives, and NSGA-II (an improved Nondominated Sorting Genetic Algorithm) was used for the optimization solution [14,92,93,94,95]. To make the optimized irrigation schedules more universal, Wu et al. [96] considered the interannual variations in rainfall and established an optimization model for irrigation scheduling based on the multi-year rainfall data and proved its strong applicability.
In addition to the Jensen model, other water-production functions have also been used for optimizing irrigation schedules. Li [97] believed that the Blank and Stewart models were also suitable for evaluating the relationship between crop yield and crop water consumption for pumpkin under drip irrigation conditions with film mulching in the Hexi Oasis area of China. Even the Stewart model was more effective than the Jensen model, and the optimal irrigation strategy was proposed based on the Stewart water-production function and TOPSIS (Technique for Order Preferences by Similarity to an Ideal Solution). Li et al. [98] also determined that the Jensen and Stewart models were applicable for revealing the relationship between crop yield and water consumption in cold and arid environments. In addition, empirical crop water-production functions were also determined through experiments, such as the quadratic relationship between the crop yield and the water consumption or irrigation amount [1,99].
Considering the importance of evaluating fruit quality, a water–fruit quality model was developed to simulate the response of fruit quality parameters to water using the water-production function for reference, including additive, multiplicative, and exponential models [100,101]. The results showed that the multiplicative model was suitable for simulating the relationships between soluble solids, reducing sugars, sugar–acid ratio, fruit hardness, and water deficit for tomato fruits [100]. However, the additive model was selected for the relationships between organic acids, vitamin C color index, comprehensive quality index, and water deficit [100]. Models for the optimization of crop irrigation scheduling were also established based on the water-production function, water–fruit quality models, and NSGA-II to obtain the optimal irrigation schedules for cash crops. This can further improve water use efficiency, crop yield, and fruit quality [102].

3.2. Optimization of Irrigation Schedules Based on Crop Model-Optimization Algorithm

When optimizing irrigation schedules based on the crop model-optimization algorithm, the first step is to validate the crop model. Subsequently, the crop model is coupled with the optimization algorithm to construct an irrigation schedule optimization model. Then, the optimal solution, set based on specific objectives, is sought. Finally, decision-making methods are used to make decisions on the optimization results. The crop models are usually agro-hydrological models that can simulate crop growth and soil water, heat, nitrogen, and salt processes. They generally have complex calculation processes and high nonlinearity [81]. Their computational complexity is much higher than that of the crop water production functions, which could result in high computational costs for these optimization solutions [81]. In addition, the crop models are generally packaged software that is difficult to split and requires specific input and output file formats [13]. Traditional optimization methods of irrigation schedules are not applicable, and evolutionary algorithms, mainly genetic algorithms, are usually used for both optimization and solution.
The AquaCrop model is the most widely used model among the many models for optimizing irrigation schedules based on the crop model-optimization algorithm, due to its advantages such as its simple structure, fewer required parameters, low computational complexity, and reasonable accuracy [34]. A flow chart of an irrigation schedule optimization based on the AquaCrop optimization algorithm is shown in Figure 2. Song et al. [13] combined the AquaCrop model with the NSGA-II model using MATLAB and constructed a multi-objective simulation–optimization model for irrigation schedules based on measured data from spring wheat fields in the arid region of Northwest China. In Song et al. [13], the optimization objectives were a maximum yield and minimum irrigation amount, and the efficiency coefficient method was used to make decisions on the optimization results. A simulation–optimization model coupling AquaCrop with NSGA-III using Python was also developed and the TOPSIS method was used for decision-making based on the Pareto optimal solution, which was generated by a multi-objective optimization from Lyu et al. [103]. In the study, four objectives were considered, i.e., maximizing crop yield, minimizing irrigation amount, maximizing irrigation water productivity, and maximizing water use efficiency [103]. Then, Wang [104] further coupled the groundwater numerical model MODFLOW with the model from Lyu et al. [103] to evaluate the impact of irrigation on the groundwater level and determined the optimal irrigation schedules for the objectives of groundwater level variation and crop yield. In addition to the AquaCrop model, the DSSAT model was also combined with a genetic algorithm to determine an optimal irrigation and fertilization plan for a maize field with drip irrigation in the Tengger Desert, China, and a maize field with surface irrigation in Shandong, China [105].
Fertilizer is one of the key factors in agricultural management, in addition to the water factor, and appropriate fertilization management has a direct impact on the economic and ecological benefits associated with agriculture. When optimizing irrigation schedules based on the crop model-optimization algorithm, it is usually accompanied by either fertilization management or nitrogen loss. For example, Wu et al. [106] modified the AquaCrop model by introducing the aboveground actual nitrogen concentration, critical nitrogen concentration, and minimum nitrogen concentration to simulate the evapotranspiration of maize under nitrogen stress in Northwest China. Then, the optimal solution was determined, with the objectives of maximizing crop yield and water use efficiency, based on the NSGA-II algorithm. Decisions were made using the TOPSIS method, and the optimal irrigation and fertilization strategy was obtained. Ma et al. [107] established a simulation–optimization model for the irrigation schedules of rice based on the AquaCrop model and the NSGA-II algorithm. A stable and efficient irrigation strategy for both yield and pollution control, suitable for different hydrological years, was proposed, with the objectives of a maximum yield, minimum nitrogen and phosphorus loss, and minimum irrigation frequency.

4. Improvement of Irrigation Schedule Optimization Methods

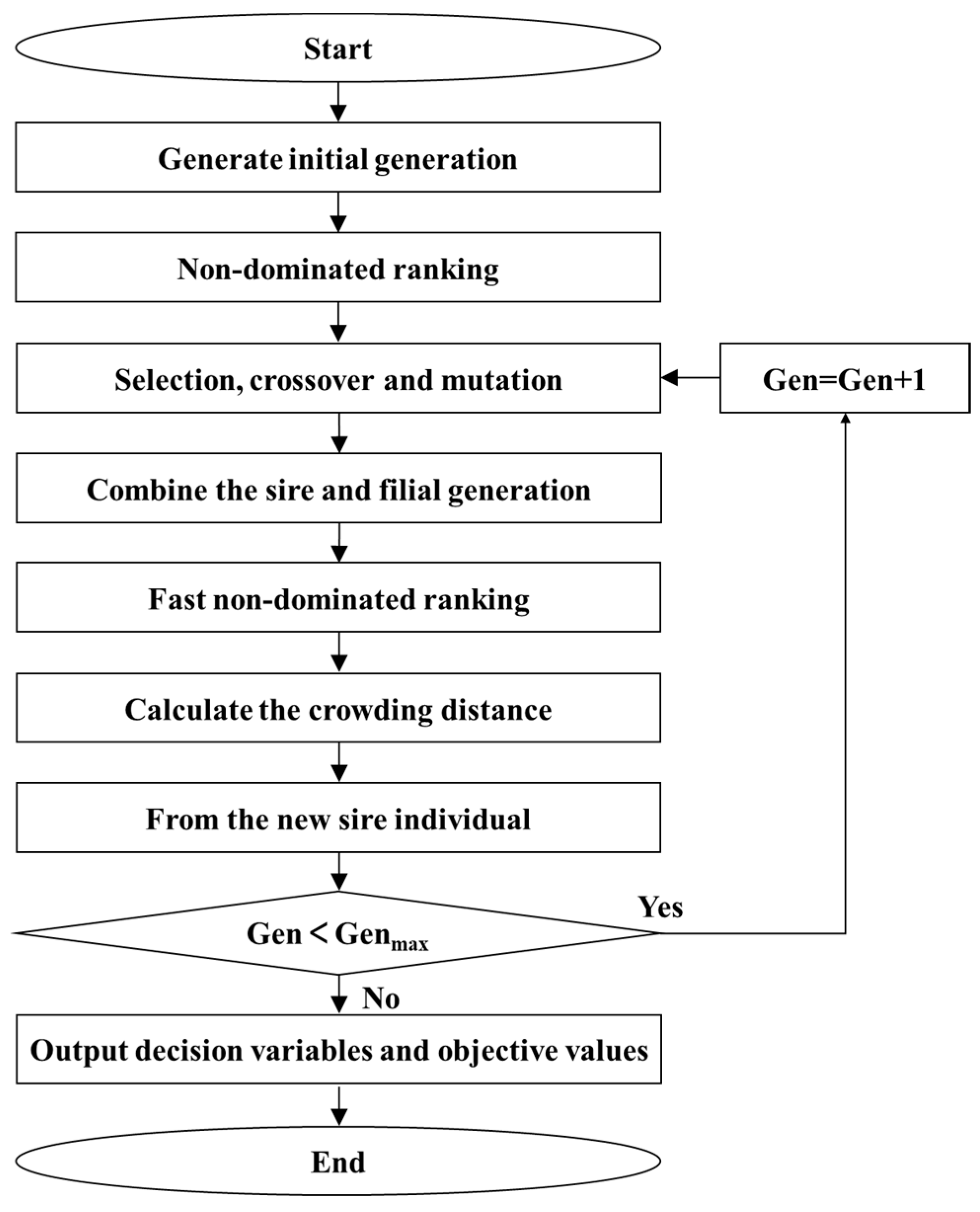
4.1. Optimization Solution Method

As the optimization objectives of irrigation schedules shifted from a single objective to multiple objectives, and crop models shifted from a simple water-production function to agro-hydrological models, the optimization methods of irrigation schedules have also evolved from traditional linear programming, nonlinear programming, and dynamic programming to an evolutionary algorithm. A comparison of the main optimization methods for irrigation schedules is shown in Table 2. The NSGA-II algorithm is currently one of the most popular multi-objective evolutionary algorithms, which was proposed based on the NSGA (Nondominated Sorting Genetic Algorithm) [108]. The NSGA, proposed in 1994, is a genetic algorithm based on the Pareto optimal concept, which layers each individual according to their dominant and nondominant relationships [109]. Then, selection operations are performed to achieve very satisfactory results for multi-objective optimization [109]. Deb et al. [78] proposed the NSGA-II, which mainly introduces an elitist strategy on the basis of the original NSGA algorithm and uses the concept of a crowding degree to sort individuals at the same level into nondominated levels, improving the algorithm speed. The NSGA-II algorithm is mainly used to solve unconstrained multi-objective optimization problems, while most historical optimization models were multi-objective optimization models with multiple constraints [107]. Currently, the improved NSGA-II algorithm is mostly used, which introduces the Deb constraint criterion into the NSGA-II algorithm [110]. A flow chart of the improved NSGA-II approach is shown in Figure 3. Due to the poor computational performance of the NSGA-II algorithm in a high-dimensional target space, the NSGA-III algorithm, with predefined multiple reference points to maintain population diversity, has also been introduced [104].
The optimization method, such as the NSGA-II, cannot provide the optimal solution to the optimization problem and can only provide several sets of Pareto solutions with good results (i.e., several irrigation schedules) [1]. Therefore, decision-making methods are necessary to further determine the optimal irrigation schedules. The decision-making methods used for optimizing irrigation schedules mainly include the analytic hierarchy process (AHP), entropy weight (EW), principal component analysis (PCA), grey relational analysis (GRA), and the technique for order preference by similarity to an ideal solution (TOPSIS) [117]. The AHP, EW, and PCA belong to a single evaluation method [117], which only evaluates a single indicator, such as evaluating the influencing factors in irrigation water efficiency or irrigation water productivity [118,119]. These methods usually cannot determine the optimal treatment and have certain limitations [120]. To address these limitations, comprehensive evaluation methods such as the GRA and TOPSIS were proposed, which greatly improved the robustness and universality of the results [121]. The TOPSIS method ranks each candidate solution by calculating the distance between the evaluation object (a solution), the ideal solution (the best value in the scheme), and the negative ideal solution (the worst value in the scheme), so as to determine the solution that is closer to the ideal solution and farther away from the negative ideal solution [122]. In the TOPSIS method, the weights of several objectives are determined, where the larger the fluctuation of the objectives, the smaller the entropy weight, and therefore the greater the weight of the objectives [122]. These comprehensive evaluation models were used for quantifying the fruit–quality index [121], developing optimal irrigation and fertilization strategies [123], as well as balancing yield, fruit quality, crop water productivity, and environmental benefits [124].

4.2. Spatiotemporal Scale of Irrigation Schedule Optimization

The optimization problem of irrigation schedules based on crop models initially focused on a field scale, while in recent years, it has been developed to solve irrigation water allocation problems on a regional scale. For example, Li et al. [1,125] considered the distribution of soil types and irrigation areas in their study area and solved the optimal irrigation plan for the typical irrigation areas in the middle reaches of the Heihe River in the arid region of Northwest China under the current situation and in typical climate years. Wang et al. [126] considered the spatial heterogeneity of the soil types, crop types, and weather types in the Yingke irrigation area in the middle reaches of the Heihe River and proposed an irrigation plan based on the maximum field water-use efficiency or the net economic benefits of using an irrigation schedule optimization model.
The traditional optimization methods were based on the time scales of the growth stage, in one month or ten days, to solve the problem of water allocation between the different stages, in order to achieve the maximum yield or benefit [90,91]. In the optimization of irrigation schedules based on the water-production function, the sensitivity index of the Jensen function is reduced to a daily scale to solve for the optimal irrigation schedule on a daily scale [90,91]. At present, irrigation schedule optimization based on crop model-optimization algorithms is usually on a daily scale. However, crop models can usually simulate smaller scales (such as an hourly scale) of crop growth and soil water, heat, and nitrogen environments [4]. Optimization research on an hourly scale irrigation schedule has been attempted, such as regulating the optimal timing of the day, duration, and pressure head threshold for irrigation based on the Hydrus-1D model [127].

5. Conclusions and Future Perspectives

This study integrated previous research and summarized how to optimize irrigation schedules based on both crop models and simulation–optimization models. It elaborated on the important links involved in the optimization process from the aspects of irrigation schedule scenarios, optimization objectives, crop model selections, optimization algorithms, and decision-making techniques. It was concluded that the method of optimizing irrigation schedules based on crop models was more mechanistic in describing the physical processes of crop growth. However, this method can only answer the “ what if” question and may not necessarily find the optimal solution. The method of optimizing irrigation schedules based on simulation–optimization models coupled with optimization algorithms could find the global optimal solution.
The problems and future prospects in the optimization of irrigation schedules based on simulation–optimization models are summarized in Table 3 and as follows:
(1)
Further Development of Crop Models.
The widely used AquaCrop model is relatively simple to apply, and several new versions have been developed in recent years, using R [128], MATLAB [129], and Python [130] languages, as the transport processes of soil water, salt, and nitrogen are relatively simple and the influence of soil heat can be ignored. This model can simulate scenarios of different irrigation methods, such as surface irrigation and drip irrigation, though it is a one-dimensional model that cannot accurately describe the two-dimensional distribution of soil water, heat, salt, and nitrogen under drip irrigation conditions. The accuracy of the optimization results for irrigation schedules based on the AquaCrop model is insufficient.
Although other crop models are more comprehensive and detailed in reflecting soil water, heat, nitrogen, salt dynamics, and crop growth, they are rarely combined with optimization algorithms for irrigation schedule optimization. They can only be used to answer the “what if?” question, that is, the optimization plan for irrigation schedules is only the optimal result in the scenario given by the user and is not necessarily the global optimum.
The HYDRUS-2D/3D model is a universal 2D/3D model, but it is currently rarely combined with optimization algorithms for irrigation schedule optimization. The model also lacks a crop growth module, which limits its development.
In summary, further development of two-dimensional or three-dimensional soil water, heat, nitrogen, and salt-coupled models with crop growth, and the exploration and resolution of the problems encountered in their coupling with the optimization algorithms are necessary. This will contribute to the precise regulation of future irrigation schedules.
(2)
Uncertain Analysis in Irrigation Schedule Optimization.
Agro-hydrological models can simulate the complex physical growth processes of crops, which involve many model parameters. These model parameters have uncertainty, which can affect the accuracy of the simulation results and ultimately affect the accuracy of the optimization results. Therefore, it is necessary to calibrate the model parameters based on intelligent optimization algorithms and explore intelligent optimization algorithm calibration tools with a strong applicability to improve model efficiency when conducting research on irrigation schedule optimization based on crop models.
In addition, there is uncertainty in the division of the typical hydrological year and in the simulation of model upscaling for irrigation schedule optimization, and this uncertainty can significantly affect the actual optimization effect. Therefore, how to further reduce this uncertainty in optimization is a key issue for future research.

Author Contributions

Conceptualization, S.L. and Y.Z.; methodology, Y.Z. and S.L.; writing—original draft preparation, Y.Z.; writing—review and editing, Y.L. and S.L.; visualization, G.L. and Y.B.; supervision, S.L.; project administration, S.L.; funding acquisition, S.L. and Y.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China (2022YFD1900801, 2022YFC3002802), Scientific Research Foundation of Binzhou University (2023Y16), Special Project for the Central Government to Guide the Development of Local Science and Technology (YDZX2022101), and Water Resource Evaluation Project of Binzhou Hydrological Center (BZSLZB2021-06-A01, BZSLZB2021-06-A02).

Data Availability Statement

Not applicable.

Acknowledgments

We greatly appreciate the careful and precise reviews provided by the anonymous reviewers.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Li, J.; Jiao, X.Y.; Jiang, H.Z.; Song, J.; Chen, L.N. Optimization of irrigation scheduling for maize in an arid oasis based on simulation–optimization model. Agronomy 2020, 10, 935. [Google Scholar] [CrossRef]
  2. Yang, H.; Wang, L.; Abbaspour, K.; Zehnder, A. Virtual water and the need for greater attention to rain-fed agriculture. Water 2006, 4, 14–15. [Google Scholar]
  3. Zheng, H.X.; Hou, H.F.; Wu, J.B.; Tian, D.L.; Miao, P. Irrigation schedule optimization for wheat and sunflower intercropping under water supply restrictions in Inner Mongolia, China. Atmosphere 2024, 15, 566. [Google Scholar] [CrossRef]
  4. Zhao, Y.; Mao, X.M.; Shukla, K.M.; Li, S.E.; Xu, Z.Q.; Bo, L.Y.; Huang, X.; Bai, Y.T.; Qi, X.C. Modelling water/heat transfer and crop growth under film mulching condition in a seed–maize field. Agric. For. Meteorol. 2023, 340, 109616. [Google Scholar] [CrossRef]
  5. Lu, J.; Shao, G.; Cui, J.; Wang, X.; Keabetswe, L. Yield, fruit quality and water use efficiency of tomato for processing underregulated deficit irrigation: A meta-analysis. Agricultural. Water Manag. 2019, 222, 301–312. [Google Scholar] [CrossRef]
  6. Galindo, A.; Collado-González, J.; Griñán, I.; Corell, M.; Centeno, A.; Martín-Palomo, M.J.; Girón, I.F.; Rodríguez, P.; Cruz, Z.N.; Memmi, H. Deficit irrigation and emerging fruit crops as a strategy to save water in Mediterranean semiarid agrosystems. Agric. Water Manag. 2018, 202, 311–324. [Google Scholar] [CrossRef]
  7. Huo, J.J.; Shang, S.H. Optimization method for crop irrigation scheduling based on simulation technique and genetic algorithms. Trans. Chin. Soc. Agric. Eng. 2007, 23, 23–28. [Google Scholar]
  8. Singh, A. An overview of the optimization modelling applications. J. Hydrol. 2012, 466, 167–182. [Google Scholar] [CrossRef]
  9. Kirkpatrick, S. Optimization by simulated annealing: Quantitative studies. J. Stat. Phys. 1984, 34, 975–986. [Google Scholar] [CrossRef]
  10. Chiang, I.; Hsu, J.Y. Incremental learning for robot control. In Proceedings of the IEEE International Conference On Systems, Man and Cybernetics, Vancouver, BC, Canada, 22–25 October 1995; pp. 4331–4336. [Google Scholar]
  11. Wang, Y.l.; Mao, X.M.; Chen, S.; Bo, L.Y. Experiments and simulation of soil moisture, temperature and salinity dynamics and oil sunflower growth in saline border irrigated farmland. Trans. Chin. Soc. Agric. Eng. 2021, 37, 76–86. [Google Scholar] [CrossRef]
  12. Solgi, S.; Ahmadi, S.H.; Sepaskhah, A.R.; Edalat, M. Wheat yield modeling under water-saving irrigation and climatic scenarios in transition from surface to sprinkler irrigation systems. J. Hydrol. 2022, 612, 128053. [Google Scholar] [CrossRef]
  13. Song, J.; Li, J.; Yang, Q.H.; Mao, X.M.; Yang, J.; Wang, K. Multi-objective optimization and its application on irrigation scheduling based on AquaCrop and NSGA-II. Trans. Chin. Soc. Agric. Mach. 2018, 49, 1284–1295. [Google Scholar] [CrossRef]
  14. Wabela, K.; Hammani, A.; Abdelilah, T.; Tekleab, S.; El-Ayachi, M. Optimization of irrigation scheduling for improved irrigation water management in Bilate Watershed, Rift Valley, Ethiopia. Water 2022, 14, 3960. [Google Scholar] [CrossRef]
  15. Linker, R.; Kisekka, I. Model-based simulation-optimization of irrigation scheduling—A field evaluation with processing tomatoes. Smart Agric. Technol. 2023, 4, 100234. [Google Scholar] [CrossRef]
  16. Li, Y.; Xu, X.; Hu, M.; Chen, Z.J.; Tan, J.W.; Liu, L.; Xiong, Y.W.; Huang, Q.Z.; Huang, G.H. Modeling water-salt-nitrogen dynamics and crop growth of saline maize farmland in Northwest China: Searching for appropriate irrigation and N fertilization strategies. Agric. Water Manag. 2023, 282, 108271. [Google Scholar] [CrossRef]
  17. Song, X.S.; Cao, H.X.; He, Z.J.; Ding, B.X.; Yao, N. Applicability of the Aquacrop model in optimization of irrigation and salt leaching schedule during the reproductive period of cotton in Northern Xinjiang of China. Trans. Chin. Soc. Agric. Eng. 2023, 39, 111–122. [Google Scholar] [CrossRef]
  18. Zhang, J.R.; Wang, C.X.; Ma, J.J.; Wang, H.X.; Wang, J.X. Dynamic simulation of Korla Fragrant pear growth and optimization of drip irrigation system based on AquaCrop model. J. Soil Water Conserv. 2023, 37, 328–336+344. [Google Scholar] [CrossRef]
  19. Zhou, S.W.; Hu, X.T.; Wang, W.E.; Allan, A.; Zhang, Y.J. Optimization of irrigation schedule based on RZWQM model for spring wheat in Shiyang River Basin. Trans. Chin. Soc. Agric. Eng. 2016, 32, 121–129. [Google Scholar] [CrossRef]
  20. Gu, Z.; Qi, Z.; Ma, L.; Gui, D.W.; Xu, J.Z. Development of an irrigation scheduling software based on model predicted crop water stress. Comput. Electron. Agric. 2017, 143, 208–221. [Google Scholar] [CrossRef]
  21. Zhang, H.H.; Ma, L.W.; Douglas, M.; Kyle, R.; Han, M.; Trout, T.J. Modeling maize production under growth stage-based deficit irrigation management with RZWQM2. Agric. Water Manag. 2021, 248, 106767. [Google Scholar] [CrossRef]
  22. Painagan, M.S.; Ella, V.B. Modeling the impact of deficit irrigation on corn production. Sustainability 2022, 14, 10401. [Google Scholar] [CrossRef]
  23. Jiang, J.; Feng, S.Y.; Ma, J.J.; Huo, Z.L.; Zhang, C.B. Irrigation management for spring maize grown on saline soil based on SWAP model. Field Crops Res. 2016, 196, 85–97. [Google Scholar] [CrossRef]
  24. Yu, Q.H.; Kang, S.Z.; Hu, S.J.; Zhang, L.; Zhang, X.T. Modeling soil water-salt dynamics and crop response under severely saline condition using WAVES: Searching for a target irrigation volume for saline water irrigation. Agric. Water Manag. 2021, 256, 107100. [Google Scholar] [CrossRef]
  25. Chen, S.; Song, C.N.; Mao, X.M.; Shang, S.H. Modeling response of spring wheat yield to soil water and salt contents and its application in scheduling brackish water irrigation. Comput. Electron. Agric. 2022, 200, 107216. [Google Scholar] [CrossRef]
  26. Lin, D.; Wang, F.; Xu, Z.Q.; Mao, X.M. Appropriate winter and spring irrigations for salt leaching in typical cotton field of Southern Xinjiang based on SHAW model. Trans. Chin. Soc. Agric. Mach. 2023, 54, 326–338+350. [Google Scholar] [CrossRef]
  27. Rakha, A.M.; Eisa, R.A.; Abourayya, M.S.; Kaseem Nabila, E.; Mahmoud, T.S.M. Effects of different sources of nitrogen fertilizer on the yield and fruit quality of persian lime under nubaria conditions. Appl. Fruit Sci. 2024, 1–7. [Google Scholar] [CrossRef]
  28. Liava, V.; Karkanis, A.; Danalatos, N.; Tsiropoulos, N. Effects of two varieties and fertilization regimes on growth, fruit, and silymarin yield of milk thistle crop. Agronomy 2022, 12, 105. [Google Scholar] [CrossRef]
  29. Cheng, M.H.; Wang, H.D.; Fan, J.L. Evaluation of AquaCrop model for greenhouse cherry tomato with plastic film mulch under various water and nitrogen supplies. Agric. Water Manag. 2022, 274, 107949. [Google Scholar] [CrossRef]
  30. Huang, Y.; Zhang, Z.; Li, Z.H.; Dai, D.Q.; Li, Y.P. Evaluation of water use efficiency and optimal irrigation quantity of spring maize in Hetao Irrigation District using the Noah-MP Land Surface Model. Agric. Water Manag. 2022, 264, 107498. [Google Scholar] [CrossRef]
  31. Wang, L.; Lin, M.W.; Han, Z.X.; Sun, W.H. Simulating the effects of drought stress timing and the amount irrigation on cotton yield using the CSM-CROPGRO-Cotton Model. Agronomy 2024, 14, 14. [Google Scholar] [CrossRef]
  32. Yang, J.; Mao, X.M.; Wang, K.; Yang, W.C. The coupled impact of plastic film mulching and deficit irrigation on soil water/heat transfer and water use efficiency of spring wheat in Northwest China. Agric. Water Manag. 2018, 201, 232–245. [Google Scholar] [CrossRef]
  33. Yin, J.; Yang, Y.; Eeswaran, R.; Yang, Z.; Ma, Z.; Sun, F. Irrigation scheduling for potatoes (Solanum tuberosum L.) under drip irrigation in an arid region using AquaCrop model. Front. Plant Sci. 2023, 14, 1242074. [Google Scholar] [CrossRef] [PubMed]
  34. Zhang, C.; Xie, Z.; Wang, Q.J.; Tang, M.; Feng, S.Y.; Cai, H.J. AquaCrop modeling to explore optimal irrigation of winter wheat for improving grain yield and water productivity. Agric. Water Manag. 2022, 266, 107580. [Google Scholar] [CrossRef]
  35. Wang, C.; Gu, F.; Chen, J.; Yang, H.; Jiang, J.; Du, T.; Zhang, J. Assessing the response of yield and comprehensive fruit quality of tomato grown in greenhouse to deficit irrigation and nitrogen application strategies. Agric. Water Manag. 2015, 161, 9–19. [Google Scholar] [CrossRef]
  36. Guizani, M.; Dabbou, S.; Maatallah, S.; Montevecchi, G.; Hajlaoui, H.; Rezig, M.; Helal, A.N.; Kilani-Jaziri, S. Physiological responses and fruit quality of four peach cultivars under sustained and cyclic deficit irrigation in center-west of Tunisia. Agric. Water Manag. 2019, 217, 81–97. [Google Scholar] [CrossRef]
  37. Shao, D.G.; Le, Z.H.; Xu, B.L.; Hu, N.J.; Tian, Y.N. Optimization of irrigation scheduling for organic rice based on AquaCrop. Trans. Chin. Soc. Agric. Eng. 2018, 34, 114–122. [Google Scholar] [CrossRef]
  38. Che, Z.; Wang, J.; Li, J.S. Modeling strategies to balance salt leaching and nitrogen loss for drip irrigation with saline water in arid regions. Agric. Water Manag. 2022, 274, 107943. [Google Scholar] [CrossRef]
  39. Zeng, W.Z.; Chi, X.U.; Wu, J.W.; Huang, J.S. Soil salt leaching under different irrigation regimes: HYDRUS-1D modelling and analysis. J. Arid. Land 2014, 6, 44–58. [Google Scholar] [CrossRef]
  40. Wei, K.; Deng, M.J.; Wang, Q.J.; Guo, Y.; Lin, S.D.; Mu, W.Y. Nitrogen application rates from dilution curve model for cotton under film mulched drip irrigation with brackish water. Trans. Chin. Soc. Agric. Eng. 2024, 40, 124–132. [Google Scholar] [CrossRef]
  41. Zhou, H.P.; Chen, J.L.; Wang, F.; Li, X.J.; Génarde, M.; Kang, S.Z. An integrated irrigation strategy for water-saving and quality-improving of cash crops: Theory and practice in China. Agric. Water Manag. 2020, 241, 106331. [Google Scholar] [CrossRef]
  42. Allard, W.; Hendrik, B.; Davide, F.; Sander, J.; Rob, K.; Daniel, K.; Iwan, S.; Raymond, W.; Kees, D. 25 years of the WOFOST cropping systems model. Agric. Syst. 2019, 168, 154–167. [Google Scholar] [CrossRef]
  43. Doro, L.; Wang, X.; Ammann, C.; Migliorati, M.; Norfleet, M.L. Improving the simulation of soil temperature within the EPIC model. Environ. Model. Softw. 2021, 144, 105140. [Google Scholar] [CrossRef]
  44. Guo, L.L.; Wang, Z.M.; Simůnek, J.; He, Y.J.; Muhamma, R. Optimizing the strategies of mulched brackish drip irrigation under a shallow water table in Xinjiang, China, using HYDRUS-3D. Agric. Water Manag. 2022, 274, 107943. [Google Scholar] [CrossRef]
  45. Shah, S.H.; Wang, J.; Hao, X.; Hao, X.Y.; Thomas, B.W. Modelling soil salinity effects on salt water uptake and crop growth using a modified denitrification-decomposition model: A phytoremediation approach. J. Environ. Manag. 2022, 301, 113820. [Google Scholar] [CrossRef]
  46. Linker, R.; Kisekka, I. Concurrent data assimilation and model-based optimization of irrigation scheduling. Agric. Water Manag. 2022, 274, 107924. [Google Scholar] [CrossRef]
  47. Lescourret, F.; Génard, M. A virtual peach fruit model simulating changes in fruit quality during the final stage of fruit growth. Tree Physiol. 2005, 25, 1303–1315. [Google Scholar] [CrossRef]
  48. Lescourret, F.; Moitrier, N.; Valsesia, P.; Génard, M. QualiTree, a virtual fruit tree to study the management of fruit quality. I. Model development. Trees 2011, 25, 519–530. [Google Scholar] [CrossRef]
  49. Génard, M.; Lescourret, F.; Gomez, L.; Habib, R. Changes in fruit sugar concentrations in response to assimilate supply, metabolism and dilution: A modeling approach applied to peach fruit (Prunus persica). Tree Physiol. 2003, 23, 373–385. [Google Scholar] [CrossRef]
  50. Chen, J.L.; Vercambre, G.; Kang, S.Z.; Bertin, N.; Gautier, H.; Génard, M. Fruit water content as an indication of sugar metabolism improves simulation of carbohydrate accumulation in tomato fruit. J. Exp. Bot. 2020, 76, 5010–5026. [Google Scholar] [CrossRef]
  51. Dai, Z.W.; Génard, M.; Li, S.; Vivin, P. Analyzing the functional association among seed traits, berry growth and chemical composition in Cabernet-Sauvignon berry (Vitis vinifera L.) using a mathematical growth function. Oeno One 2009, 43, 35–44. [Google Scholar] [CrossRef]
  52. Jorquera-Fontena, E.; Génard, M.; Franck, N. Analysis of blueberry (Vaccinium corymbosum L.) fruit water dynamics during growth using an ecophysiological model. J. Hortic. Sci. Biotechnol. 2017, 92, 646–659. [Google Scholar] [CrossRef]
  53. Liu, H.F.; Génard, M.; Guichard, S.; Bertin, N. Model-assisted analysis of tomato fruit growth in relation to carbon and water fluxes. J. Exp. Bot. 2007, 58, 3567–3580. [Google Scholar] [CrossRef]
  54. Prudent, M.; Lecomte, A.; Bouchet, J. Combining ecophysiological modelling and quantitative trait locus analysis to identify key elementary processes underlying tomato fruit sugar concentration. J. Exp. Bot. 2011, 62, 907–919. [Google Scholar] [CrossRef]
  55. Zhu, J.Q.; Génard, M.; Poni, S.; Gambetta, G.A.; Vivin, P.; Vercambre, G.; Trought, M.C.T.; Ollat, N.; Delrot, S.; Dai, Z.W. Modelling grape growth in relation to whole plant carbon and water fluxes. J. Exp. Bot. 2019, 70, 2505–2521. [Google Scholar] [CrossRef]
  56. Foster, T.; Brozovic, N.; Hsiao, T.C. AquaCrop-OS: An open source version of FAO’s crop water productivity model. Agric. Water Manag. 2017, 181, 18–22. [Google Scholar] [CrossRef]
  57. Zhang, T.; Sun, W.; Zhang, F.W. Simulation of AquaCrop model and management practice optimization for dryland maize production under whole plastic-film mulching on double ridges. Chin. J. Appl. Ecol. 2017, 28, 918–926. [Google Scholar]
  58. Deb, P.; Shrestha, S.; Babel, M. Forecasting climate change impacts and evaluation of adaptation options for maize cropping in the hilly terrain of Himalayas: Sikkim, India. Theor. Appl. Climatol. 2014, 121, 649–667. [Google Scholar] [CrossRef]
  59. Kumar, P.; Sarangi, A.; Sahoo, R.N. Simulation of salt dynamics in the root zone and yield of wheat crop under irrigated saline regimes using SWAP model. Agric. Water Manag. 2015, 148, 72–83. [Google Scholar] [CrossRef]
  60. Verma, A.K.; Gupta, S.K.; Isaac, R.K. Use of saline water for irrigation in monsoon climate and deep water table regions: Simulation modeling with SWAP. Agric. Water Manag. 2012, 115, 186–193. [Google Scholar] [CrossRef]
  61. Feng, S.Y.; Jiang, J.; Huo, Z.L.; Zhang, C.B. Optimization of irrigation scheduling under deficit irrigation with saline water for spring wheat based on SWAP model. Trans. CSAE 2014, 30, 66–75. [Google Scholar] [CrossRef]
  62. Zhou, J.; Li, W.F.; Chang, X.X. Calibration and validation of APSIM for maize grown in different seasons in southwest tropic of China. Chil. J. Agric. Res. 2022, 82, 586–594. [Google Scholar] [CrossRef]
  63. Lobell, D.B.; Hammer, G.L.; Schlenker, W. The critical role of extreme heat for maize production in the United States. Nat. Clim. Change 2013, 3, 497–501. [Google Scholar] [CrossRef]
  64. Chimonyo, V.G.P.; Modi, A.T.; Mabhaudhi, T. Simulating yield and water use of a sorghum-cowpea intercrop using APSIM. Agric. Water Manag. 2016, 177, 317–328. [Google Scholar] [CrossRef]
  65. Vogeler, I.; Cichota, R.; Werner, A. Simulating water and nitrogen runoff with APSIM. Soil Tillage Res. 2023, 227, 105593. [Google Scholar] [CrossRef]
  66. Tirfessa, A.; Getachew, F.; Hammer, G. Modeling adaptation of sorghum in Ethiopia with APSIM—Opportunities with GxExM. Agron. Sustain. Dev. 2023, 43, 15. [Google Scholar] [CrossRef]
  67. Liu, W.R.; Chen, G.Q.; Liu, E.K. The variations in winter wheat potential yields in the middle and lower reaches of the Yangtze River under the RCP scenarios. Acta Ecol. Sin. 2018, 38, 3219–3229. [Google Scholar]
  68. Shen, H.; Xu, F.; Zhao, R. Optimization of sowing date, irrigation, and nitrogen management of summer maize using the DSSAT–CERES–Maize model in the Guanzhong Plain, China. Trans. ASABE 2020, 63, 789–797. [Google Scholar] [CrossRef]
  69. Dettori, M.; Cesaraccio, C.; Duce, P. Simulation of climate change impacts on production and phenology of durum wheat in Mediterranean environments using CERES-Wheat model. Field Crops Res. 2017, 206, 43–53. [Google Scholar] [CrossRef]
  70. Ma, L.; Malone, R.W.; Heilman, P.; Karlen, D.L.; Kanwar, R.S.; Cambardella, C.A.; Saseendran, S.A.; Ahuja, L.R. RZWQM simulation of long-term crop production, water and nitrogen balances in Northeast Iowa. Geoderma 2007, 140, 247–259. [Google Scholar] [CrossRef]
  71. Ding, D.; Zhao, Y.; Sun, B.; He, J.; Feng, H. Suitability analysis of nitrogen fertilizer management on dryland of Loess Plateau based on root zone water quality model. Trans. CSAE 2015, 31, 111–121. [Google Scholar] [CrossRef]
  72. Wauchope, R.D.; Rojas, K.W.; Ma, L.W. Documenting the pesticide processes module of the ARS RZWQM agroecosystem model. Pest Manag. Sci. 2010, 60, 222–239. [Google Scholar] [CrossRef]
  73. Jiang, J.; Feng, S.Y.; Huo, Z.L.; Zhao, Z.C.; Jia, B. Application of the SWAP model to simulate water–salt transport under deficit irrigation with saline water. Math. Comput. Model. 2011, 54, 902–911. [Google Scholar] [CrossRef]
  74. Liang, H.; Hu, K.L.; Li, B.G. Parameter optimization and sensitivity analysis of soil-crop system model using PEST. Trans. Chin. Soc. Agric. Eng. 2016, 32, 78–85. [Google Scholar] [CrossRef]
  75. Zhao, Y.; Mao, X.; Shukla, M. A modified SWAP model for soil water and heat dynamics and seed-maize growth under film mulching. Agric. For. Meteorol. 2020, 108127, 292–293. [Google Scholar] [CrossRef]
  76. Hou, J.L.; Wang, Y.M.; Zhan, Z.G.; Zhang, J.; Xu, Y. Application of nonlinear least squares method to crop growth structure-function simulation model. Trans. Chin. Soc. Agric. Mach. 2005, 36, 75–79. [Google Scholar]
  77. He, J.; Jones, J.W.; Graham, W.D.; Dukes, M.D. Influence of likelihood function choice for estimating crop model parameters using the generalized likelihood uncertainty estimation method. Agric. Syst. 2010, 103, 256–264. [Google Scholar] [CrossRef]
  78. Deb, K.; Agrawal, S.; Pratap, A. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Parallel Problem Solving from Nature PPSNVI; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
  79. Wu, Y.T.; Xu, W.B.; Huang, J.X. Bayesian posterior-based winter wheat yield estimation at the field scale through assimilation of sentinel-2 data into WOFOST Model. Remote Sens. 2022, 14, 3727. [Google Scholar] [CrossRef]
  80. Bhattarai, A.; Steinbeck, G.; Khanal, S. Development of a calibration approach using DNDC and PEST for improving estimates of management impacts on water and nutrient dynamics in an agricultural system. Environ. Model. Softw. 2022, 157, 105494. [Google Scholar] [CrossRef]
  81. Guo, D.X. Growth Simulation and Regional Irrigation Schedule Optimization for Winter Wheat and Summer Maize Based on AquaCrop Model in the Fenwei Plain. Ph.D. Thesis, Northwest A&F University, Xianyang, China, 2021. [Google Scholar]
  82. Malve, S.H.; Rao, P.; Dhake, A. Evaluation of water production function and optimization of water for winter wheat (Triticum aestivum L.) under drip Irrigation. Am.-Eurasian J. Agric. Environ. Sci. 2016, 16, 1389–1398. [Google Scholar]
  83. Li, Z.K.; Liu, H.; Zhao, W.Z. Revisiting crop water production functions in terms of cross-regional applications. Chin. J. Eco-Agric. 2018, 26, 1781–1794. [Google Scholar] [CrossRef]
  84. Kang, S.Z.; Cai, H.J. Agricultural Water Management; China Agriculture Press: Beijing, China, 1996. [Google Scholar]
  85. Stewart, J.I.; Hagan, R.M.; Pruitt, W.O.; Danielson, R.E.; Franklin, W.T.; Hanks, R.J.; Riley, J.P.; Jackson, E.B. Optimizing Crop Production through Control of Water and Salinity Levels in the Soil; Reports; Paper 67; Utah State University: Logan, UT, USA, 1977. [Google Scholar]
  86. Rajputg, S.; Singh, J. Water production functions for wheat under different environmental conditions. Agric. Water Manag. 1986, 11, 319–332. [Google Scholar] [CrossRef]
  87. Jensen, M.E. Water Consumption by Agricultural Plants; Academic Press: New York, NY, USA, 1968; pp. 1–22. [Google Scholar]
  88. Minhas, B.S.; Parikh, K.S.; Srinivasan, T.N. Toward the structure of a production function for wheat yields with dated inputs of irrigation water. Water Resour. Res. 1974, 10, 383–393. [Google Scholar] [CrossRef]
  89. Rao, N.H.; Sarma, P.B.; Chander, S. A simple dated water-production function for use in irrigated agriculture. Agric. Water Manag. 1988, 13, 25–32. [Google Scholar] [CrossRef]
  90. Mao, X.M.; Shang, S.H. Application of 0-1 Programming model on optimization of crop deficit irrigation schedule. Trans. Chin. Soc. Agric. Mach. 2014, 45, 123+153–158. [Google Scholar] [CrossRef]
  91. Shang, S.H. Simulation optimization method for inadequate irrigation regime of crops. J. Tsinghua Univ. (Sci. Tecnol.) 2005, 45, 1179–1183. [Google Scholar] [CrossRef]
  92. Qie, Z.H.; Han, L.M.; Wu, X.M. Optimization of crop irrigation quantity and irrigation date based on the improved NSGA-II. Trans. Chin. Soc. Agric. Mach. 2011, 42, 106–110. [Google Scholar] [CrossRef]
  93. Tang, X.Y.; He, Y.; Peng, L.; Wang, J. Research on multi-objective optimization of Xinjiang cotton irrigation system based on CNSGA-II Algorithm. Water Sav. Irrig. 2020, 11, 59–63+67. [Google Scholar]
  94. Yu, Z.J.; Shang, S.H. Multi-objective optimization method for irrigation scheduling of crop rotation system and its application in North China. J. Hydraul. Eng. 2016, 47, 1188–1196. [Google Scholar] [CrossRef]
  95. Jie, Z. Irrigation Water Optimization Allocation Based on Intelligent Calculation. In Proceedings of the 2014 Sixth International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 10–11 January 2014. [Google Scholar] [CrossRef]
  96. Wu, X.M.; Wang, J.; Qie, Z.H. Multi-objective optimization of crop irrigation schedule based on years of rainfall data. Trans. Chin. Soc. Agric. Mach. 2013, 44, 108–112. [Google Scholar] [CrossRef]
  97. Li, X. Response of Pumpkin to Water Deficit and Optimization of Irrigation Schedule with Drip Irrigation under Mulch in the Hexi Oasis. Ph.D. Thesis, Gansu Agricultural University, Lanzhou, China, 2023. [Google Scholar]
  98. Li, F.; Zhang, H.; Li, X.; Deng, H.; Chen, X.; Liu, L. Modelling and evaluation of potato water production functions in a cold and arid environment. Water 2022, 14, 2044. [Google Scholar] [CrossRef]
  99. Zhao, J.; Yu, Y.; Lei, J.; Liu, J. Multi-objective lower irrigation limit simulation and optimization model for Lycium Barbarum based on NSGA-III and ANN. Water 2023, 15, 783. [Google Scholar] [CrossRef]
  100. Chen, J.; Kang, S.; Du, T.; Guo, P.; Qiu, R.; Chen, R.; Gu, F. Modeling relations of tomato yield and fruit quality with water deficit at different growth stages under greenhouse condition. Agric. Water Manag. 2014, 146, 131–148. [Google Scholar] [CrossRef]
  101. Chen, F.; Cui, N.B.; Jiang, S.Z.; Wang, Z.H.; Li, H.P.; Lv, M.; Wang, Y.S.; Gong, D.Z.; Zhao, L. Multi-objective deficit drip irrigation optimization of citrus yield, fruit quality and water use efficiency using NSGA-II in seasonal arid area of Southwest China. Agric. Water Manag. 2023, 287, 108440. [Google Scholar] [CrossRef]
  102. Shan, B.; Guo, P.; Guo, S.; Li, Z. A Price-Forecast-Based irrigation scheduling optimization model under the response of fruit quality and price to water. Sustainability 2019, 11, 2124. [Google Scholar] [CrossRef]
  103. Lyu, J.Y.; Jiang, Y.A.; Xu, C.; Liu, Y.J.; Su, Z.H.; Liu, J.C.; He, J.Q. Multi-objective winter wheat irrigation strategies optimization based on coupling AquaCrop-OSPy and NSGA-III: A case study in Yangling, China. Sci. Total Environ. 2022, 843, 157104. [Google Scholar] [CrossRef]
  104. Wang, K.H. Multi-Objective Optimization of Irrigation Scheduling Based on AquaCrop-FloPy-NSGA-III Coupling Model. Master’s Thesis, Northwest A&F University, Xianyang, China, 2023. [Google Scholar]
  105. Bai, Y.; Yue, W.; Ding, C. Optimize the irrigation and fertilizer schedules by combining DSSAT and GA. Environ. Sci. Pollut. Res. 2022, 29, 52473–52482. [Google Scholar] [CrossRef]
  106. Wu, H.; Yue, Q.; Guo, P.; Xu, X.Y.; Huang, X. Improving the AquaCrop model to achieve direct simulation of evapotranspiration under nitrogen stress and joint simulation-optimization of irrigation and fertilizer schedules. Agric. Water Manag. 2022, 266, 107599. [Google Scholar] [CrossRef]
  107. Ma, C.; Wu, T.A.; Zhang, W.Z.; Li, J.; Jiao, X.Y. Optimization of multi-objective irrigation schedule for rice based on AquaCrop model. J. Irrig. Drain. 2024, 43, 9–16. [Google Scholar] [CrossRef]
  108. Shafa, N.S.; Babazadeh, H.; Saremi, A. Multi-objective planning for optimal exploitation of surface and groundwater resources through development of an optimized cropping pattern and artificial recharge system. Ain Shams Eng. J. 2023, 14, 101847. [Google Scholar] [CrossRef]
  109. Srinivas, N.; Deb, K. Multi-objective optimization using non-dominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
  110. Chen, X.Q.; Hou, Z.X.; Guo, L.M.; Luo, W.C. Improved multi-objective genetic algorithm based on NSGA-II. Comput. Appl. 2006, 26, 2453–2456. [Google Scholar]
  111. Zheng, J.H.; Huang, G.H.; Huang, Q.Z.; Wang, J.; Jia, D.D.; Zhang, K.Z. Water production function and optimal irrigation schedules for onion with drip irrigation and mulch of plastic film in arid region. Trans. CSAE 2011, 27, 25–30. [Google Scholar] [CrossRef]
  112. Zheng, H.; Shi, H.; Chai, J.; Fu, W. Optimal irrigation schedule model of forage crop by RAGA-DP under deficit irrigation. Trans. CSAE 2007, 23, 65–70. [Google Scholar]
  113. Zhang, G.; Xie, C.; Pi, X.; Wang, B. Optimization model for discharge distribution of irrigation channels based on free search algorithm. Trans. CSAE 2012, 28, 86–90. [Google Scholar] [CrossRef]
  114. Wang, Q.; Yue, C.; Li, Y.; Liu, X. Optimal allocation of water resources with two-level channel based on improved particle swarm optimization algorithm. Agric. Res. Arid. Areas 2019, 37, 26–33. [Google Scholar] [CrossRef]
  115. Li, W.; Deng, H.; Tian, M.; Chen, H. Division algorithm of the rotation irrigation group for automated drip irrigation based on hybrid variable neighborhood. Trans. CSAE 2022, 38, 155–162. [Google Scholar] [CrossRef]
  116. Alibabaei, K.; Gaspar, P.; Assuncao, E. Irrigation optimization with a deep reinforcement learning model: Case study on a site in Portugal. Agric. Water Manag. 2022, 263, 107480. [Google Scholar] [CrossRef]
  117. Shi, R.; Guo, W. Research progress on the optimal allocation of agricultural irrigation water resources. Trans. CSAE 2024, 40, 1–13. [Google Scholar] [CrossRef]
  118. Li, H.; Shao, D.; Yin, X.; Chen, S.; Xu, B. Evaluation method for irrigation-water use efficiency based on principle component analysis and Copula function. Trans. CSAE 2015, 31, 96–102. [Google Scholar] [CrossRef]
  119. Zhang, N.; Zhang, J.F.; Li, T. Principal component analysis of influencing factors of winter wheat irrigation water productivity in Xi’an. J. Xi’an Univ. Technol. 2021, 37, 9–15. [Google Scholar] [CrossRef]
  120. Zhang, J.W.; Xiang, L.X.; Zhu, C.X.; Li, W.Q.; Jing, D.; Zhang, L.L.; Liu, Y.; Li, T.L.; Li, J.M. Evaluating the irrigation schedules of greenhouse tomato by simulating soil water balance under drip irrigation. Agric. Water Manag. 2023, 283, 108323. [Google Scholar] [CrossRef]
  121. Yang, X.Q.; Du, R.S.; He, D.W.; Li, D.Y.; Chen, J.R.; Han, X.L.; Wang, Z.Q.; Zhang, Z. Optimal combination of potassium coupled with water and nitrogen for strawberry quality based on consumer-orientation. Agric. Water Manag. 2023, 287, 108461. [Google Scholar] [CrossRef]
  122. Xu, C.; Ke, Y.; Li, Y.; Chu, H.; Wu, Y. Data-driven configuration optimization of an offgrid wind/PV/hydrogen system based on modified NSGA-II and CRITIC-TOPSIS. Energy Convers. Manag. 2020, 215, 112892. [Google Scholar] [CrossRef]
  123. Qu, F.; Zhang, Q.; Jiang, Z.X.; Zhang, C.H.; Zhang, Z.; Hu, X.H. Optimizing irrigation and fertilization frequency for greenhouse cucumber grown at different air temperatures using a comprehensive evaluation model. Agric. Water Manag. 2022, 273, 107876. [Google Scholar] [CrossRef]
  124. Zhang, J.W.; Xiang, L.X.; Liu, Y.X.; Dan, J.; Zhang, L.L.; Liu, Y.; Li, W.Q.; Wang, X.Y.; Li, T.L.; Li, J.M. Optimizing irrigation schedules of greenhouse tomato based on a comprehensive evaluation model. Agric. Water Manag. 2024, 295, 108741. [Google Scholar] [CrossRef]
  125. Li, J.; Shang, S.H.; Jiang, H.Z.; Song, J.; Rahman, K.U. Simulation-based optimization for spatiotemporal allocation of irrigation water in arid region. Agric. Water Manag. 2021, 254, 106952. [Google Scholar] [CrossRef]
  126. Wang, Y.Z.; Guo, S.S.; Guo, P. Crop-growth-based spatially-distributed optimization model for irrigation water resource management under uncertainties and future climate change. J. Clean. Prod. 2022, 345, 131182. [Google Scholar] [CrossRef]
  127. Fontanet, M.; Daniel, F.G.; Rodrigo, G.; Ferrer, F.; Villar, J.M. Combined simulation and optimization framework for irrigation scheduling in agriculture fields. Irrig. Sci. 2022, 40, 115–130. [Google Scholar] [CrossRef]
  128. Rodriguez, A.V.C.; Ober, E.S. AquaCropR: Crop growth model for R. Agronomy 2019, 9, 378. [Google Scholar] [CrossRef]
  129. Kelly, T.D.; Foster, T.; Schultz, D.M.; Mieno, T. The effect of soil-moisture uncertainty on irrigation water use and farm profits. Adv. Water Resour. 2021, 154, 103982. [Google Scholar] [CrossRef]
  130. Kelly, T.D.; Foster, T. AquaCrop-OSPy: Bridging the gap between research and practice in crop-water modeling. Agric. Water Manag. 2021, 254, 106976. [Google Scholar] [CrossRef]
Water 16 02545 g001
Figure 1. Flow chart of irrigation schedule optimization based on crop models.
Figure 1. Flow chart of irrigation schedule optimization based on crop models.
Water 16 02545 g001
Water 16 02545 g002
Figure 2. Flow chart of irrigation schedule optimization based on AquaCrop optimization algorithms.
Figure 2. Flow chart of irrigation schedule optimization based on AquaCrop optimization algorithms.
Water 16 02545 g002
Water 16 02545 g003
Figure 3. Flow chart of improved NSGA-II (Elitist Non-dominated Sorting Genetic Algorithm).
Figure 3. Flow chart of improved NSGA-II (Elitist Non-dominated Sorting Genetic Algorithm).
Water 16 02545 g003
Table 1. Comparison of model features for some commonly used models.
Table 1. Comparison of model features for some commonly used models.
Model NameDriving FactorsModulesCrop TypesApplication Aspects
AquaCropSoil waterMeteorological module, Crop module, Soil module (water), Management moduleMaize, wheat, barley, cotton, sunflower, potato, rice and other herbaceous crops, fruit trees, vinesBiomass and yield simulation [56]; Optimization of sowing dates [57]; Optimization of irrigation measures [57]; Climate change assessment [58]
SWAPSoil waterMeteorological module, Crop module, Soil module (water, solute, heat), Management moduleAnnual crops such as summer maize, winter wheat, spring barley, rice, soybean, sunflowerYield and biomass prediction [59]; Water and salt transport [59]; Remote-sensing assimilation [60]; irrigation optimization [61]
APSIMSoil saltMeteorological module, Crop module, Soil module (water balance, nitrogen cycle, surface organic matter, soil phosphorus), Management module, Animal module (cattle, sheep)Beans, maize, barley, wheat, rapeseed, cotton, rice, peanutBiomass and yield simulation [62]; Crop management; Climate change assessment [63]; Soil water and nitrogen processes [64,65]; The interaction between genes, management, and environment [66]
DSSATPhotosynthesisMeteorological module, Crop module, Soil module (water, organic matter, nitrogen cycle, inorganic nitrogen, phosphorus, potassium), Soil–crop–atmosphere module, Management moduleWheat, rice, maize, legumes, perennial plantsBiomass and yield prediction [67]; Irrigation, fertilization, and pesticide management [68]; Dynamic changes of carbon and nitrogen [68]; Climate risk assessment [69]
RZWQM2Soil water and saltMeteorological module, Crop module, Soil water module, Soil chemical processes, Nitrogen cycling module, Carbon cycling module, Insecticide module, Cultivation moduleMaize, wheat, soybean, potato, alfalfa, grass, treesCrop productivity assessment [70]; Optimization of irrigation and fertilization [19]; Dynamic monitoring of soil water and nitrogen [71]; Chemical simulation of insecticides [72]
Table 2. Main methods for solving simulation–optimization models for irrigation schedules.
Table 2. Main methods for solving simulation–optimization models for irrigation schedules.
Optimization MethodClassificationFeatures
Traditional mathematical programmingLinear programming [90], nonlinear programming [91], and dynamic programming [111]Simple calculation but has limitations when dealing with complex problems
Artificial intelligence searchGenetic algorithms [112], simulated annealing [113], particle swarm optimization [114], free search algorithm [115], and neural network [116]Fast computing speed, strong stability, adaptability, and robustness
Table 3. Problems and future prospects in optimization of irrigation schedules based on simulation–optimization models.
Table 3. Problems and future prospects in optimization of irrigation schedules based on simulation–optimization models.
Research ObjectsProblemsFuture Prospects
Simulation–optimization models
(1)
Only the AquaCrop model is widely used.
Other mechanism crop models should be combined with optimization algorithms.
(2)
The AquaCrop model has limitations, such as the relatively simple transport processes of soil water, salt, and nitrogen, and ignores the influence of soil heat.
(3)
Only focusing on the one-dimensional (1D) water movement process in the soil profile.
The promotion of drip irrigation technology underneath film has demonstrated the importance of quantifying the 2D/3D water movement process.
Optimization of irrigation schedules
(1)
The uncertainty of model parameters affects the accuracy of optimization results.
Based on intelligent optimization algorithms to calibrate model parameters, explore highly applicable calibration tools for intelligent optimization algorithm to improve model efficiency.
(2)
The uncertainty of the division of typical hydrological years and model upscaling simulation.
Seeking ways to reduce uncertainty in optimization.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhao, Y.; Li, G.; Li, S.; Luo, Y.; Bai, Y. A Review on the Optimization of Irrigation Schedules for Farmlands Based on a Simulation–Optimization Model. Water 2024, 16, 2545. https://doi.org/10.3390/w16172545

AMA Style

Zhao Y, Li G, Li S, Luo Y, Bai Y. A Review on the Optimization of Irrigation Schedules for Farmlands Based on a Simulation–Optimization Model. Water. 2024; 16(17):2545. https://doi.org/10.3390/w16172545

Chicago/Turabian Style

Zhao, Yin, Guoan Li, Sien Li, Yongkai Luo, and Yuting Bai. 2024. "A Review on the Optimization of Irrigation Schedules for Farmlands Based on a Simulation–Optimization Model" Water 16, no. 17: 2545. https://doi.org/10.3390/w16172545

APA Style

Zhao, Y., Li, G., Li, S., Luo, Y., & Bai, Y. (2024). A Review on the Optimization of Irrigation Schedules for Farmlands Based on a Simulation–Optimization Model. Water, 16(17), 2545. https://doi.org/10.3390/w16172545

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop