An Enhanced Horned Lizard Optimization Algorithm for Flood Control Operation of Cascade Reservoirs
Abstract
1. Introduction
- EHLOA demonstrates better robustness compared to widely used algorithms and highly cited algorithms from the past three years on both benchmark functions and the MRFCO problem.
- EHLOA exhibits superior convergence compared to widely used algorithms and highly cited algorithms from the past three years on both benchmark functions and the MRFCO problem.
- The flood control scheduling process provided by EHLOA is reasonable, making it a reliable algorithm for flood control operations.
2. Study Area and Flood Control Operation Model
2.1. Cascade Reservoirs and Flood Data
2.2. Flood Control Operation Model of Cascade Reservoirs
2.2.1. Objective Function of Flood Control Operation
2.2.2. Constraints of Flood Control Operation
- (1)
- Water balance constraint
- (2)
- Outflow constraint
- (3)
- Interval flow constraint
- (4)
- Reservoir storage capacity constraint
- (5)
- Initial condition constraint
- (6)
- Non-negative constraint
3. HLOA Algorithm
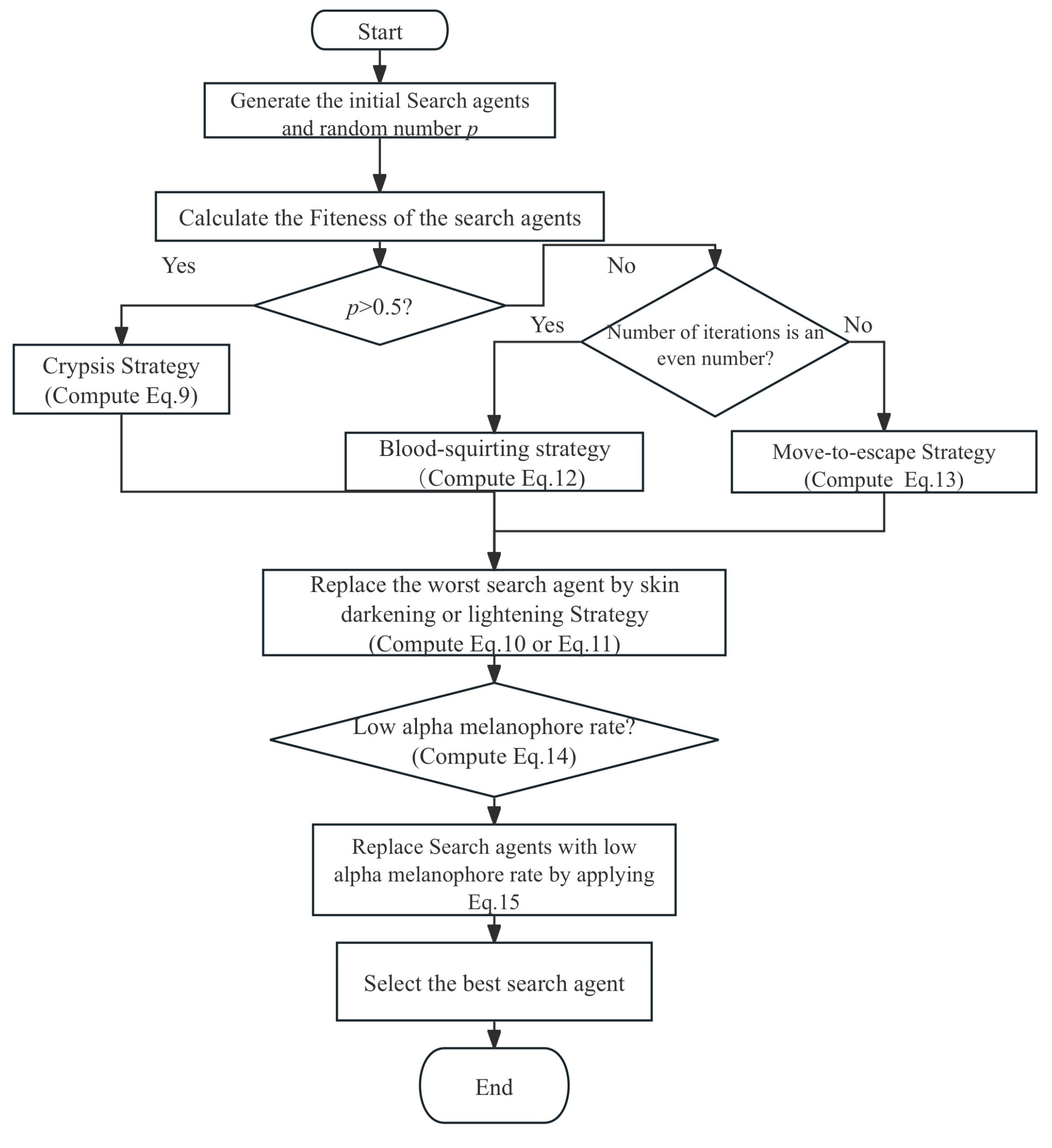
3.1. Basic HLOA Algorithm
3.1.1. Crypsis Behavior
3.1.2. Skin Darkening or Lightening
3.1.3. Blood-Squirting
3.1.4. Move-to-Escape
3.1.5. Alpha Melanophore Stimulating Hormone (α-MSH) Rate
3.2. Enhanced HLOA Algorithm
3.2.1. Circle Map Initialization
3.2.2. Trap Escaping Operator (TEO)
3.2.3. Sudden Attack Model
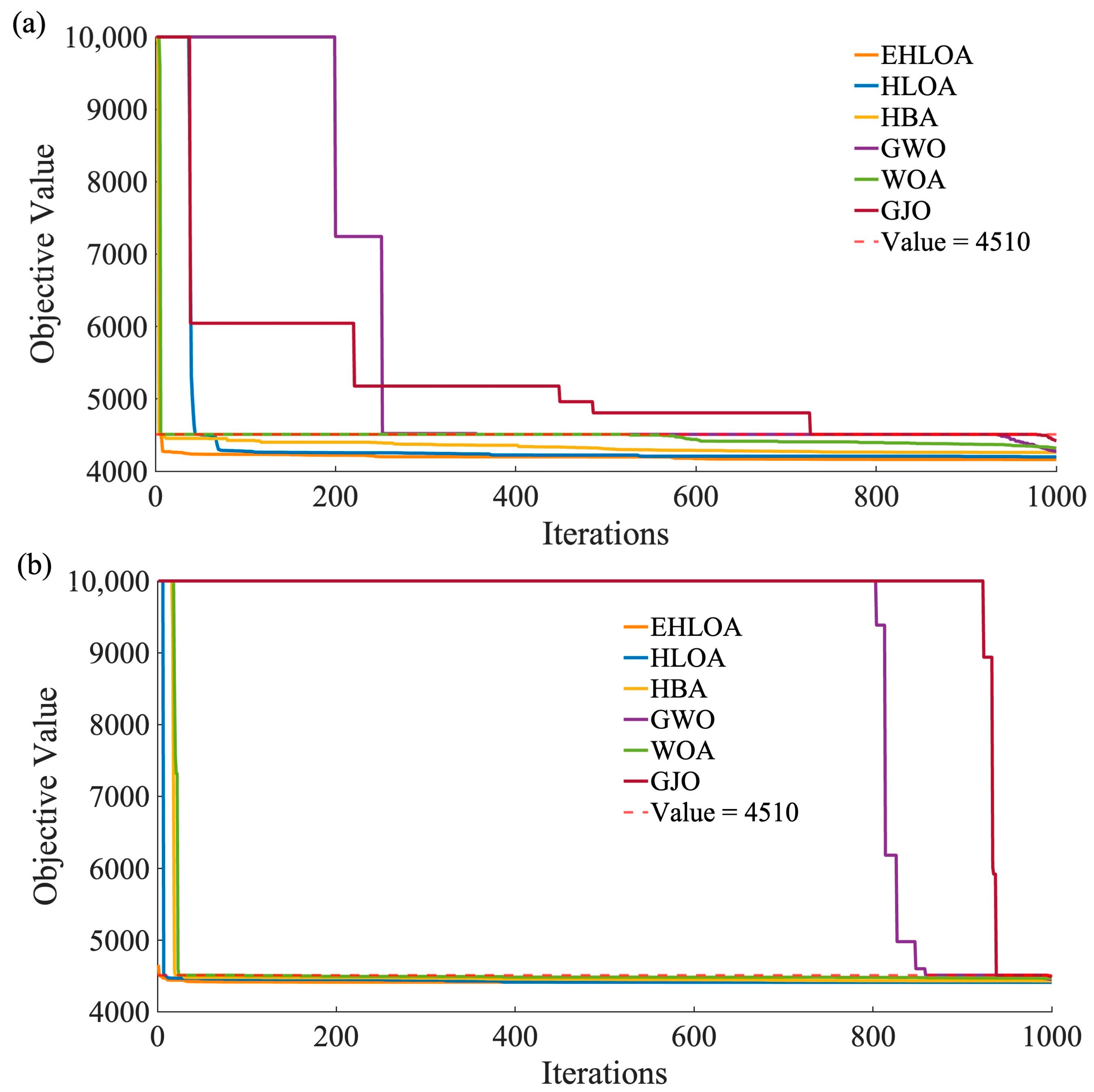
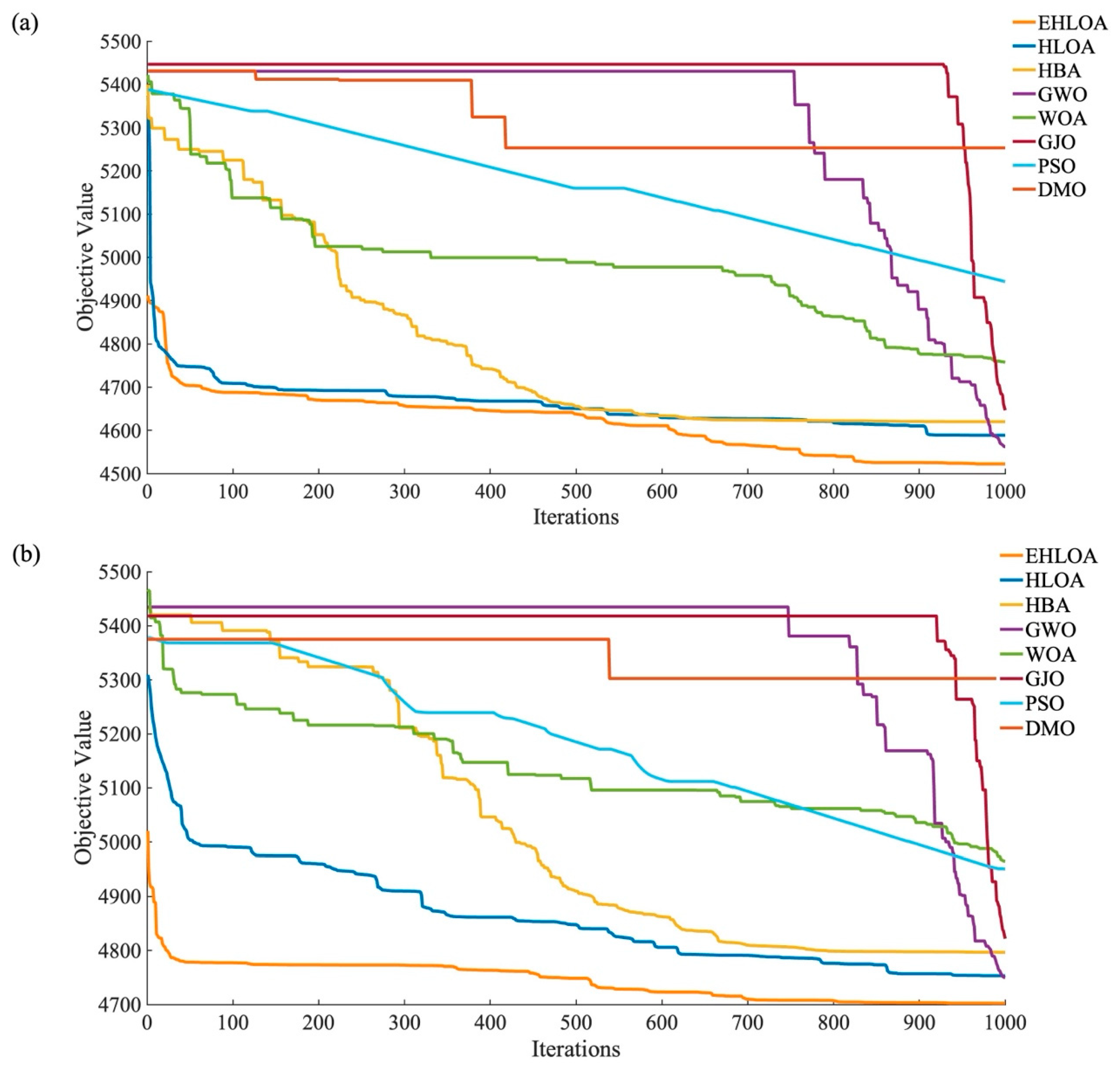
4. Experiments and Results
4.1. Experiments 1: In Benchmark Functions
4.2. Experiment 2: In the Flood Control Operation Model
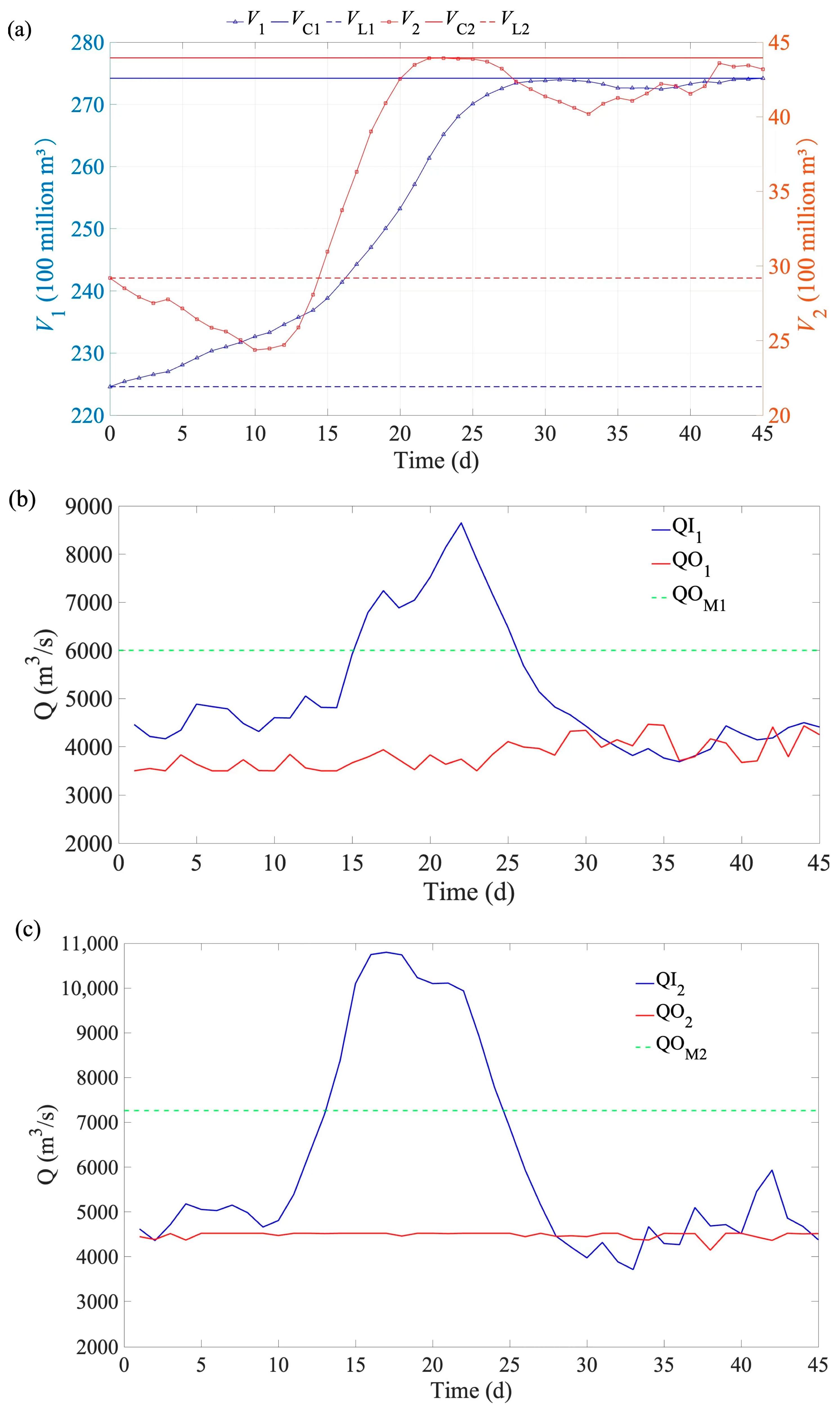
4.3. Analysis of the Flood Control Operation Process Obtained by EHLOA
5. Discussion
5.1. Robustness and Scalability of EHLOA
5.2. Reliability of EHLOA in a Multi-Reservoir Flood Control Operation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Name | Type |
| EHLOA | Enhanced Horned Lizard Optimization Algorithm | Algorithm |
| HLOA | Horned Lizard Optimization Algorithm | Algorithm |
| GWO | Grey Wolf Optimizer | Algorithm |
| WOA | Whale optimization algorithm | Algorithm |
| PSO | Particle swarm optimization | Algorithm |
| HBA | Honey badger algorithm | Algorithm |
| GJO | Golden jackal optimization algorithm | Algorithm |
| DMO | Dwarf mongoose optimization algorithm | Algorithm |
| LYX | Longyangxia | Reservoir |
| LJX | Liujiaxia | Reservoir |
Appendix A
| Fun | Dimension | Range | Theoretical Optimization Value |
|---|---|---|---|
| 30/100 | [−100, 100] | 0 | |
| 30/100 | [−10, 10] | 0 | |
| 30/100 | [−100, 100] | 0 | |
| 30/100 | [−100, 100] | 0 | |
| 30/100 | [−30, 30] | 0 | |
| 30/100 | [−100, 100] | 0 | |
| 30/100 | [−1.28, 1.28] | 0 | |
| 30/100 | [−500, 500] | 418.9829 × Dimension | |
| 30/100 | [−5.12, 5.12] | 0 | |
| 30/100 | [−32, 32] | 0 | |
| 30/100 | [−600, 600] | 0 | |
| 30/100 | [−50, 50] | 0 | |
| 30/100 | [−50, 50] | 0 |
| Fun. | Index | EHLOA | HLOA | GWO | WOA | PSO | HBA | GJO | DMO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Min | 0 | 0 | 2.85 × 10−61 | 7.49 × 10−167 | 3.25 × 10−6 | 5.06 × 10−288 | 4.08 × 10−117 | 1.02 × 10−4 |
| Mean | 0 | 0 | 7.68 × 10−59 | 1.48 × 10−148 | 4.50 × 10−5 | 1.33 × 10−276 | 1.25 × 10−110 | 4.35 × 10−4 | |
| Std | 0 | 0 | 2.25 × 10−58 | 7.39 × 10−148 | 6.73 × 10−5 | 0 | 6.81 × 10−110 | 3.35 × 10−4 | |
| F2 | Min | 0 | 8.99 × 10−264 | 1.58 × 10−35 | 9.65 × 10−115 | 8.69 × 10−5 | 8.21 × 10−152 | 2.99 × 10−68 | 3.21 × 10−4 |
| Mean | 0 | 1.06 × 10−243 | 1.16 × 10−34 | 2.79 × 10−100 | 0.33 | 1.06 × 10−146 | 2.20 × 10−66 | 7.69 × 10−3 | |
| Std | 0 | 0 | 9.46 × 10−35 | 1.53 × 10−99 | 1.83 | 2.68 × 10−146 | 3.49 × 10−66 | 1.28 × 10−2 | |
| F3 | Min | 0 | 0 | 3.92 × 10−20 | 2.29 × 103 | 1.76 × 102 | 4.71 × 10−218 | 1.34 × 10−49 | 1.81 × 104 |
| Mean | 0 | 0 | 7.19 × 10−14 | 2.04 × 104 | 8.11 × 102 | 4.01 × 10−200 | 5.9 × 10−38 | 5.14 × 104 | |
| Std | 0 | 0 | 3.73 × 10−13 | 1.06 × 104 | 1.29 × 103 | 0 | 2.47 × 10−37 | 1.45 × 104 | |
| F4 | Min | 0 | 3.62 × 10−255 | 1.05 × 10−15 | 7.7 × 10−1 | 2.47 | 6.05 × 10−124 | 1.66 × 10−36 | 3.54 × 102 |
| Mean | 0 | 2.71 × 10−239 | 2.03 × 10−14 | 3.50 × 101 | 4.55 | 5.23 × 10−117 | 5.88 × 10−33 | 4.54 × 102 | |
| Std | 0 | 0 | 3.68 × 10−14 | 2.93 × 101 | 9.6 × 101 | 2.12 × 10−116 | 2.08 × 10−32 | 4.82 | |
| F5 | Min | 2.95 × 10−12 | 4.13 × 10−4 | 2.62 × 101 | 2.69 × 101 | 2.02 × 101 | 2.11 × 101 | 2.62 × 101 | 3.57 × 102 |
| Mean | 4.25 × 10−2 | 2.2 × 101 | 2.71 × 101 | 2.73 × 101 | 1.83 × 102 | 2.18 × 101 | 2.75 × 101 | 2.43 × 103 | |
| Std | 2 × 10−2 | 1.23 × 101 | 7.62 × 10−1 | 6.28 × 10−1 | 5.42 × 102 | 4.56 × 10−1 | 7.43 × 10−1 | 2.24 × 103 | |
| F6 | Min | 3.13 × 10−11 | 5.89 × 10−6 | 1.64 × 10−5 | 1.04 × 10−2 | 4.07 × 10−6 | 2.62 × 10−9 | 1.5 | 9.28 × 10−5 |
| Mean | 1.95 × 10−5 | 1.72 × 10−4 | 5.24 × 10−1 | 1.09 × 10−1 | 6.39 × 10−5 | 1.97 × 10−8 | 2.75 | 4.93 × 10−4 | |
| Std | 2.55 × 10−5 | 1.91 × 10−4 | 2.89 × 10−1 | 1.18 × 10−1 | 9.14 × 10−5 | 1.06 × 10−7 | 4.71 × 10−1 | 2.99 × 10−4 | |
| F7 | Min | 1.54 × 10−6 | 3.44 × 10−6 | 2.05 × 10−4 | 4.28 × 10−5 | 9.03 × 10−3 | 3.71 × 10−5 | 4.99 × 10−5 | 5.1 × 10−2 |
| Mean | 4.70 × 10−5 | 1.53 × 10−4 | 9.20 × 10−4 | 1.36 × 10−3 | 2.41 × 10−2 | 1.65 × 10−3 | 1.89 × 10−5 | 8.25 × 10−2 | |
| Std | 3.94 × 10−5 | 1.48 × 10−4 | 4.43 × 10−4 | 1.52 × 10−3 | 7.63 × 10−3 | 1.02 × 10−4 | 1.31 × 10−4 | 1.74 × 10−2 | |
| F8 | Min | −12,569.487 | −10,417.75 | −7318.73 | −12,569.486 | −8897.80 | −10,291.76 | −6410.95 | infinity |
| Mean | −11,525.40 | −7412.19 | −6039.21 | −11,330.87 | −7793.66 | −8865.33 | −3928.43 | infinity | |
| Std | 1548.62 | 995.25 | 718.53 | 1633.55 | 539.36 | 952.32 | 1053.01 | infinity | |
| F9 | Min | 0 | 0 | 0 | 0 | 2.36 × 101 | 0 | 0 | 1.25 × 102 |
| Mean | 0 | 0 | 8.1 × 10−1 | 0 | 4.38 × 101 | 0 | 0 | 2.02 × 102 | |
| Std | 0 | 0 | 2.13 | 0 | 1.67 × 101 | 0 | 0 | 2.56 × 101 | |
| F10 | Min | 4.4 × 10−16 | 4.4 × 10−16 | 7.55 × 10−15 | 4.4 × 10−16 | 3.1 × 10−4 | 4.4 × 10−16 | 3.99 × 10−15 | 5.91 × 10−3 |
| Mean | 4.4 × 10−16 | 4.4 × 10−16 | 1.59 × 10−14 | 4.1 × 10−15 | 8.1 × 10−3 | 4.4 × 10−16 | 4.47 × 10−15 | 1.53 × 10−2 | |
| Std | 0 | 0 | 3.02 × 10−15 | 2.37 × 10−15 | 1.86 × 10−2 | 0 | 1.23 × 10−15 | 1.63 × 10−2 | |
| F11 | Min | 0 | 0 | 0 | 0 | 8.05 × 10−6 | 0 | 0 | 1.49 × 10−3 |
| Mean | 0 | 0 | 1.38 × 10−3 | 0 | 1.85 × 10−2 | 0 | 0 | 5.98 × 10−2 | |
| Std | 0 | 0 | 4.55 × 10−3 | 0 | 8.08 × 10−3 | 0 | 0 | 1.1 × 10−1 | |
| F12 | Min | 1.98 × 10−9 | 9.66 × 10−8 | 9.14 × 10−3 | 6.33 × 10−4 | 7.28 × 10−8 | 4.55 × 10−10 | 7.84 × 10−2 | 6.21 |
| Mean | 1.69 × 10−6 | 6.92 × 10−3 | 4.24 × 10−2 | 6.08 × 10−3 | 6.22 × 10−2 | 1.66 × 10−8 | 2.63 × 10−1 | 1.53 × 101 | |
| Std | 2.16 × 10−6 | 2.6 × 10−2 | 2.56 × 10−2 | 5.29 × 10−3 | 1.03 × 10−1 | 3.97 × 10−8 | 1.79 × 10−1 | 5.03 | |
| F13 | Min | 4.49 × 10−8 | 6.04 × 10−7 | 1.00 × 10−1 | 3.83 × 10−2 | 2.63 × 10−6 | 1.12 × 10−7 | 1.20 | 9.91 |
| Mean | 1.73 × 10−2 | 1.18 × 10−1 | 5.34 × 10−1 | 2.44 × 10−1 | 3.49 × 10−3 | 1.51 × 10−1 | 1.61 | 2.86 × 101 | |
| Std | 6.55 × 10−2 | 3.81 × 10−1 | 2.10 × 10−1 | 1.50 × 10−1 | 5.06 × 10−3 | 1.85 × 10−1 | 2.41 × 10−1 | 3.37 × 101 |
| Fun. | Index | EHLOA | HLOA | GWO | WOA | PSO | HBA | GJO | DMO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Min | 0 | 0 | 1.58 × 10−30 | 1.17 × 10−166 | 1.60 × 102 | 5.26 × 10−262 | 4.55 × 10−62 | 1.97 × 105 |
| Mean | 0 | 0 | 2.63 × 10−29 | 1.05 × 10−148 | 6.46 × 102 | 7.56 × 10−248 | 5.52 × 10−60 | 2.51 × 105 | |
| Std | 0 | 0 | 4.42 × 10−29 | 5.75 × 10−148 | 1.83 × 103 | 0 | 1.19 × 10−59 | 2.27 × 105 | |
| F2 | Min | 0 | 8.25 × 10−259 | 2.19 × 10−18 | 8.62 × 10−113 | 6.06 | 8.56 × 10−138 | 5.51 × 10−38 | 1.62 × 1016 |
| Mean | 0 | 2.36 × 10−239 | 6.54 × 10−18 | 3.83 × 10−103 | 2.08 × 101 | 6.82 × 10−132 | 4.71 × 10−37 | 7.98 × 1034 | |
| Std | 0 | 0 | 3.04 × 10−18 | 1.99 × 10−102 | 1.20 × 101 | 3.41 × 10−131 | 1.65 × 10−36 | 2.96 × 1035 | |
| F3 | Min | 0 | 0 | 2.00 × 10−2 | 5.44 × 106 | 4.34 × 104 | 1.57 × 10−186 | 3.85 × 10−19 | 7.15 × 105 |
| Mean | 0 | 0 | 9.95 | 8.87 × 106 | 6.45 × 104 | 4.02 × 10−165 | 2.00 × 10−4 | 1.06 × 106 | |
| Std | 0 | 0 | 1.92 × 101 | 1.58 × 106 | 1.30 × 104 | 0 | 6.00 × 10−3 | 2.23 × 105 | |
| F4 | Min | 0 | 3.40 × 10−256 | 3.87 × 10−5 | 1.79 × 101 | 2.60 × 101 | 9.63 × 10−89 | 6.92 × 10−13 | 9.27 × 101 |
| Mean | 0 | 5.82 × 10−241 | 1.00 × 10−2 | 7.67 × 101 | 3.34 × 101 | 7.27 × 10−83 | 1.53 | 9.53 × 101 | |
| Std | 0 | 0 | 4.00 × 10−2 | 2.26 × 101 | 3.09 | 2.18 × 10−82 | 5.20 | 1.04 | |
| F5 | Min | 9.09 × 10−11 | 4.13 × 10−4 | 9.59 × 101 | 9.67 × 101 | 1.61 × 104 | 9.24 × 101 | 9.62 × 102 | 9.64 × 108 |
| Mean | 8.59 × 10−4 | 2.20 × 101 | 9.77 × 101 | 9.77 × 101 | 5.59 × 104 | 9.57 × 101 | 9.82 × 101 | 1.12 × 109 | |
| Std | 2.58 × 10−3 | 1.23 × 101 | 8.00 × 10−1 | 4.40 × 10−1 | 3.23 × 104 | 1.99 | 6.02 × 10−1 | 8.29 × 107 | |
| F6 | Min | 2.91 × 10−10 | 5.89 × 10−6 | 6.74 | 9.10 × 10−1 | 1.23 × 102 | 2.24 | 1.55 × 101 | 1.99 × 105 |
| Mean | 9.21 × 10−5 | 1.72 × 10−4 | 9.11 | 2.13 | 6.74 × 102 | 4.16 | 1.68 × 101 | 2.43 × 106 | |
| Std | 1.15 × 10−5 | 1.91 × 10−4 | 1.02 | 9.51 × 10−1 | 1.83 × 103 | 8.41 × 10−1 | 8.36 × 10−1 | 2.11 × 105 | |
| F7 | Min | 1.34 × 10−6 | 3.44 × 10−6 | 1.14 × 10−3 | 6.55 × 10−5 | 5.33 × 10−1 | 2.44 × 10−5 | 5.31 × 10−5 | 1.06 × 103 |
| Mean | 9.21 × 10−5 | 1.53 × 10−4 | 2.43 × 10−3 | 1.31 × 10−3 | 8.10 × 10−1 | 2.68 × 10−4 | 5.98 × 10−4 | 1.77 × 103 | |
| Std | 1.15 × 10−5 | 1.48 × 10−4 | 1.21 × 10−3 | 1.53 × 10−3 | 1.70 × 10−1 | 2.92 × 10−4 | 4.33 × 10−4 | 2.08 × 102 | |
| F8 | Min | −41,898.29 | −25,513.15 | −20,216.25 | −41,897.14 | −25,484.57 | −28,539.74 | −16,502.35 | Inf |
| Mean | −37,887.25 | −22,227.35 | −15,699.06 | −37,799.01 | −21,852.99 | −24,870.91 | −9351.13 | Inf | |
| Std | 5381.91 | 1793.71 | 3511.17 | 5440.29 | 1453.26 | 3297.17 | 3940.74 | Inf | |
| F9 | Min | 0 | 0 | 2.27 × 10−13 | 0 | 2.09 × 102 | 0. | 0 | 1.45 × 103 |
| Mean | 0 | 0 | 3.71 × 10−1 | 3.78 × 10−15 | 2.94 × 102 | 0 | 0 | 1.57 × 103 | |
| Std | 0 | 0 | 1.12 | 2.07 × 10−14 | 3.97 × 101 | 0 | 0 | 5.36 × 101 | |
| F10 | Min | 4.44 × 10−16 | 4.44 × 10−16 | 9.99 × 10−14 | 4.44 × 10−16 | 3.58 | 4.44 × 10−16 | 7.55 × 10−15 | 2.05 × 102 |
| Mean | 4.44 × 10−16 | 4.44 × 10−16 | 1.13 × 10−13 | 3.28 × 10−15 | 4.81 | 2.66 | 9.44 × 10−15 | 2.08 × 102 | |
| Std | 0 | 0 | 1.10 × 10−14 | 2.36 × 10−15 | 1.28 | 6.89 | 2.91 × 10−15 | 9.45 × 10−2 | |
| F11 | Min | 0 | 0 | 0 | 0 | 2.47 | 0 | 0 | 1.91 × 103 |
| Mean | 0 | 0 | 2.8 × 10−3 | 0 | 6.47 | 0 | 0 | 2.24 × 103 | |
| Std | 0 | 0 | 8.6 × 10−3 | 0 | 1.65 | 0 | 0 | 1.53 × 102 | |
| F12 | Min | 1.33 × 10−13 | 9.66 × 10−8 | 1.38 × 10−1 | 7.23 × 10−3 | 1.96 × 101 | 2.59 × 10−2 | 4.71 × 10−1 | 1.76 × 109 |
| Mean | 5.43 × 10−7 | 1.04 × 10−3 | 2.55 × 10−1 | 1.68 × 10−2 | 9.66 × 101 | 4.52 × 10−2 | 6.19 × 10−1 | 2.71 × 109 | |
| Std | 6.12 × 10−7 | 5.68 × 10−3 | 7.55 × 10−2 | 6.3 × 10−3 | 2.25 × 102 | 1.45 × 10−2 | 7.49 × 10−2 | 3.07 × 108 | |
| F13 | Min | 2.49 × 10−9 | 1.28 × 10−5 | 5.58 | 7.62 × 10−1 | 6.23 × 102 | 5.77 | 7.88 | 3.89 × 109 |
| Mean | 7.60 × 10−3 | 9.41 × 10−3 | 6.29 | 1.97 | 7.32 × 103 | 7.41 | 8.46 | 4.93 × 109 | |
| Std | 4.06 × 10−2 | 2.61 × 10−2 | 3.38 × 10−1 | 7.41 × 10−1 | 7.50 × 103 | 7.95 × 10−1 | 2.95 × 10−1 | 3.96 × 109 |
| Fun. | Index | HLOA | GWO | WOA | PSO | HBA | GJO | DMO |
|---|---|---|---|---|---|---|---|---|
| F1 | p-value | 1 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | = | + | + | + | + | + | + | |
| F2 | p-value | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F3 | p-value | 1 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | = | + | + | + | + | + | + | |
| F4 | p-value | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F5 | p-value | 1.74 × 10−4 | 4.86 × 10−5 | 4.86 × 10−5 | 2.35 × 10−6 | 5.31 × 10−5 | 2.35 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F6 | p-value | 2.16 × 10−5 | 1.73 × 10−6 | 1.73 × 10−6 | 1.04 × 10−3 | 1.92 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | − | + | + | |
| F7 | p-value | 5.31 × 10−5 | 1.73 × 10−6 | 2.13 × 10−6 | 1.73 × 10−6 | 3.18 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F8 | p-value | 1.73 × 10−6 | 1.73 × 10−6 | 1 | 1.73 × 10−6 | 6.64 × 10−4 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | = | + | + | + | + | |
| F9 | p-value | 1 | 3.13 × 10−2 | 1 | 1.73 × 10−6 | 1 | 1 | 1.73 × 10−6 |
| +/=/− | = | + | = | + | = | = | + | |
| F10 | p-value | 1 | 1.73 × 10−6 | 7.12 × 10−6 | 1.73 × 10−6 | 1 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | = | + | + | + | = | + | + | |
| F11 | p-value | 1 | 0.25 | 1 | 1.73 × 10−6 | 1 | 1 | 1.73 × 10−6 |
| +/=/− | = | = | = | + | = | = | + | |
| F12 | p-value | 8.31 × 10−4 | 1.73 × 10−6 | 1.73 × 10−6 | 9.32 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | − | + | + | |
| F13 | p-value | 1.25 × 10−2 | 1.73 × 10−6 | 6.98 × 10−6 | 0.32 | 2.22 × 10−4 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | = | + | + | + | |
| Total | (+/=/−) | 8/5/0 | 12/1/0 | 10/3/0 | 12/1/0 | 8/3/2 | 10/3/0 | 13/0/0 |
| Fun. | Index | HLOA | GWO | WOA | PSO | HBA | GJO | DMO |
|---|---|---|---|---|---|---|---|---|
| F1 | p-value | 1 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | = | + | + | + | + | + | + | |
| F2 | p-value | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F3 | p-value | 1 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | = | + | + | + | + | + | + | |
| F4 | p-value | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F5 | p-value | 2.35 × 10−6 | 1.73 × 10−6 | 4.86 × 10−5 | 2.35 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F6 | p-value | 4.45 × 10−5 | 1.73 × 10−6 | 1.73 × 10−6 | 1.04 × 10−3 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F7 | p-value | 2.11 × 10−3 | 1.73 × 10−6 | 2.13 × 10−6 | 1.73 × 10−6 | 4.45 × 10−5 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F8 | p-value | 1.73 × 10−6 | 1.73 × 10−6 | 1 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | = | + | + | + | + | |
| F9 | p-value | 1 | 1.48 × 10−6 | 1 | 1.73 × 10−6 | 1 | 1 | 1.73 × 10−6 |
| +/=/− | = | + | = | + | = | = | + | |
| F10 | p-value | 1 | 1.61 × 10−6 | 2.93 × 10−5 | 1.73 × 10−6 | 0.12 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | = | + | + | + | = | + | + | |
| F11 | p-value | 1 | 0.25 | 1 | 1.73 × 10−6 | 1 | 1 | 1.73 × 10−6 |
| +/=/− | = | = | = | + | = | = | + | |
| F12 | p-value | 2.35 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| F13 | p-value | 1.39 × 10−2 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 | 1.73 × 10−6 |
| +/=/− | + | + | + | + | + | + | + | |
| Total | (+/=/−) | 8/5/0 | 12/1/0 | 10/3/0 | 13/0/0 | 10/3/0 | 10/2/0 | 13/0/0 |
Appendix B

References
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Xu, H.; Wang, H.; Yu, Y.; Duan, Y.; Chen, L. Quantitative attribution of historical anthropogenic warming on the extreme rainfall event over Henan in July 2021. Environ. Res. Lett. 2023, 18, 104037. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J. Significant increase of the global population exposure to increased precipitation extremes in the future. Earth’s Future 2021, 9, e2020EF001941. [Google Scholar] [CrossRef]
- Sung, J.H.; Eum, H.I.; Park, J.; Cho, J. Assessment of climate change impacts on extreme precipitation events: Applications of CMIP5 climate projections statistically downscaled over South Korea. Adv. Meteorol. 2018, 2018, 4720523. [Google Scholar] [CrossRef]
- Tew, Y.L.; Tan, M.L.; Juneng, L.; Chun, K.P.; bin Hassan, M.H.; bin Osman, S.; Samat, N.; Chang, C.K.; Kabir, M.H. Rapid extreme tropical precipitation and flood inundation mapping framework (RETRACE): Initial testing for the 2021–2022 Malaysia flood. ISPRS Int. J. Geo-Inf. 2022, 11, 378. [Google Scholar] [CrossRef]
- Manandhar, B.; Cui, S.; Wang, L.; Shrestha, S. Post-flood resilience assessment of July 2021 flood in western Germany and Henan, China. Land 2023, 12, 625. [Google Scholar] [CrossRef]
- Nanditha, J.S.; Kushwaha, A.P.; Singh, R.; Malik, I.; Solanki, H.; Chuphal, D.S.; Dangar, S.; Mahto, S.S.; Vegad, U.; Mishra, V. The Pakistan flood of August 2022 causes and implications. Earth’s Future 2023, 11, e2022EF003230. [Google Scholar] [CrossRef]
- Karbowski, A. Optimal control of single retention reservoir during flood: Solution of deterministic, continuous-time problems. J. Optim. Theory Appl. 1991, 69, 55–81. [Google Scholar] [CrossRef]
- Zha, G.; Zhou, J.; Yang, X.; Fang, W.; Dai, L.; Wang, Q.; Ding, X. Modeling and solving of joint flood control operation of large-scale reservoirs: A case study in the Middle and Upper Yangtze River in China. Water 2021, 13, 41. [Google Scholar] [CrossRef]
- Jing, Z.; Zhang, R.; Bao, H.; Zhang, S. Joint flood control scheduling strategy of large cascade reservoirs: A case study of the cascade reservoirs in the upper reaches of the Yangtze River in China. J. Flood Risk Manag. 2022, 15, e12802. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.A.; Liu, W.; Wan, X.Y.; Yeh, W.W.G. A multi-objective risk management model for real-time flood control optimal operation of a parallel reservoir system. J. Hydrol. 2020, 590, 125264. [Google Scholar] [CrossRef]
- Tao, Y.; Mo, L.; Yang, Y.; Liu, Z.; Liu, Y.; Liu, T. Optimization of Cascade Reservoir Operation for Power Generation, Based on an Improved Lightning Search Algorithm. Water 2023, 15, 3417. [Google Scholar] [CrossRef]
- Diao, Y.; Ma, H.; Wang, H.; Wang, J.; Li, S.; Li, X.; Pan, J.; Qiu, Q. Optimal flood-control operation of cascade reservoirs using an improved particle swarm optimization algorithm. Water 2022, 14, 1239. [Google Scholar] [CrossRef]
- He, J.; Guo, W.; Wang, S.; Chen, H.; Guo, X.; Li, S. Application of Multi-Strategy Based Improved DBO Algorithm in Optimal Operation of Reservoir Groups. Water Resour. Manag. 2024, 38, 1883–1901. [Google Scholar] [CrossRef]
- Zhu, D.; Chen, H.; Zhou, Y.; Mei, Y.; Xu, X.; Guo, S. A triple-stage operation method for deriving operation rules for cascade reservoirs during catastrophic flood events. Water Resour. Manag. 2022, 36, 4863–4883. [Google Scholar] [CrossRef]
- Zhu, D.; Mei, Y.; Xu, X.; Liu, Z.; Wu, Z.; Cai, H. Optimal operation of a parallel multireservoir system for flood control using a stagewise compensation method. Water Resour. Manag. 2021, 35, 1689–1710. [Google Scholar] [CrossRef]
- Mahdavi, S.; Shiri, M.E.; Rahnamayan, S. Metaheuristics in large-scale global continues optimization: A survey. Inf. Sci. 2015, 295, 407–428. [Google Scholar] [CrossRef]
- Wang, W.; Tian, W.; Chau, K.; Zang, H.; Ma, M.; Feng, Z.; Xu, D. Multi-reservoir flood control operation using improved bald eagle search algorithm with ε constraint method. Water 2023, 15, 692. [Google Scholar] [CrossRef]
- Lai, V.; Huang, Y.F.; Koo, C.H.; Ahmed, A.N.; El-Shafie, A. A review of reservoir operation optimisations: From traditional models to metaheuristic algorithms. Arch. Comput. Methods Eng. 2022, 29, 3435–3457. [Google Scholar] [CrossRef]
- Hellwig, M.; Beyer, H.G. A modified matrix adaptation evolution strategy with restarts for constrained real-world problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Fan, Z.; Fang, Y.; Li, W.; Yuan, Y.; Wang, Z.; Bian, X. LSHADE44 with an improved ε constraint-handling method for solving constrained single-objective optimization problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Sun, J.; Garibaldi, J.M. A novel memetic algorithm for constrained optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Basharu, M.; Arana, I.; Ahriz, H. Escaping local optima: Constraint weights vs. value penalties. In Proceedings of the International Conference on Innovative Techniques and Applications of Artificial Intelligence, Cambridge, UK, 10–12 December 2007; Springer: London, UK, 2007; pp. 51–64. [Google Scholar]
- Çınar, A.; Kıran, M. The performance of penalty methods on tree-seed algorithm for numerical constrained optimization problems. Int. Arab J. Inf. Technol. 2020, 17, 799–807. [Google Scholar] [CrossRef]
- Sefa AR, A.S.; Kahraman, H.T.; Gedikli, E. Determination of the effects of penalty coefficient on the meta-heuristic optimization process. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–6. [Google Scholar]
- Peraza-Vázquez, H.; Peña-Delgado, A.; Merino-Treviño, M.; Morales-Cepeda, A.B.; Sinha, N. A novel metaheuristic inspired by horned lizard defense tactics. Artif. Intell. Rev. 2024, 57, 59. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; Technical, Report; National University of Defense Technology: Changsha, China; Kyungpook National University: Daegu, Republic of Korea; Nanyang Technological University: Singapore, 2017. [Google Scholar]
- Atali, G.; PehlIvan, İ.; Gürevin, B.; Şeker, H.İ. Chaos in metaheuristic based artificial intelligence algorithms: A short review. Turk. J. Electr. Eng. Comput. Sci. 2021, 29, 1354–1367. [Google Scholar] [CrossRef]
- Ouertani, M.W.; Manita, G.; Korbaa, O. Chaotic lightning search algorithm. Soft Comput. 2021, 25, 2039–2055. [Google Scholar] [CrossRef]
- Akyol, S.; Yildirim, M.; Alatas, B. CIDO: Chaotically initialized dandelion optimization for global optimization. Int. J. Adv. Netw. Appl. 2023, 14, 5696–5704. [Google Scholar] [CrossRef]
- Gezici, H.; Livatyalı, H. Chaotic Harris hawks optimization algorithm. J. Comput. Des. Eng. 2022, 9, 216–245. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, Y.; Li, H.; Yang, H.; Zhang, B.; Gao, S. Chaotic Mapping Genetic Algorithm with Multiple Strategies. In Proceedings of the 2023 15th International Conference on Advanced Computational Intelligence (ICACI), Seoul, Republic of Korea, 6–9 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–4. [Google Scholar]
- Yang, D.; Liu, Z.; Yi, P. Computational efficiency of accelerated particle swarm optimization combined with different chaotic maps for global optimization. Neural Comput. Appl. 2017, 28, 1245–1264. [Google Scholar] [CrossRef]
- Sowmya, R.; Premkumar, M.; Jangir, P. Newton-Raphson-based optimizer: A new population-based metaheuristic algorithm for continuous optimization problems. Eng. Appl. Artif. Intell. 2024, 128, 107532. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Dwarf mongoose optimization algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization; KanGAL report, 2005005; Nanyang Technological University: Singapore, 2005. [Google Scholar]
- Woolson, R.F. Wilcoxon signed-rank test. Encycl. Biostat. 2005, 8. [Google Scholar] [CrossRef]
- Li, H.; Zhu, X.; Li, M.; Yang, Z.; Wen, M. Multi-threshold image segmentation research based on improved enhanced arithmetic optimization algorithm. Signal Image Video Process. 2024, 18, 4045–4058. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Liu, S. Cooperation search algorithm: A novel metaheuristic evolutionary intelligence algorithm for numerical optimization and engineering optimization problems. Appl. Soft Comput. 2021, 98, 106734. [Google Scholar] [CrossRef]
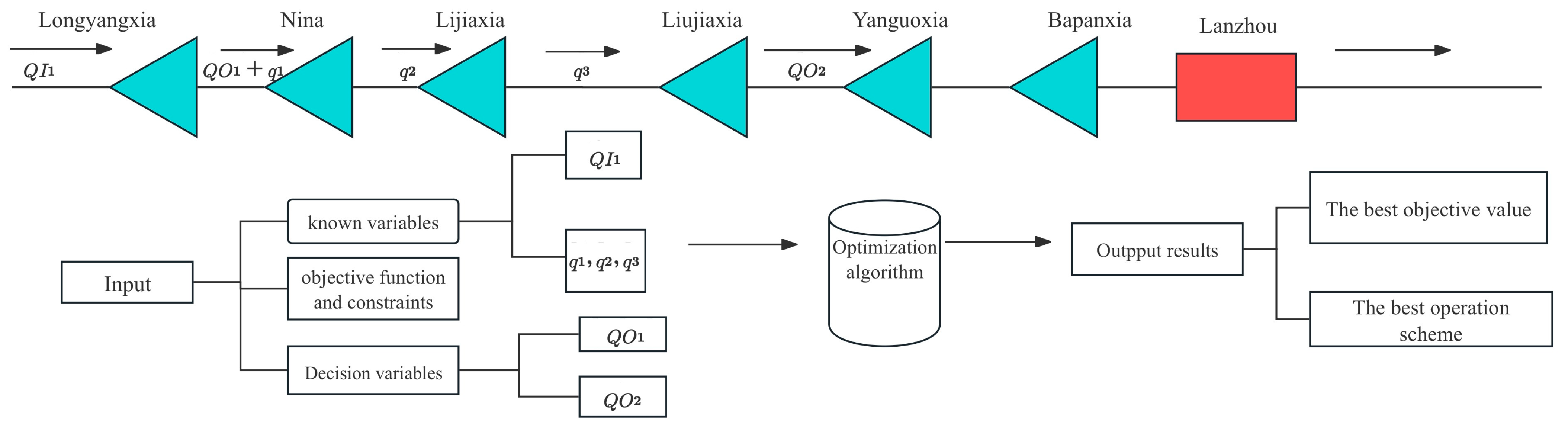
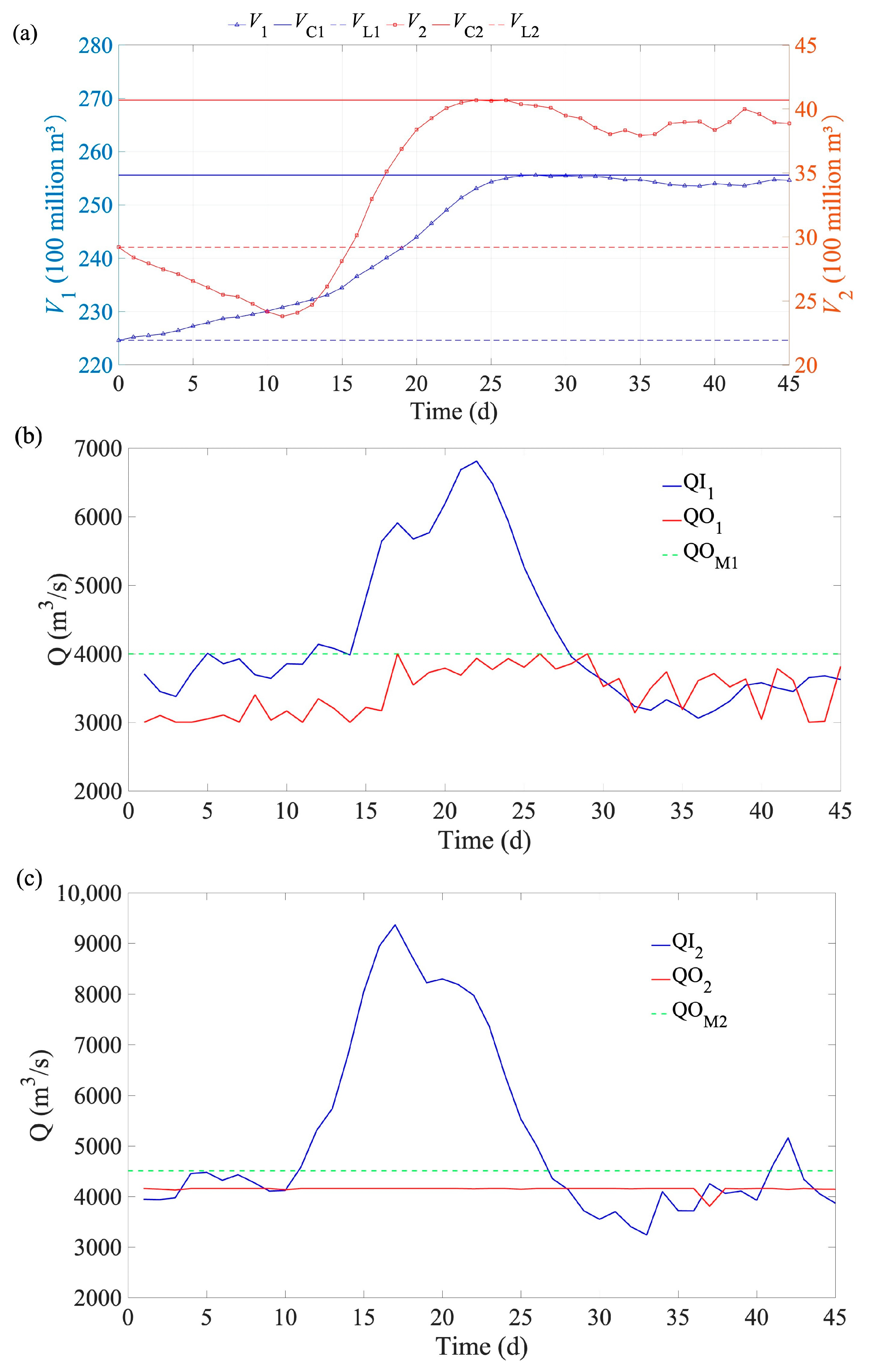

| Reservoir | VL (Billion m3) | VD (Billion m3) | VC (Billion m3) | QOM,0.1% (m3/s) | QOM,0.01% (m3/s) |
|---|---|---|---|---|---|
| LYX | 22.46 | 25.56 | 27.42 | 4000 | 6000 |
| LJX | 2.92 | 4.07 | 4.395 | 4510 | 7290 |
| Pseudo code of enhanced Horned Lizard Optimization Algorithm |
| 1: Initialize random variables such as p. Specify the number of search agents, Population Size, and Maximum number of iterations. |
| 2: Generate the initial population by Equation (16) |
| 3: While (t < max number of iterations) |
| 4: for each search agent |
| 5: if t/25 = 1,2…, n? then |
| 6: compute sudden attack, update the positions by Equation (18) |
| 7: else |
| 8: if p > 0.5? then |
| 9: compute Crypsis in HLOA, update the positions by Equation (9) |
| 10: else |
| 11: if t is an even number? then |
| 12: compute Blood-squirting in HLOA, update the positions by Equation (12) |
| 13: else |
| 14: compute Move-to-escape in HLOA, update the positions by Equation (13) |
| 15: end if |
| 16: end if |
| 17: end if |
| 18: Replace the worst search agent by randomly select Equation (10) or Equation (11) |
| 19: if Alpha melanophore rate lower than 0.3? then |
| 20: compute trap escaping operator in EHLOA, update the positions by Equation (17) |
| 21: end if |
| 22: Calculate xnew, the fitness value of the new search agents |
| 23: t = t + 1 |
| 24: end for |
| 25: end while |
| 26: find the lowest fitness value, Display it and its position xbest |
| Flood Type | Index | EHLOA | HLOA | GWO | WOA | PSO | HBA | GJO | DMO |
|---|---|---|---|---|---|---|---|---|---|
| Flood1 | Min | 4160.89 | 4201.44 | 4276.81 | 4319.78 | N/A | 4261.15 | 4421.58 | N/A |
| Mean | 4194.12 | 4295.04 | 4418.68 | 4393.19 | N/A | 4375.08 | 4504.88 | N/A | |
| Flood 2 | Min | 4408.79 | 4412.10 | 4452.01 | 4467.01 | N/A | 4430.41 | 4484.03 | N/A |
| Mean | 4421.13 | 4449.07 | 4487.36 | 4489.90 | N/A | 4468.28 | 4507.46 | N/A | |
| Flood 3 | Min | 4521.82 | 4588.62 | 4562 | 4756.93 | 4943.81 | 4619.97 | 4646.38 | 5253.01 |
| Mean | 4592.95 | 4680.02 | 4598.69 | 4923.78 | 4986.57 | 4713.98 | 4767.07 | 5332.82 | |
| Flood 4 | Min | 4701.87 | 4753.19 | 4749.66 | 4964.86 | 4950.83 | 4796.51 | 4821.83 | 5302.54 |
| Mean | 4754.32 | 4845.17 | 4780.11 | 5037.51 | 4971.29 | 4865.93 | 4897.72 | 5379.37 |
| Flood Type | Peak Values of the Design Floods (m3/s) | Peak Values after Operation (m3/s) | Peak Reduction Rates (%) |
|---|---|---|---|
| flood 1 | 9368 | 4161 | 55.6 |
| flood 2 | 9343 | 4409 | 52.8 |
| flood 3 | 10,800 | 4522 | 58.1 |
| flood 4 | 10,791 | 4702 | 56.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Xie, Y.; Liu, S.; Qin, J.; Wei, J.; Fang, H.; Du, H. An Enhanced Horned Lizard Optimization Algorithm for Flood Control Operation of Cascade Reservoirs. Water 2024, 16, 2458. https://doi.org/10.3390/w16172458
Liu C, Xie Y, Liu S, Qin J, Wei J, Fang H, Du H. An Enhanced Horned Lizard Optimization Algorithm for Flood Control Operation of Cascade Reservoirs. Water. 2024; 16(17):2458. https://doi.org/10.3390/w16172458
Chicago/Turabian StyleLiu, Chenye, Yangyang Xie, Saiyan Liu, Jiyao Qin, Jianfeng Wei, Hongyuan Fang, and Huihua Du. 2024. "An Enhanced Horned Lizard Optimization Algorithm for Flood Control Operation of Cascade Reservoirs" Water 16, no. 17: 2458. https://doi.org/10.3390/w16172458
APA StyleLiu, C., Xie, Y., Liu, S., Qin, J., Wei, J., Fang, H., & Du, H. (2024). An Enhanced Horned Lizard Optimization Algorithm for Flood Control Operation of Cascade Reservoirs. Water, 16(17), 2458. https://doi.org/10.3390/w16172458






