REV and Three-Dimensional Permeability Tensor of Fractured Rock Masses with Heterogeneous Aperture Distributions
Abstract
1. Introduction
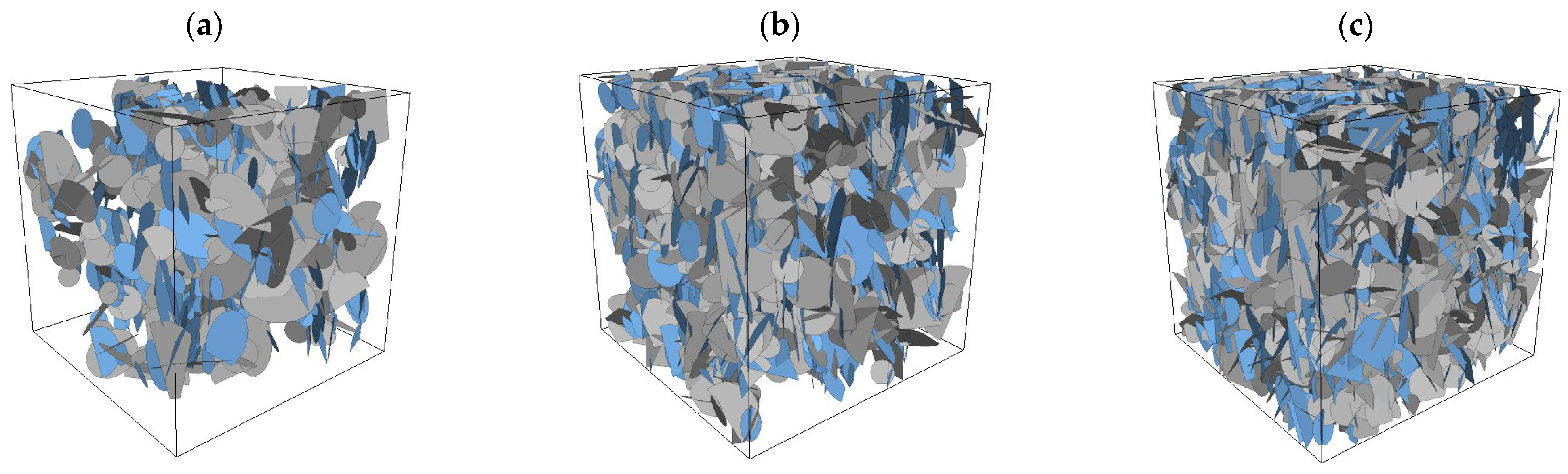
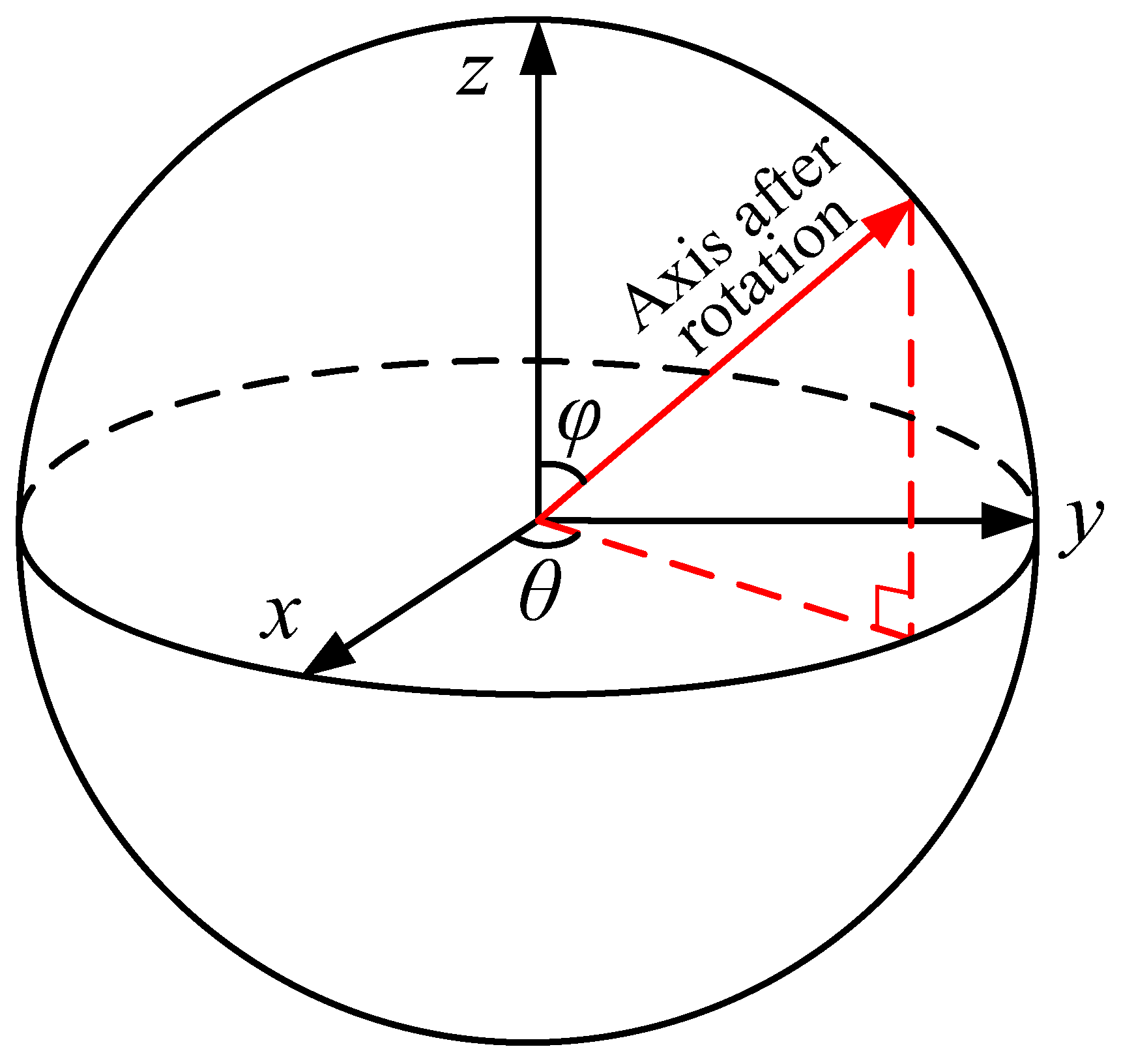
2. Model Generation
3. Flow Calculations
4. Results and Analysis
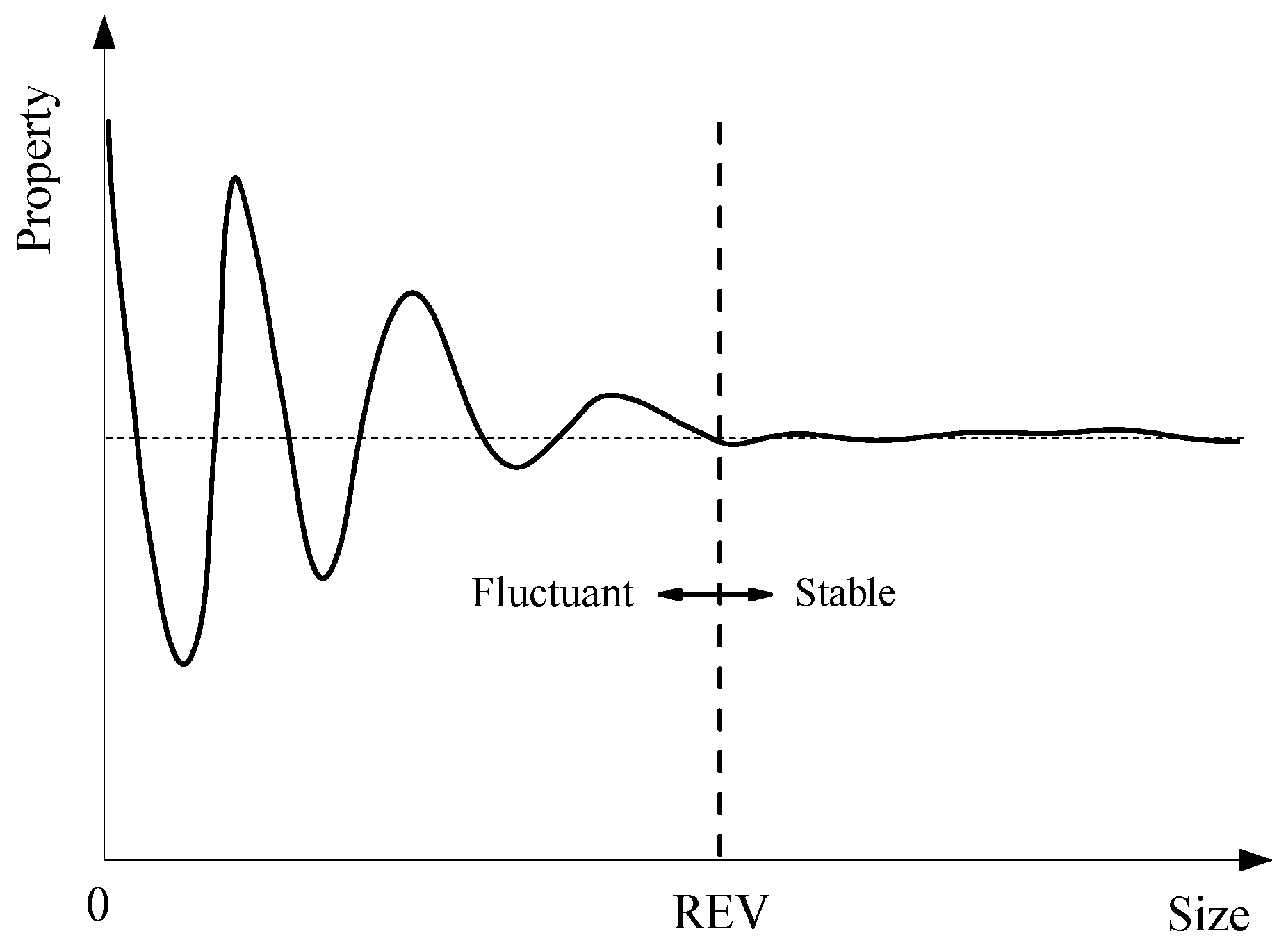
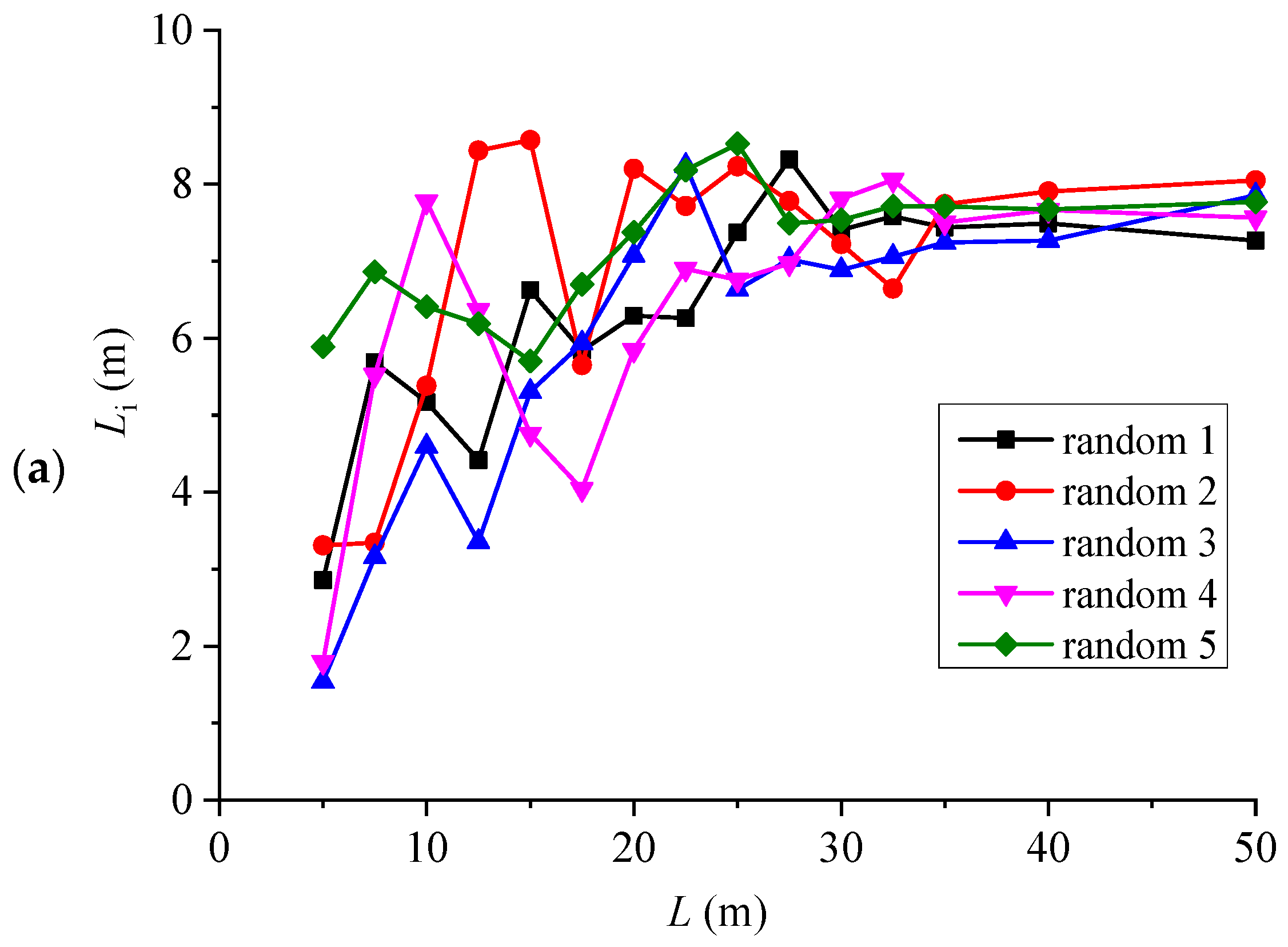
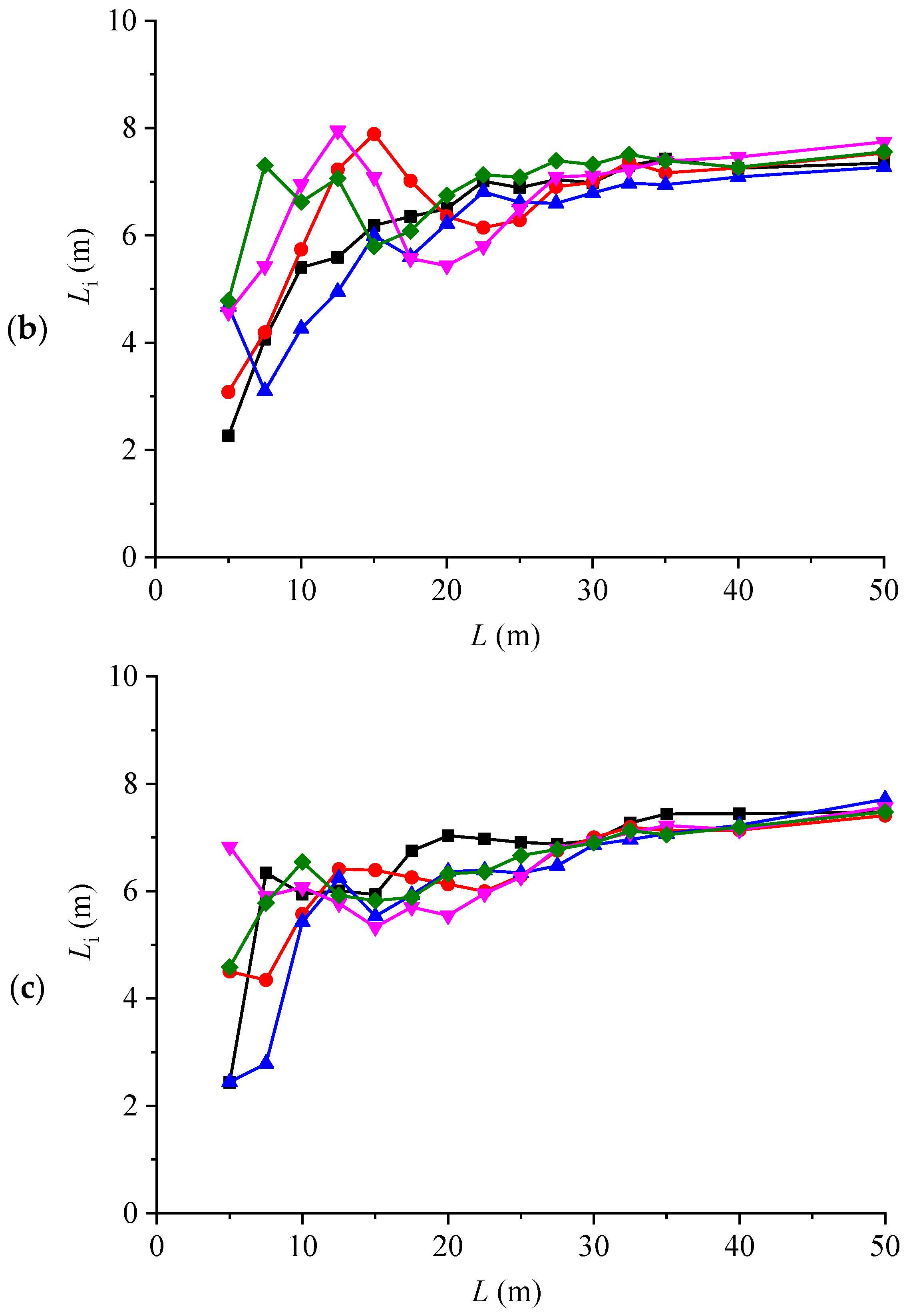
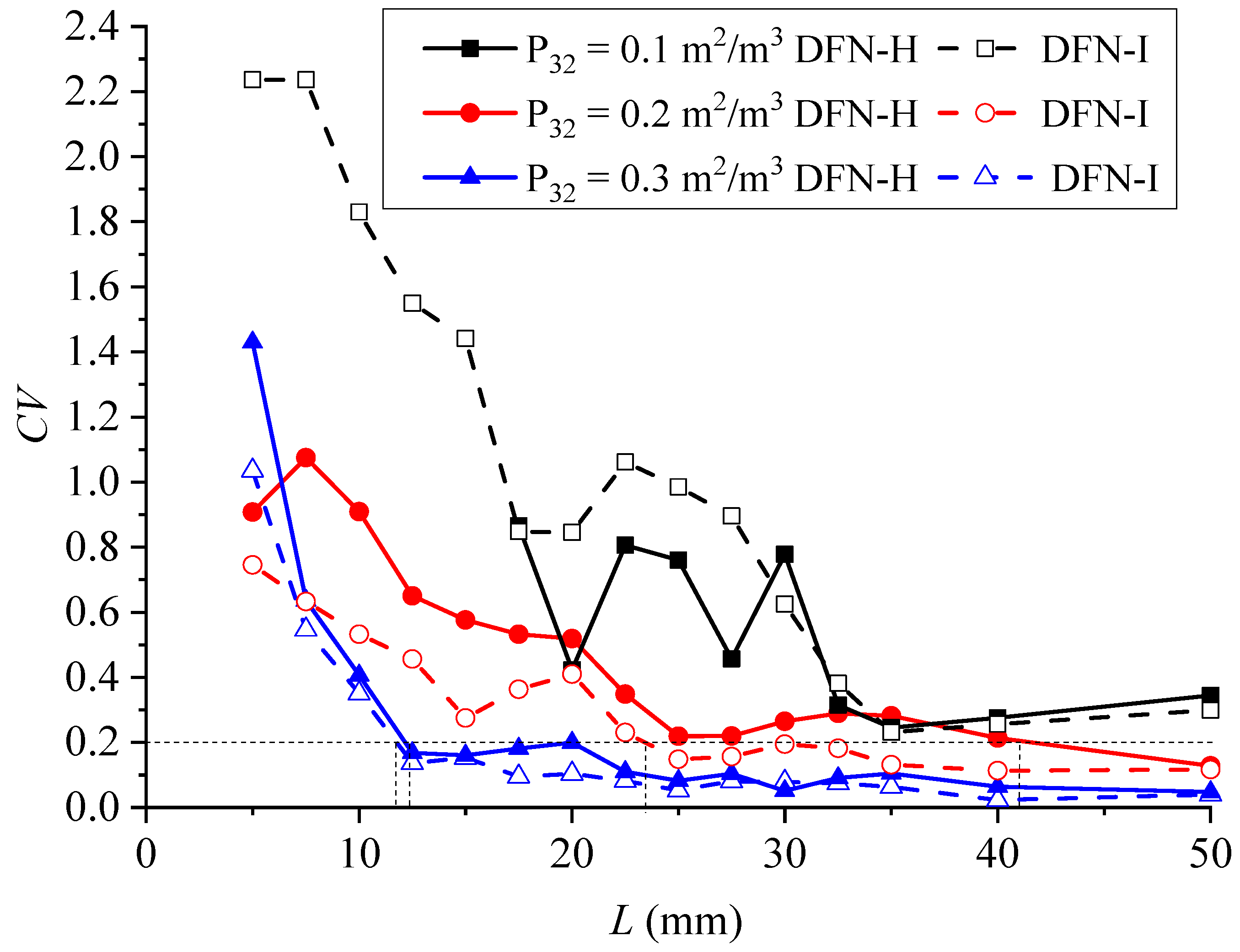
4.1. REV Based on Geometrical Indicators
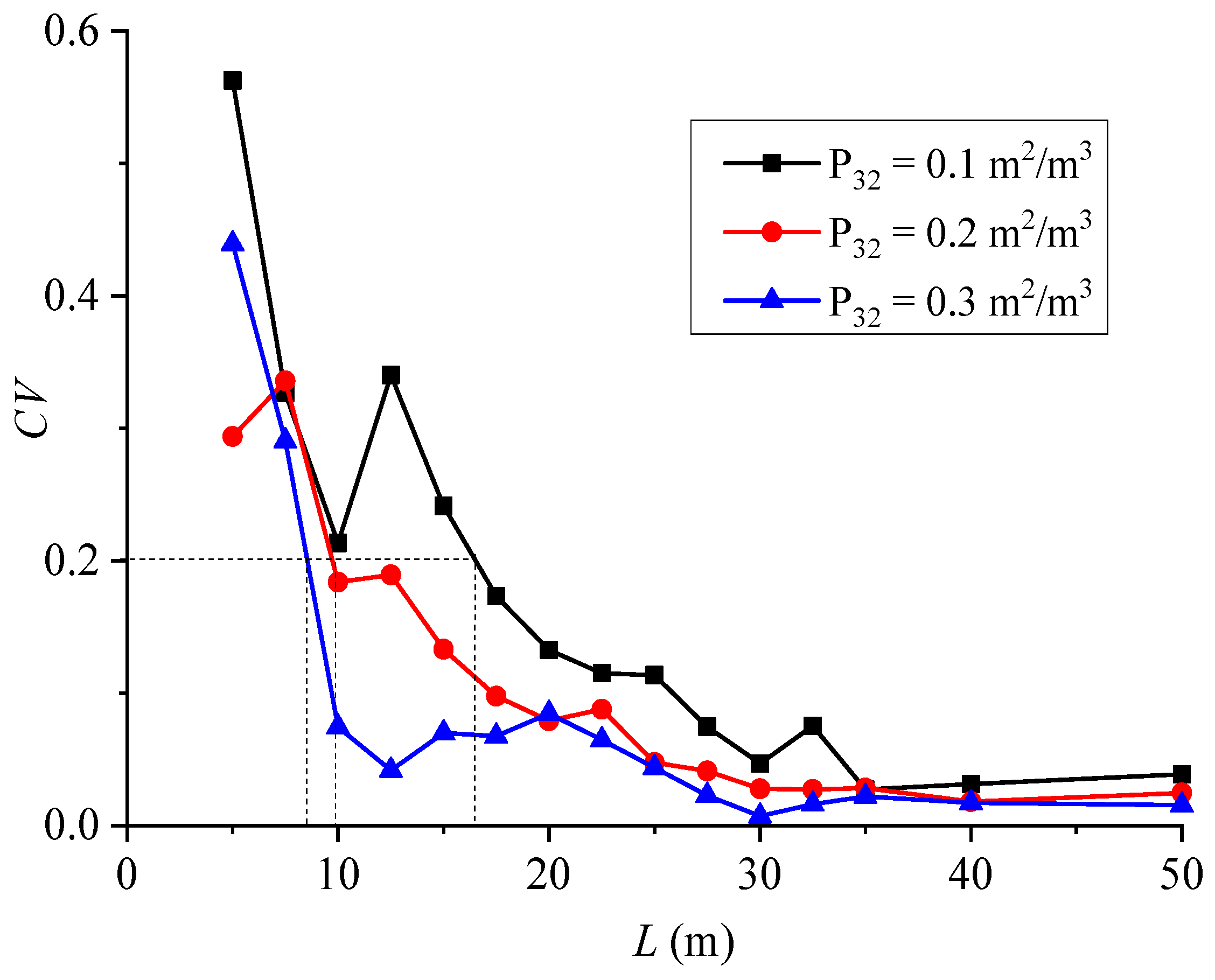
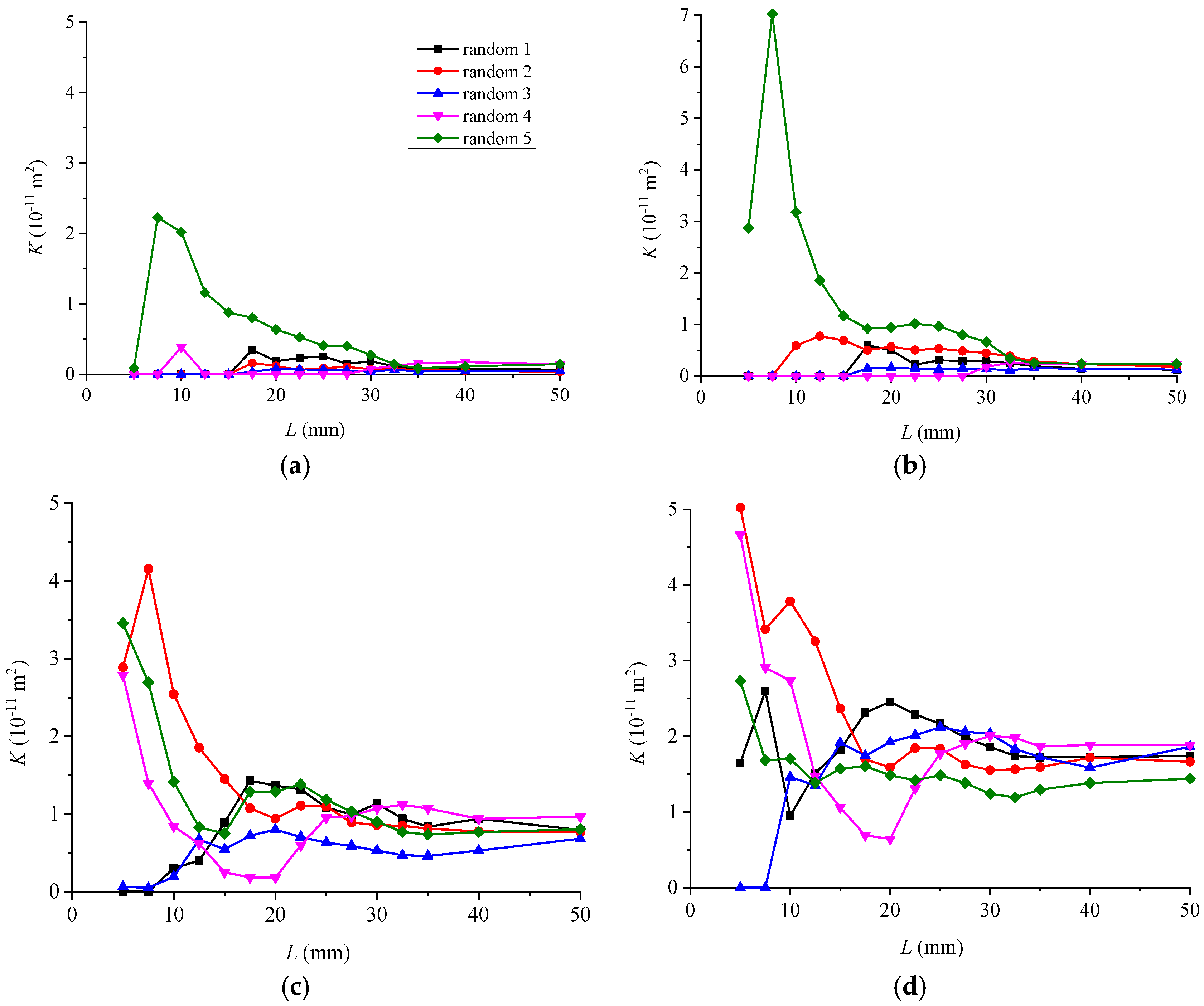
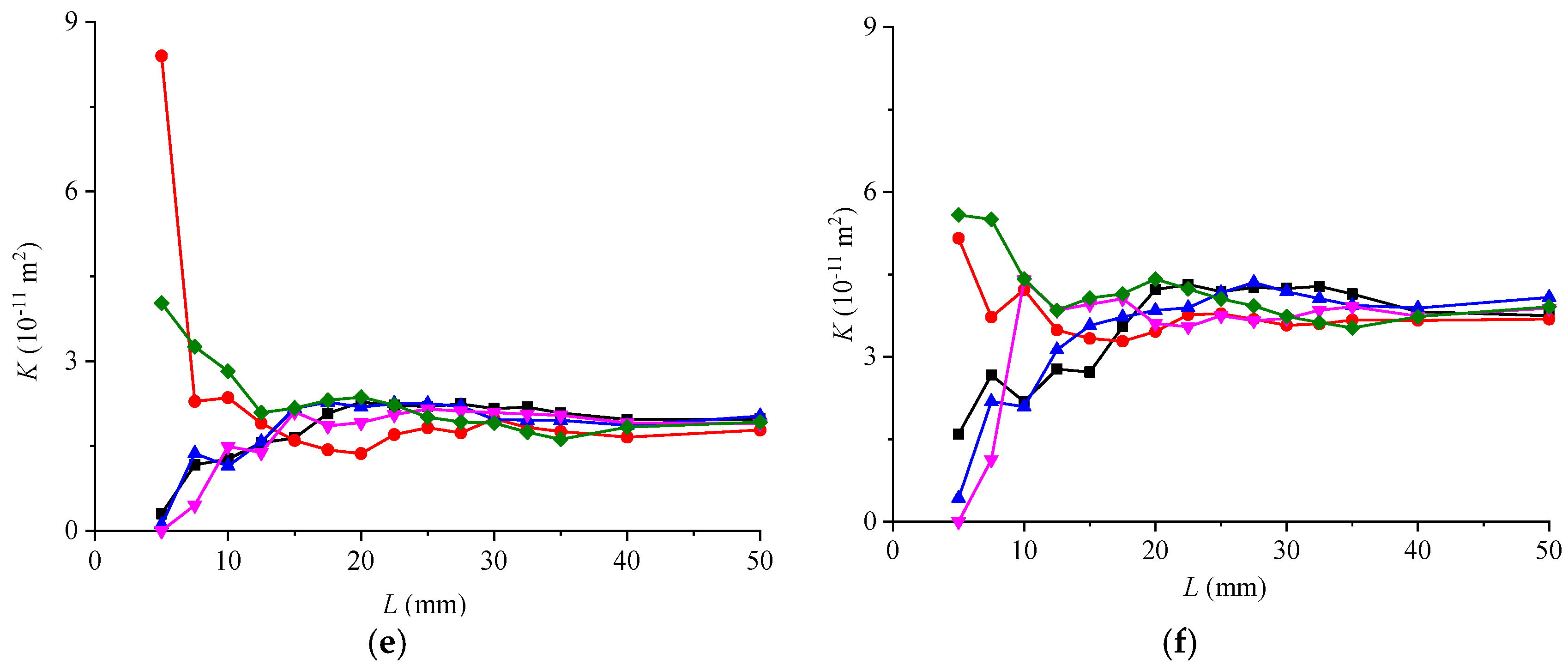
4.2. REV Based on Flow Indicators
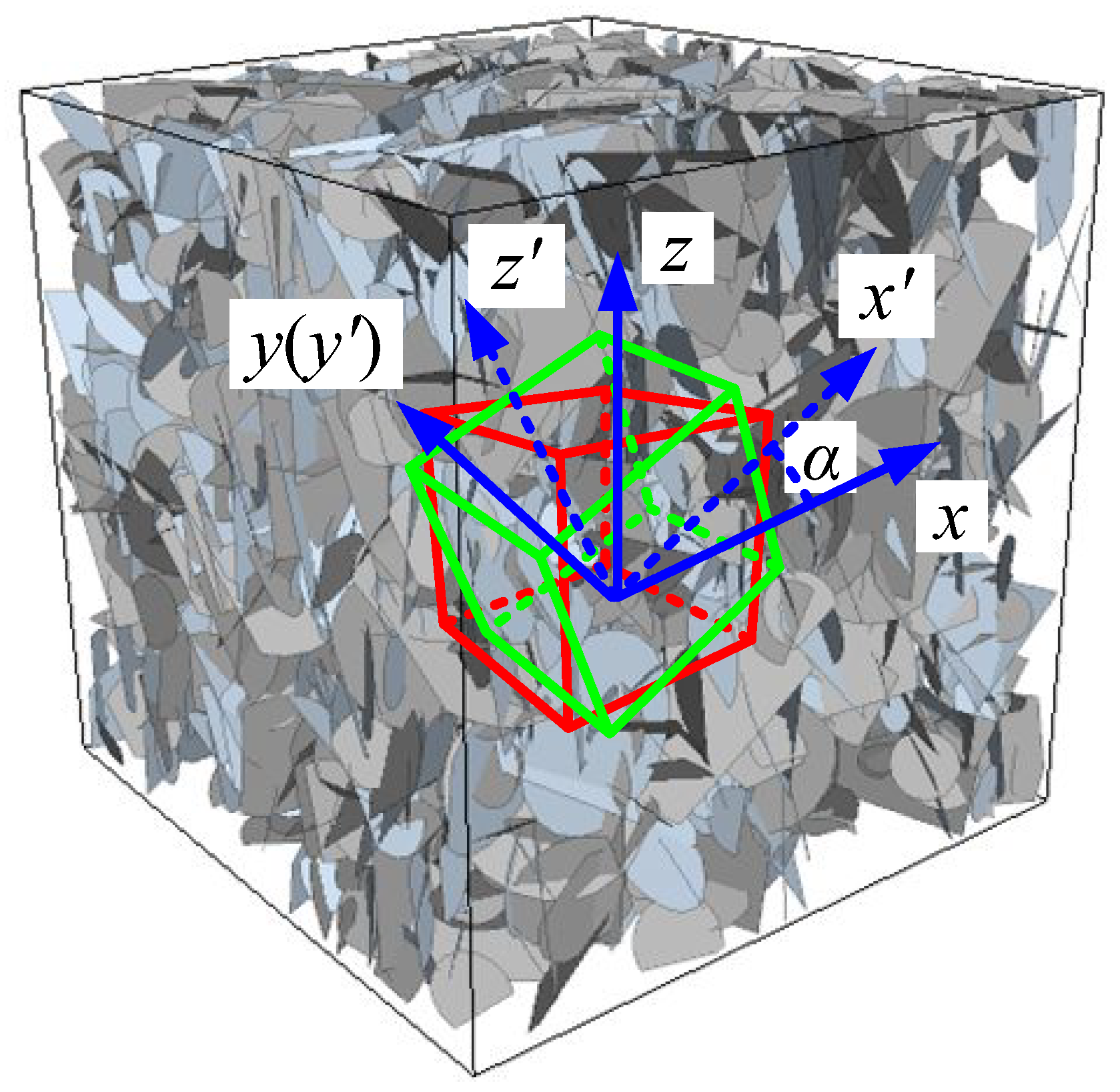
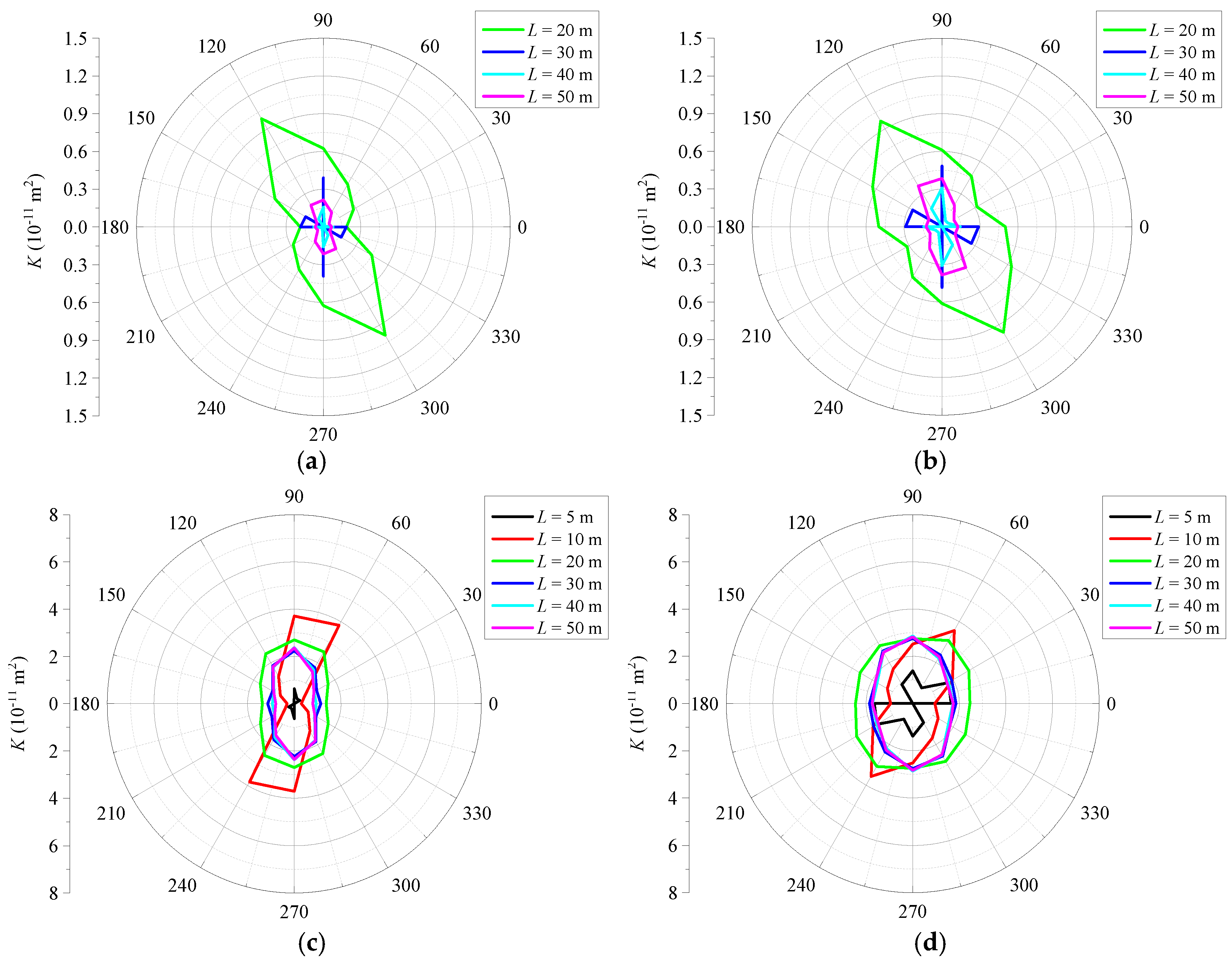
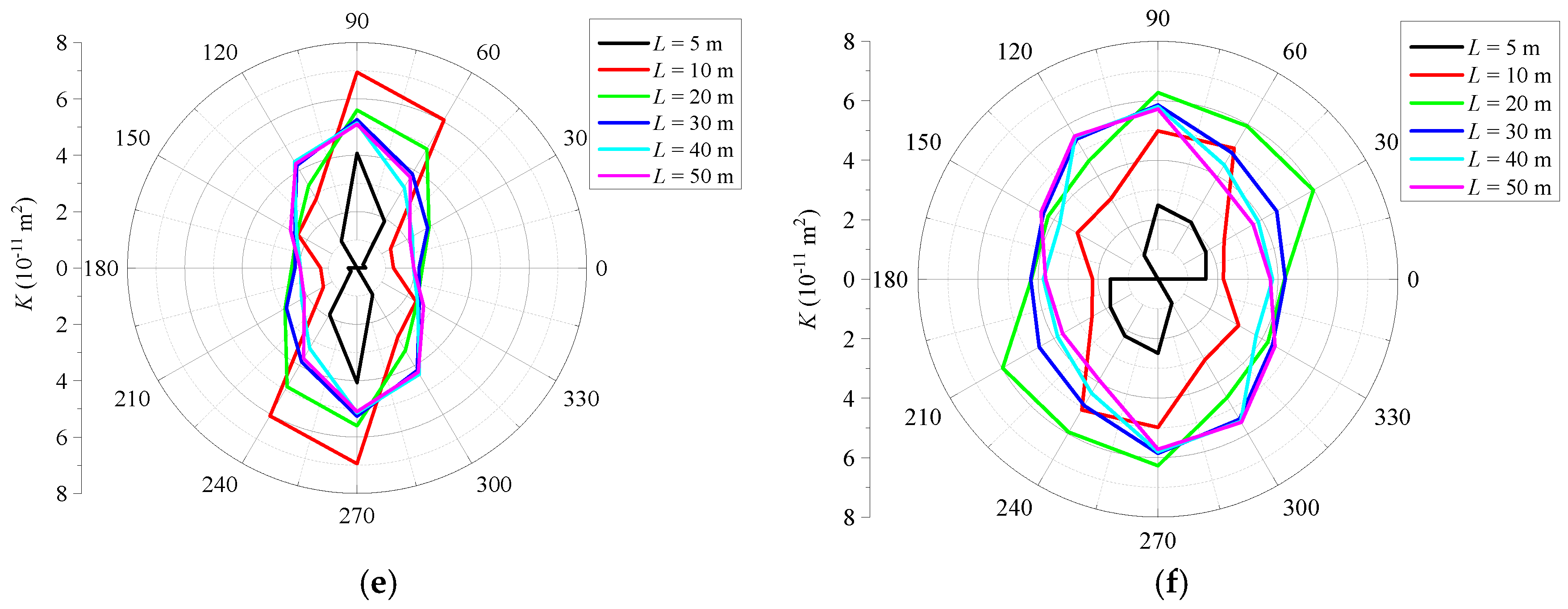
4.3. Permeability Anisotropy
5. Conclusions
- Both the average intersection length and the permeability of DFNs generated with different random numbers vary significantly when the model size is small. As the model size exceeds a certain value, their magnitudes become almost constant, and this phenomenon is more obvious with increasing fracture density.
- The calculated REV size based on the flow indicator of the permeability is obviously larger than that based on the geometrical indicator, especially when the fracture density is small. Aperture heterogeneity increases the REV size, and this effect is more obvious when the fracture density is smaller.
- The shape of the 2D permeability contour is irregular, with some breaks, when the model size is small. As the model size increases, its shape gradually tends to be smooth and approaches an ellipse, with an almost unchanged direction of the minimum or maximum permeabilities. Compared to the DFNs with uniform apertures, the shape of the permeability contours of DFNs with heterogeneous apertures is slender, indicating a larger difference between the minimum and maximum values of the permeability.
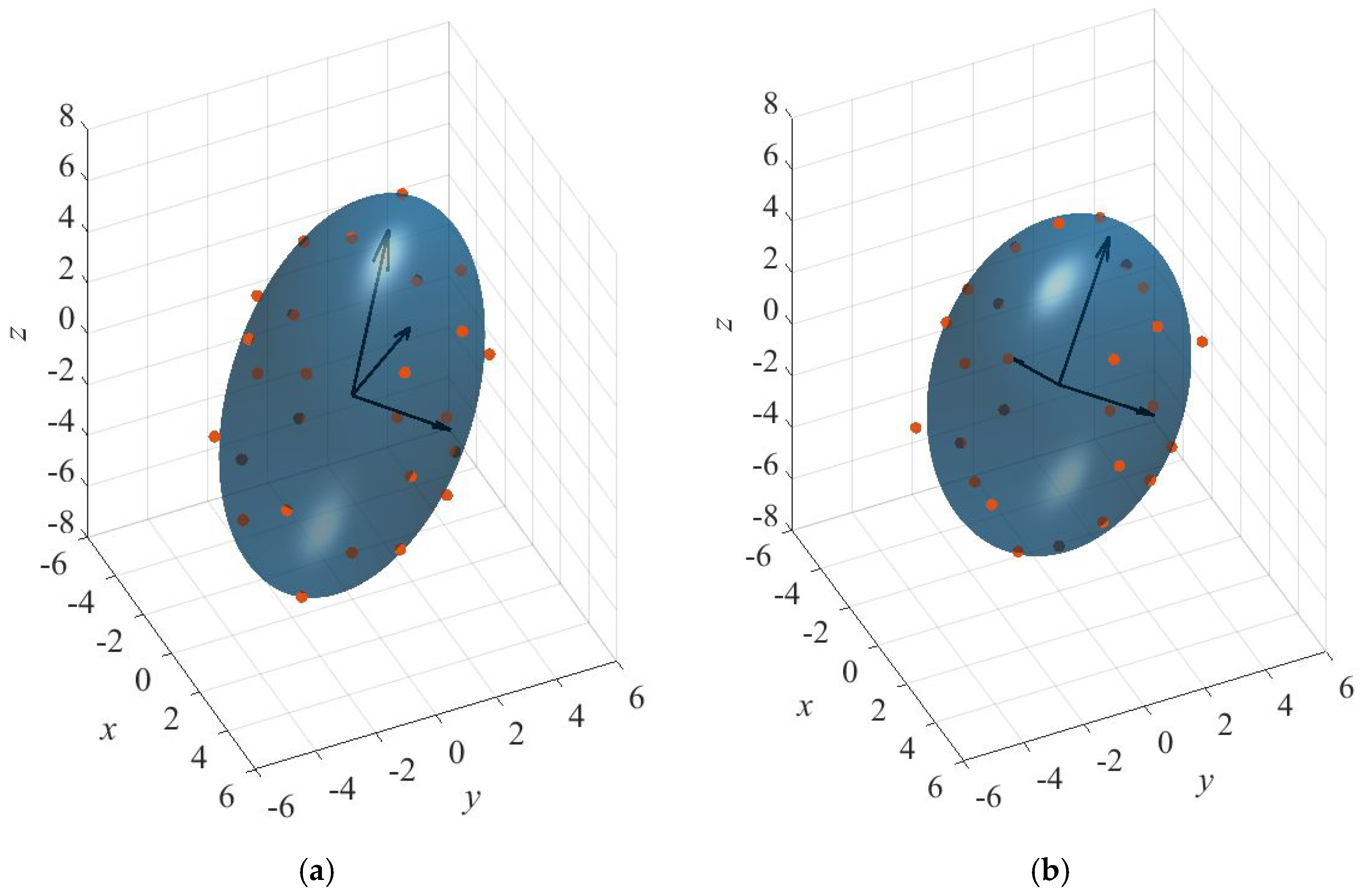
- There is no appropriate approximation of the equivalent permeability tensor over the studied model size range for the DFN-H models in this study. In contrast, for the DFN-I model, a good fit for the permeability ellipsoid is obtained, and the 3D directional permeability is calculated. The corresponding magnitude and direction of the principal permeability can be viewed as the equivalent permeability tensor for the approximated continuum medium.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bour, O.; Davy, P. On the connectivity of three-dimensional fault networks. Water Resour. Res. 1998, 34, 2611–2622. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef]
- Olson, J.E. Sublinear scaling of fracture aperture versus length: An exception or the rule? J. Geophys. Res. Solid Earth 2003, 108, 2413. [Google Scholar] [CrossRef]
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- Gale, J.F.; Laubach, S.E.; Olson, J.E.; Eichhubl, P.; Fall, A. Natural fractures in shale: A review and new observations Natural Fractures in Shale: A Review and New Observations. AAPG Bull. 2014, 98, 2165–2216. [Google Scholar] [CrossRef]
- Zhu, T.; Jing, H.; Su, H.; Yin, Q.; Du, M.; Han, G. Physical and mechanical properties of sandstone containing a single fissure after exposure to high temperatures. Int. J. Min. Sci. Technol. 2016, 26, 319–325. [Google Scholar] [CrossRef]
- Lin, Q.; Cao, P.; Wen, G.; Meng, J.; Cao, R.; Zhao, Z. Crack coalescence in rock-like specimens with two dissimilar layers and pre-existing double parallel joints under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2021, 139, 104621. [Google Scholar] [CrossRef]
- Cacas, M.C.; Ledoux, E.; de Marsily, G.; Tillie, B.; Barbreau, A.; Durand, E.; Feuga, B.; Peaudecerf, P. Modeling fracture flow with a stochastic discrete fracture network: Calibration and validation: 1. The flow model. Water Resour. Res. 1990, 26, 479–489. [Google Scholar] [CrossRef]
- Bandis, S.C.; Lumsden, A.C.; Barton, N.R. Fundamentals of rock joint deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 249–268. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y.; Huang, N. Mathematical expressions for estimating equivalent permeability of rock fracture networks. Hydrogeol. J. 2016, 24, 1623–1649. [Google Scholar] [CrossRef]
- Kirkby, A.; Heinson, G. Three-dimensional resistor network modeling of the resistivity and permeability of fractured rocks. J. Geophys. Res. Solid Earth 2017, 122, 2653–2669. [Google Scholar] [CrossRef]
- Monsalve, J.J.; Baggett, J.; Bishop, R.; Ripepi, N. Application of laser scanning for rock mass characterization and discrete fracture network generation in an underground limestone mine. Int. J. Min. Sci. Technol. 2019, 29, 131–137. [Google Scholar] [CrossRef]
- Cvetkovic, V.; Frampton, A. Solute transport and retention in three-dimensional fracture networks. Water Resour. Res. 2012, 48, W02509. [Google Scholar] [CrossRef]
- Berrone, S.; Pieraccini, S.; Scialo, S. On simulations of discrete fracture network flows with an optimization-based extended finite element method. SIAM J. Sci. Comput. 2013, 35, A908–A935. [Google Scholar] [CrossRef][Green Version]
- Hu, Y.; Xu, W.; Zhan, L.; Zou, L.; Chen, Y. Modeling of solute transport in a fracture-matrix system with a three-dimensional discrete fracture network. J. Hydrol. 2022, 605, 127333. [Google Scholar] [CrossRef]
- Gan, Q.; Elsworth, D. A continuum model for coupled stress and fluid flow in discrete fracture networks. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 43–61. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Wang, Z.; Li, W.; Bi, L.; Qiao, L.; Liu, R.; Liu, J. Estimation of the REV size and equivalent permeability coefficient of fractured rock masses with an emphasis on comparing the radial and unidirectional flow configurations. Rock Mech. Rock Eng. 2018, 51, 1457–1471. [Google Scholar] [CrossRef]
- Wang, L.; Golfier, F.; Tinet, A.J.; Chen, W.; Vuik, C. An efficient adaptive implicit scheme with equivalent continuum approach for two-phase flow in fractured vuggy porous media. Adv. Water Resour. 2022, 163, 104186. [Google Scholar] [CrossRef]
- Neuman, S.P. Stochastic continuum representation of fractured rock permeability as an alternative to the REV and fracture network concepts. In Groundwater Flow and Quality Modelling; Springer: Dordrecht, The Netherlands, 1988; pp. 331–362. [Google Scholar]
- Baghbanan, A.; Jing, L. Hydraulic properties of fractured rock masses with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2007, 44, 704–719. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Stress effects on permeability in a fractured rock mass with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2008, 45, 1320–1334. [Google Scholar] [CrossRef]
- Lang, P.S.; Paluszny, A.; Zimmerman, R.W. Permeability tensor of three-dimensional fractured porous rock and a comparison to trace map predictions. J. Geophys. Res. Solid Earth 2014, 119, 6288–6307. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, R.; Yu, L.; Li, S.; Wang, X.; Liu, D. An Equivalent Pipe Network Modeling Approach for Characterizing Fluid Flow through Three-Dimensional Fracture Networks: Verification and Applications. Water 2022, 14, 1582. [Google Scholar] [CrossRef]
- Wang, M.; Kulatilake, P.H.S.W.; Um, J.; Narvaiz, J. Estimation of REV size and three-dimensional hydraulic conductivity tensor for a fractured rock mass through a single well packer test and discrete fracture fluid flow modeling. Int. J. Rock Mech. Min. Sci. 2002, 39, 887–904. [Google Scholar] [CrossRef]
- Liu, R.; Yu, L.; Jiang, Y. Fractal analysis of directional permeability of gas shale fracture networks: A numerical study. J. Nat. Gas Sci. Eng. 2016, 33, 1330–1341. [Google Scholar] [CrossRef]
- Wang, T.; Sun, Z.; Zhang, K.; Jiang, C.; Xin, Y.; Mao, Q. Investigation on heat extraction performance of fractured geothermal reservoir using coupled thermal-hydraulic-mechanical model based on equivalent continuum method. Energies 2018, 12, 127. [Google Scholar] [CrossRef]
- Hudson, J.A.; Harrison, J.P. Engineering Rock Mechanics: An Introduction to the Principles; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Hyman, J.D.; Karra, S.; Makedonska, N.; Gable, C.W.; Painter, S.L.; Viswanathan, H.S. dfnWorks: A discrete fracture network framework for modeling subsurface flow and transport. Comput. Geosci. 2015, 84, 10–19. [Google Scholar] [CrossRef]
- Liang, Z.; Wu, N.; Li, Y.; Li, H.; Li, W. Numerical study on anisotropy of the representative elementary volume of strength and deformability of jointed rock masses. Rock Mech. Rock Eng. 2019, 52, 4387–4402. [Google Scholar] [CrossRef]
- Rong, G.; Peng, J.; Wang, X.; Liu, G.; Hou, D. Permeability tensor and representative elementary volume of fractured rock masses. Hydrogeol. J. 2013, 21, 1655–1671. [Google Scholar] [CrossRef]
- Feng, S.; Wang, H.; Cui, Y.; Ye, Y.; Liu, Y.; Li, X.; Wang, H.; Yang, R. Fractal discrete fracture network model for the analysis of radon migration in fractured media. Comput. Geotech. 2020, 128, 103810. [Google Scholar] [CrossRef]
- Brown, S.R.; Kranz, R.L.; Bonner, B.P. Correlation between the surfaces of natural rock joints. Geophys. Res. Lett. 1986, 13, 1430–1433. [Google Scholar] [CrossRef]
- Brown, S.R. Fluid flow through rock joints: The effect of surface roughness. J. Geophys. Res. Solid Earth 1987, 92, 1337–1347. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Bodvarsson, G.S. Hydraulic conductivity of rock fractures. Transp. Porous Media 1996, 23, 1–30. [Google Scholar] [CrossRef]
- Glover, P.W.J.; Matsuki, K.; Hikima, R.; Hayashi, K. Synthetic rough fractures in rocks. J. Geophys. Res. Solid Earth 1998, 103, 9609–9620. [Google Scholar] [CrossRef]
- Isakov, E.; Ogilvie, S.R.; Taylor, C.W.; Glover, P.W. Fluid flow through rough fractures in rocks I: High resolution aperture determinations. Earth Planet. Sci. Lett. 2001, 191, 267–282. [Google Scholar] [CrossRef]
- Crandall, D.; Bromhal, G.; Karpyn, Z.T. Numerical simulations examining the relationship between wall-roughness and fluid flow in rock fractures. Int. J. Rock Mech. Min. Sci. 2010, 47, 784–796. [Google Scholar] [CrossRef]
- Yin, Q.; Ma, G.; Jing, H.; Wang, H.; Su, H.; Wang, Y.; Liu, R. Hydraulic properties of 3D rough-walled fractures during shearing: An experimental study. J. Hydrol. 2017, 555, 169–184. [Google Scholar] [CrossRef]
- Huang, N.; Liu, R.; Jiang, Y.; Li, B.; Yu, L. Effects of fracture surface roughness and shear displacement on geometrical and hydraulic properties of three-dimensional crossed rock fracture models. Adv. Water Resour. 2018, 113, 30–41. [Google Scholar] [CrossRef]
- Li, B.; Cui, X.; Zou, L.; Cvetkovic, V. On the relationship between normal stiffness and permeability of rock fractures. Geophys. Res. Lett. 2021, 48, e2021GL095593. [Google Scholar] [CrossRef]
- Ishibashi, T.; Watanabe, N.; Hirano, N.; Okamoto, A.; Tsuchiya, N. Beyond-laboratory-scale prediction for channeling flows through subsurface rock fractures with heterogeneous aperture distributions revealed by laboratory evaluation. J. Geophys. Res. Solid Earth 2015, 120, 106–124. [Google Scholar] [CrossRef]
- Huang, N.; Jiang, Y.; Liu, R.; Li, B.; Sugimoto, S. A novel three-dimensional discrete fracture network model for investigating the role of aperture heterogeneity on fluid flow through fractured rock masses. Int. J. Rock Mech. Min. Sci. 2019, 116, 25–37. [Google Scholar] [CrossRef]
- Huang, N.; Jiang, Y.; Liu, R.; Li, B. Experimental and numerical studies of the hydraulic properties of three-dimensional fracture networks with spatially distributed apertures. Rock Mech. Rock Eng. 2019, 52, 4731–4746. [Google Scholar] [CrossRef]
- Hyman, J.D.; Sweeney, M.R.; Frash, L.P.; Carey, J.W.; Viswanathan, H.S. Scale-Bridging in Three-Dimensional Fracture Networks: Characterizing the Effects of Variable Fracture Apertures on Network-Scale Flow Channelization. Geophys. Res. Lett. 2021, 48, e2021GL094400. [Google Scholar] [CrossRef]
- McKay, L.D.; Cherry, J.A.; Gillham, R.W. Field experiments in a fractured clay till: 1. Hydraulic conductivity and fracture aperture. Water Resour. Res. 1993, 29, 1149–1162. [Google Scholar] [CrossRef]
- Makedonska, N.; Hyman, J.D.; Karra, S.; Painter, S.L.; Gable, C.W.; Viswanathan, H.S. Evaluating the effect of internal aperture variability on transport in kilometer scale discrete fracture networks. Adv. Water Resour. 2016, 94, 486–497. [Google Scholar] [CrossRef]
- Guo, P.; Wang, M.; Gao, K.; He, M.; Wang, Y. Influence of fracture surface roughness on local flow pattern: Visualization using a microfluidic field experiment. Hydrogeol. J. 2020, 28, 2373–2385. [Google Scholar] [CrossRef]
- Ishibashi, T.; Watanabe, N.; Tamagawa, T.; Tsuchiya, N. Three-dimensional channeling flow within subsurface rock fracture networks suggested via fluid flow analysis in the Yufutsu fractured oil/gas reservoir. J. Pet. Sci. Eng. 2019, 178, 838–851. [Google Scholar] [CrossRef]
- Guo, L.; Li, X.; Zhou, Y.; Zhang, Y. Generation and verification of three-dimensional network of fractured rock masses stochastic discontinuities based on digitalization. Environ. Earth Sci. 2015, 73, 7075–7088. [Google Scholar] [CrossRef]
- Huang, X.-W.; Wang, Z.Z.; Jiang, P.-M.; LI, K.-Q.; Tang, C.-X. Meso-scale investigation of the effects of groundwater seepage on the thermal performance of borehole heat exchangers. Appl. Therm. Eng. 2024, 236, 121809. [Google Scholar] [CrossRef]
- Han, S.; Gao, Q.; Yan, X.; Li, L.; Wang, L.; Shi, X.; Yan, C.; Wang, D. Thermally-induced cracking behaviors of coal reservoirs subjected to cryogenic liquid nitrogen shock. J. Rock Mech. Geotech. 2024, 16, 2894–2908. [Google Scholar] [CrossRef]
- Xiong, X.; Li, B.; Jiang, Y.; Koyama, T.; Zhang, C. Experimental and numerical study of the geometrical and hydraulic characteristics of a single rock fracture during shear. Int. J. Rock Mech. Min. Sci. 2011, 48, 1292–1302. [Google Scholar] [CrossRef]
- Beck, J.V.; Arnold, K.J. Parameter Estimation in Engineering and Science; Wiley: Hoboken, NJ, USA, 1977. [Google Scholar]
- Huang, N.; Jiang, Y.; Li, B.; Liu, R. A numerical method for simulating fluid flow through 3-D fracture networks. J. Nat. Gas Sci. Eng. 2016, 33, 1271–1281. [Google Scholar] [CrossRef]
- Öhman, J.; Niemi, A. Upscaling of fracture hydraulics by means of an oriented correlated stochastic continuum model. Water Resour. Res. 2003, 39, SBH-3. [Google Scholar] [CrossRef]

| Dominant Set | Orientation | Fisher Constant | |
|---|---|---|---|
| Dip (°) | Dip Direction (°) | ||
| 1 | 81.2 | 49 | 10.85 |
| 2 | 72 | 116.7 | 1.59 |
| P32 (m2/m3) | L (m) | K1 | K2 | K3 | |||
|---|---|---|---|---|---|---|---|
| Magnitude × 10−11 m2 | Direction | Magnitude ×10−11 m2 | Direction | Magnitude × 10−11 m2 | Direction | ||
| 0.2 | 30 | 6.959 | (−0.486, 0.502, −0.716) | 5.221 | (0.443, −0.564, −0.697) | 3.452 | (−0.754, −0.655, 0.051) |
| 0.3 | 20 | 6.447 | (−0.090, 0.251, 0.964) | 5.701 | (−0.681, 0.690, −0.243) | 3.579 | (0.727, 0.678, −0.109) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, N.; Han, S.; Jiang, Y.; Han, S. REV and Three-Dimensional Permeability Tensor of Fractured Rock Masses with Heterogeneous Aperture Distributions. Water 2024, 16, 2435. https://doi.org/10.3390/w16172435
Huang N, Han S, Jiang Y, Han S. REV and Three-Dimensional Permeability Tensor of Fractured Rock Masses with Heterogeneous Aperture Distributions. Water. 2024; 16(17):2435. https://doi.org/10.3390/w16172435
Chicago/Turabian StyleHuang, Na, Shengqun Han, Yujing Jiang, and Songcai Han. 2024. "REV and Three-Dimensional Permeability Tensor of Fractured Rock Masses with Heterogeneous Aperture Distributions" Water 16, no. 17: 2435. https://doi.org/10.3390/w16172435
APA StyleHuang, N., Han, S., Jiang, Y., & Han, S. (2024). REV and Three-Dimensional Permeability Tensor of Fractured Rock Masses with Heterogeneous Aperture Distributions. Water, 16(17), 2435. https://doi.org/10.3390/w16172435








