Research on Constant-Flow Water-Saving Device Based on Dynamic Mesh Transient Flow Field Analysis
Abstract
1. Introduction
2. Theoretical Analysis
2.1. Mathematical Model
- The constant-flow water-saving device adjusts the water flow rate through internal valves, and the characteristic length scale of the water-saving valve is much larger than the average free path of water molecules. In order to simplify the application of mathematical models describing the dynamic changes in water flow, it is usually assumed that the fluid is a continuous medium, ignoring the discreteness between molecules;
- When the constant-flow water-saving device is in operation, its internal fluid is usually under common temperature and pressure conditions, not under specific extreme conditions; so, the changes in water density and volume are very small. In engineering design and analysis, it can be simplified as incompressible fluid;
- Inside the water-saving device, the water flow exhibits constant viscous characteristics and a linear stress–strain relationship, which makes it reasonable to assume that the water follows the Newtonian fluid model in this process;
- Assuming that the fluid is moving under constant temperature conditions, without considering the influence of temperature changes on the flow process, the surface roughness of the water-saving device components is very small, and the flow boundary is a hydraulic smooth boundary condition.
2.1.1. Continuity Equation
2.1.2. Momentum Equation
2.2. Control of Motion Boundaries
3. The Establishment of a Transient Simulation Model Using CFD
3.1. Geometric Model
3.2. Numerical Simulation Method
3.3. Boundary Condition Setting
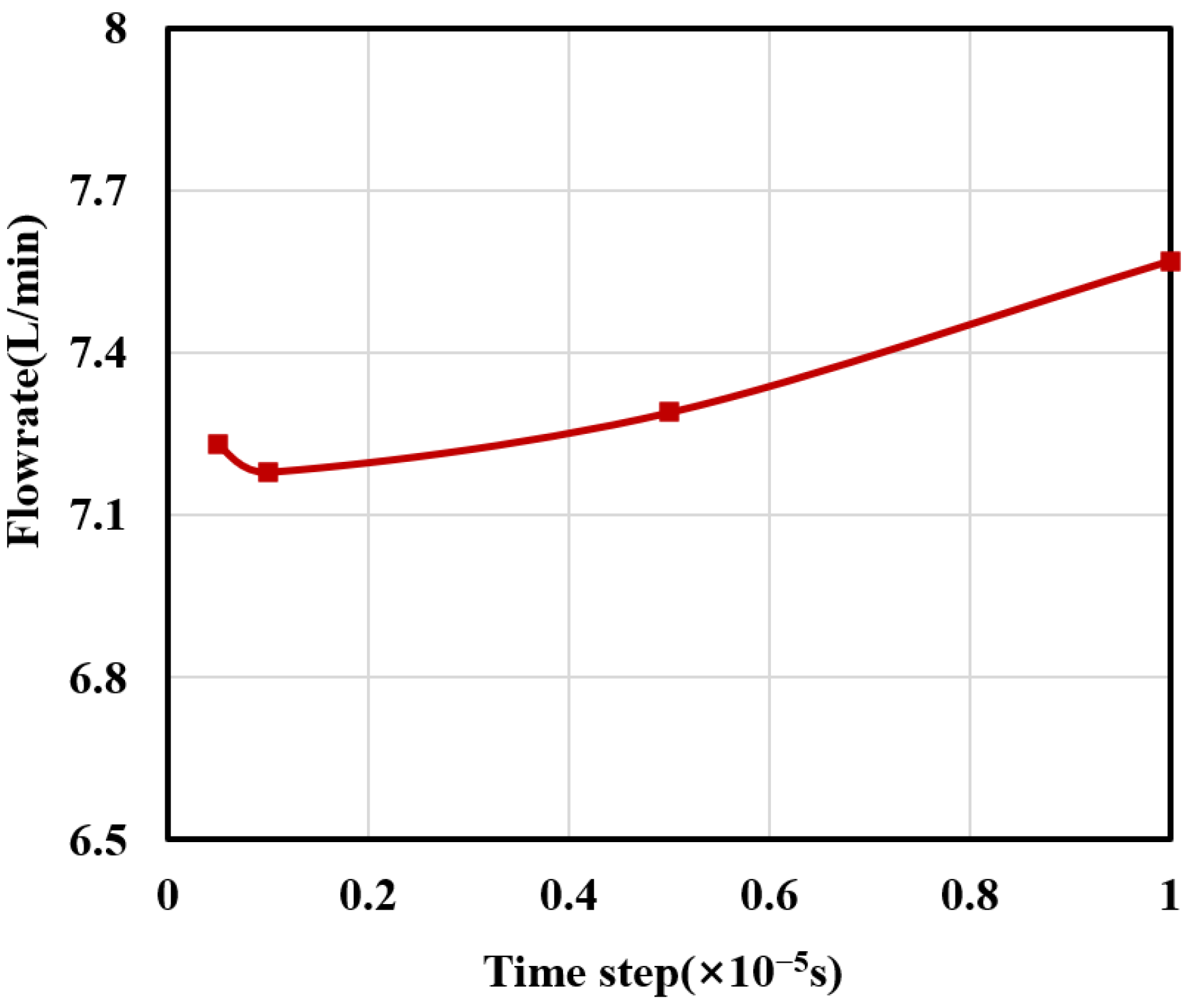
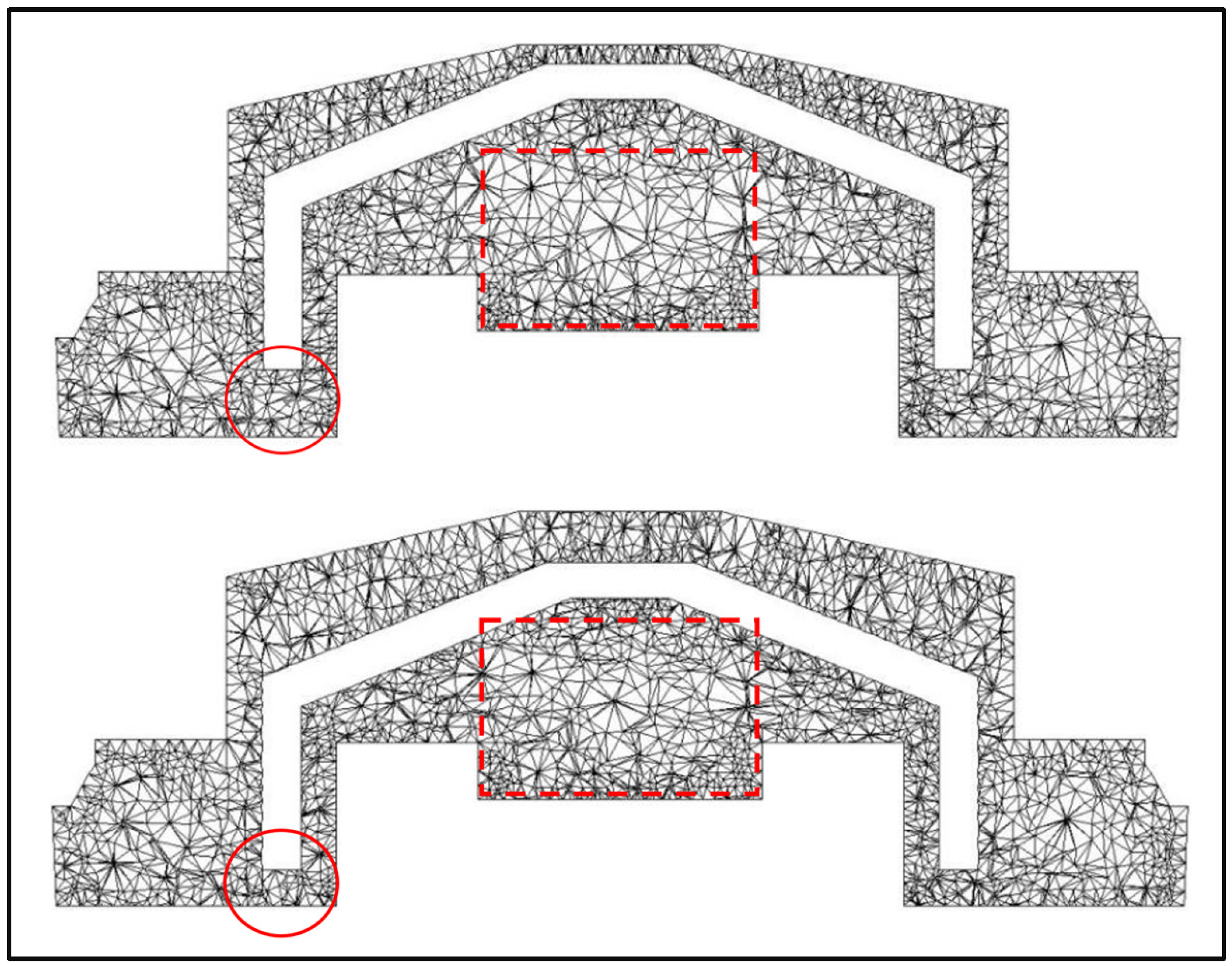
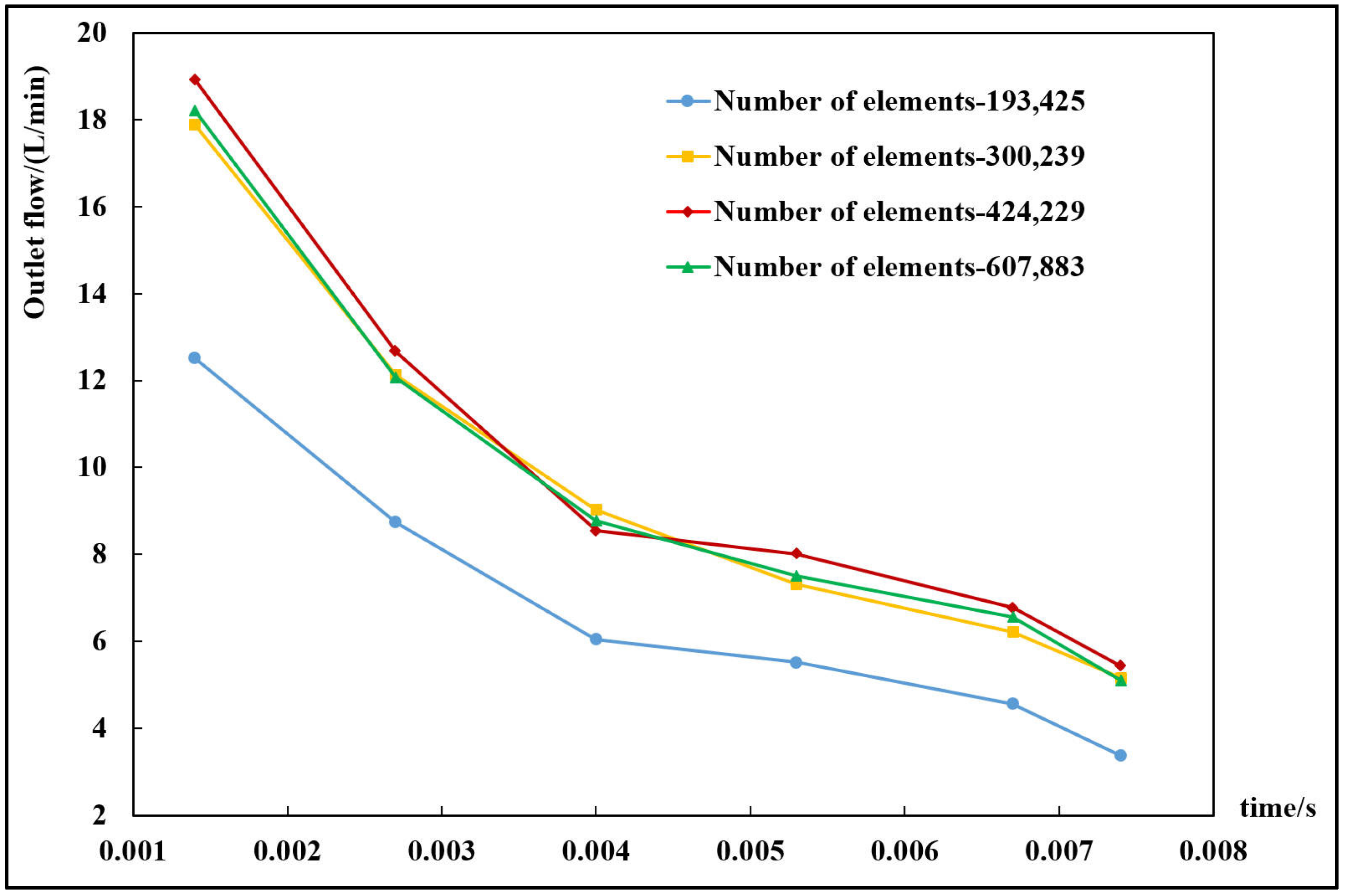
3.4. Grid Convergence Analysis
4. Experimental and Benchmark Analysis
4.1. Experimental Testing
4.2. Benchmarking Analysis
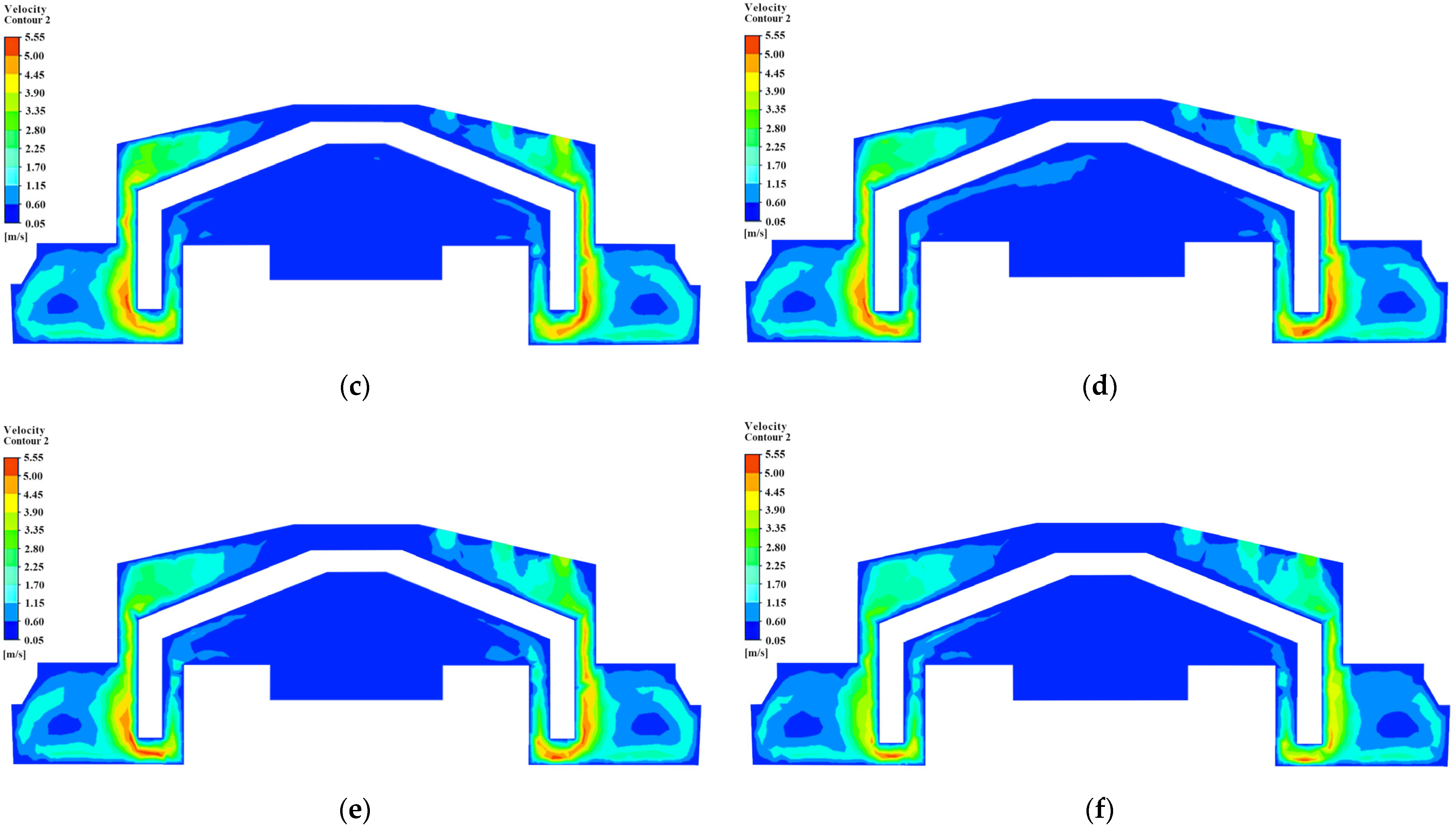
5. The Analysis of Transient Calculation Results
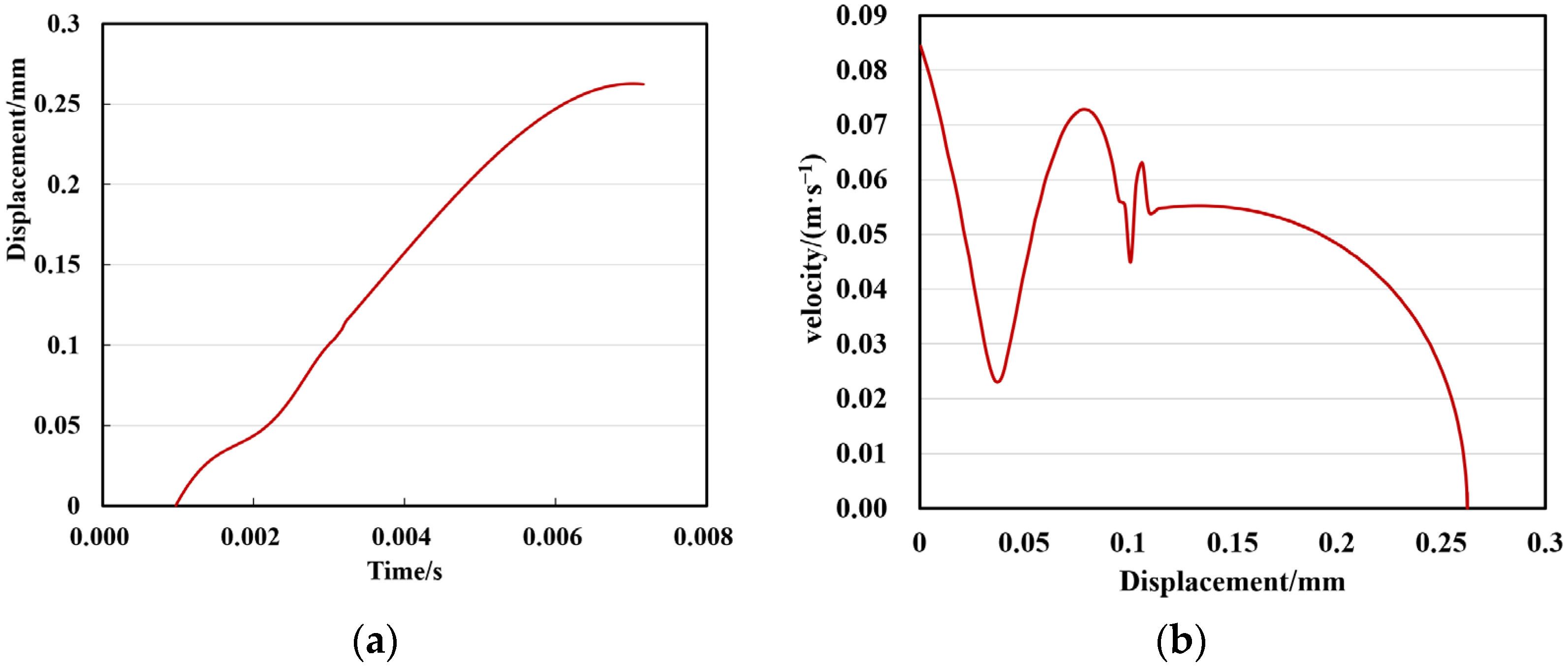
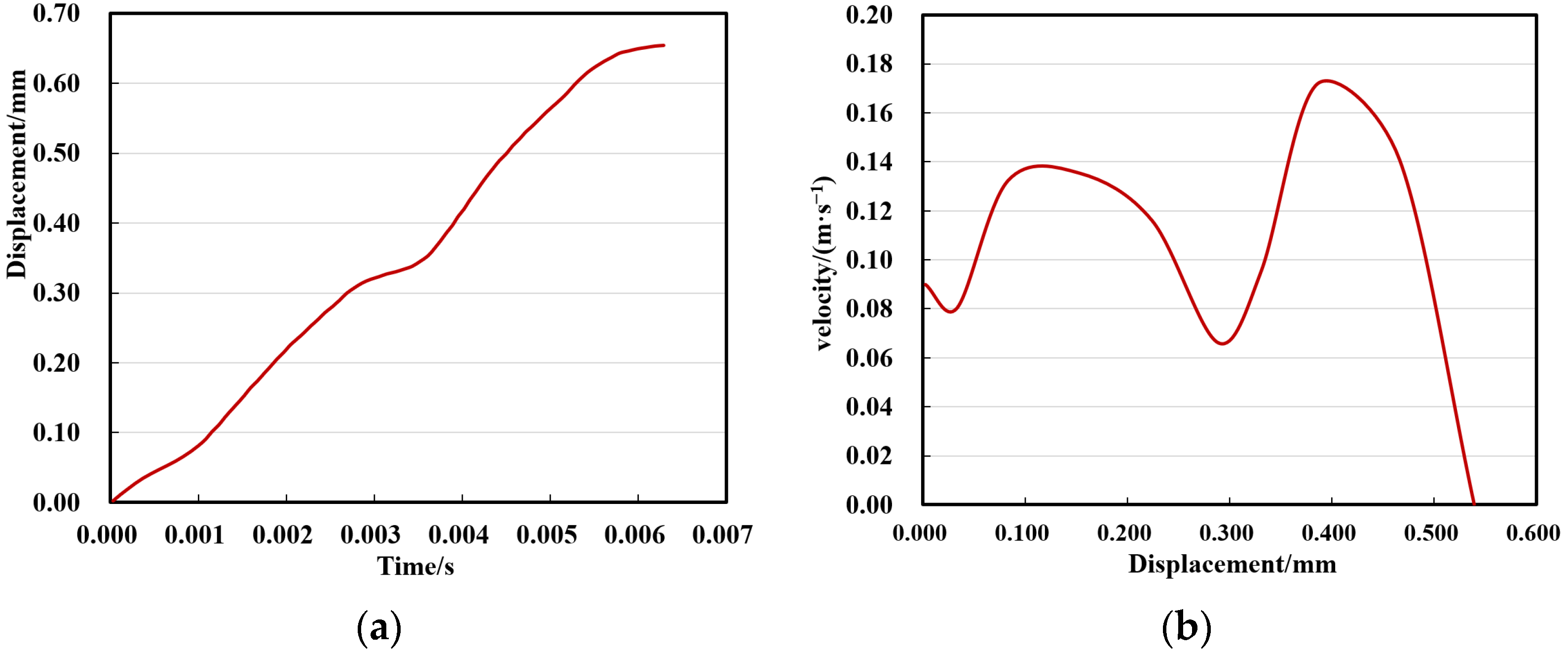
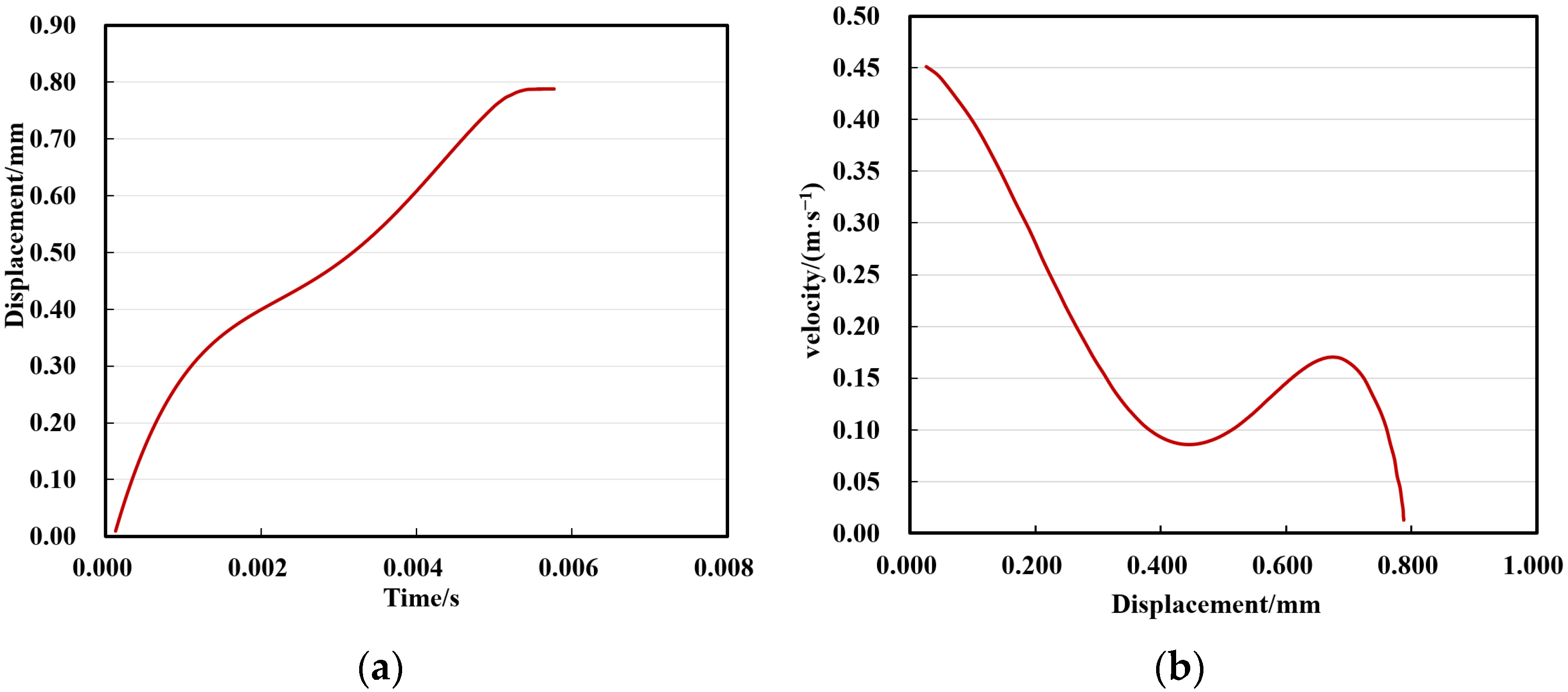
5.1. The Analysis of the Motion Parameters of the Water-Saving Valve
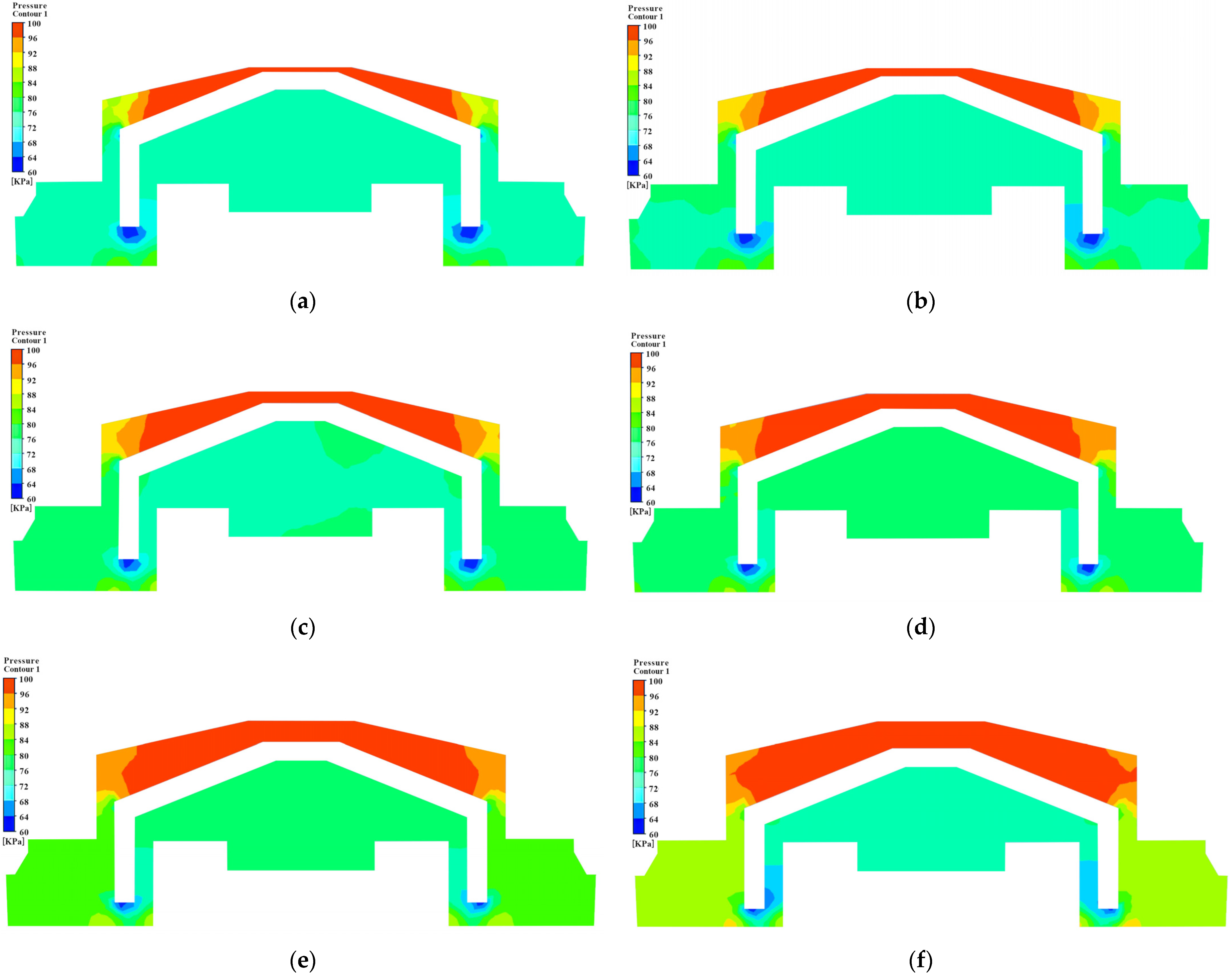
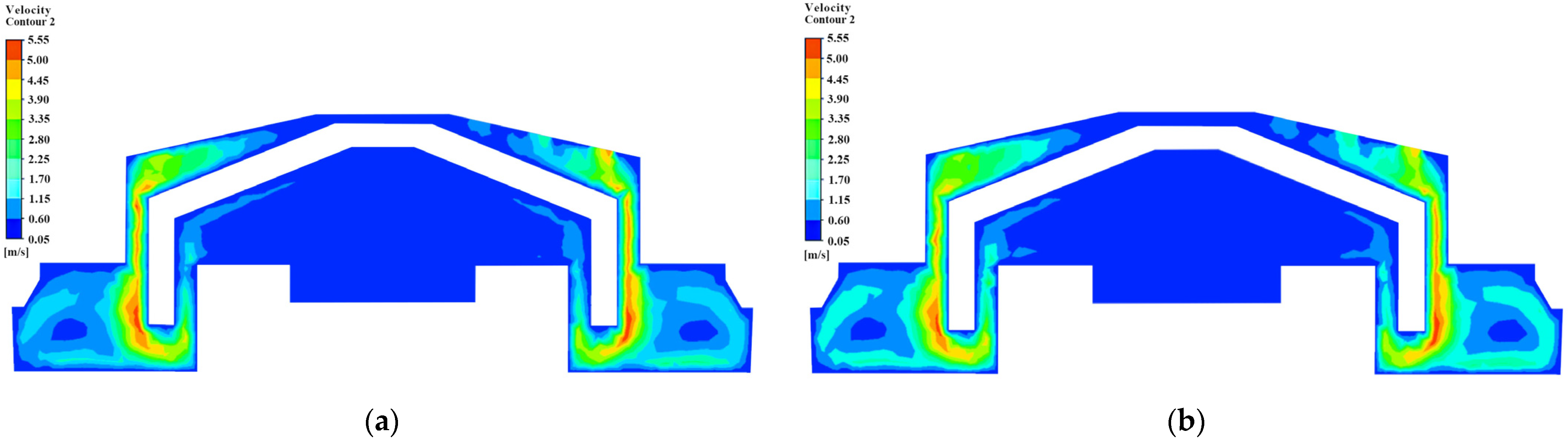
5.2. The Analysis of Pressure and Velocity in the Flow Field
6. Conclusions
- A transient CFD model of a water-saving device was successfully developed and validated using UDF program, facilitating the design of elastic component parameters in water-saving device flow control systems. Through iterative computation, the initial length of the elastic component in the flow control system was determined to be 3.5 mm, and the initial opening height of the water-saving valve was set at 1 mm;
- In response to the aforementioned simulation calculations, relevant flow testing experiments were conducted, and the results of the experimental tests were subjected to necessary processing using the Six Sigma data analysis method. Based on the comparative analysis, it was demonstrated that the relative error between the simulated and experimental results is within 5%, which provides the evidence to support the accuracy of the transient CFD simulation model employed in this paper and the feasibility of the research methodology;
- The opening height of the valve under three different pressures was determined through simulation calculations. The analysis determined the water-saving valve opening heights under three operational pressures (0.1, 0.3, and 0.5 MPa) to be 0.7383 mm, 0.3518 mm, and 0.2116 mm, respectively, with corresponding outlet flow rates of 6.207 L/min, 7.213 L/min, and 7.410 L/min. These results satisfactorily meet national regulatory standards, validating the applied methodology.
- During dynamic valve motion, internal pressure within the flow field increased while flow velocity decreased. At the valve’s limit, the pressure peaked, and the velocity was minimized, consistent with Bernoulli’s theorem and indicating rational flow field distribution dynamics. The simulation analysis of the dynamic pressure and velocity changes in the internal flow field of the constant-flow water-saving device further confirms the accuracy of the mode and provides valuable data for further design improvements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Stiffness coefficient of elastic elements () | |
| Axial displacement increment of elastic elements () | |
| The speed of the water-saving valve at time () | |
| The speed of the water-saving valve at time () | |
| Displacement of water-saving valve at time () | |
| Displacement of water-saving valve at time () | |
| Transient time-step size () | |
| Water-saving valve weight () | |
| Incoming water pressure () | |
| Elastic force of elastic components () | |
| The resultant force acting on the water-saving valve () | |
| The axial pressure component of the incoming flow water pressure on the water-saving valve () | |
| The axial area component of the water-saving valve () | |
| Turbulent kinetic energy | |
| Turbulent dissipation |
References
- Roccaro, P.; Falciglia, P.P.; Vagliasindi, F. Effectiveness of water saving devices and educational programs in urban buildings. Water Sci. Technol. 2011, 63, 1357–1365. [Google Scholar] [CrossRef]
- Martínez-Espiñeira, R.; García-Valiñas, M.Á. Adopting versus adapting: Adoption of water-saving technology versus water conservation habits in Spain. Int. J. Water Resour. Dev. 2013, 29, 400–414. [Google Scholar] [CrossRef]
- Surendran, U.; Raja, P.; Jayakumar, M.; Subramoniam, S.R. Use of efficient water saving techniques for production of rice in India under climate change scenario: A critical review. J. Clean. Prod. 2021, 309, 127272. [Google Scholar] [CrossRef]
- Du, M.; Liao, L.; Wang, B.; Chen, Z. Evaluating the effectiveness of the water-saving society construction in China: A quasi-natural experiment. J. Environ. Manag. 2021, 277, 111394. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Zhang, J.; Wang, T.; Wu, K.; You, L.; Sun, J.; Li, Y.; Li, Y.; Huang, G. Quantifying the mutual effects of water trading and systematic water saving in a water-scarce watershed of China. Water Res. 2024, 257, 121712. [Google Scholar] [CrossRef] [PubMed]
- Tsukiji, T. Flow Analysis in Oil Hydraulic Valve Using Vortex Method. In Proceedings of the 3rd International Symposium on Fluid Power Transmission and Control, Harbin, China, 7–9 September 1999; pp. 67–72. [Google Scholar]
- Milani, M.; Borghi, M.; Paoluzzi, R. Transient flow forces estimation on the pilot stage of a hydraulic valve. In Proceedings of the 1998 ASME IMECE Conference—FPST Division, Anaheim, CA, USA, 15–20 November 1998; pp. 157–162. [Google Scholar]
- Guzzomi, F.G.; O’Neill, P.L.; Tavner, A.C.R. Investigation of Damper Valve Dynamics Using Parametric Numerical Methods; School of Engineering, The University of Queensland: Brisbane, Australia, 2007. [Google Scholar]
- Dossena, V.; Marinoni, F.; Bassi, F.; Franchina, N.; Savini, M. Numerical and experimental investigation on the performance of safety valves operating with different gases. Int. J. Press. Vessel. Pip. 2013, 104, 21–29. [Google Scholar] [CrossRef]
- Vaughan, N.D.; Johnston, D.N.; Edge, K.A. Numerical Simulation of Fluid Flow in Poppet Valves. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1992, 206, 119–127. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Shafie, M. Analysis of entropy generation for mixed convection fluid flow in a trapezoidal enclosure using the modified blocked region method. J. Serbian Soc. Comput. Mech. 2020, 14, 97–116. [Google Scholar] [CrossRef]
- Mahmoodabadi, M.; Mahmoodabadi, F.; Atashafrooz, M. Development of the meshless local Petrov-Galerkin method to analyze three-dimensional transient incompressible laminar fluid flow. J. Serbian Soc. Comput. Mech. 2018, 12, 128–152. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Nassab, S.G. Simulation of three-dimensional laminar forced convection flow of a radiating gas over an inclined backward-facing step in a duct under bleeding condition. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 332–345. [Google Scholar] [CrossRef]
- de Oliveira Marum, V.J.; Reis, L.B.; Maffei, F.S.; Ranjbarzadeh, S.; Korkischko, I.; dos Santos Gioria, R.; Meneghini, J.R. Performance analysis of a water ejector using Computational Fluid Dynamics (CFD) simulations and mathematical modeling. Energy 2021, 220, 119779. [Google Scholar] [CrossRef]
- Duan, X.; Shi, B.; Wang, J.; Song, S.; Liu, H.; Li, X.; Chen, Y.; Liao, Q.; Gong, J.; Chen, S. Simulation of the hydrate blockage process in a water-dominated system via the CFD-DEM method. J. Nat. Gas Sci. Eng. 2021, 96, 104241. [Google Scholar] [CrossRef]
- Wen, T.; Lu, L.; Zhang, S.; Zhong, H. Experimental study and CFD modelling on the thermal and flow behavior of EG/water ZnO nanofluid in multiport mini channels. Appl. Therm. Eng. 2021, 182, 116089. [Google Scholar] [CrossRef]
- Moghadam, M.M.; Islami, H.R.; Ezam, M.; Mousavi, S.A. Optimizing flow uniformity and velocity fields in Aquaculture Tanks by modifying water inlets and nozzles arrangement: A Computational Fluid Dynamics Study. Aquac. Eng. 2024, 106, 102431. [Google Scholar] [CrossRef]
- Temam, R. Navier–Stokes Equations: Theory and Numerical Analysis; American Mathematical Society: Providence, RI, USA, 2024; Volume 343. [Google Scholar]
- Gaitan, F. Finding flows of a Navier–Stokes fluid through quantum computing. npj Quantum Inf. 2020, 6, 61. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Tran, L.N. Reduce the sway of the crane payload using on-off damping radial spring-damper. Mech. Eng. J. 2023, 10, 22-00321. [Google Scholar] [CrossRef]
- Gilormini, P.; Chinesta, F. Viscous drag and rod orientation kinematics in an orthotropic fluid. J. Non-Newton. Fluid Mech. 2019, 270, 96–103. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, W.; Jiang, J.; Wang, X.; Li, S.; Luo, X. Experimental and numerical investigations of flow-induced vibration of tube arrays subjected to cross flow. Int. J. Press. Vessel. Pip. 2019, 176, 103956. [Google Scholar] [CrossRef]
- Kamer, M.S.; Kaya, A.; Sisman, A. Experimental And Numerical Investigation Of The Flow Analysis Of The Water-Saving Safety Valve. Int. J. Sci. Technol. Res. 2015, 4, 189–196. [Google Scholar]
- Ding, M.; Zhang, S.; Wang, J.; Ye, F.; Chen, Z. Study on Spatial and Temporal Distribution Characteristics of the Cooking Oil Fume Particulate and Carbon Dioxide Based on CFD and Experimental Analyses. Atmosphere 2023, 14, 1522. [Google Scholar] [CrossRef]
- Fabbrocino, F.; Funari, M.F.; Greco, F.; Lonetti, P.; Luciano, R.; Penna, R. Dynamic crack growth based on moving mesh method. Compos. Part B Eng. 2019, 174, 107053. [Google Scholar] [CrossRef]
- Manning, A.; Qian, L.; Erfani, R. CFD modelling of velocity fields around a fume cupboard: Evaluating static and dynamic meshes with experimental measurements. Eur. J. Mech.-B/Fluids 2024, 105, 238–246. [Google Scholar] [CrossRef]
- Hui, T.; Chenyang, Z.; Yifei, S.; Kai, X. SuperUDF: Self-supervised UDF Estimation for Surface Reconstruction. IEEE Trans. Vis. Comput. Graph. 2023, 30, 5965–5975. [Google Scholar]
- Yi, Z.; Xuemin, L.; Maulidi, B.; Weiming, X. CFD wind turbines wake effects by using UDF. IOP Conf. Ser. Earth Environ. Sci. 2021, 766, 012025. [Google Scholar]
- Zhiming, X.; Jinhui, L.; Zhimin, H. Ash deposition characteristics of flue gas across a tube using the Eulerian multiphase model with dynamic mesh technique. Powder Technol. 2023, 419, 118369. [Google Scholar]
- Peng, L.; Chen, Z.; Hu, Y. Numerical investigation of turbocharger turbine temperature field based on conjugate heat transfer. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 09544089211039976. [Google Scholar] [CrossRef]
- Schäfle, C.; Kautz, C. Student reasoning in hydrodynamics: Bernoulli’s principle versus the continuity equation. Phys. Rev. Phys. Educ. Res. 2021, 17, 010147. [Google Scholar] [CrossRef]

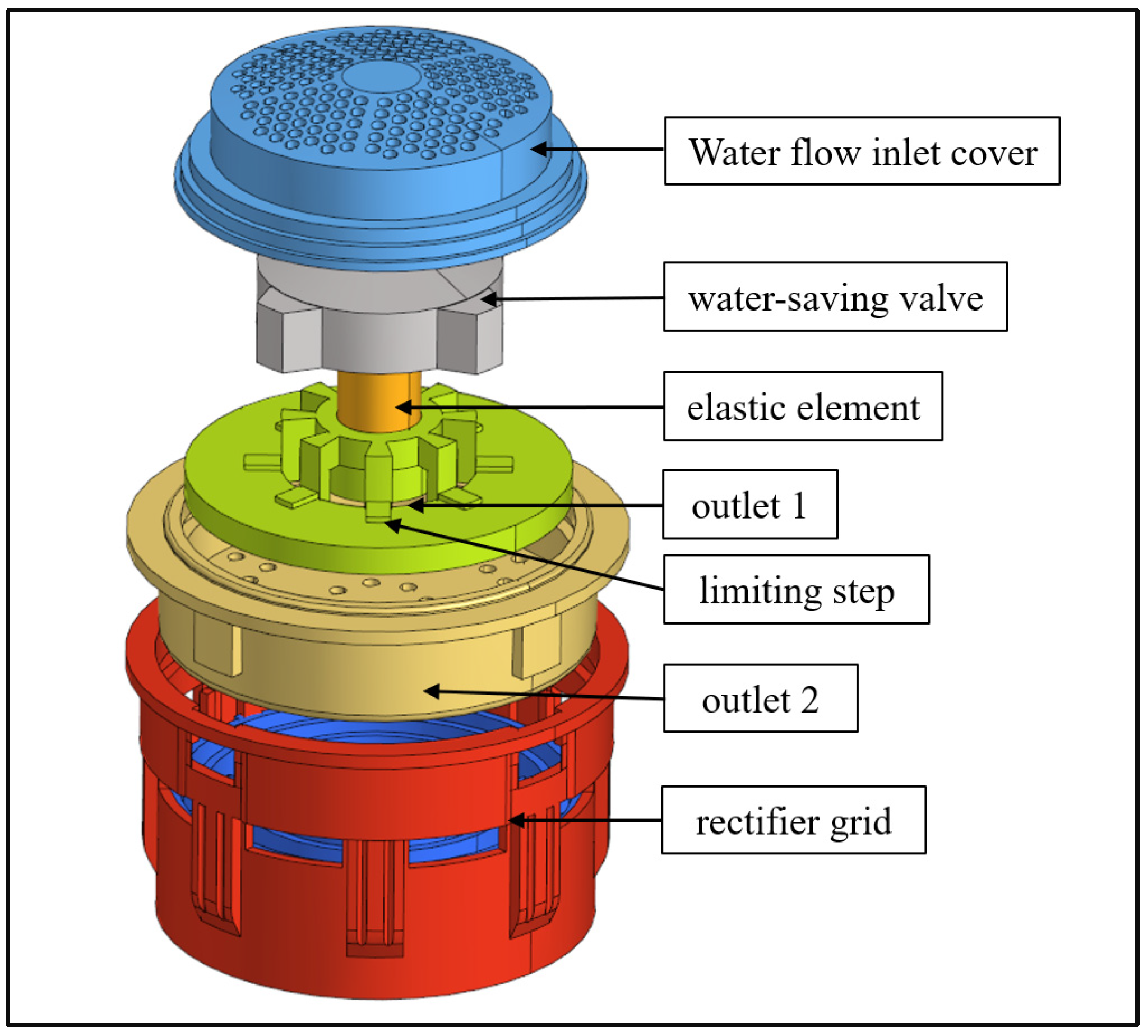
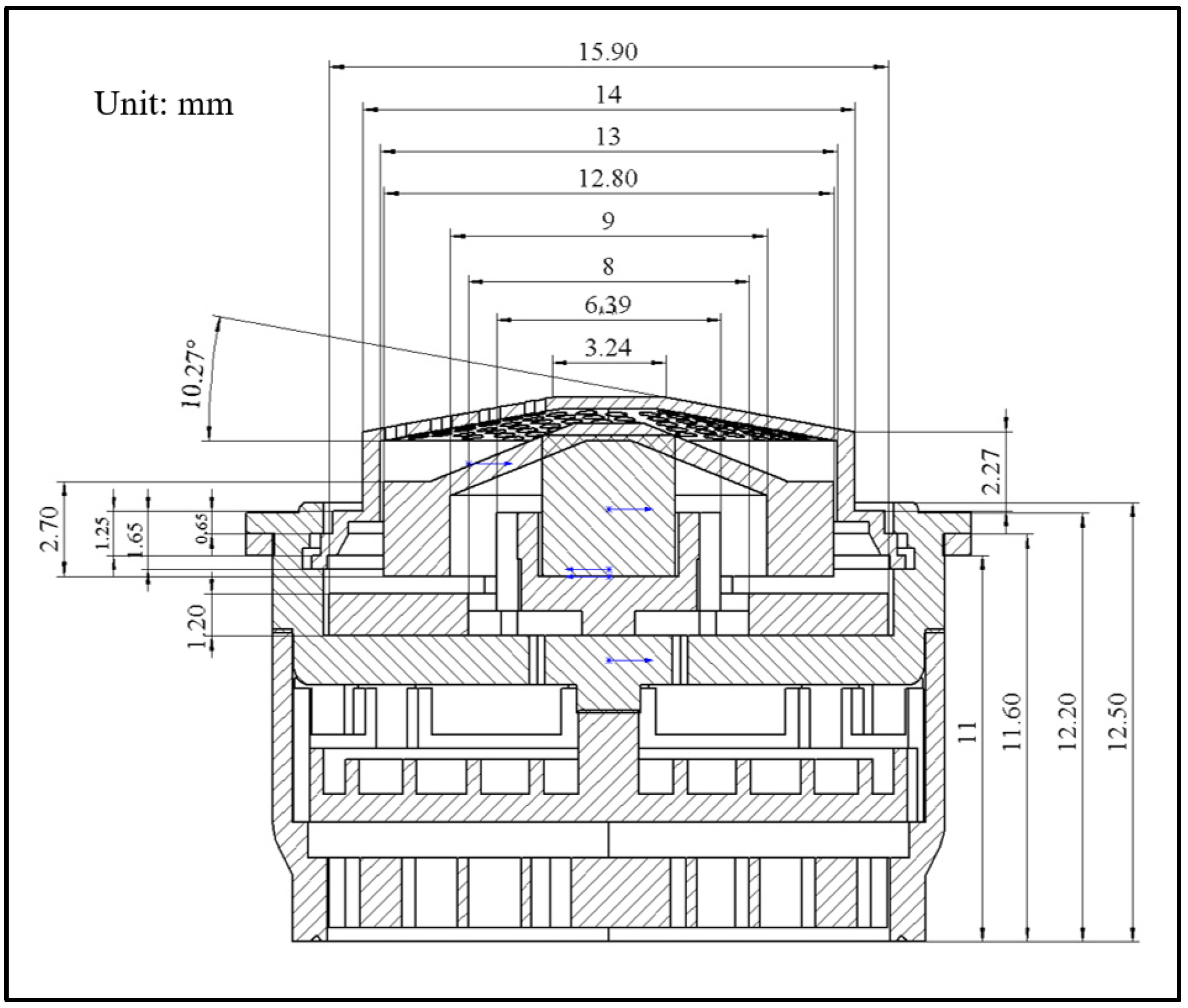
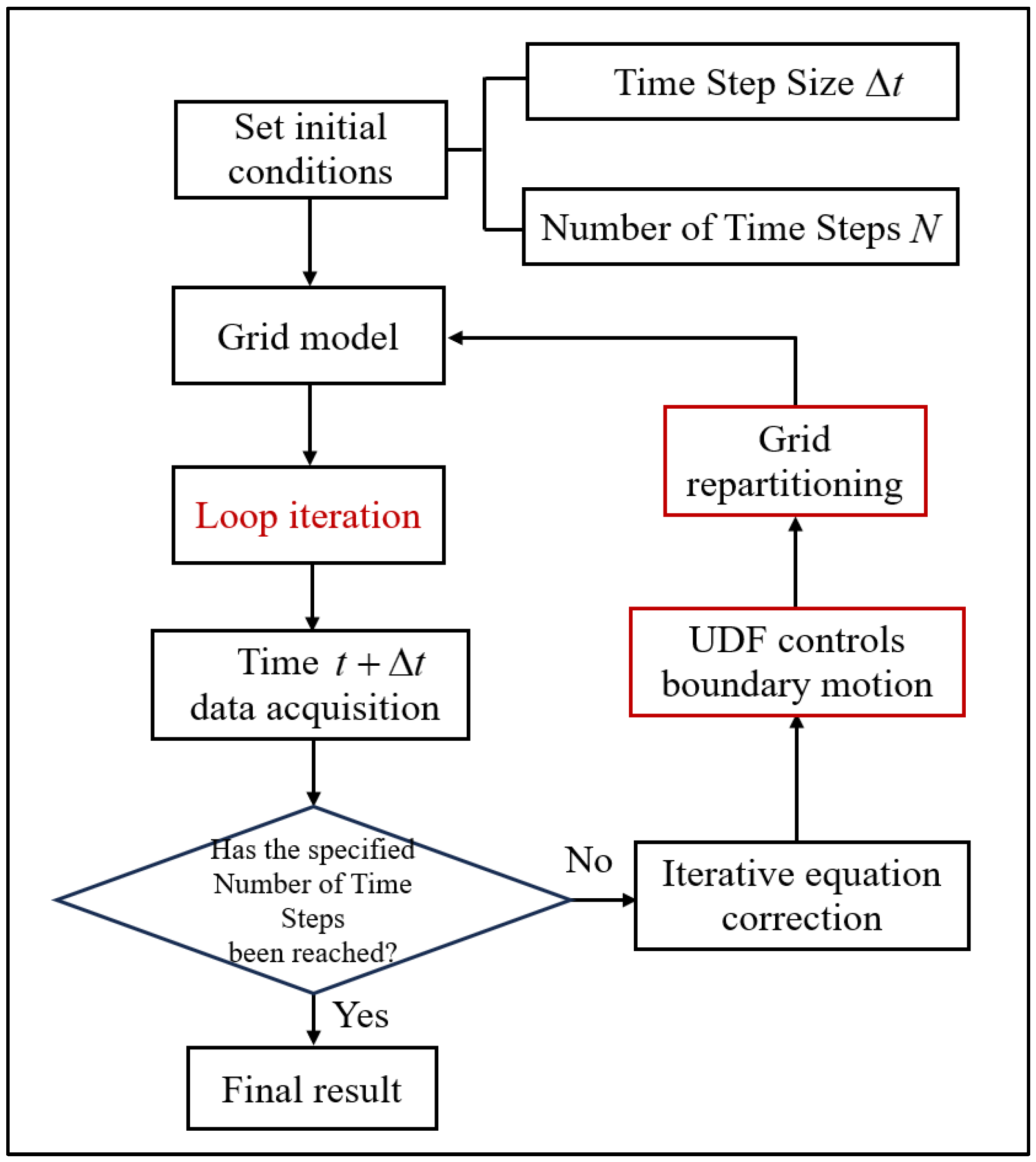
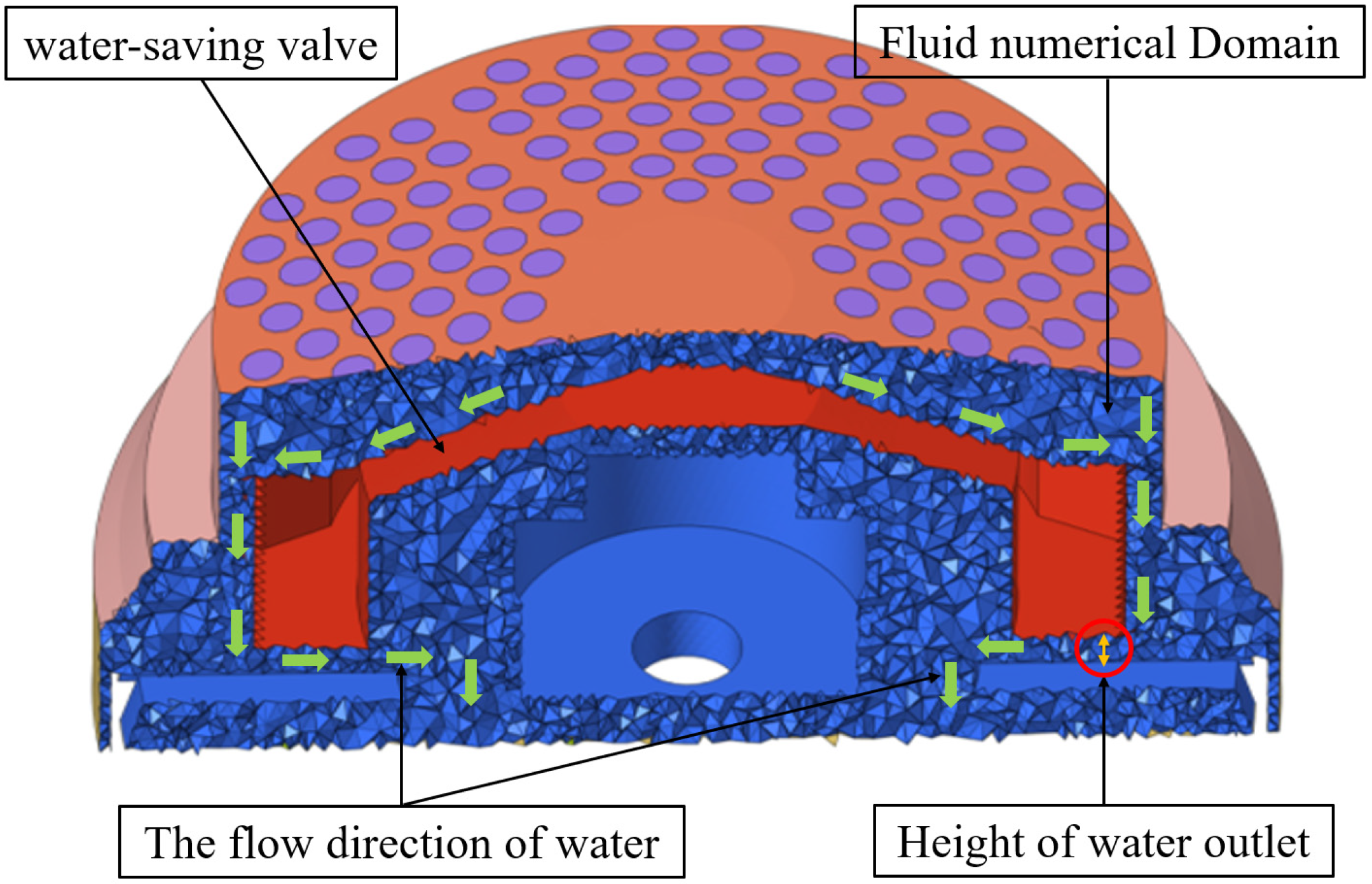


| Boundary Region | Boundary Condition Type | Parameter Setting |
|---|---|---|
| Water inlet | Pressure inlet | Gauge pressure 0.1/0.3/0.5 MPa |
| Cover | Wall | No sliding/Standard |
| Wall | Wall | No sliding/Standard |
| Water-saving valve | Wall | Motion rigid body/Dynamic mesh |
| Outlet wall | Wall | No sliding/Standard |
| Outlet for water flow | Pressure outlet | Gauge pressure 0 Pa |
| Inlet Water Pressure | 0.1 MPa | 0.3 MPa | 0.5 MPa |
|---|---|---|---|
| 1st time | 5.38 | 7.64 | 7.14 |
| 2nd time | 5.27 | 7.27 | 7.30 |
| 3rd time | 6.23 | 7.42 | 7.52 |
| 4th time | 6.01 | 7.13 | 7.12 |
| 5th time | 5.71 | 6.99 | 7.85 |
| 6th time | 5.79 | 6.92 | 7.38 |
| 7th time | 5.98 | 7.03 | 6.74 |
| 8th time | 6.13 | 7.08 | 7.25 |
| 9th time | 5.73 | 7.32 | 7.62 |
| 10th time | 5.74 | 7.37 | 7.04 |
| ori_average | 5.80 | 7.22 | 7.30 |
| max | 6.23 | 7.64 | 7.85 |
| min | 5.27 | 6.92 | 6.74 |
| amplitude | 0.48 | 0.36 | 0.56 |
| 95% | 6.01 | 7.38 | 7.55 |
| 5% | 5.77 | 7.06 | 7.27 |
| new_average | 5.93 | 7.23 | 7.41 |
| Operating Conditions | Transient Simulation Calculation Data | Experimental Data | Relative Error |
|---|---|---|---|
| 0.1 MPa | 6.207 L/min | 5.927 L/min | 4.51% |
| 0.3 MPa | 7.213 L/min | 7.234 L/min | 0.29% |
| 0.5 MPa | 7.306 L/min | 7.410 L/min | 1.42% |
| Inlet Water Pressure | 0.1 MPa | 0.3 MPa | 0.5 MPa |
|---|---|---|---|
| The time required for the motion to reach a steady state. | 0.0074 s | 0.0067 s | 0.0058 s |
| The distance travelled by the water-saving valve during motion. | 0.2617 mm | 0.6482 mm | 0.7884 mm |
| The height of the limit step of the valve. | 0.7383 mm | 0.3518 mm | 0.2116 mm |
| The maximum velocity achieved during the motion process. | 0.0849 m/s | 0.2012 m/s | 0.4512 m/s |
| The maximum resultant force exerted on the water-saving valve. | −6.9760 N | −20.9787 N | 33.8751 N |
| The steady-state flow rate at the outlet of the water outlet. | 6.207 L/min | 7.213 L/min | 7.306 L/min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Li, B.; Li, A.; Yu, B.; Chen, Z.; Jiang, P. Research on Constant-Flow Water-Saving Device Based on Dynamic Mesh Transient Flow Field Analysis. Water 2024, 16, 2427. https://doi.org/10.3390/w16172427
Zhang S, Li B, Li A, Yu B, Chen Z, Jiang P. Research on Constant-Flow Water-Saving Device Based on Dynamic Mesh Transient Flow Field Analysis. Water. 2024; 16(17):2427. https://doi.org/10.3390/w16172427
Chicago/Turabian StyleZhang, Shunyu, Boyan Li, Ang Li, Bingsong Yu, Zhenlei Chen, and Peng Jiang. 2024. "Research on Constant-Flow Water-Saving Device Based on Dynamic Mesh Transient Flow Field Analysis" Water 16, no. 17: 2427. https://doi.org/10.3390/w16172427
APA StyleZhang, S., Li, B., Li, A., Yu, B., Chen, Z., & Jiang, P. (2024). Research on Constant-Flow Water-Saving Device Based on Dynamic Mesh Transient Flow Field Analysis. Water, 16(17), 2427. https://doi.org/10.3390/w16172427





