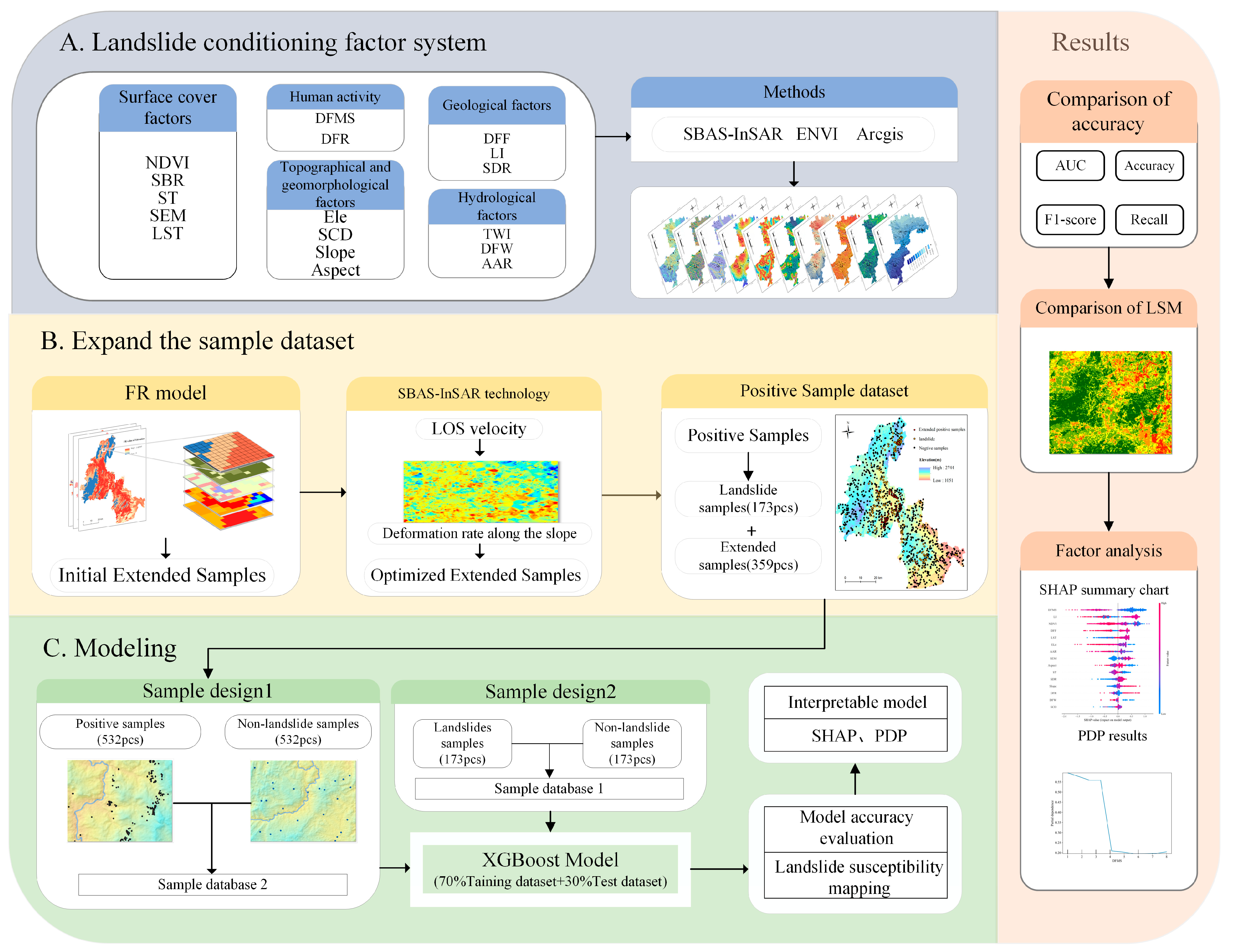
A Novel Dataset Replenishment Strategy Integrating Time-Series InSAR for Refined Landslide Susceptibility Mapping in Karst Regions
Abstract
1. Introduction
2. Study Area and Data
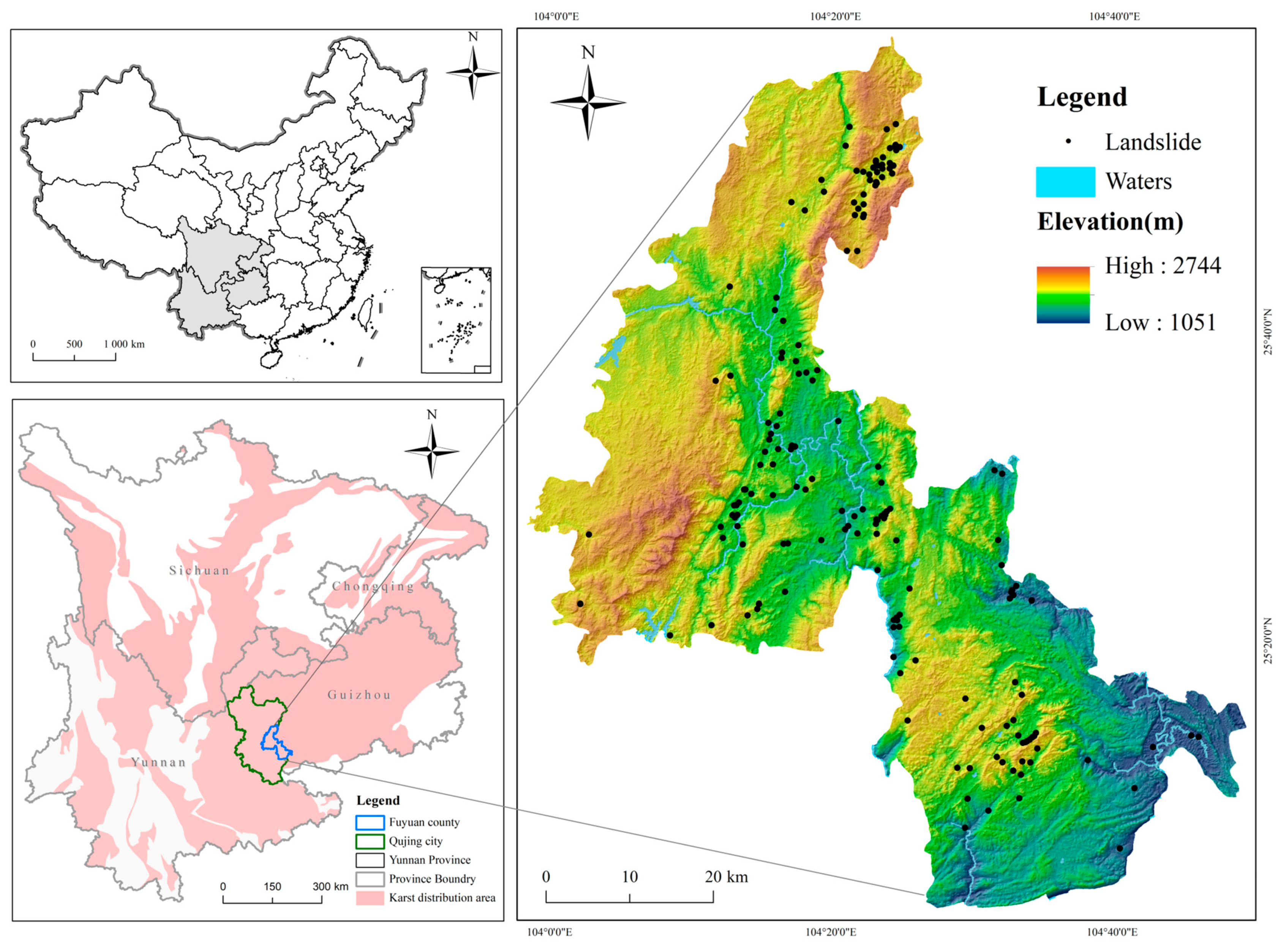
2.1. Overview of the Study Area
2.2. Conditioning Factor Spatial Database
2.2.1. Data Sources
2.2.2. Factor Selection and Processing
3. Methodology
3.1. Frequency Ratio Method
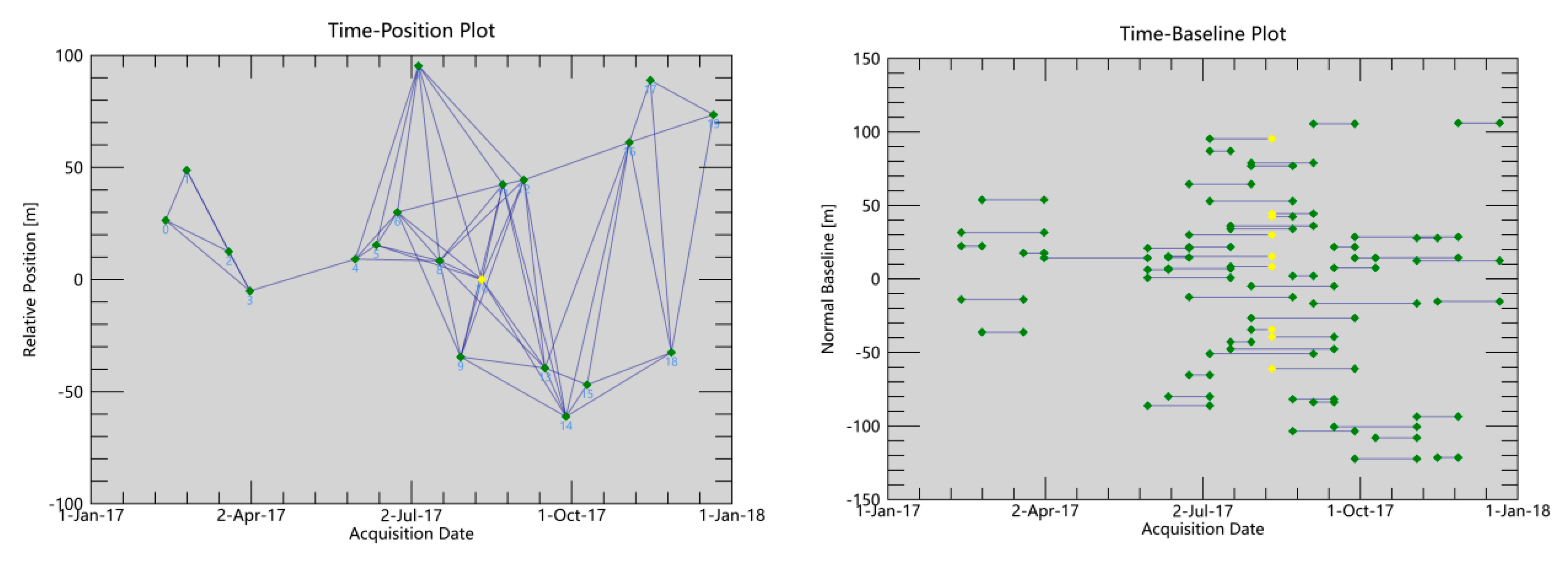
3.2. SBAS-InSAR Technology
3.3. XGBoost Algorithm
3.4. SHAP Algorithm
3.5. PDP Algorithm
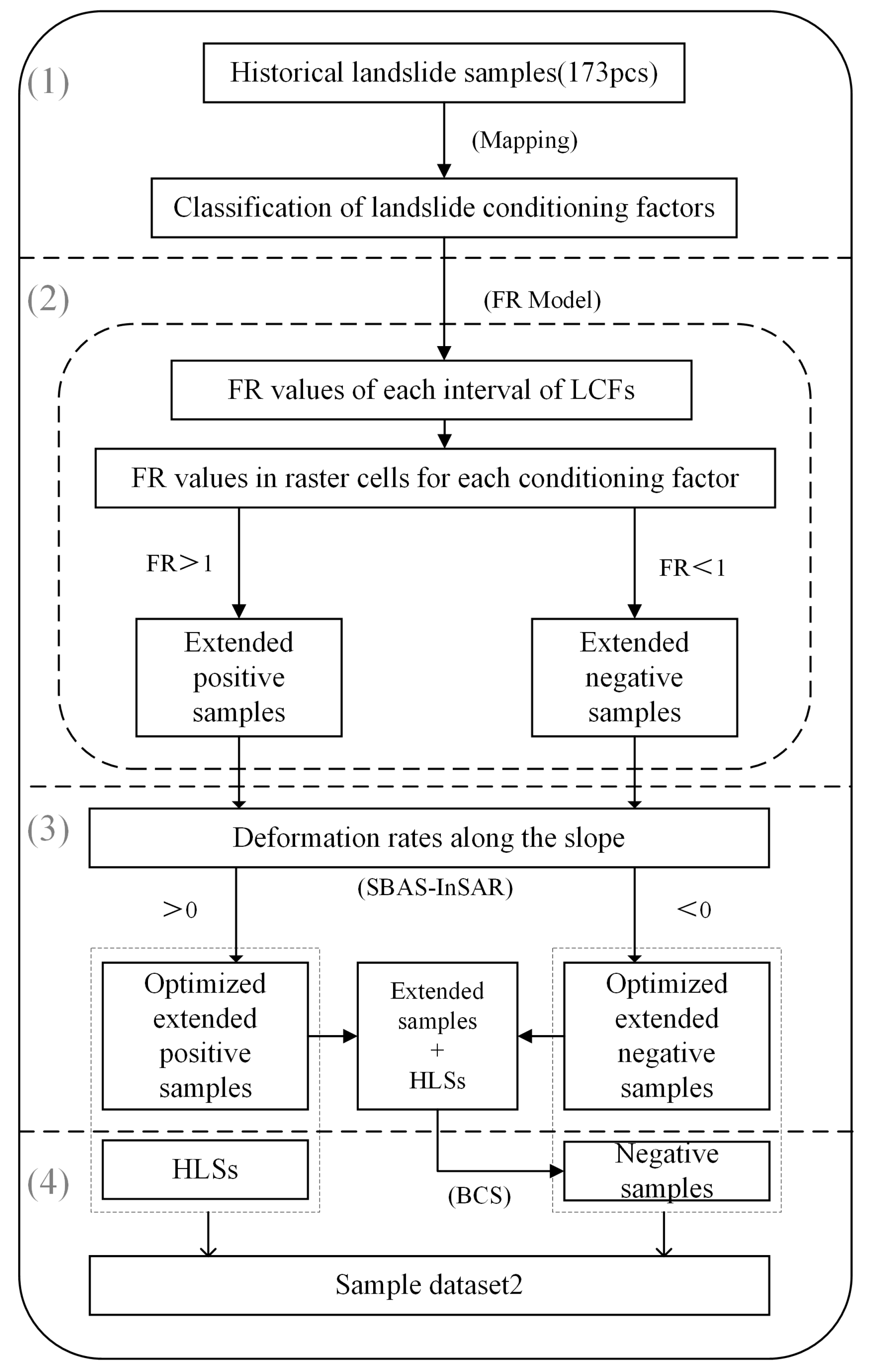
3.6. Sampling Strategies
- (1)
- Calculate the frequency ratio (FR) value for each interval of each conditioning factor to obtain an FR value attribute dataset based on raster cells.
- (2)
- Create an initial expansion sample set based on FR values. Filter samples using geographic environment indicators: select raster cells with a minimum FR value greater than 1 as expansion positive samples, totaling 955; select raster cells with a maximum FR value less than 1 as expansion negative samples, totaling 99.
- (3)
- Use the deformation rate along the slope direction obtained by SBAS-InSAR technology to refine the expanded sample dataset. The deformation rate along the line of sight (LOS) of the satellite imaging is initially deduced using SBAS-InSAR technology. However, there is some bias between this deformation information and the actual surface deformation. Therefore, the LOS deformation rate is converted to the slope direction deformation rate using a relevant formula and interpolated in ArcGIS with the inverse distance weighting method. Only negative deformation rate values are retained to obtain the final deformation rate distribution along the slope direction (Figure 7). If the deformation rate along the slope direction is less than 0, it indicates deformation in that direction; if greater than 0, it indicates no deformation. Considering surface spatial deformation factors fully, the final expanded positive samples are those with slope direction deformation rates less than 0, totaling 359, and the final expanded negative samples are those with deformation rates greater than 0, totaling 16.
- (4)
- The buffer-controlled sampling (BCS) method was used to generate random non-landslide samples. These samples, along with the expanded set of positive and negative samples and historical landslide samples, were merged to achieve a 1:1 ratio of landslide to non-landslide samples. This process created the final dataset.
4. Results
4.1. Models’ Performance Test and Comparison
4.1.1. Confusion Matrix
4.1.2. ROC Curve and AUC Value
4.2. Comparison of Landslide Susceptibility Mapping
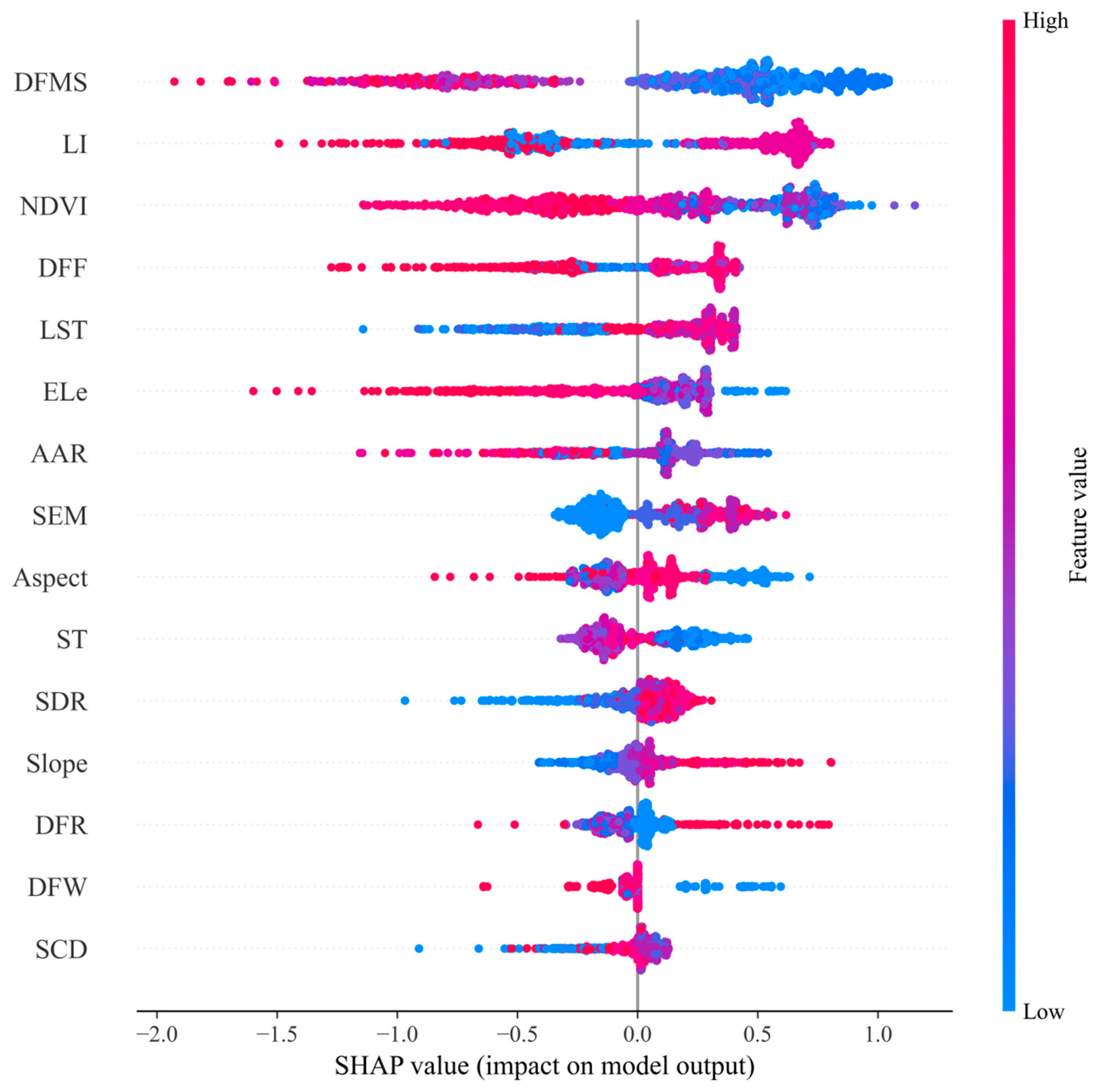
4.3. SHAP Interpretability Results
5. Discussion
5.1. Effectiveness of Combining FR and SBAS-InSAR Sample Extension Strategies
5.2. Analysis of the Primary Contributing Factors of Landslide Susceptibility in Karst Landscapes Based on SHAP Modeling
5.3. Impact Analysis of Significant Contributing Factors Based on PDP Modeling
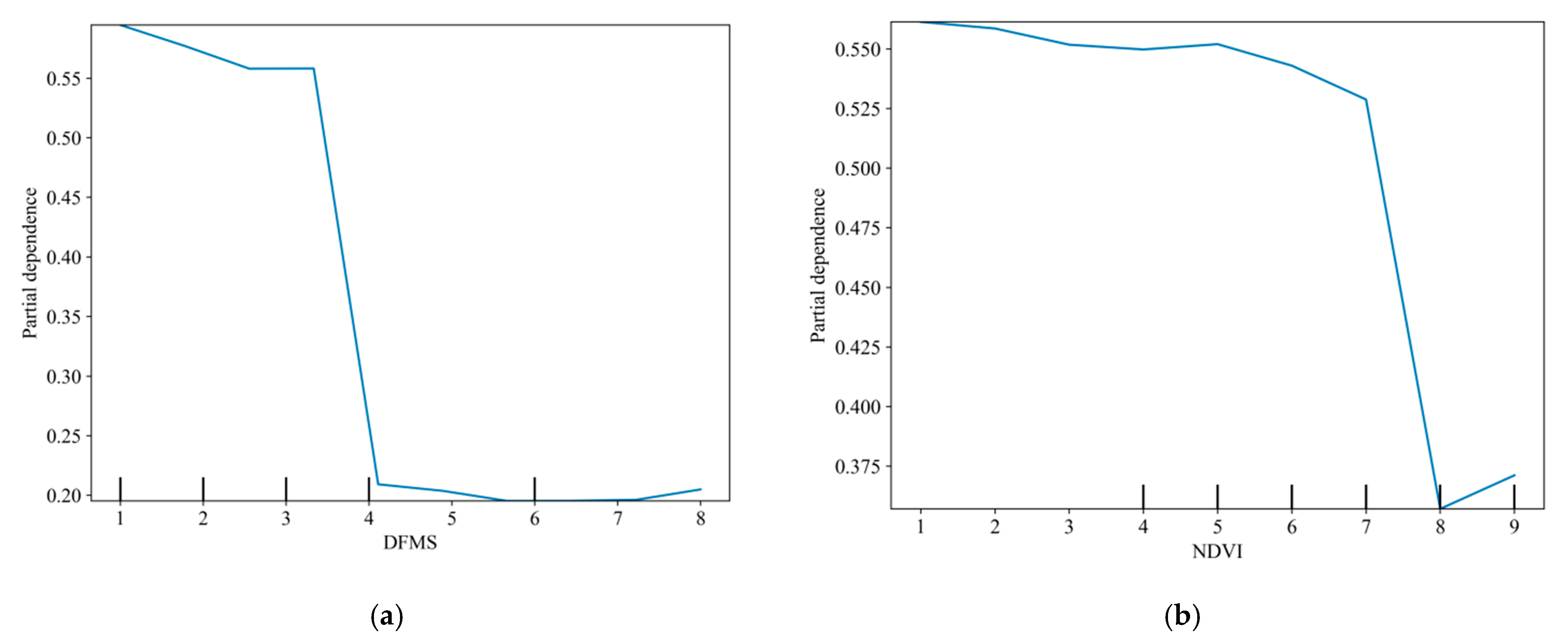
5.3.1. One-Factor Dependence Analysis of Distance from Mining Sites
5.3.2. One-Factor Dependence Analysis of NDVI
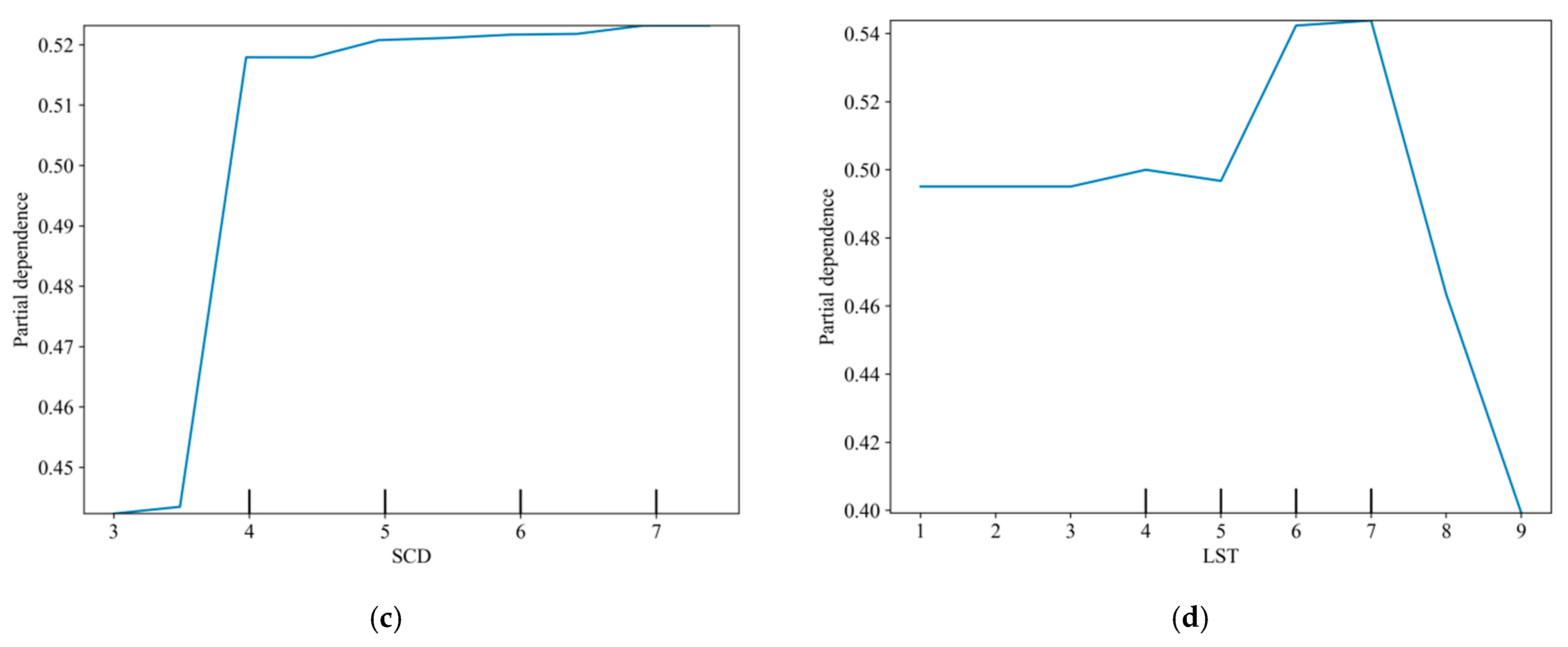
5.3.3. One-Factor Dependence Analysis of Surface Deformation Rate
5.3.4. One-Factor Dependence Analysis of Land Surface Temperature
6. Conclusions
- (1)
- The sample expansion strategy combining the frequency ratio (FR) and SBAS-InSAR technology interpretation results effectively improves model prediction accuracy and stability. The sample expansion strategy reduces the similarity between negative and positive samples, mitigating the impact of sample imbalance on model training. The optimized model can identify high-risk areas more accurately, proving the method’s effectiveness and practicality
- (2)
- The XGBoost-SHAP-PDP algorithm constructs a comprehensive interpretation framework for the landslide susceptibility assessment model, allowing exploration and interpretation from multiple perspectives. Distance from mining sites, lithology, NDVI, distance from faults, and land surface temperature are the top five contributing factors. The vulnerability of lithology and the destructive effect of mining activities on slope stability are important reasons for frequent landslides in karst areas. Meanwhile, factors such as average annual rainfall, soil erosion modulus, and surface deformation rate also greatly influence landslide occurrence.
- (3)
- Introducing factors such as soil erosion modulus, surface deformation rate, and land surface temperature significantly improves the model’s prediction ability. Applying these factors helps to understand and evaluate the spatial pattern of landslide disasters more comprehensively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
- Fang, H.; Shao, Y.; Xie, C.; Tian, B.; Shen, C.; Zhu, Y.; Guo, Y.; Yang, Y.; Chen, G.; Zhang, M. A new approach to spatial landslide susceptibility prediction in karst mining areas based on explainable artificial intelligence. Sustainability 2023, 15, 3094. [Google Scholar] [CrossRef]
- Sun, D.; Chen, D.; Zhang, J.; Mi, C.; Gu, Q.; Wen, H. Landslide susceptibility mapping based on interpretable machine learning from the perspective of geomorphological differentiation. Land 2023, 12, 1018. [Google Scholar] [CrossRef]
- Pradhan, A.; Kim, Y. Evaluation of a combined spatial multi-criteria evaluation model and deterministic model for landslide susceptibility mapping. Catena 2016, 140, 125–139. [Google Scholar] [CrossRef]
- Akgun, A. A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: A case study at İzmir, Turkey. Landslides 2012, 9, 93–106. [Google Scholar] [CrossRef]
- Wen, H.; Liu, L.; Zhang, J.; Hu, J.; Huang, X. A hybrid machine learning model for landslide-oriented risk assessment of long-distance pipelines. J. Environ. Manag. 2023, 342, 118177. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Li, B.; Zhao, C.; Li, J.; Chen, H.; Gao, Y.; Cui, F.; Wan, J. Mechanism of mining-induced landslides in the karst mountains of Southwestern China: A case study of the Baiyan landslide in Guizhou. Landslides 2023, 20, 1481–1495. [Google Scholar] [CrossRef]
- Gutiérrez, F.; Parise, M.; De Waele, J.; Jourde, H. A review on natural and human-induced geohazards and impacts in karst. Earth-Sci. Rev. 2014, 138, 61–88. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Mohammadi, A.; Shahabi, H.; Ahmad, B.B.; Al-Ansari, N.; Shirzadi, A.; Clague, J.J.; Jaafari, A.; Chen, W.; Nguyen, H. Landslide susceptibility mapping using machine learning algorithms and remote sensing data in a tropical environment. Int. J. Environ. Res. Public Health 2020, 17, 4933. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Zhang, J.; Sun, D.; Zhou, X.; Mi, C.; Wen, H. Insights into geospatial heterogeneity of landslide susceptibility based on the SHAP-XGBoost model. J. Environ. Manag. 2023, 332, 117357. [Google Scholar] [CrossRef]
- Wei, A.; Yu, K.; Dai, F.; Gu, F.; Zhang, W.; Liu, Y. Application of tree-based ensemble models to landslide susceptibility mapping: A comparative study. Sustainability 2022, 14, 6330. [Google Scholar] [CrossRef]
- Liu, L.-L.; Zhang, Y.-L.; Xiao, T.; Yang, C. A frequency ratio–based sampling strategy for landslide susceptibility assessment. Bull. Eng. Geol. Environ. 2022, 81, 360. [Google Scholar] [CrossRef]
- Ou, C.; Liu, J.; Qian, Y.; Chong, W.; Zhang, X.; Liu, W.; Su, H.; Zhang, N.; Zhang, J.; Duan, C.-Z. Rupture risk assessment for cerebral aneurysm using interpretable machine learning on multidimensional data. Front. Neurol. 2020, 11, 570181. [Google Scholar] [CrossRef]
- Ariza-Garzón, M.J.; Arroyo, J.; Caparrini, A.; Segovia-Vargas, M.-J. Explainability of a machine learning granting scoring model in peer-to-peer lending. IEEE Access 2020, 8, 64873–64890. [Google Scholar] [CrossRef]
- Can, R.; Kocaman, S.; Gokceoglu, C. A comprehensive assessment of XGBoost algorithm for landslide susceptibility mapping in the upper basin of Ataturk dam, Turkey. Appl. Sci. 2021, 11, 4993. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. Prioritization of landslide conditioning factors and its spatial modeling in Shangnan County, China using GIS-based data mining algorithms. Bull. Eng. Geol. Environ. 2018, 77, 611–629. [Google Scholar] [CrossRef]
- Sun, D.; Gu, Q.; Wen, H.; Shi, S.; Mi, C.; Zhang, F. A hybrid landslide warning model coupling susceptibility zoning and precipitation. Forests 2022, 13, 827. [Google Scholar] [CrossRef]
- Ballabio, C.; Sterlacchini, S. Support vector machines for landslide susceptibility mapping: The Staffora River Basin case study, Italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Liu, L.-L.; Yang, C.; Wang, X.-M. Landslide susceptibility assessment using feature selection-based machine learning models. Geomech. Eng 2021, 25, 1–16. [Google Scholar]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi Province, China. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Gao, H.; Fam, P.S.; Tay, L.T.; Low, H.C. Three oversampling methods applied in a comparative landslide spatial research in Penang Island, Malaysia. SN Appl. Sci. 2020, 2, 1512. [Google Scholar] [CrossRef]
- Barua, S.; Islam, M.M.; Yao, X.; Murase, K. MWMOTE--majority weighted minority oversampling technique for imbalanced data set learning. IEEE Trans. Knowl. Data Eng. 2012, 26, 405–425. [Google Scholar] [CrossRef]
- San, B.T. An evaluation of SVM using polygon-based random sampling in landslide susceptibility mapping: The Candir catchment area (western Antalya, Turkey). Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 399–412. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Zhu, A.-X.; Miao, Y.; Liu, J.; Bai, S.; Zeng, C.; Ma, T.; Hong, H. A similarity-based approach to sampling absence data for landslide susceptibility mapping using data-driven methods. Catena 2019, 183, 104188. [Google Scholar] [CrossRef]
- Erener, A.; Sivas, A.A.; Selcuk-Kestel, A.S.; Düzgün, H.S. Analysis of training sample selection strategies for regression-based quantitative landslide susceptibility mapping methods. Comput. Geosci. 2017, 104, 62–74. [Google Scholar] [CrossRef]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Optimization of landslide conditioning factors using very high-resolution airborne laser scanning (LiDAR) data at catchment scale. Remote Sens. Environ. 2014, 152, 150–165. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Zhang, Y.; Xu, J.; Zhang, W. Landslide susceptibility mapping using hybrid random forest with GeoDetector and RFE for factor optimization. Geosci. Front. 2021, 12, 101211. [Google Scholar] [CrossRef]
- Galloway, D.L.; Erkens, G.; Kuniansky, E.L.; Rowland, J.C. Preface: Land subsidence processes. Hydrogeol. J. 2016, 24, 547–550. [Google Scholar] [CrossRef]
- Abelson, M.; Baer, G.; Shtivelman, V.; Wachs, D.; Raz, E.; Crouvi, O.; Kurzon, I.; Yechieli, Y. Collapse-sinkholes and radar interferometry reveal neotectonics concealed within the Dead Sea basin. Geophys. Res. Lett. 2003, 30, 1545. [Google Scholar] [CrossRef]
- Gutiérrez, F. Gypsum karstification induced subsidence: Effects on alluvial systems and derived geohazards (Calatayud Graben, Iberian Range, Spain). Geomorphology 1996, 16, 277–293. [Google Scholar] [CrossRef]
- Pedrozzi, G. Triggering of landslides in Canton Ticino (Switzerland) and prediction by the rainfall intensity and duration method. Bull. Eng. Geol. Environ. 2004, 63, 281–291. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.-T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Xingli, J.; Qingmiao, D.; Hongzhi, Y. Susceptibility zoning of karst geological hazards using machine learning and cloud model. Clust. Comput. 2019, 22, 8051–8058. [Google Scholar] [CrossRef]
- Parise, M. Rock failures in karst. In Landslides and Engineered Slopes: From the Past to the Future; Chen, Z., Zhang, J.-M., Ho, K., Wu, F.-Q., Li, Z.-K., Eds.; RC Press: London, UK, 2008. [Google Scholar]
- Liu, Z.; Mei, G.; Sun, Y.; Xu, N. Investigating mining-induced surface subsidence and potential damages based on SBAS-InSAR monitoring and GIS techniques: A case study. Environ. Earth Sci. 2021, 80, 817. [Google Scholar] [CrossRef]
- Yalcin, A.; Bulut, F. Landslide susceptibility mapping using GIS and digital photogrammetric techniques: A case study from Ardesen (NE-Turkey). Nat. Hazards 2007, 41, 201–226. [Google Scholar] [CrossRef]
- Yao, X.; Tham, L.; Dai, F. Landslide susceptibility mapping based on support vector machine: A case study on natural slopes of Hong Kong, China. Geomorphology 2008, 101, 572–582. [Google Scholar] [CrossRef]
- Thomas, A.V.; Saha, S.; Danumah, J.H.; Raveendran, S.; Prasad, M.K.; Ajin, R.; Kuriakose, S.L. Landslide susceptibility zonation of Idukki district using GIS in the aftermath of 2018 Kerala floods and landslides: A comparison of AHP and frequency ratio methods. J. Geovis. Spat. Anal. 2021, 5, 21. [Google Scholar] [CrossRef]
- Pradhan, B.; Chaudhari, A.; Adinarayana, J.; Buchroithner, M.F. Soil erosion assessment and its correlation with landslide events using remote sensing data and GIS: A case study at Penang Island, Malaysia. Environ. Monit. Assess. 2012, 184, 715–727. [Google Scholar] [CrossRef] [PubMed]
- Habumugisha, J.M.; Chen, N.; Rahman, M.; Islam, M.M.; Ahmad, H.; Elbeltagi, A.; Sharma, G.; Liza, S.N.; Dewan, A. Landslide susceptibility mapping with deep learning algorithms. Sustainability 2022, 14, 1734. [Google Scholar] [CrossRef]
- Parise, M.; Closson, D.; Gutiérrez, F.; Stevanović, Z. Anticipating and managing engineering problems in the complex karst environment. Environ. Earth Sci. 2015, 74, 7823–7835. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A.; Mattar, C.; Ruescas, A.B.; Jimenez-Munoz, J.C.; Soria, G.; Hidalgo, V.; Atitar, M.; Franch, B.; Cuenca, J. Temporal analysis of normalized difference vegetation index (NDVI) and land surface temperature (LST) parameters to detect changes in the Iberian land cover between 1981 and 2001. Int. J. Remote Sens. 2011, 32, 2057–2068. [Google Scholar] [CrossRef]
- Shibasaki, T.; Matsuura, S.; Hasegawa, Y. Temperature-dependent residual shear strength characteristics of smectite-bearing landslide soils. J. Geophys. Res. Solid Earth 2017, 122, 1449–1469. [Google Scholar] [CrossRef]
- Sun, H.; Mašín, D.; Najser, J.; Scaringi, G. Water retention of a bentonite for deep geological radioactive waste repositories: High-temperature experiments and thermodynamic modeling. Eng. Geol. 2020, 269, 105549. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skoković, D.; Mattar, C.; Cristobal, J. Land surface temperature retrieval methods from Landsat-8 thermal infrared sensor data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Millward, A.A.; Mersey, J.E. Adapting the RUSLE to model soil erosion potential in a mountainous tropical watershed. Catena 1999, 38, 109–129. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef]
- Wang, X.; Shi, Y.; Pan, J.; Guo, Y.; Gao, Y.; Wei, J. Remote sensing monitoring evaluation of ecological environment in debris flow disaster prone area. Bull. Surv. Mapp. 2021, 11, 21–24. [Google Scholar]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (Tokat—Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Huang, J.; Wen, H.; Hu, J.; Liu, B.; Zhou, X.; Liao, M. Deciphering decision-making mechanisms for the susceptibility of different slope geohazards: A case study on a SMOTE-RF-SHAP hybrid model. J. Rock Mech. Geotech. Eng. 2024, in press. [Google Scholar] [CrossRef]
- Bailly-Comte, V.; Jourde, H.; Pistre, S. Conceptualization and classification of groundwater–surface water hydrodynamic interactions in karst watersheds: Case of the karst watershed of the Coulazou River (Southern France). J. Hydrol. 2009, 376, 456–462. [Google Scholar] [CrossRef]
- Wei, A.; Li, D.; Zhou, Y.; Deng, Q.; Yan, L. A novel combination approach for karst collapse susceptibility assessment using the analytic hierarchy process, catastrophe, and entropy model. Nat. Hazards 2021, 105, 405–430. [Google Scholar] [CrossRef]
- Bednarik, M.; Magulová, B.; Matys, M.; Marschalko, M. Landslide susceptibility assessment of the Kraľovany–Liptovský Mikuláš railway case study. Phys. Chem. Earth Parts A/B/C 2010, 35, 162–171. [Google Scholar] [CrossRef]
- Shen, C.; Feng, Z.; Xie, C.; Fang, H.; Zhao, B.; Ou, W.; Zhu, Y.; Wang, K.; Li, H.; Bai, H. Refinement of Landslide Susceptibility Map Using Persistent Scatterer Interferometry in Areas of Intense Mining Activities in the Karst Region of Southwest China. Remote Sens. 2019, 11, 2821. [Google Scholar] [CrossRef]
- Mondal, S.; Maiti, R. Integrating the analytical hierarchy process (AHP) and the frequency ratio (FR) model in landslide susceptibility mapping of Shiv-khola watershed, Darjeeling Himalaya. Int. J. Disaster Risk Sci. 2013, 4, 200–212. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Samsonov, S.; van der Kooij, M.; Tiampo, K. A simultaneous inversion for deformation rates and topographic errors of DInSAR data utilizing linear least square inversion technique. Comput. Geosci. 2011, 37, 1083–1091. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, S.; Chen, Z.; Liu, Y.; Xu, Z.; Zhao, R. Landslide susceptibility evaluation integrating weight of evidence model and InSAR results, west of Hubei Province, China. Egypt. J. Remote Sens. Space Sci. 2023, 26, 95–106. [Google Scholar] [CrossRef]
- Bianchini, S.; Herrera, G.; Mateos, R.M.; Notti, D.; Garcia, I.; Mora, O.; Moretti, S. Landslide activity maps generation by means of persistent scatterer interferometry. Remote Sens. 2013, 5, 6198–6222. [Google Scholar] [CrossRef]
- Cascini, L.; Fornaro, G.; Peduto, D. Advanced low-and full-resolution DInSAR map generation for slow-moving landslide analysis at different scales. Eng. Geol. 2010, 112, 29–42. [Google Scholar] [CrossRef]
- Herrera, G.; Gutiérrez, F.; García-Davalillo, J.; Guerrero, J.; Notti, D.; Galve, J.; Fernández-Merodo, J.; Cooksley, G. Multi-sensor advanced DInSAR monitoring of very slow landslides: The Tena Valley case study (Central Spanish Pyrenees). Remote Sens. Environ. 2013, 128, 31–43. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Qi, W.; Sun, R.; Zheng, T.; Qi, J. Prediction and analysis model for ground peak acceleration based on XGBoost and SHAP. Chin. J. Geotech. Eng. 2023, 45, 1934–1943. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems 30 (NIPS 2017); Curran Associates, Inc.: Red Hook, NY, USA, 2017. [Google Scholar]
- Lundberg, S.M.; Nair, B.; Vavilala, M.S.; Horibe, M.; Eisses, M.J.; Adams, T.; Liston, D.E.; Low, D.K.-W.; Newman, S.-F.; Kim, J. Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nat. Biomed. Eng. 2018, 2, 749–760. [Google Scholar] [CrossRef]
- Petch, J.; Di, S.; Nelson, W. Opening the black box: The promise and limitations of explainable machine learning in cardiology. Can. J. Cardiol. 2022, 38, 204–213. [Google Scholar] [CrossRef] [PubMed]
- Santo, A.; Del Prete, S.; Di Crescenzo, G.; Rotella, M. Karst processes and slope instability: Some investigations in the carbonate Apennine of Campania (southern Italy). Geol. Soc. Lond. Spec. Publ. 2007, 279, 59–72. [Google Scholar] [CrossRef]
- El-Haddad, B.A.; Youssef, A.M.; El-Shater, A.-H.; El-Khashab, M.H. Landslide mechanisms along carbonate rock cliffs and their impact on sustainable development: A case study, Egypt. Arab. J. Geosci. 2021, 14, 573. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, Y.; Li, W.; He, J.; Wu, Z. Predictive Modeling of Landslide Hazards in Wen County, Northwestern China Based on Information Value, Weights of Evidence and Certainty Factor. Geomat. Nat. Hazards Risk 2019, 10, 820–835. [Google Scholar] [CrossRef]
- Du, G.-l.; Zhang, Y.-s.; Iqbal, J.; Yang, Z.-h.; Yao, X. Landslide susceptibility mapping using an integrated model of information value method and logistic regression in the Bailongjiang watershed, Gansu Province, China. J. Mt. Sci. 2017, 14, 249–268. [Google Scholar] [CrossRef]
- Xiong, H.; Ma, C.; Li, M.; Tan, J.; Wang, Y. Landslide susceptibility prediction considering land use change and human activity: A case study under rapid urban expansion and afforestation in China. Sci. Total Environ. 2023, 866, 161430. [Google Scholar] [CrossRef]
- Gao, H.; Fan, J. Geological Disasters, the Unbearable Pain of Urban Development; China Geological Survey: Beijing, China, 2015. [Google Scholar]
- Zou, L.; Kent, J.; Lam, N.S.-N.; Cai, H.; Qiang, Y.; Li, K. Evaluating land subsidence rates and their implications for land loss in the lower Mississippi River basin. Water 2015, 8, 10. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, S.; Bai, X.; Tian, Y.; Wu, L.; Xiao, J.; Chen, F.; Qian, Q. Relationship among land surface temperature and LUCC, NDVI in typical karst area. Sci. Rep. 2018, 8, 641. [Google Scholar] [CrossRef] [PubMed]
- Pappalardo, G.; Mineo, S.; Angrisani, A.; Di Martire, D.; Calcaterra, D. Combining field data with infrared thermography and DInSAR surveys to evaluate the activity of landslides: The case study of Randazzo Landslide (NE Sicily). Landslides 2018, 15, 2173–2193. [Google Scholar] [CrossRef]
- Ma, J.; Tang, H.; Hu, X.; Bobet, A.; Yong, R.; Ez Eldin, M.A. Model testing of the spatial–temporal evolution of a landslide failure. Bull. Eng. Geol. Environ. 2017, 76, 323–339. [Google Scholar] [CrossRef]




| Data Name | Data Sources | Typology | Resolution |
|---|---|---|---|
| Historical landslide data | Chinese Academy of Sciences, Center for Resource and Environmental Data and Sciences | Vector (spatial) | - |
| DEM | Geospatial data cloud platform | Raster | 30 m |
| Landsat-8 data | Geospatial data cloud platform | Raster | 30 m |
| Geological data | National Geological Information Data Center (NGIDC) | Vector (spatial) | 1:200,000 |
| Waters | Chinese Academy of Sciences, Center for Resource and Environmental Data and Sciences | Vector (spatial) | 1:100,000 |
| Roads | Chinese Academy of Sciences, Center for Resource and Environmental Data and Sciences | Vector (spatial) | 1:100,000 |
| Multi-year average rainfall | Chinese Academy of Sciences, Center for Resource and Environmental Data and Sciences | raster | 1000 m |
| Administrative subdivision (e.g., of provinces in counties) | National Geographic Information Public Service Platform | Vector (spatial) | 1:100,000 |
| Provenance | National Address Library | Vector (spatial) | - |
| Soil data | World Soil Database (HWSD) | Raster | 1000 m |
| Sentinel-1 data | EarthData ASF Data Search | Raster | 30 m |
| Normalized Difference Vegetation Index (NDVI) | National Science and Technology Resources Sharing Service Platform | Raster | 30 m |
| Categories | Conditioning Factors | Classification/Unit | Classification Criteria |
|---|---|---|---|
| Topographic and geomorphologic factors | Elevation (Ele)/m | 11 | (1) 1051–1427; (2) 1917–2012; (3) 1427–1580; (4) 2012–2099; (5) 1580–1711; (6) 1711–1818; (7) 1818–1917; (8) 2099–2189; (9) 2189–2299; (10) 2299–2439; (11) 2439–2744 |
| Slope/° | 10 | (1) 0–5; (2) 5–10; (3) 10–15; (4) 15–20; (5) 20–25; (6) 25–30; (7) 30–35; (8) 35–40; (9) 40–50; (10) >50 | |
| Surface cutting depth (SCD)/m | 10 | (1) 0~31; (2) 31~47; (3) 47~61; (4) 61–75; (5) 75~90; (6) 90~107; (7) 107~125; (8) 125~148; (9) 148~180; (10) >180 | |
| Aspect | 10 | (1) plane (−1); (2) north (0–22.5); (3) northeast (22.5–67.5); (4) east (67.5–112.7); (5) southeast (112.5–157.5); (6) south (157.5–202.5); (7) southwest (202.5–247.5); (8) west (247.5–292.5); (9) northwest (292.5–337.5); (10) north (337.5–360) | |
| Surface cover factors | Soil bare rate (SBR) | 7 | (1) <−80; (2) −80 to −55; (3) −55 to −36; (4) −36 to −24; (5) −24 to −16; (6) −16 to −11; (7) −11 to −1 |
| Soil erosion modulus (SEM) | 9 | (1) <304; (2) 304–989; (3) 989–1749; (4) 1749–2661; (5) 2662–3802; (6) 3802–5171; (7) 5171–6920; (8) 6920–9581; (9) >9581 | |
| Land surface temperature (LST)/° | 9 | (1) <16; (2) 16–24; (3) 24–28; (4) 28–31; (5) 31–33; (6) 33–36; (7) 36–39; (8) 39–43; (9) 43–54 | |
| NDVI | 9 | (1) <0.20; (2) 0.20–0.33; (3) 0.33–0.43; (4) 0.43–0.52; (5) 0.52–0.59; (6) 0.59–0.66; (7) 0.66–0.74; (8) 0.74–0.83; (9) 0.83–0.99 | |
| Soil type (ST) | 18 | (1) Brown soil; (2) Lakes and waters; (3) Rock; (4) alluvial soil; (5) Yellow soil; (6) paddy soil; (7) Acidic purple clay; (8) Limestone; (9) Yellow-brown loamy soil; (10) Yellow-red soil; (11) black lime; (12) Yellow-brown soil; (13) mountainous red soil; (14) Red soil; (15) Red loamy soil; (16) Brick red soil; (17) calcium phosphate; (18) Dark brown soil | |
| Hydrological factors | Distance from waters (DFW)/m | 9 | (1) <500; (2) 500–1000; (3) 1000–1500; (4) 1500–2000; (5) 2000–2500; (6) 2500–3000; (7) 3000–4000; (8) 4000–9000; (9) >9000 |
| Average annual rainfall (AAR)/mm | 9 | (1) <1007; (2) 1007–1023; (3) 1023–1036; (4) 1036–1052; (5) 1052–1070; (6) 1070–1090; (7) 1090–1112; (8) 1112–1137; (9) >1137 | |
| Topographic wetness index (TWI) | 6 | (1) 2.08–4.88; (2) 4,88–6.33; (3) 6.33–8.13; (4) 8.13–10.48; (5) 10.48–13.95; (6) 13.95–30.62 | |
| Human activity factors | Distance from mining site (DFMS)/m | 10 | (1) <2300; (2) 2300–4141; (3) 4141–5889; (4) 5889–7545; (5) 7545–9201; (6) 9201–10,858; (7) 10,858–12,698; (8) 12,698–14,722; (9) 14,722–17,943; (10) >17,943 |
| Distance from road (DFR)/m | 9 | (1) <428; (2) 428–909; (3) 909–1436; (4) 1436–2029; (5) 2029–1723; (6) 2723–3535; (7) 3535–4555; (8) 4555–6208; (9) >6208 | |
| Geological factors | Lithology (Li) | 8 | (1) C1: lower Carboniferous; (2) C1P1: Carboniferous and Permian juxtaposition; (3) C2: upper Carboniferous; (4) D3C1: Devonian and Carboniferous juxtaposition; (5) P2: Upper Permian; (6) T1: Upper Triassic; (7) T2: middle Triassic; (8) T3:Lower Triassic |
| Distance from fault (DFF)/m | 9 | (1) <500; (2) 500–1000; (3) 1000–1500; (4) 1500–2000; (5) 2000–2500; (6) 2500–3000; (7) 3000–4000; (8) 4000–9000; (9) >9000 | |
| Surface deformation rate (SDR)/mm·a−1 | 9 | (1) <−78; (2) −78 to −50; (3) −50 to −35; (4) −35 to −23; (5) −23 to −12; (6) −12 to −1; (7) −1 to 9; (8) 9~26; (9) >26 |
| Parameter | Corresponding Value |
|---|---|
| Acquisition of the satellite | Sentinel-1A |
| Orbit | Ascending orbit |
| Resolution/m | 5 × 20 |
| Polarization mode | VV + VH |
| Revisit period/d | 12 |
| Incidence angle/(°) | 38.99 |
| Impact time | February 2017–December 2017 |
| Number of images/views | 34 |
| Actual Value | Predicted Value | Actual Value | Predicted Value | ||
|---|---|---|---|---|---|
| Landslide | Non-Landslide | Landslide | Non-Landslide | ||
| Landslide | 43 | 5 | Landslide | 149 | 12 |
| Non-Landslide | 15 | 41 | Non-Landslide | 23 | 136 |
| Sample | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| Before Expanding Sample | 0.8077 | 0.8913 | 0.7321 | 0.8039 |
| After Expanded Sample | 0.8906 | 0.9189 | 0.8553 | 0.8860 |
| Sample | Susceptibility Class | Probability of Landslide Occurrence | Grid Number (pcs) | Area Ratio (%) | Number of Landslide Points (pcs) | Density (pcs/km2) |
|---|---|---|---|---|---|---|
| Before Expanding Sample | Very Low Susceptibility Zone | <0.257 | 977,062 | 27.545 | 3 | 0.003412 |
| Low Susceptibility Zone | 0.257–0.392 | 849,144 | 23.938 | 13 | 0.017011 | |
| Medium Susceptibility Zone | 0.392–0.521 | 828,716 | 23.362 | 18 | 0.024134 | |
| High Susceptibility Zone | 0.521–0.662 | 565,749 | 15.949 | 54 | 0.106054 | |
| Very High Susceptibility Zone | >0.662 | 326,629 | 9.208 | 85 | 0.289149 | |
| After Expanded Sample | Very Low Susceptibility Zone | <0.123 | 1,530,467 | 43.145 | 1 | 0.000726 |
| Low Susceptibility Zone | 0.123–0.230 | 1,042,708 | 29.394 | 20 | 0.021312 | |
| Medium Susceptibility Zone | 0.230–0.418 | 547,520 | 15.435 | 34 | 0.068998 | |
| High Susceptibility Zone | 0.418–0.648 | 281,614 | 7.938 | 61 | 0.240676 | |
| Very High Susceptibility Zone | >0.648 | 144,991 | 4.087 | 57 | 0.436809 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Ma, X.; Ding, W.; Wen, H.; Sun, D. A Novel Dataset Replenishment Strategy Integrating Time-Series InSAR for Refined Landslide Susceptibility Mapping in Karst Regions. Water 2024, 16, 2414. https://doi.org/10.3390/w16172414
Yang Y, Ma X, Ding W, Wen H, Sun D. A Novel Dataset Replenishment Strategy Integrating Time-Series InSAR for Refined Landslide Susceptibility Mapping in Karst Regions. Water. 2024; 16(17):2414. https://doi.org/10.3390/w16172414
Chicago/Turabian StyleYang, Yajie, Xianglong Ma, Wenrong Ding, Haijia Wen, and Deliang Sun. 2024. "A Novel Dataset Replenishment Strategy Integrating Time-Series InSAR for Refined Landslide Susceptibility Mapping in Karst Regions" Water 16, no. 17: 2414. https://doi.org/10.3390/w16172414
APA StyleYang, Y., Ma, X., Ding, W., Wen, H., & Sun, D. (2024). A Novel Dataset Replenishment Strategy Integrating Time-Series InSAR for Refined Landslide Susceptibility Mapping in Karst Regions. Water, 16(17), 2414. https://doi.org/10.3390/w16172414






