Runoff Control Performance of Three Typical Low-Impact Development Facilities: A Case Study of a Community in Beijing
Abstract
1. Introduction
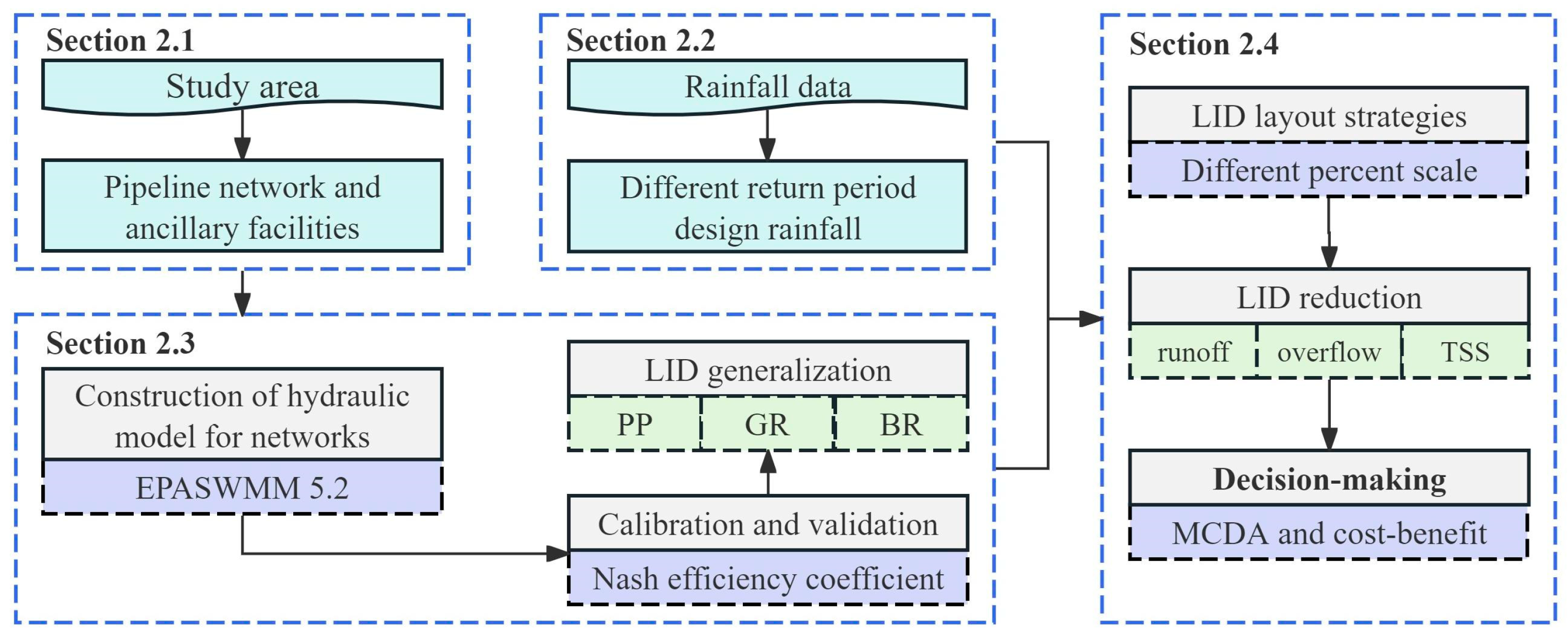
2. Materials and Methods
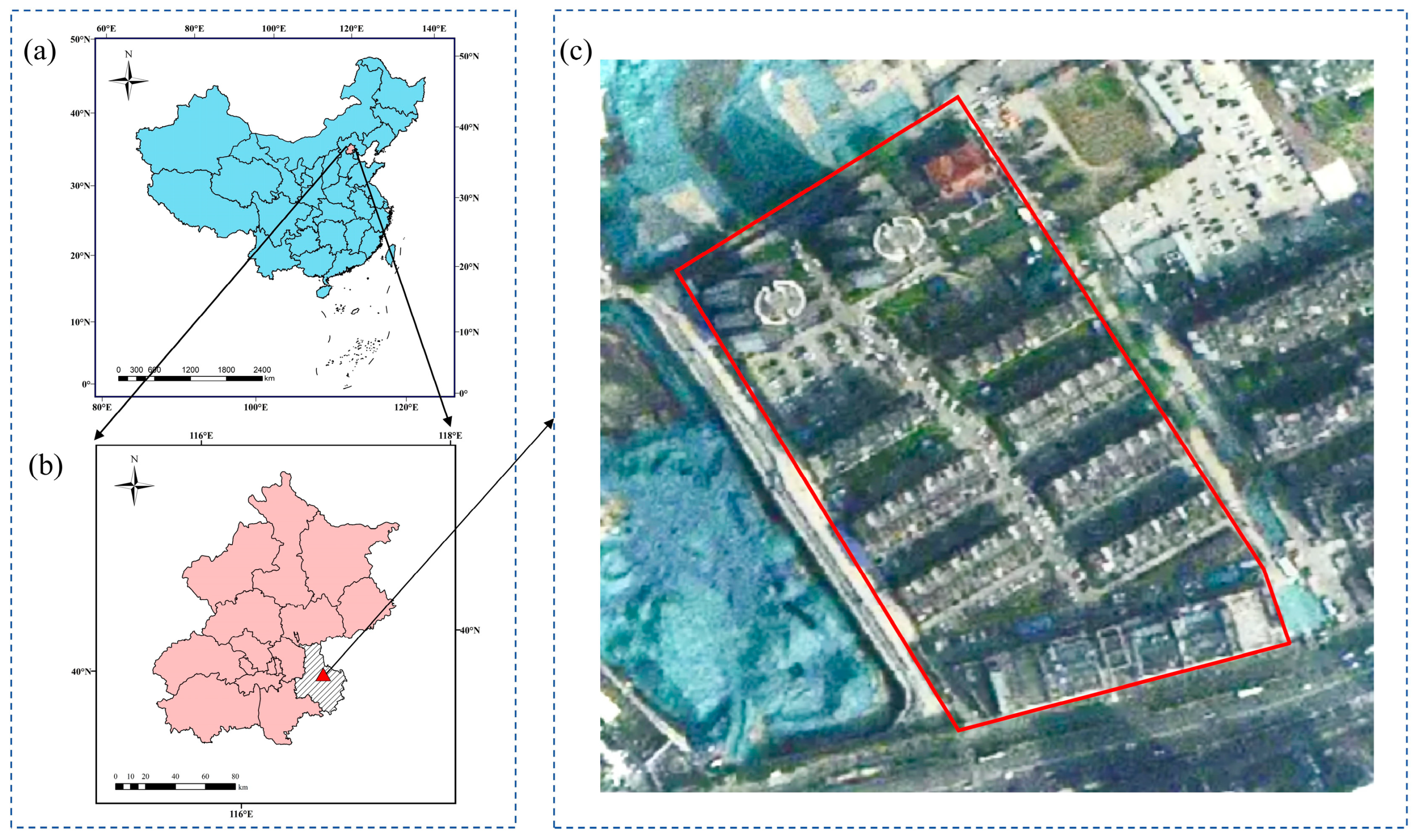
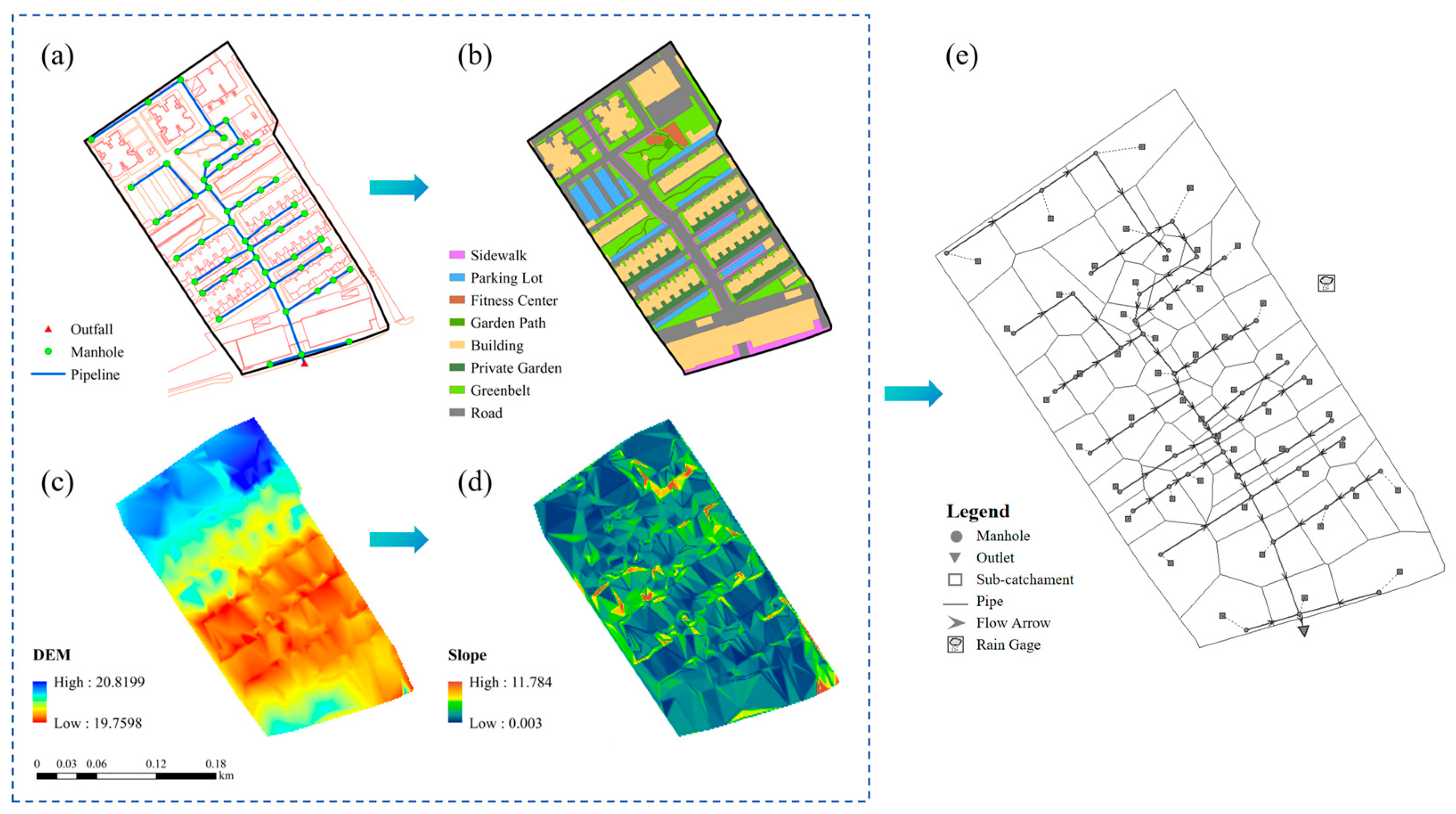
2.1. Study Area Overview
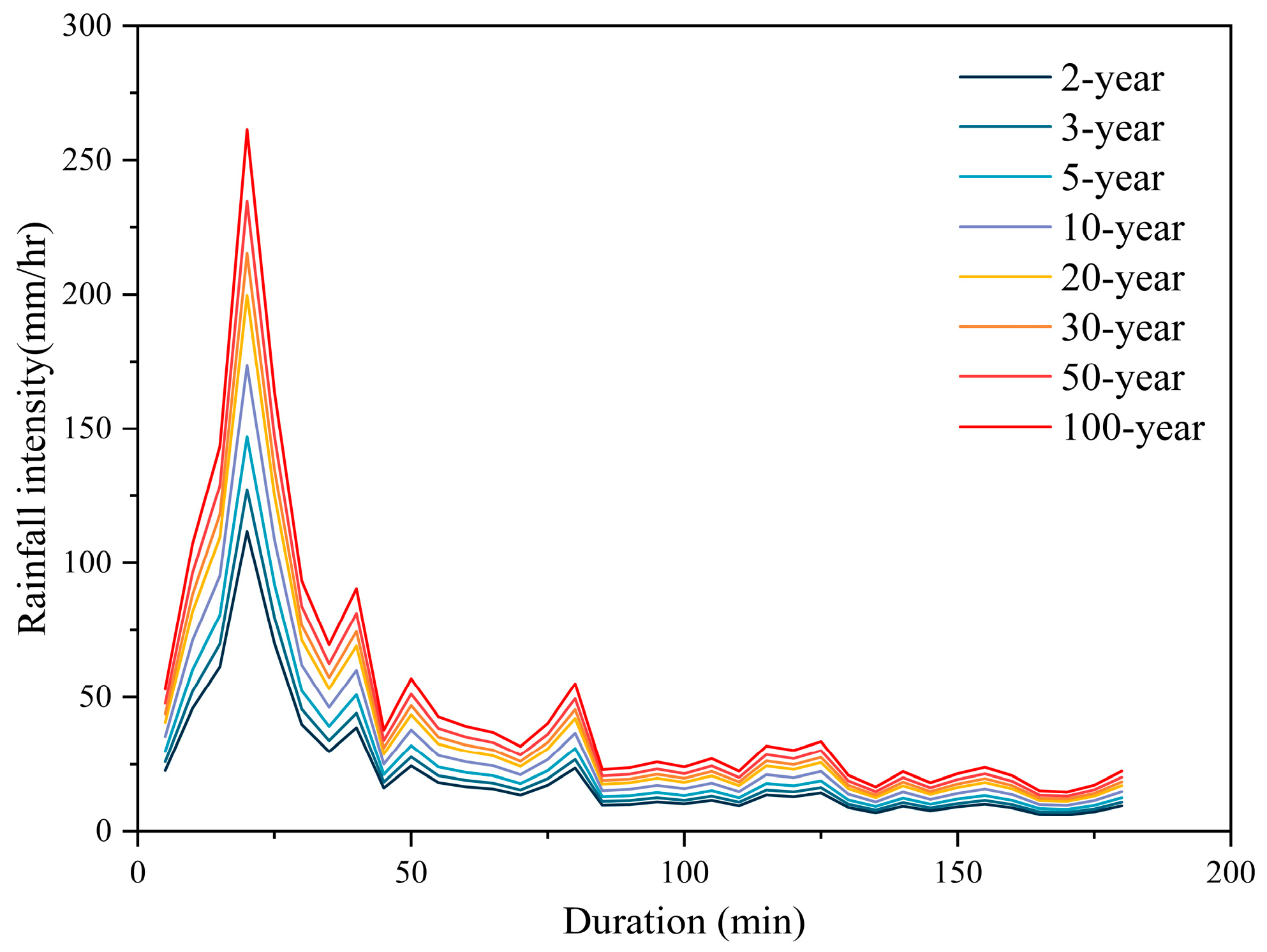
2.2. Designing Rainfall Scenarios
2.3. SWMM Model Construction
2.3.1. Hydraulic Model Setup
2.3.2. Pollution Model Setup
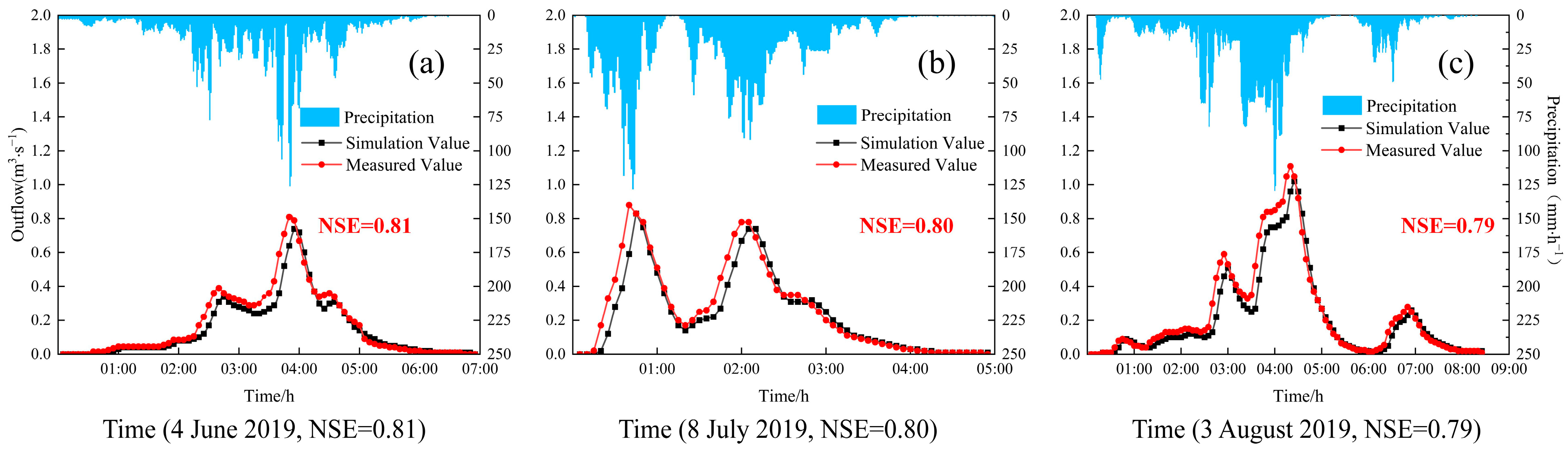
2.3.3. Calibration of Model Parameters
2.3.4. LID Facilities and Parameter Settings
2.4. Analysis of LID Facility Performance
2.4.1. Hydrological Performance Evaluation Indicators for LID
2.4.2. Spatial Layout Strategies for LID
2.4.3. Multi-Criteria Decision Analysis and Cost–Benefit Decision-Making
- In order to eliminate the dimensional influence between indicators and ensure that different indicators are compared on the same scale, the data of each indicator are standardized and standardized by min–max. The standardization formula is Equation (6).where, represents the LID layout ratio, represents the LID performance evaluation index, is the value of layout ratio on the index, is the minimum value in the index, is the maximum value in the index, and is the value of after standardization.
- The information entropy of each index is calculated and the information content and uncertainty of each index are evaluated. The higher the entropy value, the more uniform the data distribution of the index, the smaller the difference, and the weaker the influence on the decision. A lower entropy value indicates that the data distribution of the index is more different and has a stronger influence on decision-making. The calculation formula of information entropy is Equation (7).where is the information entropy of the index, is used to ensure that the entropy value is within the interval [0, 1], where represents the total number of layout proportions, and represents the proportion of layout ratio under index.
- The weight of each index is calculated. The larger the weight, the more important the index is in the evaluation system, and the more influence it has on the comprehensive evaluation of LID scheme. A smaller weight indicates a lower importance of the indicator. The weight of each index can be calculated by Equation (8).where is the weight of the indicator, and represents the total number of indexes.
- After determining the weight of each index, the comprehensive score of the layout ratio is calculated (Equation (9)). The higher the comprehensive score is, the better the comprehensive performance of the LID layout ratio in all indicators is, and it is a better choice.
3. Results
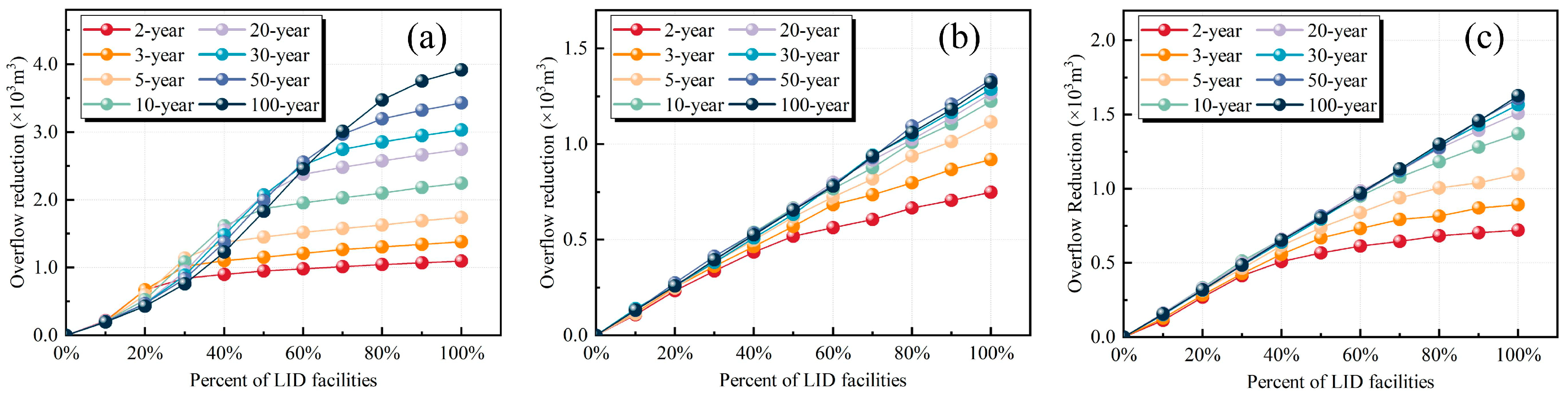
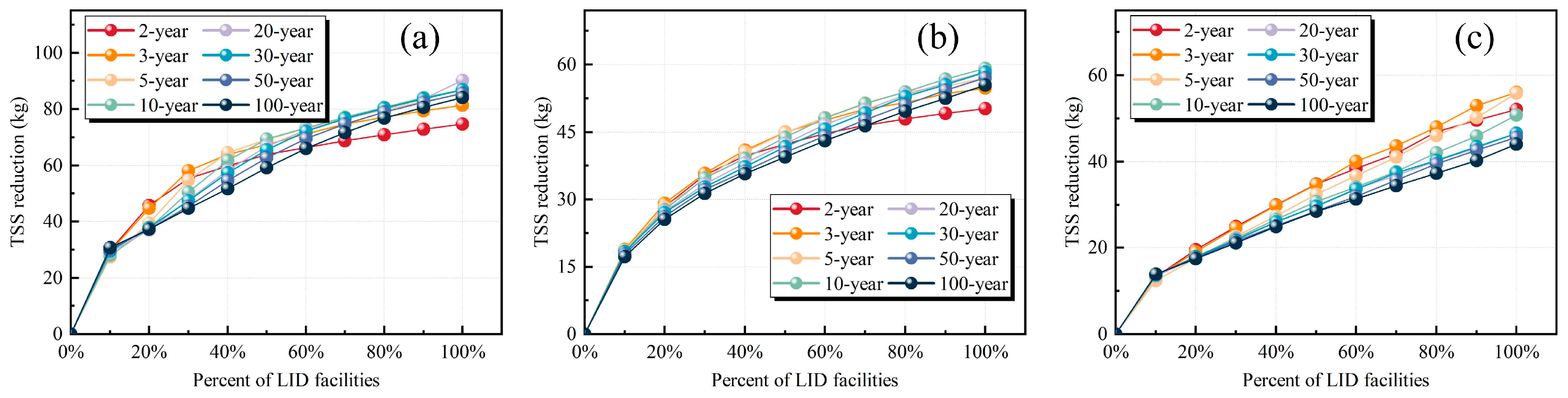
3.1. Runoff Control Performance of LID Facilities
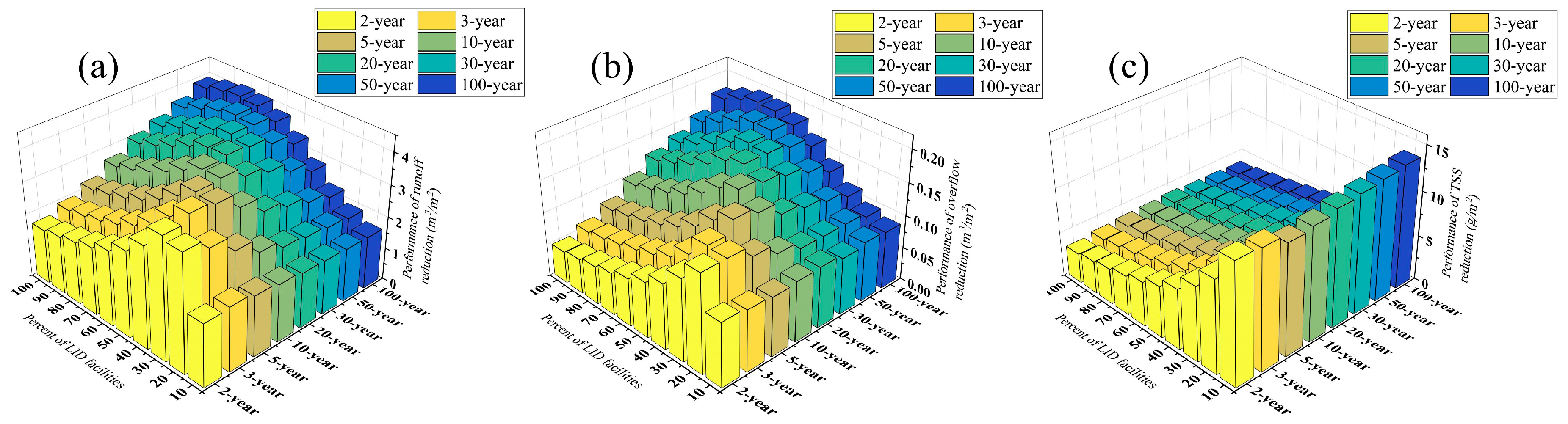
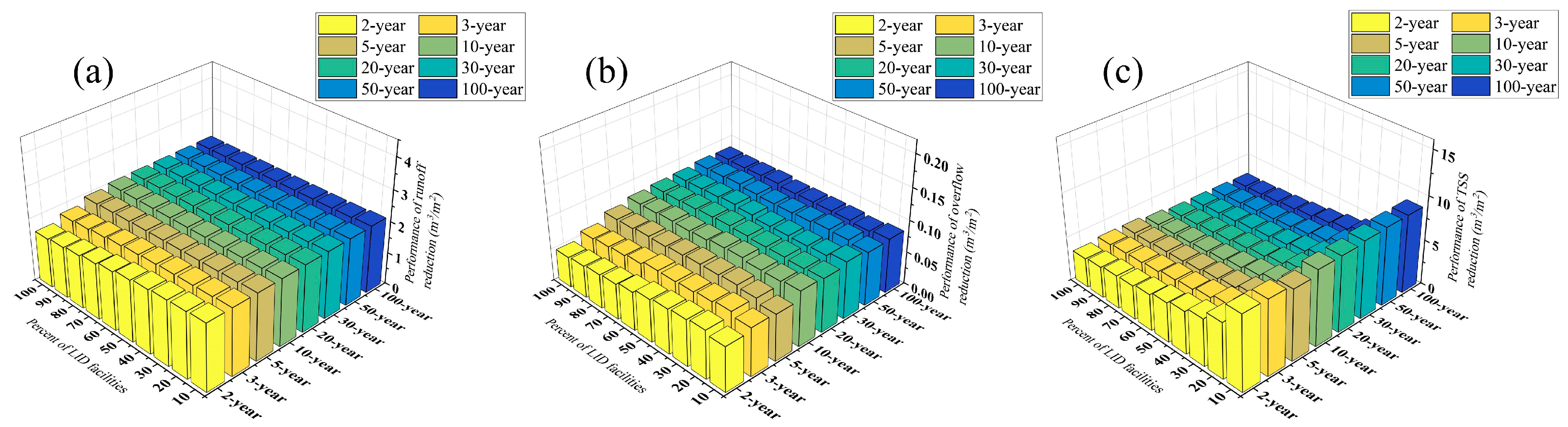
3.2. Unit Performance Analysis of LID Facilities
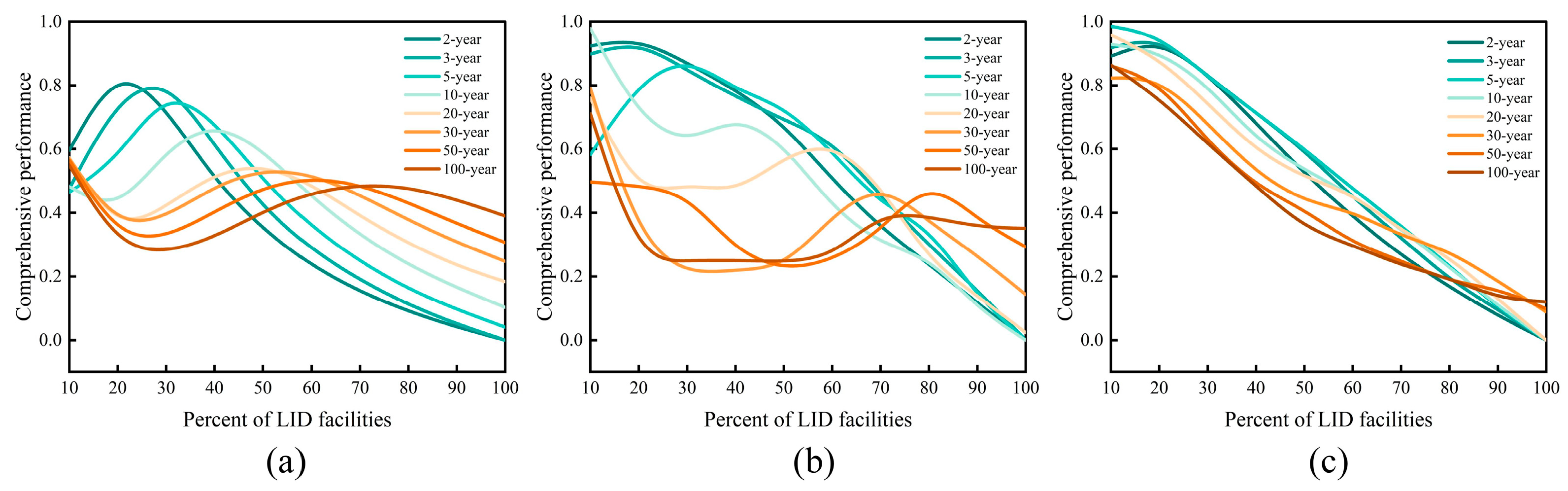
3.3. Comprehensive Performance Analysis of LID Facilities
3.4. Cost–Benefit Analysis of Combined LID Facilities
- Plan One: Increase bio-retention cells: 30% permeable pavements (PP) + 20% green roofs (GR) + (60–100%) bio-retention cells (BR);
- Plan Two: Increase permeable pavements: (30–100%) PP + 20% GR + 60% BR;
- Plan Three: Increase green roofs: 30% PP + (20–100%) GR + 60% BR.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, N.; Alipour, A. A multi-step assessment framework for optimization of flood mitigation strategies in transportation networks. Int. J. Disaster Risk. Reduct. 2021, 63, 102439. [Google Scholar] [CrossRef]
- Paulik, R.; Zorn, C.; Wotherspoon, L.; Sturman, J. Modelling national residential building exposure to flooding hazards. Int. J. Disaster Risk. Reduct. 2023, 94, 103826. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Yang, H. An integrated approach to investigate the coupling coordination between urbanization and flood disasters in China. J. Clean. Prod. 2022, 375, 134191. [Google Scholar] [CrossRef]
- Bertilsson, L.; Wiklund, K.; de Moura Tebaldi, I.; Rezende, O.M.; Verol, A.P.; Miguez, M.G. Urban flood resilience—A multi-criteria index to integrate flood resilience into urban planning. J. Hydrol. 2019, 573, 970–982. [Google Scholar] [CrossRef]
- Bayas-Jimenez, L.; Martinez-Solano, F.J.; Iglesias-Rey, P.L.; Boano, F. Economic Analysis of Flood Risk Applied to the Rehabilitation of Drainage Networks. Water 2022, 14, 2901. [Google Scholar] [CrossRef]
- Fiori, A.; Volpi, E. On the Effectiveness of LID Infrastructures for the Attenuation of Urban Flooding at the Catchment Scale. Water Resour. Res. 2020, 56, e2020WR027121. [Google Scholar] [CrossRef]
- Jean, M.; Morin, C.; Duchesne, S.; Pelletier, G.; Pleau, M. Optimization of Real-Time Control with Green and Gray Infrastructure Design for a Cost-Effective Mitigation of Combined Sewer Overflows. Water Resour. Res. 2021, 57, e2021WR030282. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Q.; He, P.; Du, Y.; Zou, Z.; Xu, S.; Han, X.; Zeng, T. Impacts of rainstorm characteristics on flood inundation mitigation performance of LID measures throughout an urban catchment. J. Hydrol. 2023, 624, 129841. [Google Scholar] [CrossRef]
- Hill, B.; Liang, Q.; Bosher, L.; Chen, H.; Nicholson, A. A systematic review of natural flood management modelling: Approaches, limitations, and potential solutions. J. Flood Risk. Manag. 2023, 16, e12899. [Google Scholar] [CrossRef]
- Pugliese, F.; Gerundo, C.; De Paola, F.; Caroppi, G.; Giugni, M. Enhancing the Urban Resilience to Flood Risk Through a Decision Support Tool for the LID-BMPs Optimal Design. Water Resour. Manag. 2022, 36, 5633–5654. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Wang, C.; Shen, R.; Gisen, J.I.A.; Mu, J. Stormwater and flood simulation of sponge city and LID mitigation benefit assessment. Environ. Sci. Pollut. R. 2023. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Yan, X.; Duan, H. Sustainable Design of Urban Stormwater Drainage Systems by Implementing Detention Tank and LID Measures for Flooding Risk Control and Water Quality Management. Water Resour. Manag. 2019, 33, 3271–3288. [Google Scholar] [CrossRef]
- Suresh, A.; Pekkat, S.; Subbiah, S. Quantifying the efficacy of Low Impact Developments (LIDs) for flood reduction in micro-urban watersheds incorporating climate change. Sust. Cities Soc. 2023, 95, 104601. [Google Scholar] [CrossRef]
- Liu, C.; Xie, T.; Yu, Q.; Niu, C.; Sun, Y.; Xu, Y.; Luo, Q.; Hu, C. Study on the response analysis of LID hydrological process to rainfall pattern based on framework for dynamic simulation of urban floods. J. Environ. Manag. 2024, 351, 119953. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, Z.; Chen, X.; Yu, G. An assessment of the hydrologic effectiveness of low impact development (LID) practices for managing runoff with different objectives. J. Environ. Manag. 2019, 231, 504–514. [Google Scholar] [CrossRef]
- Li, F.; Chen, J.; Engel, B.A.; Liu, Y.; Wang, S.; Sun, H. Assessing the Effectiveness and Cost Efficiency of Green Infrastructure Practices on Surface Runoff Reduction at an Urban Watershed in China. Water 2021, 13, 24. [Google Scholar] [CrossRef]
- Arvand, S.; Noroozi, Z.G.; Delghandi, M.; Alipour, A. Evaluating the impact of LID -BMPs on urban runoff reduction in an urban sub-catchment. Urban Water. J. 2023, 20, 604–615. [Google Scholar] [CrossRef]
- Pour, S.H.; Wahab, A.K.A.; Shahid, S.; Asaduzzaman, M.; Dewan, A. Low impact development techniques to mitigate the impacts of climate-change-induced urban floods: Current trends, issues and challenges. Sustain. Cities Soc. 2020, 62, 102373. [Google Scholar] [CrossRef]
- Xu, T.; Engel, B.; Shi, X.; Leng, L.; Jia, H.; Shaw, L.; Liu, Y. Marginal-cost-based greedy strategy (MCGS): Fast and reliable optimization of low impact development (LID) layout. Sci. Total Environ. 2018, 636, 240–251. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, T.; Li, J.; Feng, P.; Miao, Y. Optimal designs of LID based on LID experiments and SWMM for a small-scale community in Tianjin, north China. J. Environ. Manag. 2023, 334, 117442. [Google Scholar] [CrossRef]
- Palla, A.; Gnecco, I. The Web-GIS TRIG Eau Platform to Assess Urban Flood Mitigation by Domestic Rainwater Harvesting Systems in Two Residential Settlements in Italy. Sustainability 2021, 13, 7241. [Google Scholar] [CrossRef]
- Kaykhosravi, S.; Khan, U.; Jadidi, M. A simplified geospatial model to rank LID solutions for urban runoff management. Sci. Total Environ. 2022, 831, 154937. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Zhang, J.; Krebs, P. Low impact development practices mitigate urban flooding and non-point pollution under climate change. J. Clean. Prod. 2022, 347, 131320. [Google Scholar] [CrossRef]
- Martin-Miklea, C.; Kirsten, M.; Julianb, J.; Mayer, P.M. Identifying priority sites for low impact development (LID) in a mixed-use watershed. Landsc. Urban Plan. 2015, 240, 29–41. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Y.; Gitau, M.; Engel, B.; Flanagan, D.; Harbor, J. Optimal designs of LID based on LID experiments and SWMM on hydrology and water quality in a combined sewer overflow community. Sci. Total Environ. 2019, 665, 69–79. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, H.; Wang, K.; Ge, X.; Ying, X. The Application and Potential of Multi-Objective Optimization Algorithms in Decision-Making for LID Facilities Layout. Water Resour. Manag. 2024. [Google Scholar] [CrossRef]
- Tansar, H.; Duan, H.; Mark, O. Catchment-Scale and Local-Scale Based Evaluation of LID Effectiveness on Urban Drainage System Performance. Water Resour. Manag. 2022, 36, 507–526. [Google Scholar] [CrossRef]
- Lago, C.A.F.D.; Hamedani, A.S.; Mendiondo, E.M.; Giacomoni, M.H. Simulation and optimization framework for evaluating the robustness of low-impact development placement solutions under climate change in a small urban catchment. Hydrol. Sci. J. 2023, 68, 2057–2074. [Google Scholar] [CrossRef]
- Liu, K.; Chen, B.; Wang, S.; Wang, H. An urban waterlogging footprint accounting based on emergy: A case study of Beijing. Appl. Energ. 2023, 348, 121527. [Google Scholar] [CrossRef]
- Dong, Z.; Bain, D.J.; Akcakaya, M.; Ng, C.A. Evaluating the Thiessen polygon approach for efficient parameterization of urban stormwater models. Environ. Sci. Pollut. R. 2023, 30, 30295–30307. [Google Scholar] [CrossRef]
- Yazdi, M.N.; Sample, D.J.; Scott, D.; Owen, J.S.; Ketabchy, M.; Alamdari, N. Water quality characterization of storm and irrigation runoff from a container nursery. Sci. Total Environ. 2019, 667, 166–178. [Google Scholar] [CrossRef] [PubMed]
- Taghizadeh, S.; Khani, S.; Rajaee, T. Hybrid SWMM and particle swarm optimization model for urban runoff water quality control by using green infrastructures (LID-BMPs). Urban For. Urban Green. 2021, 60, 127032. [Google Scholar] [CrossRef]
- Storm Water Management Model Reference Manual (Volume 3, Water Quality); United States Environmental Protection Agency, Office of Research and Development: Washington, DC, USA, 2016. Available online: www.epa.gov/water-research (accessed on 10 November 2023).
- Agency, E.P. Storm Water Management Model User’s Manual, 5.2 ed.; United States Environmental Protection Agency, Office of Research and Development: Washington, DC, USA, 2022. Available online: www.epa.gov/water-research/storm-water-management-model-swmm (accessed on 10 November 2023).
- Saniei, K.; Yazdi, J.; MajdzadehTabatabei, M.R. Optimal size, type and location of low impact developments (LIDs) for urban stormwater control. Urban Water J. 2021, 18, 585–597. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, P.; Liu, Z.; Li, W.; Zhou, J. Optimization of LID Strategies for Urban CSO Reduction and Cost Efficiency: A Beijing Case Study. Water 2024, 16, 965. [Google Scholar] [CrossRef]
- DB11/T 1743-2020; Standard for Sponge City of Construction and Design. Beijing Municipal Commission: Beijing, China, 2021.
- Gulshad, K.; Szydlowski, M.; Yaseen, A.; Aslam, R.W. A comparative analysis of methods and tools for low impact development (LID) site selection. J. Environ. Manag. 2024, 354, 120212. [Google Scholar] [CrossRef]
- Wu, X.; Tang, R.; Wang, Y. Evaluating the cost-benefit of LID strategies for urban surface water flooding based on risk management. Nat. Hazards 2024. [Google Scholar] [CrossRef]




| Land Use Type | Max. Buildup/(kg·hm−2) | Rate Constant | Wash Off Coefficient | Wash Off Exponent |
|---|---|---|---|---|
| Road | 60 | 0.6 | 0.009 | 1.9 |
| Building | 45 | 0.5 | 0.010 | 1.8 |
| Greenbelt | 35 | 0.56 | 0.006 | 1.2 |
| Surface | Runoff Coefficient | Initial Losses (mm) | Initial Infiltration Rate (mm/h) | Minimum Infiltration Rate (mm/h) | Decay Constant (1/h) | Manning |
|---|---|---|---|---|---|---|
| Building | 0.9 | 0.15 | - | - | - | 0.012 |
| Road | 0.9 | 0.15 | - | - | - | 0.011 |
| Green | - | 2.5 | 72 | 24 | 1.2 | 0.15 |
| Process Layers | Parameter | Green Roof | Permeable Pavement | Bio-Retention Cell |
|---|---|---|---|---|
| Surface Layer | Berm Height/mm | 80 | 80 | 200 |
| Vegetation Volume Fraction | 0.3 | 0 | 0.7 | |
| Surface Roughness | 0.4 | 0.1 | 0.2 | |
| Surface Slope/% | 0.1 | 0.01 | 3 | |
| Pavement Layer | Thickness/mm | 120 | ||
| Void Ratio | 0.15 | |||
| Permeability/(mm·h−1) | 120 | |||
| Soil Layer | Thickness/mm | 150 | 700 | 200 |
| Porosity | 0.5 | 0.5 | 0.5 | |
| Field Capacity | 0.2 | 0.2 | 0.2 | |
| Wilting Point | 0.085 | 0.024 | 0.085 | |
| Conductivity/(mm·h−1) | 18 | 18 | 18 | |
| Conductivity Slope | 10 | 10 | 10 | |
| Suction Head/mm | 110 | 110 | 110 | |
| Storage Layer | Thickness/mm | - | 200 | 300 |
| Void Ratio | - | 0.75 | 0.5 | |
| Seepage Rate/(mm·h−1) | - | 18 | 18 | |
| Drainage Mat | Thickness/mm | 80 | - | - |
| Void Ratio | 0.5 | - | - | |
| Roughness | 0.1 | - | - | |
| Drain System | Drain Exponent | 0.5 | 0.5 | |
| Drain Offset Height/mm | 6 | 6 |
| Design Scale | Green Roof (ha) | Permeable Pavement (ha) | Bio-Retention Cell (ha) |
|---|---|---|---|
| 10% | 0.16 | 0.22 | 0.10 |
| 20% | 0.31 | 0.45 | 0.20 |
| 30% | 0.47 | 0.67 | 0.29 |
| 40% | 0.63 | 0.90 | 0.39 |
| 50% | 0.78 | 1.12 | 0.49 |
| 60% | 0.94 | 1.34 | 0.59 |
| 70% | 1.10 | 1.57 | 0.69 |
| 80% | 1.25 | 1.79 | 0.78 |
| 90% | 1.41 | 2.01 | 0.88 |
| 100% | 1.57 | 2.24 | 0.98 |
| LID Facilities | Unit Infrastructure Cost (RMB·m−2) |
|---|---|
| Green Roof | 300 |
| Permeable Pavement | 200 |
| Bio-retention Cell | 600 |
| Index Weight | 2-Year | 3-Year | 5-Year | 10-Year | 20-Year | 30-Year | 50-Year | 100-Year | |
|---|---|---|---|---|---|---|---|---|---|
| PP | runoff | 0.3083 | 0.3431 | 0.2314 | 0.189 | 0.1871 | 0.2122 | 0.2145 | 0.219 |
| overflow | 0.308 | 0.291 | 0.3521 | 0.3291 | 0.2408 | 0.2184 | 0.2209 | 0.2323 | |
| TSS | 0.3837 | 0.3659 | 0.4165 | 0.4819 | 0.5721 | 0.5694 | 0.5647 | 0.5487 | |
| GR | runoff | 0.3422 | 0.3271 | 0.2871 | 0.4617 | 0.4678 | 0.4233 | 0.4769 | 0.5817 |
| overflow | 0.3764 | 0.3609 | 0.4597 | 0.3582 | 0.3266 | 0.3429 | 0.2688 | 0.1358 | |
| TSS | 0.2815 | 0.3121 | 0.2532 | 0.18 | 0.2056 | 0.2338 | 0.2543 | 0.2825 | |
| BR | runoff | 0.3273 | 0.318 | 0.3002 | 0.2805 | 0.3178 | 0.3906 | 0.4939 | 0.541 |
| overflow | 0.2993 | 0.2769 | 0.2746 | 0.2588 | 0.2066 | 0.1583 | 0.1275 | 0.1261 | |
| TSS | 0.3734 | 0.405 | 0.4252 | 0.4606 | 0.4755 | 0.4511 | 0.3786 | 0.3329 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, J.; Zhou, Z.; Yang, Z.; Li, Z.; Li, X.; Zhou, J.; Wang, H. Runoff Control Performance of Three Typical Low-Impact Development Facilities: A Case Study of a Community in Beijing. Water 2024, 16, 2373. https://doi.org/10.3390/w16172373
Xiao J, Zhou Z, Yang Z, Li Z, Li X, Zhou J, Wang H. Runoff Control Performance of Three Typical Low-Impact Development Facilities: A Case Study of a Community in Beijing. Water. 2024; 16(17):2373. https://doi.org/10.3390/w16172373
Chicago/Turabian StyleXiao, Jiayi, Zhiwei Zhou, Zhiyu Yang, Zhili Li, Xiaolong Li, Jinjun Zhou, and Hao Wang. 2024. "Runoff Control Performance of Three Typical Low-Impact Development Facilities: A Case Study of a Community in Beijing" Water 16, no. 17: 2373. https://doi.org/10.3390/w16172373
APA StyleXiao, J., Zhou, Z., Yang, Z., Li, Z., Li, X., Zhou, J., & Wang, H. (2024). Runoff Control Performance of Three Typical Low-Impact Development Facilities: A Case Study of a Community in Beijing. Water, 16(17), 2373. https://doi.org/10.3390/w16172373









