Multi-Objective and Multi-Variable Optimization Models of Hybrid Renewable Energy Solutions for Water–Energy Nexus

Abstract

A new methodology, called HY4RES models, includes hybrid energy solutions (HESs) based on the availability of renewable sources, for 24 h of water allocation, using WaterGEMS 10.0 and PVGIS 5.2 as auxiliary calculations. The optimization design was achieved using Solver, with GRG nonlinear/evolutionary programming, and Python, with the non-dominated sorting genetic algorithm (NSGA-II). The study involves the implementation of complex multi-objective and multi-variable algorithms with different renewable sources, such as PV solar energy, pumped hydropower storage (PHS) energy, wind energy, grid connection energy, or battery energy, and also sensitivity analyses and comparisons of optimization models. Higher water allocations relied heavily on grid energy, especially at night when solar power was unavailable. For a case study of irrigation water needs of 800 and 1000 m³/ha, the grid is not needed, but for 3000 and 6000 m³/ha, grid energy rises significantly, reaching 5 and 14 GWh annually, respectively. When wind energy is also integrated, at night, it allows for reducing grid energy use by 60% for 3000 m³/ha of water allocation, yielding a positive lifetime cashflow (EUR 284,781). If the grid is replaced by batteries, it results in a lack of a robust backup and struggles to meet high water and energy needs. Economically, PV + wind + PHS + grid energy is the most attractive solution, reducing the dependence on auxiliary sources and benefiting from sales to the grid.

1. Introduction

Recent attention has been paid to the techno-economic viability of electrifying rural and remote areas. However, there is a dearth of awareness regarding agricultural irrigation, industrial, and drinking pump systems. Diesel generators are still employed for agricultural and industrial purposes and the utilization of facilities has led to environmental concerns and an increase in energy needs and prices. Portugal and Spanish irrigation communities have made substantial efforts to improve their infrastructure, mainly by modernizing their irrigation systems with localized methods [1]. This research presents an integrated techno-economic design of a multi-objective variable optimization model of hybrid energy for renewable energy solutions in water–energy nexus demand systems. For this purpose, optimization frameworks are required for the proper planning of a fully renewable energy system that encompasses pumped hydropower storage (PHS) and intermittent renewable source units with a grid connection or coupled batteries.

Agriculture is the fourth largest sector in the global breakdown of emissions. It is the biggest source of CO₂, which is around 13%. Furthermore, over 70% of freshwater is withdrawn globally for agriculture to keep crops such as fruits, vegetables, and grains in the water–energy–food nexus [2,3].

Therefore, growing water, energy, industry, and food security, and improving the global supply chain, hydrogen production, drinking systems, and process industry sectors present numerous opportunities and prompts for integrating renewable energy (RE) sources, to mitigate climate change and effectively manage water–energy needs. In terms of the requirement for different water sector needs [4,5,6,7], a viable option is to create a microgrid (MG) as a solution for integrating distributed intermittent and unpredictable energy resources, using optimized models towards a flexible operation.

There are many renewable and conventional generation and energy storage sources, allowing the water–energy need system improvement to cater to diverse load requirements. It is regarded as the most significant and suitable way to combine technologies into a single reliable operation platform [8,9,10,11,12]. The emergence of autonomous MG technology plays a significant role in the value of the advantages and drawbacks of renewable energy source application in different sectors [13,14,15]. To achieve a cost-effective and sustainable solution at an optimal size in terms of water and energy needs, power installed from intermittent sources like wind and solar sources, pumped hydropower storage, reservoir volume, grid connection, or stand-alone solutions are required. However, this is a complex task due to the many variables and constraints, which depend on the complexity of each system. Available power supply components, local resource data, technical and economic indicator information, and cost specifications and load profiles have to be provided. It is possible that under sizing can lead to an unsuccessful operation and a demand that is largely unmet. In the interim, the level of reliability remains high through oversizing; however, it may result in significant system costs, which is not the purpose of this research [16,17,18].

By utilizing multiple renewable energy sources (RESs) in conjunction with a pumped storage system, a hybrid renewable energy system (HRES) helps to reduce greenhouse gas emissions and increase the energy independence of the different water–energy nexus systems. Energy is stored for use in times of high demand or low production and used to meet unmet demand during times of low demand or high production [19,20,21,22,23].

To increase water–energy efficiency, a variety of strategies have been investigated. By dividing district pressure areas into water networks based on their needs for water flow and pressure, several studies suggested water network sectoring as a way to lower energy consumption. For instance, in Andalusia (Spain), irrigation district sectoring was also implemented for olive production, and the outcome was a roughly 30% decrease in energy usage. Managers and stakeholders are investing in renewable energy systems due to the need to promote more sustainable water–energy networks concerning natural resources and better social comfort. To lower energy needs and associated greenhouse gas emissions, several renewable energy technologies have recently been added to pressurized water systems. Specifically, ref. [24,25,26] created a real-time model (Smart Photovoltaic System Manager) to match the energy needed by an irrigation system in southern Portugal and Spain with the availability of PV power. Due to their ability to combine multiple conventional and renewable energy sources into a dependable and economical electricity supply, hybrid energy systems (HESs) are well suited for rural agricultural areas, process industry productions, and drinking and wastewater systems. The integration of various energy sources into HESs is a powerful approach to creating a sustainable energy supply paradigm, hybridization, digitalization, and flexibilization that is distinguished by high levels of dependability, economy, and environmental consciousness. HES effectiveness is dependent on careful planning and the consideration of several variables, including the desired water needs rate, operation schedule, and weather conditions [27,28,29].

A complicated and multifaceted relationship exists between the water sector and energy. Watering requires a significant use of energy, and simultaneously population growth, climate change, and other factors are expected to increase the amount of energy needed in the upcoming decades. Water–energy nexus systems could become more sustainable, and the cost of energy can be lowered through the energy transition with the switch from fossil fuels to renewable energy sources. The incorporation of renewable energy sources in water–energy systems is a complex process. Being intermittent, which means it is not always producing energy, is one of the primary obstacles associated with renewable energy sources. The water sector (i.e., irrigation, drinking, wastewater, and process industry), which requires a steady supply of energy to be able to have a suitable operation, may find this problematic. The water sector needs systems that integrate hybrid energy systems (HESs), can lower their carbon footprint, yield more consistent energy, and lessen their exposure to energy price fluctuations in the spot energy market that is also in transition to a fixed minimum price for the national electricity grid that allows for the return on the investment of installed equipment [30]. Refs. [31,32,33] present lessons on feasibility analyses using pumped storage and combined with, e.g., PV floating solar panels. Other studies are related to hydropower, considering relevant outcomes that can be controlled and maximized at a project level, beyond the risk mitigation requirements of environmental and social safeguard frameworks, with notable benefits that can be felt at both national and local levels throughout hydropower project planning, development, and operation within the water–energy nexus [34,35,36,37]. The overarching headline is the growth in the global hydropower fleet to 1416 GW in 2023. The conventional hydropower capacity grew from 7.2 GW to 1237 GW, while pumped storage hydropower (PSH) grew from 6.5 GW to 179 GW [36]. In Europe, there is a mature fleet of hydropower stations, and to provide the flexibility required to support Europe’s ambitions for the development of wind and solar energy, the emphasis is on the modernization of these sources, in addition to greenfield PHS development, informed by IHA’s global hydropower database, which tracks more than 13,000 stations in over 150 countries. While there is increasing global interest in hydropower, this requires action from governments to convert classical hydropower into new projects, being a cornerstone of the future energy mix. Hydropower is not only the leading supplier of renewable energy, but it is also the only sustainable and reliable method to counterbalance the variations caused by the intermittent nature of other renewable energies such as wind and solar energy. Up to 2030, a relatively small increase over the recent trend build rate, from about 20 GW/year up to about 25 GW/year, is required for hydropower to make its expected contribution to the ‘tripling up’ objective agreed to at COP28. After that, however, if net-zero emissions are to be achieved, delivery needs to more than double, to about 50 GW/year, and this rate needs to be sustained until 2050. Take Building Information Modeling (BIM), which enables the digital capture, management, and visualization of system information, facilitating both modernization and maintenance. These modernization initiatives are of paramount importance, especially in the context of a sustainable and secure energy supply. They ensure the reliable operation of these facilities while also upgrading the pumped hydropower storage capacities to meet the evolving demands of renewable power generation. A need for reliable operation with intelligent models that can offer competent and reliable support will ensure the safe, efficient, and maximum availability of these systems throughout their entire lifecycle, embracing a more digital future. Digital solutions serve to enhance the operation of hydropower plants such as in design, monitoring, optimization analyses, and diagnostic systems, using artificial intelligence (AI) to make hydropower utilization, in different sectors, more reliable and efficient [34,35,36,37]. This research work fulfilled the objective of developing advanced optimization models in the hybridization of the water sector, by the definition and design of mathematical algorithmic models within the water–energy nexus.

This research work is structured as follows: Section 1, as formerly presented, includes a detailed and recent literature review on the subject of water–energy nexus demand systems. Section 2 presents the hybrid models for renewable energy solutions (HY4RES—GRG nonlinear/evolutionary methods and Python—non-dominated sorting genetic algorithm (NSGA-II) method), the mathematical formulation used in this investigation, the proposed methodology, and the optimization algorithms developed. Section 3 presents a case study with the systems characterization and Section 4 enhances HY4RES model results and discussion for different optimization objective functions. Section 5 states different scenarios of exploration. Finally, Section 6 presents the main conclusions and limitations of this research work.

2. Methodology

2.1. HY4RES Model

Seven steps make up the suggested research methodology, which is meant to develop a hybrid model for renewable energy systems (HY4RES): (i) system characterization; (ii) definition of integrated hybrid energy solution (HES) depending on source availability and system requirements; (iii) model development using WaterGEMS (from Bentley software) for the hydraulic simulations; (iv) GRG nonlinear/evolutionary programming for the best solution optimization; (v) development of a Python software code for optimization using GA and graphical conception and system behavior analyses; (vi) sensitivity analyses for different water needs; and (vii) comparisons between models.

The main objectives of the developed models should consider the following constraints applied in the analyzed system:

• Satisfy water and energy needs of the analyzed system with a hybrid renewable energy solution;
• Primarily use solar energy to fulfill energy requirements and use its excess to pump water to the top reservoir/tank/pond, to store and later use for water needs satisfying 24 h of water when required;
• If the solar energy is not enough, water can be discharged from the top reservoir to turbine water and produce electricity during hours of non-solar generation (i.e., mainly during the night);
• Offer grid-connected solutions for selling excess solar or buy-in cases of a very low top reservoir volume;
• Water needs should/must be satisfied throughout the water scarcity period, where the top reservoir level or the associated pumped volume are key factors;
• Execute system simulation and optimization using Solver and Python; execute hydraulic simulator complementation with WaterGEMS.

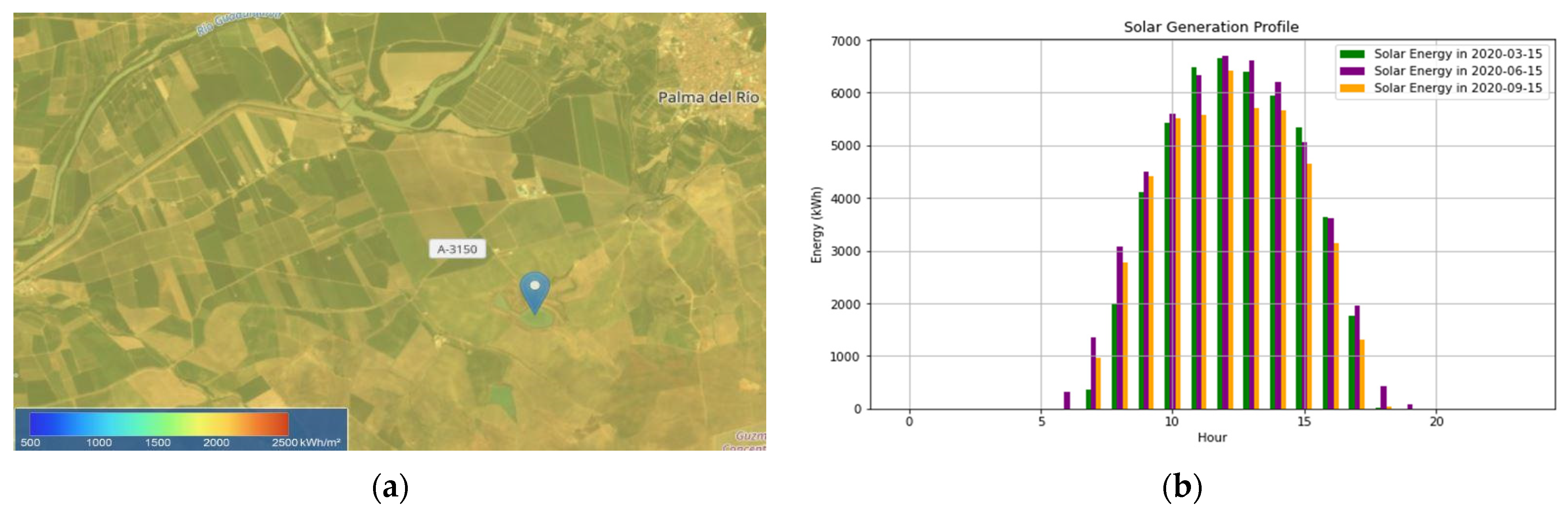
Figure 1 describes the new integrated model development (HY4RES), which requires some specific issues:

For solar/wind energy—the hourly solar/wind energy produced is retrieved from the PVGIS database; if solar energy is the main energy supplier, it is required to check if it can satisfy all the energy demand, and a solar energy surplus exists if energy needs are fulfilled and there is still solar energy available.

For pumped hydropower storage (PHS)—if solar/wind energy does not fulfill energy needs, then hydropower is required; If there is a solar/wind energy surplus, that energy can be spent on pumping water uphill to store potential energy as the water level increases in top reservoir (or tank or a pond).

Hydropower volume is only possible if the reservoir volume does not drop below the minimum after the water process.

Pumped volume is only possible if the top reservoir volume does not exceed its maximum volume after water need evaluation. Either pumps or turbines are used, since they cannot operate at the same time for only one pipe system.

For energy demand—energy needs can be fulfilled via solar/wind, hydropower, and grid electricity/batteries.

For top reservoir/tank/pond volume—the upper reservoir must have its defined capacity: maximum and minimum, and the initial volume; each hour (iteration) gives the reservoir volume by the end of it; then, after the use, it can be computed for the next hour’s volume, subtracting that hour’s input/outputs.

For water demand—water consumption refers to the water volume needed per hour for water needs; it is only possible if the reservoir has the required amount; its reliability should/must be 100%.

For grid energy—the electric grid is only required if there is an energy deficit if solar/wind energy and hydropower are not able to fulfill energy needs; it can also be used to sell excess solar/wind energy (e.g., not used by energy needs or by the pumping station); tariffs vary each hour and month for buying/selling, (i.e., energy market periods); at the end, it is computed for hourly cash flow (profits–costs); for a grid-connected solution, the energy surplus can be sold to the national grid, for profits; in the case of an energy deficit, energy can be bought from the grid to fully satisfy energy needs.

For off-grid solutions but with batteries—in an off-grid solution, batteries are used, which requires an appropriate design to fulfill energy needs, which are not satisfied by the renewable sources; if there is excess energy, after satisfying the energy needs, then it is stored in the battery system; if there is an energy deficit, i.e., with energy needs not yet fulfilled, then the batteries must feed the rest of the missing energy.

For optimization algorithms—after all parameters are defined, the HY4RES can then be optimized with Solver and Python; (i) via Solver, a general optimization is developed for the whole water need period or season in the case of irrigation (with base-fixed monthly variables for turbine and pumping) and daily selective optimization with hourly variables for turbine and pumping; (ii) via Python, a general optimization is developed for the whole season with hourly variables for turbine and pumping, with the advantage that Python does not have limited variables. The objective can be to maximize the total cash flow or minimize the energy demand from the grid or even maximize the hydropower production.

2.2. Mathematical Modeling

2.2.1. Time Definition

Regarding the timestep of the system, the default unit used is the hour, i.e., the model computes the presented parameters every hour. Nevertheless, if there is a need for lesser or greater time precision, it can be altered, for months, days, or even seconds. It is required to update the energy collected data, such as solar/wind generation, to respect the used time increment. The designated index for the timestep is the letter “i” in the superscript, which is presented in most of the parameters that are contained in the mathematical modeling.

2.2.2. Energy Consumption

The hybrid system must be able to satisfy not only the water needs but also the associated energy needs. It may resort to solar/wind energy, when available, or the hydropower that is generated when water is turbined from an upper reservoir. The objective of the hydropower solution is to compensate for the intermittency of the solar/wind production. But, as the reservoir volume is limited and there are water consumption needs, the volume that should be turbined is not always possible. Therefore, the designed system possesses two auxiliary energy sources: grid-connected sources (Alternative A) or stand-alone or battery sources (Alternative B). The energy profile could be variable through time or remain constant, depending on the case to be studied. The attributed symbol to energy consumption is E_cⁱ for each timestep.

2.2.3. Water Consumption

Another consumption requirement comes from the water supply. This model is for hybrid energy systems that plan to feed drinking communities or agricultural or industry platforms that also require a water supply. The water outflow is computed on the upstream reservoir, requiring the operation of the PHS station and subsequent overall system in the most optimized and strategic way to enable the complete satisfaction of water needs, with the least cost and energy consumption possible. The attributed symbol for water consumption is Aⁱ, from the Latin word “aqua”.

2.2.4. Solar Energy

Through the construction of a solar farm, for example, a floatable type of farm on the water reservoir, solar energy can be generated and used for feeding the pump station and energy consumption needs. Solar energy production data can be retrieved on public websites, such as PVGIS, so that the solar energy parameter (Sⁱ) can be collected and processed in kWh. Based on the retrieved solar energy generation for a given timestep, within a determined period, plus the energy needed values, the excess solar energy available can be computed with Equation (1) and denominated as the solar surplus (S_sⁱ). This solar surplus is only valid if there is no wind generation.

$$S_s^i=S^i-E_c^i ,\hspace{0.25em}\hspace{0.25em}If S^i-E_c^i>0$$

(1)

If the solar surplus is not greater than zero, either it fully satisfies the energy needs and there is no energy left, or it is insufficient to satisfy energy needs, requiring compensation from wind energy, the PHS turbine system, grid, or batteries.

2.2.5. Wind Energy

Similar to the solar energy system, wind turbines can be implemented in the model to generate additional renewable energy for the PHS system operation and energy need satisfaction. Wind power production data can be found on various public data tools/libraries/APIs, for example, NREL or renewables (Ninja). Wind energy generation is retrieved from the data for the desired timestep and period, Wⁱ, in kWh. The total renewables surplus (S_s+wⁱ) can be computed using the following Equation (2).

$$S_{s+w}^i=S^i+W^i-E_c^i ,\hspace{0.25em}\hspace{0.25em}If S^i+W^i-E_c^i>0$$

(2)

From here onwards, solar and wind production are both considered in the mathematical modeling. Nevertheless, if one of the renewable sources is not to be considered, its raw value, Sⁱ or Wⁱ, is set to zero.

2.2.6. Pumped Hydropower Storage (PHS)

The PHS station either works in the pump or turbine mode, never both, due to having only one hydraulic circuit. The math ruling the modus operandi of the station consists of a logical algorithm:

If the solar + wind energy available in a specific hour is insufficient to satisfy the energy needs, then the PHS system is set for turbine mode to produce hydropower, which is expressed by Equation (3), where H_needⁱ is the required hydropower energy to satisfy the rest of the energy needs, in kWh.

$$H_{need}^i=E_c^i-S^i-W^i ,\hspace{0.25em}\hspace{0.25em}If E_c^i-S^i-W^i>0$$

(3)

Otherwise, with the energy consumption satisfied by the solar + wind energy, and if a surplus exists, then the PHS is set for pump mode to use that same energy to pump water to the higher reservoir, expressed by Equation (4), where P_Sⁱ is the available renewable energy to be used by the pumps, in kWh.

$$P_S^i=S_{s+w}^i ,\hspace{0.25em}\hspace{0.25em}If S_{s+w}^i>0$$

(4)

Regarding the turbine operation, the PHS station only discharges if there is enough water stored in the reservoir, already discounting the water allocation:

$$V_R^{i-1}-A^i-V_t^i\ge V_{min}$$

(5)

The variable V_Rⁱ⁻¹ corresponds to the reservoir volume at the end of the previous hour and V_tⁱ to the hydropower volume, both in m³. If in Equation (5) it is fulfilled, then the hydropower volume set is executable; if not, then it is zero for that hour in the analysis. The hydropower volume is computed by the following formula, Equation (6), based on [31,32,33].

$$V_t^i={\displaystyle \frac{\alpha \times H_{need}^i\times 3600\times {10}^3}{9800\times {\eta }_t\times H_t}}$$

(6)

The variable (α) is the hydropower factor, which is a value between 0 and 1; H_needⁱ is the required hydropower energy for energy needs, in kWh; η_t is the average turbine+generator efficiency; and H_t is the average turbine head.

When the station is operating in reverse mode as a pump, the principle is quite similar. It can only pump water into the upper reservoir if this volume allows for the respective increment. The water allocation subtraction is also considered.

$$V_R^{i-1}-A^i+V_p^i\le V_{max}$$

(7)

The variable V_pⁱ corresponds to the pumped volume, in m³. If the maximum volume condition, presented in Equation (7), is respected, then the set volume for pumping can be calculated; if not, there is no flow during that specific hour. The pumped volume, V_pⁱ, results from the supplied total feasible energy used by the pump station, Pⁱ. This feasible energy for pump operation can be divided into two variables: the feasible renewable energy for the pump (P_F-Sⁱ) and the feasible alternative energy for the pump (P_F-A/Bⁱ), in kWh. Both these variables are the result of the multiplication of their available/possible energy by a factor, as presented in Equations (8) and (9):

$$P_{F-S}^i=\beta \times P_S^i$$

(8)

$$P_{F-A/B}^i=\gamma \times P_{A/B}^i$$

(9)

The possible alternative energy variable (P_A/Bⁱ) is considered equal to the nominal power of the pump station when the grid-connected alternative (A) is considered, i.e., Equation (9) transforms into Equation (10).

$$P_{F-A/B}^i=\gamma \times P_N$$

(10)

When the battery alternative (B) is considered, Equation (9) transforms into Equation (11).

$$P_{F-A/B}^i=\gamma \times B^{i-1}$$

(11)

where (Bⁱ) represents the energy stored on the battery system at a specific timestep, in kWh. Further details of parameters, in alternative B with batteries, are presented in Section 2.2.9. The pumped volume is obtained through Equation (12), based on [31,32,33].

$$V_p^i={\displaystyle \frac{\left(P^i+P_{F-A/B}^i\right)\times {\eta }_p\times 3600\times {10}^3}{9800\times H_t}}$$

(12)

which can be modified to a more complex description, as presented in Equation (13):

$$V_p^i={\displaystyle \frac{\left(P_{F-S}^i+P_{F-A/B}^i\right)\times {\eta }_p\times 3600\times {10}^3}{9800\times H_t}}={\displaystyle \frac{\left(\beta \times P_S^i+\gamma \times P_{A/B}^i\right)\times {\eta }_p\times 360\times {10}^3}{9800\times H_t}}$$

(13)

The multipliers (β) and (γ) are the solar and grid/battery factors, respectively, and these are values between 0 and 1; P_Sⁱ is the solar energy available for pumping; (P_A/Bⁱ) is the maximum pump station energy consumed from one of the alternatives (either A or B); (η_p) is the pump + motor average efficiency; and H_t is the average pump head. The total energy used for the pump operation, (Pⁱ), is equal to β × P_Sⁱ + γ × P_A/Bⁱ.

Energy from solar and wind farms is always prioritized for pumping versus grid/battery energy, as this is the primary objective to improve the system’s efficiency. The available renewable energy for the pumps considered must be greater than 20% of the nominal pump station power (P_N) and less than this same parameter. If not, it is considered zero, and this excess solar energy is free to be sold to the grid. To ensure this, the renewable energy is prioritized, its feasible energy for the pump (P_F-Sⁱ) is firstly computed, and then the feasible alternative energy for the pump operation (P_F-A/Bⁱ) already takes into account the pumped volume from the renewable energy share.

The grid contribution for the pump station operation is only doable if its value, plus the available renewable energy for the pump (P_Sⁱ) multiplied by its factor (β), is lesser or equal to the nominal power (P_N), as described by the following Equation (14).

$$P_{F-A/B}^i=\gamma \times P_{A/B}^i=\gamma \times P_N,\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}If\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\beta \times P_S^i+\gamma \times P_N\le P_N$$

(14)

Otherwise, no grid energy can be used. The grid factor is the decisive agent in evaluating if the grid can or cannot contribute to the pump station operation.

If batteries are used instead of the grid-connected alternative, then the P_A/Bⁱ variable corresponds to the battery energy available at a specific timestep, Bⁱ⁻¹, and γ is the decisive factor of how much battery energy is consumed by the pump station. This assures that a feasible value is used (P_F-A/Bⁱ). Nevertheless, the nominal pump power must also be respected in this alternative, as shown in Equation (15).

$$P_{F-A/B}^i=\gamma \times P_{A/B}^i=\gamma \times B_i,\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}If\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\beta \times P_S^i+\gamma \times B^{i-1}\le P_N$$

(15)

2.2.7. Reservoir Volume

The reservoir volume status is modeled at every timestamp, where it represents its total volume by the end of the selected instant. Therefore, the reservoir volume computation is executed after the evaluation of the water consumption and turbine/pumped volume parameters. At the beginning of the simulation period, the reservoir has a set initial volume (V_R⁰), and the following timestep volumes are computed by the iteration, in m³, through Equation (16).

$$V_R^i=V_R^{i-1}-A^i-V_t^i+V_p^i$$

(16)

At any time during the simulation, the volume at the reservoir must not be less than the defined minimum or maximum capacity. Equation (16) considers two methods. One method can serve as an inlet or outlet, which refers to the pipeline used by the PHS station, that may work in pump or turbine mode, changing the designation accordingly. The other method is to permanently use an outlet port, which corresponds to the feeding pipe for the water consumption and connects the reservoir to the irrigation network.

2.2.8. Alternative A: Grid-Connected

Whenever there is an excess of solar energy that is not used either by energy needs or by the pump station, it can be sold to the grid, resulting in a certain profit, according to the tariff; this varies monthly for the buying option. This energy surplus (E₊ⁱ), in euros [EUR], with no utilization on the water allocation system, available for sale, is computed as follows, using Equation (17).

$$E_{+}^i=S_s^i-P_s^i$$

(17)

Based on it, the hourly profits (Rⁱ) can be obtained, using Equation (18).

$$R^i=E_{+}^i\times T_S^i$$

(18)

where T_sⁱ corresponds to the selling price, in EUR/kWh, depending on the month and period of the day/hour selected.

In energy deficit scenarios, where the solar energy and the hydropower generated cannot satisfy the energy needs of the system, there is the option to buy from the grid the energy that is in debt. This amount of energy, in deficit by the system, is computed via Equation (19) in kWh. The grid energy used for the pump operation is added, so it can be considered in the cost calculation.

$$E_{-}^i=[E_c^i-S^i-H^i]+P_G^i$$

(19)

Then, the hourly costs can be computed, using Equation (20).

$$C^i=E_{-}^i\times T_B^i$$

(20)

where T_Bⁱ corresponds to the hourly price of buying energy from the grid, in EUR/kWh, which only varies according to the month of analysis.

2.2.9. Alternative B: Batteries

The second alternative for an auxiliary energy source to secure the system requirements when the renewables are insufficient or do not have the necessary power installed, is batteries, presenting a stand-alone option for this type of hybrid system. The battery plant needs to have a maximum storage capacity (B_max) capable of assuring the supply of energy whenever the solar + wind energy and hydropower are not enough. It also needs to account for the typical range of values of surplus renewable energy not used by the pumps and that can be stored in the batteries for later use. The precise and correct sizing of the batteries is a key factor for the self-sufficiency of the hybrid system as a stand-alone option. The energy stored at every timestep by the batteries is represented, in kWh, by the symbol Bⁱ.

The energy that can be charged to the battery system (B_cⁱ) is computed through Equation (21).

$$B_c^i=S_{s+w}^i-\beta \times P_S^i$$

(21)

The battery may discharge energy (B_dⁱ) to the PHS system to complement the solar+wind surplus and increase the pumping capacity or to satisfy the remaining energy needs. The energy needed (discharge) from the batteries by the system is computed as follows, using Equation (22).

$$B_e^i+B_p^i=\left[E_c^i-S^i-W^i-H^i,\hspace{0.25em}If>0\wedge B_e^i\le B^i\right]+\left[P_{F-A/B}^i\right]$$

(22)

where (B_eⁱ) represents the energy needed from the batteries for energy needs, in kWh; and (B_pⁱ) is the feasible battery energy to be used for the pump operation, in kWh.

To model the total battery energy storage status (Bⁱ), Equation (23) is used.

$$\left\{\begin{array}{c}{B}^i=B^{i-1}+B_c^i-B_p^i, B^{i-1}+B_c^i-B_d^i<0\\ B^i=B^{i-1}+B_c^i-B_d^i, 0<B^{i-1}+B_c^i-B_d^i<B_{max}\\ B^i=B_{max}, B^{i-1}+B_c^i-B_d^i>B_{max}\end{array}\right.$$

(23)

The stored energy in the battery system must never be higher than the maximum storage capacity defined (B_max), nor lower than zero. Hereby, the system may not always discharge what is required at a specific hour. This limitation results in the parameter of energy needs reliability.

2.3. Optimization Methods

The system is very versatile and complex, due to the operation and management of different energy sources, demands, and constraints; it is crucial to seek the most optimized values corresponding to each energy sector/unit. The thinnest modification of the energy balance throughout the season can produce significant deviations from optimal results. Therefore, once the input data are defined in the simulation model and the preliminary results are computed, several optimization iterations are carried out for each water allocation, seeking to improve the results obtained, depending on the type of optimization configuration selected [38,39].

2.3.1. Solver Tool

Using the tool Solver in Excel 2019, a single objective function optimization was carried out, through the nonlinear method of the generalized reduced gradient (GRG), which seeks better results through gradient patterns, making it very dependent on the initial values for the decision variables, resulting mostly in the local best solutions; nevertheless, the multistart option was selected to improve the precision of the GRG nonlinear method. The multistart option mixes the fast-computing power of the GRG method with the complexity and precision of the evolutionary method in Solver, based on genetic algorithms (GAs). With the multistart option, the optimization process can seek a global solution. The size of the population was defined to be 200, with no set initial seed; the convergence requirement was not altered from Excel’s default: 0.0001.

As mentioned in Section 2.2, the decision variables are the hydropower factor, grid factor, and solar factor. Set as constraints, all of these variables must be valued between 0 and 1. Additionally, a constraint of the total number of hours of no irrigation was set to zero, to enforce the satisfaction of the irrigation needs for the crops.

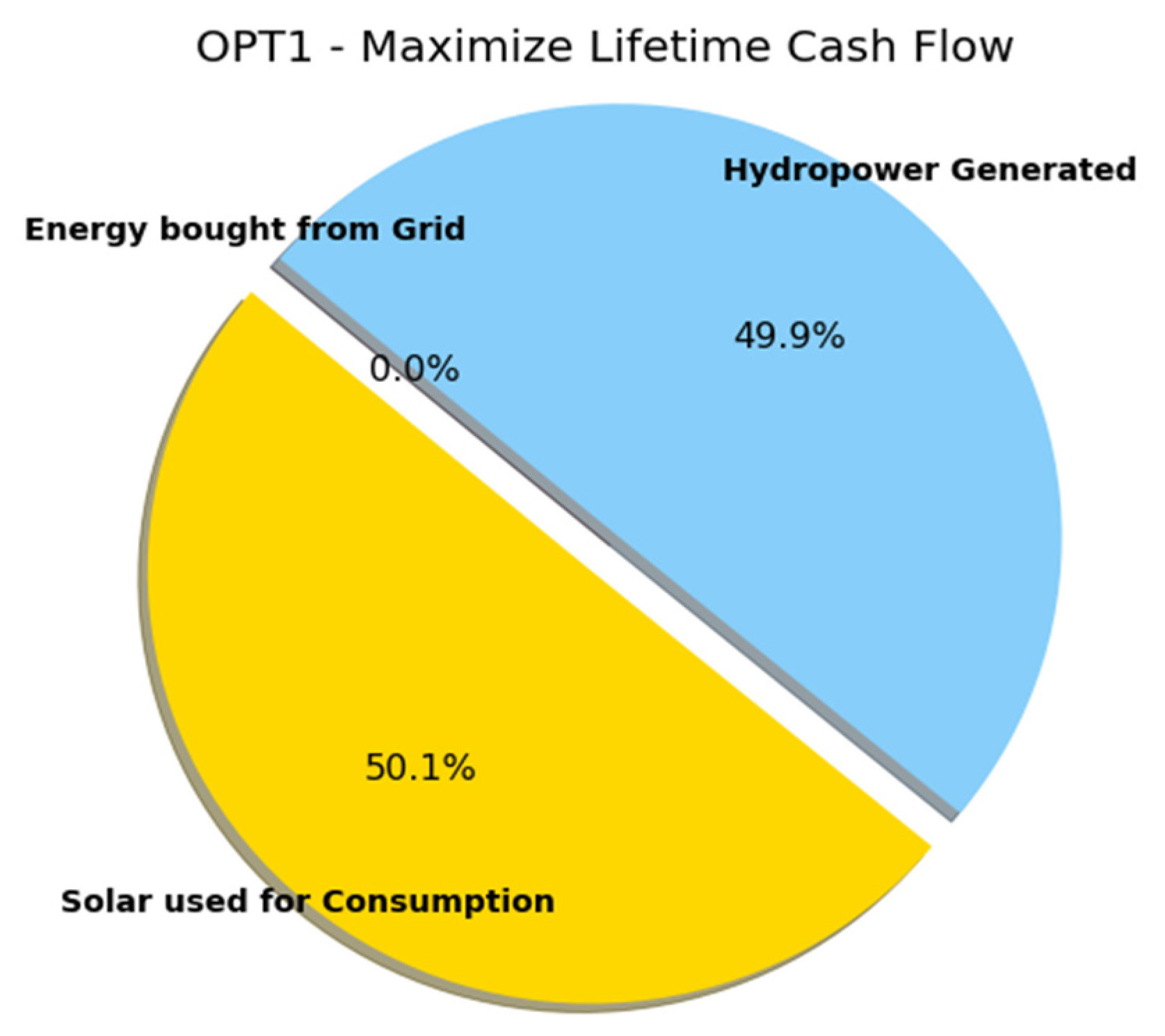
For each water allocation, three optimizations were executed, for different objective functions, labeled as OPT1, OPT2, and OPT3 in this research. OPT1: Maximize the lifetime cash flow; OPT2: minimize the consumption of grid energy used for pump operation; and OPT3: maximize the hydropower production.

Nevertheless, the cash flow and the amount of grid energy consumed are deeply related. Hence, in the results section, for some water allocations, both objective functions produce very similar optimized results. The cash flow, as it will be presented in the next chapter, corresponds to the difference between revenue (selling excess energy to the grid) and costs (buying energy from the grid).

An off-grid solution with batteries is also explored with the developed model. To enhance these results, the defined optimization objective, OPT4, aims to minimize the nominal storage capacity of the battery energy storage system, seeking to diminish the required initial investment and operation and maintenance costs associated with the installed capacity.

2.3.2. Python Algorithms

The algorithm developed in the Python language aims to optimize the hybrid system, taking into consideration two criteria. The algorithm uses the non-dominated sorting genetic algorithm (NSGA-II) method, which is capable of selecting two objective functions and seeking the best solution to both criteria. In the defined case study, the NSGA-II was used to optimize the hybrid system for two objective functions: minimize grid energy for pump operation and maximize hydropower generated. The functions were chosen due to the goal of the project to diminish grid consumption and to implement a PHS system. Therefore, the second objective function is reasonable to consider, as it explores the capability of the PHS system, to compare its potential to a simple pump station system. The algorithm is used in scenario 1 and scenario 2. Initially, the algorithm would attribute a decision variable to each hour and factor (i.e., hydropower, grid, and solar/wind energy), totaling around 25 thousand variables, which highly increases the computational time. Therefore, an approximation is identical to the one developed in Solver (i.e., variables allocated to periods of the day/month), to decrease the number of decision variables. Therefore, 315 variables were used in the Python algorithm to manipulate the energy balance during an average year. It used the open-source framework/library to construct the multi-objective optimization algorithm with a pre-defined assembly for the NSGA-II method. The biased initialization approach was adopted in this work, to improve the results from the NSGA-II. As the results could be obtained first and independently, an initial solution could then serve as a guideline for the Python code. This helped to achieve better solutions that are capable of obeying the constraints. The following parameters were selected to configure the multi-objective optimization algorithm: population size = 250, crossover probability = 0.9, mutation probability = 0.3, and number of generations = 10–15. The initial population is fixed due to the biased initialization approach.

3. A Case Study—System Definition and Configuration

For a detailed analysis and simulation of a hybrid system, an irrigation system was defined for this objective. The hybrid energy system (HES) was stated to dictate its operation status and techno-economic approach. In this case study, a symbiosis between solar and pumped storage hydropower is defined and crucial to the optimal operation, enabling the needs of the system: water allocation, and ensuring its feasibility under certain posed restrictions.

3.1. System Overview

For the modeling of the defined case study, the season of water needs was stated to start on the 1st of March and end on the 30 of September, possessing a timestep of an hour, “i”. The selected alternative is the grid-connected option. To the current date, the system unit solely uses grid energy to meet energy needs and operate the pumps to charge water to the upper reservoir. Regarding the renewable sources, solar energy and a pumped hydropower storage unit were selected, corresponding to the main scenario for analysis. This scenario will be deeply analyzed, technically and economically, by modeling it and optimizing it with the methods described in item 2. Figure 2 summarizes the energy sources in play for the defined case study and their relation.

3.2. Data Collection

3.2.1. Energy Consumption Data

The energy needs (E_cⁱ) correspond to energy requirements for the operation of agricultural activity. The energy demand presented corresponds to all the energy consumed by the agricultural field that is not directly related to the pump station operation, where the water is pumped to the upper reservoir for storage and later used in the irrigation network. For example, these include control systems (crucial in a hybrid system), auxiliary equipment (lightning, as the irrigation extends for 24 h), the operation of the irrigation network (e.g., pumps, hydrants, valves), and water treatment.

The energy demand is considered constant throughout the month, and it varies depending on the month of the irrigation season.

Table 1. Energy needs for each month.

Month	800 m3/ha [kWh]	1000 m3/ha [kWh]	3000 m3/ha [kWh]	6000 m3/ha [kWh]
March	215	269	807	1614
April	315	394	1181	2362
May	376	470	1411	2822
June	593	741	2222	4444
July	645	807	2420	4840
August	520	650	1949	3898
September	278	347	1042	2084

presents the energy demand according to the month and water allocation.

The energy values are based on a general irrigation field, where the energy consumption for a water allocation of 3000 m³/ha was retrieved and adapted for the case study under analysis and can be extended for other water allocations through a proportional factor.

3.2.2. Water Consumption Data

The agricultural area adopted in this case study has a wide variety of crops, which require different amounts of water per season fed by water pumping from a river to a top pond. Nevertheless, the total volume that is allocated every season is a fundamental parameter. For simplification purposes, the hourly water needed for irrigation is considered constant throughout each month. Nonetheless, the different water needs were taken into account throughout the season, i.e., in the peak of summer and crop growth, the water spent for irrigation is higher than at the beginning of the season (due to lower temperatures and the fact that crops have just been planted) or the end of the season (due to temperatures decreasing, evapotranspiration, and the fact that crops are being harvested). Equation (24) determines the hourly water irrigation volume attributed to a specific month.

$$A_m^i={\displaystyle \frac{Water allocation\times Irrigation area\times Month Share}{Total number of hours of that month}}$$

(24)

As stated, there is an annual limit of water that can be used for irrigation. For this study, the irrigation season was defined to start on the 1st of March and end on the 30th of September. Based on the real values of recent years, this study analyzes the system operation for water allocations of 800, 1000, 3000, and 6000 m³/ha. The monthly share attributed is presented in

Table 2. Monthly shares for water irrigation.

Month:	March	April	May	June	July	August	September	Total
Share [%]:	7	10	15	20	22	18	8	100

.

The maximum area of this hypothetic irrigation field is approximately 6000 ha. Therefore, the irrigation volume for each month is presented in

Table 3. Water irrigation volume for each month.

Month	800 m3/ha [m3]	1000 m3/ha [m3]	3000 m3/ha [m3]	6000 m3/ha [m3]
March	451.61	564.52	1693.55	3387.10
April	666.67	833.33	2500.00	5000.00
May	967.74	1209.68	3629.03	7258.07
June	1333.33	1666.67	5000.00	10,000.00
July	1419.36	1774.19	5322.58	10,645.16
August	1161.29	1451.61	4354.84	8709.68
September	533.33	666.67	2000.00	4000.00

, according to each water allocation.

Currently, the irrigation system uses the pump station for pumping water to the upper reservoir that only serves for irrigation; therefore, the allocation limit is assigned to the volume that could be pumped. This study implements a new solution for a hybrid energy system; as the PHS station either serves to pump or turbine water, it is no longer limited by this restriction. The allocation limit is only applied to the reservoir outlet that feeds the irrigation pipeline network, i.e., the water that is discharged downstream through the turbines and back to the river does not count for the water allocation limit.

3.2.3. Irrigation System

Agricultural activity requires not only water volume but also energy. Therefore, the hybrid energy system must be able to fulfill the irrigation field needs. Typically, an irrigation season begins in March and lasts up until September, 24 h a day. For this period, the regulatory authorities define the maximum water allocation for each area.

The energy needs are correlated with the allocated water, i.e., if the water consumed for irrigation increases, the energy needs also increase. Every season has a predetermined maximum amount of water that can be used by the irrigation system. Farmers must obey this restriction, as this imposition aims to prevent the risk of increasing droughts and further environmental damage to the surrounding ecosystem and the watershed.

During the off-season months, the water and energy needs are null. At the beginning of January, the water volume pumped to the upper reservoir is accounted for, plus the associated energy consumption for the pump station operation. Therefore, when the season starts, on the 1st of March, the reservoir is considered approximately full.

3.2.4. Solar Data

To collect solar irradiance from a specific location, data were retrieved from the free software PVGIS, by inputting the precise coordinates and parameters of the PV array: Peak power = 9000 MWp, optimum slope = 33°, and azimuth = 0°. A data file was then registered and solar power was obtained. As the developed model simulation has a time increment of 1 h, the power is the same as the energy in kWh, (Sⁱ).

As can be seen in Figure 3a, the selected agricultural area has a lot of advantages for this type of hybrid system. Figure 3b illustrates the solar generation for three distinct days during the season. In this hypothetical region, the selected area is very favorable for solar energy.

Apart from possessing a good elevation change for the implementation of a PHS station, it also has high irradiance values throughout the year. This location holds a huge potential for solar energy, as the daily irradiance is more or less constant throughout 12 months, and is not restricted to the summertime only.

3.2.5. Pumped Hydropower Storage Unit

The system intends to operate a PHS facility by using excess solar energy to pump water from a river to an upper reservoir, enabling the storage of water/potential energy, so that in periods of non-solar generation, water is discharged down the pipeline to run through turbines and generate the energy needed for the irrigation system. The water pumped upstream must be sufficient to satisfy the water needs for irrigation every hour, Aⁱ.

For the hypothetical case study, the pump/turbine station is located 5 m above the river height and the upper reservoir is 89 m above it when at the maximum level. The pumping capacity is 4500 L/second with a nominal power of 7.4 kW. Head losses were accounted for in the average pump head, equal to 100.14 m, by adding the average value of head losses as a function of various water flows, considering the circuits characteristics, as presented. The average pump efficiency, 60%, was computed by Equation (25), to respect the maximum flow and nominal pump power.

$${\eta }_p={\displaystyle \frac{\rho \times g\times Q\times H}{P}}$$

(25)

These conditions are achieved by four parallel pumps, maximizing the possible flow of pumping. The average turbine head follows the same principle. It is equal to 80.1 m, with the average head losses discounted. The average turbine efficiency was arbitrated to be 76%. The overall power of the turbine station is determined by analyzing the maximum hydropower generated for each water allocation and optimization method. The single pipeline of 1200 mm in diameter and a total length of approximately 3.5 km serves for both the pump and turbine operation. Therefore, the system can never perform both operations simultaneously; it either pumps or turbines.

3.2.6. Top Reservoir

The top reservoir is a pond with a maximum volume capacity of 1,078,627 m³. The water needs are discounted from this reservoir, enabling a pressurized irrigation approach. Throughout the simulation of the operation of the irrigation system, the reservoir volume is responsible for feeding the crops with the necessary water volume, and in the interim, to function as a component of the PHS system.

The minimum and maximum reservoir volumes are 118,231.16 and 1,078,627 m³, respectively. The minimum volume was settled as the estimated volume of the reservoir when it is at a 1 m depth. The reservoir shape is considered a rectangular prism, and its constant surface area was determined via satellite measurement.

The resultant area (A_R) is 118,231.16 m³. With it, an estimation of the water depth, in meters, at the reservoir can be obtained by Equation (26):

$$h_R^i={\displaystyle \frac{V_R^i}{A_R}}$$

(26)

3.2.7. Grid Tariffs

The case study’s system is currently grid-connected, and some hybrid solution analysis maintains this status. Further in the study, an alternative with batteries instead of grid energy is additionally explored. The used tariffs for the models’ simulation and optimization are presented in Figure 4, with purchasing and selling prices, respectively, based on Mibel grid prices of 2020/2021.

As a result of the considered tariffs, the hydropower and grid factors, distributed as a daily and monthly matrix, take into account the tariff period during the day, separating it into five main periods. The impact of grid tariffs on the economic results is obtained by the models and the way the optimization dictates the mode of operation of the system.

3.3. Lifetime Analysis

The optimization can proceed when the models are defined with the necessary parameters and the input data are implemented. Once the results for different water allocations have been obtained and optimized, the yearly energy and economic balance can be evaluated. In this case study, a lifetime analysis of 25 years is defined. Regarding the economic aspect, the cash flow can be calculated for every year using Equation (27).

$$Cash\hspace{0.25em}Flow\left(n\right)={\sum }_{i=1}^{k}Profits\left(i\right)-{\sum }_{i=1}^{k}Costs\left(i\right)$$

(27)

The cash flow (n) corresponds to the total annual difference between profits and costs, where “(n)” represents the year, and profits(i) and costs(i) are the hourly profits and costs, respectively. “k” is the total number of hours in the studied year. Nevertheless, in most cases, PV farms are not allowed to sell energy to the grid for the first five years, in case they are being subsidized by state funds. Therefore, the cash flow(n) in the first five years is only composed of the total annual costs portion. Hence, the cash flow part of the net present value (NPV) can already be computed by Equation (28).

$$NP{V}_{CF}=C{F}_{\left[1-5\right]}\times {\displaystyle \frac{1-{\left(1+r\right)}^{-n}}{r}}+{\displaystyle \frac{C{F}_{\left[6-25\right]}\times \frac{1-{\left(1+r\right)}^{-n}}{r}}{{\left(1+r\right)}^5}}$$

(28)

where the variables are defined as follows:

NPV_CF: Net present value due to the yearly cash flows, EUR;

CF₁₋₅: Yearly cash flow of the first five years, EUR;

CF₆₋₂₅: Yearly cash flow of the years after year five, EUR;

r: Discount rate, 10%;

n: Number of years, five and twenty at each parcel.

According to Equation (28), the yearly cash flow is constant throughout the lifetime, and the analysis presented is performed with a fixed water allocation for every year.

It is necessary to account for initial investments, operation and maintenance costs (O and M), and CO₂ emissions, which can be taxed. Considering the current situation, the irrigation system already possesses a pump station; therefore, there are no required investments regarding new pumps, pipelines, or significant valves. However, the conversion to variable speed drive pump operation (VSD/VFD) might be suitable to consider, as the energy coming from the PV panels is significantly fluctuant and fast-changing. The initial investments were implemented for PV panels and turbines for hydropower generation. The investment cost per installed kilowatt for hydro turbines is EUR 1500/kW [15,17,22]. As the nominal power of the turbine station is 1 MW, the total investment is EUR 1.5 M. Regarding the solar panels, the specific cost is EUR 850/kW [20,21], plus an inverters investment of EUR 208,000 (GW350K-UT 1500 Series, nº of inverters: 26), and considering a state subsidy of 50% of the solar system. This results in a total required photovoltaic investment of EUR 3.93 M for a 9 MWp installation for potential investors of the project.

As for the operation and maintenance costs, the hydro turbines’ annual cost is EUR 20/kW/year; the pumps are EUR 10/kW/year and the PV panels plus inverters are EUR 8.73/kW/year [20]. This amounts to a total O and M cost for each source of EUR 20,000, EUR 74,000, and EUR 78,580, respectively. Grid operation and maintenance costs were not accounted for, as valid and consistent values could not be obtained. Nonetheless, its impact is minimal for the comparison between grid-connected scenarios (1 and 2) and the off-grid solution (scenario 3).

A major difference between the current operation approach (i.e., without renewables) and the proposed hybrid solution is the environmental impact, sustainability, and grid independence. The hybrid system can be independent of the grid according to certain water allocation values. Therefore, the CO₂ emissions resulting from the operation of the system are significantly lower than the emissions resulting from the current approach. Nowadays, most EU countries tax these emissions, which increases the costs, thus requiring them to be taken into account when analyzing the economic parameters during a lifetime. The cost derivative from CO₂ emissions can be computed as follows using Equation (29).

$$E{C}_{CO2}=Grid\hspace{0.25em}Energy\hspace{0.25em}\times \hspace{0.25em}C{O}_2\hspace{0.25em}factor\hspace{0.25em}\times \hspace{0.25em}Emissions\hspace{0.25em}Tax$$

(29)

where EC_CO2 corresponds to the annual costs derivative from CO₂ emissions, in EUR; grid energy is the total annual energy consumed by the system, in kWh; the CO₂ factor is the relational value between energy and kilograms of carbon dioxide emitted, equal to 0.331 kgCO₂/kWh; and the emissions tax corresponds to the value defined by the government/authorities to penalize the emissions associated with the system operation, which is equal to EUR 0.1162/kgCO₂.

Finally, the total net present value for a lifetime period of 25 years can be determined. The final NPV is presented in Equation (30).

$$NPV=NP{V}_{CF}-Initial\hspace{0.25em}Inv\times -O\&M\times {\displaystyle \frac{1-{\left(1+r\right)}^{-25}}{r}}-E{C}_{CO2}\times {\displaystyle \frac{1-{\left(1+r\right)}^{-25}}{r}}$$

(30)

Additionally, the levelized cost of energy (LCOE) can be computed. This metric is crucial to analyze the viability of a project for an extended period. The formula to obtain the LCOE is determined using Equation (31).

$$LCOE={\displaystyle \frac{Total\hspace{0.25em}Costs}{Total\hspace{0.25em}Generated\hspace{0.25em}Energy}}$$

(31)

A comparison with the current approach (100% grid energy as the energy source) was conducted to evaluate the benefits or disadvantages of the new hybrid solution versus the current mode of operation. This comparison is based on the economic metrics presented in this section. However, the technical and social parameters should not be neglected, as the hybrid system stands as a better sustainable solution.

Regarding the other two scenarios (i.e., scenario 2: +wind and scenario 3: +wind + batteries), some modifications were required for the systems’ configuration, i.e., the number of wind turbines, installed capacity of hydropower, and battery energy storage system (BESS).

4. HY4RES Model Results and Discussion

In this section, the energy and economical results for the different water allocations are presented, according to each optimization method and configuration. The NSGA-II optimization method is only presented for 3000 and 6000 m³/ha, as for the other two scenarios, it ends up as a single objective optimization process, due to the possibility of using zero grid energy for the pump operation.

4.1. Maximum Water Allocation without Grid Consumption

Before the presentation of the results for different water allocations, it is important to analyze the performance of the system without grid assistance. The goal of this project is to develop a hybrid energy system which is capable of satisfying the requirements of consumption while only using renewable energies. Therefore, an optimization process was performed to realize what is the maximum water allocation that can be attributed to the season period, where the system does not need to buy energy from the grid to satisfy the demand.

From the GRG nonlinear optimization method with Solver, the maximum water allocation is 992 m³/ha; above it, the system will need auxiliary energy from the grid to satisfy the energy and irrigation needs. This value makes sense, as for 1000 m³/ha, no optimized values could produce a system operation without grid intervention. The configuration used to perform this optimization process consisted of fixing the hydropower and grid factors to one and zero, respectively; the first one is responsible for ensuring that hydropower satisfies the energy needs if solar energy is not capable of that, and the second one is to avoid a case where grid is used to boost the volume of water pumped uphill for storage. The only variable factor is the solar energy.

4.2. Water Needs: 800 m³/ha

Table 4. Main results according to the optimization method, 800 m³/ha.

Optimization Method:	OPT1 (Max. Lifetime Cash Flow)	OPT2 (Min. Grid Energy for Pump)	OPT3 (Max. Hydropower Generated)
Hydropower Volume [m3]	6,503,314.808	6,503,314.808	6,503,314.808
Pumped Volume [m3]	11,553,481.970	11,553,941.630	11,553,941.630
Hydropower [kWh]	1,077,716.323	1,077,716.323	1,077,716.323
Solar Energy for Pump [kWh]	5,249,196.2	5,249,405.0	5,249,405.0
Grid Energy for Pump [kWh]	0.0	0.0	0.0
Grid Energy [kWh]	0.0	0.0	0.0
Solar Excess to Grid [kWh]	8,335,480.0	8,335,271.0	8,335,271.0
Lifetime Cash Flow [EUR]	2,527,096.0	2,477,787.0	2,477,787.0

presents the total results for a single year, for 800 m³/ha water allocation, plus the lifetime (25 years) cash flow. As a reminder, the lifetime cash flow considers no selling of solar excess to the grid in the first five years, and it is described in Equation (27).

The overall results for 800 m³/ha are quite identical and equal for OPT2 and OPT3, as all the optimization methods followed the same path and obtained the “same” solution for the system operation. The three optimizations with Solver used a hydropower factor equal to 1 in all periods, reaching the maximum possible hydropower generation. OPT1 explored the profit a little bit more by selling excess solar energy to the grid; hence, there is a slightly higher cash flow. For 800 m³/ha, OPT3 did not produce a different perspective for the system, as all Solver optimizations were capable of maximizing the hydropower.

Since the water allocation is quite low and the system is flexible to this amount, for all optimizations the grid energy for the pump is zero, as the hydropower and solar energy are sufficient for satisfying energy and water needs. The solution variables for OPT2 and OPT3 are the same, yielding identical results.

Figure 5 represents the energy balance of different sources and the demand, throughout 24 h, enhancing the symbiosis between the different subsystems required to operate in harmony to fully satisfy energy needs. In both graphs, it can be noticed that at night, hydropower (blue) is responsible for assuring energy consumption needs, whereas during the day, this is carried out by solar-produced energy (yellow). The variable “energy deficit” corresponds to grid energy that is required for buying, either for pumping or to satisfy energy needs, which remains at zero.

Whenever the solar energy is in excess, after consumption and usage for pumping water by the PHS subsystem, it can be sold to the grid, seen as the variable “energy surplus”; this is prominent at mid-day if the solar factor allows it, or at the beginning and ending of solar production, where the power generation is quite low and not suitable for operating the pumps. Therefore, the system prefers to not use low-power solar energy to pump water; instead, it can be sold.

In Figure 5, there is a high peak of surplus solar energy sold to the grid, and it is accompanied by no pumped volume to the upper reservoir. This occurrence is due to the reservoir maximum volume restraint, which forbids the system to pump water uphill. Further, the surplus solar energy that is available cannot be used by the PHS. The storage level of the reservoir during every hour is important for the operation of the system and is highly influential on the energy balance obtained after optimization. Figure 6 illustrates the fullness of the uphill reservoir throughout the season for each optimization method.

The symbiosis between solar generation, reservoir current capacity, and the possible pumped volume at each hour, can also be seen in the following plot, Figure 7, for the maximizing lifetime cash flow optimization method (OPT1).

In every optimization method, the water reliability was easily fulfilled, assuring a 24 h irrigation throughout the whole defined season. Not only for the 800 m³/ha water allocation but for every allocation, the water reliability sought in the optimization methods was 100%. As the study is defined for an irrigation field, it is crucial to comply with the main objective: satisfying water needs. Additionally, the energy needs must also be always satisfied to ensure the proper operation of the agricultural activity. The pie chart below, in Figure 8, represents the shares of solar energy, hydropower, and grid energy sources to fulfill energy requirements by the system. It corresponds to the three optimization configurations in Solver.

Finally, the overall energy and water volume balance for the whole irrigation season is shown in Figure 9, for the case of lifetime cash flow maximization (OPT1). For 800 m³/ha, this optimization configuration presents the best solution, as for energy parameters, all methods have identical results, but, ultimately, this obtains the best cash flow.

4.3. Water Needs: 1000 m³/ha

The following

Table 5. Main results according to the optimization method, 1000 m³/ha.

Optimization Method:	OPT1 (Max. Lifetime Cash Flow)	OPT2 (Min. Grid Energy for Pump)	OPT3 (Max. Hydropower Generated)
Hydropower Volume [m3]	11,398.1	8,111,511.0	8,277,052.0
Pumped Volume [m3]	6,261,798.6	14,359,433.2	14,526,279.7
Hydropower [kWh]	1888.9	1,344,223.4	1,371,656.5
Solar Energy for Pump [kWh]	2,844,978.6	6,524,049.0	6,050,773.8
Grid Energy for Pump [kWh]	0.0	0.0	549,080.0
Grid Energy [kWh]	1,369,768.0	27,433.0	549,080.0
Solar Excess to Grid [kWh]	10,493,562.0	6,814,492.0	7,287,767.0
Lifetime Cash Flow [EUR]	2,050,599.0	1,667,899.0	1,395,290.0

presents the total results for a single year, for 1000 m³/ha water allocation, plus the lifetime (25 years) cash flow.

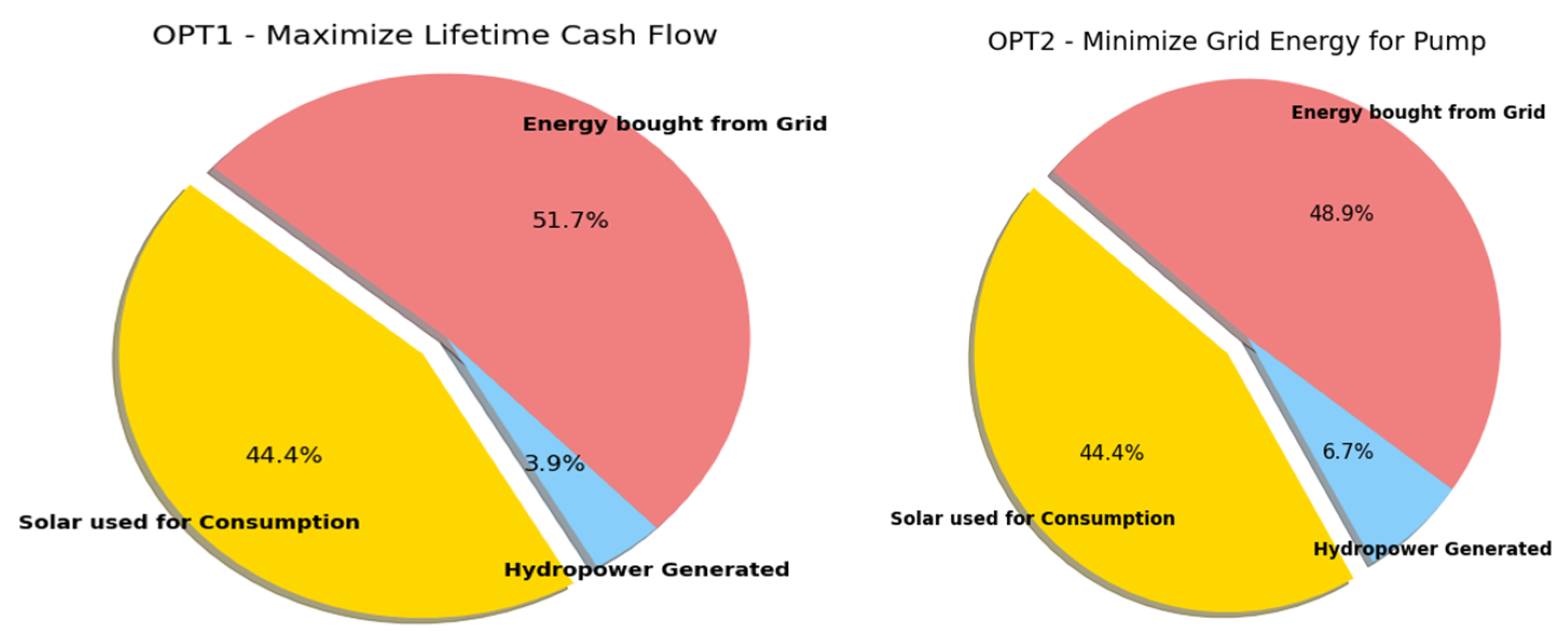
For a water allocation of 1000 m³/ha, the system can still guarantee complete irrigation satisfaction (water reliability = 100%) by solely filling the upper reservoir with solar surplus energy powering the pump station (Figure 10). From OPT1 and OPT2, only grid usage corresponds to the energy needed to satisfy the rest of the energy needs, which are not fulfilled by solar or hydropower energy. OPT1, which aims to maximize the lifetime cash flow, uses less hydropower, which in one way increases grid usage, but also enables more solar energy to be sold, as the water volume required in the reservoir throughout the season becomes less rigid. The total solar excess from OPT1 is 10,493,562 kWh, whereas for OPT2 it is 6,814,492 kWh. Although costs from grid purchase are quite inferior in OPT2, in comparison to OPT1, the profit difference between methods is much higher; hence, there is a greater cash flow for OPT1.

Regarding maximizing hydropower generation, for OPT3, the solution is similar to OPT2, but with an increase in hydropower due to a greater hydropower volume, it is also needed to compensate with grid energy to power the pumps and ensure the reservoir has enough volume for every water requirement. Therefore, the cash flow is the lowest for OPT3.

Figure 10 represents the energy balance on a selected day (1st of August) for every optimization method. Characteristic traces of each configuration can be visualized for a 24 h period. For OPT1, there is a higher dependence on grid assistance. For OPT2, there is a more balanced system. In OPT3, the influence provoked by the increase in hydropower generation is visible; and there is a need to aid the pump operation with grid energy (“energy deficit” variable).

Figure 11 presents the contribution of different energy sources for the fulfillment of energy needs. It further deepens how the system behaves according to the defined goal/optimization.

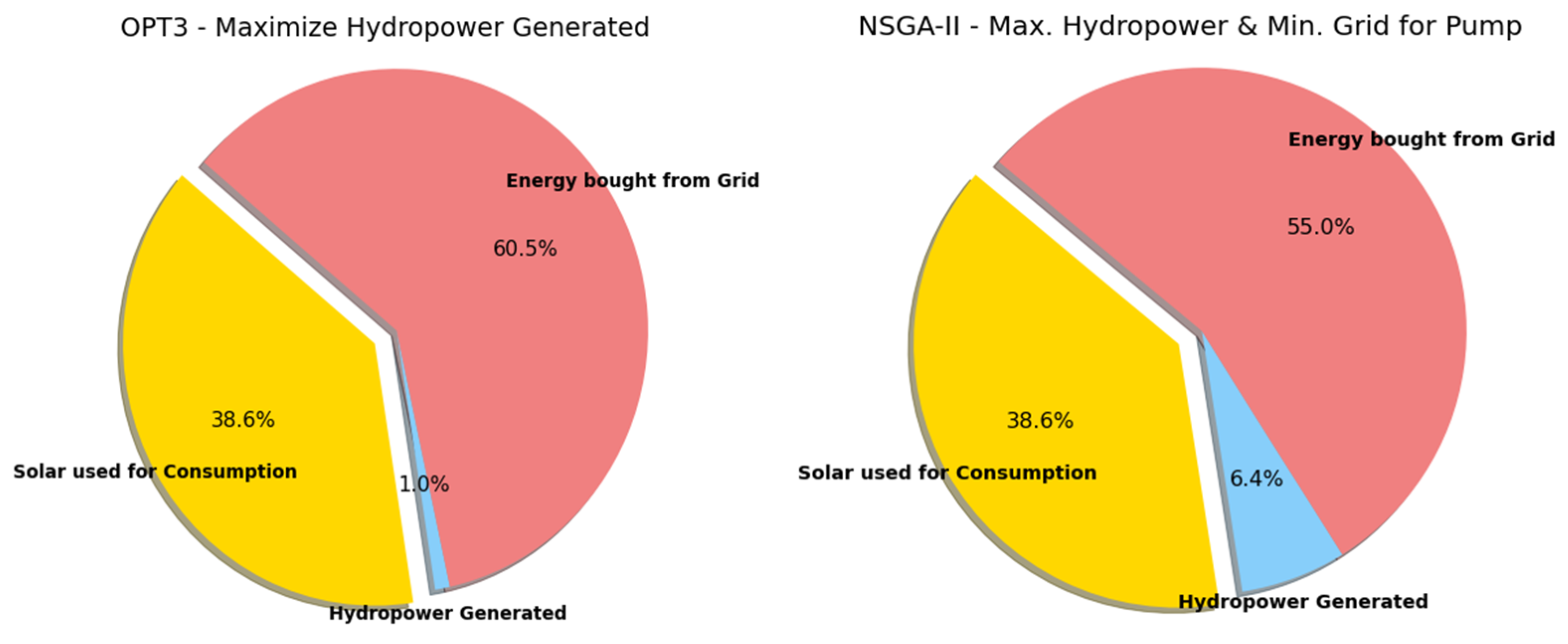
Additionally, the same type of pie chart can also present the share of solar and grid energy used by the pump station, for maximizing hydropower optimization, as shown in Figure 12.

Furthermore, the total energy consumption each month by source (needs + pump station) can be plotted for a complete year. In Figure 13, it is possible to see the main traces of each optimization method; OPT1: less hydropower is used in order to sell more solar energy and a smaller amount of pumped volume is required; OPT2: there is an increase in solar consumption to diminish grid consumption, aided by a compensation of hydropower on energy needs; and OPT3: there is an increase in grid consumption to boost the hydropower maximization.

The different approaches between the optimization methods possess a significant impact on the reservoir’s fullness throughout the season. The more optimized and refined the system is, the more likely it is for the reservoir to have a lower volume during the irrigation season. Nonetheless, this might not be desired, as it prevents flexibility in critical periods or aids other water activities in the region. Figure 14 presents the reservoir’s record of fullness throughout the irrigation season for different scenarios: OPT1 and OPT2.

4.4. Water Needs: 3000 m³/ha

Table 6. Main results according to the optimization method, 3000 m³/ha.

Optimization Method:	OPT1 (Max. Lifetime Cash Flow)	OPT2 (Min. Grid Energy for Pump)	OPT3 (Max. Hydropower Generated)	NSGA-II (OPT2 + OPT3)
Hydropower Volume [m3]	1,915,870.0	3,301,640.0	5,705,169.0	3,700,615.9
Pumped Volume [m3]	20,166,447.2	21,552,595.3	23,954,453.2	21,893,512.0
Hydropower [kWh]	317,494.1	547,141.2	945,449.3	612,989.0
Solar Energy for Pump [kWh]	4,133,361.2	5,027,692.2	5,490,393.7	4,516,647.7
Grid Energy for Pump [kWh]	5,029,040.0	4,764,490.0	5,393,046.0	5,430,426.2.0
Grid Energy [kWh]	9,219,036.0	8,724,839.0	8,955,087.0	9,324,927.6
Solar Excess to Grid [kWh]	6,940,262.0	6,045,931.0	5,583,229.0	6,556,975.2
Lifetime Cash Flow [EUR]	−7,598,476.0	−7,818,833.0	−8,325,705.0	−7,943,661.7

presents the results for a single year, for a 3000 m³/ha water allocation, plus the lifetime (25 years) cash flow.

The leap from 1000 m³/ha water allocation to 3000 m³/ha is quite prominent. From 800 m³/ha to 1000 m³/ha, there was a noticeable slight increase in grid usage, depending on how intensively the renewable sources were explored, especially hydropower. Now, the water volume for irrigation is very high and the system can no longer operate the PHS subsystem entirely on solar energy. Additionally, the feasibility of turbine water downhill to generate power for energy needs is lower and more restricted to small amounts and periods.

Regarding the NSGA-II optimization, the Python algorithm found the best solution with a maximum of 99.7% water reliability. This amounts to 16 h in the total season where the water cannot be fulfilled, which can be neglected. Nevertheless, the algorithm counts with a biased initialization to help the GA method find solutions that satisfy the constraint of water reliability (=100%).

Figure 15 presents the energy balance for the same selected day (1st of August) for 3000 m³/ha water allocations, for each optimization method.

A major evident difference present in Figure 15, in comparison to the other energy balances previously shown, is the emergence of the “energy deficit” variable, i.e., the energy bought from the grid to fulfill the leftover energy needs or to power the pumps of the PHS subsystem is used to increase the stored water volume in the reservoir. On the other hand, the “energy surplus” available to sell to the grid is greatly inferior. At a 3000 m³/ha water allocation, every opportunity to pump water uphill and store it for safekeeping for irrigation is prioritized.

Logically, the contribution of grid energy to the satisfaction of energy needs and the operation of the pumping system is much higher, in comparison to the previously analyzed water allocation, 1000 m³/ha. The pie charts in Figure 16 and Figure 17 illustrate this occurrence.

It is the significant increase in grid energy dependence that causes the solutions for the 3000 m³/ha water allocation to initiate such negative cash flows.

Hence, for 1000 m³/ha, using the OPT1 optimization configuration, the system is not pumping water uphill 85% of the hours of the defined irrigation season (1st of March till 30th of September), despite not using grid energy. But, for 3000 m³/ha and the same optimization configuration, the system is not pumping water only at 44% of the hours of the total irrigation season. Additionally, the first water need scenario (1000 m³/ha + OPT1) only uses around 3000 MWh of solar energy for the pump operation; whereas for a water need of 3000 m³/ha, it uses approximately 4600 MWh of solar energy to power the pumps. The solar contribution for the PHS increased, but still, it was not sufficient for the 100% energy and water reliability at a 3000 m³/ha water allocation.

Figure 18 presents the energy balance with the multi-objective optimization, which aims to minimize grid energy usage for the pump operation and maximize the hydropower generated (NSGA-II); the grid consumption is still highly noticeable, especially in the summer months. This is due to the energy and water need profile peaks at this period, owing to the crops’ level of growth and weather conditions.

4.5. Water Needs: 6000 m³/ha

For the 6000 m³/ha water allocation, plus the lifetime (25 years) cash flow,

Table 7. Main results according to the optimization method, 6000 m³/ha.

Optimization Method:	OPT1 (Max. Lifetime Cash Flow)	OPT2 (Min. Grid Energy for Pump)	OPT3 (Max. Hydropower Generated)	NSGA-II (OPT2 + OPT3)
Hydropower Volume [m3]	891,098.2	295,154.0	933,858.0	6,301,779.0
Pumped Volume [m3]	37,141,485.4	36,546,008.6	37,184,241.5	34,279,223.0
Hydropower [kWh]	147,671.0	48,912.3	154,757.0	1,044,281.0
Solar Energy for Pump [kWh]	3,259,265.2	3,018,760.9	2,920,753.0	1,516,573.4
Grid Energy for Pump [kWh]	13,615,556.0	13,585,512.0	13,973,494.0	14,057,810.6
Grid Energy [kWh]	23,421,659.0	23,490,374.0	23,772,511.0	22,967,303.7
Solar excess to Grid [kWh]	5,159,513.0	5,400,018.0	5,498,026.0	6,902,205.2
Lifetime Cash Flow [EUR]	−22,973,973.0	−23,250,284.0	−23,505,846.0	−21,649,585.3

presents the total results for a single year.

For a water allocation of 6000 m³/ha, the importance of using the grid as an auxiliary source to renewables increases to its peak. Most solar energy is primarily consumed for energy needs. Figure 19 shows the energy balance on the 1st of August.

With a brief analysis of Figure 19, it is easily noticeable that the pump schedule is no longer limited to sunny hours. This is due to the hydropower generation being almost nonexistent, opening the possibility to pump water during the night, or throughout the day. This is one of the reasons why grid usage also increases significantly, as the system prefers to pump water during the night as the used tariffs are less punishable during those hours. For 6000 m³/ha of water allocation, hydropower generation, with the system’s characteristics, is mostly undesirable as it requires high volumes of water to produce the needed energy for the load demand.

For this configuration, the share contribution of grid energy either for energy needs or for the pump station is much more significant, as shown in Figure 20 and Figure 21, respectively.

During the optimization process, for this irrigation volume, it was more difficult to achieve a diverse range of solutions, as the slightest modification to the energy balance would immediately compromise the water reliability. That is why, from all the water allocations studied, 6000 m³/ha presents the most similar results for each optimization method. As an exception, the NSGA-II optimization in Python could not obtain a feasible solution that was capable of ensuring 100% of water needs. The yielded “best” solution had a water reliability of 79.4%, which corresponds to a significant absence of water fulfillment throughout the season. The algorithm chose to maximize hydropower to the extent that the reservoir could never be able to store enough water volume for both hydropower and water consumption. Nevertheless, the multi-objective optimization results present a new view of the system for such a great water allocation, in terms of hydropower capabilities, as the maximum generated reached approximately 4500 kW.

Although a biased initialization was used in the algorithm, with solutions obtained previously with the GRG nonlinear method, the algorithm still could not find a solution with 100% water reliability.

4.6. Lifetime and Economic Comparison

With the model optimized and the needed results obtained, an economic analysis was developed and ultimately compared with the current approach, where the grid is the only energy source. The lifetime cash flows have already been presented at each water allocation analysis. A histogram of the hourly (full year) sales, purchases, and their difference is presented in Figure 22 for each water allocation with OPT1, which aims to minimize the lifetime cash flow. From the histogram, the evolution of sales and purchases can be analyzed. For lower water allocations, 800 and 1000 m³/ha, the hourly revenue is on average higher than the costs; hence, there is a positive cash flow overall. But, for higher water allocations, 3000 and 6000 m³/ha, it turns to the opposite, creating a negative cash flow. This turnover, provoked by the overthrow of costs over the revenues, is due to two factors; for higher water allocations, the system is not as capable of saving solar energy as excess to then sell to the grid as it is for lower water allocations. Irrigation needs are much greater; therefore, the reservoir is in constant demand to be replenished. Hence, the increase in grid energy consumption is used to aid in the pump operation and the decrease in solar energy is sold to the grid. This causes the revenue to decrease and the costs to rise, placing the cash flow on the opposite side of the axis.

It is now necessary to increment the overall initial investments, operation and maintenance costs (O and M), and CO₂ emissions taxation. The total initial investment of the hybrid solution is EUR 6,065,000. The total operations and maintenance costs each year are EUR 170,500/year. For each water allocation and optimization technique, the total amount of kilograms of CO₂ produced due to grid consumption can be obtained, as presented in Figure 23.

Table 8. Yearly CO₂ emissions taxation for each water allocation and optimization.

Solution:	800 m3/ha	1000 m3/ha	3000 m3/ha	6000 m3/ha
OPT1	0.0	52,684.3	348,940.0	900,848.5
OPT2	0.0	1055.1	335,576.5	903,491.5
OPT3	0.0	21,118.8	344,432.4	914,343.1
NSGA-II	-	-	358,657.2	883,373.0
100% Grid	162,470.5	202,454.9	630,276.5	1,256,579.8

presents the CO₂ taxes for each water allocation and optimization method in a single year.

Based on Section 3.3., it is possible to compute the final net present value for each water allocation and optimization. The respective results are presented in the following graphic of Figure 24.

The net present value of the current configuration, comprising solely the grid, was simulated with the same developed model, without the solar and hydropower sources, and optimized to ensure an appropriate change in costs from grid consumption. Every optimized solution of the hybrid system possesses a higher NPV than the grid approach. The main reason for this is the significantly lower consumption and dependence on grid energy, and a second reason is the CO₂ emissions taxation.

On average, the configuration with grid energy only uses four times more grid energy. For the lower water allocations, 800 and 1000 m³/ha, the difference is considerably more pronounced. Regarding the remaining water allocations, 3000 and 6000, the difference becomes smaller, but this is mainly due to the high energy needs and the logic behind each model design; energy needs are primarily satisfied by solar energy. Therefore, if the energy demand is high, the solar energy available will be mainly consumed for this aspect. The values attributed to energy needs may be considered to be somewhat inflated, but the intent is to explore the limits, capabilities, and sizing of the hybrid solution. It was prudent to slightly exceed the energy requirements, taking into account the topography of the area, which increases the energy consumption by the water–energy nexus system network.

To evaluate the influence of the energy needs, a simple optimization for 6000 m³/ha of water allocation was performed, with half the energy needs predefined. This configuration was capable of doubling the solar energy used by the pump station and decreased the lifetime cash flow from EUR −23 M to EUR −14.4 M (OPT1), primarily due to the reduction in grid consumption. It is a significant decrease, revealing a disadvantage of the developed model; it firstly consumes the generated solar energy for energy needs and then manages it for the PHS. Then, an auxiliary from the grid is required to comply with a 100% water need reliability. Nonetheless, this strategy was preferred, as the energy needs mainly correspond to the energy consumed by the irrigation network, i.e., the operation of pumps, valves, control devices, and hydrants present in the network are distributed through the 6000 hectares to deploy water to the crops.

Regarding the levelized cost of energy (LCOE), as stated in Equation (31), the parameter corresponds to the ratio between a system’s costs and the energy generated by it during a lifetime. Therefore, for twenty-five years, the following LCOEs for each water allocation are 0.02, 0.03, 0.05, and 0.11, in ascending order. The results were obtained through the fraction of the overall costs (initial investments, O and M, carbon dioxide taxes, and grid purchases) by the summed generated energy of solar and hydropower (the grid is not included as it is an auxiliary and external source of the system). The LCOE for each optimization technique ends up yielding the same value, apart from OPT2 and OPT3 for 1000 m³/ha, which results in 0.02.

5. Scenario Exploration

In this section, the case study model is further explored by simulating the system with other energy sources incremented, for example, wind energy paired with photovoltaic energy to satisfy energy needs and power the PHS subsystem. Additionally, auxiliary alternative B, which uses batteries, is also studied to analyze an off-grid scenario. For both scenarios (+Wind and Batteries alternative), the models were analyzed for water needs of 1000 and 3000 m³/ha.

5.1. Scenario 2: Wind Turbines Add-on

The first alternative scenario, labeled as scenario 2, increments wind energy to the hybrid system. The Vestas V110-2.0 MW wind turbine was selected, with a total of two turbines, resulting in 4 MW of output power for the present scenario. With the online tool renewables.ninja, the hourly energy production of the two turbines combined was obtained (Figure 25), extracted, and implemented in the existing model.

As described in Section 2.2., the wind energy generated is added to the solar production. Then, this sum is used to satisfy energy needs, power the pump station, or be sold, if in excess, to the grid. For scenario 2, the selected optimization methods were OPT1, to maximize the lifetime cashflow, and the defined NSGA-II algorithm. The general results obtained are presented in

Table 9. Scenario 2 results (with OPT1).

Parameter	OPT1 (1000 m3/ha)	OPT1 (3000 m3/ha)	NSGA-II (3000 m3/ha)
Hydropower Volume [m3]	753,252.0	649,022.6	642,414.7
Pumped Volume [m3]	7,002,158.7	18,899,804.0	18,890,557.9
Hydropower [kWh]	124,827.5	107,554.7	106,459.0
Solar + Wind Energy for Pump [kWh]	3,181,353.0	6,725,713.1	6,363,455.1
Grid Energy for Pump [kWh]	0.0	1,861,203	2,219,260.0
Grid Energy [kWh]	0.0	3,153,867.7	3,513,020.6
Solar + Wind Excess to Grid [kWh]	21,266,641.0	13,596,921.0	13,960,124.8
Lifetime Cash Flow [EUR]	6,738,222.0	284,781.0	−17,200.0

. The NSGA-II optimization was solely developed for 3000 m³/ha, as for 1000 m³/ha, the system is independent from the grid. For the lower water allocation, this scenario can be turned into an off-grid solution, as it can satisfy water and energy needs solely with solar, wind, and PHS systems.

There is a clear difference between the results of scenario 2 and the main scenario presented in Section 4.3 and Section 4.4, for 1000 and 3000 m³/ha, respectively. The system with wind turbine implementation has more flexibility, as the energy available from wind generation is more constant throughout the day, especially during the night, complementing the PV energy, which is not operating during the night. With this, the PV + wind variable can satisfy most energy needs during 24 h, making the system less dependent on hydropower or grid energy to fulfill the energy needs during the night. Therefore, with less obligation to hydropower volume, the reservoir is more resilient and capable of ensuring water needs; also, the grid costs to fulfill energy needs drastically decrease. This is verified by the significant difference in grid energy usage in both scenarios. Additionally, regarding the performance of the NSGA-II, for scenario 2, it was better at obtaining more feasible solutions (that satisfy the 100% water reliability), than for scenario 1. Consequently, a Pareto front, as shown in Figure 26, can be obtained with all the feasible solutions found by the optimization algorithm. In all of the trials, the number of selected wind turbines, two, was sufficient to completely ensure water and energy needs.

The overall energy and water balance throughout the defined consumption period (1st of March till 30th of September) is presented in Figure 27 and Figure 28 below for 1000 m³/ha and 3000 m³/ha, respectively.

Regarding the economic performance of scenario 2, for OPT1, it is necessary to add the wind turbine parcel to compute the NPV and LCOE. Adding to the main scenario, a wind turbine initial investment of EUR 1200/kW was considered, based on [22,23,24]. Just as for photovoltaic panels, wind turbines are subsidized by 50% by the state, also prohibiting the sale of excess energy to the grid in the first five years. Therefore, the wind turbine’s initial investment is EUR 2,400,000. The yearly wind operation and maintenance costs are EUR 60,000/year. For the carbon dioxide emissions costs, the same factor and tax were used, totaling EUR 0.0 and EUR 1,361,592.1, for 1000 and 3000 m³/ha, respectively. Therefore, the total net present value (NPV) is EUR −3,941,915.7 and EUR −11,496,444.5, for each water allocation with OPT1. Despite the additional investments required by the wind add-on, and the derived O and M costs, the final value for the NPV is greatly inferior to the NPV computed for the main scenario, with any optimization method used. In terms of grid balance (cash flow), the lifetime value is positive for both water values. As for the levelized cost of energy (LCOE), the lifetime energy generated from solar, wind, and hydropower is around 678.2 GWh and the costs are EUR 10,680,138.0 and EUR 14,907,735.0, for 1000 and 3000 m³/ha, respectively. It results in a LCOE of EUR 0.02/kWh for both. This is a significant drop in comparison to the LCOE values of scenario 1.

5.2. Scenario 3: Alternative B—Batteries (with Wind)

As for the third scenario, where the grid is replaced by a battery energy storage system (BESS), the optimization objective is different from the other two scenarios. In this case, the objective for the optimization of a system that explores battery usage as an off-grid solution is to minimize the required nominal capacity of the BESS. Therefore, OPT4 was defined, seeking to minimize the battery’s total maximum storage capacity (kWh), with the final goal of diminishing the required initial investment for the battery system.

For a water allocation need of 1000 m³/ha, the system does not need batteries, as it uses the two wind turbines from scenario 2. After the optimization process, it was confirmed that the hybrid system can be sustained solely by solar, wind, and hydropower energy sources, without requiring an auxiliary energy storage mechanism.

Nonetheless, this is not the case for 3000 m³/ha. The system was unable to satisfy both the water needs and the subsequent associated energy needs, regardless of the battery maximum storage capacity defined, in between reasonable values. Therefore, it was necessary to increase the other energy sources’ capacity, so that the system could still be an off-grid solution. Consequently, the number of wind turbines was increased to boost the amount of renewable energy available throughout 24 h. Ultimately, a total of four wind turbines were installed for scenario 3 with a water allocation of 3000 m³/ha. Additionally, the maximum hydropower generated by the system slightly increased, requiring an installed capacity of 1500 kW. This is due to the new strategy obtained by the BESS configuration, post optimization, which aims to use as much hydropower to satisfy remaining energy needs, to avoid using the battery, saving it for the pump operation assistance.

The optimization process (OPT4) was capable of managing the system to satisfy water needs in its plenitude and energy needs by 97.6% with the defined amount of wind turbines. The initial objective function solution was 10 MWh, which corresponds to the battery system’s maximum storage capacity. A second optimization run yielded a solution of 8 MWh, with an energy reliability of 97.4%. While the number of unsatisfied hours with energy requirements increased slightly, this variation is negligible in comparison to the economic benefit of decreasing the battery storage capacity. Since the energy need reliability is very close to 100% and it is only not satisfied for a maximum of 1 h per day in half the defined season, the number of wind turbines and battery storage capacity were validated.

Figure 29 represents the energy patterns for 3000 m³/ha. During June, July, and August, it is possible to visualize the system’s fragility with the battery storage dropping to its minimum on multiple occasions. Nevertheless, the optimization could still obtain results where hydropower still possesses a significant role in the fulfillment of energy needs. The hydropower volume in scenario 3, with OPT4, is higher than the volume obtained in scenario 2, where the system has greater flexibility, but the economic objective restricts the hydropower parameter to minimize the required pumped volume, which subsequently diminishes grid consumption.

Regarding the economic evaluation, for 1000 m³/ha, the results are identical to the ones of the same water allocation for scenario 2, as it does not require batteries and a grid. For 3000 m³/ha, the following requirements are needed: updating the initial investments, O and M costs for the increased number of wind turbines, the hydropower installation costs, and adding the BESS variable. The new initial investment totals EUR 14,119,000, with a BESS initial cost of EUR 2.4 M (EUR 300/kWh). The specific cost of the BESS was selected based on the current range of prices for lithium-ion batteries used in this type of stationary large-scale application [40]. For the operation and maintenance costs, it totaled EUR 422,580/year. The replacement of the grid by a BESS produces a null carbon dioxide taxation. Also, there is no cash flow variable, as the excess solar + wind energy cannot be sold to the grid, and energy cannot be purchased from it. Therefore, the resultant net present value is EUR −17,954,775.6. The levelized cost of energy is EUR 0.45/kWh.

In comparison to the other scenarios, the NPV is quite identical to the ones obtained for scenario 1, but much higher than the scenario 2 configuration. The levelized cost of energy (LCOE) also increases, but is still below scenario 1, which is a positive indicator; due to the significant increase in initial investment costs, despite a higher renewable generation, there is an increase in the number of installed wind turbines and hydropower capacity.

6. Conclusions

This research work fulfilled the objective of developing advanced optimization models in the hybridization of the water sector, by the definition and design of mathematical algorithmic models within the water–energy nexus.

For this purpose, a new methodology, based on hybrid models for renewable energy systems (HY4RES), was developed, allowing us to include different steps of design modeling: (i) different systems´ characterization; (ii) definition of integrated hybrid energy solution (HES) depending on source availability and system requirements; (iii) water allocation model development using an auxiliary WaterGEMS model for the hydraulic simulations and PVGIS auxiliary model for PV solar energy and wind production; (iv) GRG nonlinear/evolutionary programming for the best solution optimization; (v) development of a Python software code for optimization using the non-dominated sorting genetic algorithm (NSGA-II) and graphical conception and system behavior analyses; (vi) sensitivity analyses for different water needs; and (vii) comparisons between optimization algorithm models. A complex multi-variable algorithm was then implemented in each model developed, which included the following: (i) water allocation; (ii) energy consumption need; (iii) available solar source; (iv) available wind energy; (v) storage volume; (vi) grid connection or not; (vii) battery energy storage capacity or not; (viii) grid tariff; (ix) pumped capacity; (x) hydropower capacity; (xi) energy production; (xii) cash flow; and (xiii) net present value.

These models were developed to facilitate the integration of pumped hydropower storage (PHS) systems into different ranges of applications, thereby enhancing the contribution and symbiosis with other energy sources, whether renewable or not, towards net-zero carbon emissions. Although this research examines scenarios incorporating a PHS system, which fulfills both water allocation needs and energy consumption requirements, these models can be readily changed to a pumping storage system or can be modified to exclude PHS, while still addressing dual consumption needs. Although the development models were presented with two auxiliary alternatives (the grid or the battery energy storage system (BESS)), they can be adapted to use other energy sources, such as hydrogen fuel cells, which can be modeled as a BESS, requiring suitable conditions as input.

In general, the developed models fulfill the objective of energy hybridization, enabling the simulation of a variety of combinations:

• Photovoltaic + PHS + Grid—(scenario 1);
• Photovoltaic + Wind + PHS + Grid—(scenario 2);
• Photovoltaic + Wind + PHS + BESS—(scenario 3);
• PS (Pump) + Grid—(Current Approach);
• Photovoltaic + PHS + Grid + BESS
• Photovoltaic + PHS;
• Wind + PHS;
• Other possible combinations.

The models´ generalization and simplicity approaches present a limitation related to their flexibility for excess/deficit energy management. The models´ inability to simulate a system with both grid and battery components is a consequence of its single-alternative selection structure.

Regarding the optimization techniques, the developed models may be optimized through the use of either pre-established tools, such as Solver from Excel, or custom-built algorithms in Python. Both were capable of identifying an appropriate range of results for different scenarios. However, the multi-objective and multi-variable character of the non-dominated sorting genetic algorithm (NSGA-II) exhibited a higher level of complexity, which presented challenges in precisely tuning the problem to align with the modeled system. To illustrate, when an initial solution was obtained beforehand through trial and error in the Solver tool, using GRG nonlinear/evolutionary methods yielded a solution (local) that satisfied the defined reliability constraints. This proved more challenging in Python using the non-dominated sorting genetic algorithm (NSGA-II), as the system is quite complex with a lot of iterations and correlations. The optimization problem encountered difficulties in yielding solutions that adhered to the reliability constraints, particularly for a huge water allocation value (e.g., 6000 m³/ha). This is also attributable to the system’s flexibility, as a higher water consumption significantly decreases the range of feasible operating solutions for each energy source within the system. Nevertheless, the optimization process was successful and yielded appropriate results, thus enabling a further analysis of realistic variables, the system operation, and possible defined scenarios. Hence, the results demonstrate that as water consumption increases, the system’s flexibility is diminished, thereby increasing the risk of failing to meet the full water allocation and energy needs. Furthermore, in scenario 1, it is possible to observe the dependence on the grid energy for higher water allocations, in which photovoltaic energy is not enough to ensure sufficient water in the reservoir; therefore, the grid starts to power the pump station during night time, when the solar generation is null. For 800 and 1000 m³/ha, the grid did not have to power the pumps to ensure a sufficient volume for water needs; on the contrary, for 3000 and 6000 m³/ha case studies, the grid energy significantly increased to power the pumps, 5 and 14 GWh annually, respectively.

This behavior is mitigated in scenario 2, wherein wind energy can be leveraged to power the pumps during nocturnal hours if needed when water needs are particularly high. The primary distinction between the second and first scenarios is the autonomy of the renewable component of the system from the grid. For instance, with 3000 m³/ha of water allocation, the grid consumption to power the pumps drops 60% annually. This reinforces the sustainability and renewable solution for the application under study. Furthermore, with the same water allocation, scenario 2 can reproduce a positive lifetime cash flow (EUR 284,781.0), whereas scenario 1 was immensely far from yielding a positive value. In scenario 3, the system becomes more vulnerable, due to the absence of a robust and permanent backup energy source, such as the grid. If the water and energy needs are high, it becomes very challenging to satisfy them, despite the BESS capacity, consequent to the tendency for the hourly energy discharge to exceed the energy charge. During the optimization phase, the Solver tool was not able to yield any solution that could satisfy energy needs to its extent. By restricting the BESS capacity to a maximum of the total solar and wind combined installed power, the system would never fully satisfy energy requirements. Therefore, a BESS with 8 MWh was selected, which was yielded in one of the OPT4 optimization trials, and which can ensure almost every hour of the energy calendar without disproportionately increasing the initial investment required by the BESS.

From an economic standpoint, scenario 2 is the most attractive, with an NPV of EUR −12 M for 3000 m³/ha, as it facilitates a reduction in auxiliary dependence, more effectively ensures water–energy needs, and benefits more from grid sales. Scenario 3 may prove an appropriate solution, particularly for off-grid locations. However, the lifespan of the BESS will have a considerable impact on the NPV. In this research, the main components of the system’s lifetime are assumed to be twenty-five years. However, a replacement of the BESS will likely be necessary, which will harm the project’s financial costs.

For every scenario, a few additional modifications are implemented and further explored to enhance the system’s robustness and flexibility to higher water and energy demands:

• Increase the reservoir’s capacity;
• Increase the installed photovoltaic power;
• Utilize alternative A (Grid) and B (BESS) simultaneously;
• Increase pump nominal power;
• Isolate water needs volume from the hydropower volume.

An interesting issue refers to an alternative methodology that the development models´ algorithms enable us to study. This involves setting the reservoir solely for hydropower production, with the water need volume being acquired from the bottom water source (i.e., the river—in case of drinking or irrigation, the lower reservoir—in case of cascade multi-purpose dams for different water uses, and the sea—in case of desalination or hydrogen production) and modeled as a water–energy nexus need. This is performed to account for the energy required to supply water needs to its services.

Ultimately, the developed two models were successfully designed and implemented, using different environments (Excel and Python), demonstrating the capability to produce reliable results for a techno-economic analysis. Although the case study for the models´ deployment was a general agricultural field, the scope of applications in which the models are designed to operate is broader, including industry, commercial, and residential applications, as well as communities. Nonetheless, as for future research and model performance, extending the analysis for different applications is required, to refine and improve the models´ generalization goal.