Multi-Objective Optimization of the Seawall Cross-Section by DYCORS Algorithm

Abstract

The purpose of this research is to develop a new method for automatically optimizing the seawall cross-section with composite slopes and a berm, considering both overtopping discharge and construction cost. Minimizing these competing multi-objectives is highly challenging due to the intricate geometry of seawalls. In this study, the surrogate model optimization algorithm DYCORS (Dynamic COordinate search using Response Surface models) is employed to search for the optimal seawall geometry, coupled with the ANN (Artificial Neural Network) model for determining the overtopping discharge. A total of 20 trials have been run to evaluate the performance of our methodology. Even the worst-performing Trial 7 among these 20 trials shows a satisfactory performance, with a reduction of 17.67% in overtopping discharge and a 12.1% decrease in cost compared to the original solution. Furthermore, compared to other optimization schemes using GAs (Genetic Algorithms) with the same decision vectors, constraints, and multi-objective functions, the methodology has been proven to be more effective and robust. Additionally, when facing different combinations of wave conditions and water levels, there was a 27.8% reduction in objective function value compared to the original solution. The optimal results indicate that this method can still be effectively applied for optimizing the seawall cross-section as it is a general method.

1. Introduction

Many people worldwide are living near coastlines, which are increasingly utilized for more and more public activities [1]. In order to avoid danger to people’s lives and to protect property, coastal structures are often built in coastal areas to withstand waves [2]. Wave overtopping occurs when seawalls fail to completely stop waves. Due to climate change and rising sea levels, the frequency and intensity of storms are expected to increase [3], resulting in an increase in wave overtopping [4]. When facing violent wave conditions, blindly raising and reinforcing the seawall not only increases the already high economic costs but also increases the risk of breaching. Furthermore, as society and the economy continue to develop, there is an increasing emphasis on the ecological functions of natural coastlines with pristine blue seas and lush greenery. For these aesthetic, environmental, and economic reasons, it is desirable to construct a seawall with a low crest height while keeping overtopping discharge in an acceptable range. Lower overtopping discharge seems to require additional construction costs for more complex structures, such as a seawall with a berm and composite slopes, which is much more effective for wave dissipation. The highly complex nature of the structure and the need for cost-effectiveness make the optimization of the seawall cross-section a challenging task.

Traditionally, designers usually decide the seawall cross-section according to industry standards or design criteria [5,6,7,8,9]. Generally, designers need to specify the values of the cross-section variables, depending on their own accumulated knowledge and experience. The whole process is a trial-and-error selection of the variables [10,11,12], that is, if a calculated trial is impractical, a new trial is initiated and an alternative seawall solution with different variables is calculated until it meets the required design criteria. Neelamani and Sandhya [13] evaluated the performance of plane, dentated, and serrated seawalls and found that the serrated seawall has improved performance in reducing wave reflection, run-up, and run-down, as well as wave pressures. Hieu and Vinh [14] found that two optimum values of the submerged reef porosity of approximately 0.25 and 0.7 resulted in the lowest overtopping rates for a porous terrace-supported seawall. Kisacik et al. [15] optimized the various design parameters, including the pattern of gaps, blocking coefficients, and promenade, of over 150 model tests based on the urban vertical seawall of Kordon, Izmir. Dang et al. [16] researched the most optimal shape of seawalls for reducing overtopping water based on the numerical model DualSPHysics. The results indicated that a stepped-face wall most effectively reduces overtopping discharge, followed by a curved wall, an inclined wall, and a vertical wall. In conclusion, for obtaining a satisfactory solution, designers have to propose several feasible solutions. Finally, the most promising solution can be picked out from these limited comparative solutions. The quality of the final optimal solution is strongly dependent on the designer’s experience and is limited to a small number of feasible solutions to compare against. This traditional method is time-consuming, labor-intensive, and highly subjective.

Recently, there has been a growing focus on applying optimization techniques to coastal structure in order to automate the design process. While some researchers [10,17,18] have prioritized cost as the optimal objective, they have not taken into consideration the hydrodynamic processes. On the other hand, some researchers [11,12,19,20] have considered hydrodynamic conditions as constraints when seeking to maximize economic benefits, but the hydrodynamic data are obtained by empirical formulae. Elchahal et al. [21] optimized a floating breakwater with the theoretical derivation formulae from an SQP (Sequence Quadratic Program). Elchahal et al. [22] proposed an optimization approach using GAs (Genetic Algorithms) to determine the optimal layout of detached breakwaters in ports. Mahmuddin and Kashiwagi [23] combined a GA with the Boundary Element Method (BEM) to obtain the optimal shape of a two-dimensional floating breakwater model. Somervell et al. [24] employed GAs to find the pareto optimal set of solutions of a vertical cellular breakwater. Abdullah et al. [25,26] used GAs to find an optimum lateral separation ratio (S = D) for the twin pontoons of a floating breakwater. Overall, in contrast to traditional methods where design variables are manually determined by designers, optimization algorithms automatically determine these values, and the designers only need to determine the constraints and objectives to be optimized based on practical scenarios. However, despite their potential benefits, the application of optimization algorithms in coastal structure design is still limited, primarily focusing on breakwater construction with minimal application in seawall design. The design of seawalls is different from that of breakwaters, such as in terms of their objectives. Therefore, applying the optimization algorithm to the design of seawall cross-sections holds value for both research and practical engineering applications.

2. Methodology

The purpose of this research is to develop and implement an optimal cross-section for a sloping seawall with composite slopes and a berm by using the optimization algorithm, which considers the contrasting multi-objective of construction cost and the mean overtopping discharge. The surrogate model optimization algorithm DYCORS (Dynamic COordinate search using Response Surface models), developed by Regis and Shoemaker in [27], can efficiently solve optimization problems for complex multimodal objectives, especially for computationally expensive functions. The surrogate model is simply an inexpensively multivariate approximation of the evaluation function, which is computationally expensive. As the candidate points are evaluated by the surrogate model within a second, the number of expensive function evaluations is significantly reduced, resulting in a significant computational cost reduction. This is the major advantage of the DYCORS algorithm, as it can generate reasonably good solutions with a relatively small number of function evaluations compared to other algorithms, such as Genetic Algorithms (GAs), which often require a large number of evaluations. The DYCORS algorithm has demonstrated excellent applications in multiple fields [28,29,30,31,32,33,34]. It is well-regarded for its effectiveness and ability to handle complex optimization problems. Therefore, the DYCORS algorithm has been chosen to complete the optimization of the seawall cross-section.

Furthermore, the optimization of the seawall cross-section relies on accurately estimating the mean wave overtopping discharge, as it determines the cross-section geometry of the structure. Currently, there are three main methods: (a) empirical formulae, (b) numerical models, and (c) machine-learning models. The empirical formulae are restricted to the range of tested conditions, structures, and the geometry of the databases from which each parameterized formula is derived. Numerical models simulate wave overtopping with structures by solving complex flow equations, requiring significantly higher computational effort and cost compared to empirical formulae and machine-learning models. At present, machine-learning models [35,36,37,38,39,40] have gained popularity in predicting the mean overtopping discharge with good performance. These models are based on a large amount of accumulated data on historical waves and costal structures. The quantity of data should be sufficiently large and well-distributed in order to train the model and cover entire ranges of possible output values. The ANN (Artificial Neural Network) model proposed by Formentin and Zanuttigh [39,40] has been officially adopted by EurOtop, 2018 [41]. This ANN tool has been trained against the large EurOtop database, extended from the CLASH database and comprising nearly 18,000 physical model tests on wave overtopping over a wide variety of structure geometry and wave conditions. It can be accessed at www.unibo.it/overtopping-neuralnetwork (accessed on 28 July 2024). It demonstrates greater prediction accuracy than existing formulae, even considering only data falling in the range of the applicability of the formulae themselves [41]. Obviously, the ANN model takes less computational effort and cost compared to numerical models. Furthermore, specific usage instructions are detailed on the website, which provides convenient and straightforward guidance.

Therefore, in order to perform the multi-objective optimization process, the ANN model proposed by Formentin and Zanuttigh [39,40] is employed to obtain the mean overtopping discharge, while the construction cost is calculated using theoretical formulas. To find the optimal variables (that is, the optimal solution), this ANN model is integrated with the DYCORS algorithm during the optimization stage. The flowchart of the proposed methodology for multi-objective optimization of the seawall cross-section is depicted in Figure 1. This methodology consists of two phases: (a) initialization phase, step 1, and (b) iteration phase, which includes steps 2–5. During the iteration phase, the method goes through a surrogate model update, candidate points generation, and evaluation point selection and evaluation, as well as termination judgments. For each run of the ANN model, an input file containing necessary information for making predictions is required, including our decision vectors and design parameters. To be more specific:

(1)

First, all decision vectors are initialized by DYCORS to form the initial design experiment. These decision vectors are then used as inputs for the ANN model to calculate the mean overtopping discharge values, which are subsequently passed back to the DYCORS algorithm for fitting the initial surrogate model.

(2)

Then, the surrogate model based on Radial Basis Function is updated based on these evaluated points.

(3)

Next, the candidate points are generated based on the current best point (x*, f(x)*) with perturbations applied to randomly selected partial dimensions while keeping the remaining dimensions unchanged.

(4)

Subsequently, the candidate points are evaluated by the surrogate model, which is based on all the previously evaluated points and serves as an approximation of the objective function, f(x). Once a new evaluation point, x^E, is obtained, the procedure passes the newest decision vectors information to the ANN model for calculating the mean overtopping discharge and then returns the result back to DYCORS.

(5)

Finally, this procedure continues until the termination condition is satisfied. The termination condition could be a predefined number of function evaluations, or reaching a specified level of convergence.

In summary, the optimal solution (denoted as (x*, f(x)*)) can be obtained through this automated iterative optimization process without the need for manual intervention. This methodology enables designers to efficiently explore different combinations of decision vectors and find optimal solutions that meet multiple requirements and constraints.

3. Validation

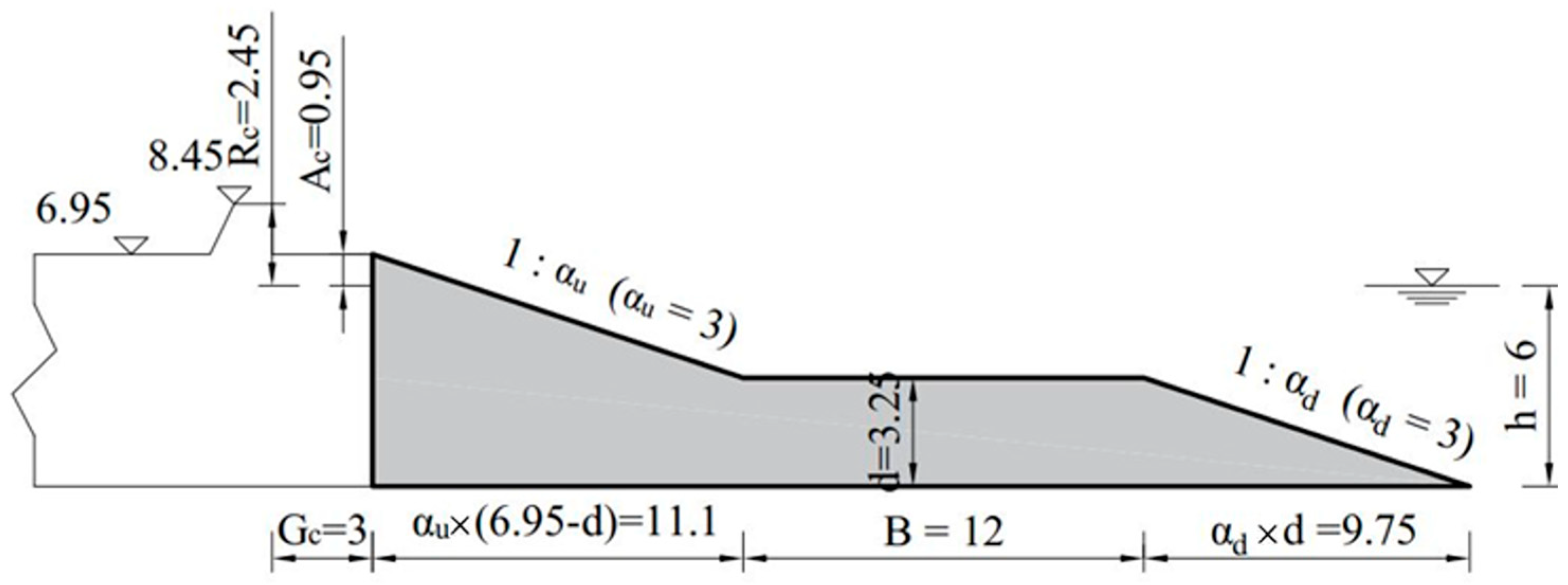
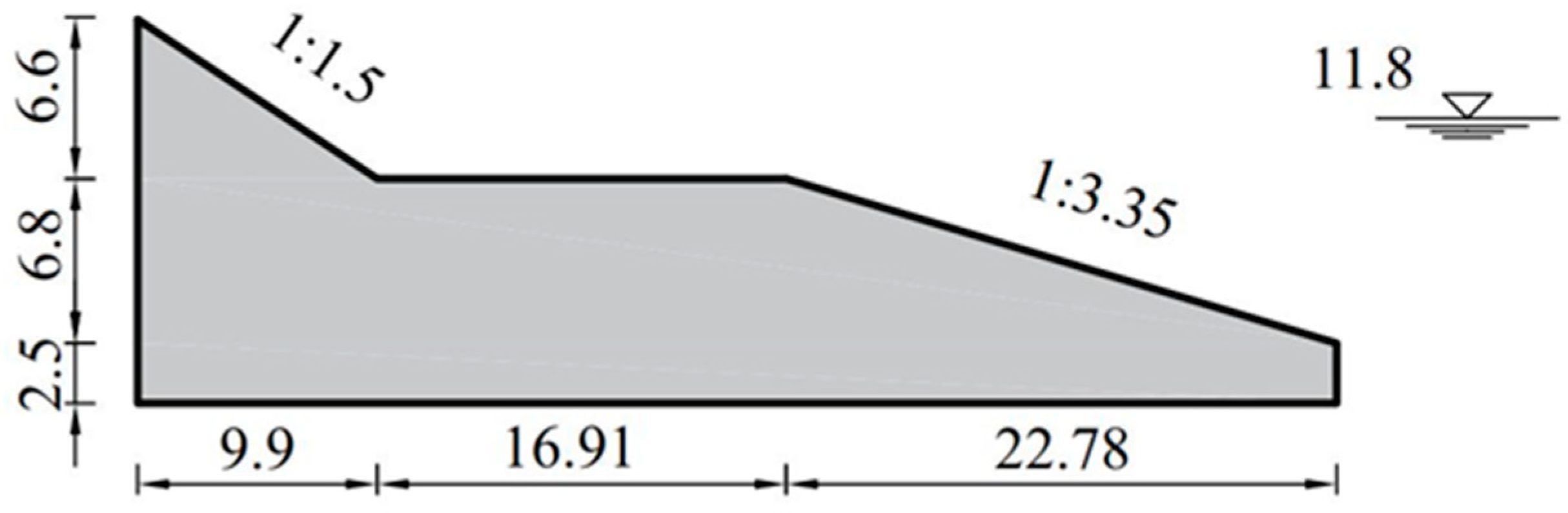
Balancing the basic function of wave prevention and disaster reduction with ecological functions such as waterfront accessibility and scenic qualities poses a significant challenge in the optimization of seawall cross-section profiles. A sloping seawall with composite slopes and a berm can effectively address this contradiction. The benefit of a berm is that the equivalent slope angle becomes smaller, which reduces wave overtopping and leads to a lower required crest level [41]. 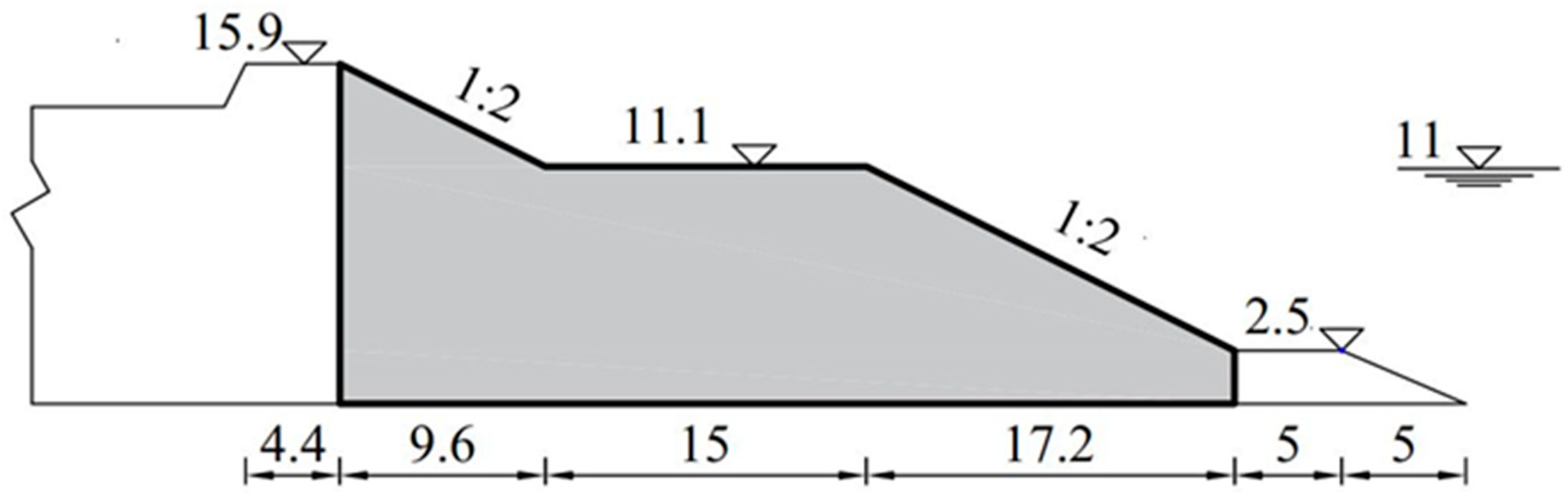As shown in Figure 2, we will use this type of seawall as an example to validate our methodology and conduct specific optimizations for this cross-section. In order to preserve the coastal view and enjoy the picturesque scenery of “wide expanse of sea and sky, with sails in full view”, we will maintain a fixed crest elevation for the seawall. However, there are various factors that affect wave overtopping discharge. For the seawall with a berm, the key to achieving the best wave dissipation efficiency lies in determining the optimal berm height and width, and the slopes of the berm. Therefore, as Figure 2 shows, we will only focus on the main structure (the shaded area within the black bold line border) of the seawall for the optimization. Here, ${\mathsf{\alpha }}_{\mathrm{d}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathsf{\alpha }}_{\mathrm{u}}$ are the cotangent of angles with respect to the horizontal direction of downslope and upslope, respectively. B is the width of the berm and d represents the height of the berm. The four decision vectors are all independent from one another. In contrast to the decision vectors, the design parameters are fixed in the whole optimization process, as given by designers, including wave conditions and structure characteristics, which are essential and indispensable in the design process. These parameters remain consistent with those used for original cross-section configuration of the seawall in a coastal area of China (Figure 2; the original cross-section configuration will be compared with our optimization solution in the following Section 3.3).

Table 1. Values of design parameters.

Design Parameters	Value
$\mathrm{the} \mathrm{still} \mathrm{water} \mathrm{level}: \mathrm{h}$ (m)	6
$\mathrm{the} \mathrm{incident} \mathrm{significant} \mathrm{wave} \mathrm{height} \mathrm{at} \mathrm{the} \mathrm{toe} \mathrm{of} \mathrm{the} \mathrm{structure}: {\mathrm{H}}_{\mathrm{m}0}$ (m)	3
$\mathrm{the} \mathrm{spectral} \mathrm{wave} \mathrm{period} \mathrm{at} \mathrm{the} \mathrm{toe} \mathrm{of} \mathrm{the} \mathrm{structure}: {\mathrm{T}}_{\mathrm{m}-1,0}$ (s)	11.2
$\mathrm{roughness} \mathrm{factor} \mathrm{for} \mathrm{the} \mathrm{downslope}: {\mathsf{\gamma }}_{fd}$	0.55
$\mathrm{roughness} \mathrm{factor} \mathrm{for} \mathrm{the} \mathrm{upslope}: {\mathsf{\gamma }}_{fu}$	0.55
$\mathrm{the} \mathrm{size} \mathrm{of} \mathrm{the} \mathrm{structure} \mathrm{elements} \mathrm{for} \mathrm{the} \mathrm{downslope}: {\mathrm{D}}_{\mathrm{d}}$ (m)	0.65
$\mathrm{the} \mathrm{size} \mathrm{of} \mathrm{the} \mathrm{structure} \mathrm{elements} \mathrm{for} \mathrm{the} \mathrm{upslope}: {\mathrm{D}}_{\mathrm{u}}$ (m)	0.75
$\mathrm{the} \mathrm{crest} \mathrm{height} \mathrm{respect} \mathrm{to} \mathrm{still} \mathrm{water} \mathrm{level}:{\mathrm{A}}_{\mathrm{c}}$ (m)	0.95
$\mathrm{the} \mathrm{wall} \mathrm{height} \mathrm{respect} \mathrm{to} \mathrm{still} \mathrm{water} \mathrm{level}:{\mathrm{R}}_{\mathrm{c}}$ (m)	2.45
$\mathrm{the} \mathrm{crest} \mathrm{width}: {\mathrm{G}}_{\mathrm{c}}$ (m)	3

presents the specified value of design parameters used in our optimization problem. According to EurOtop, 2018 [41], for two layers of rock on an impermeable core, the roughness factors for the downslope, ${\mathsf{\gamma }}_{fd}$, and the upslope, ${\mathsf{\gamma }}_{fu}$, are both 0.55.

3.1. Multi-Objective Optimization

The mean overtopping discharge is widely accepted as a primary design criterion for assessing the performance of seawalls. At the same time, the construction cost is also the focus of optimization considerations. Therefore, both construction cost and overtopping discharge are taken as the optimization objectives in this paper. The goal is to find a solution that minimizes the construction cost while also keeping the wave overtopping discharge as low as possible. By considering both objectives simultaneously, we can strike a balance between the seawall’s effectiveness in mitigating wave overtopping and the economic feasibility of the solution. The multi-objective functions for determining the optimum variables of the seawall are shown as Equations (1)–(5).

$$min: f_1\left(x\right)={\displaystyle \frac{Q\left(x\right)-Q_{min}}{Q_{max}-Q_{min}}}$$

(1)

$$min: f_2\left(x\right)={\displaystyle \frac{C\left(x\right)-C_{min}}{C_{max}-C_{min}}}$$

(2)

$$min: F\left(x\right)={\mathrm{W}}_1\times f_1\left(x\right)+{\mathrm{W}}_2\times f_2\left(x\right)$$

(3)

$${\mathrm{W}}_1+{\mathrm{W}}_2=1$$

(4)

$$C(x)=\sum _{l=1}^n{C}_l{V}_l,n=1,2,3\dots \dots$$

(5)

where $x$ represents decision vectors, $f_1\left(x\right)$ is the dimensionless form of the mean wave overtopping discharge, $f_2\left(x\right)$ is the dimensionless form of construction costs, $F\left(x\right)$ is the objective function, $C\left(x\right)$ is the cost function,$Q\left(x\right)$ is the overtopping function, obtained from the ANN model, $Q_{max}$ is the maximum value of the $Q\left(x\right)$, and $Q_{min}$ is the minimum value of the $Q\left(x\right)$. Obviously, $Q_{min}=0 {\mathrm{m}}^3/\mathrm{s}/\mathrm{m}$ (This is the value of the ideal state). Similarly, $C_{max}$ is the maximum cost function, while $C_{min}$ is the minimum one. $V_l$ is the work amount for different parts and $C_l$ is their unit price. For brevity, we assume that the cost function only relates to the amount of work as we consider a consistent unit price for each component. In practical applications, designers can adjust this function according to actual situations. ${\mathrm{W}}_1$ and ${\mathrm{W}}_2$ are adjustable coefficient used to weight cost, $C\left(x\right)$, and overtopping discharge, $Q\left(x\right)$.

When optimizing the seawall cross-section, there are virtually infinite possible combinations within the range of decision vectors. Indeed, it is impossible to identify all the solutions. However, we can determine the solutions under extreme states based on the extreme values of decision vectors. For cost, we can identify the maximum and minimum costs by considering the solutions under extreme states. Similarly, for wave overtopping, we can determine the maximum and minimum values of wave overtopping discharge. It is evident that all solutions will fall within these ranges of cost and wave overtopping discharge values. Therefore, to compare different solutions, we have performed the dimensionless normalization of construction costs and wave overtopping discharge, as shown in Equations (1) and (2), respectively.$f_1\left(x\right)$ and $f_2\left(x\right)$ represent the wave overtopping discharge ration of the proposed solution in all solutions and the cost ration of the proposed solution in all solutions, respectively. Clearly, the value of the ratio falls between 0 and 1, reflecting the effectiveness of the proposed solution relative to all other solutions. A smaller value indicates a better solution.

In order to minimize values of $f_1\left(x\right)$ and $f_2\left(x\right)$ simultaneously, we utilize the weighted sum method, combining multiple objective functions, $f_1\left(x\right)$ and $f_2\left(x\right)$, into a single objective function by linearly combining them and adjusting the weights to balance the importance of different objectives. This can be represented mathematically, as shown in Equations (3) and (4). Thus, solving the multi-objective optimization problem is transformed into minimizing the new objective function, $F\left(x\right)$. When it comes to allocating weight values, we can consider them from an economic cost perspective. If increasing the wave overtopping discharge per unit width leads to disaster losses of ${\mathrm{A}}_1$, while decreasing the cost per unit width is ${\mathrm{A}}_2$, then we have ${\mathrm{W}}_1\times {\mathrm{A}}_1={\mathrm{W}}_2\times {\mathrm{A}}_2$. This implies that ${\mathrm{W}}_1={\mathrm{W}}_2\times {\mathrm{A}}_2/{\mathrm{A}}_1$. Otherwise, ${\mathrm{W}}_1+{\mathrm{W}}_2=1$, and then ${\mathrm{W}}_2=1/(1+{\mathrm{A}}_2/{\mathrm{A}}_1)$.

In our present study, we have chosen ${\mathrm{W}}_1=0.7$ and ${\mathrm{W}}_2=0.3$ for illustrative purposes. It is important to emphasize that different weighting coefficients imply different optimization objectives, with varying emphasis on cost and wave overtopping discharge. The specific selection in practical applications can be set based on the actual requirements. This does not affect the performance of our optimization methodology as it is a general approach.

3.2. Search Space for the Optimization

The search space in an optimization problem refers to the set of decision vectors that the algorithm explores to find a solution, defined by the upper and lower bounds of the decision vectors. In the given optimization problem, there are four decision vectors, ${\mathsf{\alpha }}_{\mathrm{d}}, {\mathsf{\alpha }}_{\mathrm{u}}, \mathrm{B}$, and d. According to the Code for Design of sea dike project [8], ${\mathsf{\alpha }}_{\mathrm{d}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathsf{\alpha }}_{\mathrm{u}}$ typically range from 1.5 to 3.5. For the berm width, B, and height, d, there are specific considerations to ensure its effectiveness. According to EurOtop, 2018 [41], the berm width, B, may not be greater than 0.25 L_m−1,0 (the deep water wave length) to ensure effectiveness. Additionally, a berm lying below 2${\mathrm{H}}_{\mathrm{m}0}$ or above Ru_2% has no influence on wave run-up and wave overtopping. Therefore, B varies from 0 to 30 m and d varies from 0 to 6.95 m. The upper and lower bounds of the decision vectors are shown in

Table 2. Values of decision vectors.

Decision Vectors	Value Range
$\mathrm{the} \mathrm{slope} \mathrm{of} \mathrm{the} \mathrm{upslope}: {\mathsf{\alpha }}_{\mathrm{u}}$	1.5~3.5
$\mathrm{the} \mathrm{slope} \mathrm{of} \mathrm{the} \mathrm{downslope}: {\mathsf{\alpha }}_{\mathrm{d}}$	1.5~3.5
the width of the berm: B (m)	0~30
$\mathrm{the} \mathrm{height} \mathrm{of} \mathrm{the} \mathrm{berm}:\mathrm{d}$(m)	0~6.95

.

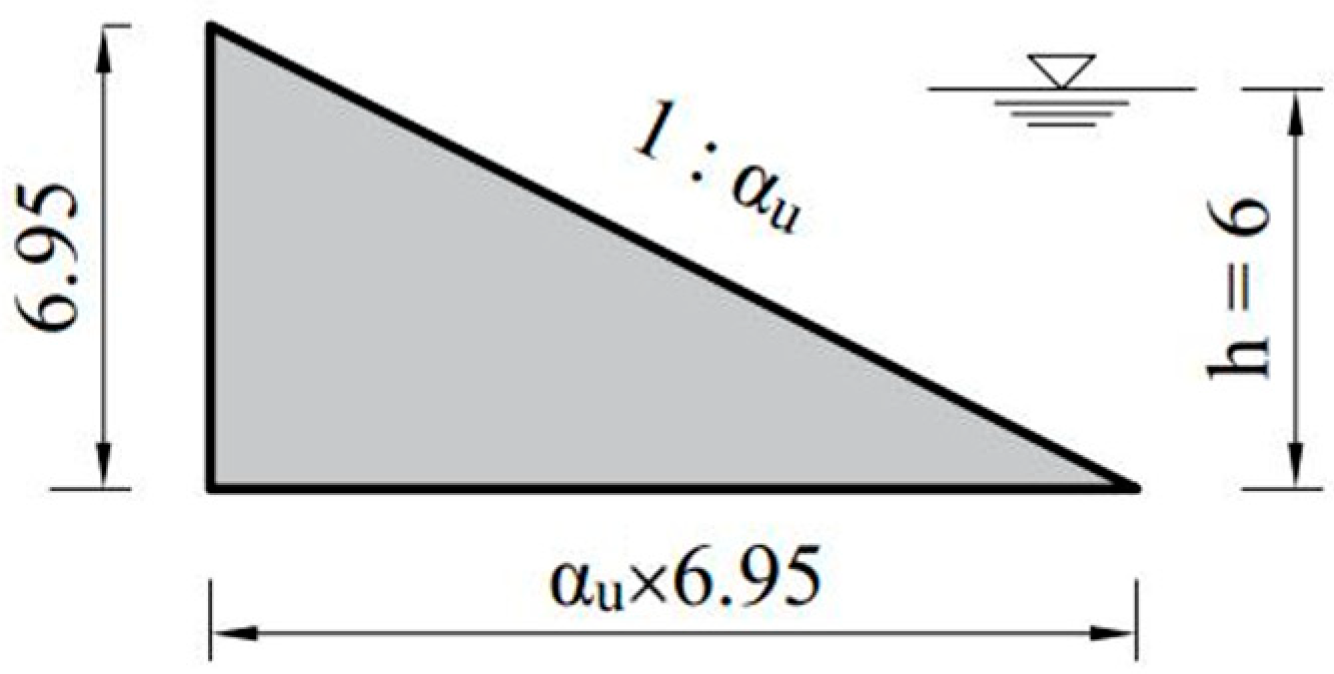
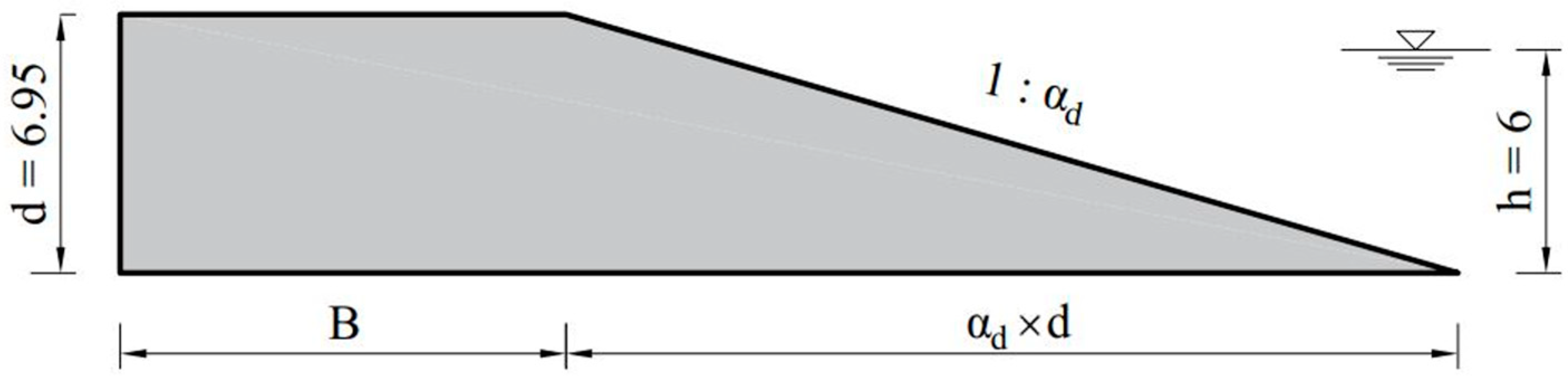
Here, when $\mathrm{d}=0 \mathrm{m}$, it means there is no berm with the seawall; the configuration becomes a single-slope seawall with the upslope, ${\mathsf{\alpha }}_{\mathrm{u}}$, see Figure 3, while when $\mathrm{d}=6.95 \mathrm{m}$, the height of the berm is flush with the crest, thereby increasing the crest width, ${\mathrm{G}}_{\mathrm{c}}$. In this configuration, the seawall becomes a single-slope structure with a downslope, ${\mathsf{\alpha }}_{\mathrm{d}}$, as depicted in Figure 4. At this height, it is appropriate to refer to it as a promenade rather than a berm, as it provides a wider space for pedestrian access and recreational purposes.

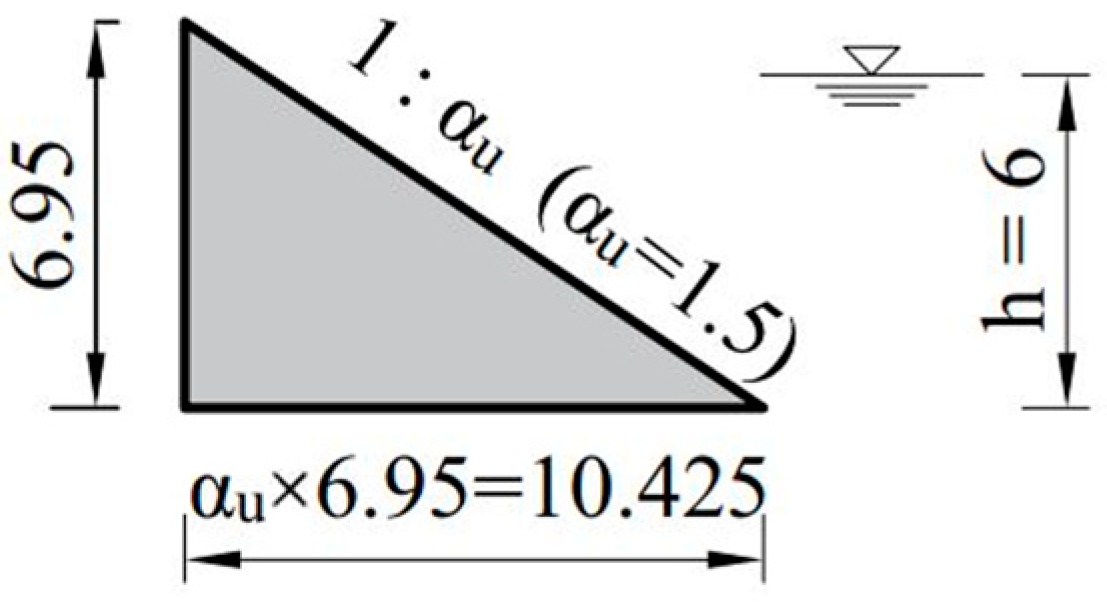
Obviously, when $\mathrm{d}=0 \mathrm{m}, {\mathsf{\alpha }}_{\mathrm{u}}=1.5,$ the seawall reaches the smallest cost solution; see Figure 5. Based on the geometrical dimensions, we can calculate $C_{min}=36.23$ (as mentioned earlier, for the sake of simplicity, we assume that the unit prices of each part are consistent, so the cost is only determined based on the size of the engineering quantity). Simultaneously, the overtopping discharge reaches its maximum at $Q_{max}=0.293 {\mathrm{m}}^3/\mathrm{s}/\mathrm{m}$ (obtained by the ANN overtopping model). Meanwhile, when ${\mathrm{d}=6.95 \mathrm{m}, \mathsf{\alpha }}_{\mathrm{d}}=3.5, \mathrm{B}=30 \mathrm{m},$ the seawall reaches its highest-cost solution; see Figure 6. After calculation, $C_{max}=293.03.$ The specified values are shown in

Table 3. Values of the function parameters.

Function Parameters	Value
the maximum value of the $Q\left(x\right)$$: Q_{max}$ (${\mathrm{m}}^3/\mathrm{s}/\mathrm{m}$)	0.293
the minimum value of the $Q\left(x\right)$$: Q_{min}$ (${\mathrm{m}}^3/\mathrm{s}/\mathrm{m}$)	0
the maximum value of the $C\left(x\right)$$: C_{max}$ (-)	293.03
the minimum value of the $C\left(x\right)$$: C_{min}$(-)	36.23

.

In conclusion, the optimization objective function at this stage is as follows:

$$min: F\left(x\right)=0.7\times {\displaystyle \frac{Q\left(x\right)}{0.293}}+0.3\times {\displaystyle \frac{C\left(x\right)-36.23}{293.03-36.23}}$$

(6)

$$C\left(x\right)=\left(2\times \mathrm{B}+{\mathsf{\alpha }}_{\mathrm{d}}\times \mathrm{d}\right)\times {\displaystyle \frac{\mathrm{d}}{2}}+\left(6.95+\mathrm{d}\right)\times {\mathsf{\alpha }}_{\mathrm{u}}\times {\displaystyle \frac{6.95-\mathrm{d}}{2}}$$

(7)

3.3. Results and Discussion

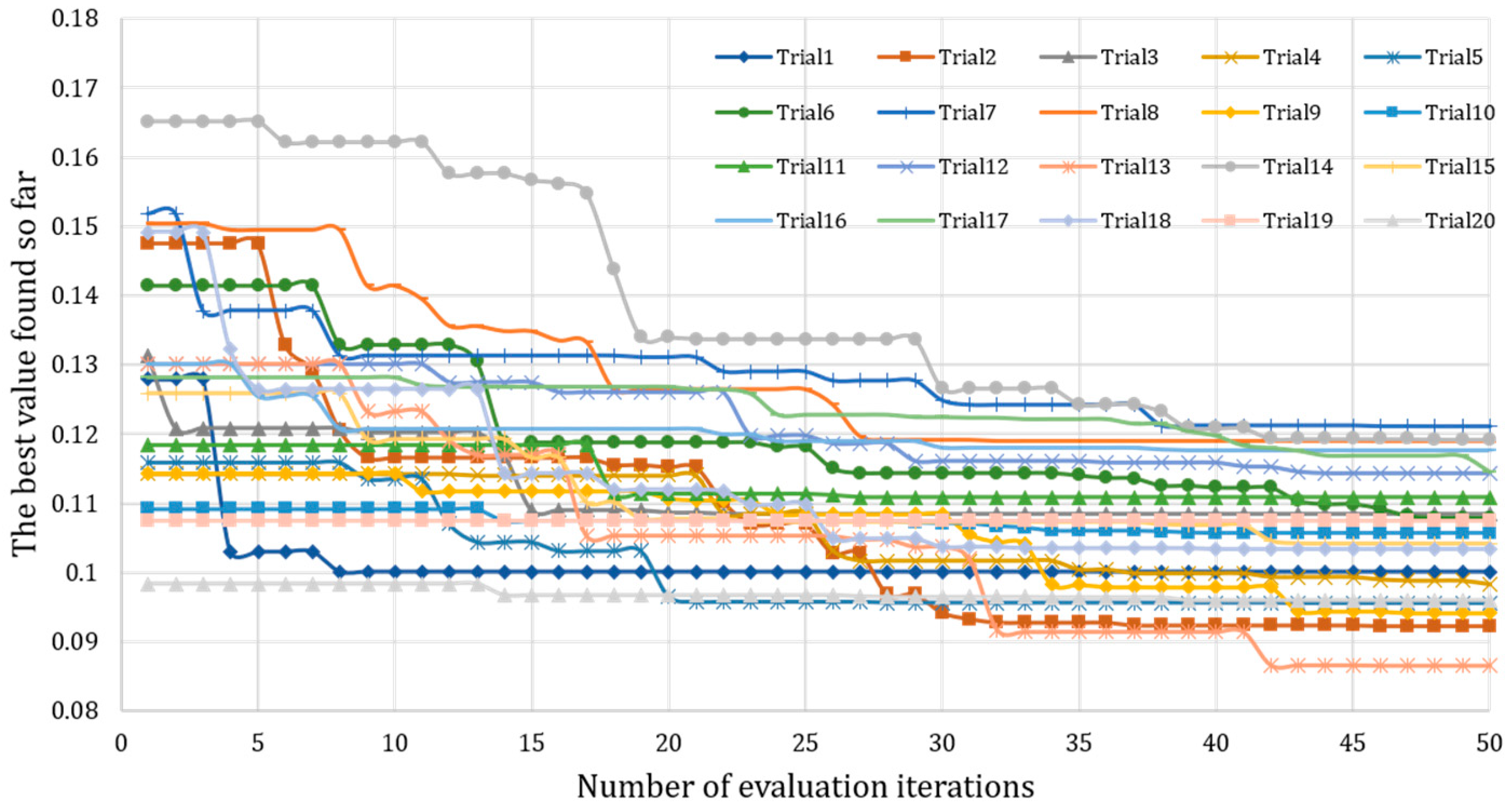
In the multi-objective optimization problem, the DYCORS algorithm is employed to find the optimal solution within the defined search space. To demonstrate the performance of our methodology in optimizing a seawall cross-section that minimizes conflicting objectives of overtopping discharge and cost, a total of 20 trials were conducted. Figure 7 illustrates the optimization process of these 20 trials (overall performance will be presented in Section 3.4 below). The x-axis represents function evaluation iterations, while the y-axis represents the best value of the objective function found so far (as Equation (6) shows). These curves provide insights into the algorithm’s convergence behavior and its ability to progressively find improved solutions over time. Convergence means that the algorithm has found a set of decision vectors that result in stable values for the optimization objectives within a given range of decision vectors. It can be observed that the results have achieved good convergence after 50 iterations for all 20 trials. Further iterations are unlikely to significantly improve the optimization objectives. This indicates that our optimization algorithm produces the optimal solution after 50 iterations.

In this section, we will focus on the worst-performing Trial 7 among these 20 trials. The optimization result obtained from Trial 7 were relatively worse compared to the other trials, with the highest value of the final objective function found among the 20 trials. By analyzing the performance of Trial 7, we can evaluate the robustness and effectiveness of the optimization algorithm in finding optimal solutions. Therefore, by analyzing the worst result, we can gain insights into the range of performance achieved by our methodology.

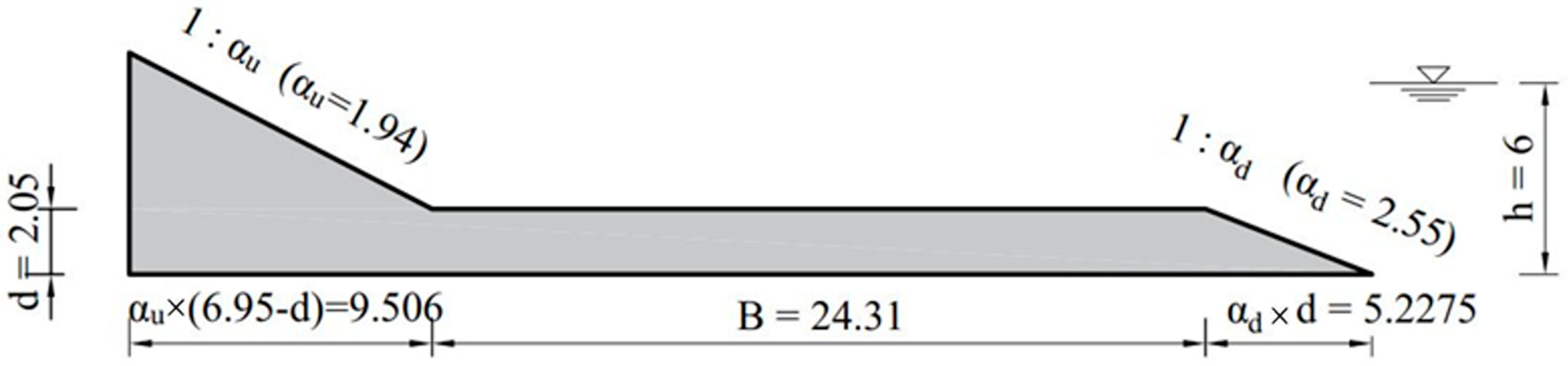
The decision vector values corresponding to the optimal solution of Trial 7 are presented in

Table 4. Values of the optimized decision vectors of Trial 7.

Decision Vectors	Value Range	Optimal Value
$\mathrm{the} \cot \mathrm{angent} \mathrm{ration} \mathrm{of} \mathrm{the} \mathrm{upslope}: {\mathsf{\alpha }}_{\mathrm{u}}$	1.5~3.5	1.94
$\mathrm{the} \cot \mathrm{angent} \mathrm{ration} \mathrm{of} \mathrm{the} \mathrm{downslope}: {\mathsf{\alpha }}_{\mathrm{d}}$	1.5~3.5	2.55
the width of the berm: B (m)	0~30	24.31
the height of the berm: d (m)	0~6.95	2.05

: the width of the berm is 24.31 m and its height is 2.05 m, while 2.55 and 1.94 are the slope cotangent of the downslope and upslope, respectively. These values represent the final optimal solution of the seawall found in Trial 7, as depicted in Figure 8.

Table 5. Comparison between the optimal solution of Trial 7 and the original solution.

Solution	${\mathsf{\alpha }}_{\mathbf{u}}$	${\mathsf{\alpha }}_{\mathbf{d}}$	B $(\mathbf{m}$)	$\mathbf{D} (\mathbf{m}$)	$\mathit{Q}\left(\mathit{x}\right)$$({\mathbf{m}}^3/\mathbf{s}/\mathbf{m}$)	$\mathit{C}\left(\mathit{x}\right)$	$\mathit{F}\left(\mathit{x}\right)$
The original solution	3	3	12	3.25	0.0249	111.45	0.147
The optimal solution	1.94	2.55	24.31	2.05	0.0205	97.97	0.121

presents the wave overtopping discharge, cost, and objective function values for both the optimal solution of Trial 7 and the original solution of the seawall (Figure 2). From Table 5, it is evident that the wave overtopping discharge for the optimal solution of Trial 7 is 0.0205 m³/s/m, while the original solution has a wave overtopping discharge of 0.0249 m³/s/m, resulting in a reduction of 17.67%. According to design standard Code for Design of sea dike project [8], to ensure the structural integrity of a seawall protected on three sides, a tolerable value of wave overtopping discharge is 0.05 m³/s/m. It is evident that the optimal cross-section solution of Trial 7 meets this standard. In terms of construction cost, the optimal solution of Trial 7 has a cost of 97.97, which is 12.1% lower compared to the original solution of 111.45. Regarding the objective function value, there is a 17.69% decrease from the original solution’s value of 0.147 to the optimal solution of Trial 7, which is 0.121. Clearly, the wave overtopping discharge and cost of the optimal solution in Trial 7 are both smaller than those of the original solution. It is worth noting that, despite being the worst result among the 20 trials, Trial 7 still demonstrates satisfactory performance in achieving our defined optimization objectives. This indicates that our methodology for finding the optimal seawall cross-section that simultaneously minimizes wave overtopping discharge and cost is effective and robust.

3.4. Comparison with GA

In this section, we will compare our method, which employs the DYCORS algorithm, with the GA (Genetic Algorithm) as the GA is a popular approach for solving global optimization problems on coastal structures [22,23,24,25,26]. In the present study, the GA solver of MATLAB(2019b) software is used and the probability of crossover and mutation operators are chosen as 0.50 and 0.4, respectively. In terms of decision vectors, design parameters, constraints, and multi-objective functions, they are the same as those of DYCORS.

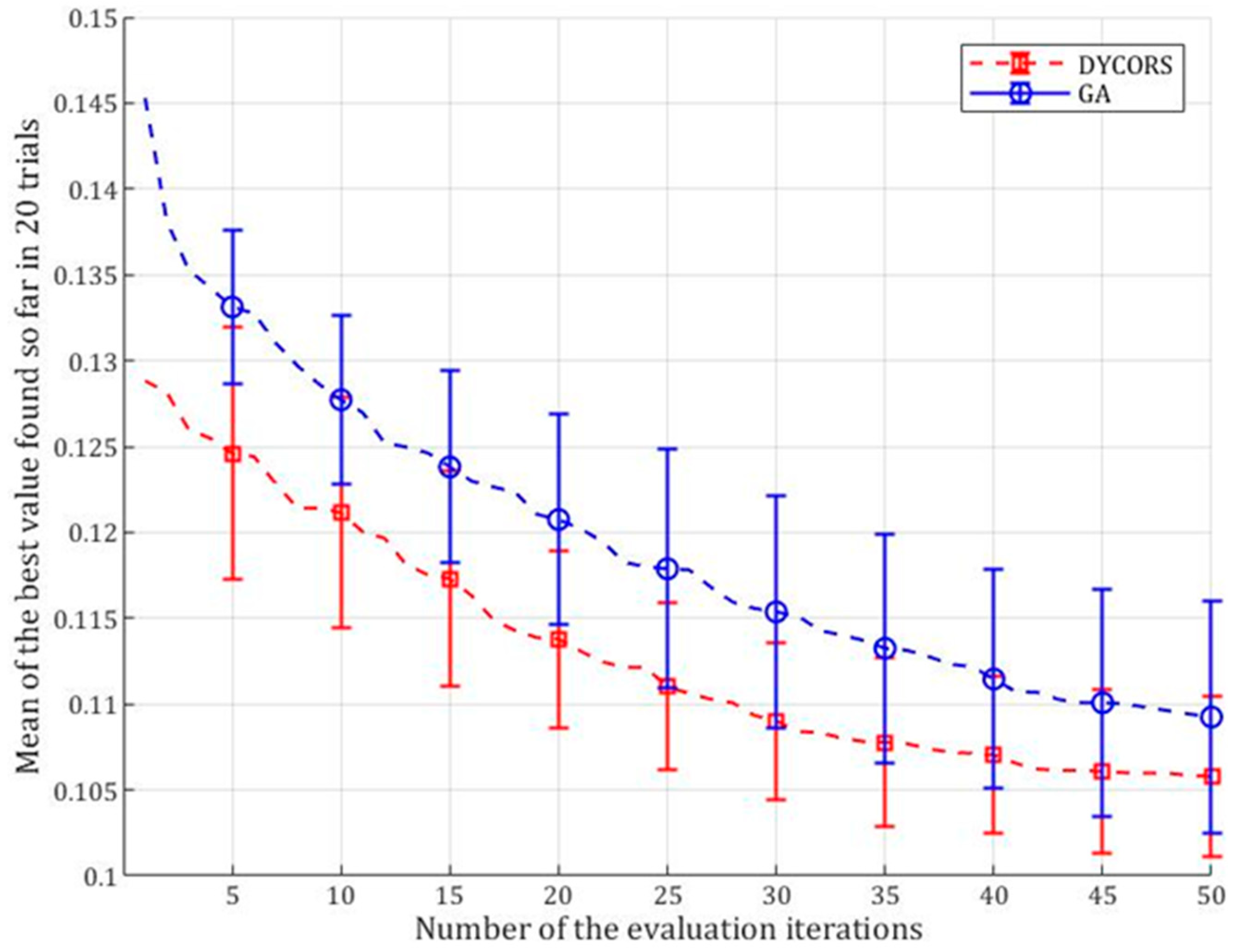
We can evaluate the performance of an algorithm for a specific problem by tracking the best objective function values obtained after each evaluation iteration. As there are multiple trials, we can calculate the average best function value for the algorithm after each evaluation iteration and present the findings in a plot known as an average progress curve. The average progress curve provides a comprehensive assessment of the algorithm’s performance and the evolution of solution quality over time for the optimize problem. It gives a clear understanding of how the quality of solutions is improved or changes throughout the evaluation process. Analyzing the average progress curve allows us to comprehend the algorithm’s behavior and make informed decisions regarding further enhancements or comparisons with other algorithms.

Convergence is an important indicator in optimization problems, signaling the approach or attainment of the optimal solution. As demonstrated in Section 3.4, favorable convergence is achieved after 50 iterations. Consequently, we determine the relative performance of the two algorithms after 50 evaluation iterations by looking at the values indicated by their respective average progress curves in 20 trials.

Figure 9 shows the average progress curves of these two optimization algorithms applied to the optimization problem of the seawall cross-section with error bars representing 95% t-confidence intervals for the mean. These error bars provide insights into the stability and reliability of the results, allowing us to assess the consistency of each algorithm’s performance across multiple trials. The length of the error bars indicates the potential range of variation in the mean at a given confidence level. The larger the error bar, the greater the variability in the results. From Figure 9, it can be observed that the data reliability of the DYCORS algorithm is higher. Furthermore, the average progress curve for the DYCORS algorithm consistently falls below that of the GA for this optimization problem, signifying that DYCORS consistently achieves a lower average best function value compared to the GA. Therefore, it can be concluded that DYCORS outperforms the GA throughout the entire dynamic optimization process, consistently producing better results over each evaluation iteration.

In addition,

Table 6. Statistics of the best objective function value from 20 trials of the algorithms.

Algorithms	Best	Worst	Mean	Median	Std Error
DYCORS	0.0865	0.1211	0.1058	0.1066	0.0100
GA	0.0925	0.1321	0.1093	0.1042	0.0144

provides the statistical data for the optimization problem after 50 evaluation iterations, including the best value (minimum), the worst value (maximum), the median value, the mean value, and the standard error of the mean of the best function values over the 20 trials for both algorithms. Upon analyzing the statistical data from Table 6, it can be observed that, for the statistical measures of the 20 trials, both the best value and the worst value for DYCORS are smaller than those for the GA. The mean value, commonly used to measure the central tendency and representativeness of statistical data, provides an estimate of the overall level of the entire dataset. Additionally, it is smaller for DYCORS in comparison to the GA. Furthermore, the standard error is a crucial statistical measure assessing the precision and reliability of the trials’ results. A smaller standard error suggests higher reliability and precision. Comparing the standard error of the mean value, it can be concluded that the data results of DYCORS are more reliable and accurate. The median, which is the value located in the middle position of a sorted dataset, is slightly larger for DYCORS compared to GA. However, overall, DYCORS performs better than GA because we are more concerned with the mean values and standard errors of the mean.

Taking these findings above into account, it can be concluded that, overall, the DYCORS algorithm consistently outperformed the GA for seawall cross-section optimization.

4. Application

4.1. Background

In general, during the design of seawalls, various tidal and wave combinations should be taken into consideration. Therefore, it is necessary to optimize the seawall cross-section for different conditions, such as wave heights, periods, and tidal combinations with different return periods. Next, taking the seawall cross-section profile as an example, as Figure 10 shows, the optimization aims to maximize economic benefits and wave prevention effects while considering design conditions and verification conditions simultaneously. The slope ratio of both the upslope and downslope surfaces is 1:2. The height of the berm is 8.6 m (distance from the toe to the top of the berm), and the width of the berm is 15 m, representing the original solution. Similar to Section 3, the optimization will focus only on the main structural part of the seawall (the shaded area bounded by thick black lines) and will be compared with the final optimal solution. The decision vectors include ${\mathsf{\alpha }}_{\mathrm{d}}$ and ${\mathsf{\alpha }}_{\mathrm{u}}$ (the cotangent of angles with respect to the horizontal direction of downslope and upslope, respectively), B (the width of the berm), and d (the height of the berm). These four decision vectors are all independent from one another.

Table 7. Values of decision vectors.

Decision Vectors	Value Range
$\mathrm{the} \mathrm{slope} \mathrm{of} \mathrm{the} \mathrm{upslope}: {\mathsf{\alpha }}_{\mathrm{u}}$	1.5~3.5
$\mathrm{the} \mathrm{slope} \mathrm{of} \mathrm{the} \mathrm{downslope}: {\mathsf{\alpha }}_{\mathrm{d}}$	1.5~3.5
the width of the berm: B (m)	0~30
$\mathrm{the} \mathrm{height} \mathrm{of} \mathrm{the} \mathrm{berm}:\mathrm{d}$(m)	0~13.4

presents the upper and lower bounds for these decision vectors.

Table 8. Values of design parameters used in optimizing the seawall cross-section profile.

Design Parameters	Value
$\mathrm{the} \mathrm{still} \mathrm{water} \mathrm{level} \mathrm{of} \mathrm{design} \mathrm{condition}: {\mathrm{h}}^1$ (m)	11
$\mathrm{the} \mathrm{incident} \mathrm{significant} \mathrm{wave} \mathrm{height} \mathrm{of} \mathrm{design} \mathrm{condition}:{\mathrm{H}}_{\mathrm{m}0}^1$ (m)	3.6
$\mathrm{the} \mathrm{spectral} \mathrm{wave} \mathrm{period} \mathrm{of} \mathrm{design} \mathrm{condition}: {\mathrm{T}}_{\mathrm{m}-1,0}^1$ (s)	8.8
$\mathrm{the} \mathrm{still} \mathrm{water} \mathrm{level} \mathrm{of} \mathrm{verification} \mathrm{condition}:{\mathrm{h}}^2$ (m)	11.8
$\mathrm{the} \mathrm{incident} \mathrm{significant} \mathrm{wave} \mathrm{height} \mathrm{of} \mathrm{verification} \mathrm{condition}: {\mathrm{H}}_{\mathrm{m}0}^2$ (m)	4.75
$\mathrm{the} \mathrm{spectral} \mathrm{wave} \mathrm{period} \mathrm{of} \mathrm{verification} \mathrm{condition}: {\mathrm{T}}_{\mathrm{m}-1,0}^2$ (s)	10.2
$\mathrm{roughness} \mathrm{factor} \mathrm{for} \mathrm{the} \mathrm{downslope}: {\gamma }_{f\mathrm{d}}$	0.55
$\mathrm{roughness} \mathrm{factor} \mathrm{for} \mathrm{the} \mathrm{upslope}:{\gamma }_{fu}$	0.55
$\mathrm{the} \mathrm{size} \mathrm{of} \mathrm{the} \mathrm{structure} \mathrm{elements} \mathrm{for} \mathrm{the} \mathrm{downslope}: {\mathrm{D}}_{\mathrm{d}}$ (m)	0.85
$\mathrm{the} \mathrm{size} \mathrm{of} \mathrm{the} \mathrm{structure} \mathrm{elements} \mathrm{for} \mathrm{the} \mathrm{upslope}:{\mathrm{D}}_{\mathrm{u}}$ (m)	0.85
$\mathrm{the} \mathrm{crest} \mathrm{height} \mathrm{in} \mathrm{respect} \mathrm{to} \mathrm{still} \mathrm{water} \mathrm{level} \mathrm{of} \mathrm{design} \mathrm{condition}: {\mathrm{A}}_c^1$(m)	4.9
$\mathrm{the} \mathrm{wall} \mathrm{height} \mathrm{in} \mathrm{respect} \mathrm{to} \mathrm{still} \mathrm{water} \mathrm{level} \mathrm{of} \mathrm{design} \mathrm{condition}: {\mathrm{R}}_c^1$(m)	4.9
$\mathrm{the} \mathrm{crest} \mathrm{height} \mathrm{in} \mathrm{respect} \mathrm{to} \mathrm{still} \mathrm{water} \mathrm{level} \mathrm{of} \mathrm{verification} \mathrm{condition}: {\mathrm{A}}_c^2$ (m)	4.1
$\mathrm{the} \mathrm{wall} \mathrm{height} \mathrm{in} \mathrm{respect} \mathrm{to} \mathrm{still} \mathrm{water} \mathrm{level} \mathrm{of} \mathrm{verification} \mathrm{condition}: {\mathrm{R}}_c^2$ (m)	4.1
$\mathrm{the} \mathrm{crest} \mathrm{width}: {\mathrm{G}}_c$ (m)	4.4

presents values for the design parameters used in optimizing the seawall cross-section profile, and the wave conditions and wave overtopping control standards are shown in

Table 9. The tolerable mean wave overtopping for design condition and verification condition.

Conditions	$\mathbf{h}$ (m)	${\mathbf{H}}_{\mathbf{m}0}$ (m)	${\mathbf{T}}_{\mathbf{m}-1,0}$ (S)	QT (L/s/m)
Design condition	11.0	3.80	9.0	0.3
Verification condition	11.8	4.75	10.2	50.0

. Under the design condition involving a combination of a 100-year return period high tide and a 100-year return period wave, referring to EuroTop, 2018 [41], the tolerable mean wave overtopping is Q^T = 0.3 L/s/m. At this time, people can enjoy the picturesque view of the sea and sky from the top of the seawall. Under the verification condition of the combination of a 200-year return period high tide and a 200-year return period wave, referring to design standard Code for Design of sea dike project [8], the tolerable mean wave overtopping is Q^T = 50 L/s/m. This aims to ensure that the structures behind the seawall, which are protected on three sides, are not damaged.

4.2. The Optimization Problem

It is important to emphasize that the optimization methodology established in this study is a general approach. Modifying decision vectors, constraints, and objective functions does not affect the effectiveness of the method. It merely represents variations in the objectives to be optimized based on specific circumstances. Therefore, when facing design conditions and verification conditions simultaneously, we can modify the objective function according to Equations (1)–(4), as shown below:

$$min: F\left(x\right)={\mathrm{W}}_1\times {\displaystyle \frac{Q_1\left(x\right)-Q_{1min}}{Q_{1max}-Q_{1min}}}+{\mathrm{W}}_2\times {\displaystyle \frac{Q_2\left(x\right)-Q_{2min}}{Q_{2max}-Q_{2min}}}{+\mathrm{W}}_3\times {\displaystyle \frac{C\left(x\right)-C_{min}}{C_{max}-C_{min}}}$$

(8)

where $Q_1\left(x\right)$ represents the mean overtopping discharge for the design condition and $Q_{1min}$ and $Q_{1max}$ are the minimum and maximum value of $Q_1\left(x\right)$, respectively. Similarly, $Q_2\left(x\right)$ represents the mean overtopping discharge for the design condition and $Q_{2min}$ and $Q_{2max}$ are the minimum and maximum value of $Q_2\left(x\right)$, respectively. $C\left(x\right)$ is the cost function. $C_{min}$ and $C_{max}$ are the minimum and maximum value of $C\left(x\right)$, respectively. $W_1$,$W_2$, and $W_3$ are adjustable coefficient used to weight cost, $C\left(x\right)$, and overtopping discharge, $Q_1\left(x\right)$ and $Q_2\left(x\right)$.

In our present study, we have selected ${\mathrm{W}}_1=0.5,$ ${\mathrm{W}}_2=0.3$, and ${\mathrm{W}}_3=0.2$ for illustrative purposes. It is important to emphasize that different weighting coefficients imply different optimization objectives, with varying emphasis on cost and wave overtopping discharge. The specific selection in practical applications can be set based on the actual requirements. Obviously, when $\mathrm{d}=0 \mathrm{m}, {\mathsf{\alpha }}_{\mathrm{u}}=1.5$, the seawall reaches the smallest cost solution, and we can calculate $C_{min}=184.92$ (as mentioned earlier, for the sake of simplicity, we assume that the unit prices of each part are consistent, so the cost is only determined based on the size of the engineering quantity). At the same time, the overtopping discharge reaches its maximum, $Q_{1max}=11.4 \mathrm{L}/\mathrm{s}/\mathrm{m}, { Q}_{2max}=241 \mathrm{L}/\mathrm{s}/\mathrm{m}$ Meanwhile, when $\mathrm{d}=13.4 \mathrm{m}, {\mathsf{\alpha }}_{\mathrm{d}}=3.5, \mathrm{B}=30 \mathrm{m}$, the seawall reaches the biggest cost solution, $C_{max}=908.48$. The specified values are shown in

Table 10. Values of the function parameters.

Function Parameters	Value
$\mathrm{the} \mathrm{maximum} \mathrm{value} \mathrm{of} \mathrm{the} Q_1\left(x\right)$: $Q_{1max}$ (L/s/m)	11.4
$\mathrm{the} \mathrm{minimum} \mathrm{value} \mathrm{of} \mathrm{the} Q_1\left(x\right)$: $Q_{1min}$ (L/s/m)	0
$\mathrm{the} \mathrm{maximum} \mathrm{value} \mathrm{of} \mathrm{the} Q_2\left(x\right)$: $Q_{2max}$ (L/s/m)	241
$\mathrm{the} \mathrm{minimum} \mathrm{value} \mathrm{of} \mathrm{the} Q_2\left(x\right):$ $Q_{2min}$(L/s/m)	0
$\mathrm{the} \mathrm{maximum} \mathrm{value} \mathrm{of} \mathrm{the} C\left(x\right)$: $C_{max}$ (-)	908.48
$\mathrm{the} \mathrm{minimum} \mathrm{value} \mathrm{of} \mathrm{the} C\left(x\right)$: $C_{min}$ (-)	184.92

.

In conclusion, the optimization objective function at this stage is as follows:

$$min: F\left(x\right)=0.5\times {\displaystyle \frac{Q_1\left(x\right)}{11.4}}+0.3\times {\displaystyle \frac{Q_2\left(x\right)}{241}}+0.2\times {\displaystyle \frac{C\left(x\right)-184.92}{908.48-184.92}}$$

(9)

$$C\left(x\right)=\left(2\times \mathrm{B}+{\mathsf{\alpha }}_{\mathrm{d}}\times \mathrm{d}\right)\times {\displaystyle \frac{\mathrm{d}}{2}}+2.5\times \left(\mathrm{B}+{\mathsf{\alpha }}_{\mathrm{d}}\times \mathrm{d}\right)+\left(15.9+2.5+\mathrm{d}\right)\times {\mathsf{\alpha }}_{\mathrm{u}}\times {\displaystyle \frac{13.4-\mathrm{d}}{2}}$$

(10)

4.3. Results and Discussion

The optimal solution is obtained by implementing the established method of optimizing seawall cross-section profiles. The optimized decision vector results are presented in

Table 11. Values of the optimized decision vectors.

Decision Vectors	Value Range	Optimal Value
$\mathrm{the} \cot \mathrm{angent} \mathrm{ration} \mathrm{of} \mathrm{the} \mathrm{upslope}: {\mathsf{\alpha }}_{\mathrm{u}}$	1.5~3.5	1.50
$\mathrm{the} \cot \mathrm{angent} \mathrm{ration} \mathrm{of} \mathrm{the} \mathrm{downslope}: {\mathsf{\alpha }}_{\mathrm{d}}$	1.5~3.5	3.35
the width of the berm: B (m)	0~30	16.91
the height of the berm: d (m)	0~13.4	6.8

. The cotangent slope ratio of the upslope slope, ${\mathsf{\alpha }}_{\mathrm{u}}$, and downslope slope, ${\mathsf{\alpha }}_{\mathrm{d}}$, are 1.5 and 3.35, respectively. The width, B, and the height of the berm, $\mathrm{d}$, are 16.91 m and 6.8 m, respectively. The final optimal solution for the seawall cross-section profile is illustrated in Figure 11.

Table 12. Comparison between the optimal solution and the original solution.

Solution	${\mathsf{\alpha }}_{\mathbf{u}}$	${\mathsf{\alpha }}_{\mathbf{d}}$	B $(\mathbf{m}$)	$\mathbf{d} (\mathbf{m}$)	${\mathit{Q}}_1\left(\mathit{x}\right)$$(\mathbf{L}/\mathbf{s}/\mathbf{m}$)	${\mathit{Q}}_2\left(\mathit{x}\right)$ $(\mathbf{L}/\mathbf{s}/\mathbf{m}$)	$\mathit{C}\left(\mathit{x}\right)$	$\mathit{F}\left(\mathit{x}\right)$
The original solution	2	2	15	8.6	0.288	25.5	413.060	0.115
The optimal solution	1.5	3.35	16.91	6.8	0.142	9.95	416.405	0.083

presents the wave overtopping discharge, cost, and objective function values for both the optimal solution (Figure 11) and the original solution of the seawall (Figure 10). There was a 27.8% reduction in objective function value compared to the original solution. In more detail, the optimal solution only incurs a marginal 0.81% increase in cost while achieving a significant reduction in wave overtopping discharge. Specifically, for the design condition, the wave overtopping discharge has been reduced from 0.288 L/s/m to 0.142 L/s/m, resulting in a decrease of 50.69%. For the verification condition, the wave overtopping discharge has been reduced from 25.5 L/s/m to 9.95 L/s/m, resulting in a decrease of 60.98%. Clearly, the optimal cross-section solution meets the tolerable mean overtopping discharge, as Table 9 shows.

From this, it can be seen that our methodology for determining the optimal seawall cross-section, which simultaneously minimizes wave overtopping discharge and cost, is effective and robust when facing design conditions and verification conditions simultaneously. Additionally, it is important to note the general applicability and effectiveness of our methodology, as long as Equation (1) to Equation (4) are followed when modifying decision vectors, constraints, and objective functions based on specific circumstances.

5. Summary and Conclusions

The purpose of this research is to develop an optimization methodology for a seawall cross-section with a berm and composite slopes. One of the main challenges is the conflicting nature of simultaneously minimizing the overtopping discharge and construction costs. Therefore, we utilize the optimization algorithm DYCORS, which efficiently explores the decision vectors to identify solutions that satisfy multi-objective functions and constraints. Additionally, the ANN model is employed to obtain the mean overtopping discharge. The main conclusions are as follows:

(1)

The worst-performing Trial 7 among 20 trials shows a satisfactory performance, with an overtopping discharge 0.0205 ${\mathrm{m}}^3/\mathrm{s}/\mathrm{m}$ and a construction cost of 97.97, which are both smaller than those of the original solution.

(2)

Compared to GA, the DYCORS-based methodology proposed has been proven to be more effective and robust, as evidenced by the statistical data and the average progress curve.

(3)

When facing different combinations of water levels and wave conditions, the optimal solution has a 27.8% reduction in objective function value compared to the original solution.

In summary, the results show that the new method established in this study can provide a technical solution tool for the optimization design of seawall cross-sections. Designers only need to focus on determining decision vectors, the objective function, and constraints without worrying about how they interact with one another. The selection of decision vectors and the determination of the optimal solution are all made by the optimization algorithm DYCORS.

6. Future Outlooks

The proposed optimization methodology is an innovative study for optimizing the cross-section of real-word seawalls, which really still requires practical data and experience to support its implementation. In the application showcases provided, the cost function has been simplified for demonstration purposes. Actually, it is important to consider variations in materials, such as the selection of core stones, armor layers, and changes in their dimensions. In addition, factors such as the difficulty of construction, land acquisition, and utilization also need to be taken into account. Furthermore, the stability constraints of the structure, such as the armor layer and wave wall, should also be considered. We will strive to incorporate more realistic considerations and constraints into the optimization model. This will involve close collaboration with experienced engineering professionals to better align the optimization process with the practical requirements of seawall design and construction. Therefore, it is essential to further improve our optimization methodology based on the optimization algorithm DYCORS to solve the optimization problem under these multiple complex constraints.