Abstract
The majority of existing numerical simulations of the effect of bridge piers on water’s movement are based on a limited number of bridge piers at a laboratory scale. Furthermore, some 2D numerical simulations for actual bridge projects have deficiencies, including the use of overly large meshes and an inadequate treatment of bridge piers. In this study, we compare three methods (structural mesh encryption, suspension mesh, and non-structural mesh) based on Delft3D, and we apply the optimisation scheme to a real bridge project. It is demonstrated that optimal results can be achieved by utilising a grid size comparable to the pier diameter (Dp) in the region away from the pier. In the vicinity of the pier, the grid cell size should be no larger than 1/9 Dp. The suspended grid technique (DD Boundary) can yield results consistent with those obtained using a full-area high-resolution grid, provided that the total grid number can be reduced and the computational time is considerably reduced. In this study, the unstructured mesh (Delft3D Flexible Mesh) scheme was unable to capture the oscillations in the wake flow behind the bridge piers. However, the application of the optimised scheme in bridge engineering demonstrated its practical value. The findings of this study on mesh resolution and suspension mesh schemes can be applied to the Delft3D software and are also useful for other numerical simulation work.
1. Introduction
Piers and columns represent a common and important class of hydraulic structures. Examples of such structures include the piers of various bridges, dividing piers of porous sluice gates, structural support columns inside underground lock chambers, rectification piers/columns of pumping station inlet/outlet basins and inlet/outlet canals, and support columns of high-pile piers. In contrast to the unimpeded flow of water in natural rivers, the introduction of piers and columns into the waterway results in a number of changes to the characteristics of the water’s movement. These include alterations to the velocity of the water, the water level, the shear force, and several other factors. These changes are sometimes beneficial, such as the use of a variety of rectification piers/columns to homogenise the pumping station’s inlet and outlet water flow, in order to improve the pumping station’s inlet and outlet water flow pattern and unit inlet/outlet conditions. However, some may be unfavourable; for instance, the pier impedes the movement of water caused by the upstream channel’s surface congestion, which affects the river’s flood control. Additionally, the pier/columns’ localised changes in the local flow, caused by local scouring, affect the project’s safety. Consequently, the impact of piers and columns on water’s movement has been a significant area of investigation within the field of water conservancy engineering [,,,,,].
In the field of pier/columns’ winding flow, physical modelling tests represent a significant and widely employed research methodology [,,]. Some scholars have previously observed that “sixty years ago, it was believed that the flow field at bridge piers was too complex to be measured or even visualised” []. Subsequently, with the advent of sophisticated measurement techniques such as ADV and PIV, the intricate flow field around bridge piers has been successfully quantified and continues to be a pivotal aspect of related research. Keshavarzi, A. et al. [], in their study of coherent turbulence around a single circular bridge pier and its influence on the scour pattern of the riverbed, employed an acoustic Doppler velocimeter (micro-ADV) to measure the flow field around an open-channel bed at 102 locations in the vicinity of an open channel. Pagliara, S. et al. [] conducted a study to investigate the effect of spacing between two in-line circular columns on the flow structure. This was achieved by utilising a micro-acoustic Doppler velocimeter (ADV) at 102 points near the bed of an open channel. The objective was to develop a reliable method for predicting the maximum depth of localised scour around a bridge pier. Furthermore, Vijayasree, B.A. et al. [] employed three-dimensional micro-acoustic Doppler velocimetry (ADV) to measure the instantaneous velocity of individual piers of various shapes, including rectangular, oblong, trapezoidal, triangular, and lenticular; they then discussed the changes in mean velocity and Reynolds stress induced by the shape of the piers and compared them with a flat plate surface. In their study, Li, J. et al. [] employed particle image velocimetry (PIV) to quantify the flow field in the vicinity of the pier. U. Jenssen and M. Manhart [] employed stereoscopic particle image velocimetry (PIV) to examine the turbulent flow within a scour hole surrounding a cylinder in a sand bed; their objective was to elucidate the flow dynamics and the underlying turbulent structure. J. Unger and W. H. Hager [] utilised PIV to investigate the internal flow characteristics surrounding a circular bridge pier; their aim was to characterise the turbulent flow. The internal flow characteristics around a circular bridge pier were investigated via particle image velocimetry, resulting in a quasi-spatial visualisation of the velocity field. The temporal evolution of the vertical deflected flow in front of the pier and the horseshoe vortex in the enlarged scour hole were investigated, and velocity and vorticity distributions were derived.
Another significant approach to the investigation of pier-deflected flow is the CFD technique. Although CFD emerged later than physical modelling tests, it has developed at a rapid pace and has gradually become an important research tool in recent years, as a result of the continuous progress of technology [,,]. The combination of a physical model and a mathematical model has become the dominant research programme in the field of pier and column flow.
In numerous CFD studies, FLUENT is employed for three-dimensional fine numerical simulation of the flow field around bridge piers, with the objective of obtaining more realistic and comprehensive flow information. K. H. M. Ali and O. Karim [] utilised FLUENT to predict the three-dimensional flow field around a cylinder, resulting in the identification of the rule governing the change in shear stress within the bed in proximity to the cylinder. Solutions were obtained for rigid beds and scour holes of different sizes due to different durations. M. Salaheldin Tarek et al. [] employed a three-dimensional numerical model, FLUENT, to simulate the separation turbulence around a vertical circular pier in clear water. Calculations were conducted using a variety of turbulence models, with the results being compared with several sets of experimental data that were available in the literature. W. Cui et al. [] conducted a numerical simulation of the flow around a combined pier with a Reynolds number in the range of 1.0 × 10⁶ to 2.76 × 10⁶ using the fluid dynamics software FLUENT. The time courses of lift and drag coefficients for three different types of combined piers (i.e., combined cylindrical piers, truncated conical piers, and combined truncated conical piers) were analysed for different water depths based on the detached eddy simulation (DES). M. Nasim et al. [] simulated the flooding effect of bridge piers using the finite volume method in the ANSYS FLUENT software package. The shape of the pier’s cross-section was found to have a significant effect on the fluid pressure exerted on the pier under flood loading. K. Lahsaei et al. [] simulated the three-dimensional flow around a river pier under rigid riverbed conditions using ANSYS FLUENT software.
Another frequently used 3D fine numerical simulation software platform is FLOW-3D. In their study, M. Ghasemi and S. Soltani-Gerdefaramarzi [] employed the Flow-3D modelling function to simulate local scour around a cylindrical bridge pier in a non-cohesive bed sediment. The simulations were conducted at different flow rates of 5, 10, 19, and 30 L/s, investigating parameters such as flow velocity, fluid depth, Froude number, height of filled sediment, and change in net sediment motion. M. Jafari et al. [] investigated the hydrodynamic behaviour around the piers of a diagonal bridge complex settling on a foundation, using the FLOW-3D numerical model. It was demonstrated that the flow pattern around a bridge pier cluster is distinct from that of a single pier due to nonlinearity and interactions between different phenomena. Consequently, the results of the flow pattern around a single pier cannot be generalised to a bridge pier cluster. H. K. Jalal and W. H. Hassan [] conducted a numerical investigation of the problem of localised scour around a circular bridge pier using the FLOW-3D model. The results were compared with those of the experimental model of Melville Laboratory. The findings indicated that the proposed Flow-3D model is an effective tool for predicting and simulating scour depths around bridge piers, as well as being an economical method for predicting the potential outcomes. Man, C. et al. [] analysed the influence of different turbulence models on abutment scour pits using Flow-3D software. The simulated scour results were found to diverge significantly from the observed data collected from previous studies, due to the inapplicability of the meshing method in the Flow-3D software.
Due to the high computational effort required for 3D numerical simulations, they are predominantly employed for laboratory-scale studies and are primarily conducted on a limited number of bridge piers (1–2). In contrast to laboratory-scale studies, real bridges tend to have large spans and many piers, and the length of the river section affected is much larger than at the laboratory scale. To accurately reflect the impact of real bridges on water’s movement, numerous scholars have conducted related studies utilising two-dimensional mathematical models with a greater applicability area and superior computational economy. Cetina and Mario Krzyk [] employed a two-dimensional depth-averaged mathematical model, PCFLOW2D, on a 600 m long river segment. The investigation examined the alterations to the velocity field and free surface elevation resulting from the designed piers of a new bridge. Some local flow details, such as increases in the upstream water level and the velocity between the piers, were accurately predicted. J. G. Duan [] employed a two-dimensional depth-averaged hydrodynamics model to simulate the flow field around a circular bridge pier in clear water. The two-dimensional model not only simulated vortex shedding in the turbulent wake, it also simulated the distribution of bed shear stress. The simulated bed shear stress contours were in close agreement with the experimental measurements and three-dimensional (3D) modelling results. The 2D model is considerably more straightforward than the 3D model and requires a much shorter computational time, suggesting that the enhanced 2D model is an effective tool for simulating the bed shear stress distribution around bridge piers. W. Wang et al. [] investigated the impact of bridge piers on the flood hazard of the Jialing River using the 2D numerical model Mike 21 FM. A comparison of the numerical results with and without bridge piers enabled the analysis of the influence of the backwater effect on the flow field.
X. Zhang et al. [] constructed a hydrodynamics model based on MIKE21, taking elliptical bridge piers as an example, and applied it to the numerical simulation of the hydrodynamics of the river downstream of the Yellow River. This simulation examined the influence of changes in the morphology of the bridge piers on the river’s flow rate, water level, and flow field. In a similar vein, H. Xiong et al. [] employed the MIKE 21 hydrodynamics module and transportation module to investigate the hydrodynamics and water quality of the Wuhan river section under varying pier densities. Z. Sun et al. [] employed the Delft3D mathematical model to conduct a series of numerical experiments on the flow field of the estuary of the Qiantang River under various combinations of single and multiple bridges in order to investigate the complex response of tidal currents to multiple bridges. C. Xiaocen et al. [] also employed the Delft3D model to investigate the flow field of the Ningbo River under different combinations of single and multiple bridges in order to investigate the complex response of tidal currents to multiple bridges. C. Xiaocen et al. [] established a two-dimensional non-constant-flow mathematical model of the Yongjiang River in order to study the influence of the built bridges on flood control and tidal flow. The Delft3D model was employed to determine and verify parameter rates, which were then used to conduct a study on the influence of the bridges on the Yongjiang River’s flow rate and water level under typical flood and tidal conditions. C. Jun et al. [] conducted a study on the cumulative effects of bridge and pier groups on river flooding under typical flood and tide conditions based on the Delft3D mathematical model. The study compared the effects of single-type and dual-type engineering groups on the flood level and flow rate of the river. A. Abdou et al. [] employed the Delft3D mathematical model to simulate a straight river channel and investigate the effects of different configurations (i.e., the number of bridge piers, the span characteristics, and the different reach characteristics) on the flow rate and water level of the Ningbo River. The characteristics, number of piers, and different reach locations of bridge pier clusters in a river cross-section were investigated for their influence on the morphodynamics. The study focused on sandy lowland rivers that exhibit stable alternating bars and low Froude numbers.
The majority of researchers engaged in these two-dimensional numerical simulations utilise a single computational grid cell to simulate a bridge pier. This method contravenes the recommendations set out in the majority of user manuals. These manuals stipulate that a minimum of five grid cells is required to accurately capture a hydrodynamic feature. Furthermore, some scholars have proposed adjusting the local roughness or local topography of the riverbed as a method for the treatment of bridge piers [,]. The aforementioned treatments do not accurately reflect the complex water movement in the vicinity of the bridge pier, nor do they guarantee the reliability of the long-term cumulative effects of phenomena such as local scour.
For this reason, this study employed Delft3D software, which is based on measured data, and took the computational accuracy and computational efficiency as the criteria. Numerical experiments were carried out and compared and analysed for a variety of schemes for the numerical simulation of bridge piers’ winding flow. An optimised scheme was proposed and applied to an engineering example to prove the feasibility of the scheme. The findings of this study can serve as a reference point for future scientific research and engineering design projects.
2. Research Objects and Basic Data
The research objects, which are aligned with the content of this study, include a physical model of a flume for basic research and a bridge project for programmatic application.
2.1. Flume Physical Model
The flume physical model test system comprises a transparent glass flume, water pipeline, electromagnetic flow meter, pump, electric valve, and water storage tank. The glass flume has a total length of 15.0 m, a width of 0.42 m, and a height of 0.48 m. The effective working section of the flume is 12.0 m long and is located between sections A-A and D-D (Figure 1). A cylindrical model pier is located in the middle of the flume. The diameter of the model pier (Dp) is 5 cm.
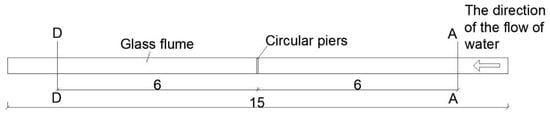
Figure 1.
Effective working section of the flume.
2.2. Basic Data for the Physical Model of the Flume
Table 1 presents the measured water level in section A-A when there is no pier and a single cylindrical pier is set up, with a flow rate of Q = 20 L/s and a water level of 13.40 cm in section D-D (the bottom of the model sink is horizontal and its height is defined as 0 cm). The maximum flow velocity was measured in the vicinity of the bridge pier, occurring on both sides. The average value of the maximum flow velocity was found to be 0.55 m/s.

Table 1.
Incoming flow rate and the water level of the main section.
Figure 2 presents the planar flow distribution obtained via particle image velocimetry (PIV). In the time-averaged state (Figure 2a), the flow in the vicinity of the piers is essentially symmetrical, and the wake zone downstream of the piers is stable. The instantaneous flow field image (Figure 2b) demonstrates that the wake flow downstream of the bridge pier is subject to oscillatory behaviour.

Figure 2.
Flow field measured by PIV: (a) Time-averaged flow velocity distribution. (b) Instantaneous flow velocity distribution.
In the numerical simulation presented in this paper, the measured water level in section A-A, the measured maximum flow velocity on both sides of the bridge pier, and the oscillating phenomenon of the flow downstream of the bridge pier were employed as criteria for the verification and discernment of the advantages and disadvantages of the calculation scheme.
2.3. Example Bridge Project
A highway bridge crosses a river, with the river and the bridge intersecting diagonally. The length of the river is approximately 1.2 km. There are six groups of piers in the bridge, with four piers in each group. Each pier has a diameter of 1.4 m. Due to the necessity of engineering transformation, the original diameter of the piers was increased from 1.4 m to 2.4 m. Figure 3 presents the river channel pier layout. The project design flow rate is 800 m3/s, with a downstream water level of 47.0 m.
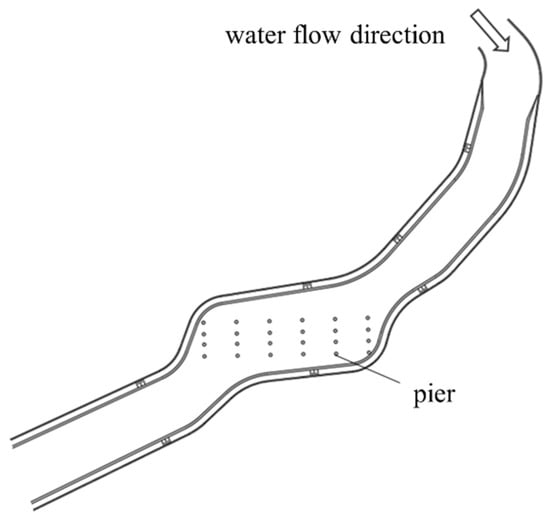
Figure 3.
Schematic diagram of the bridge project’s pier locations.
3. Mathematical Model and Calculation Scheme
3.1. Mathematical Model
3.1.1. Governing Equations []
In this study, Delft3D software was used for two-dimensional numerical simulations. The software plane adopted an orthogonal curve coordinate system, and the vertical direction adopted σ coordinate transformation. The control equations are as follows:
The σ-grid was introduced by Phillips (1957) for atmospheric models. The vertical grid consists of layers bounded by two σ-planes, which are not strictly horizontal but follow the bottom topography and the free surface. Because the σ-grid is boundary fitted both to the bottom and to the moving free surface, a smooth representation of the topography is obtained. The number of layers over the entire horizontal computational area is constant, irrespective of the local water depth (see Figure 4) [].
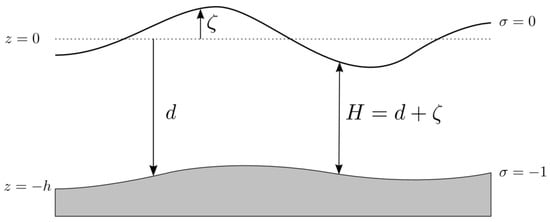
Figure 4.
Definition of water level (ζ), depth (h) and total depth (H).
The σ coordinate system is defined as follows:
where
z: The vertical coordinate in physical space;
ζ: The free surface elevation above the reference plane (at z = 0);
d: The depth below the reference plane;
H: The total water depth.
The depth-averaged continuity equation is as follows:
where and are the transformation coefficients from rectangular coordinates to curvilinear coordinates in the ξ- and η-directions, respectively, while U and V are the depth-averaged velocities.
Q represents the contributions per unit area due to the discharge or withdrawal of water, precipitation, and evaporation:
where and are the local sources and sinks of water per unit of volume [1/s], respectively, P is the non-local source term of precipitation, and E is the non-local sink term due to evaporation. In this study, the effects of precipitation and evaporation were ignored (P = 0, E = 0).
The momentum equations in the ξ- and η-directions are given by
where
: The vertical eddy viscosity coefficient;
: The Coriolis parameter (1/s);
: The reference density of water (kg/m3);
, : The pressure gradients in the ξ- and η-directions, respectively (kg/(m2s2));
, : The imbalance of horizontal Reynold’s stresses in the ξ- and η-directions, respectively (m/s2).
, : The contributions due to external sources or sinks of momentum in the ξ- and η-directions, respectively (m/s2).
The forces Fξ and Fη are of the form:
where : the horizontal eddy viscosity coefficient;
The Coriolis parameter f depends on the geographic latitude and the angular speed of rotation of the earth, Ω: f = 2Ω sin φ.
Where φ: deg latitude co-ordinate in spherical co-ordinates (32° N latitude for Nanjing)
Vertical velocities:
The vertical velocity ω in the adapted σ coordinate system is computed from the continuity equation:
The vertical velocity ω is defined at the iso σ-surfaces; ω is the vertical velocity relative to the moving σ-plane; it may be interpreted as the velocity associated with up- or downwelling motions. The “physical” vertical velocities w in the Cartesian coordinate system are not involved in the model equations. Computation of the physical vertical velocities is only required for post-processing purposes. These velocities can be expressed in the horizontal velocities, water depths, water levels, and vertical ω-velocity according to
3.1.2. Mathematical Model Parameters
The flume mathematical model’s simulation range is the effective working section of the flume, which is a rectangular area with a length of 12.0 m, a width of 0.42 m, a height of 0.48 m, and a cylindrical pier with a diameter of 5 cm. The model inlet is given the flow boundary Q = 20 L/s, and the outlet is given the water level boundary H = 0.134 m.
The calculation range of the bridge project is consistent with Figure 3. The total length of the river is approximately 1.2 km, the width of the river is 60–80 m, and the riverbed elevation is set according to the measured data. The diameter of the bridge piers was set at 1.4 m prior to engineering modification and 2.4 m thereafter. The upstream boundary of the model is defined by a flow rate of 800 m3/s, while the downstream boundary is defined by a water level of 47.0 m.
The solid wall and pier surface of the mathematical model are defined by a no-slip boundary and a specified roughness height (ks).
In this study, the effect of wind was ignored, so the boundary condition at the free surface was w = 0.
The initial condition of the mathematical model is defined as a cold start condition, with the initial water level (h0) specified.
The horizontal eddy viscosity uses the default value provided by Delft3D (1.0).
3.2. Mesh-Independent Analysis
In order to obtain a more ideal grid resolution, four grids with different resolutions (R1, R2, R3, and R4) were set up in the numerical simulation. The grid scale is expressed as a proportion of the diameter of the bridge pier (Dp), and the specific data are given in Table 2.

Table 2.
Grid parameters for different resolutions.
The R1 grid size is Dp, which is the same as the model pier diameter. One grid cell can approximate the simulation unit pier. The R2 grid size is 1/5Dp, which contains five grid cells within a pier diameter. This is in accordance with the user manual, which suggests that at least five grid cells are needed to capture a feature’s size. The R3 grid size is 1/7Dp, which contains seven grid cells within a pier diameter. Finally, the R4 grid size is 1/9Dp, which contains nine grid cells within one pier diameter. Schematic diagrams of the grids for R1 and R4 are provided in Figure 5 and Figure 6, respectively.

Figure 5.
Grid R1.

Figure 6.
Grid R4.
For each grid, numerical simulations were conducted without piers and with a single cylindrical pier, and the results were subjected to analysis.
Table 3 presents the numerical simulation results of the water level in section A-A with varying grid resolutions.

Table 3.
Numerical simulation of water level in section A-A.
The data presented in the table indicate that when there is no bridge pier in the flume, the water level in section A-A remains consistent across the various grid cell sizes. This finding is consistent with the physical model outcomes.
When a 5 cm diameter cylindrical pier is set in the flume, there is a significant difference in the numerical simulation results. As the grid cell size is reduced, the numerical calculation error is gradually reduced. When the grid cell size is 1/9Dp, the error is reduced to −0.009 cm.
Figure 7 presents the variation in the maximum flow velocity at different grid cell scales. As the grid resolution is increased, the calculated maximum flow velocity also gradually increases. The change is gradual and smooth. When the grid cell size is 1/9Dp, the maximum calculated flow velocity is 0.557 m/s, which coincides with the physical model’s measurement of 0.55 m/s. The location of the emergence of the bridge pier is on both sides of the bridge.
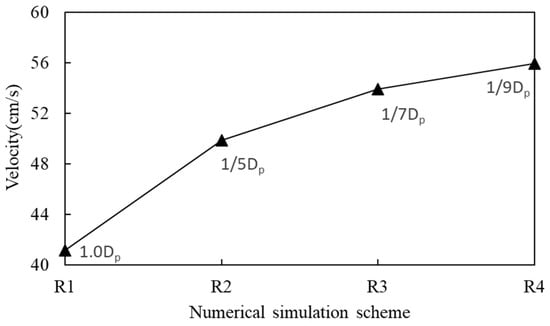
Figure 7.
Maximum flow velocity at different grid cell sizes.
Figure 8 presents the setting of the pier case, with R1 and R4, as pertains to the calculation of the region of the planar water flow pattern. As presented in Figure 8, when the grid cell size is 1.0 Dp (R1), the calculated flow pattern is a stable, symmetric distribution. This pattern does not exhibit the oscillating wake flow observed in the physical model experiments (Figure 2b). When the grid cell size is 1/9 Dp (R4), the computational calculations are able to clearly reflect the oscillating wake flow downstream of the bridge pier.
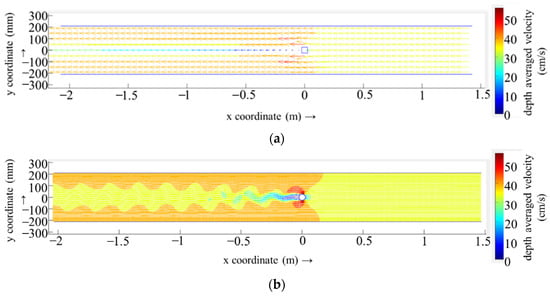
Figure 8.
Planar flow pattern under different grid cell sizes: (a) cell size 1.0 Dp; (b) cell size 1/9 Dp.
The results of the grid-independent analysis demonstrate that, when there is no bridge pier in the river, or in the region away from the bridge pier, the use of a size and diameter of the bridge pier (Dp) comparable to the grid can accurately reflect the characteristics of the water’s flow. In the vicinity of the bridge pier area, it is recommended to adopt a 1/9 Dp or smaller grid size.
3.3. Numerical Simulation Program
In numerical simulations, the number of grid cells has a profound impact on the efficiency and economy of calculation. Consequently, to guarantee the precision of the numerical simulation results, it is essential to minimise the number of computational grids. In the context of bridge piers’ winding flow, an effective method is to utilise a higher-resolution grid for the area in proximity to the bridge pier and, subsequently, reduce the grid resolution for the area situated beyond the bridge pier.
In Delft3D, two methods are available for local encryption of the mesh:
The first method is to utilise suspended mesh technology, specifically DD Boundary. DD Boundary is a domain decomposition technique in which a model is divided into several smaller model domains. The subdivision is based on the horizontal and vertical model resolution required for adequately simulating physical processes. Then, the computations can be carried out separately on these domains. The communication between the domains takes place along internal boundaries, or so-called DD-boundaries. If these computations are carried out concurrently, it is called parallel computing, which can reduce the turnaround time of multiple domain simulations.
The second method is to employ an unstructured mesh, i.e., Delft3D Flexible Mesh.
To facilitate a comparison of the relative merits of the various methods, three numerical simulation schemes were designed for the sink model in this study.
Scheme 1 employs a square mesh with a mesh size of 1/9 Dp throughout the numerical simulation computational area. This scheme is designated as the R4 scheme in the mesh-independent analysis.
Scheme 2 employs a three-level suspension grid based on the DD Boundary. The first level of the region is situated closest to the pier of the calculation area (pier upstream of 6 Dp, and pier downstream of 10 Dp). The grid cell is scaled to 1/9 Dp. The second level of the region is situated in close proximity to the first level of the upstream and downstream region (pier upstream of 6–20 Dp, pier downstream of 10–40 Dp); the grid cell scale is 1/3 Dp. The remaining region for the third level of the calculation area is represented by a grid cell scale of 1/9 Dp. The computational region is defined by a grid cell scale of 1 Dp, with a hanging grid ratio of 1:3 between the regions of all levels. The total number of grid cells is 17,846 (Figure 9).

Figure 9.
DD Boundary numerical simulation grid.
Scheme 3 employs the non-structural computational grid utilised in the Delft3D Flexible Mesh method. This grid is triangular in nature and has a minimum cell scale of 0.1 Dp within the range of 10 Dp upstream and 20 Dp downstream of the bridge pier. The remainder of the area utilises a square grid with a grid scale of 1.0 Dp, resulting in a total of 6716 grid cells (Figure 10). The Delft3D Flexible Mesh is capable of more accurately representing the profile of the cylindrical bridge pier.

Figure 10.
Delft3D Flexible Mesh numerical simulation mesh.
In the case of the bridge project example presented in Section 2.3, a suspension mesh with a suspension ratio of 1:3 is employed, with the calculation area divided into three levels. The area where the bridge piers are located is a level 1 region. Each group of four piers constitutes a polygonal partition, resulting in a total of six mutually independent polygonal regions. The grid scale is 0.15 m, which is equivalent to one-ninth of the pier diameter of 1. The diameter of each pier must contain at least nine grid cells, ensuring that the grid scale for the first level of the region is three times that of the second level. The grid scale for the second level of the region is three times that of the third level. One or two regions outside the river are included in the third level of the region, with the grid scale for the second and third levels of the region being three times that of the level 2 areas. Figure 11 presents the suspension grid for each level of the bridge project example, and the zoomed-in image in the upper left corner clearly shows the variation between the levels. The total grid number is 122,043.
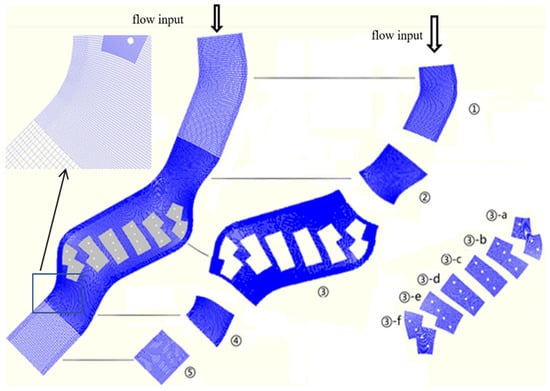
Figure 11.
Grid division of the bridge project example.
A variety of scenarios were subjected to numerical simulation in this study. In order to ensure the stability of the numerical simulation results, the length of the calculation period for the flume flow was unified to 20 min, with a calculation timestep of 0.0001 min. The length of the calculation period for the bridge project example was 12 h, with a calculation timestep of 0.001 min.
4. Results
4.1. Numerical Simulation of Flume Flow
4.1.1. Water Level
Table 4 presents the numerical simulation results for the water level upstream of the bridge pier and the upper boundary (section A-A) under three distinct numerical simulation schemes. Figure 12 presents the planar distribution of water level in the flume under various numerical simulation schemes. The data presented in the table indicate that the results of the R4 scheme and the suspended grid (DD Boundary) scheme are identical for the upstream of the bridge pier and for section A-A. In contrast, the results of the Delft-3D FM scheme are slightly larger.

Table 4.
Numerical simulation results of the water level.
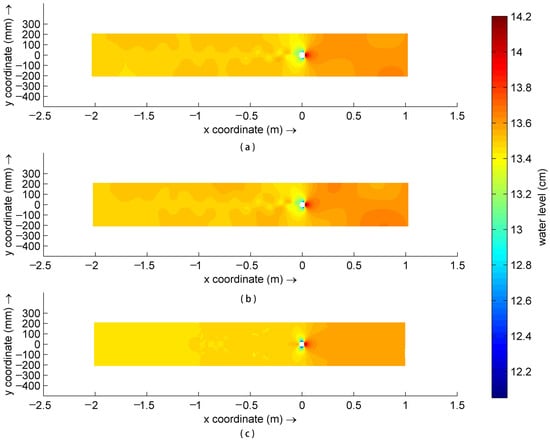
Figure 12.
Planar water level distribution under different numerical simulation schemes: (a) R4 scheme; (b) DD Boundary scheme; (c) Delft3D Flexible Mesh scheme.
4.1.2. Flow Pattern
Figure 13 presents the distribution of the planar flow pattern in the vicinity of the bridge pier under three distinct numerical simulation schemes. As illustrated in Figure 13, the numerical simulation results obtained using the R4 scheme and the suspended grid (DD Boundary) scheme are more accurate in reflecting the oscillation phenomenon of the tail current downstream of the bridge pier, as well as in reproducing the results of the physical model test. The numerical simulation yielded a Strouhal number of 0.22, which is in close agreement with the theoretical value of 0.21. The resolution of the flow distribution maps is slightly lower under the DD Boundary scheme due to the gradual reduction in the grid scale in the secondary and tertiary regions. However, the wake oscillations can still be clearly recognised. However, the computational results of the Delft3D FM scheme demonstrate a completely symmetric flow pattern, which is more consistent with the time-averaged flow pattern of the physical model (Figure 2a). This pattern does not capture the wake oscillations behind the bridge pier.
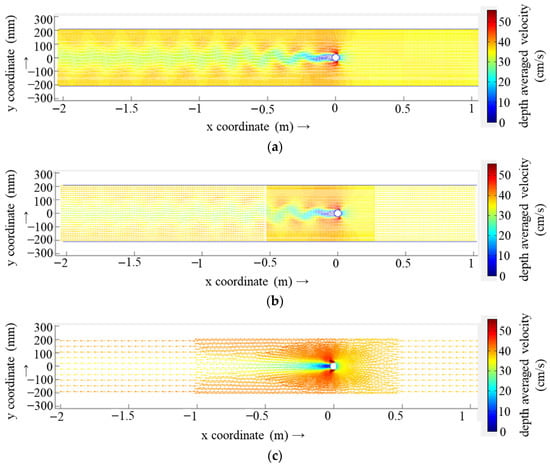
Figure 13.
Planar flow distribution under different numerical simulation schemes: (a) R4 scheme; (b) DD Boundary scheme; (c) Delft3D Flexible Mesh scheme.
The maximum flow velocities obtained from the numerical simulation and the discrepancies with the model test results for the three distinct numerical simulation schemes are presented in Table 5. As can be observed from the data presented in the table, the maximum flow velocity obtained from the numerical simulation was 55.7 cm/s for both the R4 scheme and the DD Boundary, which represents a difference of only 1.27% from the model test. The maximum flow velocity obtained from the Delft3D FM scheme was 51.1 cm/s, which is a discrepancy of −7.09% from the model test. The maximum flow velocity obtained from R4 and DD Boundary was more accurate.

Table 5.
Numerical simulation results of the maximum flow velocity.
4.1.3. Computational Efficiency
Table 6 presents the computational time required under distinct numerical simulation schemes. The data in the table indicate that the computation time under the DD Boundary scheme is 40 min, which is only one-twentieth of that of the R4 scheme. This is due to two factors: First, the total grid number in the DD Boundary scheme is 17,846, which is only one-eleventh of the total grid number in the R4 scheme (197,559). Second, the computation area is divided into five areas by the DD Boundary scheme. Conversely, in the suspended grid (DD Boundary) scheme, the computation area is divided into five regions by DD Boundary, with each region assigned a CPU core for parallel computation.

Table 6.
Calculation time of different numerical simulation schemes.
In the case of the Delft3D FM flexible mesh scheme, the total number of meshes is further reduced to 6716, but the computation time is 57 min, which is higher than that of the suspended mesh. The primary reason for this discrepancy is that the Delft3D FM scheme employs a distinct computational methodology from that of Delft3D, which necessitates enhanced computer performance.
The numerical simulation of flume flow presented above demonstrates that the suspended grid (DD Boundary) scheme exhibits clear advantages in all aspects, as evidenced by the comparison of water levels, flow patterns, and computational efficiency.
4.2. Example of a Bridge Project
Figure 14 presents a cloud diagram of the water level distribution in the river channel before and after the thickening of the bridge abutment piers. Figure 15 presents the distribution of the water level along the middle of the river channel before and after the thickening of the bridge abutment piers. Figure 16 presents the change in water level along the middle of the river channel before and after the thickening of the bridge abutment piers. As illustrated in the figures, the thickening of the bridge abutment results in an increase in the obstruction to the water flow, with the majority of the changes in the water level of the river channel occurring in the upstream section and in the section where the bridge abutment is located. The water level of the river channel upstream of the bridge abutment is demonstrably elevated. The greatest increase in water level is observed in the upstream section of the first set of bridge piers, with a rise of 30 cm. This localised rise is caused by congestion in front of the bridge piers and has no significant impact on flood control. It is of particular interest to note the maximum value of the water level rise in the upstream channel, which is 25 cm, occurring 50 m upstream of the bridge abutment. This has the greatest impact on the flood control of the river. As the river flows upstream, the water level in the river channel gradually decreases, while the water level at the upper boundary increases by 16 cm. There is no significant change in the water level in the river section downstream of the bridge abutment.
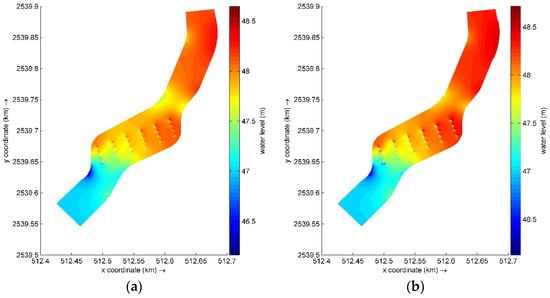
Figure 14.
Distribution of water level before and after thickening of the bridge pier: (a) pier diameter of 1.4 m; (b) pier diameter of 2.4 m.
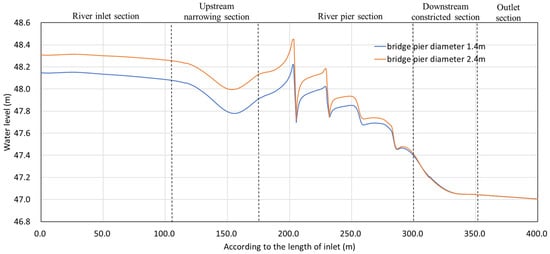
Figure 15.
Water level changes in the middle of the river channel before and after the thickening of the bridge pier.
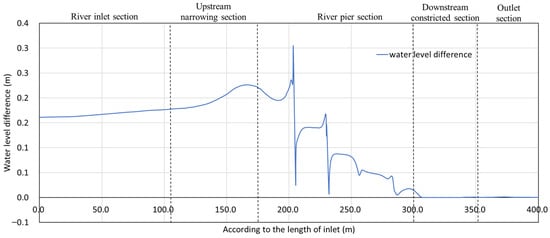
Figure 16.
Water level difference in the middle of the river channel before and after the thickening of the bridge pier (water level at pier diameter of 2.4 m − water level at pier diameter of 1.4 m).
Figure 17 presents a comparison of the cloud diagram of the flow velocity distribution in the river before and after the thickening of the bridge abutment. As illustrated in the figure, following the thickening of the bridge piers, the upstream section of the river, due to the increase in water depth, exhibits a slight reduction in flow velocity, with no discernible alteration in the flow velocity distribution pattern. In the vicinity of the bridge piers, the narrowing of the overwater cross-section between the piers resulted in a slight increase in local flow velocity. The water level in the downstream section remained unaltered, resulting in a correspondingly unchanging flow velocity distribution. It can thus be concluded that the thickening of the bridge abutment has the most significant impact on the water level upstream of the river. Further consideration must therefore be given to whether the upstream embankment is capable of meeting the requirements of flood control, in order to ensure regional safety. The results of the calculations demonstrate that the suspended grid scheme is an effective method for illustrating the changes in the water flow pattern before and after the thickening of the bridge abutment. This provides a basis for evaluating the engineering scheme. Our findings indicate that the numerical simulation method employed here is a suitable approach for the actual project.
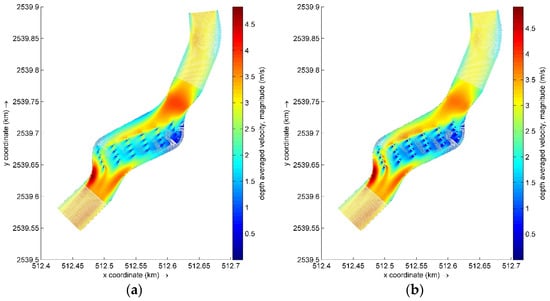
Figure 17.
Distribution of river flow velocity before and after thickening of the bridge pier: (a) pier diameter of 1.4 m; (b) pier diameter of 2.4 m.
5. Conclusions
This study employed physical model test data to analyse the influence of mesh size on water flow motion, utilising Delft3D. The numerical simulation scheme was optimised, with three schemes (i.e., mesh encryption in the overall calculation area, a suspended mesh technique, and a non-structural mesh method) being calculated and compared. The optimised scheme was then applied to an actual bridge project.
(1) This study demonstrated that the grid resolution has a significant effect on the calculation results when Delft3D is applied to the numerical simulation of bridge piers’ winding flow. For the area situated at a distance from the bridge pier, a grid size that is comparable to the diameter of the bridge pier (Dp) can be employed in order to accurately reflect the motion of the water flow. In the area close to the bridge pier, the mathematical model is unable to simulate the oscillation of the wake downstream of the bridge pier when the grid size is comparable to the pier diameter (Dp). Even the condition that the minimum grid size recommended by the user manual should not be less than 1/5 Dp is still on the conservative side. In order to obtain more optimal calculation results, it is recommended that the grid cell size in the vicinity of the bridge pier be less than or equal to 1/9 Dp.
(2) In the numerical simulation of bridge piers’ winding flow, the number of grid cells has a profound impact on the efficiency and economy of calculation. In addition to the computational scheme of using high-resolution grids for the entire computational area, Delft3D also allows for the use of suspended grid technology (DD Boundary) and unstructured grid models (Delft3D Flexible Mesh) to achieve local grid encryption. In the case of the bridge project example, a suspension mesh with a suspension ratio of 1:3 is employed, with the calculation area divided into three levels.The numerical simulation results of the three different schemes demonstrate that the suspended mesh technique (DD Boundary) can obtain highly consistent results with the full-area high-resolution mesh, even when the total number of meshes is reduced. The results are in close agreement with those of the physical model test. The suspended grid technology has the potential to significantly reduce the time required for computation. From one perspective, the reduction in the number of meshes results in a reduction in the computational effort required. Conversely, the DD Boundary is a domain decomposition technique that divides a model into several smaller model domains. Parallel computation can be performed on these domains, which can shorten the computation time of the model.
(3) The numerical simulation results of the non-structural mesh (Delft3D Flexible Mesh) scheme indicate that the total number of computational grid cells in this scheme is the smallest. However, the results demonstrate completely symmetric flow patterns, which are more consistent with the time-averaged flow patterns of the physical model (Figure 2a). Additionally, they do not capture the oscillating phenomenon of the tail flow behind the bridge pier. Conversely, the computational time consumption is relatively high. Given that the Delft3D Flexible Mesh technology is a relatively new development from Delft, it may require further investigation and research before it can be fully understood.
(4) The grid cell size of less than 1/9 Dp near the bridge pier, obtained from the flume flow calculation and the suspended mesh technology, was applied to the bridge engineering example. The numerical simulation results were employed to examine the patterns and alterations in the distribution of river flow velocity and water level distribution prior to and following the thickening of the bridge piers. Based on these findings, the study offers practical engineering suggestions. The practical engineering value of the scheme is proved.
(5) The findings of this study on grid resolution and the suspended grid scheme can be applied not only to the numerical simulation of a hydrodynamic study of a bridge abutment bypassing flow, but also to the hydrodynamic study of porous sluice gates on a river channel, high piling wharf on a bank, and so forth. The findings of this study provide a foundation for subsequent research on material transport processes influenced by water and sediment movement. Three-dimensional calculations are a promising avenue for further investigation. Additionally, the insights gained from this study have implications beyond Delft3D-Flow, offering technical guidance for the utilisation of other related numerical simulation software.
Author Contributions
Conceptualisation, X.L., Q.-S.C. and Z.D.; methodology, X.L.; software, Z.D.; validation, X.L. and Z.-N.Z.; formal analysis, X.L. and Z.-N.Z.; resources, Z.D.; data curation, X.L. and Z.-N.Z.; writing—original draft preparation, X.L. and Z.-N.Z.; writing—review and editing, Q.-S.C. and Z.D.; visualisation, X.L. and Z.-N.Z.; supervision, Z.D.; project administration, Z.D.; funding acquisition, Z.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Melville, B.W.; Raudkivi, A.J. Flow characteristics in local scour at bridge piers. J. Hydraul. Res. 1977, 15, 373–380. [Google Scholar] [CrossRef]
- Melville Bruce, W. Live-bed Scour at Bridge Piers. J. Hydraul. Eng. 1984, 110, 1234–1247. [Google Scholar] [CrossRef]
- Melville, B.W.; Sutherland, A.J. Design Method for Local Scour at Bridge Piers. J. Hydraul. Eng. 1988, 114, 1210–1226. [Google Scholar] [CrossRef]
- Ahmed, F.; Rajaratnam, N. Flow around Bridge Piers. J. Hydraul. Eng. 1998, 124, 288–300. [Google Scholar] [CrossRef]
- Tafarojnoruz, A.; Gaudio, R.; Dey, S. Flow-altering countermeasures against scour at bridge piers: A review. J. Hydraul. Res. 2010, 48, 441–452. [Google Scholar] [CrossRef]
- Melville Bruce, W. Pier and Abutment Scour: Integrated Approach. J. Hydraul. Eng. 1997, 123, 125–136. [Google Scholar] [CrossRef]
- Beheshti, A.A.; Ataie-Ashtiani, B. Experimental Study of Three-Dimensional Flow Field around a Complex Bridge Pier. J. Eng. Mech. 2010, 136, 143–154. [Google Scholar] [CrossRef]
- Tafarojnoruz, A.; Gaudio, R.; Calomino, F. Evaluation of Flow-Altering Countermeasures against Bridge Pier Scour. J. Hydraul. Eng. 2012, 138, 297–305. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Shrestha, C.K.; Zahedani, M.R.; Ball, J.; Khabbaz, H. Experimental study of flow structure around two in-line bridge piers. Proc. Inst. Civ. Eng. Water Manag. 2018, 171, 311–327. [Google Scholar] [CrossRef]
- Ettema, R.; Constantinescu, G.; Melville, B.W. Flow-Field Complexity and Design Estimation of Pier-Scour Depth: Sixty Years since Laursen and Toch. J. Hydraul. Eng. 2017, 143, 03117006. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Melville, B.; Ball, J. Three-dimensional analysis of coherent turbulent flow structure around a single circular bridge pier. Environ. Fluid Mech. 2014, 14, 821–847. [Google Scholar] [CrossRef]
- Pagliara, S.; Carnacina, I. Bridge pier flow field in the presence of debris accumulation. Proc. Inst. Civ. Eng. Water Manag. 2013, 166, 187–198. [Google Scholar] [CrossRef]
- Vijayasree, B.A.; Eldho, T.I.; Mazumder, B.S.; Ahmad, N. Influence of bridge pier shape on flow field and scour geometry. Int. J. River Basin Manag. 2019, 17, 109–129. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Yang, Z. Influence of Scour Development on Turbulent Flow Field in Front of a Bridge Pier. Water 2020, 12, 2370. [Google Scholar] [CrossRef]
- Jenssen, U.; Manhart, M. Flow around a scoured bridge pier: A stereoscopic PIV analysis. Exp. Fluids 2020, 61, 217. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W.H. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef]
- Richardson John, E.; Vijay, G.P. Three-Dimensional Simulation of Scour-Inducing Flow at Bridge Piers. J. Hydraul. Eng. 1998, 124, 530–540. [Google Scholar] [CrossRef]
- Tseng, M.-H.; Yen, C.-L.; Song, C.C.S. Computation of three-dimensional flow around square and circular piers. Int. J. Numer. Methods Fluids 2000, 34, 207–227. [Google Scholar] [CrossRef]
- Chang, W.-Y.; Constantinescu, G.; Lien, H.-C.; Tsai, W.-F.; Lai, J.-S.; Loh, C.-H. Flow Structure around Bridge Piers of Varying Geometrical Complexity. J. Hydraul. Eng. 2013, 139, 812–826. [Google Scholar] [CrossRef]
- Ali, K.H.M.; Karim, O. Simulation of flow around piers. J. Hydraul. Res. 2002, 40, 161–174. [Google Scholar] [CrossRef]
- Salaheldin, T.M.; Imran, J.; Chaudhry, M.H. Numerical Modeling of Three-Dimensional Flow Field Around Circular Piers. J. Hydraul. Eng. 2004, 130, 91–100. [Google Scholar] [CrossRef]
- Cui, W.; Zhang, X.; Li, Z.; Li, H.; Liu, Y. Three-dimensional numerical simulation of flow around combined pier based on detached eddy simulation at high Reynolds numbers. Int. J. Heat Technol. 2017, 35, 91–96. [Google Scholar] [CrossRef]
- Nasim, M.; Setunge, S.; Zhou, S.; Mohseni, H. An investigation of water-flow pressure distribution on bridge piers under flood loading. Struct. Infrastruct. Eng. 2019, 15, 219–229. [Google Scholar] [CrossRef]
- Lahsaei, K.; Vaghefi, M.; Sedighi, F.; Chooplou, C.A. Numerical simulation of flow pattern at a divergent pier in a bend with different relative curvature radii using ansys fluent. Eng. Rev. 2022, 42, 63–85. [Google Scholar] [CrossRef]
- Ghasemi, M.; Soltani-Gerdefaramarzi, S. The Scour Bridge Simulation around a Cylindrical Pier Using Flow-3D. J. Hydrosci. Environ. 2017, 1, 46–54. [Google Scholar]
- Jafari, M.; Ayyoubzadeh, S.A.; Esmaeilivaraki, M.; Rostami, M. Simulation of Flow Pattern around Inclined Bridge Group Pier using FLOW-3D Software. Water Soil 2017, 30, 1860–1873. [Google Scholar]
- Jalal, H.K.; Hassan, W.H. Three-dimensional numerical simulation of local scour around circular bridge pier using Flow-3D software. IOP Conf. Ser. Mater. Sci. Eng. 2020, 745, 012150. [Google Scholar] [CrossRef]
- Man, C.; Zhang, G.; Hong, V.; Zhou, S.; Feng, Y. Assessment of turbulence models on bridge-pier scour using Flow-3D. World J. Eng. Technol. 2019, 7, 241–255. [Google Scholar] [CrossRef]
- Cetina, M.; Krzyk, M. A Depth-Averaged Mathematical Model of a River Flow around Bridge Piers; WIT Press: Cambridge, MA, USA, 2002; Volume 52. [Google Scholar]
- Duan, J.G. Two-Dimensional Model Simulation of Flow Field around Bridge Piers. Impacts of Global Climate Change. 2005, pp. 1–12. Available online: https://ascelibrary.org/doi/abs/10.1061/40792%28173%29449 (accessed on 13 June 2024).
- Wang, W.; Zhou, K.; Jing, H.; Zuo, J.; Li, P.; Li, Z. Effects of Bridge Piers on Flood Hazards: A Case Study on the Jialing River in China. Water 2019, 11, 1181. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, T.; Duan, B. Study on the effect of morphological changes of bridge piers on water movement properties. Water Pract. Technol. 2021, 16, 1421–1433. [Google Scholar] [CrossRef]
- Xiong, H.; Chen, L.; Sun, Z.; Li, Z.; Zhou, K.; Chen, Z. Simulating the impact of piers on hydrodynamics and pollutant transport: A case study in the Middle Yangtze River. PLoS ONE 2021, 16, e0260527. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Huang, S.; Zhu, L. Complex response of tidal flow to multiple bridges in Qiantang River. J. Sichuan Univ. Eng. Sci. Ed. 2007, 39, 10. [Google Scholar]
- Chu, X.; Tang, H.; Yuan, S.; Chen, J. Effects of a group of bridges on flood and tide control of Yongjiang River. J. Hohai Univ. (Nat. Sci.) 2015, 42, 223–229. [Google Scholar]
- Jun, C.; Yu, M.; Deng, L.; Lu, Y. Cumulative influence of bridge and wharf engineering groups on flood propagation in tidal rivers. Adv. Sci. Technol. Water Resour. 2021, 41, 49–56. [Google Scholar]
- Abdou, A.; Valero, D.; Crosato, A. Large-Scale Morphodynamic Impact of Groups of Piers on Low-Land Rivers. In Proceedings of the 8th International Junior Researcher and Engineer Workshop on Hydraulic Structures (IJREWHS 2021), Galway, Ireland, 5–8 July 2021. [Google Scholar] [CrossRef]
- Deltares, Delft3D-FLOW User Manual. 2017, pp. 182–185. Available online: https://download.deltares.nl/delft3d-4-suite (accessed on 13 June 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).