Abstract
Local regulations control the additional runoff produced by urbanization processes. Sustainable urban drainage systems can mitigate the issues associated with increased runoff by employing infiltration basins, detention ponds, wet ponds, and constructed wetlands. Traditionally, the Water Level Pool Routing Method, which relies on an implicit calculation scheme, has been used to calculate outflow hydrographs in reservoirs. In this research, an explicit scheme for the Water Level Pool Routing Method has been developed. The proposed model is applied to a case study where the reservoir has a surface area of 9.12 hectares. The influence of weir width and the discharge coefficient is also analyzed. Additionally, the variation in time step does not significantly affect the response of the proposed model, demonstrating its adequacy as a novel method. The proposed model is compared to the traditional method, yielding similar results in an analyzed ornamental reservoir (low percentage reduction in peak flow). However, a case study with experimental data reveals that the proposed model provides better accuracy than the traditional method. In addition, the proposed model is more efficient as it reduces computational time compared to the implicit scheme (conventional method). Finally, the proposed model is simplified for small watersheds by applying the rational method for computing an inflow hydrograph.
1. Introduction
Reservoirs serve as permanent or temporary storage systems that regulate peak flows, making it essential to have a straightforward tool for their analysis. These structures are commonly used to reduce the maximum water flows of inflow hydrographs in engineering projects such as dams [1], sustainable urban drainage systems [2], and others. A suitable reservoir routing technique is required for computing an outflow hydrograph [3,4], which depends on discharge hydraulic structures [5,6], the relation of storage versus water level, and an inflow hydrograph.
Outflow hydrographs can be estimated using hydraulic or hydrological routing techniques [7,8,9]. Hydraulic routing methods can be applied regardless of the shapes and longitudinal slopes of reservoirs, as the numerical solution is derived using the Saint-Venant equations [10,11,12], which consider local and convective accelerations and friction slopes. To achieve accurate numerical resolution, reservoirs should be divided with an appropriate selection of spatial and time steps. The larger the spatial steps, the greater the computational time required during simulations. Consequently, hydraulic methods demand more computational time compared to hydrological methods.
When reservoirs can be considered with a circular surface area, and the inverted elevation along them remains practically constant, the water surface elevation tends to be uniform within the reservoirs, forming what is known in the literature as a water level pool [9,13]. Under this assumption, outflow hydrographs can be estimated using hydrological routing methods. However, if large reservoirs have significant longitudinal slopes, then, hydrological routing methods are unsuitable for computing outflow hydrographs.
Typically, reservoirs are modeled using hydrological methods since they do not cover large surface areas. Nematollahi et al. (2001) [9] proposed analytical and numerical solutions using different shapes of inflow hydrographs. Some investigations have presented the disadvantages of employing the numerical resolution of Laurenson–Pilgrim, fourth-order Runge–Kutta, and fixed-order Cash–Karp methods [14], where the time step should be carefully selected to avoid computational problems. Guang et al. (2009) [15] developed a Runge–Kutta–Fehlberg-Reverse method for routing reservoir floods. Several authors have created many schemes for numerical resolution for reservoir routing considering different shapes of inflow hydrographs [16]. Other studies have focused on the numerical resolution of risk analysis in reservoir routings considering different conditions [16]. These numerical resolutions are based on implicit scheme methods for reservoir routings.
An explicit scheme was recently proposed by the authors for channel routing [17], which simplifies calculations compared to the traditional methods known as Kinematic Wave [18], Muskingum [19], and Muskingum–Cunge [20,21] This method saves computational time compared to traditional ones, as conventional methods employ an implicit scheme for computing an outflow hydrograph using three formulations (water-surface-elevation–storage relation, weir discharge rating curve, and storage–outflow function) [9]. In contrast, the proposed model uses only one equation for this computation: the hydraulic head over a weir crest.
This research presents the development of an explicit scheme for reservoir routing considering a hydrological or lumped analysis. The numerical resolution of the proposed model is conducted using Newton’s binomial theorem [22] and considering a rectangular weir as a discharge outlet. The resolution is also performed for small watersheds by applying the rational method, which can be used to determine the percentage of attenuation in a selected reservoir. A case study located in Cartagena de Indias, Colombia, is presented to show the proposed model’s advantages. The proposed model is compared with the traditional reservoir methods named the water level pool [11], where both methods practically give the same outflow hydrographs for the different analyzed scenarios considering a reservoir for ornamental purposes. During the validation stage, the proposed model demonstrates better accuracy than the traditional method, using the input data provided by De Martino et al. (2012) [23] as the case study. Experimental data are important for calibration purposes considering steady and unsteady flow conditions [24,25].
2. Materials and Methods
This section presents the damping effect generated by a reservoir when an inflow hydrograph is passing through it. A rectangular weir is considered as the discharge structure. Figure 1a,b describe inflow () and outflow () hydrographs in a reservoir for the times and , respectively. An analyzed reservoir maintains a constant surface area and a horizontal water surface. Figure 1c illustrates a schematic of an inflow hydrograph, where a linear increasing trend for demonstration purposes has been considered. This trend can vary in shape based on the morphometric characteristics of watersheds. A frontal view of an uncontrolled rectangular overflow is presented in Figure 1d.
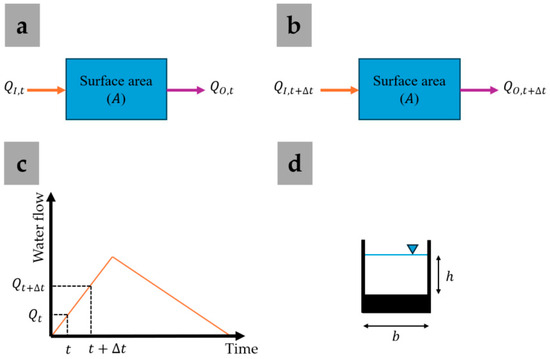
Figure 1.
Components of a system: (a) relationship between and at time ; (b) relationship between and at time ; (c) water flow hydrograph; and (d) rectangular weir.
2.1. Proposed Model
2.1.1. Assumptions
The proposed model has the following assumptions:
- A horizontal water surface is considered in a reservoir.
- The conservation of mass equation is used for considering inflow and outflow hydrographs.
- The discharge curve is evaluated using a rectangular weir.
2.1.2. General Governing Equations
When considering the inflow volume of water () into a reservoir over intervals of duration and comparing it to the outflow volume () within the same time interval, the following relationship can be established:
where = inflow hydrograph occurring at times and , and = outflow hydrograph occurring at times and .
By applying the conservation of mass equation, Equation (3) can be derived, which serves to calculate the increase or decrease in water surface () within a reservoir for a time interval ():
where = surface area.
The outlet discharge depends on the selected hydraulic structure, such as a morning glory spillway, drop inlet spillway, culvert structure, or controlled and uncontrolled ogee crest [1]. In this case, the outlet discharge is represented by a rectangular weir. Thus,
where = discharge coefficient, = width of weir crest measured perpendicular to the main direction of the flow, and = hydraulic head measured over a weir crest.
The discharge coefficient depends on several factors: the hydraulic head measured over a weir crest, the relationship between the crest and ideal nappe shapes, tailwater conditions, downstream submergence, and the sloping upstream face.
In order to determine the values of an outflow hydrograph at times and in relation to water surface levels and , the following procedure is employed:
Utilizing Newton’s binomial theorem and disregarding terms beyond the third, the computation proceeds as follows:
where = power of the final term in the binomial theorem
Substituting Equation (7) into Equation (3) and arranging the terms yields:
2.2. Solution for Small Watersheds
The computation of inflow hydrographs for small watersheds can be established considering a triangular hydrograph, as shown in Figure 2. The peak flow () is occurring at peak time (), while the base time () depends on the value of . The value of in mountainous basins results in a shorter hydrograph duration compared to that of normal gravel rivers.
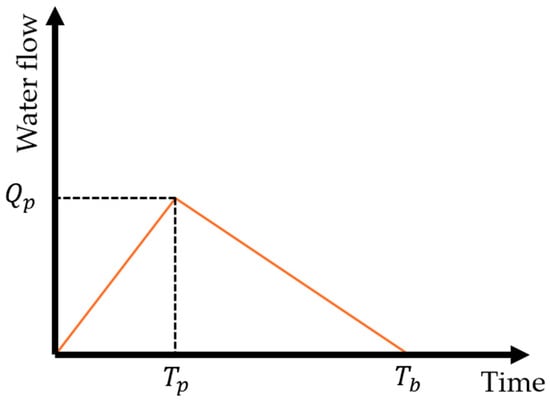
Figure 2.
Characteristics of a triangular hydrograph.
The direct runoff volume of the triangular hydrograph can be determined by evaluating the excess rainfall () over a watershed with a drainage area . Subsequently, the peak flow can be expressed as follows:
If Equation (9) is reformulated with in hectares (ha), in millimeters (mm), and in hours (h), it takes the following form:
The dimensionless peak flow () is given as follows:
2.3. Methodology
The objective of this research is to develop an Explicit Water Level Pool Method (EWLPM) for reservoir routing, which can be used as a new approach for practical applications. The proposed methodology consists of five steps, as illustrated in Figure 3.
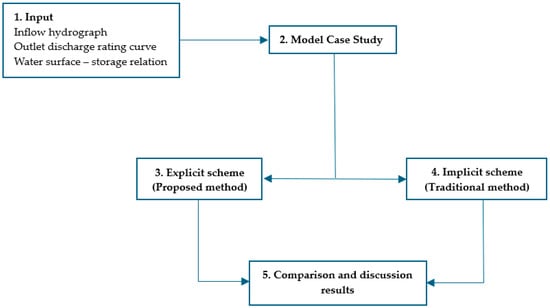
Figure 3.
Methodology.
The input data for the case study are defined in Section 3. The proposed methodology can be applied to reservoir routing in any watershed, representing a general development. The EWLPM was developed as presented in Section 2. The implicit scheme was simulated using the traditional method, Implicit Water Level Pool Routing (IWLPR). Section 4 and Section 5 present a comparison and discussion of the results of the EWLPM and IWLPM.
3. Case Study
The case study was obtained from a report conducted by Ecociencias for the Environmental Agency of the area, known as CARDIQUE (Corporación Autónoma del Canal del Dique) [26]. Figure 4 illustrates the general location of the city of Cartagena de Indias, as well as the location of the neighborhood Barcelona de Indias (Figure 4a). The reservoir is situated within the neighborhood of Barcelona de Indias, encompassing a surface area of 9.12 ha (Figure 4b). Additionally, aerial photographs numbered 000009, 000010, 000011, 000012, 000013, 000047, 000048, 000049, 000050, 000051, 000064, 000065, and 000066 from flight C-2714 and photographs numbered 000064, 000065, and 000066 from flight C-2722, taken in 2004, were sourced from the Agustín Codazzi Geographic Institute (IGAC) [27]. Cartographic maps numbered 23-II-A, 23-I-D, 23-II-C, 23-II-D, 23-I-D, 23-III-B, 23-II-C, 23-III-D, 23-IV-A, and 23-IV-A at a scale of 1:25,000 were also utilized (Figure 4c).
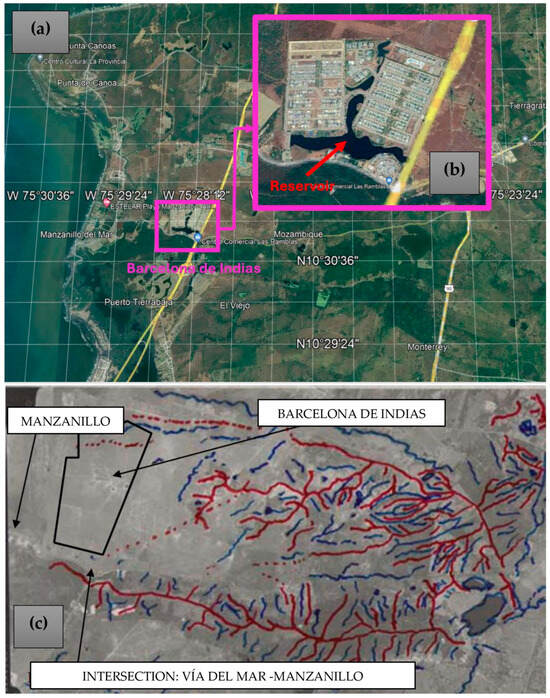
Figure 4.
Location of the case study: (a) general location of the city of Cartagena, Colombia; (b) location of the neighborhood Barcelona de Indias; and (c) aerial photographs for delineation of the watershed.
The case study is in Cartagena, specifically in the northern region, between the entrance to the neighborhood of Manzanillo del Mar and parallel to the road known as Vía del Mar. According to the topography of the area, it is observed that the watershed has a drainage area of 1388 ha. The watershed discharge is perpendicular to the road Vía del Mar.
The selected rainfall intensities ranged from 82.5 to 125.9 mm/h for the four sub-basins of the case study, considering a return period of 100 years. The outflow hydrograph was computed for a 100-year return period, which was determined at the entrance of the reservoir in the project’s technical report [28]. Figure 5 shows the results of the inflow hydrograph. The peak flow is 97.72 m3/s, which occurs at 1.5 h. The base time of the inflow hydrograph is 4.3 h.
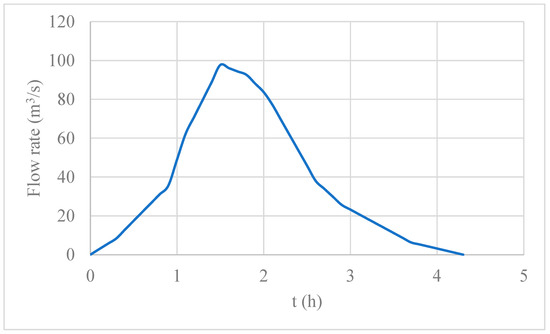
Figure 5.
Inflow hydrograph.
According to the results of the topography and bathymetry of the reservoir, it currently has an average depth of 1.95 m. The crest of the outlet structure is located at 2.50 m a.s.l. The outlet weir has a width of 80 m.
4. Results
The proposed model was applied to perform a water level pool routing in the reservoir situated in the neighborhood of Barcelona de Indias, Cartagena (Colombia), as outlined in Section 3. The analysis incorporated the following data: discharge coefficient () 1.42, a weir width () of 80 m, and a reservoir surface area () of 9.12 ha. A time step () of 0.1 h was used during simulations. The analysis was carried out with the crest elevation considered at 2.50 m a.s.l. The inflow hydrograph is illustrated in Figure 4. Figure 6 displays the outcomes of applying the proposed model in this study. The peak value of the outflow hydrograph is 92.58 m3/s (occurring at 1.8 h). The highest water level in the reservoir reaches 0.872 m, which is calculated concerning the crest elevation. The total discharge occurs over a period exceeding 5 h. Appendix A shows the numerical results for the case study, where maximum values are highlighted in gray. An explanation of all columns is presented below in Appendix A. This simulation is identified as a baseline since it is compared to other ones in the following sections.
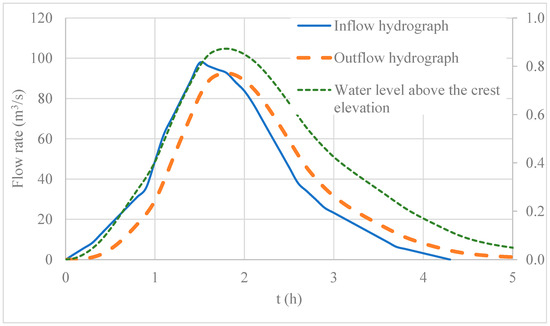
Figure 6.
Outflow hydrograph and water level inside the reservoir.
A sensitivity analysis was conducted to ascertain the influence of weir width () and discharge coefficient () when the proposed model is applied. The variation in parameters is shown in Table 1, while the obtained results of the outflow hydrograph are presented in Figure 7.

Table 1.
Range of parameters.
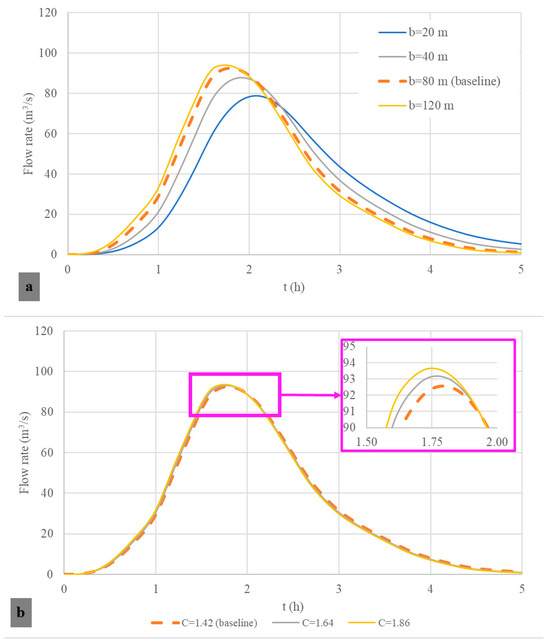
Figure 7.
Sensitivity analysis for the water level pool routing: (a) weir width; and (b) discharge coefficient.
As expected, the weir width significantly influences the outflow hydrograph, as depicted in Figure 7a. The greater the weir width, the higher the maximum value of the outflow hydrograph, which implies a lower capacity for flood control. For instance, with a weir width of 120 m, a peak flow of 93.97 m3/s is reached, close to the inflow hydrograph’s maximum value (97.72 m3/s). In contrast, when a weir width of 20 m is selected, the reservoir can reduce the maximum value of the inflow hydrograph by 19.4%, achieving a peak value of 78.73 m3/s. The selection of weir width also influences the occurrence of peak times for the outflow hydrograph. The narrower the weir width, the higher the peak times obtained. Figure 7b illustrates the results obtained by varying the discharge coefficient of the weir between 1.42 and 1.86. In this case, no significant variations are detected since the purpose of the reservoir is ornamental and not intended for flow reduction as the weir width is 80 m, and the outflow hydrograph is not reduced in a high percentage as shown in Figure 5. Based on the higher value of the discharge coefficient, the maximum values of the outflow hydrograph are computed. The discharge coefficient does not significantly affect the results, as the weir’s large width produces a low percentage of reduction in the peak inflow hydrographs.
5. Discussion
5.1. Proposed Model
This section focuses on two aspects: (i) varying the time step for running the analyzed parameters in the baseline simulation; and (ii) comparing the proposed model’s results with the traditional method for performing a water level pool routing in the case study.
The time step ranged from 0.05 to 0.5 h; the results are depicted in Figure 8. A linear interpolation was used to compute the inflow hydrograph, adjusting for the varying time steps, as shown in Figure 4. This interpolation method was also applied to calculate the outflow hydrograph, ensuring consistency in the time step used for computations. Most simulations tend to produce a similar outflow hydrograph in comparison to the baseline simulation. The worst results were obtained using a time step of 0.5 h, as this represents a high time step in comparison to the values of the inflow hydrograph. This is of utmost importance since time steps should be suitably selected. However, the peak flow for a time step of 0.5 h was 92.53 m3/s (occurring at 2 h), which can be compared to the peak flow reached in the baseline simulation of 92.58 m3/s (occurring at 1.8 h). This robust performance of the proposed model confirms its potential impact in the field of hydrological modeling.
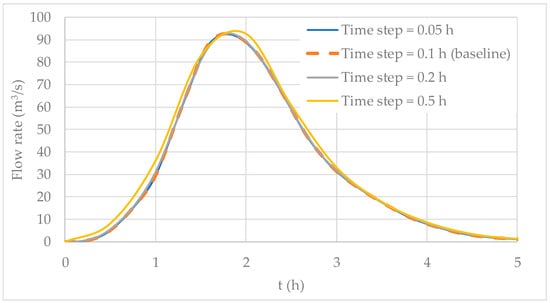
Figure 8.
Analysis of time step using the proposed model.
The IWLPM was applied to validate the proposed model. The numerical resolution of IWLPM requires the solution of the two following formulations:
- The conservation of mass equation given bywhere = storage in a reservoir.
- The storage–outflow function expressed as follows:
Applying IWLPM requires computing the water-surface-elevation–storage relation, the weir discharge rating curve, and the storage–outflow function. These were calculated using the data for the baseline problem (see Section 4). The results are presented in Figure 9.
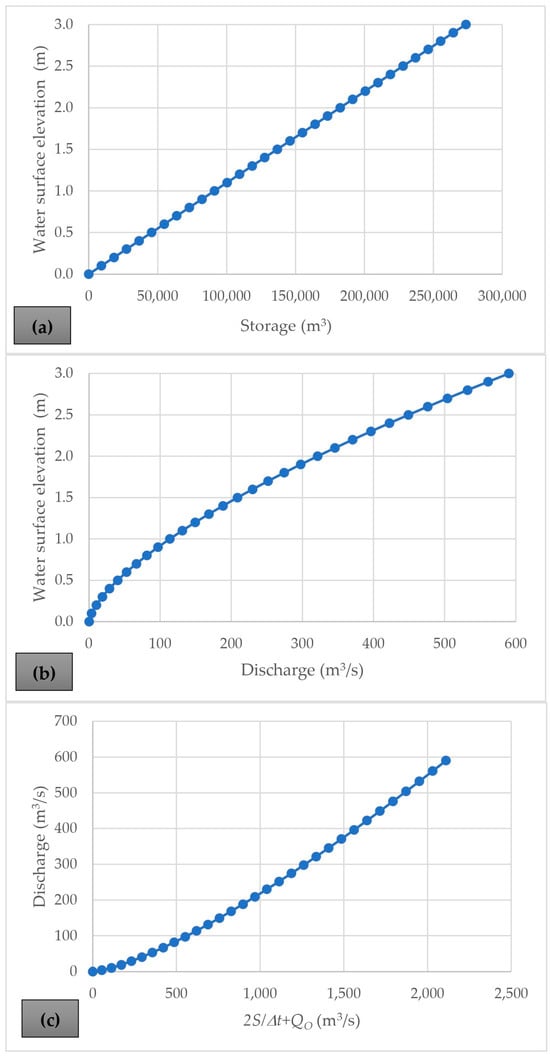
Figure 9.
Assessing the storage–outflow relation: (a) water-surface-elevation–storage relation; (b) weir discharge rating curve; and (c) storage–outflow function.
Figure 10 compares the EWLPM (proposed model) and the IWLPM. The results confirm that the proposed model is suitable for simulating water level pool routing since both outflow hydrographs are similar. EWLPM is easier to implement compared to the IWLPM and requires less computational time. For this practical application, the IWLPM takes around 0.04 s, while the EWLPM takes values lower than 0.01 s.
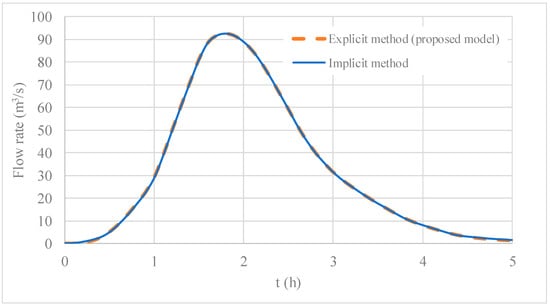
Figure 10.
Comparison of the outflow hydrograph considering the explicit (proposed model) and implicit methods for water level pool routing.
The Root Mean Square Error () and the R-squared () were calculated to check the adequacy of the proposed model, using the following formulas:
where = computed values of the outflow hydrograph using the proposed model (EWLPM), = calculated values of the outflow hydrograph using IWLPM, and = total number of analyzed water flows of the outflow hydrograph.
where = sum of squares of residual ( and ), and = total sum of squares of the analyzed variable . The obtained values of and are 0.16 m3/s and 0.9999, respectively. These results confirm that the proposed model can be used as an alternative method for computing water level pool routing.
Figure 11 presents the dispersion graph related to the outflow hydrograph. The proposed model (EWLPM) can replicate the results of the IWLPM, as most computed values align with the orange line, indicating a suitable adjustment.
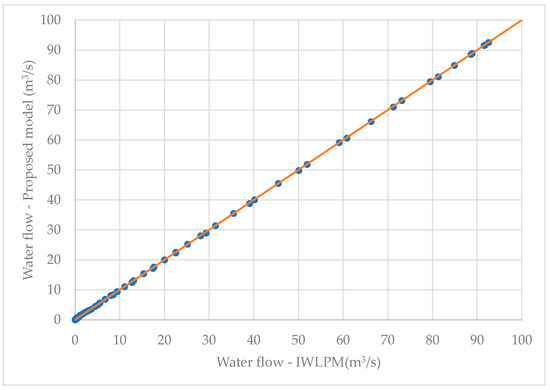
Figure 11.
Dispersion graph of the outflow hydrograph (EWLPM—proposed model—versus IWLPM).
5.2. Solution for Small Watersheds
For this specific solution, the authors have considered . Equation (16), which defines the final shape of outflow hydrographs, can be used to establish a practical solution for small watersheds. This Equation can compute the variation in the water surface level over the crest of a weir and its corresponding water flow.
Substituting Equation (11) into Equation (8), the following is obtained:
where = parameter that defines the percentage of reduction in an outflow hydrograph, which depends on surface area, width of a weir, discharge coefficient, and time step.
The parameter is expressed as follows:
Figure 12 shows the results based on the proposed methodology. The parameter was varied from 1 to 20 to compare different percentages of reduction in outflow hydrographs. This variation is a function of the surface area of a reservoir, weir width, discharge coefficient, and time step.
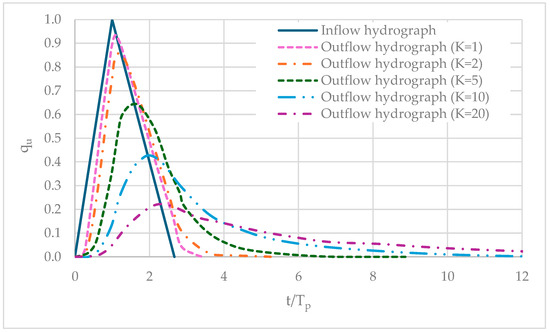
Figure 12.
Representation of the triangular unit inflow hydrograph and outflow hydrographs as a function of the parameter .
5.3. Validation
The validation of the proposed model using experimental data was conducted with measurements by De Martino et al. (2012) [23]. The hydraulic system comprises a gate valve to control the inflow hydrograph, a reservoir with a surface area of 29.12 m2, and a flood gate for outflow discharge. The inflow hydrograph was generated and recorded within the reservoir system. The stage-area curve, accounting for a floodplain, was used for analysis, implying that Configuration 1 from De Martino et al. (2012) [23] was analyzed.
The outlet discharge occurred through a floodgate system with a width () of 0.45 m and a gate height () of 0.05 m. For the discharge structure, a gate discharge coefficient () of 0.645 was employed, as this value was determined during the calibration process [23]. Considering the outflow discharge structure, the hydraulic modeling utilized an orifice discharge approach:
Following a similar procedure to that described in Section 2.1, it is possible to demonstrate that the change in the water surface can be computed as follows:
The measured inflow and outflow hydrographs are presented in Figure 13. Additionally, the proposed model, utilizing Equation (19), was compared with the traditional implicit scheme for computing the outflow hydrograph, also shown in Figure 13. The results indicate that the explicit method (proposed model) provides superior results compared to the implicit method, as it predicts the peak outflow more accurately and better captures the hydrograph patterns.
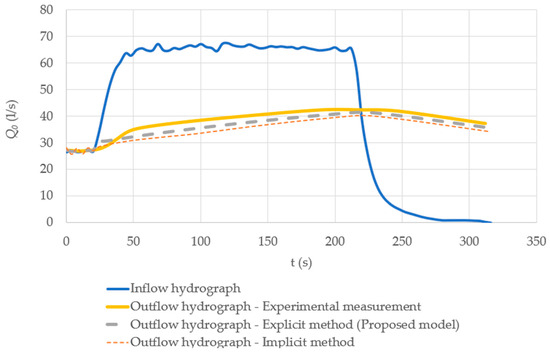
Figure 13.
Comparison of outflow hydrographs: experimental measurements versus calculated results from EWLPM (explicit method) and IWLPM (implicit or traditional method).
5.4. Limitations of the Proposed Model
This section presents the limitations of the EWLPM as follows: (i) it cannot be applied to large surface areas where longitudinal bed slopes can produce a non-water surface pool level; (ii) for outlet discharge structures other than rectangular weirs, Equation (8) needs to be reformulated as presented in Section 5.3; and (iii) rain-runoff models must be applied to compute inflow hydrographs.
6. Conclusions
The Water Level Pool Routing Method has been utilized to understand the movement of an inflow hydrograph within a reservoir, ultimately determining the corresponding outflow hydrograph. This method can be applied to spillways, wetlands, ponds, and similar hydraulic structures. Traditionally, the technique involves an implicit numerical resolution scheme.
This research presents the development of an Explicit Water Level Pool Routing Method with a numerical resolution that avoids numerical stability issues. The proposed model uses straightforward equations and does not demand significant computational resources. It can be employed to determine an appropriate weir width in a reservoir based on its function and the desired reduction percentage in the outflow hydrograph. Although the proposed model was developed with a rectangular weir (an economical solution for urban areas), it can be extended to different hydraulic structures.
The efficiency of the proposed model is demonstrated in a practical case study of a reservoir near Barcelona de Indias, Cartagena (Colombia), with a surface area of 9.1 ha. All numerical calculations are provided, enabling engineers to readily apply the proposed model. The model’s performance is evaluated by varying the weir width and discharge coefficient. Notably, changes in the time step do not significantly alter the results, affirming the robustness of the proposed model. A comparison with the traditional method (implicit resolution scheme) reveals that both methods exhibit similar behaviors in the analyzed outflow hydrograph.
Furthermore, the proposed model is adapted for small watersheds, where a triangular unit inflow hydrograph is used to compute outflow hydrographs. The model takes into account the reservoir’s surface area, weir width, discharge coefficient, and time step, providing a comprehensive tool for water resource management in these areas.
The model for small watersheds presented in this research corresponds to a specific scenario but can be extended to accommodate any morphometric characteristics of basins.
Future research should focus on developing practical formulas for different shapes of inflow hydrographs for small watersheds, such as the modified rational method.
Author Contributions
Conceptualization, A.A.-P.; methodology, A.A.-P., and O.E.C.-H.; validation, A.A.-P.; formal analysis, A.A.-P., O.E.C.-H., and V.S.F.-M.; writing—original draft preparation, A.A.-P., and O.E.C.-H.; supervision, V.S.F.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research project did not receive external or internal funding.
Data Availability Statement
Data may be acquired by contacting the corresponding author (A.A-P.).
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
The following abbreviations were used in this manuscript:
| : | surface area of a reservoir (m2) |
| : | drainage area of a watershed (ha) |
| : | Weir width (m) |
| : | discharge coefficient of a weir |
| : | hydraulic head measured over the weir crest (m) |
| : | parameter that defines the percentage of reduction in an outflow hydrograph |
| power of the final term in the binomial theorem (-) | |
| : | total number of analyzed water flows of an outflow hydrograph (-) |
| : | storage in a reservoir (m3) |
| : | time (s) |
| : | base time of a hydrograph (s) |
| : | peak time of a hydrograph (s) |
| : | base time of a hydrograph (s) |
| : | amount of precipitation (mm) |
| Root Mean Square Error (m3/s) | |
| : | R-squared (-) |
| : | sum of squares of residual (m6/s2) |
| : | dimensionless peak flow (-) |
| : | inflow hydrograph (m3/s) |
| : | outflow hydrograph (m3/s) |
| : | peak flow (m3/s) |
| : | total sum of squares of the analyzed variable (m6/s2) |
| : | inflow volume of water (m3) |
| : | outflow volume of water (m3) |
| : | time step (s) |
| : | variation in water surface (m) |
Appendix A

Table A1.
Numerical results for the case study.
Table A1.
Numerical results for the case study.
| t (h) [1] | (m3/s) [2] | (m) [3] | (m) [4] | (m3/s) [5] |
|---|---|---|---|---|
| 0 | 0.00 | 0 | 0.0055 | 0.0000 |
| 0.1 | 2.79 | 0.006 | 0.0159 | 0.046 |
| 0.2 | 5.58 | 0.021 | 0.0249 | 0.357 |
| 0.3 | 8.37 | 0.046 | 0.0350 | 1.133 |
| … | … | … | … | … |
| 1.4 | 88.87 | 0.7334 | 0.0676 | 71.232 |
| 1.5 | 97.72 | 0.800 | 0.0472 | 81.318 |
| 1.6 | 96.03 | 0.847 | 0.0198 | 88.619 |
| 1.7 | 94.34 | 0.867 | 0.0053 | 91.741 |
| 1.8 | 92.65 | 0.872 | −0.0065 | 92.580 |
| … | … | … | … | … |
| 5.0 | 0.00 | 0.049271 | −0.0046 | 1.242 |
Notes: column [1] represents the time; column [2] is the inflow hydrograph (Figure 4); column [3] is computed as ; column [4] is calculated using Equation (8); and column [5] is computed using Equation (5). The numbers highlighted in color indicate the maximum values.
References
- Crookston, B.M.; Erpicum, S. Hydraulic Engineering of Dams. J. Hydraul. Res. 2022, 60, 184–186. [Google Scholar] [CrossRef]
- D’Ambrosio, R.; Longobardi, A.; Schmalz, B. SuDS as a Climate Change Adaptation Strategy: Scenario-Based Analysis for an Urban Catchment in Northern Italy. Urban Climb 2023, 51, 101596. [Google Scholar] [CrossRef]
- Kim, B.; Sanders, B.F. Dam-Break Flood Model Uncertainty Assessment: Case Study of Extreme Flooding with Multiple Dam Failures in Gangneung, South Korea. J. Hydraul. Eng. 2016, 142, 05016002. [Google Scholar] [CrossRef]
- Dotson, H.W. Watershed Modeling with HEC-HMS (Hydrologic Engineering Centers-Hydrologic Modeling System) Using Spatially Distributed Rainfall. In Coping with Flash Floods; Springer: Berlin/Heidelberg, Germany, 2001; pp. 219–230. [Google Scholar]
- Gabriel-Martin, I.; Sordo-Ward, A.; Garrote, L.; Granados, I. Hydrological Risk Analysis of Dams: The Influence of Initial Reservoir Level Conditions. Water 2019, 11, 461. [Google Scholar] [CrossRef]
- Bruwier, M.; Erpicum, S.; Pirotton, M.; Archambeau, P.; Dewals, B.-J. Assessing the Operation Rules of a Reservoir System Based on a Detailed Modelling Chain. Nat. Hazards Earth Syst. Sci. 2015, 15, 365–379. [Google Scholar] [CrossRef]
- Todini, E. Hydraulic and Hydrologic Flood Routing Schemes. In Recent Advances in the Modeling of Hydrologic Systems; Bowles, D.S., O’Connell, P.E., Eds.; Springer: Dordrecht, The Netherlands, 1991; pp. 389–405. [Google Scholar] [CrossRef]
- Fenton, J.D. Flood Routing Methods. J. Hydrol. 2019, 570, 251–264. [Google Scholar] [CrossRef]
- Nematollahi, B.; Niazkar, M.; Talebbeydokhti, N. Analytical and Numerical Solutions to Level Pool Routing Equations for Simplified Shapes of Inflow Hydrographs. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 3147–3161. [Google Scholar] [CrossRef]
- Theodor, S. Numerical Solution of Saint-Venant Equations. J. Hydraul. Div. 1970, 96, 223–252. [Google Scholar] [CrossRef]
- Chow, V. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Tseng, M.-H. Kinematic Wave Computation Using an Efficient Implicit Method. J. Hydroinform. 2010, 12, 329–338. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill Science/Engineering/Math: Columbus, OH, USA, 1988. [Google Scholar]
- Fiorentini, M.; Orlandini, S. Robust Numerical Solution of the Reservoir Routing Equation. Adv. Water Resour. 2013, 59, 123–132. [Google Scholar] [CrossRef]
- Guang, L.X.; Ben, D.W.; Hua, S.R. Numerical Solution to Reservoir Flood Routing. J. Hydrol. Eng. 2009, 14, 197–202. [Google Scholar] [CrossRef]
- Basha, H.A. Nonlinear Reservoir Routing: Particular Analytical Solution. J. Hydraul. Eng. 1994, 120, 624–632. [Google Scholar] [CrossRef]
- Arrieta-Pastrana, A.; Coronado-Hernández, O.E.; Coronado-Hernández, J.R. Explicit Scheme for a Hydrological Channel Routing: Mathematical Model and Practical Application. Water 2024, 16, 1480. [Google Scholar] [CrossRef]
- Smith, A.A. A Generalized Approach to Kinematic Flood Routing. J. Hydrol. 1980, 45, 71–89. [Google Scholar] [CrossRef]
- Salvati, A.; Moghaddam Nia, A.; Salajegheh, A.; Shirzadi, A.; Shahabi, H.; Ahmadisharaf, E.; Han, D.; Clague, J.J. A Systematic Review of Muskingum Flood Routing Techniques. Hydrol. Sci. J. 2024, 69, 810–831. [Google Scholar] [CrossRef]
- Barry, D.A.; Bajracharya, K. On the Muskingum-Cunge Flood Routing Method. Environ. Int. 1995, 21, 485–490. [Google Scholar] [CrossRef]
- Tang, X.N.; Knight, D.W.; Samuels, P.G. Volume Conservation in Variable Parameter Muskingum-Cunge Method. J. Hydraul. Eng. 1999, 125, 610–620. [Google Scholar] [CrossRef]
- Liu, C. The Essence of the Generalized Newton Binomial Theorem. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2766–2768. [Google Scholar] [CrossRef]
- De Martino, G.; De Paola, F.; Fontana, N.; Marini, G.; Ranucci, A. Experimental Assessment of Level Pool Routing in Preliminary Design of Floodplain Storage. Sci. Total Environ. 2012, 416, 142–147. [Google Scholar] [CrossRef]
- Tafarojnoruz, A.; Gaudio, R.; Calomino, F. Bridge Pier Scour Mitigation under Steady and Unsteady Flow Conditions. Acta Geophys. 2012, 60, 1076–1097. [Google Scholar] [CrossRef]
- Giuseppe, D.; Ali, T.; Giampiero, S.; Claudia, A.; Francesco, C.; Roberto, G. Modified Einstein Sediment Transport Method to Simulate the Local Scour Evolution Downstream of a Rigid Bed. J. Hydraul. Eng. 2016, 142, 04016041. [Google Scholar] [CrossRef]
- Ecociencias. Evaluación de La Hidrología Superficial de La Cuenca de Cienaga de La Virgen Compuesta Por Los Municipios de Turbaco, Santa Rosa y Villanueva Distrito de Cartagena—Departamento de Bolívar; Ecociencias: Cartagena, Colombia, 2005. [Google Scholar]
- Sierra-Sánchez, A.; Coronado-Hernandez, O.E.; Paternina-Verona, D.A.; Gatica, G.; Ramos, H.M. Statistical Analysis to Quantify the Impact of Map Type on Estimating Peak Discharge in Non-Instrumented Basins. Trans. Energy Syst. Eng. Appl. 2023, 4, 1–17. [Google Scholar] [CrossRef]
- Arrieta-Pastrana, A.; Martínez-Padilla, E. Drenajes Pluviales Principales—Urbanización Barcelona de Indias; Universidad de Cartagena: Cartagena, Colombia, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).