Experimental Investigation of Film Thickness in Wastewater Airlift Pumps by an Image Processing Method
Abstract
1. Introduction
2. Theoretical Analysis of a Film Thickness
3. Experiment
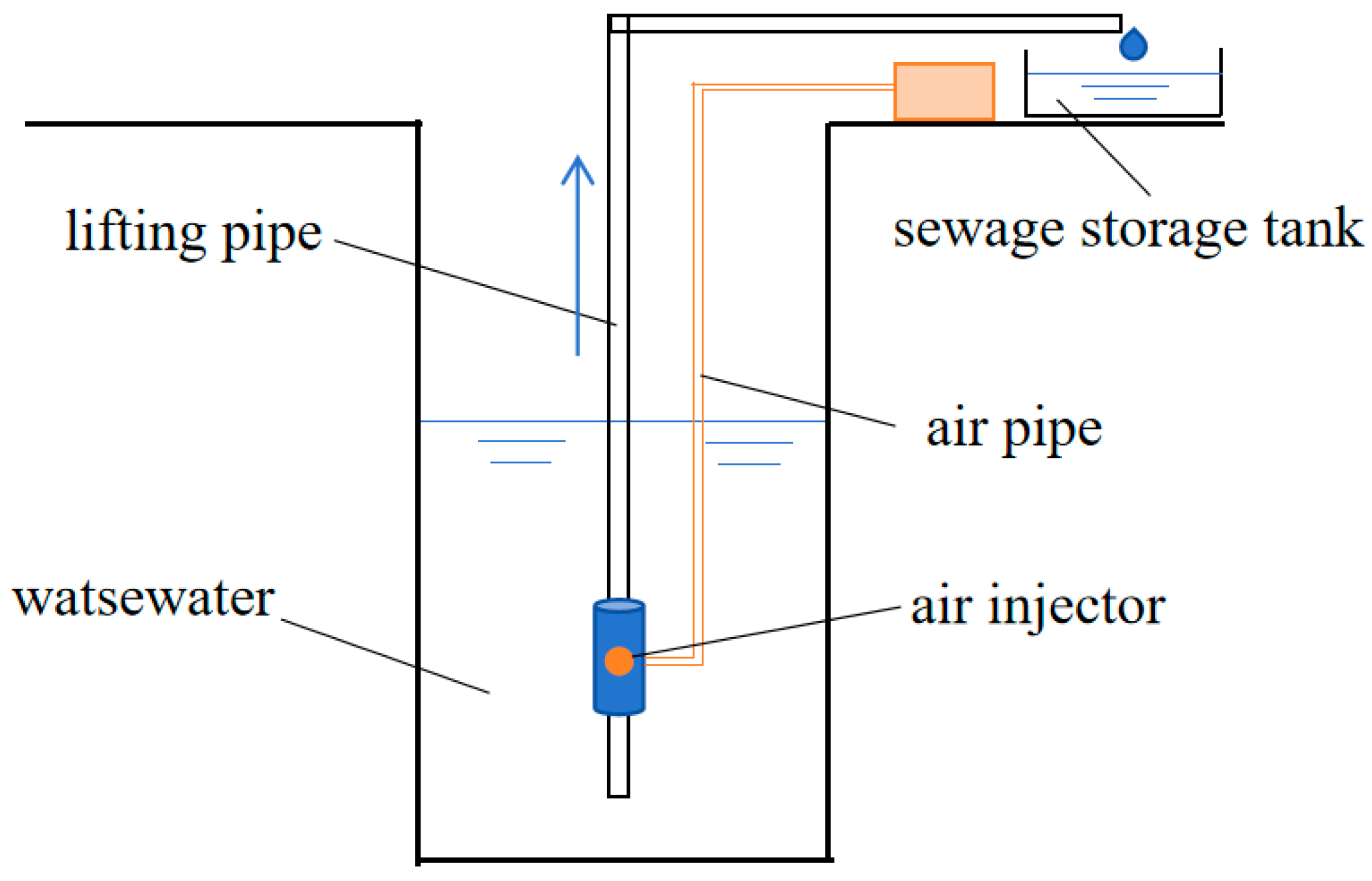
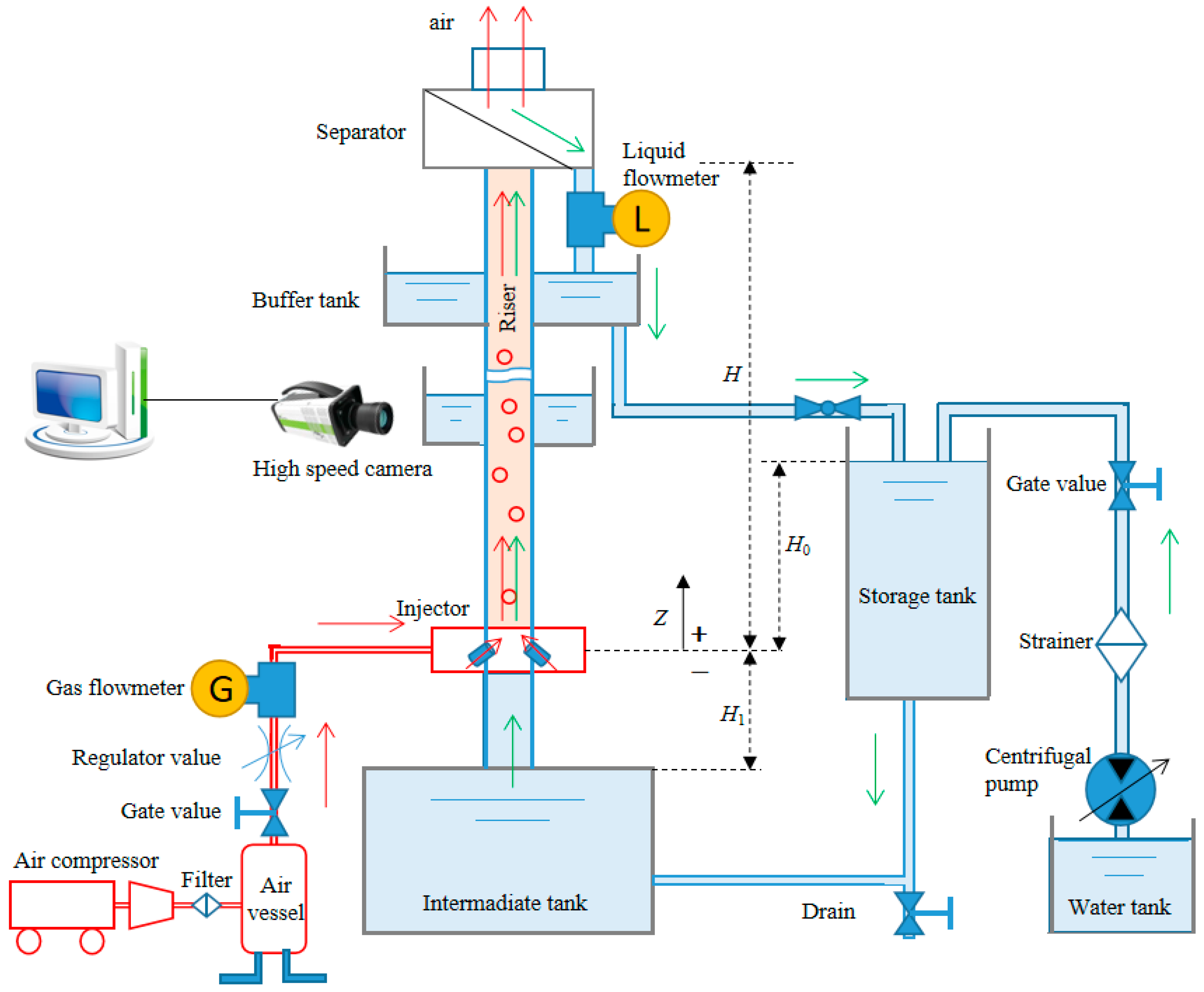
3.1. Experimental Device
3.2. High-Speed Photography
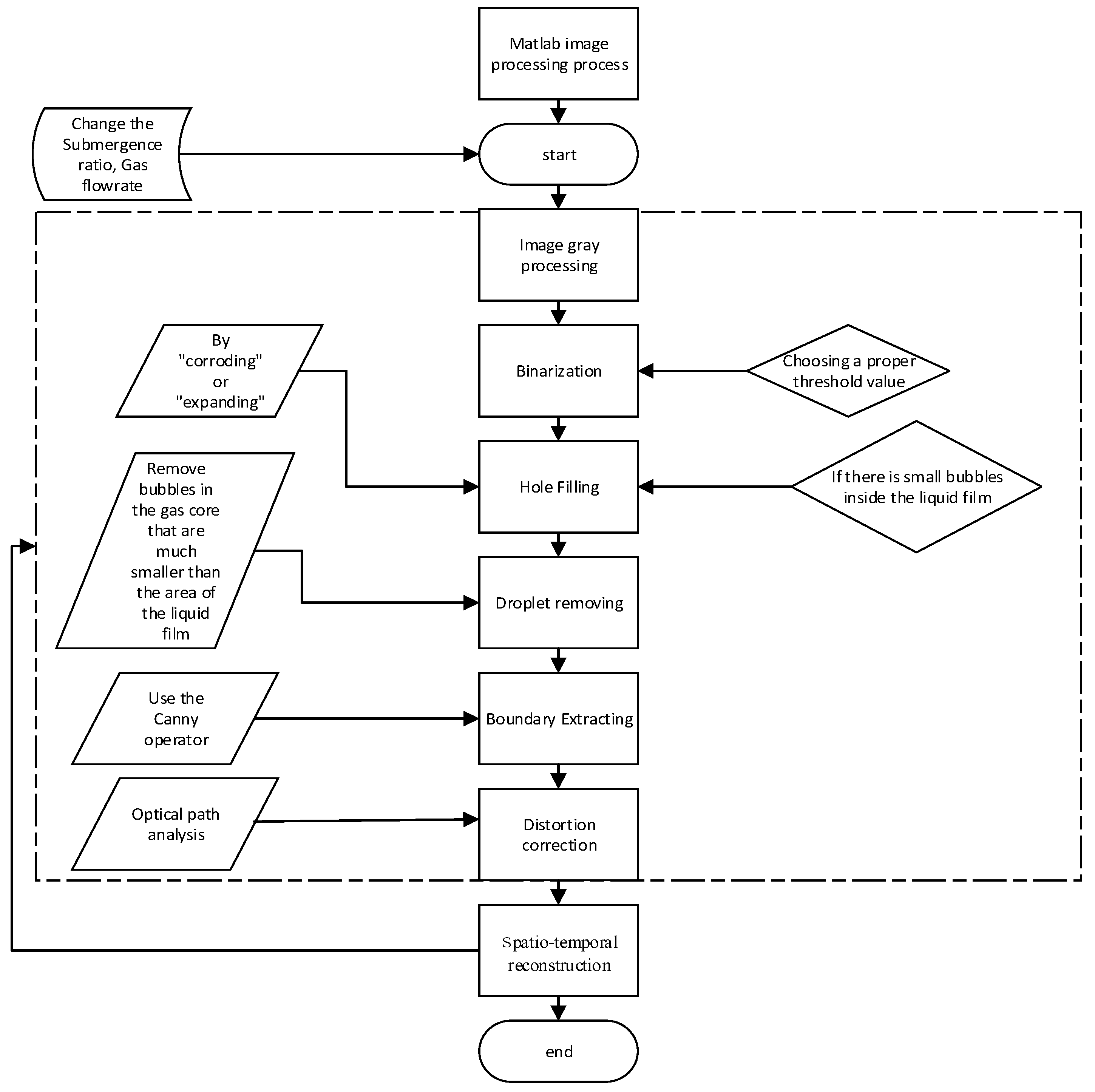
3.3. Image Processing for a Film Thickness
- (1)
- Grayscale processing. The original image was transformed into a grayscale image. The gray levels of the gas and liquid phase were obviously different, as shown in Figure 8b. The gray level of the gas core was much smaller than that of the water phase because the gas core is colorless in airlift pumps.
- (2)
- Image binarization processing. The point of the colorless gas core in the gray image was treated as a background, while the point of the liquid phase was treated as a target. An image threshold was employed to distinguish these two different phases and then to transform the grayscale image into a binary image.
- (3)
- Image hole filling. There existed some small holes in the film structure because some small bubbles were entrained in this film structure. Thus, these small holes in the liquid film were effectively filled using a hole-filling method, as shown in Figure 8c.
- (4)
- Droplets removing. Some droplets were suspended in the gas core in the rising pipe, which may affect the estimation of the film thickness. These droplets usually had a much smaller size than that of the liquid film. Thus, the areas of the droplets were removed by setting the gray level of small areas to 0, as shown in Figure 8d.
- (5)
- Boundary extraction. The gas–liquid interfaces can be seen in Figure 9a. To achieve the coordinate values of the left and right interfaces, the binary image without liquid droplets was divided into two figures from the pipe central axis. An edge-detection algorithm was employed to extract the two gas–liquid interfaces.
- (6)
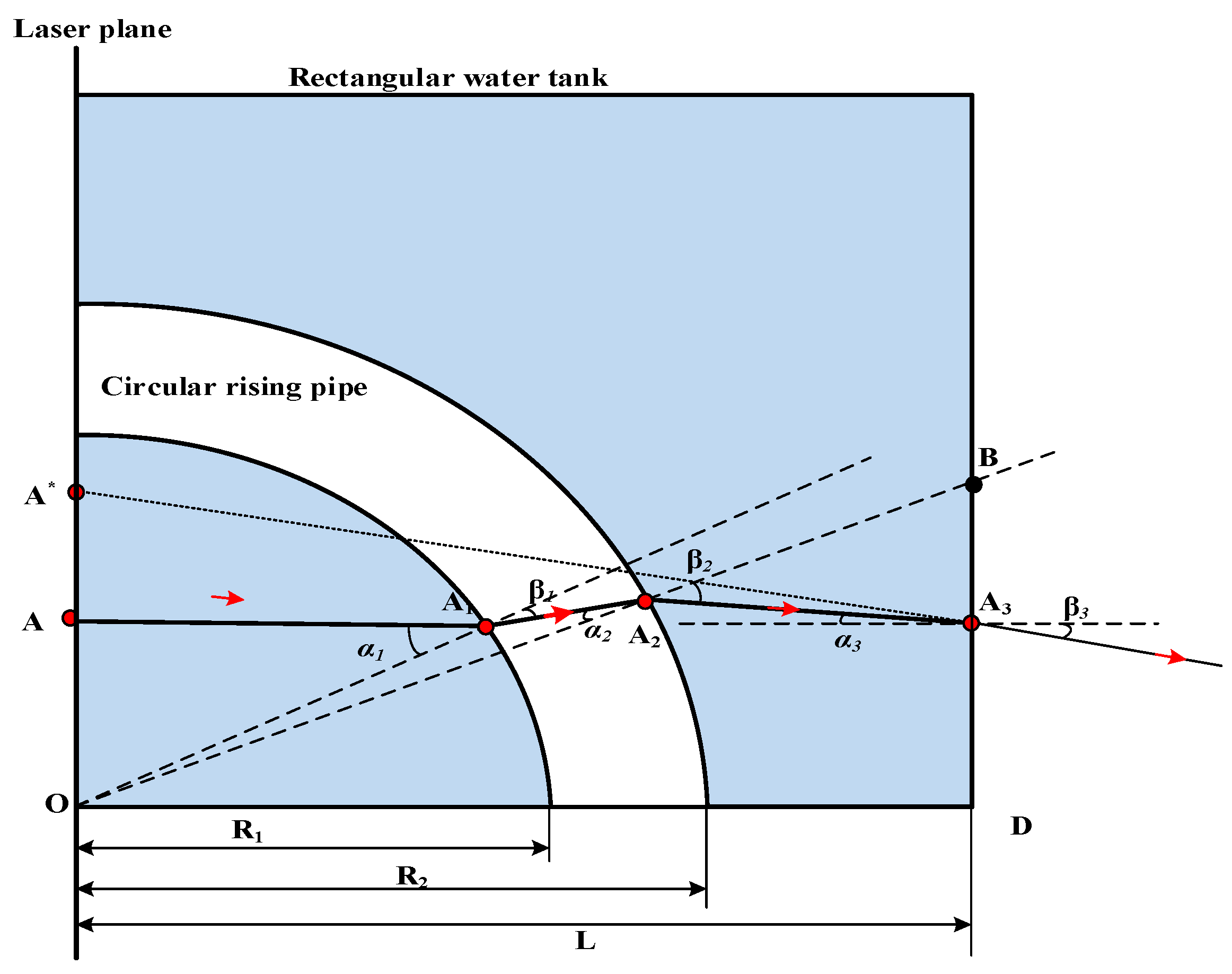
- Image distortion correction. According to the correction function in Equation (13), the real coordinate of the gas–liquid interface can be calculated, as shown in Figure 9b.
3.4. Validation of the Image-Processing Method
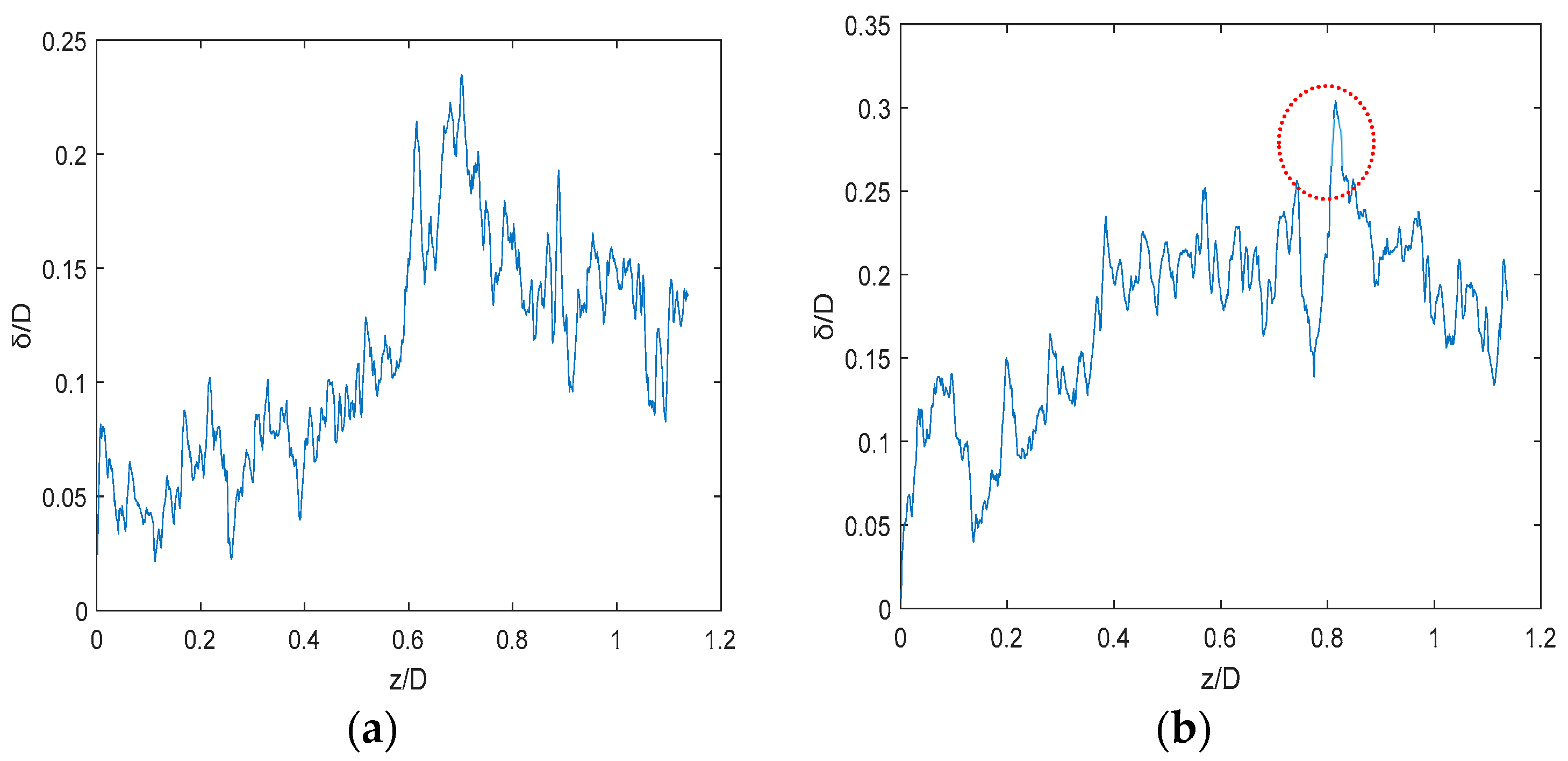
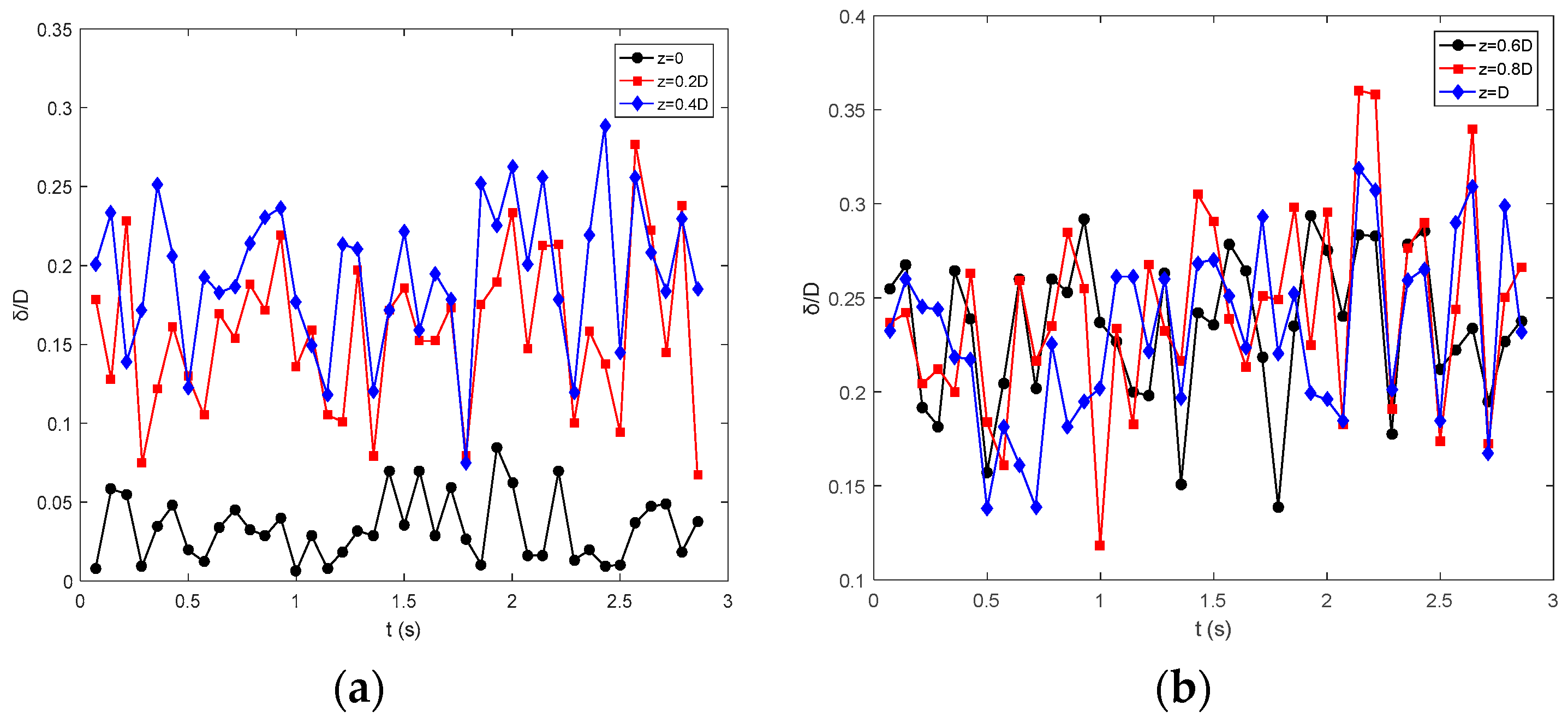
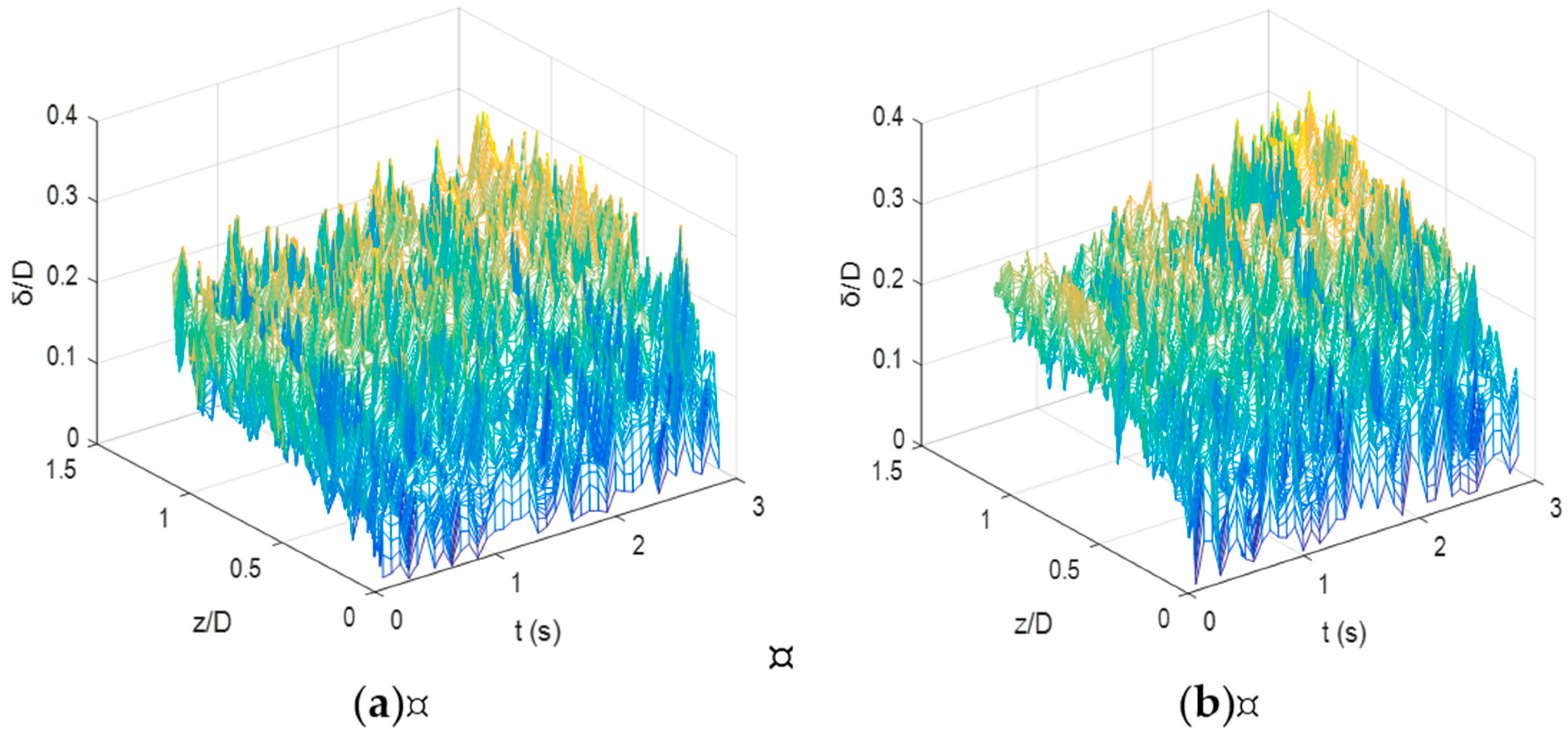
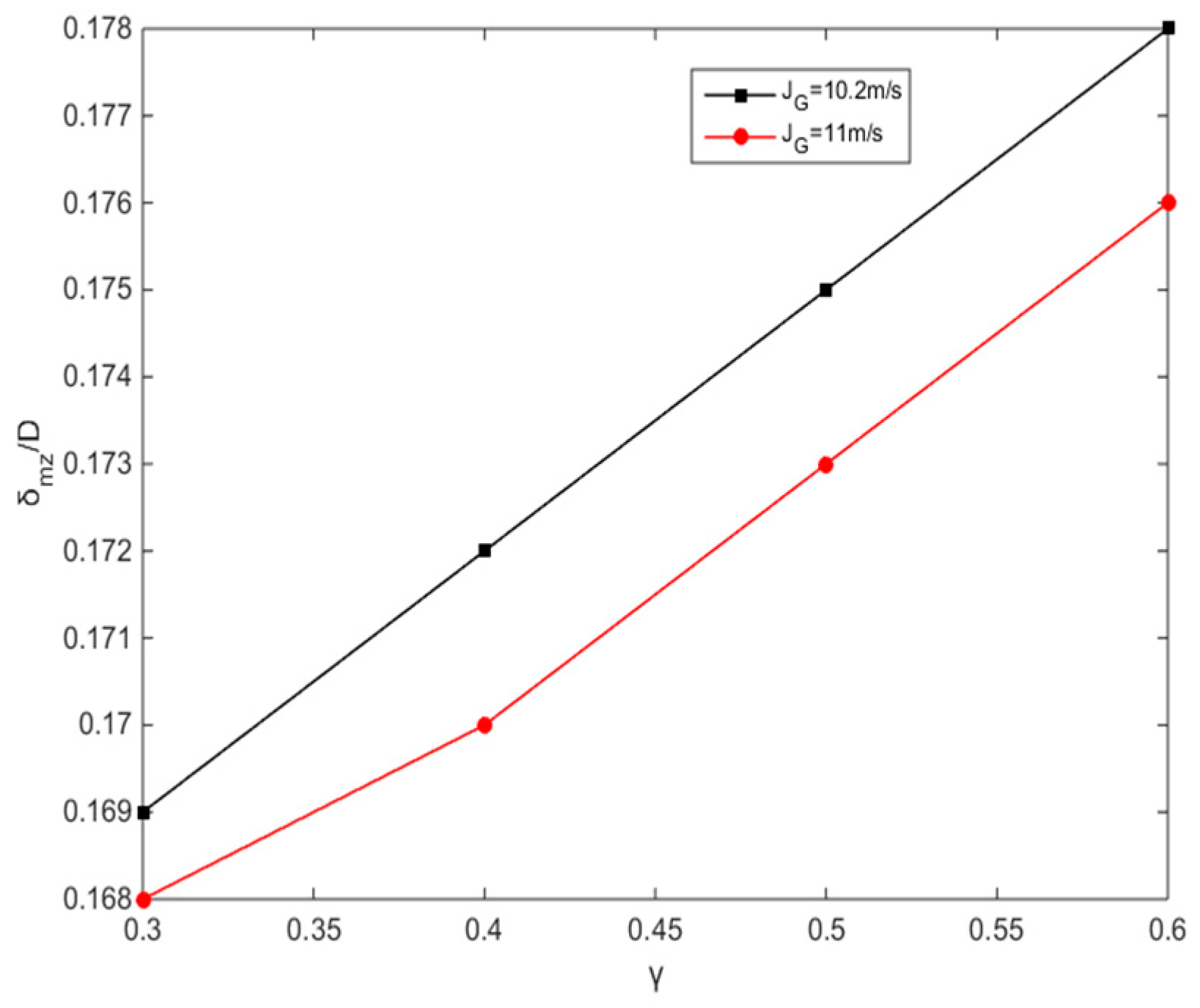
4. Results and Discussions
5. Conclusions
- (1)
- A film structure with a large thickness ranging from 0.15 D to 0.24 D was found in airlift pumps in a high gas flow rate. This film thickness greatly exceeded the maximal thickness of an annular flow and maintained a high discharge of the liquid flow in airlift pumps.
- (2)
- The film thickness first increased with an increase in the gas flow rate and then maintained a constant with a further increase in the gas flow rate. A large submergence ratio was a benefit to the film thickness. One of the key parameters the ability of lifting depends on is the film thickness. Excellent liquid film has a greater efficiency when lifting and picking up; the film thickness is one of the topics of focus in the airlift pump of wastewater treatment equipment.
- (3)
- Some huge turbulent waves existed in the gas–liquid interface. It largely enhanced the momentum exchange between the gas–liquid phase and made a great contribution to improving the performance of the airlift pump working at a high gas flow rate.
- (4)
- The paper investigated the film thickness under a gas–liquid phase flow condition based on limited experimental conditions, and the impacts of other factors on film thickness are still unknown. Further research of film thickness under gas–liquid phase flow in an actual working environment is suggested to be planned in the future.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AG | cross-sectional area of the gas core | u | actual velocity |
| AL | cross-sectional area of the liquid film | z | flow distance |
| D | pipe diameter | δ | film thickness |
| f | friction factor | α | incidence angle |
| g | acceleration of gravity | β | departure angle |
| J | superficial velocity | ρ | Density |
| L | half of the length of the rectangular box | τi | Gas–liquid interface shear force |
| n1 | water refractive index | τL | friction between the liquid film and the lifting pipe wall |
| n2 | pipe refractive index | γ | submergence ratio |
| n3 | atmosphere refractive index | Subscripts: | |
| Si | Gas–liquid interface area | G | gas phase |
| SL | film-wall contact area | L | liquid phase |
References
- Lingyun, J.; Guangming, Z.; Huifang, T. Current state of sewage treatment in China. Water Res. 2014, 66, 85–98. [Google Scholar]
- Meijer, D.; Van Bijnen, M.; Langeveld, J.; Korving, H.; Post, J.; Clemens, F. Identifying Critical Elements in Sewer Networks Using Graph-Theory. Water 2018, 10, 136. [Google Scholar] [CrossRef]
- Abed, R.; Hussein, M.M.; Ahmed, W.H.; Abdou, S. Two-Phase Flow Mass Transfer Analysis of Airlift Pump for Aquaculture Applications. Fluids 2021, 6, 226. [Google Scholar] [CrossRef]
- Fadlalla, D.; Joshua, R.; Shahriyar, G.H.; Wael, H.A. Airlift pumps characteristics for shear-thinning non-Newtonian fluids: An experimental investigation on liquid viscosity impact. Exp. Therm. Fluid Sci. 2023, 149, 110994. [Google Scholar] [CrossRef]
- Zhao, L.; Gu, Y.; Peng, C.; Tang, Z. Scale-up of the cross-flow flat-plate airlift photobioreactor. Asia-Pac. J. Chem. Eng. 2020, 15, e2518. [Google Scholar] [CrossRef]
- Pi, K.; Huang, L.; Li, Z.; Gao, L.; Gerson, A.R. Oxygen mass transfer characteristics in an internal-loop airlift reactor with preset trumpet-shaped riser. Asia Pac. J. Chem. Eng. 2014, 9, 834–844. [Google Scholar] [CrossRef]
- Qiang, Y.F.; Fan, W.; Xiao, C.B.; Pan, Y.; Chen, Y. Effects of operating parameters and injection method on the performance of an artificial upwelling by using airlift pump. Appl. Ocean Res. 2018, 78, 212–222. [Google Scholar] [CrossRef]
- Ahmed, W.H.; Badr, H.M. Dual-Injection Airlift Pumps: An Enhanced Performance. Part. Sci. Technol. 2012, 30, 497–516. [Google Scholar] [CrossRef]
- Ahmed, W.; Aman, A.M.; Badr, H.; Al-Qutub, A. Air injection methods: The key to a better performance of airlift pumps. Exp. Therm. Fluid Sci. 2016, 70, 354–365. [Google Scholar] [CrossRef]
- Catrawedarma, I.; Deendarlianto; Indarto. Statistical Characterization of Flow Structure of Air–water Two-phase Flow in Airlift Pump–Bubble Generator System. Int. J. Multiph. Flow 2021, 138, 103596. [Google Scholar] [CrossRef]
- Hanafizadeh, P.; Karimi, A.; Saidi, M.H. Effect of Step Geometry on the Performance of the Airlift Pump. Int. J. Fluid Mech. Res. 2011, 38, 387–408. [Google Scholar] [CrossRef]
- Kassab, S.Z.; Kandil, H.A.; Warda, H.A.; Ahmed, W.H. Air-lift pumps characteristics under two-phase flow conditions. Int. J. Heat Fluid Flow 2009, 30, 88–98. [Google Scholar] [CrossRef]
- Stenning, A.H.; Martin, C.B. An Analytical and Experimental Study of Air-Lift Pump Performance. J. Eng. Power 1968, 90, 106–110. [Google Scholar] [CrossRef]
- Hall-Taylor, N.S.; Hewitt, G.F.; Lacey, P.M.C. The motion and frequency of large disturbance waves in annular two-phase flow of air-water mixtures. Chem. Eng. Sci. 1963, 18, 537–552. [Google Scholar] [CrossRef]
- Han, H.; Zhu, Z.; Gabriel, K. A study on the effect of gas flow rate on the wave characteristics in two-phase gas–liquid annular flow. Nucl. Eng. Des. 2006, 236, 2580–2588. [Google Scholar] [CrossRef]
- Zhao, Y.; Markides, C.N.; Matar, O.K.; Hewitt, G.F. Disturbance wave development in two-phase gas–liquid upwards vertical annular flow. Int. J. Multiph. Flow 2013, 55, 111–129. [Google Scholar] [CrossRef]
- Kang, H.C.; Kim, M.H. The development of a flush-wire probe and calibration method for measuring liquid film thickness. Int. J. Multiph. Flow 1992, 18, 423–437. [Google Scholar] [CrossRef]
- Klausner, J.F.; Zeng, L.Z.; Bernhard, D.M. Development of a film thickness probe using capacitance for asymmetrical two-phase flow with heat addition. Rev. Sci. Instrum. 1992, 63, 3147–3152. [Google Scholar] [CrossRef]
- Asano, H.; Takenaka, N.; Fujii, T.; Hayashi, H.; Wakabayashi, T. Visualization and void fraction measurement of gas-liquid two-phase flow in a commercial plate heat exchanger by thermal neutron radiography. IEEE Trans. Nucl. Sci. 2005, 52, 280–284. [Google Scholar] [CrossRef]
- Wang, Z.N.; Deng, Y.J.; Pan, Y.; Jin, Y.; Huang, F. Experimentally investigating the flow characteristics of airlift pumps operating in gas-liquid-solid flow. Exp. Therm. Fluid Sci. 2019, 112, 109988. [Google Scholar] [CrossRef]
- Wang, Z.N.; Liao, Y.S.; Wang, X.C. An intermittent glow structure in an airlift pump by using an annular venturi injector. J. Appl. Fluid Mech. 2021, 14, 949–961. [Google Scholar]
- Wang, Z.N.; Jin, Y.P.; Huang, F. Investigation of the inner structure of gas–liquid flow in airlift pumps by laser-high speed visualization technology. Asia-Pac. J. Chem. Eng. 2020, 15, e2509. [Google Scholar] [CrossRef]
- Muntasir, A.-O.; Tiemin, Z.; Wenbo, Y. Mixing Efficiency of Compost Tea Brewing Machines with Various Airlift Pump Air Jacket Structures and Air Injection Pressures. J. Inst. Eng. 2019, 100, 111–116. [Google Scholar] [CrossRef]
- Hu, D.; Kang, Y.; Tang, C.-L.; Wang, X.-C. Modeling and analysis of airlift system operating in three-phase flow. China Ocean Eng. 2015, 29, 121–132. [Google Scholar] [CrossRef]
- Hanafizadeh, P.; Saidi, M.H.; Karimi, A.; Zamiri, A. Effect of Bubble Size and Angle of Tapering Upriser Pipe on the Performance of Airlift Pumps. Part. Sci. Technol. 2010, 28, 332–347. [Google Scholar] [CrossRef]
- Cho, N.-C.; Hwang, I.-J.; Lee, C.-M.; Park, J.-W. An experimental study on the airlift pump with air jet nozzle and booster pump. J. Environ. Sci. 2009, 21, S19–S23. [Google Scholar] [CrossRef] [PubMed]
- Wallis, G.B. One Dimensional Two Phase Flow; McGraw-Hill Book Co. Inc.: New York, NY, USA, 1969. [Google Scholar]
- Henstock, W.H.; Hanratty, T.J. The interfacial drag and the height of the wall layer in annular flows. AIChE J. 1976, 22, 990–1000. [Google Scholar] [CrossRef]
- Kabir, C.S.; Hasan, A.R. Simplified Wellbore-Flow Modeling in Gas/Condensate Systems. SPE Prod. Op. 2006, 21, 89–97. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, M.; Wang, Z.; Chen, B. Experimental Investigation of Film Thickness in Wastewater Airlift Pumps by an Image Processing Method. Water 2024, 16, 2010. https://doi.org/10.3390/w16142010
Jiang M, Wang Z, Chen B. Experimental Investigation of Film Thickness in Wastewater Airlift Pumps by an Image Processing Method. Water. 2024; 16(14):2010. https://doi.org/10.3390/w16142010
Chicago/Turabian StyleJiang, Min, Zhineng Wang, and Bingzheng Chen. 2024. "Experimental Investigation of Film Thickness in Wastewater Airlift Pumps by an Image Processing Method" Water 16, no. 14: 2010. https://doi.org/10.3390/w16142010
APA StyleJiang, M., Wang, Z., & Chen, B. (2024). Experimental Investigation of Film Thickness in Wastewater Airlift Pumps by an Image Processing Method. Water, 16(14), 2010. https://doi.org/10.3390/w16142010




