Abstract
Groundwater flow systems are influenced by the changes in surface waters as well as climatic factors. These teleconnections significantly increase in cases of extreme weather conditions. To prepare and mitigate the effect of such phenomena, the background factors that create and influence natural processes must be recognized. In the present study, 94 shallow groundwater (SGW) wells’ water level time series were analyzed in the inner delta of the River Danube (Europe) the Szigetköz region to explore which factors contribute to the development of diurnal periodicity of SGW and what its drivers are. The relationship between surface meteorological processes and SGW dynamics in the Szigetköz region was investigated using hourly data from monitoring wells. Hourly water temperature data exhibited weak correlations with meteorological parameters. However, daily averaged data revealed stronger correlations, particularly between SGW levels and air temperature and potential evapotranspiration. Diurnal periodicity in SGW fluctuations correlated strongly with potential evapotranspiration. The study also demonstrated the role of capillary fringe dynamics in linking surface evapotranspiration with SGW fluctuations. Changes in groundwater levels, even small, can significantly affect soil moisture, vegetation, and ecosystem functioning, highlighting the sensitivity of the unsaturated zone to SGW fluctuations driven by surface processes.
1. Introduction
Groundwater is a crucial freshwater resource supporting domestic, agricultural, and industrial needs [1,2]. However, over the past decades, worldwide depletion of groundwater storage has become increasingly prevalent due to its extensive use in rapid agricultural, industrial, and urban development globally, e.g., [3,4,5,6]. Ongoing groundwater shortages in many countries pose significant threats to the long-term sustainability of regional economies and ecosystem services [7]. Groundwater flow systems are influenced by the changes of dependent surface waters [8] and in determining climatic factors (e.g., precipitation, evapotranspiration [9,10]). The governing hydraulic processes of groundwater and surface water are quite well understood, and knowledge of how to address specific conditions is rapidly increasing [11]. However, to protect water resources (surface or subsurface), it is vital to gain a better and quantified knowledge of the exchange processes, pathways between surface and subsurface waters [12], and the drivers of these (e.g., meteorology, anthropogenic activity, etc.) [13,14]. It is well known that the short term (from diurnal to weekly) changes in the groundwater table are adversely influenced by local meteorological conditions in addition to hydrogeological circumstances [7,15,16]. The magnitude of the effects of these phenomena is multiplied in the case of extremities such as extreme rainfall, floods [17], or groundwater droughts [15]. Thus, it is important to recognize how changing environmental conditions may affect surface waters [18,19] and groundwater [20,21], since this may allow for the prediction not only of groundwater levels but also of the water balance of the vadose zone.
Groundwater levels and water quality are generally affected by extreme rainfall events [22], or by their opposite, i.e., rainfall-free (drought) periods [23], which are increasingly likely to occur in the future because of climate change [24,25,26,27]. These events affect not only agriculture [28] but also the urban environment, and through endangering the drinking water supply system [29], they also affect the quality of life [30,31].
In order to develop effective mitigation strategies, it is essential to thoroughly assess the direct impact of meteorological conditions in the form of imprints of surface and atmospheric processes on SGW levels. There is a known strong relationship between inter-annual precipitation variability and groundwater recharge driven by climate change [32]. Therefore, teleconnection factors directly influence regional precipitation and consequently impact groundwater dynamics, thereby affecting the lag time in the transmission of meteorological drought to groundwater conditions [15]. Understanding the sub-catchment (small)-scale temporal and local spatial patterns of groundwater requires high-resolution observations and data interpretation beyond long- and regional-scale investigations. For small-scale studies, basic properties of groundwater such as the water level and temperature are the most suitable parameters due to the fact that these are easily measurable by automatic instruments [18].
If data are available, this phenomenon should be explored in detail, on scales ranging from hourly to weekly. Such analysis not only aids in detecting short-term groundwater fluctuations but also enables the inference of long-term impacts influenced by varying climate conditions. Ultimately, this comprehensive understanding will facilitate the development of more effective strategies to prepare for climate change-induced changes across various spatial scales. A more frequent temporal sampling relative to the frequency prescribed by the authorities’ regulations, e.g., as explored in [13,33,34], allows for the determination of such processes influencing subsurface water levels on the daily level. Analysis of this fine scale is usually of subordinate importance, despite its proven importance [33]. As the measurement of the physical parameters of surface and riparian groundwater has a sufficient time resolution, the possibility for such detailed analysis became a reality in the case of the River Danube, specifically in its inner delta, the Szigetköz in Hungary.
The River Danube has the second largest river basin in Europe (801,463 km2; total channel length: 2857 km [30]), with an inner delta located in its middle section in NW Hungary bordering Slovakia near Austria. The delta, called “Szigetköz”, displays the characteristics of numerous human-induced problems. The river itself fundamentally affects the ecological balance of the floodplain. The natural value of the area is outstanding; among others, it is a designated Natura 2000 area. As of October 1992, a 58 km section of the Danube in the Szigetköz has been diverted into a 27 km long cemented power canal [35] at river kilometer (rkm) 1851.75 for the Gabčíkovo powerplant (Figure 1A) [36]. In 1989, Hungary decided to no longer participate in a bilateral hydropower plant construction project planned for the Szigetköz; thus, in 1992, Slovakia finished a version of the project that circumvented Hungary [35]. Up until this point, the level of the SGW of a several hundred-meter-thick hydrogeologically quasi-homogeneous and izotropic aquifer had been uniform [37] and was determined mainly by the natural water level fluctuation of the Danube [38,39]. Thus, the long-term changes in river runoff—caused, e.g., by climate change [34] or direct anthropogenic influences [40]—will have an effect on SGW table fluctuations. After the diversion, 80% of the Danube’s flow was redirected to an insulated power plant canal that re-joins the original riverbed only at Palkovicovo (Szap) at rkm 1811, creating a quasi-well-balanced flow in the Old Danube (Figure 1A) [40,41]. Not taking into account the floods, the river water level fluctuates between a couple of tens of centimeters and a meter [38,42].
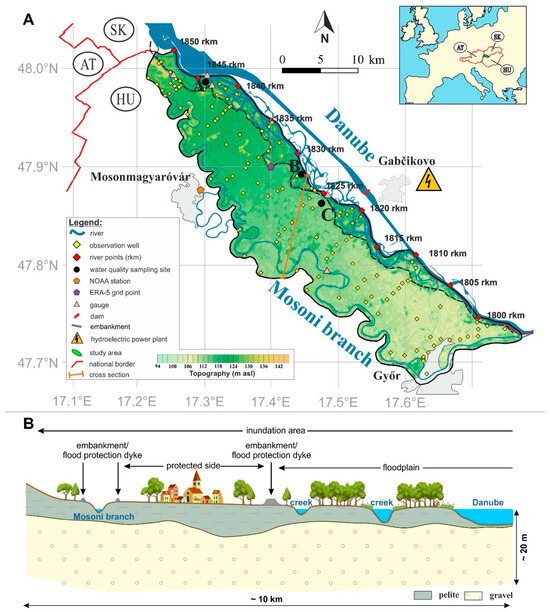
Figure 1.
(A) Study area of the Szigetköz itself and its monitoring sites, along with the branches of the Danube and the “new” canal with the hydroelectric power plant at Gabčikovo. HU: Hungary, SK: Slovakia, AT: Austria. The two-letter country codes follow the ISO 3166-1 alpha-2 standards. (B) Cross-section summarizing the different parts of inundation area; modified after Trásy [43].
For historical reasons, the Szigetköz has a monitoring network with a high spatial resolution (especially perpendicular to the Danube), making it an excellent study area. The investigated part of the Szigetköz (Figure 1) has an area of 342.7 km2 and is represented by 94 wells; a 1 well per 4 km2 average density. In the Szigetköz area, the water flow of the river is balanced with low variability [42], which provides an opportunity to study the background processes causing the variability in the groundwater level without the superimposing effect of extreme hydrometeorological events (e.g., extreme rainfall, long droughts, etc.).
Aims
In view of the previous, the aim of the study is to answer the following three major questions using the Szigetköz inner Danube Delta as a pilot area:
- Do the diurnal patterns of the groundwater level and temperature exhibit mutually consistent characteristics, and if so, are there any spatial attributes of these ?
- What factors contribute to the development of diurnal periodicity in SGW, and what are its drivers?
- Is the Szigetköz area susceptible to forecasted changes in climatic conditions and/or human activity concerning groundwater levels and the extent (thickness) of the unsaturated zone? What specific alterations in groundwater levels might be anticipated in the future? Are there spatial variations within the area’s response to climatic changes?
2. Materials and Methods
2.1. Study Area—Geological Conditions
It is a general notion that the imprint of surface processes (e.g., evapotranspiration, precipitation, floods, etc.) decreases proportionately with depth in the subsurface layers. However, this can be assessed from a vertical and a horizontal perspective. Regarding the aforementioned information, it is viable to explore to what extent the parameters measured in the subsurface water respond to changes in surface processes with respect to SGW level depth, i.e., distance from the surface. Regarding the latter, the lithological characteristic (grain size, permeability, porosity, etc.) of the strata in which the water level is located must be identified as an additional—horizontal—major factor. If the water level is located in, e.g., fine-grained strata, the horizontal interconnectivity will be much lower than in the case of a well-classified gravel strata.
A pelitic Holocene cover strata (avg. depth 2–6 m) with low hydraulic conductivity is the most characteristic in the Szigetköz, which is characteristically different from the couple of 100 m thick underlying well-classified Pleistocene gravel strata (high hydraulic conductivity; Figure 1B). Due to this characteristic vertical difference in aquifer host rock quality, the area was split up into two main lithological units. In the (i) NW part of the Szigetköz, the SGW levels are mainly located in gravel strata, whereas in the (ii) SE parts, those are in the pelitic cover layer [44]. These two sets of SGW wells were quite clearly defined by their location. However, those particular SGW wells (iii) in which the water levels cannot be characterized as situated in the gravel or pelitic strata but are rather located in an alternating way due to their annual periodic behavior, were handled as the third set.
2.2. Data
Two sets of data were used in the study. The so-called response parameters set was comprised of SGW levels and water temperature time series from 94 wells (average screen interval: 7.3 m, min: 3.7 m, max: 14.5 m; Figure 1A) over the period 1 February 2009–31 October 2009. The subsurface water levels were measured hourly by the North-Transdanubian Water Directorate using, in most cases, high-resolution automatic loggers in accordance with the Water Framework Directive [45]. This was the interval covering the second-largest flood in the last 20 years with the greatest number of active monitoring wells operating to record it.
The other set includes the explanatory parameters that are expected to drive SGW levels. It is known that not geology, but rather the local meteorological conditions, are the stronger drivers of weekly, diurnal fluctuations in shallow water [13]. Thus, hourly temperature [°C], relative humidity [%], wind speed [m s−1], and air pressure [Pa] acquired from the National Oceanic and Atmospheric Administration (NOAA) were chosen as explanatory parameters for the interval from 1 February 2009 to 31 October 2009, represented by one station located in Mosonmagyaróvár. In addition, potential evapotranspiration (PET) [mm day−1] was considered and calculated with the FAO56-PM formula [46,47]. The input data for this task included insolation [J] from the ERA5 database [48] and the other variables from the NOAA [49].
2.3. Steps of the Study in Identifying the Main Driving Factors of the Diurnal Periodicity of Groundwater Levels
In determining the driving factors of the SGW levels, the following steps were taken:
- First, it was investigated whether a significant linear relationship exists between the surface explanatory variables and the subsurface response variables at each SGW well using Pearson’s correlation coefficient [50], including cross-correlation on an hourly and diurnal basis to obtain those parameters that are in close relation with the water levels. If any periodic pattern is observed in a SGW level time series resembling that of the meteorological parameters, it may be suspected that a causal relationship may obtain between them, and that this will be driven mainly by insolation/radiation [51,52]. In order to draw general conclusions from any such particular instance of the coincidence between periodic meteorological behavior and SGW, a thorough investigation is required as to the extent to which temperature, PET, relative humidity, and air pressure are able to explain the variance in the SGW levels. It is suggested that this investigation precedes that of the periodic patterns.
- The periodic behavior of the response parameters was assessed using wavelet spectrum analysis (Section 2.4) to determine what percentage of the investigated time period is a diurnal period present in the SGW levels and temperature records, and to try to relate this behavior to local geology.
- Using wavelet transform coherence (WTC, Section 2.4), we investigated whether the periodic signals of the independent explanatory parameters are transferred to the subsurface. This is necessary to determine the delay in the change in SGW levels caused by the given surface processes.
2.4. Wavelet Spectrum Analysis and Wavelet Transform Coherence
Wavelet spectrum analysis was employed to assess the periodic behavior of the independent variables and identify time intervals lacking periodicity of a given frequency. Subsequently, WTC was utilized to identify common periodic signals between water quality parameters and the independent variables, as in other cases, to explore the relationship between water levels and chlorophyll-a in Lake Baiyangdian [53] or to uncover the relationship between climate indices and streamflow variability [54]. This approach was also used, e.g., on stable isotopes in precipitation and T [55], on speleothems and climate variables [13], or in assessing low-frequency variability in hydroclimatic records from east Central Europe [56].
Wavelet spectrum analysis is considered to be a function localized in both frequency and time with a zero mean [57]; it could also be taken as the convolution of the data and the wavelet function [58] for a time series. Wavelet transformation Wn(s) could be defined as the convolution of the data and the wavelet function; Equation (1):
Here, n stands for the length of the time series, ψ the wavelet function, s the scale, and (*) represents the complex conjugate. In the present case, to generate daughter wavelets, the Morlet mother wavelet [59] was used as the source function. In this study, those wells that did not indicate a significant daily period for at least 20% of the investigated time were discarded from the group of those possessing a diurnal periodicity.
Numerous studies exist in which WTC has been applied to find a relationship between, e.g., climate indices, streamflow variability [54], and subsurface water levels. It is widely used in other disciplines as well, e.g., in paleoclimate research on speleothems and climate variables [60], or in assessing low-frequency variability in hydroclimate records from eastern Central Europe [56].
WTC is able to indicate the common power of two variables, being in this way similar to a correlation coefficient but localized in the frequency-time space [57]. WTC takes into account the period, power, and localization of two variables in the time-frequency space in 4D, because the phase differences, which represent the temporal lags, are included as well.
In the present study, only the positive significant signals (α = 0.01) against a thousand first-order autoregressive AR(1) surrogate time series were considered [61]. Periods of <20 h were highpassed. It should be noted that since the wavelet functions at each scale are normalized, the wavelet transforms of the results are comparable even to other time series [62]. Three main characteristics of the wavelet transform coherence were considered:
- The presence of the coherent periods in time, which meant that significant periodic behavior—coherence—at a certain frequency was transformed into a percentage, while taking the presence of the coherence/period throughout the whole investigated time as 100%;
- The maximum global wavelet power, which is the average cross-wavelet power in the frequency domain (averages over time) [61];
- The phase differences between the pairs of water quality parameters and meteorological parameters, which show which series is the leading one in this relationship [43].
The calculations were conducted in R 4.3.2 [63] using gstat for mapping and the WaveletComp package for wavelet spectrum and coherence analysis [61]. The grids were obtained with the sp and raster packages, and the mapping was performed in Golden Software Surfer 11 and CorelDraw 2021.
3. Results and Discussion
3.1. Analysis of Shallow Groundwater Table Fluctuation
It was found that hourly, the water temperature data of the SGW wells did not correlate well with the meteorological response parameters (air temperature, PET, relative humidity, and air pressure). In addition, no lagged correlation structure was found between surface meteorological parameters and those of the SGW.
However, on a daily basis (that is, with daily averages derived from the hourly data), higher correlations (r) than those experienced with the hourly data were obtained in the case of SGW levels, air temperature, and PET (r > ∣0.7∣). In the case of water levels, the highest values for r were observed in relation to temperature and PET. In contrast, the GW temperature and meteorological parameters were characterized by low correlation values (r < ∣0.3∣). Again, no lagged correlation structure was found between the surface meteorological and SGW parameters (Figure 2). The critical correlation coefficients were calculated for the 5% significance levels, thus correlation coefficients r > ∣0.118∣ were considered significant for the daily, and practically all coefficients (r > ∣0.024∣) for the hourly measurements (Figure 2).
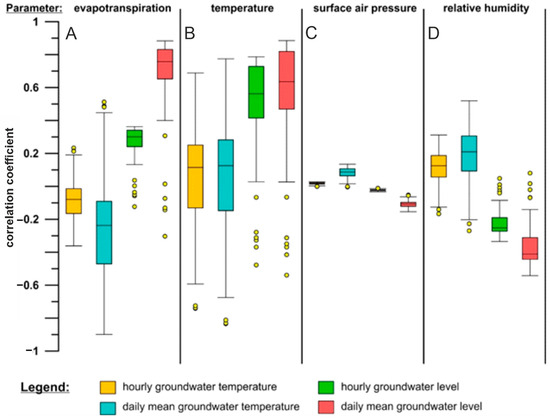
Figure 2.
Box-and-whiskers plots showing the correlation coefficients between the given meteorological parameters of (A) PET, (B) temperature, (C) surface air pressure, and (D) relative humidity and groundwater temperatures as well as groundwater levels. The boxes indicate the interquartile range, the black line in the middle the median, and the values outside 1.5 times the interquartile range are indicated by a yellow circle [64].
It may therefore be concluded that the “high-frequency” hourly variation in the meteorological parameters is not transferred directly to the SGW. Nevertheless, in the low-frequency domain (daily changes), a much stronger common linear pattern was indicated between the SGW data and PET and air T (Figure 2A,B).
Taking an overall look at the correlation coefficients’ values between the assessed meteorological data and parameters measured in SGW wells, it becomes clear that in general, the linear relationship of the hourly observations shows a much smaller variability than that of the daily ones. If the different meteorological parameters are investigated, surface air pressure and relative humidity do not correlate well with the SGW level or temperature, with the latter indicating a larger variability, in some cases reaching values of ±0.5 (Figure 2C,D). On the contrary, PET and air temperature did have meaningful correlations with SGW level and temperature, although SGW temperature (hourly and daily) still did not show such a relationship that would be worth exploring further. The most meaningful linear relationship was seen between PET and air T with the SGW level (Figure 2A,B). Thus, in the following, these will be explored in detail.
3.2. Detection of the Effect of Surface Processes in the Groundwater by Periodicity Analysis
For each SGW well, the periodic behavior of temperature and water levels was investigated, along with the meteorological parameters both within and beyond a 24 h period. The exercise was to first remove large-scale trends from the signal, since these may hinder the estimation of small-case periodicity. Thus, a centered 24 h moving average was subtracted from the measured hourly water level signal [65]. In the case of the meteorological parameters (temperature, PET, relative humidity, air pressure), diurnal (24 h) periodicity was present with the highest average power, e.g., in PET (Figure 3).
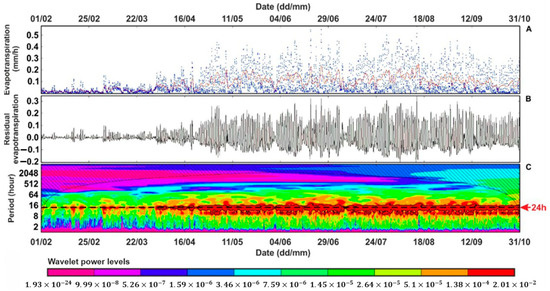
Figure 3.
PET of the area (blue dots) with the 24 h moving average (red line) (A); the residual PET after the 24 h moving average was subtracted (B); and its power spectrum density graph (C). The 5% significance level against red noise is shown as a thick black contour. The black-shaded areas mark the cone of influence (COI). The black dashed horizontal line indicates those domains in which 24 h (diurnal) periodicity could be found.
Interestingly, SGW temperature did not display any diurnal periodicity, despite the fact that the measurements had an uncertainty of just 0.1 °C. In the case of the SGW levels, at p = 0.95, only 41% (n = 39) of the wells displayed diurnal periodicity in at least 50% of the total investigated time (Figure 4B).
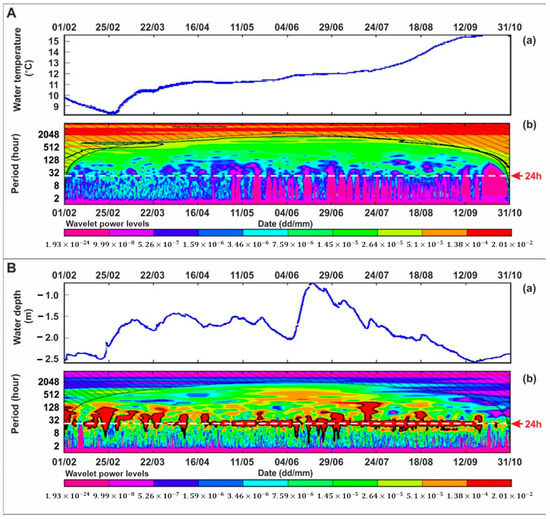
Figure 4.
Wavelet spectrum power density graphs of temperature of SGW monitoring well No. 110691 (A) and the groundwater level (B). Upper panels (a) show the time series, lower ones (b) the power spectrum density graphs. The 5% significance level against red noise is shown as a thick black contour. The black-shaded areas mark the COI. The white dashed horizontal line indicates those domains in which 24 h (diurnal) periodicity could be found.
3.3. Relationship between the Intensity of Evapotranspiration and the Periodic Behavior of Shallow Groundwater Fluctuation
Since air temperature and PET displayed a strong daily correlation with the SGW data (Section 3.1), their time series were compared.
As a first step, the number of SGW wells behaving periodically (n = 39) was determined following [58]. These were the ones indicating a diurnal periodicity in at least 20% of the investigated time between 1 February 2009 and 31 October 2009. Next, the ratio of wells (%) in which diurnal periodicity was found was determined and empirically compared to the daily PET. It became clear that during summer, most of the SGW wells displayed diurnal periodicity (Figure 5).
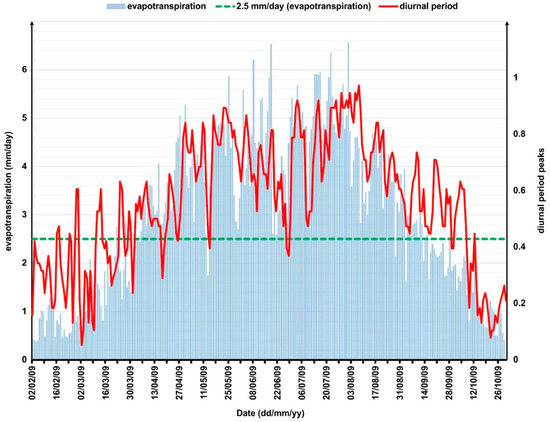
Figure 5.
Change in the ratio of wells with diurnal SGW periodicity was along with change in PET (blue bars). Regarding the diurnal period peaks (right Y axis), 1.0 indicates the total number of wells available on that particular day. If the red line corresponds to one, it means that all the SGW wells indicated diurnal periodicity on that particular day. The linear correlation coefficient between the two datasets is 0.81. The green dashed line represents the 2.5 mm day−1 PET.
In the growing season, in the Carpathian Basin (1 April–31 September) [66], more than 50% of the wells display diurnal periodicity. In the time periods when PET was low (<2.5 mm day−1), the number of SGW wells displaying periodicity was low, as well (37% of all the wells). On the contrary, in the warmer months (April–September), when PET is characteristically higher (>2.5 mm day−1), the number of wells displaying diurnal periodicity increases as well (to approx. 69%; Figure 5).
This pattern (Figure 5) concurs with the intra-annual variability in temperature and PET (r = 0.75 and r = 0.81 respectively, p < 0.0001 implying a close linear relationship between SGW table diurnal periodicity and surface meteorological parameters of PET (r = 0.81, p < 0.0001) and air temperature (r = 0.76, p < 0.0001) (this is in accordance with the findings of, e.g., Thornthwaite [67]). In the following analyses, only the results obtained with PET will be shown. With the other surface meteorological parameters, the diurnal periodicity frequency time series showed correlations of 0.1, (–0.44), and 0.65 for air pressure, relative humidity, and dew point, respectively.
Assessing the location of the wells leads to the conclusion that those wells that do not display diurnal periodicity throughout the whole year (Figure 6) and/or do not behave periodically at all (n = 55) mostly tap SGW from the gravelly layer. This is true for 93% of the non-periodic wells. Moreover, those SGW wells that do display diurnal periodic behavior are located on either the pelitic strata or at least in places varying between gravel and the pelite. These, in turn, are mostly located in the southern part of the area (Figure 6). Based on these observations, three different groups were distinguished, i.e., a “gravelly type”, a “pelitic type”, and a “fluctuating type”.
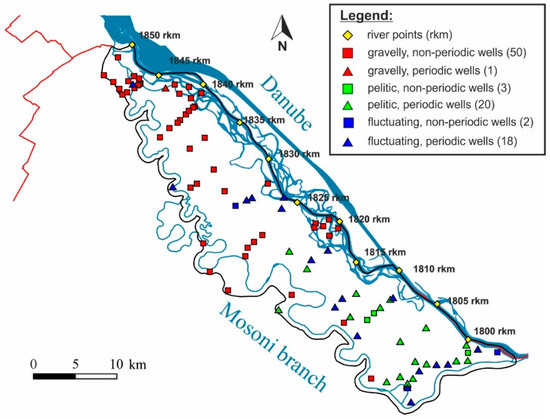
Figure 6.
Map presenting the SGW wells classified by the lithological facies in which they are located in and whether they display diurnal periodicity. Red markers indicate gravelly wells, black the pelitic wells, and blue color markers represents lithology characteristic of the dominant water table. SGWs indicated by triangles have diurnal periodicity based on wavelet spectrum analysis; rectangles represent non-periodic wells.
3.4. Temporal Relationship between Evapotranspiration and Groundwater Level Fluctuation
Most of the parameters describing surface meteorological processes (including PET) display diurnal periodicity (e.g., Figure 3), as might be expected [68]. Thus, the connection between the periodically behaving SGW time series and PET may be investigated in terms of any lagged relationship as well, using WTC (Section 2.4). The highest power was observed in the summer months (Figure 7).
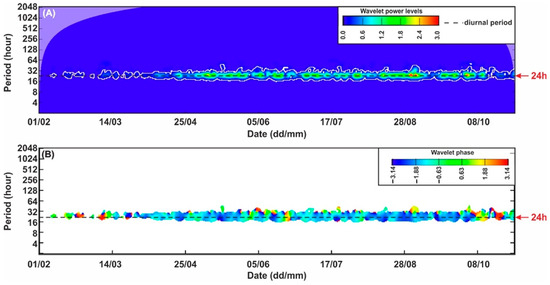
Figure 7.
Power spectrum density (A) and phase difference (B) indicating the presence of diurnal periodicity in the PET and SGW level time series at sampling SGW well 110772. The white contours in the panels show the 95% confidence levels calculated against a thousand AR (1) surrogates. It should be noted that wavelet spectrum analysis coherence and wavelet transform coherence produce edge artifacts, since the wavelet is not completely localized in time; thus, the introduction of a cone of influence (dimmed area on the left panels) is suggested, in which edge effects cannot be ignored [62].
The mean phase difference between PET and the SGW time series is −1.44 (Q1: −1.73, Q3: −1.14). This, in turn, indicates that evapotranspiration is leading the SGW levels by ~5–12 h. This, although it cannot be taken in itself as indicating correlation [69], is nonetheless in accord with the high correlation between the SGW time series and PET (Figure 5).
The weak Pearson (cross)correlation between surface processes and the fluctuation of the subsurface water table on an hourly scale suggests that surface processes are not transferred downwards into the ground in a linear way. This characteristic, lacking directness, is presumably caused by the “insulation” effect of covering layers [70], especially in the unsaturated/vadoze zone, which has the effect of dampening heat flux from insulation [71,72], or night cooling and surface evaporation [73,74]. A higher degree of correlation was observed between surface and sub-surface parameters on a daily scale than on a diurnal one, most probably because diurnal changes occurring in meteorological conditions (e.g., short-term change in cloud cover, etc.) are not transferred to the SGW. Nevertheless, in the low-frequency domain (daily averages), changes in local meteorology are able to manifest themselves, due to their higher persistence/residence time [70].
Groundwater table fluctuation is driven by the warming of the SGW by insolation [75]. In the Great Hungarian Plain, for example, SGW table fluctuation was thought to be driven by thermo-osmosis [76]. However, in the present case, evapotranspiration, and not direct insolation heating the SGW, was found to be the most important factor in determining SGW table fluctuation. This is most explicitly demonstrated by the insignificant degree of diurnal fluctuation in SGW temperature (Section 3.2).
In this case, if temperature was indeed the major factor controlling SGW table fluctuation, then diurnal air temperature fluctuations should have been detected in most of the SGW wells. This, however, cannot be regarded as proven by the results indicating the low degree of correlation between the surface and sub-surface (Figure 2), despite the exceptionally low uncertainty of the measurements. On the contrary, PET displayed a high degree of correlation with fluctuations in the SGW table (Figure 2), as has in fact been previously documented [68]. In summer, in riparian environments, such as the study area, if it is impossible for the flora to take up water from the river due to its low-water level, then the primary source of water for the flora is the SGW. Its fluctuation reflects the daily cycle of water uptake by flora; thereby, evapotranspiration has a great influence on SGW levels [77,78,79].
Such a physical process could serve as an explanation for this phenomenon, which would be capable of creating a direct connection between the shallow subsurface and deeper underground zones, thus enabling surface effects to be communicated to the groundwater. For this reason, a discussion of the relationship between the geological medium and water is necessary. In those periods when evapotranspiration is low (the predawn and dawn hours), SGW table fluctuation is low as well [80], as reflected in the observation (Section 3.3, Figure 5) that in periods with low PET < 2.5 mm day−1, the number of SGW wells displaying diurnal periodicity was much lower (37%). However, in the time intervals characterized by higher PET (>2.5 mm day−1), 69% of the SGW wells displayed diurnal periodicity, also indicated by the wavelet coherence results (Figure 7).
3.5. Capillary Fringe as a ”Conveyor Belt”
In the case of near-surface groundwater, groundwater rising via capillary fringe is a crucial factor in vertical transport of fluids. It is basically the replenishment of soil moisture from the SGW via capillaries in the soil when soil moisture decreases due to surface evapotranspiration. The amount of water transported to the surface from the SGW by the capillary system depends mainly on the grain size and sediment of the sub-surface layers and decreases proportionately to the distance from the SGW table in the direction of the surface [70,81]. The effective rise in groundwater level via capillary fringe differs in relation to grain size and quality. In fine-grained layers (e.g., clay), it can reach up to 10 m [81], although its speed is quite low.
The output of water and its flow towards the surface from the capillary zone the groundwater appears when the soil’s humidity content and the humidity potential decreases gradually on the way up. This phenomenon is caused by adhesion, which is the force of attraction that causes the soil particulars and water molecules to join. Due to evaporation, the humidity of the upper soil layer, as well as the matrix potential and the hydraulic potential, decreases even further, so the potential difference between the upper and the lower layers of the soil-saturated capillary zone keeps on increasing.
The observation, that capillary action is most prominent in the covering layer of fine-grained sediment is in accord with general knowledge. Results show that SGW wells indicating diurnal periodicity are mostly located in the pelitic sequence (Section 3.3), that is, much deeper (4–5 m) than the screening depth of the wells both closer and parallel to the Danube (1–3 m in depth), which do not display diurnal periodicity. It may be said that the presence of diurnal periodicity depends not on the screening depth of the SGW wells, nor on the depth of the water table, but to a much greater degree on the local surroundings of the water table, i.e., the lithology and its physical properties (Figure 8). The main reasons for the more characteristically diurnal periodic behavior in the pelitic sequence are as follows:
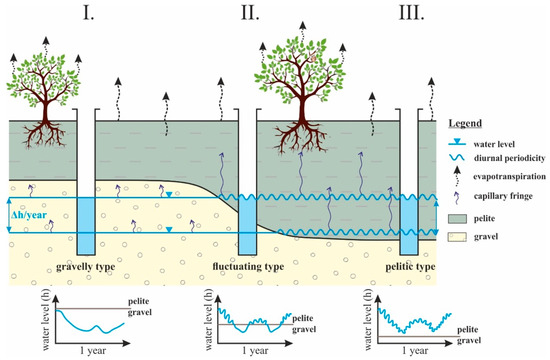
Figure 8.
Conceptual model showing different types of fluctuation. Roman numbers I.–III. are used to refer to the underlying processes explained in the main text.
- The higher reaction time to changes in the SGW table due to the smaller pore space;
- The fact that the water can reach the root zone, due to the great extent of capillary action, enabling plants to take up water [81].
The SGW table decreases proportionate to the transpiration of vegetation, as indicated by the wavelet coherence analysis (Figure 7). Therefore, capillary action functions as a vector between the evapotranspiration of the fauna and SGW table, but only in those locations where the average pore size (<40 µm) enables it to do so [81,82,83], and the SGW table reaches this fine-grained strata (Figure 8), contributing to soil moisture [81]. This notion is reinforced by the “fluctuating wells” themselves, because the only main factor that affects their behavior is the intra-annual change in lithology (pelite, gravel) of the strata where the SGW table is to be found throughout the year. In the case of the SGW wells, the water level depth at which these are mostly located is in the pelitic strata, and it is here that diurnal periodicity becomes characteristic. However, in the SGW wells typified as the “fluctuating type”, in which the SGW table is located in the gravelly zone, capillary action is insignificant, and no periodic behavior is to be seen (Figure 8). Moreover, if the SGW table is located exclusively in the gravelly zone, no periodic behavior resembling surface climatology is to be observed. In the case that the level of the subsurface water remains throughout the year in a gravelly layer (case I, “gravelly type”), it is subordinate to capillary fringe, and therefore, a diurnal periodic pattern is not apparent. However, in case II (“fluctuating type”), due to annual water level fluctuation, the groundwater table rises into the fine-grained covering layer thanks to capillary fringe, and therefore, it is in daily connection with surface evapotranspiration, and diurnal periodicity is able to develop. In case III (“pelitic type”), this connection obtains year-round (Figure 8).
The three conditions (”gravelly”, ”pelitic”, and ”fluctuating” wells, see details in Figure 6) can be generalized to other similar settings, since the observed behavior is significantly present in 95% of the cases: pelite—periodic, gravel—aperiodic behavior that is generalized (Figure 8). Near Wageningen (Netherlands), a case study of two closely (~60 m) situated SGW wells documented a characteristic difference, in which one indicated a diurnal periodicity of the SGW table, whereas the other did not, though in this case, lithological conditions were not investigated [84]. The explanation was to be found in the vegetation, although lithological differences such as those presented could be the reason for this particularly strange behavior. In the pattern of variation in the wells, the spatial element is such as might be expected in a situation in which their significant lithological differences obtain. In the case of similar lithological settings, on the basis of the results presented here, a distinction between wells is not to be expected, except in those cases in which the vegetation is completely different [85].
3.6. Sensitivity of Unsaturated Zone to Possible Future Changes in Groundwater Level
The processes introduced above make it clear that even slight changes (of the order of tens of centimeters) in the position of water levels can have significant consequences, depending on the direction of water level change [83]. The latter may affect vegetation diversity [83] and the landscape functionality [86], since the vegetation is an immensely vulnerable part of the ecosystem, due to its water demand and the effect of soil humidity [87]. Several studies call attention to the subject in relation to the Danube [88,89,90], as well as to other large rivers [91] and their immediate environments [92]. The general water level decrease following the 1992 diversion of the Danube (in certain places, these were on the order of several meters [35]) made the Szigetköz especially sensitive in those areas where the all-time water level is close to or directly into the gravel layer (Upper Szigetköz and floodplain zone of the Danube). The map in Figure 6 shows the zones where groundwater reaches as far as the gravel layer. There is no traceable diurnal period in the wells in those areas, and as a consequence, no direct connection to the surface process can be traced.
On the basis of the above, and from the perspective of “good housekeeping” in water governance, it is apparent that when one examines the water balance, it is precisely those areas where the all-time water level is close to the boundary of the two lithological units that are the most sensitive to contingent GW water level changes. Consequently, the decreasing water level, whether due to anthropogenic factors like water governance practices or climate change—natural or human-induced—can significantly affect the water balance of the upper layer and its moisture factors. These impacts can be direct and widespread. In order to highlight these changes, the given water level distance from the boundary of the two lithological units was determined for each point, and an average was calculated for each well over the entire investigated period. The map (Figure 9) compiled from these data shows the difference between the all-time water level and the lithological boundary.
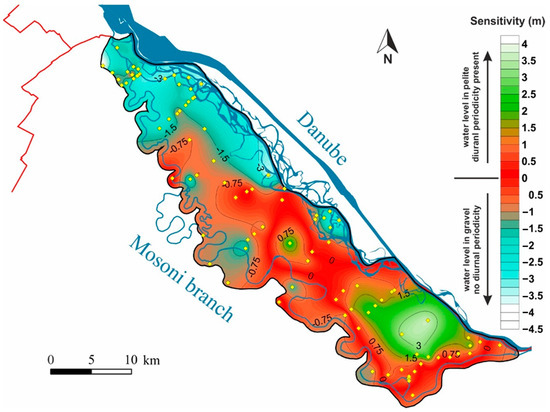
Figure 9.
Map showing sensitivity of moisture content of the unsaturated zone of the Szigetköz. Warmer colors represent areas where small changes in groundwater level could lead to significant alteration in capillary fringe, and colder colors indicate the opposite. The red hairline indicates the country border. Yellow markers indicate the SGW monitoring wells and the thick dark-blue line indicates the main riverbed.
A considerable part of the groundwater in the middle and eastern (lower) part of Szigetköz would lie beyond the pelitic zone if there were a further 75 cm decrease in the water level. If the respective water level reaches the gravelly zone, the capillary system, which hitherto had drawn support from the GW, will not be able to constitute itself, so no capillary fringe of any great significance will develop. Consequently, the water balance of the entire cover layer is transformed, its humidity content decreases, and only water arriving from above as a result of precipitation events can humidify the soil to any great extent. Due to the cessation of the constant capillary fringe, the groundwater loses its direct connection with the rhizosphere, so daily water absorption by vegetation does not affect groundwater levels directly.
It is a known fact that one of the dominant background factors behind the variance in groundwater levels is the flow regime of the Danube in the area [38,39]. As a result, it should be expected that in such cases, a negative development can be observed in the connection between the discharge of rivers and/or the communication between the surface water and groundwater. For instance, riverbed clogging emerges [93], and less water infiltrates beneath the surface [94]. This, in turn, results in a decrease in the water level and a lack of water in a major part of the cover layer. One of the remarkable driving factors of interaction between surface waters and groundwater in the Szigetköz is the riverbed clogging found in the lower sections of the Danube [34,40,44]. This is the product of the altered conditions of deposition, which was caused by a decrease in runoff largely attributable to anthropogenic impact.
Identifying the processes that significantly affect the diurnal periodicity of groundwater allows establishing that the physical properties of the water table medium are crucial in determining the extent to which surface influences penetrate below the surface.
At the current groundwater level, even a small rise of tens of centimeters can affect the gravel zone from the upper layer. While the capillary effect does not cease entirely, it weakens and cannot raise water further (<∼cm), leading to the drying of the unsaturated zone. Conversely, if the groundwater level rises, previously dry soils can absorb more water. Thus, even minor changes in water level can significantly alter soil moisture, and evapotranspiration can impact the water balance in the unsaturated zone. The long-term effects of the altered moisture conditions can be expected as follows:
- Due to the lack of moisture in the upper layers of the soil, the productivity and actual yield of agriculture decreases.
- The altered moisture conditions may affect natural ecological communities, changing the plant community and, as a result, the habitat as well. A habitat change of such a nature usually results in a decrease in biodiversity [95] and contributes to the spreading of pioneer and invasive species [96], which can then alter the landscape [86].
- The changing water balance may affect the physical and chemical properties of soils and may even cause the degradation of the soil, which can be to the further detriment of the water balance of the soil.
- Groundwater levels decreasing due to localized anthropogenic effects or major evapotranspiration resulting from climate change (e.g., drought) may affect vulnerable water tables directly, and these events thus have a serious negative impact on groundwater supply.
A potential general solution to the problem of the decreasing elevation of the water table, which modifies the groundwater flow systems and affects the location of the recharge and the discharge areas (e.g., [97]), are managed aquifer recharge (MAR) systems. These provide various technical solutions to restore subsurface flow systems and support groundwater-dependent ecosystems [98,99]. Finite element numerical modeling has been carried out to investigate the artificial recharge mechanism over time in two Hungarian study areas: the Danube-Tisza Interfluve [100] and the Nyírség (NE Hungary) [101]. These simulations confirm the effectiveness of MAR technology in local-scale groundwater flow systems before construction. The Szigetköz is also considered a potential MAR site, where the infiltration water is provided by the surface water, the Danube. Of course, the primary solution would be the targeted and joint water management of the area by the neighboring countries, since the Danube water level is the primary driving factor of the subsurface water level [39].
4. Conclusions and Outlook
The study focused on understanding the relationship between surface meteorological parameters and SGW dynamics within the inner-delta of the River Danube, the Szigetköz region. The findings reveal distinct behaviors between hourly and daily data analyses, shedding light on the complex interactions governing these systems.
The daily periodic fluctuation in the surface water level time series was investigated by applying wavelet spectrum analysis, resulting in the observation that the presence of daily periodicity is significant in part of the wells (41%, Figure 4B). By contrast, the diurnal periodic fluctuations in the water temperature cannot be identified (Figure 4A). According to the results of the wavelet coherence test, the water level time series pattern follows the change in the time series pattern of PET by a time period of between 5 and 12 h. On the basis of the results, it can be concluded that daily fluctuation is influenced by evapotranspiration.
Hourly water temperature data from SGW wells showed poor correlation with surface meteorological parameters, indicating minimal direct influence of high-frequency meteorological variations on groundwater dynamics. Conversely, daily averages exhibited stronger correlations, particularly with air temperature and PET. This shift suggests that low-frequency variations are more influential in shaping SGW behavior. PET emerged as a key driver influencing SGW fluctuations, with a significant correlation observed on a daily scale. The close relationship between PET and SGW dynamics underscores the importance of surface processes in regulating groundwater levels, especially during warmer months characterized by higher evapotranspiration rates.
The physical properties of lithological units play a crucial role in determining the periodicity of SGW fluctuations. The periodic daily behavior of SGW does not primarily depend on the depth of the groundwater level, but rather on the physical properties of the lithological unit characteristic of a given depth. Wells tapping into fine-grained sediment exhibited diurnal periodicity, driven by capillary action facilitating water movement between groundwater and the surface. In contrast, wells situated solely within gravelly layers displayed aperiodic behavior, indicating limited capillary influence all year round, and capillary elevation was found to be the determining factor of periodic water level fluctuations (Figure 8), creating a teleconnection between the groundwater table and the upper stratigraphic layer.
The change in the degree of capillary water elevation is important with regard to both the water balance of the unsaturated zone (above the groundwater table) and from an ecological point of view. Therefore, the reduction in the water level needed to make the existing groundwater table shift from the upper fine-grained strata to the underlying gravel strata is an important issue.
Changes in groundwater levels, driven by factors such as evapotranspiration and lithological composition, can directly impact soil moisture, vegetation patterns, and ecosystem stability. Sensitivity maps highlight areas vulnerable to even minor fluctuations in groundwater levels, emphasizing the need for informed water governance strategies.
The anthropogenically altered hydrological conditions in the Szigetköz region now closely resemble those anticipated globally due to climate change. Consequently, this analysis not only exemplifies processes occurring in similarly modified river sections—serving as a pilot area—but also those expected to experience aridification.
Author Contributions
B.T. was responsible for conceptualization, data curation, writing the original draft, writing—review and editing, funding acquisition, methodology, visualization, data curation, formal analysis, and software development. I.G.H. contributed to writing the original draft, writing—review and editing, and methodology. T.G. was involved in writing the original draft, methodology, visualization, formal analysis, and software development. I.K.-S. focused on writing—review and editing, and validation. N.M. worked on writing the original draft, formal analysis, and writing—review and editing. J.K. contributed to conceptualization, writing—review and editing, funding acquisition, methodology, data curation, and validation, and T.T.-H. was responsible for writing the original draft, project administration, and formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This work was completed in the ELTE Institutional Excellence Program (grant number: TKP2020-IKA-05) financed by the Hungarian Ministry of Human Capacities. We would also like to thank Green Geo Hungary Ltd., leading Hungarian provider of intelligent green energy solutions, for providing financial, theoretical, and technical background for the study (grant number: CSR-#101).
Data Availability Statement
The data presented in this study are available on request from the North-Transdanubian Water Directorate and the first author.
Acknowledgments
The core of this paper was the Ph.D. dissertation of the first author, Trásy B., not published elsewhere.
Conflicts of Interest
Authors Balázs Trásy and Tamás Garamhegyi were employed by the company Green Geo Hungary Ltd. Author József Kovács was employed by the company Midori-Öko Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Alley, W.M.; Healy, R.W.; LaBaugh, J.W.; Reilly, T.E. Flow and Storage in Groundwater Systems. Science 2002, 296, 1985–1990. [Google Scholar] [CrossRef] [PubMed]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef]
- MacDonald, A.M.; Bonsor, H.C.; Dochartaigh, B.É.Ó.; Taylor, R.G. Quantitative maps of groundwater resources in Africa. Environ. Res. Lett. 2012, 7, 024009. [Google Scholar] [CrossRef]
- Hughes, J.D.; Petrone, K.C.; Silberstein, R.P. Drought, groundwater storage and stream flow decline in southwestern Australia. Geophys. Res. Lett. 2012, 39, L03408. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.H.; van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, L20402. [Google Scholar] [CrossRef]
- Xanke, J.; Liesch, T. Quantification and possible causes of declining groundwater resources in the Euro-Mediterranean region from 2003 to 2020. Hydrogeol. J. 2022, 30, 379–400. [Google Scholar] [CrossRef]
- Qi, P.; Zhang, G.; Xu, Y.J.; Wang, L.; Ding, C.; Cheng, C. Assessing the Influence of Precipitation on Shallow Groundwater Table Response Using a Combination of Singular Value Decomposition and Cross-Wavelet Approaches. Water 2018, 10, 598. [Google Scholar] [CrossRef]
- Tóth, Á.; Baják, P.; Szijártó, M.; Tiljander, M.; Korkka-Niemi, K.; Hendriksson, N.; Mádl-Szőnyi, J. Multimethodological Revisit of the Surface Water and Groundwater Interaction in the Balaton Highland Region—Implications for the Overlooked Groundwater Component of Lake Balaton, Hungary. Water 2023, 15, 1006. [Google Scholar] [CrossRef]
- Czauner, B.; Erőss, A.; Szkolnikovics-Simon, S.; Markó, Á.; Baják, P.; Trásy-Havril, T.; Szijártó, M.; Szabó, Z.; Hegedűs-Csondor, K.; Mádl-Szőnyi, J. From basin-scale groundwater flow to integrated geofluid research in the hydrogeology research group of Eötvös Loránd University, Hungary. J. Hydrol. X 2022, 17, 100142. [Google Scholar] [CrossRef]
- Galsa, A.; Tóth, Á.; Szijártó, M.; Pedretti, D.; Mádl-Szőnyi, J. Interaction of basin-scale topography- and salinity-driven groundwater flow in synthetic and real hydrogeological systems. J. Hydrol. 2022, 609, 127695. [Google Scholar] [CrossRef]
- Barthel, R.; Banzhaf, S. Groundwater and Surface Water Interaction at the Regional-scale—A Review with Focus on Regional Integrated Models. Water Resour. Manag. 2016, 30, 1–32. [Google Scholar] [CrossRef]
- Kalbus, E.; Reinstorf, F.; Schirmer, M. Measuring methods for groundwater–surface water interactions: A review. Hydrol. Earth Syst. Sci. 2006, 10, 873–887. [Google Scholar] [CrossRef]
- Garamhegyi, T.; Kovács, J.; Pongrácz, R.; Tanos, P.; Hatvani, I.G. Investigation of the climate-driven periodicity of shallow groundwater level fluctuations in a Central-Eastern European agricultural region. Hydrogeol. J. 2018, 26, 677–688. [Google Scholar] [CrossRef]
- Magyar, N.; Hatvani, I.G.; Arató, M.; Trásy, B.; Blaschke, A.P.; Kovács, J. A New Approach in Determining the Decadal Common Trends in the Groundwater Table of the Watershed of Lake “Neusiedlersee”. Water 2021, 13, 290. [Google Scholar] [CrossRef]
- Han, Z.; Huang, S.; Huang, Q.; Leng, G.; Wang, H.; Bai, Q.; Zhao, J.; Ma, L.; Wang, L.; Du, M. Propagation dynamics from meteorological to groundwater drought and their possible influence factors. J. Hydrol. 2019, 578, 124102. [Google Scholar] [CrossRef]
- Molnar, S.; Molnar, M.; Csabragi, A. Impact Assessment Of Mitigation Strategies in the Hungarian Agriculture. J. Agric. Inform. 2011, 2, 10–17. [Google Scholar] [CrossRef][Green Version]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, 1–22. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; MacQuarrie, K.T.B.; Voss, C.I. Climate change impacts on the temperature and magnitude of groundwater discharge from shallow, unconfined aquifers. Water Resour. Res. 2014, 50, 3253–3274. [Google Scholar] [CrossRef]
- Whitehead, P.G.; Wilby, R.L.; Battarbee, R.W.; Kernan, M.; Wade, A.J. A review of the potential impacts of climate change on surface water quality. Hydrol. Sci. J. 2009, 54, 101–123. [Google Scholar] [CrossRef]
- Bouraoui, F.; Vachaud, G.; Li, L.Z.X.; Le Treut, H.; Chen, T. Evaluation of the impact of climate changes on water storage and groundwater recharge at the watershed scale. Clim. Dyn. 1999, 15, 153–161. [Google Scholar] [CrossRef]
- Spane, F.A. Considering barometric pressure in groundwater flow investigations. Water Resour. Res. 2002, 38, 14-11–14-18. [Google Scholar] [CrossRef]
- Robins, N.S.; Finch, J.W. Groundwater flood or groundwater-induced flood? Q. J. Eng. Geol. Hydrogeol. 2012, 45, 119–122. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Famiglietti, J. Groundwater Variability across Temporal and Spatial Scales in the Central and Northeastern U.S. J. Hydrol. 2015, 525, 769–780. [Google Scholar] [CrossRef]
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.G.; Sivapalan, M.; et al. Twenty-three unsolved problems in hydrology (UPH)—A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef]
- Liu, S.; Huang, S.; Xie, Y.; Leng, G.; Huang, Q.; Wang, L.; Xue, Q. Spatial-temporal changes of rainfall erosivity in the loess plateau, China: Changing patterns, causes and implications. CATENA 2018, 166, 279–289. [Google Scholar] [CrossRef]
- Edenhofer, O.; Seyboth, K. Intergovernmental Panel on Climate Change (IPCC); United Nations: Vienna, Austria, 2013; pp. 48–56. [Google Scholar]
- Molnár, S.; Molnar, M. Comprehensive assessment of climate change policies and measures in Hungary: Concerns and tasks in an underestimated challenge. Idojaras 2012, 116, 297–321. [Google Scholar]
- Zeng, R.; Cai, X. Analyzing streamflow changes: Irrigation-enhanced interaction between aquifer and streamflow in the Republican River basin. Hydrol. Earth Syst. Sci. 2014, 18, 493–502. [Google Scholar] [CrossRef]
- Jaramillo, M. Riverbank filtration: An efficient and economical drinking-water treatment technology. DYNA 2012, 79, 148–157. [Google Scholar]
- Chapman, D.V.; Bradley, C.; Gettel, G.M.; Hatvani, I.G.; Hein, T.; Kovács, J.; Liska, I.; Oliver, D.M.; Tanos, P.; Trásy, B.; et al. Developments in water quality monitoring and management in large river catchments using the Danube River as an example. Environ. Sci. Policy 2016, 64, 141–154. [Google Scholar] [CrossRef]
- Winter, T.C.; Harvey, J.W.; Franke, O.L.; Alley, W.M. Ground Water and Surface Water: A Single Resource; Circular 1139; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 1998. [Google Scholar]
- Apurv, T.; Sivapalan, M.; Cai, X. Understanding the Role of Climate Characteristics in Drought Propagation. Water Resour. Res. 2017, 53, 9304–9329. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.-W.; Sethi, R. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Eng. Appl. Artif. Intell. 2012, 25, 1670–1676. [Google Scholar] [CrossRef]
- Trásy, B.; Magyar, N.; Havril, T.; Kovács, J.; Garamhegyi, T. The Role of Environmental Background Processes in Determining Groundwater Level Variability—An Investigation of a Record Flood Event Using Dynamic Factor Analysis. Water 2020, 12, 2336. [Google Scholar] [CrossRef]
- Smith, S.E.; Büttner, G.; Szilagyi, F.; Horvath, L.; Aufmuth, J. Environmental Impacts of River Diversion: Gabcikovo Barrage System. J. Water Resour. Plan. Manag. 2000, 126, 138–145. [Google Scholar] [CrossRef]
- Jansky, L.; Pachova, N.I.; Murakami, M. The Danube: A case study of sharing international waters. Glob. Environ. Chang. 2004, 14, 39–49. [Google Scholar] [CrossRef]
- Völgyesi, I. A Kisalföld talajvíz-és rétegvíz helyzete. Hidrol. Közlöny 1994, 74, 260–268. [Google Scholar]
- Trásy, B.; Garamhegyi, T.; Laczkó-Dobos, P.; Kovács, J.; István Gábor, H. Geostatistical screening of flood events in the groundwater levels of the diverted inner delta of the Danube River: Implications for river bed clogging. Open Geosci. 2018, 10, 64–78. [Google Scholar] [CrossRef]
- Kovács, J.; Márkus, L.; Szalai, J.; Kovács, I.S. Detection and evaluation of changes induced by the diversion of River Danube in the territorial appearance of latent effects governing shallow-groundwater fluctuations. J. Hydrol. 2015, 520, 314–325. [Google Scholar] [CrossRef]
- Trásy, B.; József, K.; István Gábor, H.; Timea, H.; Tibor, N.; Péter, S.; Csaba, S. Assessment of the interaction between surface- and sub-surface waters after the diversion in the inner delta of the River Danube using multivariate statistics. Anthropocene 2018, 22, 14. [Google Scholar] [CrossRef]
- Deák, J.; László, F.; Liebe, P. A felszín alatti vizek utánpótlódásának, áramlási viszonyainak, szintjének és minőségének változása. In Proceedings of the A Szigetközi Környezeti Monitoring Eredményei, Mosonmagyaróvár, Budapest, Hungary, 20–21 February 2002. [Google Scholar]
- ÉDUKÖVIZIG. (North-Transdanubian Water Directorate); ÉDUKÖVIZIG: Győr, Hungary, 2014. [Google Scholar]
- Trásy, B. The Effects of River-Diversion on the Behavior of Shallow Groundwater in the Szigetköz Inner Delta of the River Danube (Hungary). Ph.D. Thesis, Eötvös Loránd University, Budapest, Hungary, 2018. [Google Scholar]
- Scharek, P.; Don, G.; Horvath, I.; Toth, G. Results of the modern depositional process and hydrogeologic investigations in Szigetkoz, Hungary. Operation of a geologic monitoring system by the geological institute of Hungary. Acta Geol. Hung. 2000, 43, 85–106. [Google Scholar]
- EC. EU Water Framework Directive; EC Directive; EC: Maastricht, The Netherlands, 2000; Volume 60. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Allen, R.G.; Pruitt, W.O.; Wright, J.L.; Howell, T.A.; Ventura, F.; Snyder, R.; Itenfisu, D.; Steduto, P.; Berengena, J.; Yrisarry, J.B. A recommendation on standardized surface resistance for hourly calculation of reference ETo by the FAO56 Penman-Monteith method. Agric. Water Manag. 2006, 81, 1–22. [Google Scholar] [CrossRef]
- Available online: https://cds.climate.copernicus.eu (accessed on 2 February 2018).
- Available online: https://www.ncei.noaa.gov (accessed on 2 February 2018).
- Pearson, K. Note on Regression and Inheritance in the Case of Two Parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- Pörtge, K.-H. Tagesperiodische Schwankungen des Abflusses in Kleinen Einzugsgebieten als Ausdruck Komplexer Wasser-und Stoffflüsse; E. Goltze: Berlin, Germany, 1996. [Google Scholar]
- Dingman, S.L. Physical Hydrology; Waveland Press: Long Grove, IL, USA, 2015. [Google Scholar]
- Wang, F.; Wang, X.; Zhao, Y.; Yang, Z. Long-term changes of water level associated with chlorophyll a concentration in Lake Baiyangdian, North China. Procedia Environ. Sci. 2012, 13, 1227–1237. [Google Scholar] [CrossRef][Green Version]
- Nalley, D.; Adamowski, J.; Khalil, B.; Biswas, A. Inter-annual to inter-decadal streamflow variability in Quebec and Ontario in relation to dominant large-scale climate indices. J. Hydrol. 2016, 536, 426–446. [Google Scholar] [CrossRef]
- Salamalikis, V.; Argiriou, A.A.; Dotsika, E. Periodicity analysis of δ18O in precipitation over Central Europe: Time–frequency considerations of the isotopic ‘temperature’ effect. J. Hydrol. 2016, 534, 150–163. [Google Scholar] [CrossRef]
- Sen, A.K.; Kern, Z. Wavelet analysis of low-frequency variability in oak tree-ring chronologies from east Central Europe. Open Geosci. 2016, 8, 478–483. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Kovács, J.; Hatvani, I.G.; Korponai, J.; Kovács, I.S. Morlet wavelet and autocorrelation analysis of long-term data series of the Kis-Balaton water protection system (KBWPS). Ecol. Eng. 2010, 36, 1469–1477. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory—Part I: Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Hatvani, I.G.; Kern, Z.; Leél-Őssy, S.; Demény, A. Speleothem stable isotope records for east-central Europe: Resampling sedimentary proxy records to obtain evenly spaced time series with spectral guidance. Earth Syst. Sci. Data 2018, 10, 139–149. [Google Scholar] [CrossRef]
- Rösch, A.; Schmidbauer, H. WaveletComp 1.1: A guided Tour through the R Package. 2014. Available online: http://www.hs-stat.com/projects/WaveletComp/WaveletComp_guided_tour.pdf (accessed on 2 February 2018).
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Kovács, J.; Márkus, L.; Szalai, J.; Barcza, M.; Bernáth, G.; Kovácsné Székely, I.; Halupka, G. Exploring Potentially Hazardous Areas for Water Quality Using Dynamic Factor Analysis. In Water Quality; Kostas, V., Dimitra, V., Eds.; IntechOpen: Rijeka, Croatia, 2012; Chapter 9. [Google Scholar]
- Nagy, B.; Ignéczi, Á.; Kovács, J.; Szalai, Z.; Mari, L. Shallow ground temperature measurements on the highest volcano of the Earth, the Mt. Ojos del Salado, Arid Andes, Chile. Permafr. Periglac. Process. 2018; in press. [Google Scholar]
- Karátson, D. Pannon enciklopédia. In Magyarország Földje–Kitekintéssel a Kárpát-Medence Egészére (Pannonian Encyclopedia: The Land of Hungary with an Outlook to the Whole Carpathian Basin); Kertek: Budapest, Hungary, 2000. [Google Scholar]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Gribovszki, Z.; Szilágyi, J.; Kalicz, P. Diurnal fluctuations in shallow groundwater levels and streamflow rates and their interpretation—A review. J. Hydrol. 2010, 385, 371–383. [Google Scholar] [CrossRef]
- Hatvani, I.G.; Clement, A.; Korponai, J.; Kern, Z.; Kovács, J. Periodic signals of climatic variables and water quality in a river–eutrophic pond–wetland cascade ecosystem tracked by wavelet coherence analysis. Ecol. Indic. 2017, 83, 21–31. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M. Capturing the influence of groundwater dynamics on land surface processes using an integrated, distributed watershed model. Water Resour. Res. 2008, 44, W02402. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. An Overview of Unsaturated Soil Behaviour. In Proceedings of the ASCE Specialty Session Unsaturated Soil Properties, Dallas, TX, USA, 24–28 October 1993. [Google Scholar]
- Fredlund, D. The scope of unsaturated soil mechanics: An overview. In Proceedings of the First International Conference on Unsaturated Soils, Paris, France, 6–8 September 1995. [Google Scholar]
- De Vries, D. Simultaneous transfer of heat and moisture in porous media. Eos Trans. Am. Geophys. Union 1958, 39, 909–916. [Google Scholar]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology; Wiley: New York, NY, USA, 1998; Volume 506. [Google Scholar]
- Kozeny, J. Das tägliche periodische steigen und fallen des grundwasserspiegels. Die Wasserwirtsch. 1933, 31, 424–427. [Google Scholar]
- Ubell, K. Über die gesetzmassigkeiten des grundwassergangs and des grundwasserhaushalts in flachlandgebieten. Wasserwirtsch. Wassertech. 1961, 11, 366–372. [Google Scholar]
- Meyboom, P. Three observations on streamflow depletion by phreatophytes. J. Hydrol. 1965, 2, 248–261. [Google Scholar] [CrossRef]
- Reigner, I.C. A method of estimating steamflow loss by evapotranspiration from the riparian zone. For. Sci. 1966, 12, 130–139. [Google Scholar]
- Bond, B.J.; Jones, J.A.; Moore, G.; Phillips, N.; Post, D.; McDonnell, J.J. The zone of vegetation influence on baseflow revealed by diel patterns of streamflow and vegetation water use in a headwater basin. Hydrol. Process. 2002, 16, 1671–1677. [Google Scholar] [CrossRef]
- White, W.N. A Method of Estimating Ground-Water Supplies Based on Discharge by Plants and Evaporation from Soil: Results of Investigations in Escalante Valley, Utah; US Government Printing Office: Washington, DC, USA, 1932; Volume 659. [Google Scholar]
- Rodríguez-Iturbe, I.; Porporato, A. Ecohydrology of Water-Controlled Ecosystems: Soil Moisture and Plant Dynamics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Bauer, P.; Thabeng, G.; Stauffer, F.; Kinzelbach, W. Estimation of the evapotranspiration rate from diurnal groundwater level fluctuations in the Okavango Delta, Botswana. J. Hydrol. 2004, 288, 344–355. [Google Scholar] [CrossRef]
- Nachabe, M.; Shah, N.; Ross, M.; Vomacka, J. Evapotranspiration of Two Vegetation Covers in a Shallow Water Table Environment. Soil Sci. Soc. Am. J. 2005, 69, 492–499. [Google Scholar] [CrossRef]
- Thal-Larsen, J.H. Fluctuations in the level of the phreatic surface with an atmospheric deposit in the form of dew. Bodenkd. Forsch. 1934, 4, 223–233. [Google Scholar]
- Moreo, M.T.; Andraski, B.J.; Garcia, C.A. Groundwater Discharge by Evapotranspiration, Flow of Water in Unsaturated Soil, and Stable Isotope Water Sourcing in Areas of Sparse Vegetation, Amargosa Desert, Nye County, Nevada; 2328-0328; US Geological Survey: Reston, VA, USA, 2017. [Google Scholar]
- Euliss, N.H.; Mushet, D.M. Water-level fluctuation in wetlands as a function of landscape condition in the prairie pothole region. Wetlands 1996, 16, 587–593. [Google Scholar] [CrossRef]
- Loheide, S.P.; Butler, J.J.; Gorelick, S.M. Estimation of groundwater consumption by phreatophytes using diurnal water table fluctuations: A saturated-unsaturated flow assessment. Water Resour. Res. 2005, 41, W07030. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Hirschi, M.; Mueller, B.; Dorigo, W.; Seneviratne, S.I. Using remotely sensed soil moisture for land–atmosphere coupling diagnostics: The role of surface vs. root-zone soil moisture variability. Remote Sens. Environ. 2014, 154, 246–252. [Google Scholar] [CrossRef]
- Heiler, G.; Hein, T.; Schiemer, F.; Bornette, G. Hydrological connectivity and flood pulses as the central aspects for the integrity of a river-floodplain system. Regul. Rivers Res. Manag. 1995, 11, 351–361. [Google Scholar] [CrossRef]
- Hudon, C. Impact of water level fluctuations on St. Lawrence River aquatic vegetation. Can. J. Fish. Aquat. Sci. 1997, 54, 2853–2865. [Google Scholar] [CrossRef]
- Trebitz, A.S. Characterizing Seiche and Tide-driven Daily Water Level Fluctuations Affecting Coastal Ecosystems of the Great Lakes. J. Great Lakes Res. 2006, 32, 102–116. [Google Scholar] [CrossRef]
- Schälchli, U. The clogging of coarse gravel river beds by fine sediment. In Sediment/Water Interactions: Proceedings of the Fifth International Symposium; Hart, B.T., Sly, P.G., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 189–197. [Google Scholar]
- Lewandowski, J.; Lischeid, G.; Nützmann, G. Drivers of water level fluctuations and hydrological exchange between groundwater and surface water at the lowland River Spree (Germany): Field study and statistical analyses. Hydrol. Process. 2009, 23, 2117–2128. [Google Scholar] [CrossRef]
- Van Tol, G.; Dobben, H.v.; Schmidt, P.; Klap, J. Biodiversity of Dutch forest ecosystems as affected by receding groundwater levels and atmospheric deposition. Biodivers. Conserv. 1998, 7, 221–228. [Google Scholar]
- Pyšek, P.; Richardson, D.M. Invasive species, environmental change and management, and health. Annu. Rev. Environ. Resour. 2010, 35, 25–55. [Google Scholar] [CrossRef]
- Trásy-Havril, T.; Szkolnikovics-Simon, S.; Mádl-Szőnyi, J. How Complex Groundwater Flow Systems Respond to Climate Change Induced Recharge Reduction? Water 2022, 14, 3026. [Google Scholar] [CrossRef]
- Dillon, P.; Pavelic, P.; Page, D.; Beringen, H.; Ward, J. Managed Aquifer Recharge: An Introduction; Waterlines Report Series no. 13, February 2009; National Water Commisssion: Canberra, Australia, 2009. [Google Scholar]
- Imig, A.; Szabó, Z.; Halytsia, O.; Vrachioli, M.; Kleinert, V.; Rein, A. A review on risk assessment in managed aquifer recharge. Integr. Environ. Assess. Manag. 2022, 18, 1513–1529. [Google Scholar] [CrossRef] [PubMed]
- Szabó, Z.; Szijártó, M.; Tóth, Á.; Mádl-Szőnyi, J. The Significance of Groundwater Table Inclination for Nature-Based Replenishment of Groundwater-Dependent Ecosystems by Managed Aquifer Recharge. Water 2023, 15, 1077. [Google Scholar] [CrossRef]
- Simon, S.; Déri-Takács, J.; Szijártó, M.; Szél, L.; Mádl-Szőnyi, J. Wetland Management in Recharge Regions of Regional Groundwater Flow Systems with Water Shortage, Nyírség Region, Hungary. Water 2023, 15, 3589. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).