Using Machine Learning Models for Short-Term Prediction of Dissolved Oxygen in a Microtidal Estuary
Abstract
1. Introduction
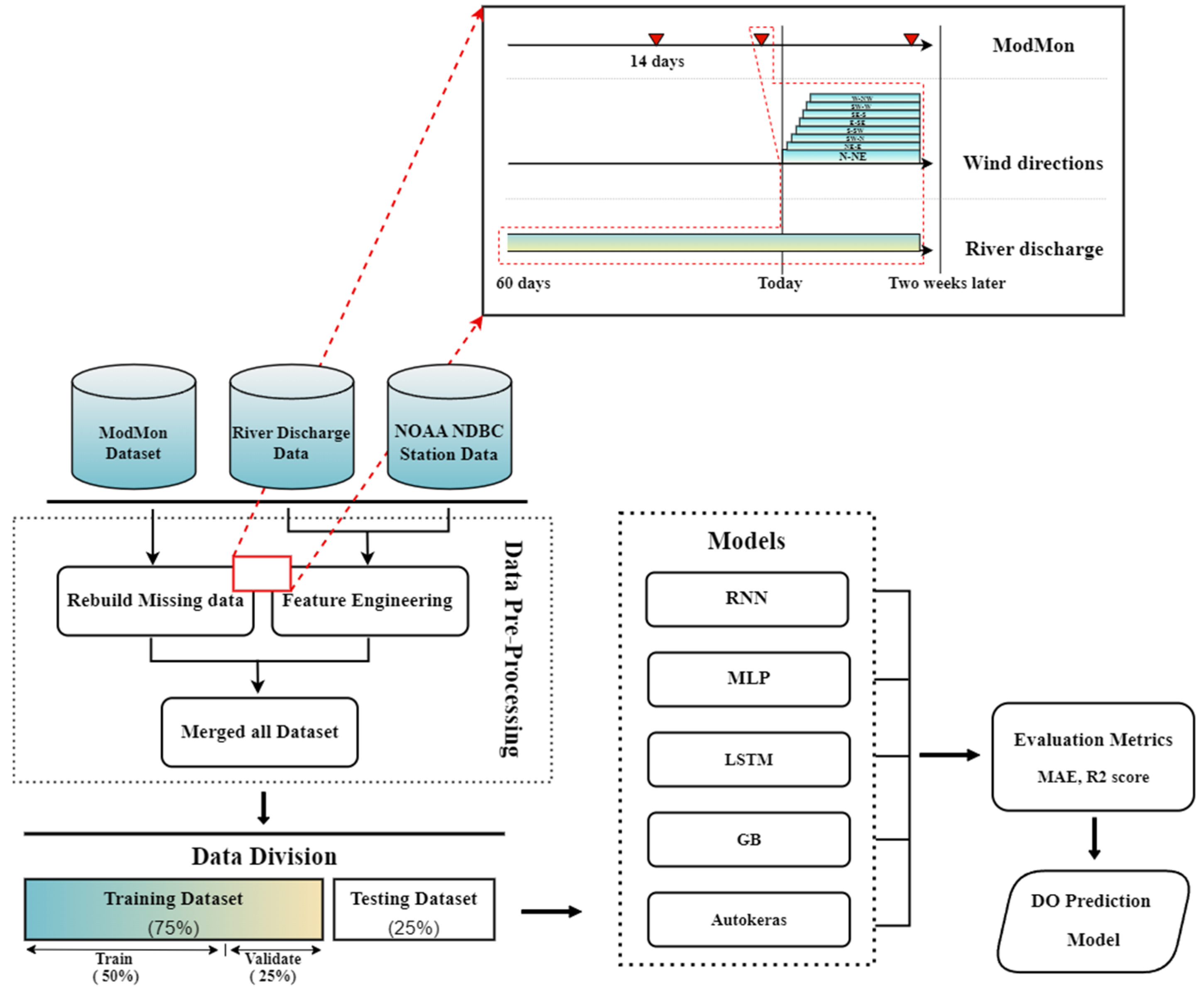
2. Materials and Methods
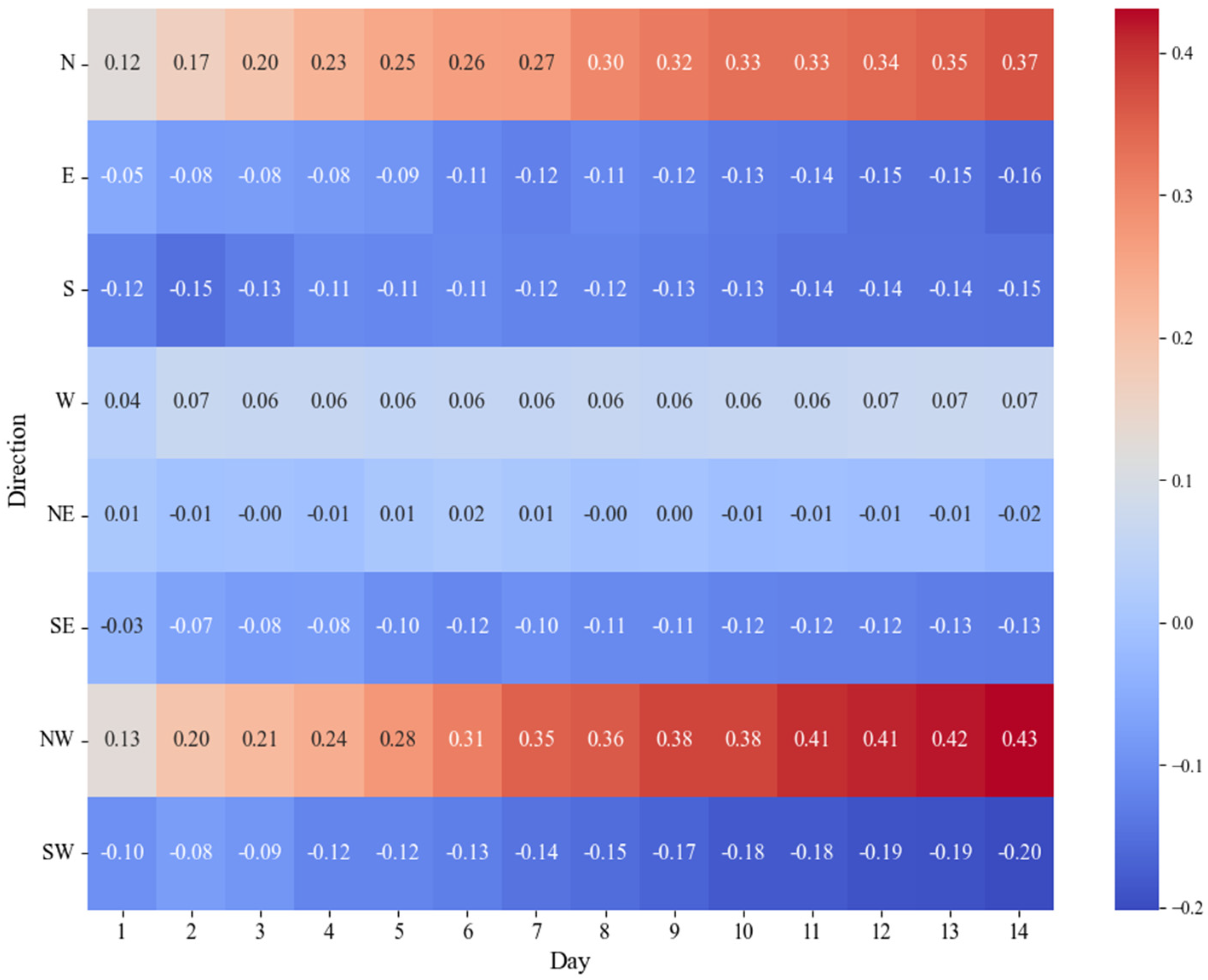
2.1. Study Area and Data
2.2. Machine Learning Models
2.2.1. The Multi-Layer Perceptron (MLP)
2.2.2. The Recurrent Neural Network (RNN)
2.2.3. Long Short-Term Memory (LSTM) Networks
2.2.4. Gradient Boosting (GB)
2.2.5. AutoKeras
2.3. The Model Application Process
2.4. Model Parameter Tuning
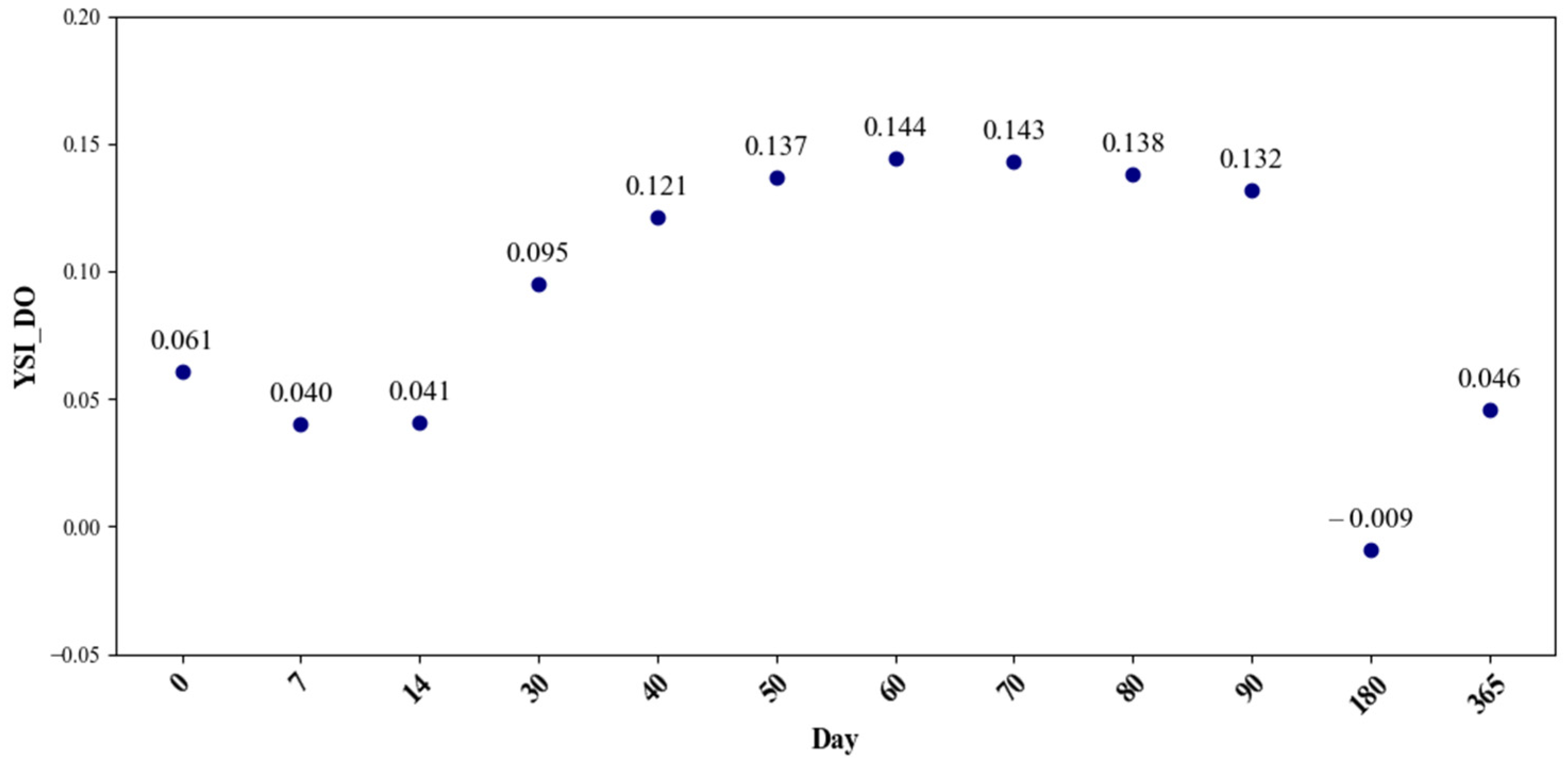
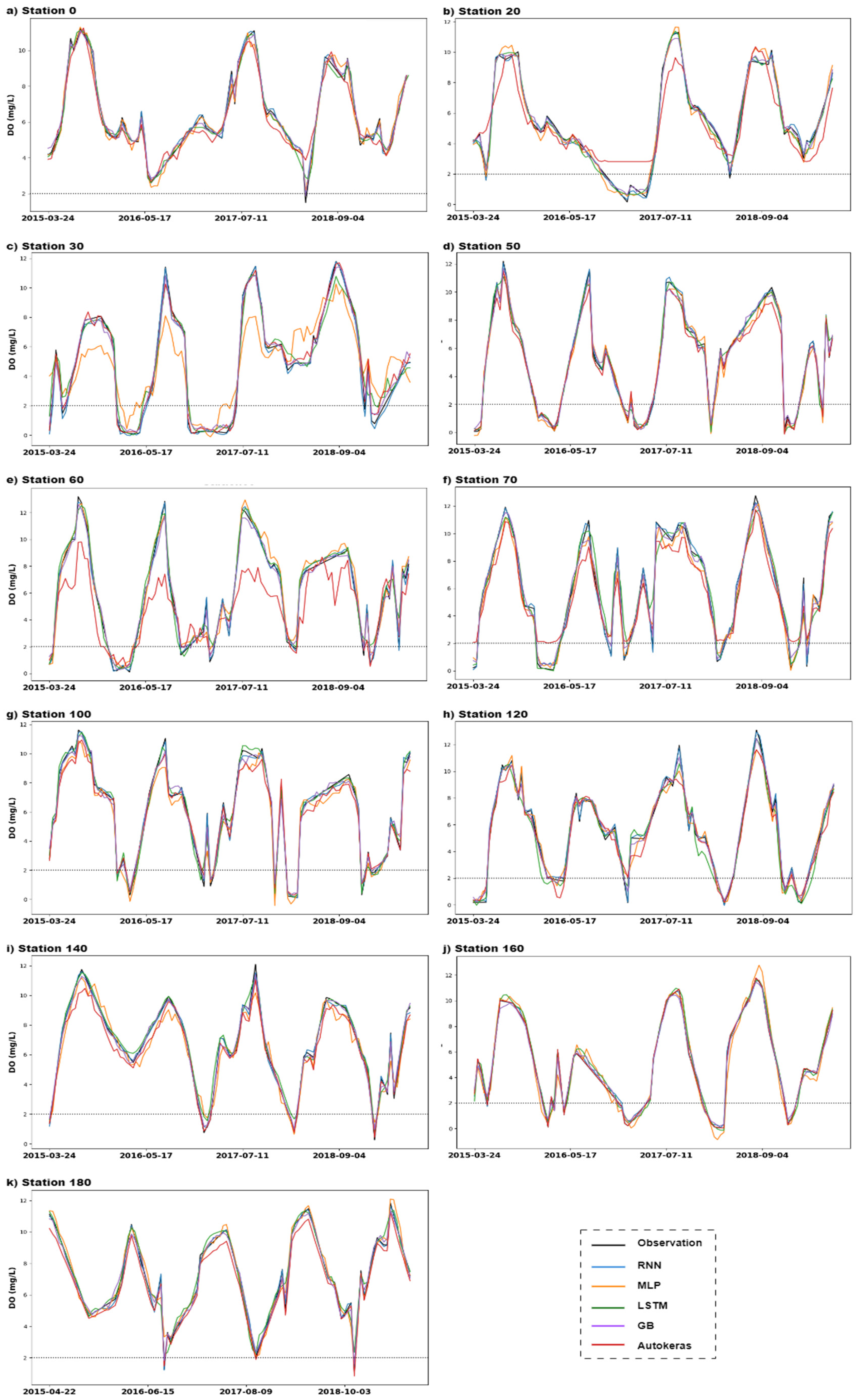
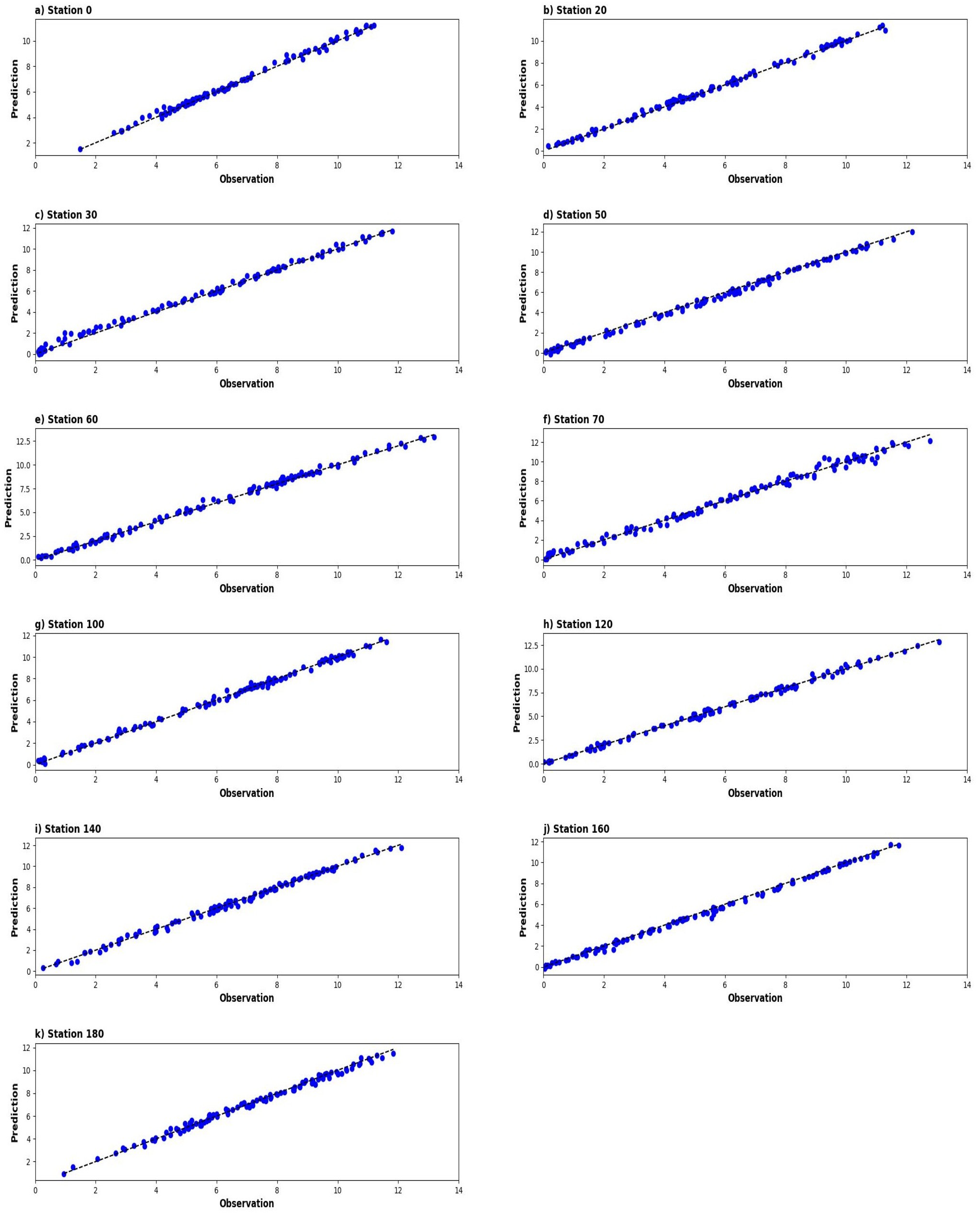
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paerl, H.W.; Rossignol, K.L.; Hall, S.N.; Peierls, B.L.; Wetz, M.S. Phytoplankton Community Indicators of Short- and Long-Term Ecological Change in the Anthropogenically and Climatically Impacted Neuse River Estuary, North Carolina, USA. Estuaries Coasts 2010, 33, 485–497. [Google Scholar] [CrossRef]
- Latif, S.D.; Azmi, M.S.B.N.; Ahmed, A.N.; Fai, C.M.; El-Shafie, A. Application of Artificial Neural Network for Forecasting Nitrate Concentration as a Water Quality Parameter: A Case Study of Feitsui Reservoir, Taiwan. IJDNE 2020, 15, 647–652. [Google Scholar] [CrossRef]
- Ziyad Sami, B.F.; Latif, S.D.; Ahmed, A.N.; Chow, M.F.; Murti, M.A.; Suhendi, A.; Ziyad Sami, B.H.; Wong, J.K.; Birima, A.H.; El-Shafie, A. Machine Learning Algorithm as a Sustainable Tool for Dissolved Oxygen Prediction: A Case Study of Feitsui Reservoir, Taiwan. Sci. Rep. 2022, 12, 3649. [Google Scholar] [CrossRef]
- Zhi, W.; Feng, D.; Tsai, W.-P.; Sterle, G.; Harpold, A.; Shen, C.; Li, L. From Hydrometeorology to River Water Quality: Can a Deep Learning Model Predict Dissolved Oxygen at the Continental Scale? Environ. Sci. Technol. 2021, 55, 2357–2368. [Google Scholar] [CrossRef]
- Vaquer-Sunyer, R.; Duarte, C.M. Thresholds of Hypoxia for Marine Biodiversity. Proc. Natl. Acad. Sci. USA 2008, 105, 15452–15457. [Google Scholar] [CrossRef]
- Farrell, A.P.; Richards, J.G. Chapter 11 Defining Hypoxia: An Integrative Synthesis of the Responses of Fish to Hypoxia. In Fish Physiology; Richards, J.G., Farrell, A.P., Brauner, C.J., Eds.; Hypoxia; Academic Press: Cambridge, MA, USA, 2009; Volume 27, pp. 487–503. [Google Scholar]
- Biddanda, B.A.; Weinke, A.D.; Kendall, S.T.; Gereaux, L.C.; Holcomb, T.M.; Snider, M.J.; Dila, D.K.; Long, S.A.; VandenBerg, C.; Knapp, K.; et al. Chronicles of Hypoxia: Time-Series Buoy Observations Reveal Annually Recurring Seasonal Basin-Wide Hypoxia in Muskegon Lake—A Great Lakes Estuary. J. Great Lakes Res. 2018, 44, 219–229. [Google Scholar] [CrossRef]
- Rowe, M.D.; Anderson, E.J.; Wynne, T.T.; Stumpf, R.P.; Fanslow, D.L.; Kijanka, K.; Vanderploeg, H.A.; Strickler, J.R.; Davis, T.W. Vertical Distribution of Buoyant Microcystis Blooms in a Lagrangian Particle Tracking Model for Short-Term Forecasts in Lake Erie. J. Geophys. Res. Ocean. 2016, 175, 238. [Google Scholar] [CrossRef]
- Moshogianis, A. A Statistical Model for the Prediction of Dissolved Oxygen Dynamics and the Potential for Hypoxia in the Mississippi Sound and Bight. Master’s Thesis, University of Southern Mississippi, Hattiesburg, MS, USA, 2015. [Google Scholar]
- Katin, A.; Del Giudice, D.; Obenour, D.R. Temporally Resolved Coastal Hypoxia Forecasting and Uncertainty Assessment via Bayesian Mechanistic Modeling. Hydrol. Earth Syst. Sci. 2022, 26, 1131–1143. [Google Scholar] [CrossRef]
- Chubarenko, I.; Tchepikova, I. Modelling of Man-Made Contribution to Salinity Increase into the Vistula Lagoon (Baltic Sea). Ecol. Model. 2001, 138, 87–100. [Google Scholar] [CrossRef]
- Marcomini, A.; Sute, G.W., II; Critto, A. (Eds.) Decision Support Systems for Risk-Based Management of Contaminated Sites; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISBN 978-0-387-09722-0. [Google Scholar]
- Scavia, D.; Justić, D.; Obenour, D.R.; Craig, J.K.; Wang, L. Hypoxic Volume Is More Responsive than Hypoxic Area to Nutrient Load Reductions in the Northern Gulf of Mexico—And It Matters to Fish and Fisheries. Environ. Res. Lett. 2019, 14, 024012. [Google Scholar] [CrossRef]
- Borsuk, M.E.; Higdon, D.; Stow, C.A.; Reckhow, K.H. A Bayesian Hierarchical Model to Predict Benthic Oxygen Demand from Organic Matter Loading in Estuaries and Coastal Zones. Ecol. Model. 2001, 143, 165–181. [Google Scholar] [CrossRef]
- Katin, A.; Del Giudice, D.; Obenour, D.R. Modeling Biophysical Controls on Hypoxia in a Shallow Estuary Using a Bayesian Mechanistic Approach. Environ. Model. Softw. 2019, 120, 104491. [Google Scholar] [CrossRef]
- Ahmed, A.A.M. Prediction of Dissolved Oxygen in Surma River by Biochemical Oxygen Demand and Chemical Oxygen Demand Using the Artificial Neural Networks (ANNs). J. King Saud. Univ.—Eng. Sci. 2017, 29, 151–158. [Google Scholar] [CrossRef]
- Yu, X.; Shen, J.; Du, J. A Machine-Learning-Based Model for Water Quality in Coastal Waters, Taking Dissolved Oxygen and Hypoxia in Chesapeake Bay as an Example. Water Resour. Res. 2020, 56, e2020WR027227. [Google Scholar] [CrossRef]
- Agatonovic-Kustrin, S.; Beresford, R. Basic Concepts of Artificial Neural Network (ANN) Modeling and Its Application in Pharmaceutical Research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 6th ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2021; ISBN 978-1-119-57872-7. [Google Scholar]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Lu, H.; Ma, X. Hybrid Decision Tree-Based Machine Learning Models for Short-Term Water Quality Prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Asadollah, S.B.H.S.; Sharafati, A.; Motta, D.; Yaseen, Z.M. River Water Quality Index Prediction and Uncertainty Analysis: A Comparative Study of Machine Learning Models. J. Environ. Chem. Eng. 2021, 9, 104599. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods Used for the Development of Neural Networks for the Prediction of Water Resource Variables in River Systems: Current Status and Future Directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Antanasijević, D.; Pocajt, V.; Povrenović, D.; Perić-Grujić, A.; Ristić, M. Modelling of Dissolved Oxygen Content Using Artificial Neural Networks: Danube River, North Serbia, Case Study: Environmental Science & Pollution Research. Environ. Sci. Pollut. Res. 2013, 20, 9006–9013. [Google Scholar] [CrossRef]
- Huang, J.; Liu, S.; Hassan, S.G.; Xu, L.; Huang, C. A Hybrid Model for Short-Term Dissolved Oxygen Content Prediction. Comput. Electron. Agric. 2021, 186, 106216. [Google Scholar] [CrossRef]
- Nair, J.P. Analysing and Modelling Dissolved Oxygen Concentration Using Deep Learning Architectures. Int. J. Mech. Eng. 2022, 7, 12–22. [Google Scholar]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A Comparative Analysis of XGBoost. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Taud, H.; Mas, J.F. Multilayer Perceptron (MLP); Springer: Berlin/Heidelberg, Germany, 2017; Volume 2024. [Google Scholar]
- Jin, H.; Song, Q.; Hu, X. Auto-Keras: An Efficient Neural Architecture Search System. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 1946–1956. [Google Scholar]
- Thompson, P.A.; Paerl, H.W.; Campbell, L.; Yin, K.; McDonald, K.S. Tropical Cyclones: What Are Their Impacts on Phytoplankton Ecology? J. Plankton Res. 2023, 45, 180–204. [Google Scholar] [CrossRef]
- Stow, C.A.; Roessler, C.; Borsuk, M.E.; Bowen, J.D.; Reckhow, K.H. Comparison of Estuarine Water Quality Models for Total Maximum Daily Load Development in Neuse River Estuary. J. Water Resour. Plann. Manag. 2003, 129, 307–314. [Google Scholar] [CrossRef]
- Paerl, H.; Pinckney, J.; Fear, J.; Peierls, B. Ecosystem Responses to Internal and Watershed Organic Matter Loading:Consequences for Hypoxia in the Eutrophying Neuse River Estuary, North Carolina, USA. Mar. Ecol. Prog. Ser. 1998, 166, 17–25. [Google Scholar] [CrossRef]
- Wool, T.A.; Davie, S.R.; Rodriguez, H.N. Development of Three-Dimensional Hydrodynamic and Water Quality Models to Support Total Maximum Daily Load Decision Process for the Neuse River Estuary, North Carolina. J. Water Resour. Plann. Manage. 2003, 129, 295–306. [Google Scholar] [CrossRef]
- Lin, J.; Liu, Q.; Song, Y.; Liu, J.; Yin, Y.; Hall, N.S. Temporal Prediction of Coastal Water Quality Based on Environmental Factors with Machine Learning. J. Mar. Sci. Eng. 2023, 11, 1608. [Google Scholar] [CrossRef]
- Peirce, C.S. The numerical measure of the success of predictions. Science 1884, 4, 453–454. [Google Scholar] [CrossRef]
- Raheli, B.; Aalami, M.; El-Shafie, A.; Ghorbani, M.; Deo, R. Uncertainty Assessment of the Multilayer Perceptron (MLP) Neural Network Model with Implementation of the Novel Hybrid MLP-FFA Method for Prediction of Biochemical Oxygen Demand and Dissolved Oxygen: A Case Study of Langat River. Environ. Earth Sci. 2017, 76, 503. [Google Scholar] [CrossRef]
- Ismail, M.R.; Awang, M.K.; Rahman, M.N.A.; Makhtar, M. A Multi-Layer Perceptron Approach for Customer Churn Prediction. Int. J. Multimed. Ubiquitous Eng. 2015, 10, 213–222. [Google Scholar] [CrossRef]
- Niroobakhsh, M. Prediction of Water Quality Parameter in Jajrood River Basin: Application of Multi Layer Perceptron (MLP) Perceptron and Radial Basis Function Networks of Artificial Neural Networks (ANNs). Afr. J. Agric. Res. 2012, 7, 4131–4139. [Google Scholar] [CrossRef]
- Selvin, S.; Ravi, V.; Gopalakrishnan, E.A.; Menon, V.; Kp, S. Stock. In Price Prediction Using. LSTM, RNN and CNN-Sliding Window Model. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; p. 1647. [Google Scholar]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, Y.; Zhao, Y.; Xie, M.; Zhong, J.; Tu, Z.; Liu, J. A Water Quality Prediction Method Based on the Deep LSTM Network Considering Correlation in Smart Mariculture. Sensors 2019, 19, 1420. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic Gradient Boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Bolick, M.M.; Post, C.J.; Naser, M.-Z.; Mikhailova, E.A. Comparison of Machine Learning Algorithms to Predict Dissolved Oxygen in an Urban Stream. Env. Sci. Pollut. Res. 2023, 30, 78075–78096. [Google Scholar] [CrossRef]
- Prasad, D.V.V.; Venkataramana, L.Y.; Kumar, P.S.; Prasannamedha, G.; Harshana, S.; Srividya, S.J.; Harrinei, K.; Indraganti, S. Analysis and Prediction of Water Quality Using Deep Learning and Auto Deep Learning Techniques. Sci. Total Environ. 2022, 821, 153311. [Google Scholar] [CrossRef]


| Models | Parameters | Value | Models | Parameters | Value |
|---|---|---|---|---|---|
| RNN | Learning rate | 0.001 | LSTM | Learning rate | 0.001 |
| Loss | Mean squared error | Loss | Mean squared error | ||
| Epochs | 200 | Epochs | 200 | ||
| Batch size | 32 | Batch size | 32 | ||
| The units of the RNN | 100 | The units of the LSTM | 100 | ||
| MLP | Learning rate | 0.001 | GB | Learning rate | 0.1 |
| Loss | Mean squared error | Number of estimators | 100 | ||
| Epochs | 300 | Random state | 32 | ||
| Batch size | 32 | AutoKeras | Epochs | 300 | |
| The units of the MLP | 128, 64 and 32 | The units of AutoKeras | 32, 32, 32, and 1 |
| Station | 0 | 20 | 30 | 50 | 60 | 70 | 100 | 120 | 140 | 160 | 180 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RNN | MAE | 0.13 | 0.17 | 0.18 | 0.13 | 0.14 | 0.16 | 0.12 | 0.16 | 0.14 | 0.11 | 0.11 |
| R2 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | |
| PSS | 1.00 | 1.00 | 0.96 | 1.00 | 0.90 | 1.00 | 0.94 | 0.90 | 1.00 | 0.97 | 0.99 | |
| MLP | MAE | 0.24 | 0.31 | 1.43 | 0.29 | 0.48 | 0.52 | 0.51 | 0.41 | 0.54 | 0.46 | 0.31 |
| R2 | 0.98 | 0.98 | 0.77 | 0.98 | 0.96 | 0.96 | 0.95 | 0.96 | 0.94 | 0.96 | 0.96 | |
| PSS | 1.00 | 0.88 | 0.85 | 0.93 | 0.83 | 0.68 | 0.92 | 0.40 | 0.86 | 0.49 | 0.00 | |
| LSTM | MAE | 0.24 | 0.24 | 0.46 | 0.29 | 0.45 | 0.53 | 0.30 | 0.45 | 0.28 | 0.29 | 0.31 |
| R2 | 0.98 | 0.98 | 0.96 | 0.98 | 0.96 | 0.95 | 0.98 | 0.96 | 0.98 | 0.98 | 0.96 | |
| PSS | 0.00 | 0.87 | 0.86 | 0.96 | 0.83 | 0.85 | 0.74 | 0.88 | 0.99 | 0.85 | 0.00 | |
| GB | MAE | 0.15 | 0.19 | 0.28 | 0.28 | 0.31 | 0.32 | 0.29 | 0.26 | 0.19 | 0.23 | 0.21 |
| R2 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.99 | 0.98 | 0.98 | |
| PSS | 1.00 | 0.88 | 0.93 | 0.98 | 0.79 | 0.86 | 0.94 | 0.82 | 0.75 | 0.90 | 1.00 | |
| AutoKeras | MAE | 0.39 | 0.93 | 0.26 | 0.32 | 1.45 | 0.93 | 0.41 | 0.50 | 0.38 | 0.12 | 0.39 |
| R2 | 0.93 | 0.82 | 0.98 | 0.98 | 0.69 | 0.90 | 0.97 | 0.95 | 0.96 | 0.99 | 0.96 | |
| PSS | 0.00 | 0.94 | 0.57 | 0.84 | 0.61 | 1.00 | 0.97 | 0.98 | 0.99 | 0.87 | 1.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gachloo, M.; Liu, Q.; Song, Y.; Wang, G.; Zhang, S.; Hall, N. Using Machine Learning Models for Short-Term Prediction of Dissolved Oxygen in a Microtidal Estuary. Water 2024, 16, 1998. https://doi.org/10.3390/w16141998
Gachloo M, Liu Q, Song Y, Wang G, Zhang S, Hall N. Using Machine Learning Models for Short-Term Prediction of Dissolved Oxygen in a Microtidal Estuary. Water. 2024; 16(14):1998. https://doi.org/10.3390/w16141998
Chicago/Turabian StyleGachloo, Mina, Qianqian Liu, Yang Song, Guozhi Wang, Shuhao Zhang, and Nathan Hall. 2024. "Using Machine Learning Models for Short-Term Prediction of Dissolved Oxygen in a Microtidal Estuary" Water 16, no. 14: 1998. https://doi.org/10.3390/w16141998
APA StyleGachloo, M., Liu, Q., Song, Y., Wang, G., Zhang, S., & Hall, N. (2024). Using Machine Learning Models for Short-Term Prediction of Dissolved Oxygen in a Microtidal Estuary. Water, 16(14), 1998. https://doi.org/10.3390/w16141998







