Abstract
In order to better understand the role of coral reefs around an isolated island in mitigating tsunami hazards, this study performed a horizontally two-dimensional (2DH) numerical study of tsunami-like solitary wave propagation and run-up around an idealized reef-fringed island. The shock-capturing Boussinesq wave model, the FUNWAVE-TVD is used in the present study and well-validated with existing experimental data for its robustness in predicting 2DH solitary wave processes around an island. Based on the validated model, the typical solitary propagation process around the reef-fringed island and the effects of morphological and hydrodynamic parameters on the maximum run-up heights were systematically investigated. It is found that coral reefs can effectively reduce maximum run-up heights around an isolated island. The reef flat’s water depth, reef flat width, and reef surface roughness are the main factors affecting maximum run-up heights around an island, while the fore-reef slope has little impact. For the idealized reef-fringed island in this study, sea-level rise will cause coral reefs to lose their protective capability on the lee side, and the presence of coral reefs may even enhance tsunami hazards around an island when the reef flat width is very narrow or coral bleaching happens.
1. Introduction
Tsunamis, mostly generated by earthquakes or landslides, can cause extensive property damage in coastal areas. Therefore, it is of scientific and technical importance to study nearshore tsunami wave propagation and run-up. Although real tsunamis often appear as a combination of depressions and elevations, solitary waves are believed to model some important aspects of tsunamis and are commonly used as a theoretical form of tsunamis in numerous experimental and numerical studies (e.g., [1,2,3,4,5]). Analytical solutions of solitary waves have been found via various mathematical techniques for different governing equations (e.g., [6,7,8,9,10])
Since the Indian Ocean Earthquake in 2004, scholars have been increasingly interested in the protective capabilities of coastal forests and coral reefs against tsunami hazards. The mitigation effects of mangrove forests on tsunami hazards have been reported and confirmed in many field surveys (e.g., [11,12]), while the effects of coral reefs reported in field surveys were anecdotal. Some studies suggest coral reefs may provide minimal or no protection for the reef-fringed coasts [13,14], while some indicate coral reefs may effectively dissipate tsunami energy [15,16,17]. To better understand the role of coral reefs in mitigating tsunami hazards, several scholars have resorted to laboratory experiments or numerical models to further study the effects of morphological and hydrodynamic parameters, which characterize the state of fringing reefs, on tsunami transformation and run-up. Quiroga and Cheung [18] conducted laboratory experiments to investigate how reef roughness affects solitary wave propagation over an idealized reef model, and Yao et al. [19] developed empirical formulas based on experimental data to predict solitary wave run-up height on the back-reef beach. Compared to laboratory experiments, numerical models provide a more convenient approach for studying wave-reef interactions. Morphological and hydrodynamic parameters, such as the fore-reef slope, water level of the reef flat, and width of the reef flat, can be readily modified to explore their impacts on wave processes. Kunkel et al. [20] conducted a pioneer numerical work based on a nonlinear shallow water model to study the effects of reefs on tsunami-like solitary wave run-up. However, their numerical model lacked validation through experimental or field data. Compared to nonlinear shallow water equations, Boussinesq equations are reported better in reproducing wave processes under deeper water due to the inclusion of dispersive terms [21]. Therefore, over the last decade, Boussinesq-type models have been widely used as an accurate and efficient method to model wave processes over reef bathymetry (e.g., [21,22,23,24,25,26]). As for the role of coral reefs against tsunamis, Zhou et al. [27] applied a Boussinesq-type model to investigate the effects of reef morphological and hydrodynamic parameters on solitary wave breaking, reflection, and transmission. Yao et al. [19] and Ning et al. [28] utilized Boussinesq-type models to investigate the effects of morphological and hydrodynamic parameters on solitary wave run-up height. Liu et al. [29] investigated maximum momentum flux within solitary wave run-up zone over back-reef slopes. More recently, Qu et al. [30] also applied a non-hydrostatic numerical model to study the effect of permeable layers of coral reefs on the run-up processes of solitary waves. These studies contribute to understanding the importance of different factors associated with coral reefs in mitigating tsunami hazards, especially in the face of climate change.
However, so far, both experimental and numerical studies about solitary wave-reef interactions reduced wave processes to a horizontally one-dimensional (1DH) problem, which ignores the two-dimensional complexity of reef bathymetry and longshore wave motions [31]. This simplification may be more suitable for wave motions over fringing reefs distributed along continental coasts; however, for isolated reef-fringed islands abundant in the open ocean, wave refraction and diffraction associated with longshore wave motions, which are usually observed around an island [2] and responsible for unexpectedly large tsunami run-up heights on the lee of islands [32], cannot be considered. Therefore, the knowledge of how coral reefs affect three-dimensional tsunami wave propagation and impact around an island is still limited. To remedy existing studies, this study employs a Boussinesq-type model, FUNWAVE-TVD (https://fengyanshi.github.io/build/html/index.html, accessed on 1 July 2024) [33], to simulate horizontally two-dimensional (2DH) propagation and run-up of tsunami-like solitary waves around an idealized reef-fringed island at the prototype scale. The model was first validated by existing experimental data [2] to demonstrate its robustness in predicting 2DH solitary wave processes around an island. Then, based on the validated model, the typical solitary wave propagation process around the idealized reef-fringed island was simulated and investigated. The maximum run-up heights around the island with and without coral reefs were compared to demonstrate the basic role of coral reefs against tsunamis. Finally, the effects of main morphological and hydrodynamic parameters, such as the water depth over the reef flat, the width of the reef flat, fore-reef slope, and reef surface roughness, on the distribution of maximum run-up height around the reef-fringed island were studied through a series of numerical experiments.
2. Model and Validation
2.1. Introduction of the Numerical Method
The FUNWAVE-TVD [33] is a public-domain model in the nearshore and coastal communities. It is the most recent implementation of the well-known FUNWAVE, originally proposed by Kirby et al. [34]. FUNWAVE-TVD is developed based on a complete set of fully nonlinear Boussinesq equations with the vertical vorticity correction derived by Chen [35], incorporating a moving reference level introduced by Kennedy et al. [36]. The depth-integrated conservation equation and momentum equation are expressed as follows:
where η is the surface elevation, the subscript t indicates partial derivatives with regard to time, and g is the gravitational acceleration. Term M is the horizontal volume flux:
where D = η + h denotes the total local water depth, h is the local water depth measured from still water level, and uα represents the horizontal velocity at the moving reference elevation zα (zα = −0.53h + 0.47η). Term is the depth-averaged contribution to the horizontal velocity field, given by
with and . Term is the depth-dependent correction of velocity at , and ( is the frequency dispersion parameter equal to the ratio of water depth to wavelength) and written as follows:
Terms V1 and V2 in Equation (2) are dispersive Boussinesq terms which can be expressed as follows:
Term V3 represents vertical vorticity at and may be written as follows:
where
Here, term is the unit vector in the z direction.
Term R stands for diffusive and dissipate terms, which include subgrid lateral turbulent mixing and bottom friction. The bottom friction used in this paper is calculated by a quadratic friction law:
where n is the Manning coefficient, which has been used as a convenient parameter to characterize the surface roughness of coral reefs in previous studies [20,37].
In FUNWAVE-TVD, the governing equations are reformulated to a well-balanced conservative form and solved numerically using a hybrid finite volume-finite difference TVD scheme. Boussinesq-type models with this TVD-type solver are believed to provide more stable solutions compared to their finite-difference counterparts [38]. With this hybrid scheme, the dissipation effects associated with wave breaking can be modeled by locally switching the Boussinesq equations to the nonlinear shallow-water equations when the ratio of surface elevation to water depth exceeds a threshold of 0.8 [39] without relying on empirical breaking models. Shoreline movement can be managed efficiently as part of the Riemann solver that underlies the finite volume scheme. Since the first official release of FUNWAVE-TVD, the model has been applied and extended to study various practical problems, such as ship-wakes [40], wave-structure interactions [41], and wave-induced hydrodynamics in coastal wetlands [42]. As for 1DH wave processes over the rapidly changing reef topography, the model has also successfully been applied to reproduce the solitary [28] and irregular wave [25,43] propagation and run-up. Shao et al. [44] compared the performance of FUNWAVE-TVD and the previous version FUNWAVE with an eddy-viscosity type breaking model for solitary wave processes over fringing reefs. The present model demonstrates the ability to simulate wave shoaling, breaking, reflection, energy transform, and run-up over rapidly changing reef-beach topography quite effectively, utilizing appropriate values of the Manning coefficient without the need for threshold tuning.
2.2. Model Validation
Besides cross-shore wave motions over the reef bathymetry, solitary wave propagation and run-up around a reef-fringed island must consider wave refraction and diffraction associated with longshore wave motions. Therefore, we first used the model to reproduce the laboratory experiments conducted by Briggs et al. [2] to demonstrate its capability to predict 2DH solitary wave processes around an island.
The numerical setup based on the experiments of Briggs for model validation is shown in Figure 1 (top view and side view). The numerical wave basin is 40 m wide and 40 m long. An idealized circular island is implemented, whose center is located at x = 23 m, y = 19 m. The slope of the island is 1:4, and the diameter at the base is 7.2 m. An incident solitary wave was generated by an internal wave-maker at x = 7 m. The initial values of surface elevation and velocity of the incident solitary wave were defined based on Wei and Kirby [45]. Sponge layers were arranged to absorb the reflected and radiated energy. The water depth of the basin is 0.32 m. In Briggs’s experiments, twenty-seven wave gauges were installed around the island to measure surface water elevations. Maximum run-up heights, Rmax, were measured visually at 20 shoreline locations around the perimeter of the island.
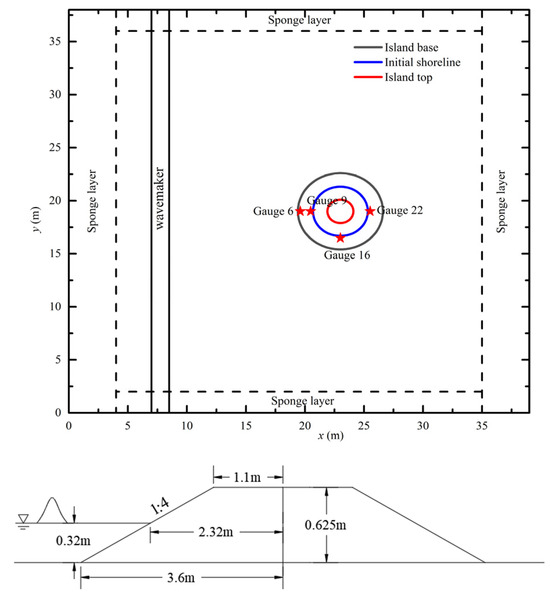
Figure 1.
Numerical setup based on the experiments of Briggs.
Two typical wave cases with incident solitary wave heights (H) of 0.01442 m and 0.05792 m were selected for model validation. Numerical simulations were performed with the grid size dx = dy = 0.05 m. Manning coefficient was set to 0.012 to characterize the surface roughness of smooth concrete used in Briggs’s experiments. Figure 2 shows the measured and computed results of time-varying surface water elevations at Gauge 6, Gauge 9, Gauge 16, and Gauge 22, whose locations are indicated in Figure 1. Figure 2 also shows the quantified model performance calculated by
where Xmod is the computed value, Xexp is the measured value, and is the mean of measured values. As seen in Figure 2, the agreement between experimental data and numerical results is good overall. Model skills at four gauges of each case are around 0.95. Figure 3 shows the measured and computed non-dimensionalized maximum run-up heights around the island. The angle α is measured counterclockwise around the island from the incident wave direction, and comparisons at 12 locations are presented, while the other eight locations can be inferred from symmetry. It can be seen that for both cases, the model effectively reproduced the maximum run-up heights around the island, including the enhanced run-up heights on the lee side of the island caused by the collision of the trapped waves [32]. Model skills at four gauges of both cases are 0.99. The validation results presented in this section are similar to results obtained from the previous version of FUNWAVE presented by Chen et al. [46]. However, for the solitary wave case with H = 0.05792 m, Chen’s model obviously overestimates the leading wave height at Gauge 22, while the present model predicts the surface water fluctuations at Gauge 22 better. Correspondingly, the present model also predicts the run-up heights around the island more accurately. This may somehow reveal the advantages of the present model in predicting 2DH wave processes.
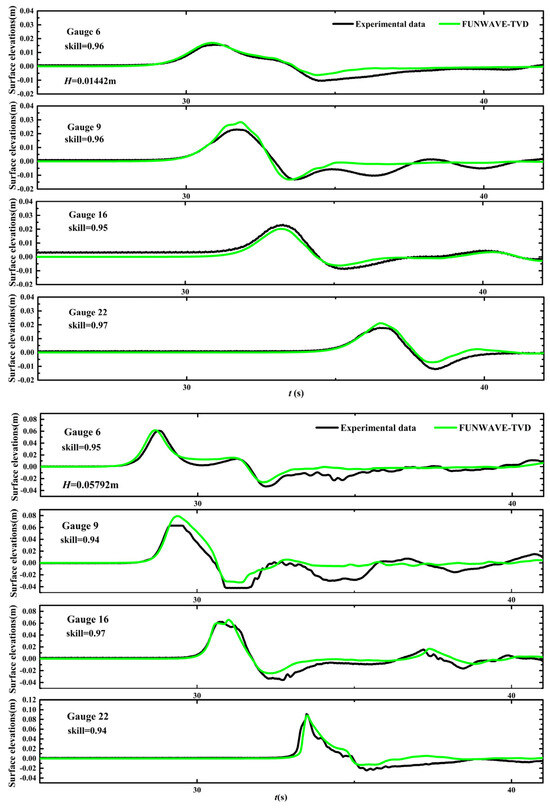
Figure 2.
The measured and computed results of time-varying surface water elevations for the incident solitary waves with H = 0.01442 m and H = 0.05792 m.
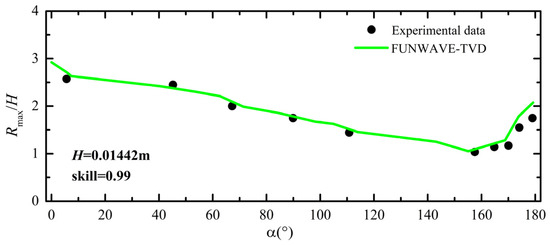
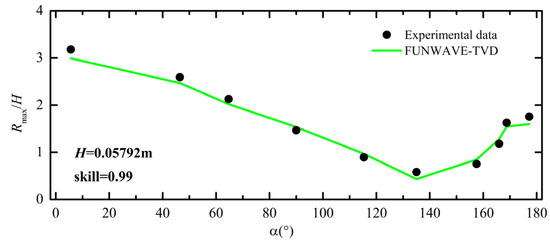
Figure 3.
The measured and computed results of normalized maximum run-up heights around the island for the incident solitary waves with H = 0.01442 m and H = 0.05792 m.
3. Typical Propagation Process around a Reef-Fringed Island
After validation of the present model, we first designed an idealized circular reef-fringed island based on an actual coral reef island in the numerical basin and investigated the typical propagation process of solitary waves. The numerical setup is shown in Figure 4. As shown in Figure 4, the numerical basin measures 16 km in length and 16 km in width, with the center of the reef-fringed island located at x = 8 km, y = 8 km. The internal wave maker was implemented at x = 3 km. The size of the reef-fringed island, such as the diameter of the initial shoreline circle and the reef edge circle, was determined based on the prototype, Babi Island (Figure 5), a typical coral reef island in Indonesia. Briggs’s physical model [2], the circular island, was also designed based on its mathematical simplicity and realistic geometry of Babi Island, but without considering fringing reefs. Using Google Earth, we measured the length of the shoreline of Babi Island (the inner red line in Figure 5), and it is about 6400 m. Taking this length as the circumference of the initial shoreline circular in Figure 4, the diameter of the initial shoreline circle Di is 2016 m. Similarly, we measured the length along the reef edge (the outer white line in Figure 5), which is about 9000 m, and the corresponding diameter of the reef edge circle in Figure 4 is 2816 m. Moreover, the back-reef slope (cot β) was set to be 4, the same as the slope of Briggs’s circular island. The reef flat’s water depth (hr) and fore-reef slope (cot θ) were set to be 3 m and 4, falling within the common ranges of these parameters as reported by Quataert et al. [47]. Then the reef flat (w) is about 400 m, which also falls within the range of reef flat widths reported by Quataert et al. [47]. Table 1 summarizes the conditions of numerical experiments in this section. As seen in Table 1, the incident wave height (H) and deep water depth (hd) were set to be 2 m and 60.5 m, in which case the height-to-depth ratio (ε = H/hd = 0.033), measuring the nonlinearity of incident solitary wave, is within the range of experiments of Briggs. As suggested by previous studies [20,37], the Manning coefficient of fore-reef slop and reef flat (n2) was set to be 0.09 for healthy and prosperous coral reefs, while the Manning coefficient for the back-reef slope (n3) and basin bottom(n1) were set to be 0.04 (cobbles) and 0.02 (sand), respectively. Moreover, based on the above conditions of case 1, we also set case 1A just without fringing reefs for comparison. The total simulation time is 450 s and the time interval for data output is 1 s for both case 1 and case 1A.
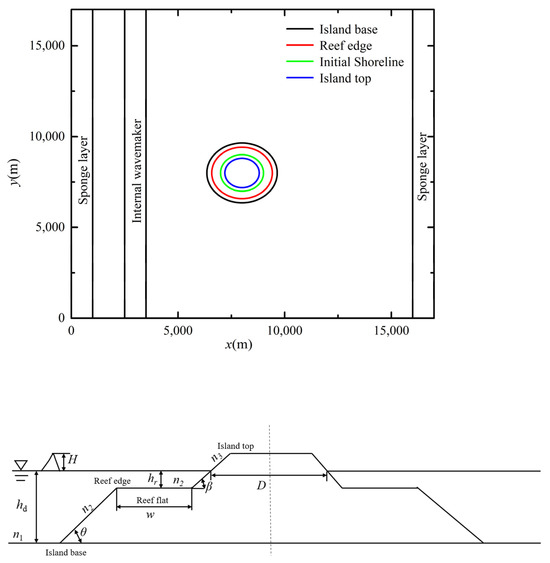
Figure 4.
Numerical experiment setup.
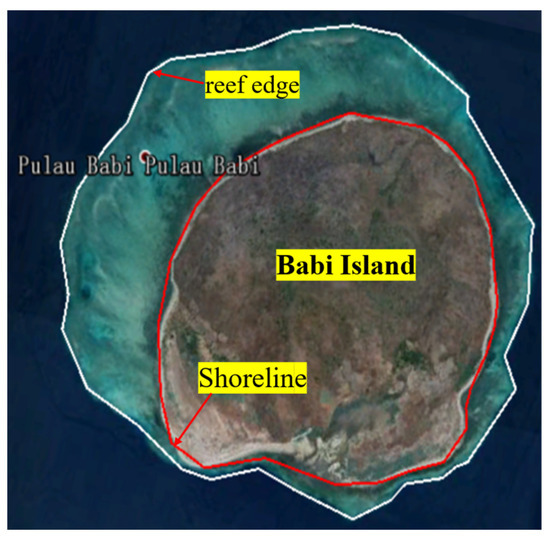
Figure 5.
Babi Island from Google Earth.

Table 1.
Conditions of numerical experiments for solitary wave propagation.
Figure 6 shows the typical snapshots of free-surface profiles and corresponding velocity fields at different times for case 1. As seen in Figure 6, when t = 150 s, the incident solitary wave has reached the front of the island (in the following content of this article, “island” means the land portion inside the shoreline). Large onshore velocity and run-up can be observed along the front of the island, with a portion of the solitary wave starting to diffract on both sides of the island. When t = 225 s, diffracted waves on both sides have reached the middle part of the island. Because of the very shallow water depth over the reef flat, the wave celerity over the reef flat is much slower than that outside the reef flat, so the diffracted waves on both sides seem to separate into two parts. However, the velocity over the reef flat is much greater than outside it. When t = 295 s, the diffracted waves outside the reef flat are trapped by the reef-fringed island and collide at the lee side of it, generating large onshore velocity. Then, the diffracted waves over the reef flat also collide (t = 320 s) on the lee side, and these two collisions of diffracted waves finally lead to the run-up at the back of the island (t = 375 s). The propagation process around the reef-fringed island revealed in Figure 6 is somehow different from the one around the island without reefs. As revealed by Liu et al. [32], diffracted waves around the island without reefs do not separate, and the corresponding run-up at the back of the island is generated only by one collision of trapped waves.
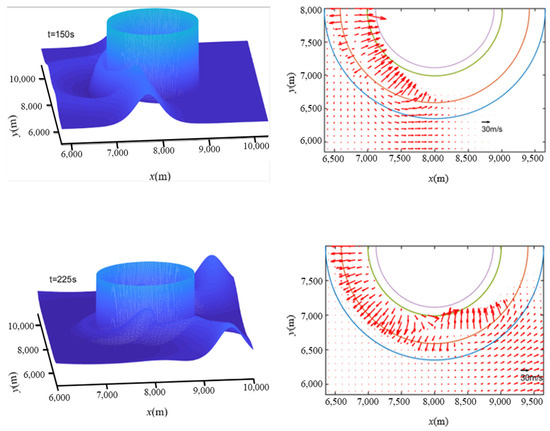
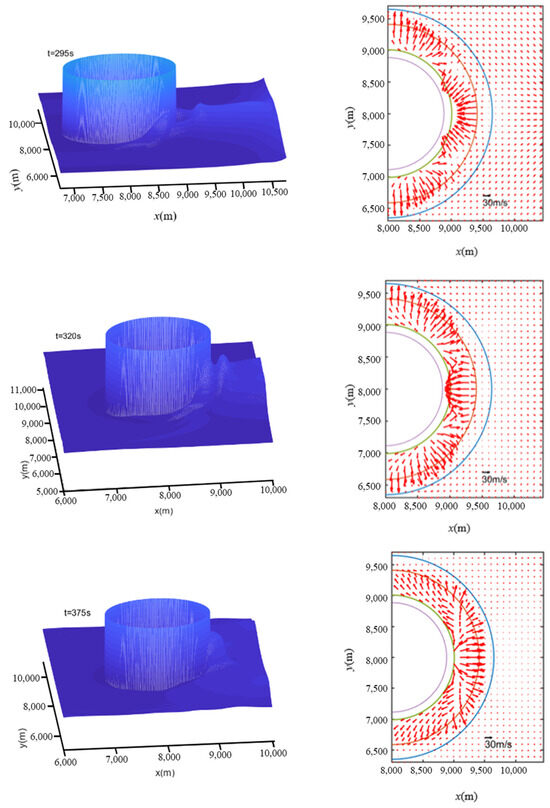
Figure 6.
Computed free-surface profiles (left) and corresponding velocity field (right) at different times for Case 1 (the semi-circular lines in the right pictures from inside to outside stand for the island top, initial shoreline, reef edge and island base respectively).
Figure 7 compares the numerical results of dimensionless maximum run-up heights around the island for case 1 and case 1A. As seen in Figure 7, the maximum run-up heights along the island are reduced with the presence of reefs, including the run-up enhancement on the lee side of the island. The maximum run-up height can be reduced by 36% at α = 0°, 47% at α = 90°, and 56% at α = 180°, in which α means the angle measured from the point of direct tsunami impact. The results of Figure 6 and Figure 7 clearly reveal the typical solitary wave propagation process around a reef-fringed island and the basic role of coral reefs in mitigating tsunami hazards around an isolated island.
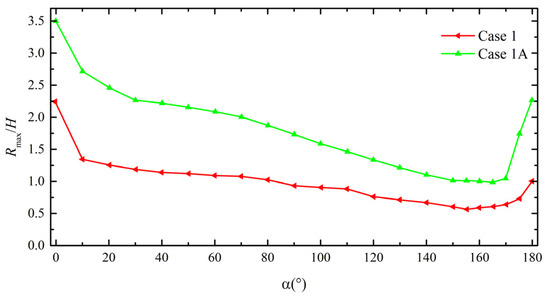
Figure 7.
Numerical results of normalized maximum run-up heights around the island for case 1 and case 1A.
4. Effects of Morphological and Hydrodynamic Parameters
The typical state of a fringing reef is defined by the fore-reef slope, reef flat width, water depth of the reef flat, and the roughness of the reef surface. Due to differences in coral species, geology, and tidal conditions, these parameters exhibit significant variations across different locations. Based on the numerical setup in Section 3, a series of parameterized numerical experiments were further designed and conducted to systematically investigate the effects of these morphological and hydrodynamic parameters on the maximum solitary wave run-up heights around the island.
The parameterized numerical experimental conditions are shown in Table 2. As seen in Table 2, by changing only one parameter in each group, four groups were designed to investigate the effects of these parameters independently. Values of unchanged parameters in all groups are the same as the ones in case 1. The varying ranges of hr, Cot θ, and w in Group 1, Group 2, and Group 3 were set based on the reef parameter ranges reported by Quataert et al. [47]. We have to mention that Quataert et al. [47] report that the reef flat’s water depth is usually less than 4m, and the previous research [48,49] also indicated the potential for a 2-meter rise in sea level by the year 2100. Hence, the maximum value of hr in Table 2 was established as 6 m to account for the effect of sea-level rise. The varying range of n2 in Group 4 was set based on Gelfenbaum et al. [37], who suggest the Manning coefficient of 0.02 can represent the smooth surface roughness of dead coral reefs.

Table 2.
Conditions of parameterized numerical experiments.
Figure 8 illustrates calculated non-dimensionalized maximum run-up heights around the reef-fringed island with different reef flat water depths for Group 1. The distribution of non-dimensionalized maximum run-up heights around the conical island without fringing reefs (case 1A) is also presented for comparison. As shown in Figure 8, maximum run-up heights around the reef-fringed island increase with an increase in the reef flat’s water depth, and the area of run-up enhancement in the lee side also expands as the reef flat’s water depth increases. It is noted that when the reef flat’s water depth is larger than 4m, the run-up heights enhanced by collisions of trapped waves on the lee side are almost comparable to those without coral reefs. This indicates that with the intensification of global warming, sea-level rise will cause coral reefs to lose their protective capability on the lee side of the island first.
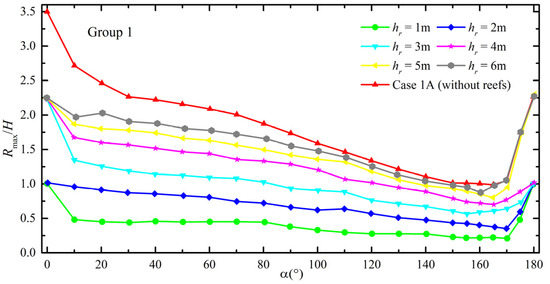
Figure 8.
The numerical results of non-dimensionalized maximum run-up heights around the reef-fringed island with different reef flat’s water depths for Group 1.
Figure 9 illustrates calculated non-dimensionalized maximum run-up heights around the reef-fringed island with different for-reef slopes for Group 2. The distribution of non-dimensionalized maximum run-up heights around the conical island without fringing reefs (case 1A) is also presented for comparison. As shown in Figure 9, in general, the fore-reef slope has little impact on solitary wave maximum run-up heights around the reef-fringed island. This phenomenon is similar to what was reported in the previous 1DH studies [28], which demonstrated that over two-dimensional fringing reef bathymetries, the solitary wave run-up height is insensitive to the change of the fore-reef slope. Ning et al. [28] demonstrate that although a gentler fore-reef slope results in a reduced reflection, it also changes the position of the breaking point, causing the solitary wave to break earlier and consume more energy. Moreover, for this study, it should be noted that when Cot θ is larger than 14, the maximum run-up heights on the lee side of the reef-fringed island are very close to the ones of case 1A. Figure 10 further demonstrates the calculated maximum surface elevations around the island when Cot θ = 4 and Cot θ = 16. As seen in Figure 10, the impact range on wave propagation of reef-fringed islands with Cot θ = 16 is much larger than the one of reef-fringed islands with Cot θ = 4. Maximum surface elevations on the lee side of the reef-fringed island with Cot θ = 16 generated by two collisions of trapped waves outside and on the reef flat are also larger than the ones on the lee side of the reef-fringed island with Cot θ = 4. Based on these results, we think that when the fore-reef slope gets mild to a certain extent, a larger body of water will be trapped by the reef-fringed islands, resulting in collisions on the lee side and finally increasing the run-up heights around the back of the island.
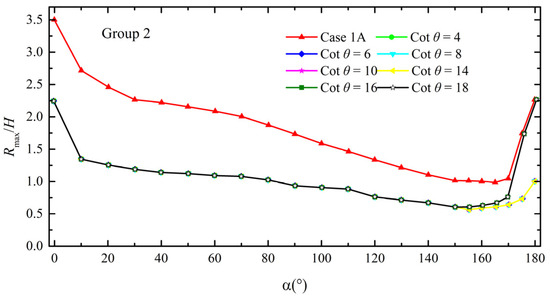
Figure 9.
Numerical results of non-dimensionalized maximum run-up heights around the reef-fringed island with different for-reef slopes for Group 2.
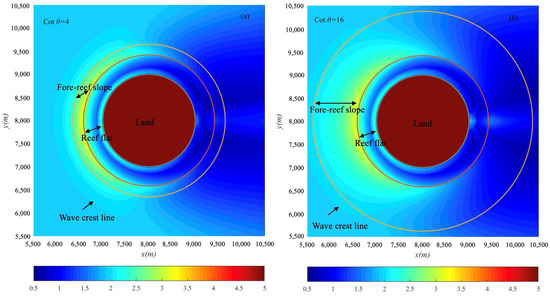
Figure 10.
Calculated maximum surface elevations around the island when (a) Cot θ = 4 and (b) Cot θ = 16.
Figure 11 illustrates calculated non-dimensionalized maximum run-up heights around the reef-fringed island with different reef flat widths for Group 3. The distribution of nondimensionalized maximum run-up height around the conical island without fringing reefs (case 1A) is also presented for comparison. As shown in Figure 11, maximum run-up heights around the reef-fringed island decrease with an increase in the reef flat width. This makes sense because the wider the reef flat, the greater the frictional losses during the wave propagation over fringing reefs. It also can be seen that when the reef flat width is 100 m, the maximum run-up heights are very close to those of case 1A, and when the reef flat width is 50 m, the maximum run-up heights are even larger than those of case 1A. Figure 12 further illustrates calculated cross-shore distributions of the maximum surface elevation at the positions of α = 10° and α = 90° when the reef flat width is 50 m, 100 m, and 400 m. As seen in Figure 12, when the reef flat width is long enough (i.e., w = 400 m), before increasing in front of the back-reef slope due to the shoaling effect, the maximum surface elevation can undergo attenuation over a certain distance after solitary wave propagates onto the reef flat, resulting in a final run-up height still lower than the one without coral reefs. However, for the cases of w = 100 m and w = 50 m, the maximum surface elevations over the reef flat do not exhibit significant attenuation and instead rise quickly due to the shoaling effect of back-reef slope, resulting in final run-up heights close to and even larger than the one without coral reefs. This phenomenon is consistent with the viewpoint of some researchers [37] who argue that the presence of coral reefs may not always mitigate tsunami hazards, especially when the energy dissipation induced by coral reefs is weak. The present results reveal that tsunami hazards may even be enhanced when the reef flat width is very narrow, and this should be paid attention to for the site selection of coastal structures on the reef flat.
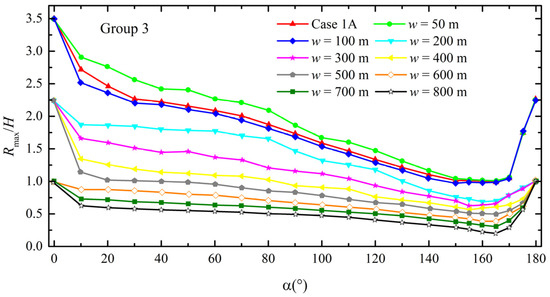
Figure 11.
Numerical results of non-dimensionalized maximum run-up heights around the reef-fringed island with different reef flat widths for Group 3.
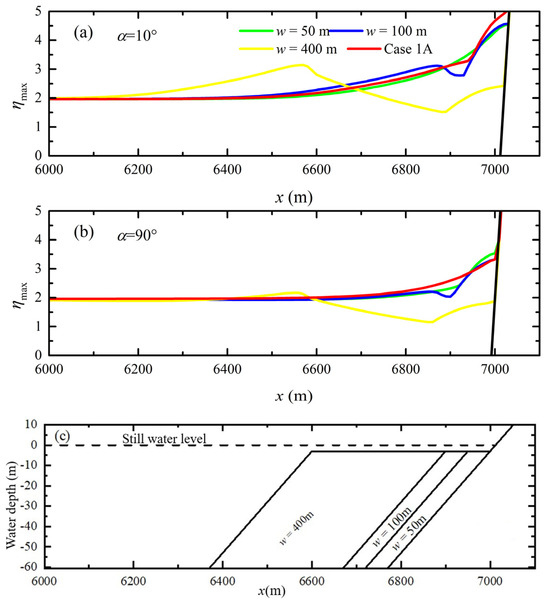
Figure 12.
The calculated cross-shore distributions of the maximum surface elevation at the positions of (a) α = 10° and (b) α = 90° over (c) reef profiles when the reef flat width is 50 m, 100 m, and 400 m.
Figure 13 illustrates the calculated non-dimensionalized maximum run-up height distribution around the reef-fringed island with different reef surface roughness for Group 4. The distribution of non-dimensionalized maximum run-up height around the conical island without fringing reefs (case 1A) is also presented for comparison. As seen in Figure 13, the maximum run-up heights around the reef-fringed island increase with a decrease in reef roughness. Similar to the effect of reef flat water depth, when n2 reduces to 0.05, the enhanced run-up heights on the lee side are almost the same as those without coral reefs. Moreover, similar to the effect of reef flat width, when the surface roughness of coral reefs decreases to 0.03 and 0.02, the maximum run-up heights around the reef-fringed island are even higher than those without coral reefs. Figure 14 further illustrates calculated cross-shore distributions of the maximum surface elevation at the positions of α = 10° and α = 90° when the reef surface roughness is 0.02, 0.03, and 0.09. As seen in Figure 14, when coral reefs are healthy and prosperous (i.e., n2 = 0.09), before increasing in front of the back-reef slope due to the shoaling effect, the maximum surface elevation can undergo enough attenuation after solitary wave propagates onto the reef flat, resulting in a final run-up height still lower than the one without coral reefs. However, for the cases of n2 = 0.03 and n2 = 0.02, the maximum surface elevations over the reef flat do not exhibit significant attenuation before rising due to the shoaling effect of back-reef slope, resulting in final run-up heights close to or even larger than the one without coral reefs. These results indicate that when the surface roughness of coral reefs is small to a certain extent, coral reefs will first lose their protective capability on the lee side, and when the roughness of coral reefs is small enough, the presence of coral reefs may even enhance tsunami hazards around an island. Since the above-average seawater temperatures caused by global warming are the leading cause of coral bleaching [50], it is believed that climate change will not only reduce the defensive effect of coral reefs against tsunami hazards but also exacerbate the degree of tsunami disasters around the island.
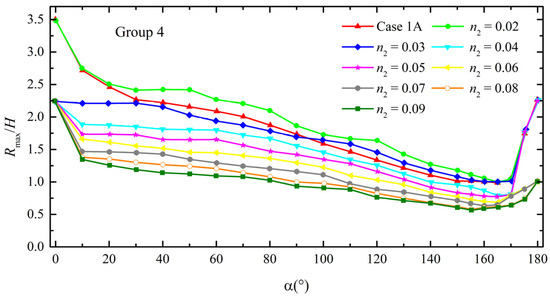
Figure 13.
Numerical results of non-dimensionalized maximum run-up heights around the reef-fringed island different reef surface roughness for Group 4.
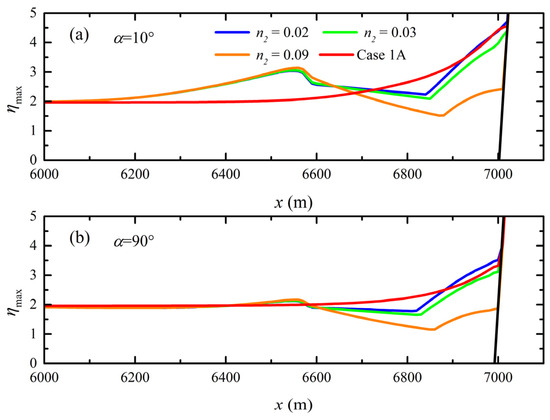
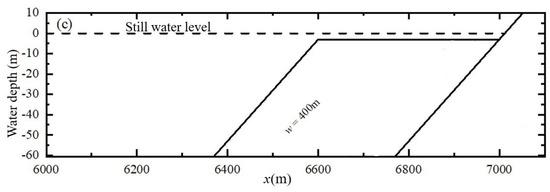
Figure 14.
The calculated cross-shore distributions of the maximum surface elevation at the positions of (a) α = 10° and (b) α = 90° over (c) the reef profile when the reef surface roughness is 0.02, 0.03, and 0.09.
5. Conclusions
In this study, the fully nonlinear shock-capturing Boussinesq wave model FUNWAVE-TVD was employed to simulate the propagation and run-up of solitary waves around an idealized reef-fringed circular island. Compared to existing experimental data, the present model shows its robustness in predicting 2DH solitary wave processes around an island. Based on the validated model, the typical solitary propagation process around an idealized reef-fringed island and the effects of morphological and hydrodynamic parameters on maximum run-up heights around the island were systematically investigated. For the idealized reef-fringed island set in this study, we reach the following conclusions:
- (1)
- The presence of coral reefs effectively reduces the maximum run-up heights around an island. Run-up enhancement at the back of the reef-fringed island is induced by collisions of trapped waves.
- (2)
- Maximum run-up heights around the reef-fringed island and the area of run-up enhancement on the lee side increase with an increase in reef flat water depth. Sea-level rise associated with climate change will cause coral reefs to lose their protective capability on the lee side of the island.
- (3)
- The maximum run-up heights around the reef-fringed island decrease as the reef flat width increases. When the reef flat width is very narrow, the presence of coral reefs may even enhance the tsunami hazards around the island. Similarly, the maximum run-up heights around the reef-fringed island decrease as the reef surface roughness increases. Coral bleaching associated with climate change will not only reduce the defensive effect of coral reefs against tsunami hazards but also exacerbate the degree of tsunami disasters around the island.
- (4)
- The fore-reef slope has little impact on the maximum run-up heights around the reef-fringed island. But when the fore-reef slope gets mild to a certain extent, a larger body of water will be trapped by the reef-fringed island and increase the run-up heights around the back of the island.
We have to confess that the solitary wave and idealized topography we used in the present numerical study are a simplification of the real tsunami wave and reef-fringed island topography; however, the basic characteristics of tsunami wave propagation and run-up can be achieved from the present study enhancing the comprehension of coastal engineers and managers regarding the influence of key parameters on potential tsunami hazards around a reef-fringed island.
Author Contributions
Conceptualization, W.L.; software, F.Q. and Y.N.; validation, Y.N.; investigation, R.C.; writing—original draft preparation, W.L.; writing—review and editing, F.Q. and Y.N.; project administration, R.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Zhejiang Provincial Natural Science Foundation of China, grant number (LY21E090007), State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering of China, grant number (2019nkms03) and the National Natural Science Foundation of China, grant number (51809234).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Feng Qian was employed by the company Zhejiang Yuquan Environmental Technology Engineering Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Synolakis, C.E. The runup of solitary waves. J. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Briggs, M.J.; Synolakis, C.E.; Harkins, G.S.; Green, D.R. Laboratory experiments of tsunami runup on a circular island. Pure Appl. Geophys. 1995, 144, 569–593. [Google Scholar] [CrossRef]
- Maiti, S.; Sen, D. Computation of solitary waves during propagation and runup on a slope. Ocean Eng. 1999, 26, 1063–1083. [Google Scholar] [CrossRef]
- Lin, P. A numerical study of solitary wave interaction with rectangular obstacles. Coast. Eng. 2004, 51, 35–51. [Google Scholar] [CrossRef]
- Chang, Y.-H.; Hwang, K.-S.; Hwung, H.-H. Large-scale laboratory measurements of solitary wave inundation on a 1:20 slope. Coast. Eng. 2009, 56, 1022–1034. [Google Scholar] [CrossRef]
- Shakeel, M.; Attaullah; Shah, N.A.; Chung, J.D. Modified Exp-Function Method to Find Exact Solutions of Microtubules Nonlinear Dynamics Models. Symmetry 2023, 15, 360. [Google Scholar] [CrossRef]
- Shakeel, M.; Attaullah; El-Zahar, E.R.; Shah, N.A.; Chung, J.D. Generalized Exp-Function Method to Find Closed Form Solutions of Nonlinear Dispersive Modified Benjamin–Bona–Mahony Equation Defined by Seismic Sea Waves. Mathematics 2022, 10, 1026. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Geng, B.; Jiao, S. Fractional Order Fuzzy Dispersion Entropy and Its Application in Bearing Fault Diagnosis. Fractal Fract. 2022, 6, 544. [Google Scholar] [CrossRef]
- Attaullah; Shakeel, M.; Ahmad, B.; Shah, N.A.; Chung, J.D. Solitons Solution of Riemann Wave Equation via Modified Exp Function Method. Symmetry 2022, 14, 2574. [Google Scholar] [CrossRef]
- Shakeel, M.; Attaullah; Kbiri Alaoui, M.; Zidan, A.M.; Shah, N.A.; Weera, W. Closed-Form Solutions in a Magneto-Electro-Elastic Circular Rod via Generalized Exp-Function Method. Mathematics 2022, 10, 3400. [Google Scholar] [CrossRef]
- Danielsen, F.; Sørensen, M.K.; Olwig, M.F.; Selvam, V.; Parish, F.; Burgess, N.D.; Hiraishi, T.; Karunagaran, V.M.; Rasmussen, M.S.; Hansen, L.B.; et al. The Asian Tsunami: A Protective Role for Coastal Vegetation. Science 2005, 310, 643. [Google Scholar] [CrossRef] [PubMed]
- Yanagisawa, H.; Koshimura, S.; Goto, K.; Miyagi, T.; Imamura, F.; Ruangrassamee, A.; Tanavud, C. The reduction effects of mangrove forest on a tsunami based on field surveys at Pakarang Cape, Thailand and numerical analysis. Estuar. Coast. Shelf Sci. 2009, 81, 27–37. [Google Scholar] [CrossRef]
- Adger, W.N.; Hughes, T.P.; Folke, C.; Carpenter, S.R.; Rockström, J. Social-Ecological Resilience to Coastal Disasters. Science 2005, 309, 1036. [Google Scholar] [CrossRef] [PubMed]
- Baird, A.H.; Campbell, S.J.; Anggoro, A.W.; Ardiwijaya, R.L.; Fadli, N.; Herdiana, Y.; Kartawijaya, T.; Mahyiddin, D.; Mukminin, A.; Pardede, S.T.; et al. Acehnese Reefs in the Wake of the Asian Tsunami. Curr. Biol. 2005, 15, 1926–1930. [Google Scholar] [CrossRef] [PubMed]
- Fernando, H.J.S.; McCulley, J.L.; Mendis, S.G.; Perera, K. Coral poaching worsens tsunami destruction in Sri Lanka. Eos Trans. Am. Geophys. Union 2005, 86, 301–304. [Google Scholar] [CrossRef]
- Goff, J.; Liu, P.L.F.; Higman, B.; Morton, R.; Jaffe, B.E.; Fernando, H.; Lynett, P.; Fritz, H.; Synolakis, C.; Fernando, S. Sri Lanka Field Survey after the December 2004 Indian Ocean Tsunami. Earthq. Spectra 2006, 22, 155–172. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Samarawickrama, S.P.; Balasubramanian, S.; Hettiarachchi, S.S.L.; Voropayev, S. Effects of porous barriers such as coral reefs on coastal wave propagation. J. Hydro-Environ. Res. 2008, 1, 187–194. [Google Scholar] [CrossRef]
- Quiroga, P.D.; Cheung, K.F. Laboratory study of solitary-wave transformation over bed-form roughness on fringing reefs. Coast. Eng. 2013, 80, 35–48. [Google Scholar] [CrossRef]
- Yao, Y.; He, F.; Tang, Z.; Liu, Z. A study of tsunami-like solitary wave transformation and run-up over fringing reefs. Ocean Eng. 2018, 149, 142–155. [Google Scholar] [CrossRef]
- Kunkel, C.M.; Hallberg, R.W.; Oppenheimer, M. Coral reefs reduce tsunami impact in model simulations. Geophys. Res. Lett. 2006, 33, L23612. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, Z.; Monismith, S.G.; Lo, E.Y.M. 1DH Boussinesq modeling of wave transformation over fringing reefs. Ocean Eng. 2012, 47, 30–42. [Google Scholar] [CrossRef]
- Nwogu, O.; Demirbilek, Z. Infragravity Wave Motions and Runup over Shallow Fringing Reefs. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 295–305. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K. Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Fang, K.; Liu, Z.; Zou, Z. Fully nonlinear modeling wave transformation over fringing reefs using shock-capturing Boussinesq model. J. Coast. Res. 2016, 32, 164–171. [Google Scholar] [CrossRef]
- Ning, Y.; Liu, W.; Zhao, X.; Zhang, Y.; Sun, Z. Study of irregular wave run-up over fringing reefs based on a shock-capturing Boussinesq model. Appl. Ocean Res. 2019, 84, 216–224. [Google Scholar] [CrossRef]
- Liu, W.; Ning, Y. Numerical simulation of wave propagation over coral reef bathymetries based on fully-dispersive Boussinesq equations. J. Chang. Univ. Sci. Technol. (Nat. Sci.) 2023, 20, 47–54. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhan, J.-M.; Li, Y.S. Parametric Investigation of Breaking Solitary Wave Over Fringing Reef Based on Shock-Capturing Boussinesq Model. Coast. Eng. J. 2016, 58, 1650007. [Google Scholar] [CrossRef]
- Ning, Y.; Liu, W.; Sun, Z.; Zhao, X.; Zhang, Y. Parametric study of solitary wave propagation and runup over fringing reefs based on a Boussinesq wave model. J. Mar. Sci. Technol. 2019, 24, 512–525. [Google Scholar] [CrossRef]
- Liu, W.; Shao, K.; Ning, Y. A Study of the Maximum Momentum Flux in the Solitary Wave Run-Up Zone over Back-Reef Slopes Based on a Boussinesq Model. J. Mar. Sci. Eng. 2019, 7, 109. [Google Scholar] [CrossRef]
- Qu, K.; Liu, T.W.; Chen, L.; Yao, Y.; Kraatz, S.; Huang, J.X.; Lan, G.Y.; Jiang, C.B. Study on transformation and runup processes of tsunami-like wave over permeable fringing reef using a nonhydrostatic numerical wave model. Ocean Eng. 2022, 243, 110228. [Google Scholar] [CrossRef]
- Su, S.-F.; Ma, G. Modeling two-dimensional infragravity motions on a fringing reef. Ocean Eng. 2018, 153, 256–267. [Google Scholar] [CrossRef]
- Briggs, M.J.; Cho, Y.-S.; Kanoglu, U.; Liu, P.L.F.; Synolakis, C.E. Runup of solitary waves on a circular Island. J. Fluid Mech. 1995, 302, 259–285. [Google Scholar] [CrossRef]
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean Model. 2012, 43–44, 36–51. [Google Scholar] [CrossRef]
- Kirby, J.T.; Wei, G.; Chen, Q.; Kennedy, A.B.; Dalrymple, R.A. FUNWAVE 1.0. Fully Nonlinear Boussinesq Wave Model. Documentation and User’s Manual; Center for Applied Coastal Research, Department of Civil and Environmental Engineering, University of Delaware: Newark, DE, USA, 1998; Available online: www.udel.edu/kirby/papers/kirby-etal-cacr-98-06.pdf (accessed on 1 July 2024).
- Chen, Q. Fully nonlinear Boussinesq-type equations for waves and currents over porous beds. J. Eng. Mech. 2006, 132, 220–230. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Chen, Q.; Kirby, J.T.; Dalrymple, R.A. Boussinesq modeling of wave transformation, breaking, and runup. I: 1D. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 39–47. [Google Scholar] [CrossRef]
- Gelfenbaum, G.; Apotsos, A.; Stevens, A.W.; Jaffe, B. Effects of fringing reefs on tsunami inundation: American Samoa. Earth-Sci. Rev. 2011, 107, 12–22. [Google Scholar] [CrossRef]
- Choi, Y.-K.; Shi, F.; Malej, M.; Smith, J.M. Performance of various shock-capturing-type reconstruction schemes in the Boussinesq wave model, FUNWAVE-TVD. Ocean Model. 2018, 131, 86–100. [Google Scholar] [CrossRef]
- Tonelli, M.; Petti, M. Hybrid finite volume—Finite difference scheme for 2DH improved Boussinesq equations. Coast. Eng. 2009, 56, 609–620. [Google Scholar] [CrossRef]
- Shi, F.; Malej, M.; Smith, J.M.; Kirby, J.T. Breaking of ship bores in a Boussinesq-type ship-wake model. Coast. Eng. 2018, 132, 1–12. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y.; Zhao, X. Numerical study of Bragg reflection of regular water waves over fringing reefs based on a Boussinesq model. Ocean Eng. 2019, 190, 106415. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Brandt, S.R.; Chen, Q.; Shi, F. Boussinesq modeling of wave-induced hydrodynamics in coastal wetlands. J. Geophys. Res. Ocean 2017, 122, 3861–3883. [Google Scholar] [CrossRef]
- Su, S.-F.; Ma, G.; Hsu, T.-W. Boussinesq modeling of spatial variability of infragravity waves on fringing reefs. Ocean Eng. 2015, 101, 78–92. [Google Scholar] [CrossRef]
- Shao, K.; Liu, W.; Gao, Y.; Ning, Y. The influence of climate change on tsunami-like solitary wave inundation over fringing reefs. J. Integr. Environ. Sci. 2019, 16, 71–88. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T. Time-Dependent Numerical Code for Extended Boussinesq Equations. J. Waterw. Port Coast. Ocean Eng. 1995, 121, 251–261. [Google Scholar] [CrossRef]
- Chen, Q.; Kirby James, T.; Dalrymple Robert, A.; Kennedy Andrew, B.; Chawla, A. Boussinesq Modeling of Wave Transformation, Breaking, and Runup. II: 2D. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 48–56. [Google Scholar] [CrossRef]
- Quataert, E.; Storlazzi, C.; Rooijen, A.; Cheriton, O.; Van Dongeren, A. The influence of coral reefs and climate change on wave-driven flooding of tropical coastlines. Geophys. Res. Lett. 2015, 42, 6407–6415. [Google Scholar] [CrossRef]
- Vermeer, M.; Rahmstorf, S. Global sea level linked to global temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 21527. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Reconstructing sea level from paleo and projected temperatures 200 to 2100 ad. Clim. Dyn. 2010, 34, 461–472. [Google Scholar] [CrossRef]
- Michael, S. The Great Barrier Reef: A catastrophe laid bare. The Guardian, 7 June 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).