Research on Suspended Particle Size Measurement Based on Ultrasonic Backscattered Amplitude Analysis
Abstract
1. Introduction
2. Materials
2.1. Experimental Particles
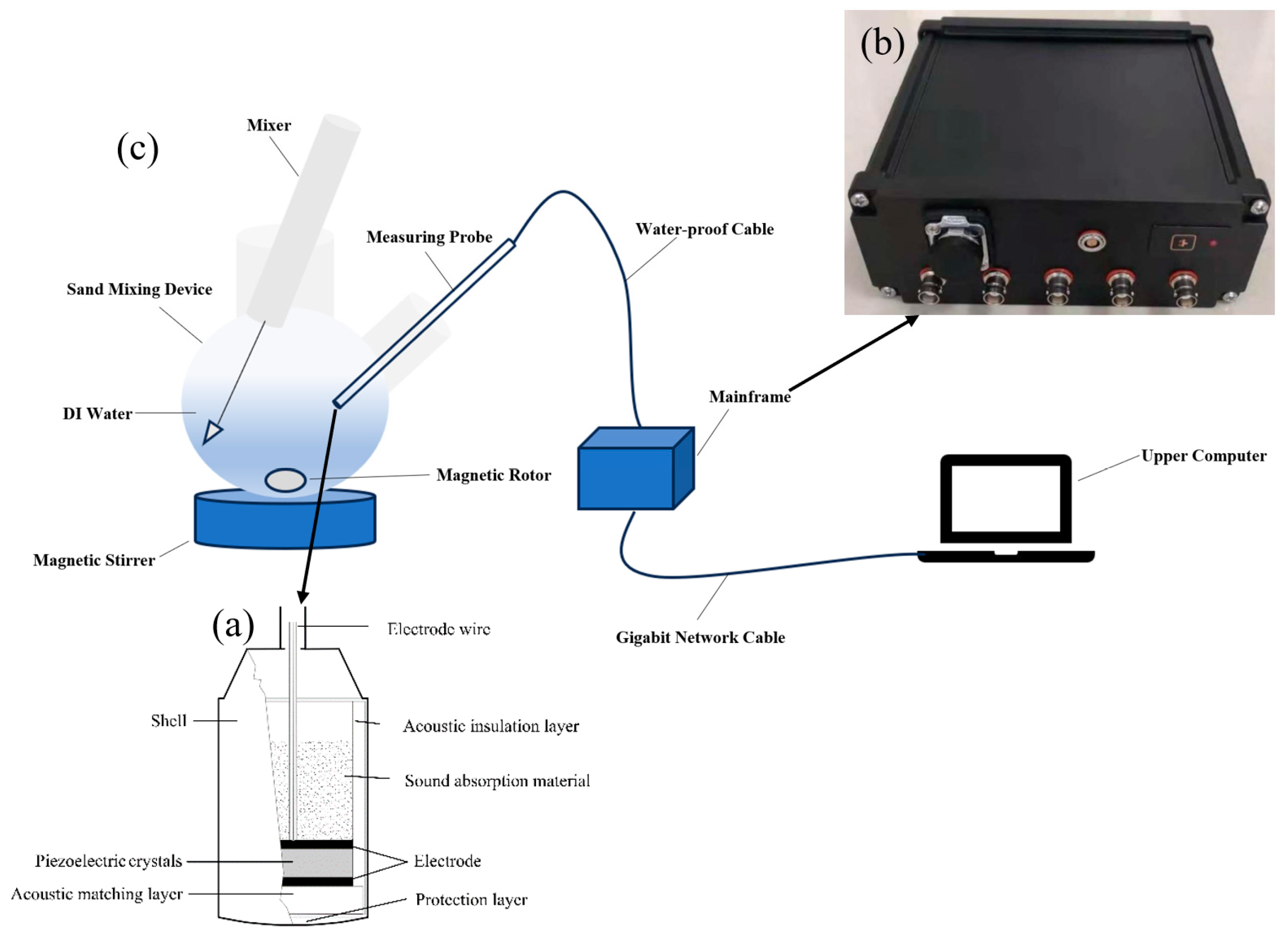
2.2. Experimental Setup
2.3. Experimental Procedures
- (1)
- Configuration of suspension: First, 0.05 kg to 1.60 kg of particles of 0.006 mm to 0.030 mm in size were weighed with an analytical balance with an accuracy of 0.001 g and put into a stirring device; then, we added 1000 mL of DI water, started the stirring device, and configured the suspension to SSC = 0.05 kg/m3 to 1.60 kg/m3.
- (2)
- Measurement: The control software based on QT6.5 programming was opened in the host computer and the parameters of the measuring instrument were set as follows: pulse width, 200 ns; transmit pulse wave 6; gain, 45 dB; signal acquisition frequency, 50 Hz; acquisition time, 90 s. Each group of experiments collected 4500 frames of signals.
- (3)
- Data analysis: The internal SOC of the measuring instrument performed FFT operation. The signals from four kinds of probes covering the studied bandwidth were converted from the time domain to the frequency domain in MATLAB2023a software with reference to Equation (5) [47]. This was performed for each group of experiments with 4500 frames measuring the signal data, which underwent splicing, integration, and noise abatement after the time-averaged normalisation analysis. Then, Equation (6) was used to calculate the particle size-Amp conversion error value for the analysis and evaluation.
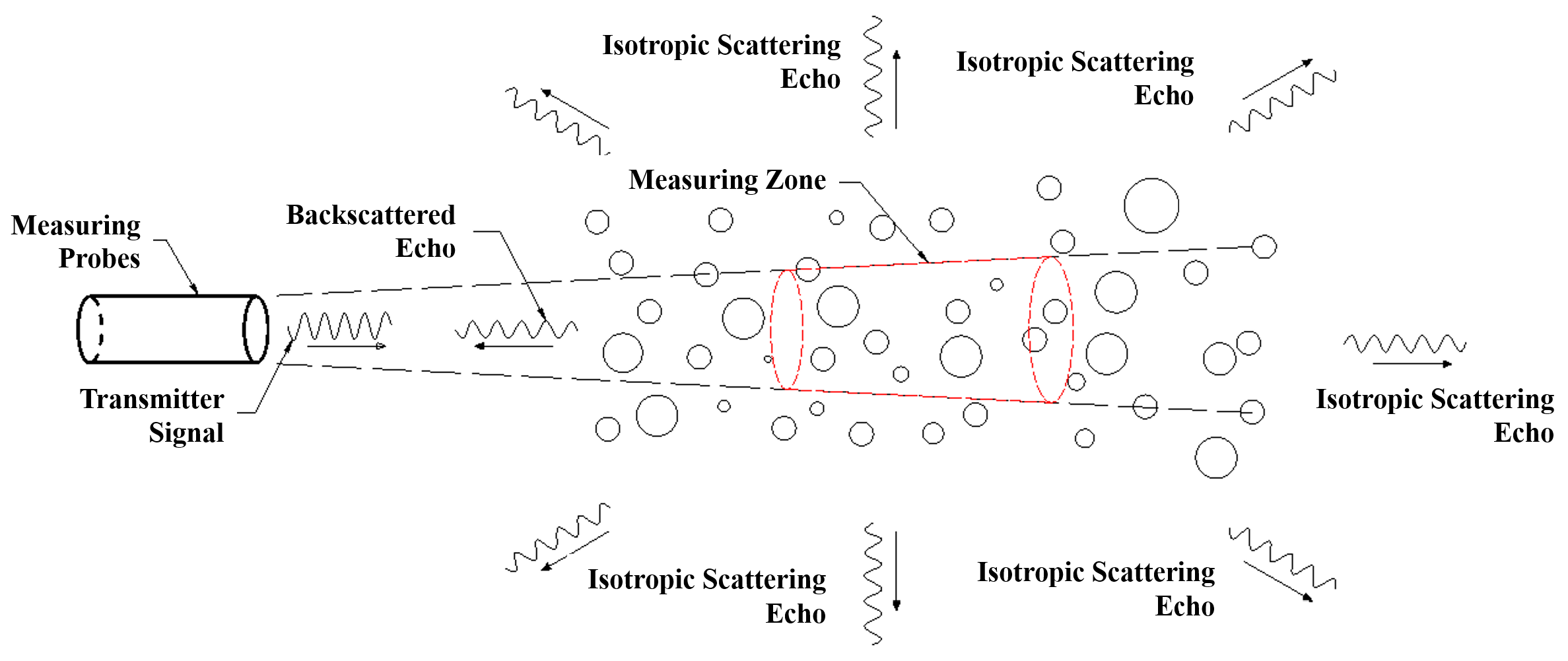
3. Methods
4. Results
4.1. Time-Averaged Normalised Spectrograms
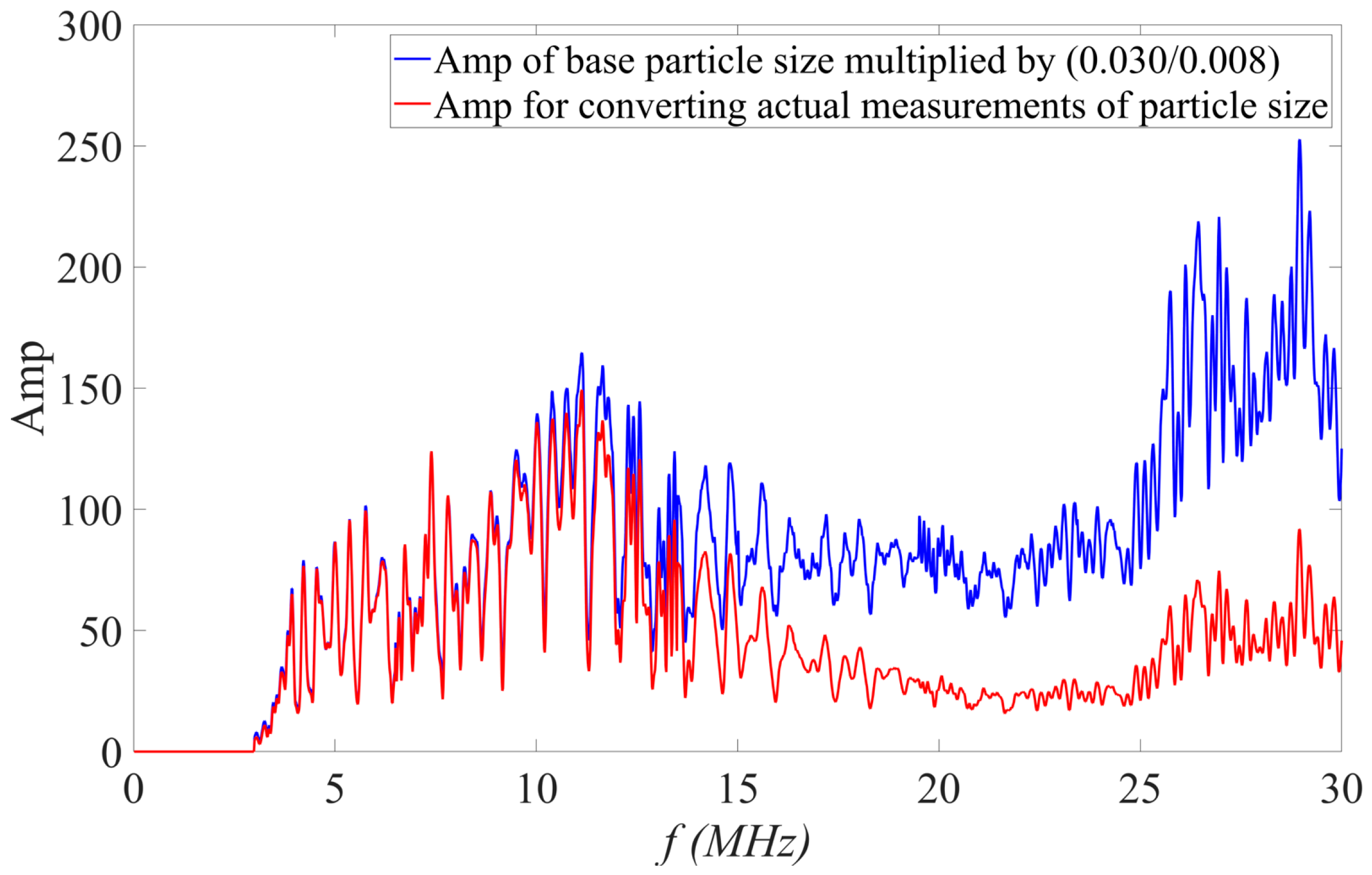
4.2. Particle Size-Amp Conversion
5. Discussion
6. Conclusions
- (a)
- The multi-frequency measurement experiments of a single particle size showed that the shape of the time-averaged normalised spectral map will not change with the change in concentration; only the corresponding Amp value will change at a certain proportion. The law of change in the Amp value is in line with the relevant studies of other scholars [12,15,37,48,49]; the smaller the particle size is, the higher the frequency corresponding to the peak is, and the larger the particle size is, the lower the frequency corresponding to the peak is.
- (b)
- The particle size-Amp theory (the positive correlation between the Amp of the backscattered signal of suspended particles and the first power of the particle size) was verified on the basis of the measured results, which is useful for verifying the actual range of measurable particle sizes of the probes and for converting the Amp for other sizes when only the Amp for a certain particle size is available.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahammad, M.; Czuba, J.; Curran, C. In-Stream Laser Diffraction for Measuring Suspended Sediment Concentration and Particle Size Distribution in Rivers: Insights from Field Campaigns. J. Hydraul. Eng. 2023, 149, 05022007. [Google Scholar] [CrossRef]
- Dutu, F.; Dutu, L.T.; Catianis, I.; Ispas, B.A. Sediment dynamics and hydrodynamical processes in the Danube Delta (Romania): A response to hydrotechnical works. Z. Fur Geomorphol. 2022, 63, 365–378. [Google Scholar] [CrossRef]
- Parra, L.; Ahmad, A.; Sendra, S.; Lloret, J.; Lorenz, P. Combination of Machine Learning and RGB Sensors to Quantify and Classify Water Turbidity. Chemosensors 2024, 12, 34. [Google Scholar] [CrossRef]
- Lee, J.; Kwon, J.H.; Kim, J.; Koo, J.; Lee, S. In-situ turbidity sensor system for residential water quality monitoring. Int. J. Nanotechnol. 2024, 21, 9. [Google Scholar] [CrossRef]
- Dishman, K.L.; Doolin, P.K.; Hoffman, J.F. Comparison of particle size of cracking catalyst determined by laser light scattering and dry sieve methods. Ind. Eng. Chem. Res. 1993, 32, 1457–1463. [Google Scholar] [CrossRef]
- Faers, M.A.; Kneebone, G.R. Application of rheological measurements for probing the sedimentation of suspension concentrate formulations. Pestic. Sci. 1999, 55, 312–325. [Google Scholar] [CrossRef]
- Graham, M.D. The Coulter Principle: Foundation of an Industry. J. Assoc. Lab. Autom. 2003, 8, 72–81. [Google Scholar] [CrossRef]
- Saleh, O.A.; Sohn, L.L. Quantitative sensing of nanoscale colloids using a microchip Coulter counter. Rev. Sci. Instrum. 2001, 72, 4449–4451. [Google Scholar] [CrossRef]
- Bin Omar, A.F.; Bin MatJafri, M.Z. Turbidimeter Design and Analysis: A Review on Optical Fiber Sensors for the Measurement of Water Turbidity. Sensors 2009, 9, 8311–8335. [Google Scholar] [CrossRef] [PubMed]
- White, D. The Measurement of Particle Size Distribution Using the Single Particle Optical Sizing (SPOS) Method; Cambridge University Department of Engineering: Cambridge, UK, 2002. [Google Scholar]
- Ochiai, S.; Kashiwaya, K. Measurement of suspended sediment for model experiments using general-purpose optical sensors. Catena 2010, 83, 1–6. [Google Scholar] [CrossRef]
- Challis, R.E.; Povey, M.J.W.; Mather, M.L.; Holmes, A.K. Ultrasound techniques for characterizing colloidal dispersions. Rep. Prog. Phys. 2005, 68, 1541. [Google Scholar] [CrossRef]
- Epstein, P.S.; Carhart, R.R. The Absorption of Sound in Suspensions and Emulsions. I. Water Fog in Air. J. Acoust. Soc. Am. 1953, 25, 553–565. [Google Scholar] [CrossRef]
- Yuan, A.; Mingxu, S.U.; Yongming, L.I.; Cai, X.; Yin, P. Application of ultrasonic method on particle concentration in gas-liquid two-phase flow. In Proceedings of the UK-China International Particle Technology Forum, Shanghai, China, 30 June 2014. [Google Scholar]
- Kulon, J.; Malyan, B.E.; Balachandran, W. Simultaneous measurement of particle size and electrostatic charge distribution in DC electric field using phase Doppler anemometry. IEEE Trans. Ind. Appl. 2003, 39, 1522–1528. [Google Scholar] [CrossRef]
- Harris, R.A.; Shi, Y.; Cina, J.A. On the measurement of superpositions of chiral amplitudes by polarized light scattering. J. Chem. Phys. 1994, 101, 3459–3463. [Google Scholar] [CrossRef]
- Fei, S. Several Commonly Used Powder Size Test Methods. In Physical Testing and Chemical Analysis (Part A: Physical Testing); Oriprobe: Windsor, ON, Canada, 2012. [Google Scholar]
- Nishiguchi, K.; Utani, K.; Gunther, D.; Correction, M.O. to Gas to Particle Conversion-Gas Exchange Technique for Direct Analysis of Metal Carbonyl Gas by Inductively Coupled Plasma Mass Spectrometry. Anal. Chem. 2014, 86, 11925–11926. [Google Scholar] [CrossRef]
- Kang, R.; Wang, X.; Zhao, M.; Henihan, L.E.; O’Donnell, C.P. A comparison of benchtop and micro NIR spectrometers for infant milk formula powder storage time discrimination and particle size prediction using chemometrics and denoising methods. J. Food Eng. 2022, 329, 111087. [Google Scholar] [CrossRef]
- Deines, K.L. Backscatter Estimations Using Broadband Acoustic Doppler Current Profilers. Application Note. In Proceedings of the IEEE Sixth Working Conference on Current Measurement, Stoughton, WI, USA, 11–13 March 1999. [Google Scholar]
- Guerrero, M.; Rüther, N.; Archetti, R. Comparison under controlled conditions between multi-frequency ADCPs and LISST-SL for investigating suspended sand in rivers. Flow Meas. Instrum. 2014, 37, 73–82. [Google Scholar] [CrossRef]
- Ji, X.; Su, M.; Chen, J.; Wang, X.; Cai, X. A novel method for plastic particle sizing in suspension based on acoustic impedance spectrum. Ultrasonics 2017, 77, 224–230. [Google Scholar] [CrossRef]
- Mingxu, S.U.; Anli, Y.; Jianming, Z.; Yongming, L.I.; Xiaoshu, C. Measurement of steam droplet size and content: A comparison of ultrasonic attenuation and light scattering. J. Cent. South Univ. (Sci. Technol.) 2016, 47, 654–660. [Google Scholar]
- Lang, M.J.; Duarte-Dominguez, M.; Arnold, W. Extension of frequency spectrum methods for phase velocity measurements in ultrasonic testing. Rev. Sci. Instrum. 2000, 71, 3470–3473. [Google Scholar] [CrossRef]
- Urick, R.J. The Absorption of Sound in Suspensions of Irregular Particles. J. Acoust. Soc. Am. 1948, 20, 283–289. [Google Scholar] [CrossRef]
- Rayleigh, L.; Nachtrieb, N.H. The Theory of Sound. Phys. Today 1856, 10, 32–34. [Google Scholar] [CrossRef]
- Weser, R.; Wöckel, S.; Wessely, B.; Hempel, U. Particle characterisation in highly concentrated dispersions using ultrasonic backscattering method. Ultrasonics 2013, 53, 706–716. [Google Scholar] [CrossRef] [PubMed]
- Thorne; Peter, D.; Hanes; Daniel, M. A review of acoustic measurement of small-scale sediment processes. Cont. Shelf Res. 2002, 22, 603–632. [Google Scholar] [CrossRef]
- Thorne, P.D.; Agrawal, Y.C.; Cacchione, D.A. A Comparison of Near-Bed Acoustic Backscatter and Laser Diffraction Measurements of Suspended Sediments. IEEE J. Ocean. Eng. 2007, 32, 225–235. [Google Scholar] [CrossRef]
- Thorne, P.D.; Hardcastle, P.J. Acoustic measurements of suspended sediments in turbulent currents and comparison with in-situ samples. J. Acoust. Soc. Am. 1997, 101, 2603–2614. [Google Scholar] [CrossRef]
- Thorne, P.D.; Vincent, C.E.; Hardcastle, P.J.; Rehman, S.; Pearson, N.D. Measuring suspended sediment concentrations using acoustic backscatter devices. Mar. Geol. 1991, 98, 7–16. [Google Scholar] [CrossRef]
- Rai, A.K.; Kumar, A. Continuous measurement of suspended sediment concentration: Technological advancement and future outlook. Measurement 2015, 76, 209–227. [Google Scholar] [CrossRef]
- Fugate, D.C.; Friedrichs, C.T. Determining concentration and fall velocity of estuarine particle populations using ADV, OBS and LISST. Cont. Shelf Res. 2002, 22, 1867–1886. [Google Scholar] [CrossRef]
- Arora, N.; Kumar, A.; Singal, S.K. Technological advancement in measurements of suspended sediment and hydraulic turbine erosion. Measurement 2022, 190, 110700. [Google Scholar] [CrossRef]
- Li, W.; Yang, S.; Yang, W.; Xiao, Y.; Fu, X.; Zhang, S. Estimating instantaneous concentration of suspended sediment using acoustic backscatter from an ADV. Int. J. Sediment Res. 2018, 34, 422–431. [Google Scholar] [CrossRef]
- Holdaway, G.P.; Thorne, P.D.; Flatt, D.; Jones, S.E.; Prandle, D. Comparison between ADCP and transmissometer measurements of suspended sediment concentration. Cont. Shelf Res. 1999, 19, 421–441. [Google Scholar] [CrossRef]
- Kuang, Z.; Yang, W.; Lin, H.; Bi, S.; Chen, Y.; Gao, Y.; Jing, S.; Li, J. Research on sediment concentration measurement based on multi-frequency ultrasonic signal response. Measurement 2023, 208, 112485. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, W.; Lin, H.; Li, B.; Jing, S. Modified kernel density-based algorithm for despiking acoustic Doppler velocimeter data. Measurement 2022, 204, 112043. [Google Scholar] [CrossRef]
- Hay, A.E.; Sheng, J. Vertical profiles of suspended sand concentration and size from multifrequency acoustic backscatter. J. Geophys. Res. Ocean. 1992, 97, 15661–15677. [Google Scholar] [CrossRef]
- Flammer, G.H. Ultrasonic Measurement of Suspended Sediment; Us Geological Survey Bulletin A Government Printing Office: Washington, DC, USA, 1962. [Google Scholar]
- Rajaee, T.; Jafari, H. Two decades on the artificial intelligence models advancement for modeling river sediment concentration: State-of-the-art. J. Hydrol. 2020, 588, 125011. [Google Scholar] [CrossRef]
- Shui, Y.; Xue, Q. A dynamic model for piezoelectric composite transducers and coupling coefficient kt. J. Acoust. Soc. Am. 1994, 96, 3299. [Google Scholar] [CrossRef]
- Shui, Y.; Xue, Q. Dynamic characteristics of 2-2 piezoelectric composite transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 44, 1110–1119. [Google Scholar] [CrossRef]
- Nyquist, H. Certain topics in Telegraph Transmission Theory. Trans. Am. Inst. Electr. Eng. 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Sun, H.; Nie, S.; Packman, A.I.; Zhang, Y.; Chen, D.; Lu, C.; Zheng, C. Application of Hausdorff fractal derivative to the determination of the vertical sediment concentration distribution. Int. J. Sediment Res. 2022, 38, 12–23. [Google Scholar] [CrossRef]
- Santos, A.I.; Carinhas, D.; Oliveira, A.; Pinto, J.P.; Hanes, D.M. A statistical interpretation of acoustic backscatter and laser responses to suspended particle variations in the coastal shelf. Mar. Geol. 2021, 436, 106474. [Google Scholar] [CrossRef]
- Panda, S.K.; Nag, S.; Jana, P.K. Normalization-Based Task Scheduling Algorithms for Heterogeneous Multi-Cloud Environment. In Proceedings of the International Conference on Parallel, Beijing, China, 1–4 September 2015. [Google Scholar]
- Yuyang, S.; Jerome, M. Comparisons of Different Instruments for Measuring Suspended Cohesive Sediment Concentrations. Water 2017, 9, 968. [Google Scholar] [CrossRef]
- Wang, W.; Xu, Z.; Zhang, C.; Liu, G.; Tian, J. Study of Coal Water Slurry Particle Size Distribution with Ultrasonic Testing Theory. In Proceedings of the Power and Energy Engineering Conference (APPEEC), 2010 Asia-Pacific, Chengdu, China, 28–31 March 2010. [Google Scholar]



| (MHz) | (MHz) | (MHz) | (mm) | (mm) |
|---|---|---|---|---|
| 5.0 | 3.0 | 6.5 | 0.007 | 0.094 |
| 10.0 | 6.5 | 13.5 | 0.004 | 0.043 |
| 15.0 | 13.5 | 19.5 | 0.002 | 0.020 |
| 20.0 | 19.5 | 30.0 | 0.002 | 0.014 |
| Experimental Group | (mm) | SSC (kg/m3) |
|---|---|---|
| Single particle size group | 0.006 | 0.05, 0.10, 0.20, 0.40, 0.80, 1.60 |
| 0.008 | ||
| 0.012 | ||
| 0.015 | ||
| 0.020 | ||
| 0.025 | ||
| 0.030 |
| (MHz) | (mm) | (mm) | (mm) |
|---|---|---|---|
| 5.0 | 6.0 | 30.0 | 35.0 |
| 10.0 | 5.0 | 42.0 | 65.0 |
| 15.0 | 1.8 | 9.0 | 23.0 |
| 20.0 | 1.8 | 11.0 | 23.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yang, W.; Lin, H.; Kuang, Z.; Chen, Y.; Han, C.; Gao, Y.; Li, T. Research on Suspended Particle Size Measurement Based on Ultrasonic Backscattered Amplitude Analysis. Water 2024, 16, 1973. https://doi.org/10.3390/w16141973
Li Y, Yang W, Lin H, Kuang Z, Chen Y, Han C, Gao Y, Li T. Research on Suspended Particle Size Measurement Based on Ultrasonic Backscattered Amplitude Analysis. Water. 2024; 16(14):1973. https://doi.org/10.3390/w16141973
Chicago/Turabian StyleLi, Yixu, Wenjun Yang, Haili Lin, Zhen Kuang, Yue Chen, Chang Han, Yinggang Gao, and Tingting Li. 2024. "Research on Suspended Particle Size Measurement Based on Ultrasonic Backscattered Amplitude Analysis" Water 16, no. 14: 1973. https://doi.org/10.3390/w16141973
APA StyleLi, Y., Yang, W., Lin, H., Kuang, Z., Chen, Y., Han, C., Gao, Y., & Li, T. (2024). Research on Suspended Particle Size Measurement Based on Ultrasonic Backscattered Amplitude Analysis. Water, 16(14), 1973. https://doi.org/10.3390/w16141973





