Identifying the Optimal Layout of Low-Impact Development Measures at an Urban Watershed Scale Using a Multi-Objective Decision-Making Framework

Abstract

This study introduces a spatial layout framework for the multi-objective optimization of low-impact development (LID) measures at an urban watershed scale, targeting the mitigation of urban flooding and water pollution exacerbated by urbanization. The framework, tailored for the Dahongmen area within Beijing’s Liangshui River Watershed, integrates the storm water management model (SWMM) with the nondominated sorting genetic algorithm II (NSGA-II). It optimizes LID deployment by balancing annual costs, volume capture ratio of rainfall, runoff pollution control rate, and the reduction in heat island potential (HIPR). High-resolution comprehensive runoff and land use data calibrate the model, ensuring the realism of the optimization approach. The selection of optimal solutions from the Pareto front is guided by weights determined through both the entropy weight method and subjective weight method, employing the TOPSIS method. The research highlights the positive, nonlinear correlation between cost and environmental benefits, particularly in reducing heat island effects, offering vital decision-making insights. It also identifies a critical weight range in specific decision-making scenarios, providing a scientific basis for rational weight assignment in practical engineering. This study exemplifies the benefits of comprehensive multi-objective optimization, with expectations of markedly improving the efficacy of large-scale LID implementations.

1. Introduction

With the accelerating pace of urbanization, the area of impervious surfaces has been expanding, significantly disrupting the natural hydrological cycle and ecological balance [1]. This has led to pressing urban water issues, including flooding, water pollution, and ecological degradation, which we urgently need to address [2]. For instance, Yang’s study [3] found that rapid urbanization negatively impacts the water environment of urban lakes, manifested by notable increases in runoff depth, runoff coefficient, and pollutant loads. Traditional grey infrastructure (GREI) has been considered a primary solution in response to these challenges. However, its rapid drainage capability has not effectively controlled runoff pollution and may even exacerbate water environment pressures [4,5]. Additionally, the high construction and maintenance costs of GREI limit its widespread application, and its inadequate drainage capacity during intense rainfall events often leads to flooding disasters [6,7].

To effectively address these challenges, China introduced the concept of sponge cities in 2012, an innovative stormwater management strategy to improve urban water environment issues by enhancing rainwater infiltration, purification, and utilization [8]. The planning of sponge cities not only enhances urban flood control and drainage capacity but also promotes the efficient use of rainwater resources [9]. Despite sponge cities’ social, environmental, and economic feasibility [10], differences in public willingness to pay and the slow realization of long-term benefits of LID measures result in insufficient private investment interest in such projects. This poses significant challenges for the government to achieve sponge city goals solely with public funds [11,12,13]. Therefore, rational planning and optimization of the spatial layout of LID measures to maximize cost-effectiveness are crucial for advancing sponge city construction, particularly in controlling runoff and reducing pollutant emissions [14].

However, the spatial optimization of LID measures is a complex issue that requires consideration of various factors, such as soil type, permeability, land cover, and land use [15], to ensure hydrology and water quality improvements. In optimizing LID measures, the “scenario-model” and “model-algorithm” are two commonly used methods. The “scenario-model” approach is straightforward to implement. Still, it is based on simulations and evaluations of a limited number of specific scenarios, potentially yielding the best solution among only a few alternatives, making it more suitable for small-scale study areas [16]. For example, in Su et al.’s study [17], by comparing the runoff control effects of four scenarios, the optimal scheme was selected as a reference for constructing a “sponge campus.” However, this method may not comprehensively capture all possible solutions.

In contrast, the “model-algorithm” approach uses optimization algorithms to automatically simulate many scenarios while considering multiple objectives, resulting in a series of excellent feasible solutions [18]. This method avoids local optima and is closer to the global optimum, making it applicable to study areas of various scales. Integrating multiple algorithms with numerical models has become the mainstream trend in selecting optimization tools for LID planning [16]. This model-coupled optimization algorithm can solve multi-objective optimization problems in the LID layout, providing optimal solutions for the types and scales of LID measures within sub-catchments. This method can more effectively handle numerous simulated scenarios to find the best spatial layout for LID measures, particularly at the watershed scale.

Compared to small and medium-scale studies, large-scale studies have unique advantages in optimizing the spatial layout of LID measures. They can effectively avoid fragmentation during implementation, enhancing the coherence and efficiency of runoff management [16]. As understanding in this field deepens, optimizing the LID spatial layout in large-scale study areas is gaining increasing attention [19]. However, current research still focuses primarily on small to medium-sized areas [16]. There are two main reasons for this situation. First, optimizing LID spatial layout typically relies on model-coupled algorithms for calculations. In large-scale study areas, the algorithm needs to search for the optimal solution within a vast search space, often requiring thousands or more simulations, significantly increasing the time needed for optimization from hours to days or even longer [18,20]. Second, obtaining the necessary accurate data, such as network data, elevation data, and water level and flow data, during model construction, calibration, and validation, is particularly challenging in urban watersheds [21]. The difficulty in acquiring these data limits the in-depth development of large-scale studies.

Despite numerous challenges, large-scale studies play an indispensable role in realizing the comprehensive benefits of LID measures. They help foster synergies between different regions and provide a broader assessment and optimization of LID implementation at a macro level. In small- to medium-scale studies, the solutions derived are often locally optimal, failing to fully consider the drainage characteristics’ interdependence between the study area and its surroundings. In contrast, large-scale studies, such as those optimizing the spatial layout of LID measures at the urban watershed scale, can address this gap by more comprehensively reflecting the hydrological connections and interactions between regions [16]. For instance, Liu’s study [22] in the Crooked Creek watershed in Indiana, USA, optimized the types and scales of LID facilities by dividing the watershed into hydrological response units (HRUs) and considering water flow exchanges between these units. This approach underscores the importance of considering hydrological process continuity and spatial heterogeneity at larger scales.

However, most current research still divides urban watersheds based on functional zoning rather than hydrological zoning, leading to uniform LID measure ratios within the same functional zone after optimization [23]. While this method simplifies the search for optimal solutions, it overlooks the specific requirements for LID types and proportions based on different surface hydrological conditions. The applicability of the results is thus limited, mainly targeting particular functional zones and failing to provide general guidance for LID selection and layout at the watershed scale. To enhance the practicality and effectiveness of LID spatial optimization, researchers need to focus more on hydrological zoning and the adaptability analysis of LID layouts under different hydrological conditions. This will help devise more precise and efficient LID layout plans at the watershed scale, promoting comprehensive urban stormwater management, ecological protection and sustainable development.

In urban stormwater management, soil infiltration and evapotranspiration processes are crucial for soil characteristics and the siting decisions of LID measures. This study considers several critical factors, including soil type, permeability, roughness coefficient, land cover and use, precipitation, and terrain slope. These factors collectively determine the suitability and effectiveness of LID deployment plans. For instance, green roofs (GR) can effectively reduce rooftop runoff volume and pollution load, contributing positively to energy savings and emissions reductions. However, implementing GR requires considerations such as the roof’s load-bearing capacity, waterproofing, slope, and available space, typically suitable for roofs with gentler slopes [24]. Additionally, different types of LID measures and their combinations affect hydrological and water quality improvements differently. For instance, GR outperforms permeable pavements (PP) in terms of reducing peak flow. However, PP has advantages in durability, infiltration capacity, and water quality purification compared to traditional asphalt pavements [25], making them more suitable for hardened areas such as roads and squares. Rain gardens (RG), known as bioretention cells, are another effective LID measure. They enhance soil and vegetation filtration, effectively reducing runoff and removing suspended solids, heavy metals, phosphorus, fats, oils, and other pathogens [26,27], and are usually placed in green areas to maximize ecological benefits.

Implementing LID measures is a multi-criteria decision-making process that comprehensively considers numerous factors. While hydrological performance is critical, the full life-cycle cost is also a key factor in determining the type, scale, and layout of LID measures [28]. LID measures play an essential role in controlling runoff pollution. By slowing down the flow of rainwater and filtering pollutants, they significantly reduce the risk of contaminants entering water bodies, thereby enhancing the overall quality of the water environment [29,30]. Furthermore, LID measures have the potential to mitigate the urban heat island effect. By increasing vegetation cover and using permeable materials, LID measures help lower temperatures in urban areas and improve the microclimate [31]. For example, Giacomoni et al. [32] used Monte Carlo simulation, targeting the reduction of peak runoff and node overflow, to study the spatial layout of GR and PP. The results indicated that LID measures effectively reduce peak flow and total runoff volume. Yu et al. [33] developed an LID spatial layout optimization system based on the SWMM model and PICEA-g, aiming to reduce the peak inflow rate into retention ponds and costs, optimizing bioretention facilities, RG, PP, and GR layout. This demonstrated the potential to achieve watershed hydrological benefits at a lower price. Therefore, when evaluating the benefits of LID measures, it is crucial to consider multiple objectives, including environmental, economic, and social benefits. This comprehensive approach promotes environmental sustainability and maximizes economic and social benefits. This study aims to comprehensively evaluate the spatial layout of LID measures through a multi-objective optimization assessment framework, providing scientific, economical, and practical strategies for urban stormwater management.

When finalizing the spatial layout plan for LID measures, selecting a comprehensively optimal alternative is critical. This involves multiple elements, such as the scale, type, and specific locations of the LID measures [33]. In addressing multi-objective optimization problems, model-coupled optimization algorithms can provide a set of Pareto solutions. These solutions balance multiple objectives, with no single solution being the absolute best across all objectives. However, real-world decision-making requires selecting the most suitable plan from these Pareto solutions. To address this challenge, among various multi-criteria decision-making methods, TOPSIS (technique for order preference by similarity to ideal solution) is widely popular due to its intuitiveness and effectiveness [34,35]. The core of the TOPSIS method lies in calculating the distance of each potential solution from the ideal and negative ideal solutions and then assessing each plan’s relative merits based on these distances. This method helps decision makers make quantitative comparisons in multi-objective optimization problems and provides a systematic decision-support tool. By applying the TOPSIS method, we can identify the most cost-effective and environmentally beneficial LID layout plan, considering all relevant goals and constraints. This is crucial for achieving sustainability and comprehensiveness in urban stormwater management.

In recent years, Beijing has frequently faced extreme rainfall events [36,37]. The Dahongmen area, an essential part of Beijing’s central urban region, has a high degree of urbanization but the existing drainage system struggles to meet the increasing demands of stormwater management. This contradiction has led to a high risk of urban flooding during heavy rains, resulting in a “flood-prone” situation [38]. Given the severe challenges posed by climate change and the typicality and representativeness of the Dahongmen area in urban stormwater issues, this study focuses on the Dahongmen section of the Liangshui River Basin in Beijing. We aim to deeply explore the stormwater characteristics and formulate targeted strategies. This choice of study area is crucial for optimizing the spatial layout of LID measures. It has significant implications for enhancing the overall flood control capacity of the city, safeguarding residents’ lives and property, and promoting environmental sustainability. Through precise planning and scientific implementation, we hope to significantly enhance the resilience of urban infrastructure, laying a solid foundation for effectively addressing potential extreme weather events in the future.

This study aims to develop a multi-objective optimization framework focused on the spatial layout optimization of LID measures at the scale of a typical urban watershed. By comprehensively considering the types, scales, and locations of LID measures, this framework seeks to identify the optimal alternative that achieves the best multi-criteria decision-making solution. Given the high building density and diverse surface types in the study area, including construction area, roads and squares, and grassland, this study selects three typical LID measures and their combinations: RG, PP, and GR, to suit the specific characteristics of the area. We utilize the SWMM model coupled with the NSGA-II optimization algorithm, targeting cost, volume capture ratio of annual rainfall, annual runoff pollution control rate, and heat island mitigation benefits as evaluation objective functions, aiming to determine the spatial layout scheme of LID measures at the urban watershed scale. Since the NSGA-II optimization algorithm provides a set of Pareto frontier solutions that meet multi-objective and constraint conditions, and actual engineering practice often requires a specific implementation plan with varying emphasis on each objective function; this study combines the entropy weight method and subjective weighting method to determine the weight matrix of the objective functions. Further, we apply the TOPSIS method to rank these solutions, identifying the best LID measure spatial layout scheme that prioritizes specific objective functions under both subjective and objective conditions. Through this comprehensive evaluation method, this study aims to provide a scientific and systematic decision support tool for urban stormwater management, enhancing the adaptability and resilience of urban infrastructure to address the challenges posed by future climate change effectively.

2. Materials and Methods

2.1. Research Area

Beijing has a monsoon climate, with an average annual precipitation of 550 mm and an average annual temperature of 11–13 °C [39]. The precipitation distribution is uneven both temporally and spatially, with over 60% of the annual precipitation occurring during the flood season (June–October). The windward slopes in the urban area at the foot of the mountains are prone to flash floods and flood disasters [40]. The Dahongmen area is situated in the southwest foothills of Beijing, upstream of the Liangshui River basin, with terrain sloping from southwest to northeast, covering a total area of 130 km². During the flood season, the mountains obstruct moisture moving southeastward, often leading to localized heavy rainfall in this area. As one of Beijing’s central urban areas, Dahongmen covers over 30% of the city’s central urban district. The predominant land use types include road squares, green spaces, and built-up areas. Due to high urbanization rates and relatively low existing drainage capacity, coupled with the additional drainage burden from 30% of the central urban area during the flood season, the area has faced a higher probability of flash floods in recent years, often experiencing localized flooding after heavy rains. Statistics show that during the “7.21” torrential rain and urban flooding event in Beijing in 2012, more than 50% of the severe flooding points with water depths exceeding 30 mm were located in the Dahongmen area [38].

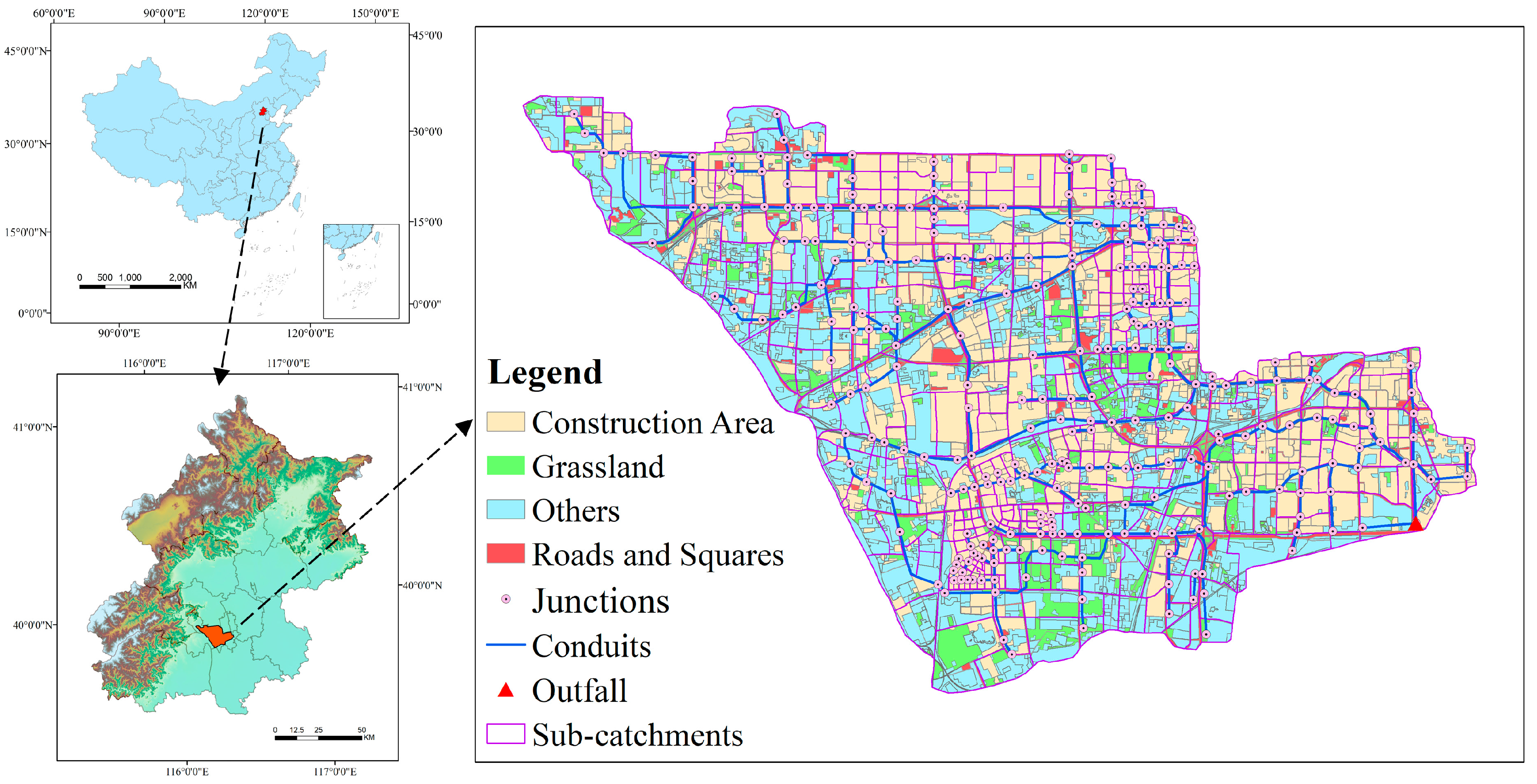
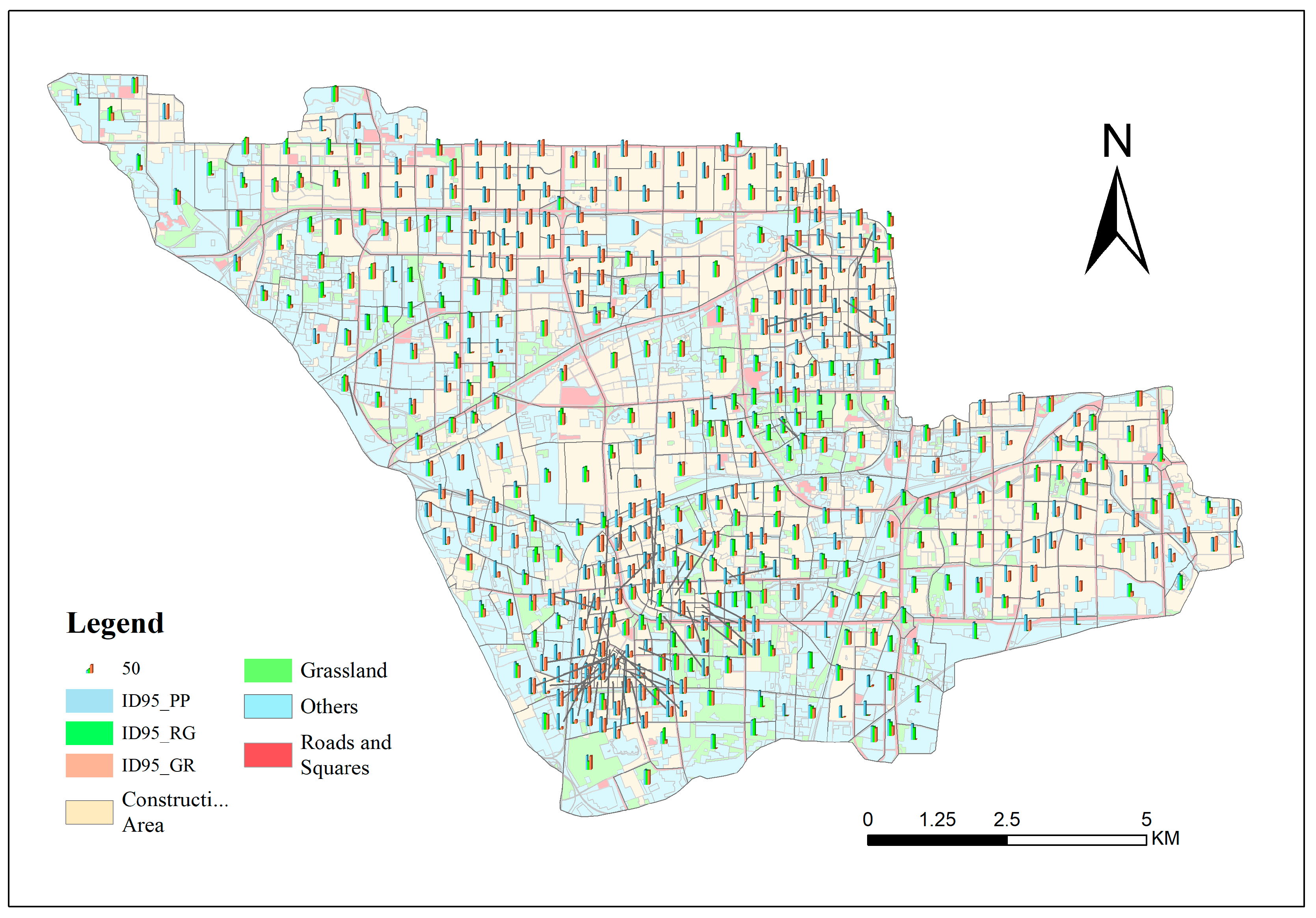
To mitigate the impact of flash floods, GREI methods such as increasing pipe diameters, adding pumping stations, and constructing detention basins have been employed to enhance the drainage capacity of the existing drainage system. However, during heavy rainfall, when the water level of the Liangshui River is higher than the ground level, it is challenging to rely solely on pumping stations to force rainwater into the river. To further improve drainage capacity, enhance water environmental quality, and mitigate the urban heat island effect, the study proposes the implementation of LID measures and their combinations alongside existing GREI. Considering the existing land use types in the study area, LID measures including PP, RG, and GR are selected for retrofitting road and squares, grassland, and construction area. Reflecting the hydrological characteristics of the study area, it is subdivided into 461 sub-catchments, including 292 pipes (of which 125 are river sections) and 295 nodes. The sub-catchments are interconnected hydraulically, with outflows from one sub-catchment directed to another sub-catchment or pipe node. Detailed geographic location, elevation, land use, and drainage system information of the study area are illustrated in Figure 1.

2.2. Datasets

The data used in this study primarily serve to construct, calibrate, and validate the SWMM model. To evaluate the performance of different LID spatial layout schemes in terms of cost-effectiveness, volume capture ratio of annual rainfall, annual runoff pollution control rate, and HIPR, this study established a baseline scenario without any LID measures as a control for the simulation results. The simulation data for this baseline scenario (excluding the annual rainfall sequence) were sourced from the period between 2010 and 2012, during which no LID measures were implemented in the study area. The rainfall and runoff (outflow at the outfall) data used for model calibration and validation also came from the same period, ensuring data completeness and reliability.

Furthermore, when assessing the effectiveness of the baseline scenario and LID layout schemes, the core objective of sponge city planning—to improve the ecological environment under normal hydrological conditions—was considered. Therefore, the model simulations used rainfall sequences from an average rainfall year known as a normal year as input. A normal year is one where the annual precipitation is close to the long-term average, facilitating more accurate simulation and evaluation of the effectiveness of LID measures under normal climatic conditions.

The fundamental data utilized in this study encompasses runoff data, drainage network data, river network data, rainfall data, surface elevation data, and land use data within the research area.

Runoff data were provided by the Liangshui River Basin Management Bureau, covering lateral inflow and outflow discharge data for the main and tributary streams of the Liangshui River during the flood seasons from 2010 to 2012. Data were collected before the implementation of LID measures. The outflow at the outfall was used to calibrate the SWMM model (baseline scenario, the model without LID). Drainage network data were sourced from the Beijing Municipal Institute of City Planning & Design, including the spatial distribution of primary stormwater drainage networks and the geographic locations of drainage nodes. River network data were obtained from the Beijing Hydrological Station, detailing river alignments, cross sections, and watershed boundary conditions. Rainfall data were sourced from the National Meteorological Center, utilizing hourly precipitation data from observation stations over nearly 60 years. The precipitation pattern from 1966, considered a normal year, was selected through frequency analysis as the model input to simulate and calculate the volume capture ratio of annual rainfall for each LID spatial layout scheme under planned design conditions.

Surface elevation data were derived from 30 m resolution data provided by the Beijing Institute of City Planning and 7.29 m resolution remote sensing images from Google Earth. These were resampled using ArcGIS 10.8 software to generate 10 m resolution elevation information. These data were further checked and corrected around river channels, roads, and buildings, incorporating land use information. Land use data were obtained by interpreting high-resolution imagery of the Beijing area from 2012, supplemented by field surveys, with a spatial resolution of 1 m. Based on the surface runoff characteristics of the Dahongmen area and the layout characteristics of LID measures, we categorized the land use data as follows: urban roads and squares were grouped under Roads and Squares, suitable for the installation of PP; building areas and bungalow areas were grouped under Construction Area, suitable for the installation of GR; arable land, forest land, river surfaces, ditches, lake surfaces, pond surfaces, beach land, industrial and mining land, railway land, other construction land, and unused land were grouped under Others, with LID measures not currently considered for these areas; grassland remained unchanged, suitable for the installation of RG.

Due to data confidentiality and availability constraints, this study only utilized primary trunk sewer network data from the Dahongmen area for runoff simulation and sub-catchment delineation. The primary trunk sewer network in the study area is primarily laid along urban roads (without LID measures). When setting up LID measure deployment schemes, PP is proportionally installed based on the area of roads within each sub-catchment area, without altering the network’s alignment and layout.

2.3. Optimization Framework

The SWMM model is widely used for stormwater simulation and evaluating the effectiveness of LID measures [41]. Research indicates that SWMM is particularly suitable for urban areas with complex hydrological and hydraulic conditions, especially those primarily relying on piped drainage systems [42]. The model can simulate and assess the potential effects of various LID measures on reducing runoff, controlling peak flow, and improving water quality. 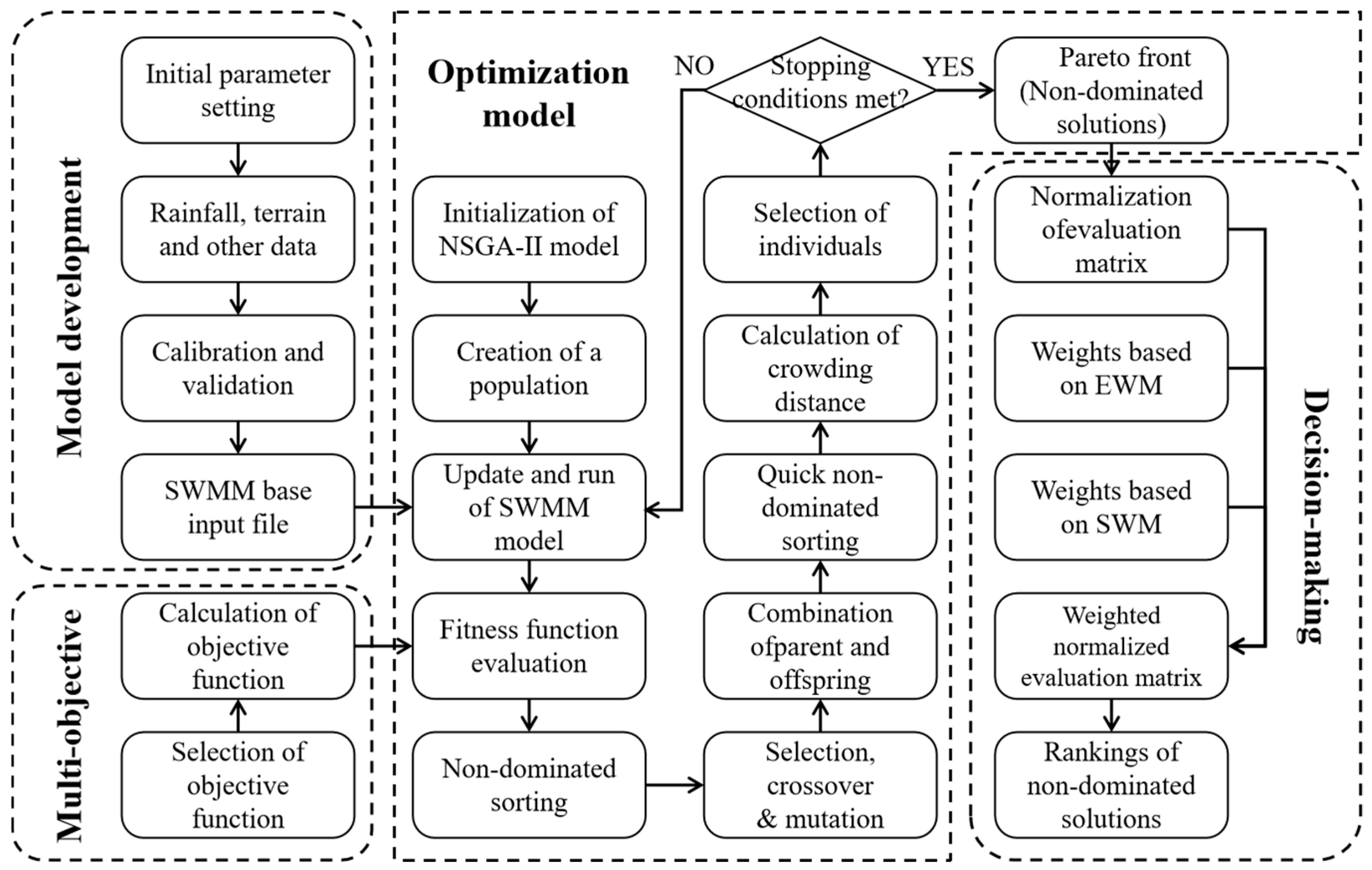The NSGA-II was chosen for optimization due to its incorporation of an elitist strategy and uniform solutions distribution, enabling the algorithm to explore the entire Pareto front effectively [43]. This makes NSGA-II highly applicable and efficient for handling multi-objective optimization problems. Therefore, we adopted the coupled SWMM model and NSGA-II algorithm for multi-objective optimization of the spatial layout of LID measures. To facilitate decision makers in selecting a specific scheme, we used the TOPSIS algorithm for multi-criteria decision making on the Pareto front to choose the final scheme. The exact technical framework is illustrated in Figure 2. The framework can be divided into the following three steps.

Step 1: Initial parameters, annual rainfall data, terrain slope, and drainage network information are input into the SWMM model; the model is calibrated and validated before conducting simulations of the baseline scenario (SWMM model without LID).

Step 2: Parameters for various LID measures are meticulously set, referencing volume capture ratio of annual rainfall from recent Beijing studies, their rationality [44]. These parameters are then input into the swmm_api computational package for scenario simulations. Based on the heat island mitigation benefits analysis of various LID measures, decision variables, objective functions, and constraints are further selected.

Step 3: The SWMM model code integrated with the NSGA-II algorithm is utilized for computation to obtain the Pareto front, which represents the multi-objective optimization solution set for LID practices spatial layout schemes. By determining the weights of objective functions through the entropy weight method (EWM) and subjective weight method (SWM), the final optimal spatial layout scheme is obtained through TOPSIS ranking.

2.4. Components of Optimization Problems

2.4.1. Multi-Objective Optimization Algorithms

The NSGA (nondominated sorting genetic algorithm) is a nondominated sorting genetic algorithm designed to address multi-objective optimization problems. This algorithm categorizes potential solution sets hierarchically based on individual ranks, resulting in a relatively uniform distribution of the solution set and quickly yielding satisfactory nondominated solutions. However, it has drawbacks such as high computational complexity and the need for manually specified parameters. To address these issues, Indian scholar Deb [45] and colleagues improved the NSGA algorithm, proposing the NSGA-II algorithm. Compared to NSGA, the NSGA-II algorithm introduces an elitism strategy, effectively preventing the loss or omission of excellent parent individuals, significantly reducing computational complexity. Additionally, this algorithm does not require manually specified parameters, thereby improving computational efficiency and robustness, making it widely applicable in various fields of multi-objective optimization.

In this study, the NSGA-II algorithm is selected to solve the multi-objective optimization problem of spatial layout for LID measures. This algorithm efficiently identifies and generates Pareto optimal solutions, which together form the Pareto front. When mapped through the objective function, these solutions constitute the Pareto front of the multi-objective optimization problem. The optimization module in Figure 2 provides a detailed overview of the basic principles and core steps of the NSGA-II algorithm.

2.4.2. Multi-Criteria Decision Making

TOPSIS is a multi-criteria decision-making method that evaluates the performance of each alternative by comparing their relative closeness to the ideal solution and the negative ideal solution. In the TOPSIS method, the determination of criterion weights directly affects the identification of the ideal and negative ideal solutions. Currently, common methods for determining TOPSIS weights include the entropy weight method and subjective weighting methods. The entropy weight method is an objective approach that determines weights based on the variability of the indicators, reflecting the inherent information in the data and reducing the influence of subjective judgment. However, the entropy weight method may not accurately reflect the weighting relationships in certain special cases. For instance, when the values of an indicator are equal or very close, the weight of that indicator may be underestimated. Subjective weighting methods, such as the analytic hierarchy process (AHP), convert the decision maker’s experience and judgments into quantitative weights through pairwise comparisons. Nevertheless, these methods carry a degree of subjectivity, as the construction of the judgment matrix relies to some extent on the expert’s experience and preferences, potentially introducing subjective bias.

In the real world, different decision makers prioritize various objective functions differently depending on the forecast period. Therefore, this study not only compares the performance of the optimal layout schemes selected by the TOPSIS method under the two weighting schemes across various objectives but also conducts a sensitivity analysis of weight assignments by setting multiple decision scenarios. This analysis explores the potential impact of weight changes on the optimal scheme decisions under different decision scenarios.

2.4.3. The Decision Variables

As previously mentioned, based on the current underlying surface conditions of the study area, this research selects three LID measures (PP, RG, and GR) and their combinations for spatial layout optimization. In other words, the area of each sub-watershed was chosen as the decision variable to optimize the layout of these three LID measures.

2.4.4. The Objective Functions

Research indicates that increasing the implementation of LID measures such as PP, RG, and GR can enhance urban surface reflectivity and heat capacity, reduce surface temperatures, and subsequently mitigate urban heat island intensity [15,46]. By strategically planning and combining LID measures based on urban climate conditions and hydrological cycle characteristics, it is possible to create an effective network to alleviate heat island effects, improve urban ecological comfort, promote low-carbon emissions, and support sustainable development. Therefore, in this study, while optimizing the spatial layout of LID measures, we not only consider cost, volume capture ratio of annual rainfall, and annual runoff pollution control rate as objective functions but also include the reduction in heat island potential (HIP) [46], referred to as HIPR. The aim of the research is to use multi-objective optimization to identify solutions that minimize costs while maximizing volume capture ratio of annual rainfall, annual runoff pollution control rate, and HIPR. This approach seeks to balance cost-effectiveness, environmental impact mitigation, and sustainable urban development.

$$F=\left\{\begin{array}{c}\begin{array}{l}\min C(\mathrm{X})\\ \max R\left(\mathrm{X}\right)\end{array}\\ \begin{array}{l}\max P(\mathrm{X})\\ \max H(\mathrm{X})\end{array}\end{array}\right.$$

(1)

C(X), R(X), P(X), and H(X), respectively, represent the annual cost, volume capture ratio of annual rainfall, annual runoff pollution control rate, and HIPR of all LID measures.

• Cost

This study conducted the cost accounting for various LID measures using the annual cost method. Specifically, we defined the annual cost as the ratio of the total life-cycle cost of an LID measure to its expected service life. This method considers the economic inputs throughout the entire cycle, from construction to operation and maintenance, providing a comprehensive indicator of the economic performance of LID measures. Using this approach, we can more accurately assess and compare the cost-effectiveness of different LID measures, offering scientific support for decision makers in urban planning and water resource management.

According to previous research, the annual cost method is employed to evaluate financial expenditures related to LID measures, including construction, operation, and maintenance costs [47]. According to the latest monetary policy issued by the People’s Bank of China, the annual cost of infrastructure expenses calculated at the discount rate of 5% is as follows in Equations (2) and (3) [41]:

$$C_{\mathrm{k}}=C_{0k}\frac{r{(1+\mathrm{r})}^{lk}}{{(1+r)}^{lk}-1} ,$$

(2)

$$C={\displaystyle \sum _{k=1}^3{S}_{\mathrm{k}}}{C}_{\mathrm{k}},$$

(3)

where C_k is the annual cost of certain LID measures per area (CNY/m²); C_0k is the life-cycle cost of certain LID measures per unit area (CNY/m²); r is the discount rate; l_k is service life (year); C is annual cost of LID measures (CNY); S_k is the construction area of certain LID measures (m²); k is the type of LID measures [41]. The annual costs of LID measures are shown in

Table 1. Construction and annual cost of implemented LID measures [41].

LID Measure	GR	PP	RG
Life period (year)	30	10	15
Construction cost (CNY/m2)	1110.5	1032.1	800
Annual construction cost (5% discount rate) (CNY/m2)	72.2	82.8	77.07
Annual maintenance and administration cost (CNY/m2)	25.4	6.2	6.55
Annual cost (CNY/m2)	97.6	89.0	83.62

.

• Runoff control effectiveness

The indicator of volume capture ratio of annual rainfall refers to the proportion of the cumulative annual controlled rainfall within the site through natural and artificially enhanced infiltration, storage, utilization, evaporation, transpiration, etc., to the total annual rainfall. The calculation formula is as follows in Equation (4).

$$R=(1-\frac{R_0}{R_1})\times 100\%,$$

(4)

where R₁ and R₀ are the annual rainfall and simulated surface runoff resulting from the hypothetical implementation of LID measures within the sub-catchment, respectively, and the unit is mm.

• Runoff pollutant control effectiveness

Annual runoff pollutant reduction rate represents the percentage reduction of pollutant load after the implementation of LID measures. The model calculates pollutant reduction using suspended solids (SS) for water quality assessment, with the calculation formula as follows in Equation (5).

$$P=(1-\frac{P_1}{P_0})\times 100\%,$$

(5)

where P represents the pollution reduction rate, P₁ denotes the pollutant load after the deployment of LID measures, and P₀ refers to the pollutant load in the initial state.

• The benefits of mitigating urban heat islands

In research, the wet bulb globe temperature (WBGT) and heat island intensity (HII) indices are commonly utilized to assess the intensity of urban heat environments. However, these indices do not provide a quantitative measure of the mitigation benefits of LID measures on the urban heat island effect. The HIP index [46] offers a quick and simple means to assess the urban heat island effect in planned residential areas, which can be calculated using Equation (6) through 3D-based thermal simulation tools [48]. This study employs HIPR (the reduction value of HIP) to evaluate the mitigation benefits of urban heat island, with the calculation formula as follows in Equation (7).

$$HIP=\frac{{\displaystyle \sum _{i=1}^n(T_{si}-T_{\mathrm{a}})}\Delta s}{s},$$

(6)

where T_si is the surface temperature of a mesh (°C), T_a is the ambient air temperature (°C), Δs is the area of a mesh (m²), S is the area of the analyzed urban block (m²), n is the number of meshes.

$$H={\displaystyle \sum _1^k{H}_i}{S}_i,$$

(7)

where H represents HIPR (the reduction value of HIP), S represents LID area; there are k types of LID measures (there are three types in this paper, i.e., k = 3), where i represents the i-th type of LID measure. The HIPR of each LID measure is shown in

Table 2. The HIPR of each LID implemented measure [49].

LID Measure	GR	PP	RG
HIPR	173.88	166.53	36.04

.

2.4.5. The Constraints

By referencing relevant research and regulatory requirements, it has been determined to establish the volume capture ratio of annual rainfall and the annual runoff pollution control rate as specific constraints, as outlined in the following Equations (8) and (9):

$$75\%\le R\le 85\%,$$

(8)

$$\mathsf{\psi }\ge 50\%,$$

(9)

where R and ψ represent volume capture ratio of annual rainfall and the annual runoff pollution control rate, respectively.

2.5. Storm Water Modeling

This study utilized the SWMM model developed by the Environmental Protection Agency of the United States to assess the hydrological improvement effects of LID measures. The Horton model and dynamic wave method within the SWMM model were used to simulate the hydrological and hydraulic processes of sub-catchments and drainage systems, respectively [50].

Dividing the study area into 461 sub-catchments within the Dahongmen area, the impervious area percentage and slope data for each sub-catchment were calculated using ArcGIS and 1 m resolution land use data. The feature width in the sub-catchment parameters was determined based on an empirical Equation (10).

$$width=K\times \sqrt{Area},$$

(10)

where “width” stands for feature width, “K” represents the coefficient (with a range of 0.2 to 5, and in this study, K is set to 0.5), and “Area” denotes the area of the sub-catchment.

Due to the variations in percent of impervious area and feature width of the original sub-catchments caused by the application of different LID measure layouts, this study conducted an automatic adjustment of these two parameters using the Python programming language. The corrected parameters were then integrated into the SWMM model code for simulation.

2.6. Model Calibration and Validation

In the SWMM model, most parameters have clear physical meanings, and theoretically, they can be obtained through actual measurements. However, it is often difficult to obtain exat and initial values for these parameters in practical applications due to various constraints. Therefore, for the ranges of other related model parameters in the sub-catchment area, we primarily referred to the SWMM user manual, hydrological manuals, and relevant literature [44]. The parameter value ranges for the sub-catchment area are presented in

Table 3. Model parameter value ranges and calibration outcomes.

Model Parameter	Physical Significance	The Range of Values	Results of Calibration
NLSH	Roughness of Liangshuihe	0.010~0.03	0.019
RoughnessG	Roughness of conduit	0.010~0.026	0.026
N-Imperv	Manning’s coefficient of pervious	0.011~0.05	0.05
N-Perv	Manning’s coefficient of impervious	0.011~0.41	0.41
S-Imperv	Depth of depression storage on the impervious/mm	1~20	5.6
S-Perv	Depth of depression storage on the pervious/mm	1~50	49.8
MaxRate	Maximum infiltration rate/(mm·h−1)	80~150	149.9
MinRate	Minimum infiltration rate/(mm·h−1)	1~50	50
Decay	Decay constant	1~10	1
DryTime	Time in days for a fully saturated soil to dry completely/day	3~10	9.86

. Additionally, to ensure the reliability of the model simulation results, we conducted model calibration and validation work.

In the Dahongmen area, due to differences in the sources and timing of rainfall and runoff data acquisition, there is incomplete temporal matching. Considering the integrity and representativeness of the data, we selected three typical rainfall events on 20100709, 20120721, and 20110623, which differ in their causes and characteristics, for the calibration and validation of model parameters [38]. The calibration of model parameters used data from the first two events, while the validation utilized data from the last event. The model calibration and validation were assessed using the Nash efficiency coefficient (NSE), primarily comparing simulated runoff values at the outlet of the entire study area with measured runoff values. The specific calculation formula for NSE is shown in Equation (11).

$$NSE=1-\frac{{\displaystyle \sum _{\mathrm{t}=1}^n{\left(Q_o-Q_{\mathrm{m}}\right)}^2}}{{\displaystyle \sum _{t=1}^n{\left(Q_o-\overline{Q_o}\right)}^2}}$$

(11)

where NSE stands for the Nash-Sutcliffe efficiency coefficient (closer to 1 indicates better calibration results), t represents the value at time t, Q_o denotes the measured value, Q_m denotes the simulated value, and Q_o (overline) represents the mean of observed values.

The Nash efficiency coefficients of the simulated rainfall-runoff processes for the three aforementioned events were 0.959, 0.812, and 0.707, all exceeding 0.7. These results indicate a satisfactory calibration and validation performance of the model, suitable for multi-objective optimization of LID measures in the Dahongmen drainage area. The calibration results of specific model parameters are detailed in Table 3.

3. Results

3.1. The Pareto Front

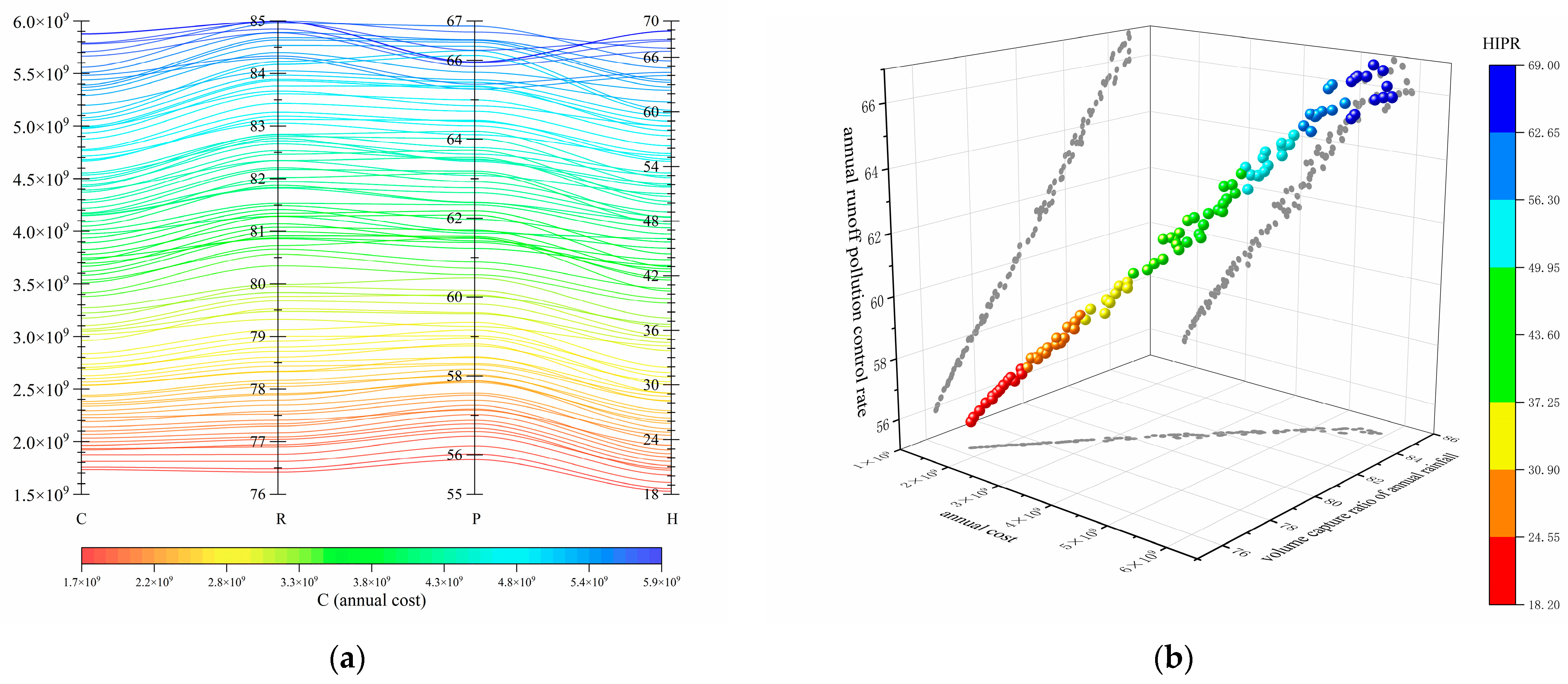
Based on the aforementioned multi-objective optimization framework, we obtained a Pareto front consisting of 100 Pareto optimal solutions. These solutions achieve a comprehensive balance among the four key objective functions: annual cost, volume capture ratio of annual rainfall, annual runoff pollution control rate, and HIPR. 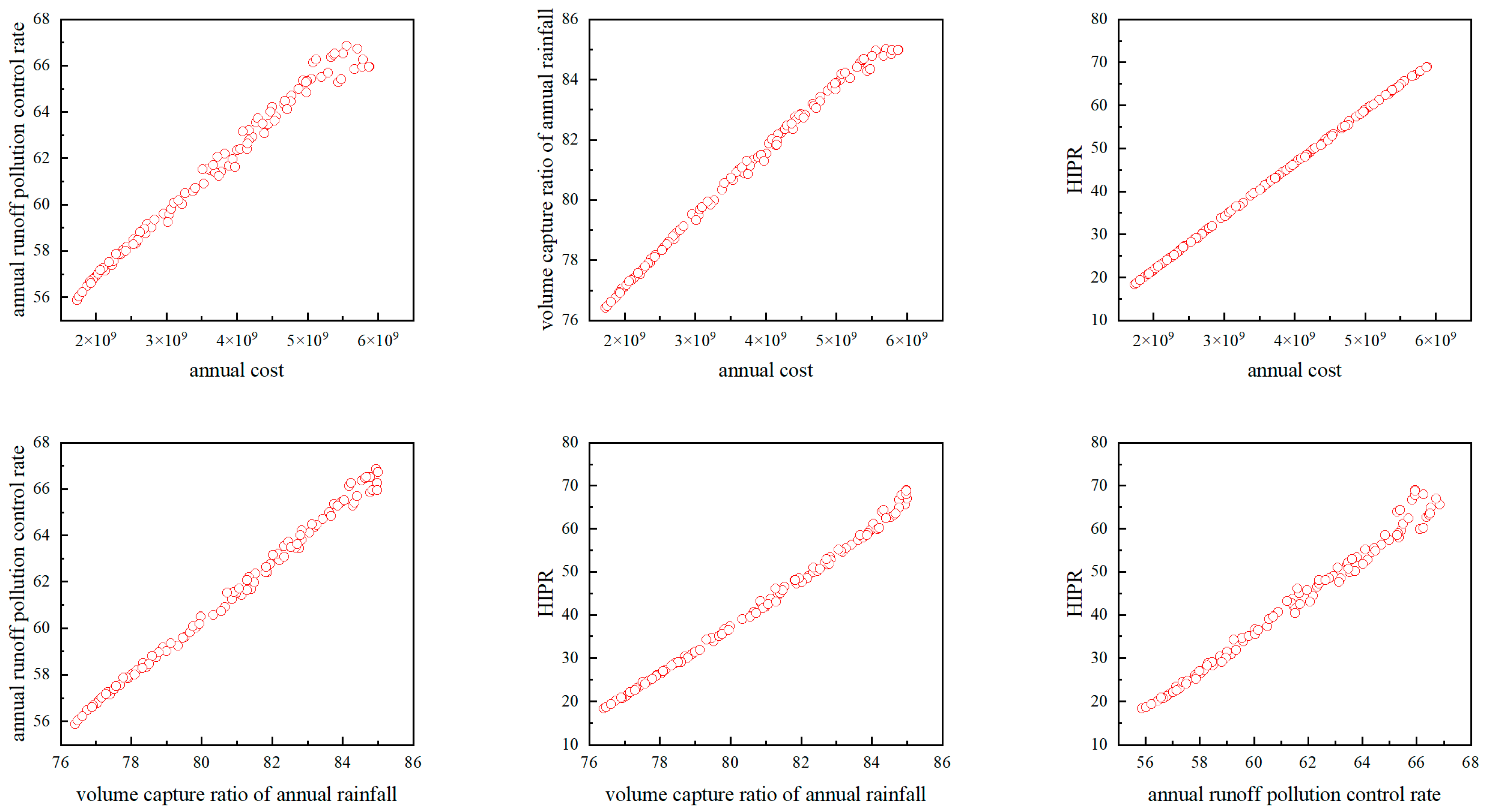The values of the four key objective functions for the 100 Pareto optimal solutions are detailed in the parallel coordinate plot (Figure 3a) and the four-dimensional scatter plot (Figure 3b). The pairwise mapping relationships of the four objective functions are shown in Figure 4, illustrating the trade-offs between different objectives.

Based on the analysis results from Figure 3 and Figure 4, we observe a significant positive correlation between annual cost, volume capture ratio of annual rainfall, annual runoff pollution control rate, and HIPR. This indicates that as investment increases, we can achieve better runoff control, more effective pollution management, and more benefits of mitigating urban heat islands. This positive correlation highlights an important decision-making insight: by moderately increasing investment, we can significantly enhance the overall effectiveness of LID measure implementation. However, this positive correlation does not imply that an increase in cost will proportionally enhance the outcomes. For example, considering the annual cost, when the cost increases from CNY 2,000,000 to CNY 6,000,000 (a 200% increase), the annual runoff pollution control rate rises from 56% to 67%, an improvement of 19.6%. Similarly, the annual runoff volume control rate increases from approximately 77% to 85%, an improvement of about 10.4%. These data indicate that while higher costs do lead to better outcomes, the rate of improvement is not linear with the increase in cost.

Notably, for the HIP reduction value, the improvement associated with increased costs is particularly significant. When the cost rises from CNY 2,000,000 to CNY 6,000,000, the HIP reduction value increases from 20 to 70, representing an improvement of approximately 250%. This substantial enhancement suggests that for urban heat island mitigation benefits, reasonable financial investment can significantly boost effectiveness.

3.2. Comparison of Annual Runoff Control Effectiveness among Sub-Catchments in the Study Area

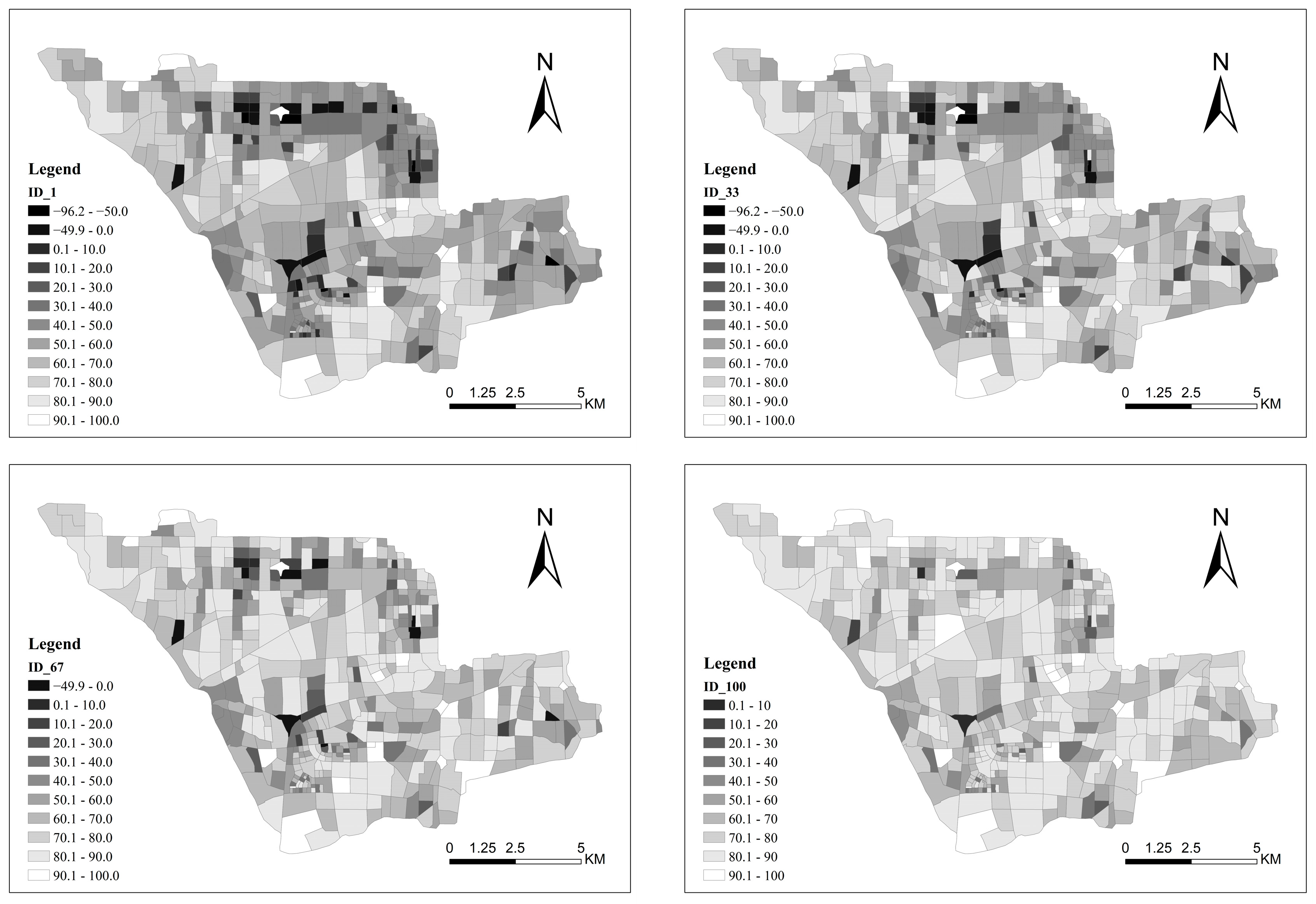
The study considered the hydrological connections and influences between sub-watersheds and surrounding areas by setting hydraulic connections among sub-watersheds. To explore the effectiveness of multi-objective optimization for LID measures at the watershed scale, the study selected several optimal schemes from the Pareto front. These selected schemes were compared to analyze the volume capture ratio of annual rainfall of each sub-watershed when volume capture ratio of annual rainfall for the entire watershed meets the target (exceeding 75%). The selection steps for the optimal schemes are as follows: first, all schemes on the Pareto front were numbered in ascending order based on their annual cost, from 1 to 100. Then, the schemes ID 1, 33, 67, and 100 were selected. The spatial distribution maps of volume capture ratio of annual rainfall for each sub-watershed under these schemes were plotted, as shown in Figure 5. The total annual runoff control rates for the entire watershed under these four schemes are presented in

Table 4. Volume capture ratio of annual rainfall for schemes ID 1, 33, 67, and 100.

ID	Volume Capture Ratio of Annual Rainfall (%)
1	76.41904522
33	79.32455422
67	82.76227081
100	84.9858232

.

Figure 5 reveals a significant phenomenon: when considering the hydraulic connections among sub-watersheds and their surrounding areas, we found that not all sub-watersheds achieved the target volume capture ratio of annual rainfall among the four optimal solutions. Particularly in the southwest part of the study area, where there is high building density, the runoff control rates in some sub-watersheds are as low as 50%. This observation may be attributed to the way these sub-watersheds discharge into downstream confluences connected with surrounding green spaces and rivers. This finding underscores the importance of optimizing LID measure layouts at the watershed scale. By comprehensively considering hydraulic connections between regions, we can more effectively evaluate the effectiveness of LID measure layouts and formulate globally meaningful optimal deployment strategies.

Simultaneously, we noted negative values in volume capture ratio of annual rainfall for some sub-watersheds. The occurrence of negative volume capture ratio may stem from these sub-watersheds receiving runoff from other sub-watersheds, causing the inflow of runoff to exceed the amount that can be controlled through infiltration, evaporation, and other means in that area. In other words, the net runoff in these sub-watersheds increases due to incoming runoff, resulting in a negative control rate. Such inter-sub-watershed runoff transfers not only complicate water resource management but may also adversely affect hydrological conditions downstream. For instance, it could elevate flood risks downstream or degrade water quality in downstream water bodies. Therefore, it is advisable to consider implementing large-scale runoff control measures such as RG or detention ponds in these areas to mitigate potential risks.

Of course, the occurrence of a significant negative volume capture ratio of annual rainfall in certain sub-catchments might be related to the precision of the model. If more detailed data on the pipe network and river network, as well as information reflecting the hydraulic connections between different plots within each sub-catchment, could be obtained, we would achieve more refined sub-catchment delineation results. Additionally, if longer data series or higher spatiotemporal resolution rainfall-runoff data were available for model calibration and validation, the annual volume capture ratio of annual rainfall simulated for each sub-catchment could change accordingly. However, even though the precision of the model can influence the simulation results, the phenomena observed from the current simulations—the importance of hydraulic connections between sub-catchments and the complexity of cross-regional runoff transfer—remain valid.

In Section 2.4.2, the author thoroughly discussed the practical necessity of selecting the optimal solution from the Pareto front. In the final spatial layout of LID measures, the goal is to balance the objective functions within the Pareto front to choose the best layout scheme. This process not only reflects the complexity of multi-objective optimization but also underscores the importance of seeking balance in practical applications. The next section will detail the results related to the above discussion. These results will further elucidate how to achieve the best balance among objective functions in real-world projects and how to maximize cost-effectiveness through reasonable financial investment. Through specific case studies, we will demonstrate how to effectively control costs while ensuring runoff control, runoff pollution control, and urban heat island mitigation, thereby achieving optimal resource assignment.

3.3. Comparison and Analysis of TOPSIS Ranking Results Based on Entropy Weight and Subjective Weight Methods

This study aims to evaluate the differences between two weighting methods—subjective weighting and entropy weighting—in applying the TOPSIS method to select the optimal spatial layout for LID measures. Beyond the decision scenario determined by the entropy weighting method, we further established four decision scenarios, each focusing on annual cost, volume capture ratio of annual rainfall, annual runoff pollution control rate, and heat island effect reduction rate, respectively.

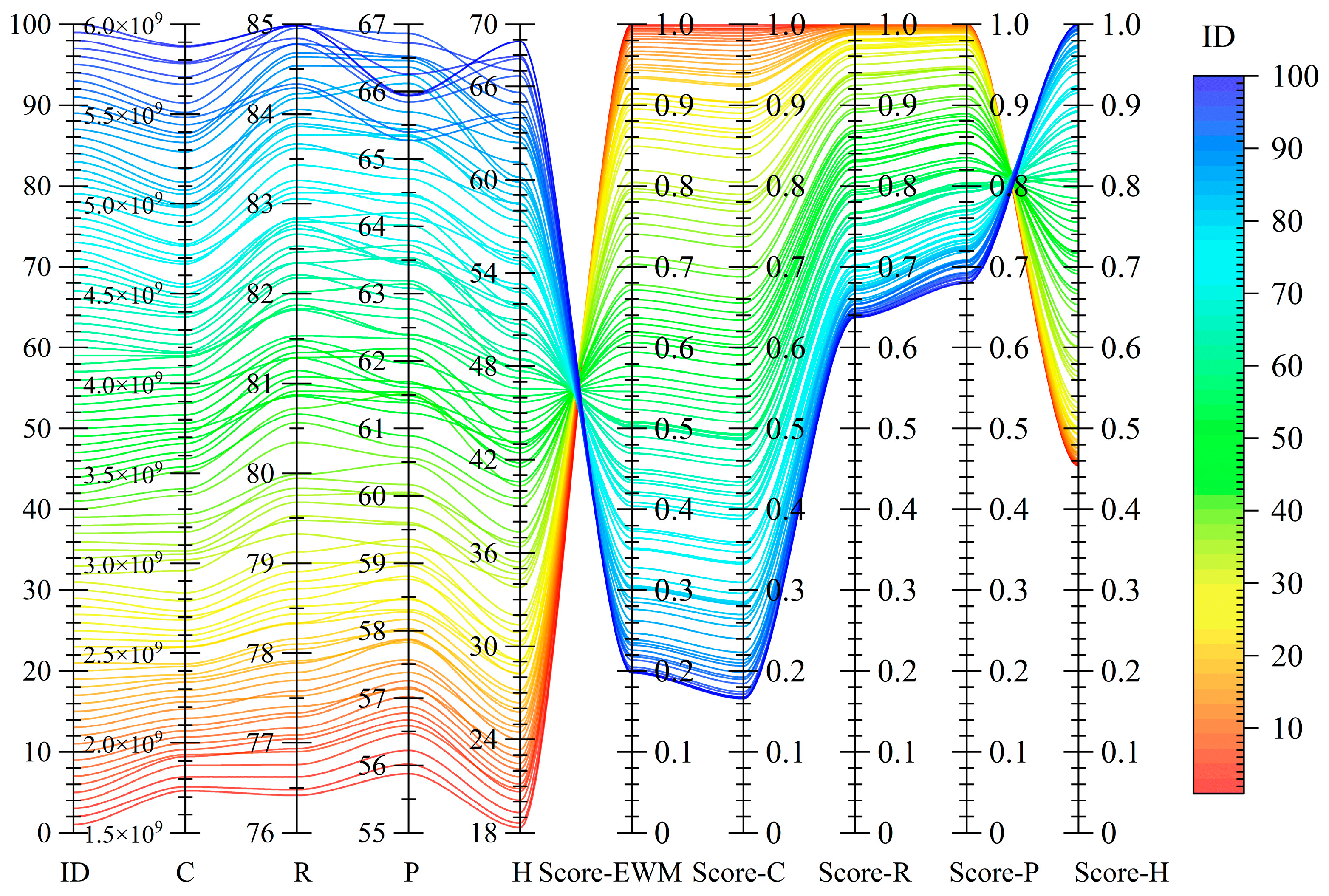
Using the entropy weight method (EWM), we calculated the weight matrix for the four objective functions as [0.74050017, 0.0059645, 0.00934035, 0.24419498]. Based on these weights, we ranked 100 Pareto frontier solutions using the TOPSIS algorithm to determine the best and the worst solutions. These ranking scores are presented in Figure 6 as Score-EWM (results using the EWM). Additionally, we applied the subjective weighting method, assigning the weight matrices [0.55, 0.15, 0.15, 0.15], [0.15, 0.55, 0.15, 0.15], [0.15, 0.15, 0.55, 0.15], and [0.15, 0.15, 0.15, 0.55] for the four decision scenarios mentioned above. In Figure 6, we display the TOPSIS scores for these four scenarios, labeled as Score-C (annual cost priority), Score-R (volume capture ratio of annual rainfall priority), Score-P (annual runoff pollution control rate priority), and Score-H (HIPR priority).

Table 5. Scores of each scheme in the TOPSIS ranking after weight assignment using the entropy weight method.

ID	Annual Cost (CNY)	Volume Capture Ratio of Annual Rainfall (%)	Annual Runoff Pollution Control Rate (%)	HIPR	Score
1	1,734,325,555	76.41904522	55.87695543	18.33748439	1
2	1,757,574,735	76.48142314	56.0175713	18.6234859	0.999940476
3	1,811,654,494	76.62172096	56.22340482	19.28857098	0.999264568
-	-	-	-	-	-
98	5,787,590,176	84.98036251	66.25488756	67.92692459	0.199167739
99	5,872,725,183	84.98561317	65.95611594	68.87289457	0.197822838
100	5,877,741,736	84.9858232	65.94021643	68.89818525	0.197702316

presents the TOPSIS ranking scores and corresponding values of the four objective functions for the three highest and lowest scoring schemes determined using the entropy weighting method. Similarly, Figure 6, Figure 7, Figure 8 and Figure 9 list the TOPSIS scores and objective function values for the three highest- and lowest-scoring schemes under the four decision scenarios, assigned through the subjective weighting method.

By analyzing Figure 6, we found that the TOPSIS ranking results using the entropy weighting method are largely consistent with those of the other three decision schemes when the heat island effect reduction rate is not considered. Further comparison of Table 5 and

Table 6. Scores of each scheme in the TOPSIS ranking after weight assignment using subjective weight method with annual cost priority.

ID	Annual Cost (CNY)	Volume Capture Ratio of Annual Rainfall (%)	Annual Runoff Pollution Control Rate (%)	HIPR	Score
1	1,734,325,555	76.41904522	55.87695543	18.33748439	1
2	1,757,574,735	76.48142314	56.0175713	18.6234859	0.999949214
3	1,811,654,494	76.62172096	56.22340482	19.28857098	0.999138532
-	-	-	-	-	-
98	5,787,590,176	84.98036251	66.25488756	67.92692459	0.167596406
99	5,872,725,183	84.98561317	65.95611594	68.87289457	0.165906268
100	5,877,741,736	84.9858232	65.94021643	68.89818525	0.165795121

reveals that under the cost-priority scenario, the TOPSIS ranking results from the entropy weighting method are identical to those from the subjective weighting method. This indicates that, when cost is given the highest weight, the LID layout scheme that minimizes cost is the best solution. This outcome aligns with the fact that cost exhibits the greatest variance among the four objective functions and thus is assigned the highest weight in the entropy weighting matrix.

Additionally, comparing Table 5 with

Table 7. Scores of each scheme in the TOPSIS ranking after weight assignment using subjective weight method with volume capture ratio of annual rainfall priority.

ID	Annual Cost (CNY)	Volume Capture Ratio of Annual Rainfall (%)	Annual Runoff Pollution Control Rate (%)	HIPR	Score
4	1,874,465,728	76.75802827	56.47062848	20.10217554	1
3	1,811,654,494	76.62172096	56.22340482	19.28857098	0.999910532
2	1,757,574,735	76.48142314	56.0175713	18.6234859	0.999828636
-	-	-	-	-	-
97	5,779,214,182	84.84552538	65.9354158	67.77365545	0.638673308
99	5,872,725,183	84.98561317	65.95611594	68.87289457	0.637747234
100	5,877,741,736	84.9858232	65.94021643	68.89818525	0.637437182

and

Table 8. Scores of each scheme in the TOPSIS ranking after weight assignment using subjective weight method with annual runoff pollution control rate priority.

ID	Annual Cost (CNY)	Volume Capture Ratio of Annual Rainfall (%)	Annual Runoff Pollution Control Rate (%)	HIPR	Score
9	2,032,430,261	77.1669502	57.02085005	22.08792564	1
5	1,923,565,430	76.93634092	56.67539141	20.64523544	0.999792734
4	1,874,465,728	76.75802827	56.47062848	20.10217554	0.999752458
-	-	-	-	-	-
97	5,779,214,182	84.84552538	65.9354158	67.77365545	0.682220439
99	5,872,725,183	84.98561317	65.95611594	68.87289457	0.679945036
100	5,877,741,736	84.9858232	65.94021643	68.89818525	0.679475105

, we observe that in the scenarios prioritizing annual runoff control rate and annual runoff pollution control rate, the TOPSIS ranking results are generally similar to those from the entropy weighting method. Compared to Table 5 and

Table 9. Scores of each scheme in the TOPSIS ranking after weight assignment using subjective weight method with HIPR priority.

ID	Annual Cost (CNY)	Volume Capture Ratio of Annual Rainfall (%)	Annual Runoff Pollution Control Rate (%)	HIPR	Score
95	5,664,801,752	84.77369626	65.84552727	66.66511731	1
98	5,787,590,176	84.98036251	66.25488756	67.92692459	0.999717158
94	5,560,200,498	84.95473925	66.86393989	65.60141954	0.999593537
-	-	-	-	-	-
3	1,811,654,494	76.62172096	56.22340482	19.28857098	0.454347291
2	1,757,574,735	76.48142314	56.0175713	18.6234859	0.454067597
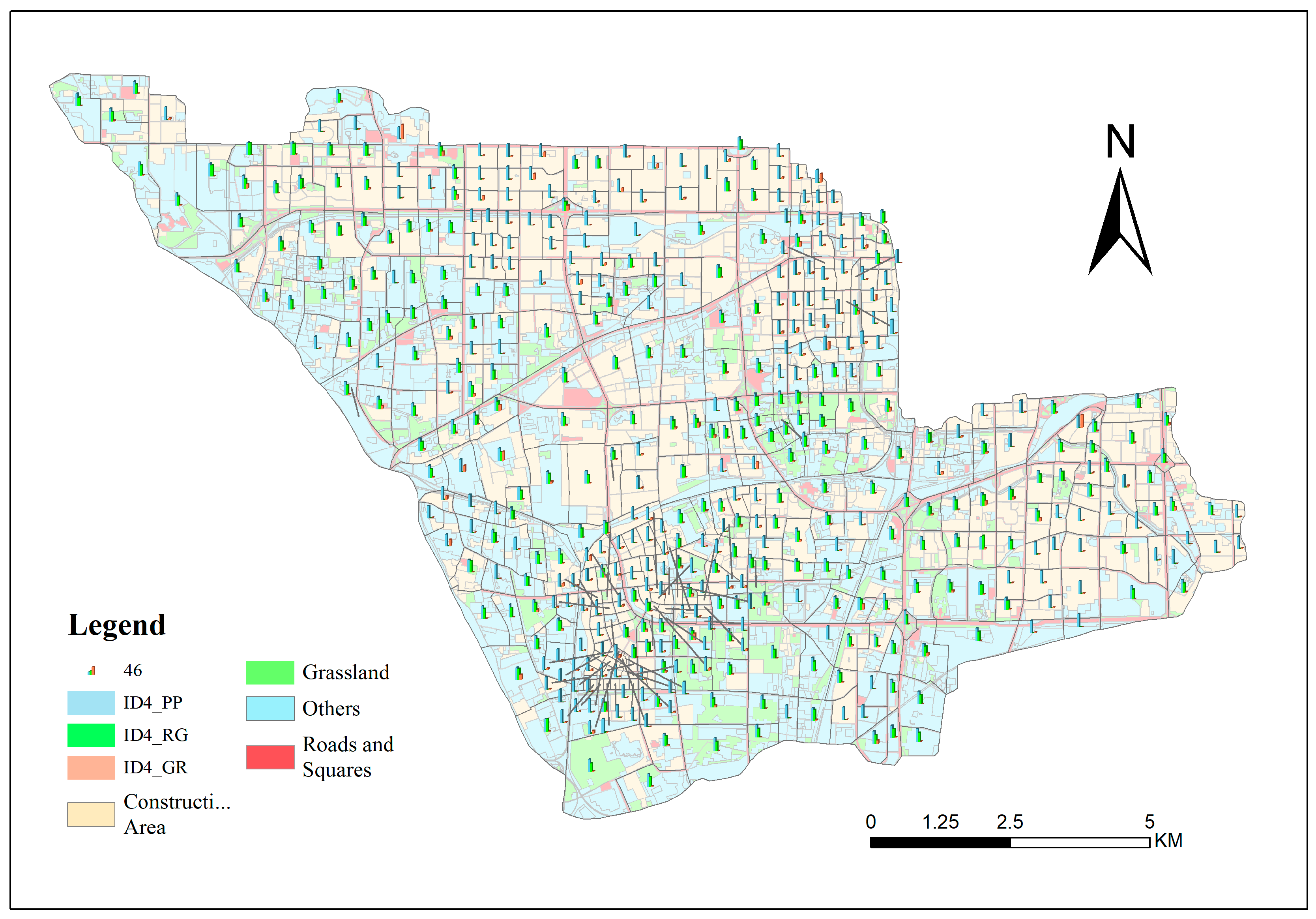
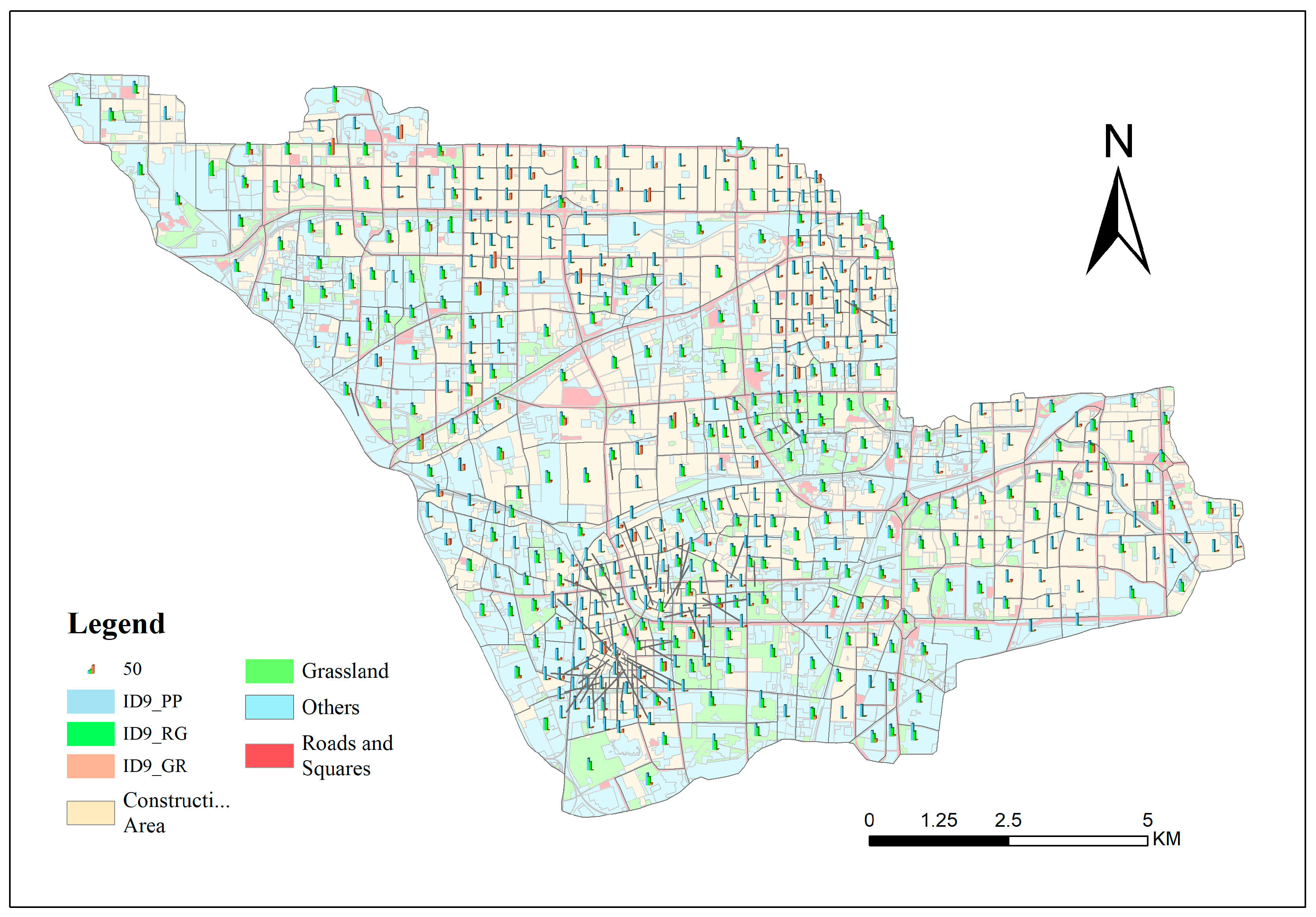
1	1,734,325,555	76.41904522	55.87695543	18.33748439	0.45402553

, we observe that in the scenarios prioritizing HIPR, the TOPSIS ranking results are generally opposite to those from the entropy weighting method. However, the selected optimal solutions, while ensuring cost minimization, place greater emphasis on either the annual runoff control rate or the annual runoff pollution control rate. In terms of the types and proportions of LID measures, this is reflected in a relatively higher proportion of RG and a relatively lower proportion of GR, as shown in Figure 7, Figure 8 and Figure 9.

Notably, under the scenario prioritizing HIPR, the LID layout scheme that minimizes cost turned out to be the least favorable solution. In terms of the types and proportions of LID measures, the proportion of GR significantly increased from 50–60% to 60–100%, and the spatial deployment of RG also expanded noticeably, with an increase in their proportion, as shown in Figure 7 and Figure 10.

These observations indicate that the assignment of weights has a significant impact on the optimal LID layout scheme selected by the TOPSIS method. Under different decision priorities, even the same LID measures will have their proportions and types adjusted according to the varying weights to meet specific decision-making objectives.

3.4. Analysis of the Impact of Weight Variation in Specific Decision Scenarios on TOPSIS Ranking Results

In the actual decision-making process, different decision makers may prioritize different objectives. For example, some decision-makers may focus more on short-term runoff control effectiveness, while others may prioritize long-term environmental benefits. Therefore, there may be variations in how weights are assigned to different objective functions by each decision maker. Based on the analysis results in Section 3.3 of this study, we found that different weight assignments can lead to differences in the selection of optimal solutions.

To further explore the potential impact of weight variations in specific decision scenarios on the selection of optimal solutions, we conducted a series of sensitivity analyses. These analyses help reveal the specific effects of different weight distributions on decision outcomes, thereby providing decision makers with more flexible and adaptable decision support.

For specific decision scenarios where one objective function is prioritized, we varied the weight of that objective function from 0.01 to 0.91, with increments of 0.09. Assuming the weight of the prioritized objective function is denoted as x, the weights of the remaining three objective functions were set to (1 − x)/3. For instance, in a decision scenario prioritizing cost, if the weight of cost is set to 0.01, the weights of the other three objective functions are each set to 0.33. Using this approach, we obtained 10 different sets of weight matrices and derived 10 sets of Pareto front solutions.

Figure 11 illustrates the scores of the Pareto front solutions as the weights vary in decision scenarios prioritizing cost (Figure 11a), runoff control effectiveness (Figure 11b), runoff pollution control effectiveness (Figure 11c), and the benefits of heat island mitigation (Figure 11d).

Analysis of Figure 11 reveals three typical trends in the scores of optimal solutions within the Pareto front:

The first type of optimal solutions exhibit high and stable scores at low weights, but their scores rapidly decrease within a specific range of weights as the weight increases.

The second type of optimal solutions show low and stable scores at low weights, but their scores rapidly increase within a specific range of weights as the weight increases.

The third type of optimal solutions exhibit a trend between the first two types: their scores are moderate at low weights, increase initially with increasing weights, peak within a specific range of weights, and then decline. Within this specific range of weights, they transition into the globally optimal solution. We refer to this specific range of weights as the “critical weight range”.

In the scenario prioritizing annual cost (Figure 11a), schemes numbered 90 to 100 belong to the first type, 1 to 10 belong to the second type, and 11 to 89 belong to the third type, with a critical weight range from 0.1 to 0.19. When the weight assigned to annual cost exceeds 0.55, further increases in weight no longer affect the TOPSIS ranking results.

In the scenario prioritizing volume capture ratio of annual rainfall (Figure 11b), the classification of schemes into the first and second types is opposite to that in the annual cost prioritization scenario, with a critical weight range from 0.73 to 0.91. Specifically, when the weight reaches 0.82, certain schemes from the third type, such as scheme number 41, become optimal. When the weight assigned to volume capture ratio of annual rainfall is below 0.73 or above 0.91, variations in weight no longer affect the TOPSIS ranking results.

In the scenario prioritizing annual runoff pollution control rate (Figure 11c), similar to the volume capture ratio of annual rainfall prioritization scenario, the critical weight range is from 0.64 to 0.82. When the weight assigned to annual runoff pollution control rate exceeds this range, variations in weight no longer affect the TOPSIS ranking results.

The scenario prioritizing HIPR (Figure 11d) exhibits score variation trends similar to the cost prioritization scenario, with a critical weight range from 0.28 to 0.37. Similarly, when the weight assigned to HIPR exceeds this range, variations in weight do not affect the TOPSIS ranking results.

These results indicate that in specific decision scenarios, there exists a critical weight range where crossing this range significantly alters the TOPSIS ranking results. However, variations in weight within one side of this range do not impact the ranking results.

3.5. The Enhancement Effect of Different Optimization Schemes on Maximum Pipe Fullness

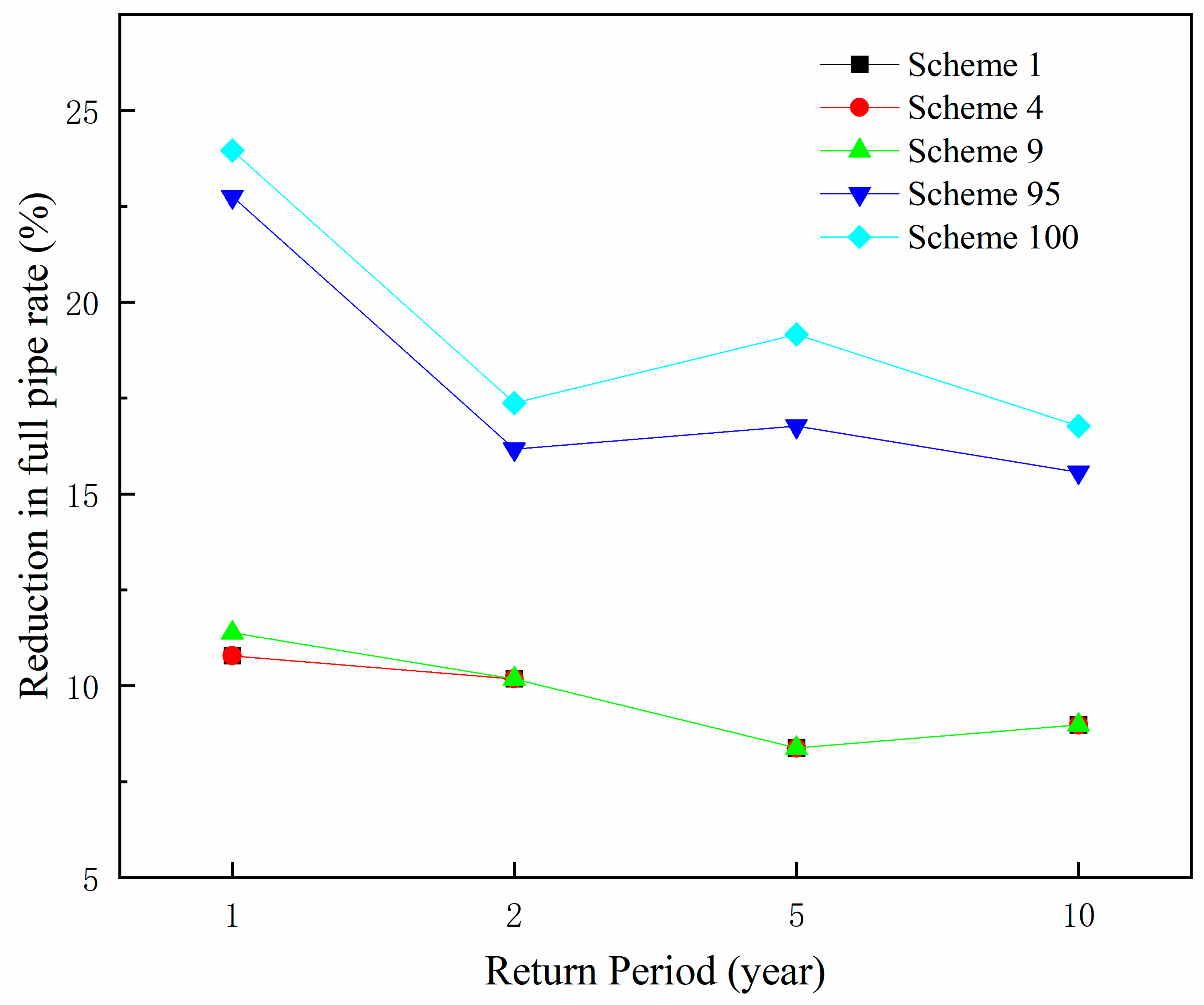
This study aims to evaluate the effectiveness of the constructed multi-objective optimization framework at the urban watershed scale in enhancing the drainage capacity of the study area. To this end, we selected the optimal alternative schemes numbered 1, 4, 9, and 95, as identified using the TOPSIS ranking method under the five decision scenarios described in Section 3.2, along with the worst-performing scheme numbered 100. Thus, a total of five schemes (1, 4, 9, 95, and 100) were subjected to simulation and comparative analysis. The full pipe rate was chosen as the key indicator to measure the improvement in drainage capacity. This rate represents the proportion of pipes operating at full capacity to the total number of pipes.

The simulation analysis adopted rainfall return period scenarios of 1-year, 2-year, 5-year, and 10-year events. The results show that compared to the scheme without LID measures, the five LID spatial layout schemes significantly reduced the full pipe rate. The specific values are summarized in

Table 10. Reduction in full pipe rate of each scheme compared to the control scheme (no LID) under different rainfall return periods.

Return Periods	Scheme 1 (%)	Scheme 4 (%)	Scheme 9 (%)	Scheme 95 (%)	Scheme 100 (%)
1-year	10.78	10.78	11.38	22.75	23.95
2-year	10.18	10.18	10.18	16.17	17.37
5-year	8.38	8.38	8.38	16.77	19.16
10-year	8.98	8.98	8.98	15.57	16.77

and illustrated in Figure 12. Under the 1-year return period rainfall scenario, the full pipe rate was reduced by an average of 10.78% to 23.95%. Although the improvement effect diminishes with increasing rainfall return periods, it still effectively alleviates the pressure on the drainage system, demonstrating that the rational deployment of LID measures can enhance the resilience of the drainage system.

Table 10 shows that among the optimal alternative schemes selected under the five decision scenarios, scheme number 95 performed the best in improving regional drainage capacity. Under the 1-year return period rainfall scenario, implementing this scheme reduced the full pipe rate by 22.75%. The other three schemes, ID 9, 4, and 1, reduced the full pipe rate by 11.38%, 10.78%, and 10.78%, respectively. Although scheme number 100 provided the greatest reduction in the full pipe rate (23.95%), it also incurred the highest cost. The analysis indicates that the effectiveness of schemes 95 and 100 is attributed to their extensive deployment of GR and RG, which enhanced rainwater storage and regulation capacities, effectively mitigating the load on the drainage system.

4. Discussion

Implementing spatial layout optimization of LID measures at the urban watershed scale significantly impacts the efficiency and effectiveness of urban water management. This optimization considers the interdependencies of hydrological interactions and drainage characteristics both within and beyond the region. Through comprehensive evaluation, it aids in the precise selection and adjustment of LID measure types and scales. Moreover, large-scale optimization strategies can avoid solutions effective only in localized areas, providing a more scientific and systematic approach to stormwater management for urban watersheds.

Within the multi-objective optimization framework, the model-coupled optimization algorithm provides a set of Pareto solutions, representing a balance between multiple objectives. In real-world decision making, we must select the most suitable solution from these sets. Different decision makers may prioritize different objectives—some may emphasize short-term runoff control effectiveness, while others may focus on long-term environmental protection and ecological benefits. Therefore, they may assign weights to objective functions differently. The entropy weight method, as an objective weighting method, accurately reflects the relative importance of objective functions. Conversely, the subjective weight method offers decision makers the flexibility to adjust weights based on specific contexts. By comparing these two methods, we can provide more comprehensive considerations for selecting LID measures under specific decision scenarios, ensuring that the chosen scheme meets the requirements of multi-objective optimization and the specific needs of different engineering practices.

This study aims to find the optimal spatial layout of LID measures through multi-objective optimization at the urban watershed scale, to minimize costs and maximize environmental benefits, achieving a balance between cost-effectiveness, environmental impact reduction, and promoting urban sustainable development. The study selected solutions from the Pareto front and conducted a comparative analysis of the annual runoff volume control rate for each sub-watershed. It explored the effectiveness of multi-objective optimization of LID measures at the watershed scale and evaluated the differences between the subjective weighting method and the entropy weighting method in selecting the optimal LID spatial layout scheme using the TOPSIS method. By setting multiple decision scenarios, the study conducted a sensitivity analysis of weight assignment, exploring the impact of weight variations on optimal solution decision outcomes.

The study revealed a significant positive correlation between annual cost and volume capture ratio of annual rainfall, annual runoff pollution control rate, and HIPR. This indicates that with increased costs, higher runoff control, more effective runoff pollution management, and more significant heat island mitigation can be achieved. However, this positive correlation does not imply a linear relationship between the improvement of effects and cost increase. Particularly for the benefits of mitigating urban heat islands, the enhancement brought by increased costs is especially notable, providing important decision-making insights for urban heat island mitigation benefits.

The study also found that optimizing LID measure layout at the watershed scale is crucial. By comprehensively considering the hydraulic connections between regions, a more thorough evaluation of the layout effects of LID measures can be conducted, resulting in globally significant optimal deployment schemes. Additionally, cross-regional runoff transfer increases the complexity of water resource management and may adversely affect downstream hydrological conditions. It is recommended to deploy large runoff control measures, such as retention pond, in these areas to mitigate risks.

When not considering the heat island effect reduction rate, the TOPSIS ranking results using entropy weighting were generally consistent with the results of other decision scenarios. However, in the scenario prioritizing HIPR, the LID measure layout scheme minimizing annual cost became the least favorable solution. This phenomenon indicates that weight assignment significantly influences the optimal LID measure layout scheme selected by the TOPSIS method. Under different decision priorities, even the same LID measures will have their proportions and types adjusted according to varying weights to meet specific decision management goals.

Moreover, the study observed that there is a critical weight range in specific decision schemes. Crossing this range leads to significant changes in the TOPSIS ranking results. This finding emphasizes the importance of rational weight determination in practical engineering practice and the necessity of seeking a balance between different objectives.

In summary, this study not only provides scientific decision support for urban hydrological management but also offers practical application guidance for the spatial layout of LID measures at the urban watershed scale. Rational deployment of LID measures can enhance regional drainage capacity, improve the resilience of urban drainage systems under different rainfall scenarios, and maximize environmental benefits within an acceptable cost range. This has significant practical application value for promoting urban sustainable development and building eco-friendly cities.

5. Conclusions

This study successfully developed a comprehensive evaluation framework to optimize the spatial layout of LID measures at the urban watershed scale. Focusing on densely built urban watersheds, this research specifically optimized the types, scales, and spatial layout of LID measures such as RG, PP, and GR. The study employed the SWMM model coupled with the NSGA-II optimization algorithm, using annual cost, volume capture ratio of annual rainfall, annual runoff pollution control rate, and HIPR. The Pareto front obtained from the optimization algorithm, combined with weight matrices determined by the entropy weight method and the subjective weighting method, were ranked using the TOPSIS method to identify the optimal LID measure layouts prioritizing different objective functions under various subjective and objective conditions.

The innovative aspects of this study can be summarized as follows:

Multi-Objective Optimization Method: A novel multi-objective optimization method was proposed for the spatial layout of LID measures at the urban watershed scale. This method comprehensively considers hydrological interactions and drainage characteristics, providing a systematic stormwater management strategy for urban areas.

Pareto Solution Set Analysis: The Pareto front obtained through the model-coupled optimization algorithm were used to conduct an in-depth analysis of volume capture ratio of annual rainfall for different sub-watersheds, offering a solid theoretical foundation for selecting the optimal solution.

Comparison of Weighting Methods: A comparative analysis of the entropy weight method and the subjective weighting method in the TOPSIS method revealed the impact of weight variations on scheme selection under different decision scenarios, enhancing the flexibility and adaptability of decision making.

Relationship Between Annual Cost and HIPR: The study identified a positive correlation between annual cost and HIPR, particularly noting the nonlinear relationship in urban heat island mitigation, providing important decision support for urban heat island reduction.

Critical Weight Range Identification: The study identified a critical weight range under specific decision scenarios, offering important guidance for the rational determination of weights in practical engineering practice.

In summary, this study not only provides scientific decision support for urban hydrological management but also offers practical application guidance for the spatial layout of LID measures at the urban watershed scale. By rationally deploying LID measures, it is possible to enhance regional drainage capacity, improve the resilience of urban drainage systems under different rainfall scenarios, and maximize environmental benefits within an acceptable cost range. This has significant practical application value for promoting sustainable urban development and building eco-friendly cities.