Abstract
Fine sediment infiltration and subsequent clogging in a gravel bed affect several fluvial, ecological, and biological processes, resulting in the degradation of the river ecosystem. Despite many experimental and a few numerical studies, the process is yet to be entirely understood. We employed a pure Lagrangian framework, called the Discrete Element Method (DEM), to numerically investigate the infiltration process. Special attention is given to tackling the issue of non-spherical and irregular particle shapes and particle size distributions (PSDs) in numerical simulations. Due to computational limitations, these aspects were either not considered or simplified in previous numerical studies. We implicitly included non-spherical and irregular shape effects through rolling resistance models, which do not cause excessive computational overhead. Our study shows that rolling resistance models greatly influence packing and fine sediment infiltration. However, they may also lead to unphysical particle behavior; thus, they should be carefully used in numerical simulations. Oversimplified PSDs do not mirror natural systems, and full PSDs pose computational challenges. Sufficient grain classes are needed to mimic the non-homogeneity and poly-dispersity found in natural fluvial sediments. The infiltrating characteristics of sand concerning PSD and shape effects are linked to size ratio D15,Gravel/D85,Sand, assuring physical and realistic modeling of the infiltration process.
1. Introduction
The gravel bed and the pore space within the bed structures are crucial in sustaining a healthy river ecosystem [1,2,3]. Fish and other microorganisms utilize the pore space in the gravel bed for reproduction and living purposes. Fine sediment clogging (e.g., sand, silt, and clay) in the gravel bed harms several ecological processes, such as fish spawning [4], macrophytes’ root length [5], and habitat of subsurface invertebrates, and may cause subsurface contamination [6,7]. Additionally, it hinders surface–subsurface interaction, which is a function of pore space and permeability of the gravel bed [8,9]. Fine sediments are flushed during dam removal operations, which are a standard practice to recover the reservoir’s capacity [10,11,12,13,14,15,16]. Fine sediment can also join the river systems through landslides, forest fires, changes in land use and land cover, mining activities, and dredging [17,18,19,20,21]. The fine sediment, joining the river system, fills the coarse sediment deposit downstream, decreasing the pore space in the gravel bed and eventually degrading the river ecology. An understanding of variation in pore space along the depth of the gravel bed, as a result of fine sediment infiltration, is required to have a better sediment management strategy to sustain the healthy river ecosystem.
The fluvial sediments consist of different particle sizes and non-spherical and irregular particles, which pose a major challenge in accurately predicting packing structures and pore space variation. The process of infiltration/packing can be mainly studied using three different approaches: (a) experimental investigations, (b) analytical and stochastic models, and (c) numerical simulations. In this regard, a set of experimental works has been conducted to study the packing and infiltration process. Experimental investigations are most accurate but time- and resource-consuming. Furthermore, controlling all the interdependent parameters in the experimental investigations is difficult. The second approach is analytical and stochastic models, which are usually based on simple process equations. A limited number of analytical models have been developed to predict the packing behavior. In analytical and stochastic approaches, simple equations are developed and solved. The two most famous analytical models are linear and linear-mixture packing models [22,23,24], which were developed to model the random packing of particles. However, these analytical approaches are limited to a binary or ternary mixture. Moreover, incorporating the shape effects in the existing analytical models is very challenging since sediment particles have random shapes, which might differ significantly from one another. Some stochastic models, based on relative pore space geometry and particle size, have also been developed [25,26]. The analytical and stochastic models have many constraints in relation to particle shape, particle size distributions (PSDs), and water flow effects. Therefore, simple analytical and stochastic models cannot be directly used to replicate the infiltration process in the natural systems, where these aspects become significantly important. The third approach, so-called numerical simulations, can also be employed to study the sand infiltration process. In numerical simulations, equations based on physical laws describing the process are numerically solved. Compared to the experimental, analytical, and stochastic approaches, the numerical simulations allow us to have better control over parameters, which are mainly responsible for the physical process under consideration. Additionally, numerical simulations can provide more detailed information with relatively fewer resources such as money and time. Numerical simulations can be categorized into 1D, 2D, and 3D modeling approaches, which solve fluid flow to a certain extent of detailing, coupled with sediment transport equations. The relatively simple empirical equations for sediment transport are governed by mean flow, which is usually a function of resistance parameters. The flow resistance formulations that consider different effects can be found elsewhere [27]. However, simple sediment transport and flow resistance equations are not enough to obtain particle scale information. Therefore, one has to consider more advanced simulation approaches (e.g., Lagrangian particle tracking), which resolve each particle present in the system.
With recent advancements in computational architecture, efficient solution algorithms, and relatively easy accessibility to high-performance computing (HPC) facilities, numerical simulations can be performed in much greater detail, which was almost impossible a decade ago. One such advanced numerical method allows us to track each particle individually, along with its interaction with fluid and other contacting particles (Lagrangian particle tracking). Such a detailed numerical simulation can be further subcategorized into coupled or uncoupled approaches, which can be adopted depending on the process under consideration, the level of complexity, and the computational resources available to accommodate that level of complexity. In the coupled approach, computational fluid dynamics (CFD) is utilized to solve flow fields, and particles are tracked in the Lagrangian framework using Newton’s second law of motion, also called the Discreet Element method (DEM). The coupled CFD–DEM approach allows for a comprehensive inclusion of fluid–particle interaction terms in the governing DEM equations; however, it adds computational overhead on top of expensive DEM computations. In the uncoupled approach, particles can be tracked simply with the DEM equations, neglecting the flow effects. In this paper, we employ the pure Lagrangian framework (DEM) to simulate and investigate the sand infiltration process by considering PSDs and implicitly accounting for the effects of non-sphericity and irregularities in particle shape.
The process of sand infiltration into the gravel bed has been experimentally studied for over 75 years, from the first study by Einstein [28] to many other experimental studies [19,29,30,31,32,33,34,35,36,37]. These experiments were performed on different experimental setups with different flow conditions and different gravel and sand compositions and by using various measurement techniques. The experimental investigations have resulted in the development of empirical equations, usually limited to similar scenarios as experimental conditions. A straightforward comparison between different experimental works is not possible, yet researchers have been able to observe two distinct infiltration processes. One of them, where the filling of the gravel bed occurs from the bottom to the top, is called unimpeded static percolation, and the other is called bridging or clogging, where most of the sand becomes clogged in the upper surface layer. The occurrences of these two distinct infiltration processes are mainly a function of the relative sizes of sand and gravel, more precisely on D15,Gravel/D85,Sand [38,39]. D15,Gravel and D85,Sand represent the gravel and sand sizes at which 15 and 85 percent of the material is finer. Some studies have observed only unimpeded static percolation [28,29,30,31,32,33]. In contrast, many researchers have claimed that the bridging type on infiltration is predominant, and percolation is simply an artifact of a shallow gravel bed [8,19,34,35,36,37]. This behavior is also supported by recent studies [8,40], which advocates that the bridging behavior is dominant in the natural fluvial systems. However, both bridging and percolation behavior in sufficiently thick gravel beds have been observed in the recent experimental [38] and numerical investigations [41,42,43].
The sand infiltration process has also been studied with advanced numerical simulations (e.g., particle tracking methods). Recently, Bui et al. [41,42] replicated Gibson’s experiment numerically and were able to obtain quite good agreement with experimental data. However, they neglected the effects of flowing water (modeled in a pure DEM framework), simplified the PSD with a simple distribution with a mean and standard deviation, and did not consider the effects of non-sphericity and irregularities in particle shape as well. The work has been extended by Jaiswal et al. [43] by including the effects of flowing water on the infiltration process (modeled in the coupled CFD–DEM framework). However, they only considered the binary mixture to represent the gravel–sand system with free-rolling spherical particles. Despite several simplifications in the above-mentioned numerical studies, significant contributions to the understanding of the sand infiltration process have been made. Jaiswal et al. [43] numerically showed that bridging and percolation could occur within the same gravel deposit despite being subjected to the same flow conditions, as reported in the experimental study of Gibson et al. [38]. Jaiswal et al. [43] emphasized that the gravel bed should be sufficiently thick to distinguish between the above-mentioned two distinct infiltration processes, and accordingly, they suggested a suitable gravel bed thickness (minimum of five times the coarsest gravel diameter) for such a purpose. Furthermore, they also confirmed that the process of sand infiltration into static gravel beds is mainly gravity-dominated, which was first hypothesized by Cui et al. [40]. However, the above-mentioned numerical studies, based on the Lagrangian framework [41,42,43], have entirely neglected the effect of particle shape on the overall packing and sand infiltration process. Additionally, in previous numerical studies [41,42,43], particle size distributions (PSDs) of gravel and sand are simplified by a binary mixture or simple PSDs with a mean and standard deviation.
Particle size distributions (PSDs), particle shape, and texture are essential in how gravel bed packing is formulated and how fine sediment infiltrates into the gravel deposit. As mentioned above, previous numerical studies have neglected these aspects. Many studies on various fluid–particle systems have indicated that particle shape can have a significant role in the particle–particle and fluid–particle interaction terms [44,45,46,47]; thus, it cannot be neglected. The particle shape effects can be either included by resolving the actual particle shape or by including the shape effects implicitly by adding some rolling resistance to the particles [45]. Resolving different shapes is computationally expensive and adds an extra burden on top of the complexity and limitations in the Lagrangian framework, especially when dealing with a large number of particles. Some simplified non-spherical objects (e.g., ellipsoid, cube, multi-sphere, and super-quadric) can be used to consider non-spherical particles [48,49,50,51]. However, they also do not represent natural sand and gravel shapes, which can be very different from one another. Another approach to consider particle shape effects implicitly is by restricting the rolling of the particles with simple models, which seem to be an efficient tool to investigate shape effects on the sand infiltration process. Other physical and chemical factors may also become relevant depending on the particle size and system under consideration. Several studies on the fine sediment migration in porous media that considered the effects of these factors and focused on chemical engineering applications can be found in the recent literature [52,53,54,55]. The current study focuses on the sand–gravel system, where these effects seem insignificant. We employ three different rolling resistance models and compare their abilities to capture particle shape effects on the process of sand infiltration into the static gravel bed.
Moreover, the inclusion of exact/full PSDs of gravel and sand (poly-disperse nature of sediments) in the analytical and stochastic models is incredibly difficult and not well-established. Considering full PSDs is also a challenging issue in numerical simulations, where broader PSDs result in a larger number of particles. When full PSDs are included, instead of simpler PSDs with fewer grain classes, a larger number of particles are required for the same mass or volume of sediments. Most of the numerical studies on the infiltration process have simplified the PSDs by considering fewer grain classes than exact gravel and sand compositions. In this paper, we test both full PSDs and simplified versions of PSDs for the adapted experiment to shed more light on the effect of particle size distribution on the numerical simulation of the sand infiltration process.
To our knowledge, there are very few studies on the process of sand infiltration into the gravel bed using the Lagrangian framework, where each particle is resolved and tracked. However, with the recent advancements in computational architecture, solution algorithms, and accessibility to supercomputing facilities, advanced numerical methods (e.g., Lagrangian particle tracking) are becoming popular tools for investigating complex physical problems. Nevertheless, the previous pure DEM and coupled CFD–DEM studies have simplified the particle size distributions (PSDs) and entirely neglected particle shape effects on the sand infiltration process. Considering the fact that the process of sand infiltration into the static gravel bed is gravity-dominated, and due to computational constraints, we chose to perform pure DEM simulations and focus on particle shape and PSD aspects. Thus, we model the particle shape (non-sphericity and irregularity) effects by including it implicitly with rolling resistance models in the DEM equations. Several infiltration cases (corresponding to bridging and percolation) are considered, dealing with a wide range of gravel sand compositions. Special attention is given to the conditions, which might lead to situations where rolling resistance should be avoided to obtain the correct behavior of infiltrating sand particles. Moreover, we tested the effects of the particle size distributions (PSDs) on the sand infiltration into the static gravel bed by reducing the number of grain classes in sand and gravel PSDs. The paper is arranged into the following sections: first, the governing equations and rolling resistance models are described; this is followed by the numerical setup of the adopted experiments; after that, the results are presented and discussed, followed by the main conclusions of this study.
2. Governing Equations and Rolling Resistance Models
The advanced numerical approach in the pure Lagrangian framework is considered to track each particle (sand and gravel), along with their interaction with each other. Particles are described as discrete entities and tracked using Newton’s second law of motion, and the so-called Discrete Element Method (DEM) is employed. The DEM simulates the interactions between individual grains. It is of special interest because it is able to investigate particulate systems at the particle scale, in which the packing structure of a particle assembly is observable and the process of particle rearrangement can be traced through the time domain. The DEM approach was first proposed by Cundell and Strack [51] to model the mechanical behavior of granular materials with the consideration of particle interaction with other particles and walls using the soft-sphere approach. The translational and rotational motion of particle i with mass and moment of inertia can be described with the following equations:
where and are translational and angular velocities of the particle i and is the number of particles interacting with the particle i. The forces acting on particles are contact forces and gravity, i.e., the gravitational force and inter-particle forces, which include the normal particle–particle contact force and tangential particle–particle contact force . The torque acting on particle i by particle j includes two components, i.e., , generated by tangential force, and , commonly known as the rolling friction torque and caused mainly by the non-sphericity of particles. The normal and tangential forces between particles are calculated based on the linear spring dashpot model, usually known as the Hertz–Mindlin model. More details on the Hertz–Mindlin model can be found elsewhere [56] and are not discussed here as the model is well-established and widely accepted. Figure 1 illustrates schematics of the rolling friction torque model (due to non-spherical particles) in addition to sliding and damping force models.
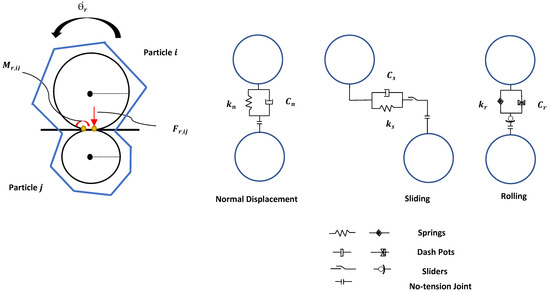
Figure 1.
Rolling resistance torque acting on the rotating particle, along with the contact models for normal and tangential forces, and rolling resistance torque calculations [47,57].
In the conventional DEM approach [51], the particle–particle (and particle–wall) interactions consist of contact spring and damping forces in both normal and tangential directions with the “free rolling” of particles . The normal and tangential components of sliding and damping forces are calculated by the famous Hertz–Mindlin contact model [56]. However, the significance of the rotational inertia and energy loss in the rotation of particles has been highlighted in both numerical studies [57,58,59] and physical experiments [60,61,62]; therefore, rolling friction (rolling torque ) should not be neglected. The rolling resistance can also arise from other contact behaviors, including micro-slip, friction on the contact surface, plastic deformation around the contact, viscous hysteresis, surface adhesion, and particle shape [63]. However, in our numerical simulations, we assume that the particle shape is the main factor restricting the particle’s rotation.
The rolling friction models can be mainly categorized into four subgroups, namely Constant Directional Torque (CDT) models, Viscous models, Elastic-Plastic Spring-Dashpot (EPSD) models, and contact-independent models. The contact-independent models have been shown to be highly deficient because the contact pair torques are not in equilibrium and Viscous models do not provide any quasi-static torque; so, it is not effective in modeling pseudo-static systems [63]. Therefore, we considered and compared CDT and EPSD models. These rolling friction models are briefly touched upon in the following subsections. It must be mentioned that a thorough investigation of the fundamental mechanisms of rolling is beyond the scope of this paper. Rather, we focus on the effects of rolling resistance models in simulating a quasi-static system of sand infiltration into the static gravel bed.
2.1. Constant Directional Torque (CDT) Model
The CDT model and its derivatives apply a constant torque on a particle, which restricts the particle’s rotation and implicitly takes into account particle shape [63]. The direction of the rolling friction torque is always in the opposite direction of the relative rotation between the particles in contact. The CDT model uses a simple equation (Equation (3)) to model the rolling friction between contacting particles, which is a function of relative angular velocity () of contacting particles i and j.
where and are the angular velocities of particles i and j, respectively, is the coefficient of rolling resistance, and is the rolling radius, with and representing the radii of particles i and j, respectively.
2.2. Elastic-Plastic Spring-Dashpot (EPSD) Model
The EPSD model and its derivatives (e.g., EPSD2 and EPSD3) divide the rolling friction torque into two components: a mechanical spring torque and a viscous damping torque , shown in Equation (4) and Equation (5), respectively [63].
If the spring torque at time is and the incremental torque in is , the following relations can be established.
is the limiting torque, which is achieved at a full mobilization rolling angle, is the coefficient of rolling friction, is the incremental relative rotation between two particles, and and are the normal contact and rolling friction stiffness, respectively.
The viscous damping torque is assumed to be dependent on the relative angular velocity between the two contacting particles and the damping constant .
where is the rolling viscous damping coefficient, is the rolling viscous damping ratio, is the critical viscous damping constant, is the factor controlling full mobilization (damping is disabled at full mobilization ), and is the equivalent moment of inertia for the relative rotational vibration mode about the contact point between the two contacting particles.
Another version of the Elastic-Plastic Spring-Dashpot type of the rolling resistance model is called the EPSD2 model. The EPSD2 model neglects the contribution of the viscous damping torque , and the original rolling stiffness is modified (Equation (6)) and assumed to be a function of the tangential stiffness ( and rolling radius .
In this study, we test the CDT, EPSD, and EPSD2 rolling resistance models for a pseudo-static system of sand infiltration into the static gravel bed. The ability of these models to capture the correct infiltration behavior is tested, and accordingly, the most suitable rolling resistance model for the sand infiltration process is proposed.
3. Methodology and Numerical Setup
To investigate the effects of non-sphericity and irregularities in particle shape (implicitly with rolling resistance models) and particle size distributions (PSDs) on infiltrating characteristics of sand in the gravel bed, we adapted the infiltration experiment [38], also considered in previous pure DEM [41,42] and coupled CFD–DEM studies [43]. Previous numerical studies have simplified the particle size distributions of sand and gravel and have completely neglected the particle shape effects (without any consideration of rolling resistance). Several experiments, covering a wide range of gravel and sand combinations, are considered. We chose to perform DEM simulations for experiments 1, 2, and 3, which are run1, run2, and run3 of the reference flume experiment. Experiments 1 and 2 correspond to the bridging type of infiltration, and experiment 3 corresponds to the percolation type of infiltration.
The simulations are performed in LIGGGHTS−PFM (version-23.02), a CPU-based DEM code written in C++, developed by Johannes Kepler University, Linz, Austria. LIGGGHTS−PFM allows parallel computations by utilizing the MPI (Message Passing Interface), which decomposes the 3D domain into specified numbers of sub-domains in each direction and assigns one processor per sub-domain. It must be mentioned here that the DEM calculations are computationally demanding and limited to a definite number of particles [64]. The maximum number of particles that can be simulated with the DEM approach, even in large clusters/supercomputers, is in the order of 107 [65]. Unfortunately, LIGGGHTS−PFM has not yet been extended and modified to run on GPU systems. Due to these limitations and heavy computational requirements in the DEM method, a reduced domain size (0.15 m in length, 0.075 m in width, and 0.25 m in height) is considered, which is much smaller than the actual flume experiment but sufficient to capture the bulk behavior of particles. This strategic decision allowed us to perform the simulations in a reasonable timeframe with limited computational resources.
The simulations are performed in two stages. In the first stage, a gravel bed is prepared by pouring gravel particles into the domain under gravity. Once the gravel particles have reached equilibrium and achieved a steady-state condition after 1 s, where almost no gravel particle is moving and the system’s kinetic energy is minimal, sand particles are inserted in the second stage, from 2 s onwards. Particle size distributions have a significant impact on the created gravel bed; for example, mono-sized (mono-disperse) and poly-sized (poly-disperse) particle assemblies have porosities of 0.454 and 0.407, respectively [66]. Considering this, we prepared a gravel bed with predefined bulk porosities of 0.454 and 0.407 for mono-disperse and poly-disperse cases, respectively, which resulted in a graved bed with a height of 0.1 m precisely, the same as in the original experiment. Sand particles are inserted from a region above the gravel bed with a specified mass flow rate for a specified duration. Several sets of DEM simulations are performed to investigate the effects of particle shape and size distribution on sand infiltration. We tested CDT, EPSD, and EPSD2 rolling resistance models while keeping the same PSD and other DEM settings. For the particle size distribution test, PSDs for gravel and sand are simplified, and different cases corresponding to full PSDs, simplified PSDs, and oversimplified PSDs are simulated. The simulations are performed until the bridging layer is formed in the upper gravel layer, precluding subsequent infiltration (bridging behavior). However, in some cases, especially for smaller sand sizes and cases resulting in undesired results, simulations were not further pursued until the final steady-state condition. The following sections will mention these cases explicitly, explaining the reason for not pursuing them further upon their arrival. The main reason is the limitation concerning the number of particles, which is explained in greater detail in the following paragraphs.
In total, 10 cases are simulated, taking references from three experiments (two corresponding to bridging and one corresponding to percolation, which are run1, run2, and run3 of the reference flume experiment, respectively). These 10 cases aim to cover this study’s intended objectives: investigating particle shape and PSD effects on the sand infiltration process. Experiment 1 (run1), a bridging case, is simulated without any rolling resistance model (free-rolling) and with CDT, EPSD, and EPSD2 rolling resistance models. It must be noted that simplified PSDs (four gravel and five sand classes) are considered for rolling resistance tests (in our first set of simulations). This decision should not lead to any non-physical results as simulations aim to test the effects of rolling resistance, keeping the particle size distribution constant. This decision is taken strategically to perform several simulations within a limited timeframe and computational resources. From the first set of simulations, the best-performing rolling resistance model (EPSD model) is found and considered for the following sets of simulations. Two cases for each experiment (experiments 2 and 3) are simulated without and with the EPSD rolling resistance model. Moreover, experiment 1 is simulated, considering different PSDs for sand and gravel, resulting in three cases (full PSDs, simplified PSDs, and oversimplified PSDs). More details of each set of simulations covering rolling resistance and particle size distribution tests are summarized in Table 1.

Table 1.
Overview of different sets of simulations performed.
Figure 2 shows the PSDs considered for sand and gravel for the rolling resistance test. The median sand diameter (D50) in experiment 1 was 0.4 mm, while it was 0.22 mm and 0.21 mm in experiments 2 and 3, respectively. It must be noted that experiment 2 and experiment 3 had 2,527,852 and 2,872,822 particles, respectively, after 5 and 4 s of simulation, while experiment 1 had 2,267,073 particles even after 17 s of simulation (substantially fewer than experiments 2 and 3). The number of particles directly correlates with particle size because more particles are required to represent the same mass for smaller than larger particles. Therefore, experiments 2 and 3 were not further (until the steady-state condition) simulated due to computational limitations, especially concerning the number of particles (max. number of particles, which could be simulated in LIGGGHTS ~ O (107)).
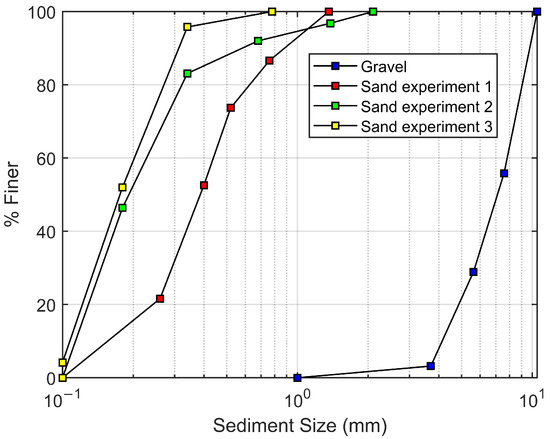
Figure 2.
The considered PSDs for gravel and sand (in simplified form) for the rolling resistance test. Note: the gravel bed is the same across the different experiments.
In the third set of simulations, the effects of PSDs on the infiltrating characteristics of sand are tested. Here, the rolling resistance model is kept the same (based on the best-performing rolling resistance model from the first set of simulations), and PSDs for gravel and sand are varied by considering the full particle size distributions (full PSDs: 9 gravel and 10 sand classes), simplified particle size distributions (simplified PSDs: 4 gravel and 5 sand classes), and oversimplified particle size distributions (oversimplified PSDs: 1 gravel and 1 sand classes). The particle size classes are grouped with the weighted average method to simplify the full (exact) PSDs of sand and gravel. If two particle classes have diameters and with respective fractions and , then the new size class and its corresponding size fraction are calculated using Equations (7a) and (7b). Figure 3 shows the considered PSDs for several cases examined for the particle size distribution test.
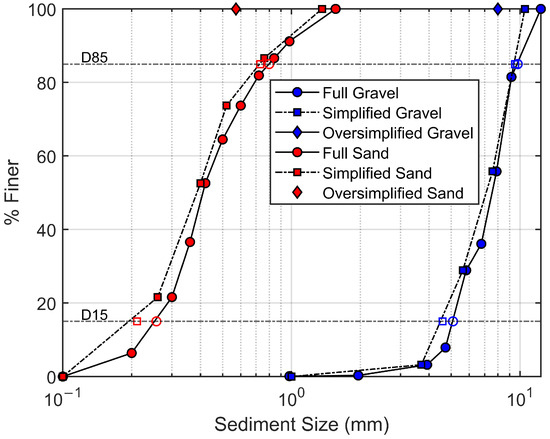
Figure 3.
The considered PSDs for gravel and sand in experiment 1 in their full, simplified, and oversimplified versions. Note: empty squares and circles represent D15 and D85 of different PSDs.
In DEM simulations, the time step is determined by the Rayleigh and Hertz time criteria (Equations (8a) and (8b)), which should be between 10 and 20% of Rayleigh and Hertz times to avoid unphysical particle behavior. In all the numerical simulations, it is ensured that the DEM time step does not exceed 15% of the Rayleigh ( and Hertz ( times.
where is the particle density, is the shear modulus, is the Poisson’s ratio, , , are the effective mass, effective radius, and effective Young’s modulus, and is the maximum relative velocity. It is evident from the equations above that the Rayleigh time is dependent on individual particle characteristics, but the Hertz time is dependent on the characteristics of contacting particles. The time step requirements are proportional to particle size, which is one of the major challenges in dealing with many particles with a wide range of particle size distributions.
DEM simulations are computationally demanding, and this requirement increases exponentially with smaller particles and (or) a greater number of particles. We had a total number of particles (sand + gravel) in the order of 106, which is only one order smaller than the method’s limitation concerning a maximum number of particles (O~107). All the simulations were performed on SuperMUC (High-Performance Computing; HPC) with 240 processors. The 240 processors were distributed over five nodes with 96 GB RAM. Each simulation was run for a minimum of 48 physical h, costing a minimum of 11,520 CPU h for a simulation. The decision to use 240 processors for the simulations was based on initial trials for finding the optimal number of processors for the considered domain size and particles.
As mentioned, some cases are not pursued until the final steady state/equilibrium infiltration state due to computational and time constraints. For those unfinished cases, the infiltration state is qualitatively analyzed only by comparing the snapshot of the gravel bed at the achieved simulation time. The cases that could be simulated until the final steady state/equilibrium infiltration state are both qualitatively and quantitatively analyzed. Other than looking at snapshots of the infiltration state, the final infiltration state in terms of porosity and sand fraction profiles along the depth of the gravel bed was compared to experimental data. Sand fraction content and porosity profiles were extracted from simulated results. A similar methodology was used to plot the sand content and porosity profiles along the depth of the gravel bed, as considered by Jaiswal et al. [43] in their study. The 3D bed is cut at several cross-sections, generating circles of different diameters, which represent sediments of different sizes. The porosity and sand content are calculated based on the area of sand and gravel particles at the cross-sections. A total of 100 such cross-sections are generated, cutting over 10 cm of the depth of the gravel bed, resulting in sand content and porosity values at 1 mm from the top to the bottom of the gravel bed. More details can be found in their paper, as demonstrated in Figure 4.
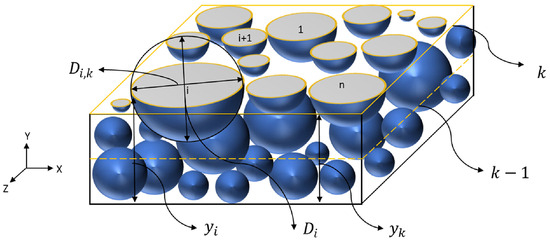
Figure 4.
A plane cutting and generating circles across the cutting plane in 3D packing of the gravel bed [43].
Only the sand content profiles were available from the experimental data. Therefore, simulated sand and measured sand content were used to perform statistical analysis to evaluate the simulation’s efficiency. We calculated four different statistical parameters to evaluate the performance of our simulation against the experimental data. Four statistical parameters were considered, as shown in the following equations: Mean Average Error (MAE), Mean Square Error (MSE), Root Mean Square Error (RMSE), and Correlation Coefficient (R), where n is the number of data points, and are the measured and simulated values, respectively, and and are the means of measured and simulated data, respectively.
4. Results and Discussion
4.1. Effects of Non-Sphericity and Irregularities in Particle Shape
Natural sediment particles are non-spherical and irregular. To investigate particle shape effects on the infiltration characteristics of sand in the gravel bed, we implicitly included their effects by restricting the particle’s rotational movement with simple models. Experiment 1 (run1) of the reference flume experiment is considered with simplified PSDs for gravel and sand (four gravel and five sand classes). Experiment 1 corresponds to the bridging type of infiltration process, which means that the numerical simulations should also capture most of the sand particles in the upper surface layer, precluding subsequent infiltration. Three rolling resistance models, i.e., CDT, EPSD, and EPSD2, were tested for their ability to capture shape effects. A separate case without any rolling resistance (free-rolling) is also simulated.
The simulations are performed until the bridging layer is formed (minimum of 17 s). The bulk porosity of the initial clean gravel bed (at 1 s) and of infiltration at different times (14, 17, and 18 s) are summarized in Table 2. One can see that a marginal change in porosity occurs after 17 s, indicating that a steady-state condition has been reached at 17 s of simulation. The case with the free-rolling (without any rolling resistance model) is an exception as it has not been pursued further after observing that it results in percolation instead of the desired bridging behavior. The bulk porosities of the gravel bed before and after the sand infiltration at different simulation times for different rolling resistance models considered in this study result in very similar values, indicating that all the rolling resistance models can capture shape effects. Depending on the model used, time and resources allotted to them, each case was run till different simulation times. All three cases were run for a minimum of 17 s and seemed to reach the steady state/equilibrium state; therefore, the results for different simulations are compared after 17 s.

Table 2.
Bulk porosities of the initial clean gravel bed and infiltrated gravel bed at different simulation times with different rolling resistance models.
Figure 5 and Figure 6 show the snapshots of the infiltration state after 17 s of simulation for all four cases from frontal and top perspectives, respectively. It must be emphasized that the reference case (experiment 1; run1) is a bridging case, and numerical simulation should also result in a bridging type of infiltration behavior. It is evident that sand fills the coarse gravel deposit predominantly by percolation for the free-rolling case (no rolling resistance case; Figure 5a and Figure 6a), which is the exact opposite of what had been observed in the reference flume experiment 1. Ideally, as observed in experiment 1, most of the sand particles should have been clogged in the upper surface layer. In the numerical simulation of the free-rolling case, this incorrect behavior of sand particles can be related to the simplification made in DEM simulations, where gravel and sand particles are simplified as spheres. In the reference flume experiment, natural sediments were considered, which are indeed non-spherical in shape. To capture the shape effects in the infiltration process, it should be considered in numerical simulations. Here, we have included the shape effects with simple rolling resistance models. Contrary to the free-rolling case, the bridging behavior is captured in the three cases with rolling resistance models, as observed in the reference experiment, where most of the sand particles become clogged in the upper surface layer. This indicates that particle shape effects can be implicitly included with simple models but could capture the physically correct infiltration behavior. Figure 5b–d show the infiltration state after 17 s from the frontal perspective for CDT, EPSD, and EPSD2 models, respectively. Figure 6b–d show the infiltration state after 17 s from the top perspective for CDT, EPSD, and EPSD2 models, respectively. Qualitatively, all the rolling resistance models perform very similarly and could capture the anticipated bridging behavior of sand in the static gravel bed.

Figure 5.
Front view of snapshots of sand infiltration state after 17 s of simulation for experiment 1 with (a) free-rolling (without any rolling resistance model), (b) CDT model, (c) EPSD model, and (d) EPSD2 model. Note: the particles are colored by their types (sand in red and gravel in blue).
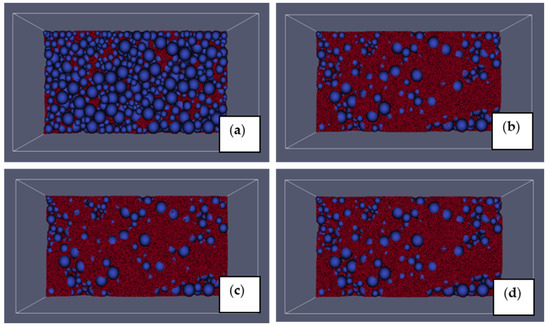
Figure 6.
Top view of snapshots of sand infiltration state after 17 s of simulation for experiment 1 with (a) free-rolling (without any rolling resistance model), (b) CDT model, (c) EPSD model, and (d) EPSD2 model. Note: the particles are colored by their types (sand in red and gravel in blue).
To evaluate the performance of considered rolling friction models in greater detail, the sand content and porosity profiles are shown in Figure 7. Figure 7a compares the measured and simulated sand content profiles along the depth of the gravel bed for CDT, EPSD, and EPSD2 rolling resistance models, along with the free-rolling case. The profiles are plotted after a steady state/equilibrium has been reached (after 17 s of simulation). We can see that all the rolling resistance models could capture the bridging behavior, as observed in the reference experiment. Most sand particles become trapped in the upper surface layer, precluding subsequent infiltration, resulting in an exponential decay function for sand content. The maximum sand content is found at the top of the gravel bed, which keeps on decreasing along the depth of the gravel bed. The simulated sand content for CDT, EPSD, and EPSD2 rolling resistance models overlap, indicating that all the rolling resistance models considered could be used to include the particle shape effects and capture more particles in the upper surface layer. Compared to the cases with rolling resistance models, the free-rolling case results in very different sand content and porosity profiles and is far from the observed data in experiment 1. It must be mentioned that the free-rolling case was not pursued further after realizing that it results in percolation instead of bridging behavior. It also means that the data used in the free-rolling case has not reached the steady-state/equilibrium condition. Another important point is that in the free-rolling case (without rolling resistance models), bridging behavior is not captured (see Figure 5a and Figure 6a). An outlier in the experimental data that could have resulted from human, measurement, and/or process-based errors was not compared to the simulated data. Figure 7b shows the porosity profiles along the depth of the gravel bed before and after the infiltration process (steady-state/equilibrium) for different rolling resistance models considered for numerical simulations. Here, CDT, EPSD, and EPSD2 rolling resistance models again resulted in overlapping porosity profiles similar to simulated sand content profiles. The free-rolling case shows very low porosity at the bottom of the gravel bed, indicating that most of the sand particles are reaching the bottom and that the filling of the gravel bed occurs from the bottom to the top. For the cases with rolling resistance models, the bridging type of infiltration is evident from the porosity profile curve, where significant porosity is reduced in the upper surface layer (approx. first 3–4 cm of the gravel bed), and the reduction in porosity is minimal below this depth. This depth is termed bridging or clogging depth. In the experimental studies, the bridging depth is usually 2–5 times the D90,Gravel [31,34,67]. The D90,Gravel is 10 mm in the considered experiment, and accordingly, the bridging depth should be 2–5 cm. Our simulated bridging depth (3–4 cm) aligns well with previously observed bridging depth.
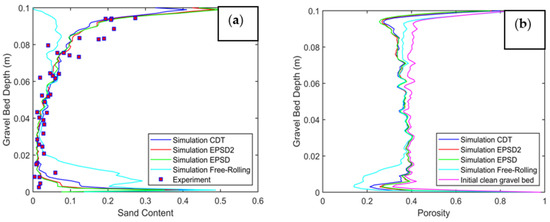
Figure 7.
Sand content (a) and porosity (b) profiles along the depth of the gravel bed after 17 s of simulation for experiment 1.
Furthermore, we evaluated the efficiency of different cases performed for the rolling resistance test with some statistical parameters. The results of the statistical evaluation are summarized in Table 3. While the opposite trend of percolation instead of bridging is evident with a negative correlation coefficient for the free-rolling case, rolling resistance models perform very well with high efficiency and lower error. The CDT model is the least efficient in capturing the shape effects compared to EPSD and EPSD2 models. EPSD and EPSD2 models result in almost the same efficiency, but the EPSD model seems to be slightly better. The EPSD2 model neglects the contribution of the viscous damping torque but EPSD considers both mechanical spring torque and a viscous damping torque . Although the viscous damping torque is marginal compared to the mechanical spring torque, it can be said that both torques should be included to capture correct particle behaviors with high efficiency. We conclude that the EPSD model is most efficient in capturing the particle shape effects for pseudo-static systems such as the process of sand infiltration into the static gravel bed. Therefore, we considered EPSD models for further sets of simulations.

Table 3.
Statistical evaluation of different rolling resistance models against the experiment data.
The second set of simulations, considering experiment 2 (run2) and experiment 3 (run3) of the reference flume experiment, is performed. Experiment 2 corresponds to bridging behavior, and experiment 3 corresponds to the percolation type of infiltration processes. We simulated four cases for the second set of simulations, where the efficiency of the EPSD model is further evaluated. In total, four cases referring to experiments 2 and 3 are simulated without (free-rolling) and with the EPSD rolling resistance model. Unfortunately, these cases are not pursued until the final steady state/equilibrium due to computational and time constraints. Reaching the final infiltration state for experiments 2 and 3 could have resulted in many more particles than the method’s limitation concerning the number of particles (O~107). As mentioned before, the numbers of particles in numerical simulations were ~2.6 × 106 (in 5 s) and ~2.8 × 106 (in 4 s) for experiment 2 and experiment 3, respectively, approaching the maximum number of particles in the DEM method. Additionally, the simulation becomes extremely slow with an increase in the number of particles and a decrease in the particle size, which further requires extremely small DEM time steps. Furthermore, the time and computational resources available for this study could not have allowed us to simulate experiments 2 and 3 further within a reasonable timeframe. Considering the above-mentioned constraints, we could not simulate these cases for a longer duration. Although these cases were not simulated until the steady state/equilibrium, the results could still be used to investigate shape effects and, thus, the rolling friction model.
Figure 8 shows the snapshot of the infiltration state after 5 s of simulation for experiment 2. Figure 8a shows the infiltration state for the free-rolling case (without any rolling resistance), and Figure 8b shows the infiltration state for the EPSD rolling friction model. It is evident that more sand particles are clogged when the EPSD rolling friction model is considered, while with the free-rolling case, sand particles directly infiltrate into the bottom of the gravel bed. Since experiment 2 is also a bridging case, most sand particles should be clogged in the upper surface layer. Figure 8c shows the sand content profiles for free-rolling and EPSD model cases in the first 5 cm of gravel bed depth. One can see that sand content is almost zero for the free-rolling case. Contrary to the free-rolling case, the bridging layer appears in the upper layer, where the sand content is higher. More bridges would have been formed, precluding further infiltration of sand, if the case had been persuaded further. The fact that more particles are becoming clogged when the rolling resistance model (ESPD) is also considered for experiment 2. The above discussion indicates that particle shape (thus rolling resistance) is important in capturing the physically correct particle behavior and justifies our approach of including particle shape effects implicitly.

Figure 8.
Front view of snapshots of sand infiltration state after 5 s of simulation for experiment 2 with (a) free-rolling (without any rolling resistance model), (b) EPSD model, and (c) the sand content in the first 5 cm of the gravel bed for free-rolling and EPSD model cases. Note: the particles are colored by their types (sand in red and gravel in blue).
Figure 9 shows the snapshot of the infiltration state after 4 s of simulation for experiment 3. Figure 9a shows the infiltration state for the free-rolling case (without any rolling resistance), and Figure 9b shows the infiltration state with the EPSD rolling friction model. Experiment 3 corresponds to the percolation type of infiltration, where sand particles fill the coarse gravel deposit from the bottom to the top without being clogged in the upper layers of the gravel bed. Figure 9c shows the sand content profiles for free-rolling and EPSD model cases in the first 5 cm of gravel bed depth. Here, the sand content is almost zero in the upper layer for the free-rolling case, indicating that all sand particles first reach the bottom of the gravel bed, and filling occurs from the bottom to the top. Sand particles become clogged throughout the gravel bed when the rolling resistance model (EPSD) is considered. We observe that numerical simulations result in a percolation type of behavior when the particles are free to roll (without any rolling resistance model). On the other hand, when the rolling resistance (EPSD) model is considered, the particles start to become clogged in the upper surface layer of the gravel bed. Compared to previous cases (bridging cases), where the rolling resistance model helped us obtain the correct infiltration behavior, it leads towards an incorrect trend for the percolation case. Among all the cases considered for the rolling resistance test (particle shape), it can be stated that the inclusion of rolling resistance could help capture more particles in the upper layer and indirectly consider shape effects in the infiltration process. In percolation cases, the inclusion of rolling resistance seems to be unnecessary, and the percolation trend was evident with free-rolling particles (see Figure 9a).

Figure 9.
Front view of snapshots of sand infiltration state after 4 s of simulation for experiment 3 with (a) free-rolling (without any rolling resistance model), (b) EPSD model, and (c) the sand content in the first 5 cm of the gravel bed for free-rolling and EPSD model cases. Note: the particles are colored by their types (sand in red and gravel in blue).
Our observation that rolling resistance models are not necessary for percolation cases could probably be explained by the concept of controlling constriction size (smallest pore size) and its relation to sand and gravel sizes. Percolation occurs when controlling constriction is larger than the coarsest sand particle. Hence, no sand particle should become clogged until it reaches the bottom of the gravel bed. On the other hand, if the controlling constriction size is smaller than the sand particles (at least some), sand particles start to become clogged at the pores that are more diminutive than their sizes, forming bridges. Once some pores are blocked, they subsequently preclude sand infiltration, forming more bridges. For bridging cases (experiments 1 and 2), D15,Gravel/D85,Sand < 10.6, and for percolation cases (experiment 3), D15,Gravel/D85,Sand > 15.4. Here, D85,Sand represents the larger portion of sand as 85% of sand is smaller than that size, and D15,Gravel not only indicates that 15% of gravel is smaller than that size but also indirectly represents the approx. size of the pores in the gravel bed [68,69,70,71]. It must be emphasized that D15,Gravel representing the pore sizes, is only a simplified representation, but the pore sizes vary from one another and follow size distributions like particles. However, D15,Gravel can represent the average pore size in a gravel bed to a reasonable approximation and is useful in practical engineering applications. For percolation to happen, pore size (D15,Gravel) must be at least 15.4 times larger than D85,Sand. In other words, percolation occurs when the sand size is extremely small compared to pore sizes in the gravel bed. Because of considerable differences in the largest sand particle and pore size, particle shape could not remain significant in governing infiltration. This also suggests that when there is a huge difference in the largest sand particle and pore space, the sand particles shape (in terms of shpericity and irregularities) does not play any role within the context of infiltration. Shape effects are important and can play a significant role when they are of similar sizes, at least of the same order. This indicates that rolling resistance models are not necessary for smaller sand sizes (D15,Gravel/D85,Sand > 15.4).
Another possible reason for our observation that rolling resistance is not required for percolation cases, more specifically when D15,Gravel/D85,Sand > 15.4, could be related to the history of sand particles (how and since when the sand particles are in the river system) and the fluvial process (how sand particles have been transported in the river system). There is a possibility that smaller sand particles tend to be rounder and more spherical than larger sand particles. The rounding of sand particles is possible, and a study has shown that any rounding of sand grains by aqueous traction transportation requires transportation over many thousands of miles [72]. Sand particles found in natural river systems go through several fluvial processes from their origin to several transport regimes in the river system, resulting in shape evolution by bed load transport [73]. Smaller sand particles in the river system could become smoother, rounder, and probably spherical as a result of erosive and abrasive actions, which happen during transportation. Additionally, flowing water can favor the smoothing of sand grains, which could become more significant as particles become smaller and smaller. It is possible that smaller sand particles are rounder and spherical and, therefore, might not necessarily require any treatment (explicitly or implicitly) to include non-sphericity. If non-sphericity is included for spherical particles, it would result in an incorrect behavior, as seen in the numerical simulation of experiment 3. However, historical information is very difficult to acquire and generally not available. Further field investigations are necessary to gather more evidence for the hypothesis that sand particles become rounder, smoother, and spherical as they become smaller due to the fluvial transport process.
Another interesting observation could be made from performed DEM simulations: irrespective of the infiltration process (bridging or percolation), some sand particles could always reach the bottom of the gravel bed. This behavior is also persistent in cases where the rolling resistance models are considered or discarded. In other words, a small portion of sand particles could always reach the bottom of the gravel bed, at least at the beginning of the infiltration process, even in bridging cases. Gibson et al. [38] also observed this behavior and called it granular sorting, which is predominant in the infiltration process. Smaller particles preferentially pass through pore spaces, advancing deeper into the gravel framework. The infiltration process is primarily a function of the pore throat and sand gradation distributions. There is always a possibility that some sand particles are smaller than some pore throats and traverse through the pore connections until they approach pore throat (opening of pore connection) smaller than approaching sand particle, which restricts the subsequent sand to be trapped, resulting in the formation of bridges. Additionally, the large values of sand fraction and porosity reduction at the bottom could be related to wall effects and wall–particle interactions. A sudden increase in the sand content at the bottom of the gravel bed could be due to the wall effects as larger pore sizes between walls and gravel particles result in more pore space available for sand particles to accumulate.
4.2. Effects of Particle Size Distribution (PSD)
The third set of simulations was aimed at investigating the effects of different PSDs on the process of sand infiltration into a static gravel bed. Natural sediments contain a wide range of particle sizes. To simplify the system, the grain sizes are grouped with corresponding fractions, resulting in particle size distribution (PSD) curves. The more grain classes there are, the more accurately the PSD represents the natural system. On the other hand, considering wide particle sizes in numerical simulations, especially in the Lagrangian framework (DEM method), is very challenging due to the heavy computational requirements and limitations of the method concerning number of particles. As mentioned in several instances in this paper, the maximum number of particles that could be simulated with the DEM method in LIGGGHTS software (version 23.02) is in O~107; therefore, considering a decent domain size with a PSD resembling the complex natural sediments is difficult and may cross the limit concerning the maximum number of particles depending on the particle size range. Our simulations of experiments 2 and 3 approached the maximum number of particles despite the consideration of simplified PSDs (four gravel and five sand classes for experiment 2 and four gravel and four sand classes for experiment 3). Experiment 3, a percolation case, would be especially vulnerable to limitations concerning the maximum number of particles in the DEM method. A simplification of PSDs is necessary to simulate the infiltration processes. However, the question remains: What simplification is justified enough to capture the required process?
We aim to answer this question by considering three different combinations of PSDs for gravel and sand, varying from exact to very simplified PSDs. Three separate cases are simulated by considering full PSDs (9 gravel and 10 sand classes), simplified PSDs (4 gravel and 5 sand classes), and oversimplified PSDs (1 gravel and 1 sand classes), keeping the same rolling resistance model (EPSD) and other DEM settings. The simulation time each case takes to reach the steady state/equilibrium differs from one another, depending on the number of particles and particle sizes. Experiment 1 (run1) of the flume experiment [38] is considered, which is a bridging case, for particle size distribution (PSD) effects on the sand infiltration process. Snapshots of the infiltration state are compared for different cases. Furthermore, porosity and sand content profiles are compared, and statistical analysis is performed against the experimental data regarding their ability to capture correct results.
Figure 10 shows the snapshots of the infiltration state for numerical simulations for experiment 1 with different PSD combinations. Figure 10a–c show the snapshots from the frontal perspective for full PSDs, simplified PSDs, and oversimplified PSDs, respectively. Figure 10d–f show the snapshots from the top perspective for full PSDs, simplified PSDs, and oversimplified PSDs, respectively. Cases for full, simplified, and oversimplified PSDs are run for 15.8, 18, and 40 s of simulation, respectively. One can see that bridging behavior is observed in the cases of full and simplified PSDs. However, in the oversimplified PSD case, the percolation type of infiltration is observed instead of the desired bridging process. It is evident from the full PSD case (Figure 10a,d) that it captures most of the sediments in the upper surface layer, and by the time the steady state/equilibrium is approaching (15.8 s), a bridging layer is distinctly visible. A small portion of sand could still reach the bottom of the gravel bed, but it is marginal, and the overall behavior is mainly the bridging type of infiltration. Similarly, the sand clogging pattern in the upper layer of the gravel bed is observed for the case of simplified PSDs (see Figure 10b,e). Compared to the full PSD case, more sand particles could reach the bottom of the gravel bed for the simplified PSD case, but the overall infiltration behavior is still a bridging type of infiltration. A portion of sand could always reach the bottom of the gravel bed due to gradational sorting until larger sand particles approach the pore and bridges are formed, precluding subsequent infiltration, described in greater detail in Section 4.1. Both the full and simplified PSD cases could capture the bridging behavior observed in experiment 1. The case with oversimplified PSDs resulted in the opposite behavior, where the filling of the gravel bed occurs from the bottom to the top (percolation behavior). One can see that pores in the lower layer of the gravel bed are fully packed with sand particles at 40 s of simulation, and the upper layer of the gravel bed still has some unclogged pores (see Figure 10c,f). The rest of the gravel bed (upper layer) would have been also filled with sand particles, resulting in a fully packed gravel bed, if the case was run further beyond 40 s of simulation. We intentionally did not pursue the oversimplified case after 40 s. The oversimplified PSD case resulted in an incorrect infiltration behavior (percolation instead of bridging). Therefore, it would have been a waste of computational resources if pursued further. The full PSD case requires much more computational time and resources to reach the steady-state condition, while the simplified PSD case is faster and is able to capture the correct bridging behavior, indicating that the grain classes can be simplified and that the correct particle behavior can be captured. However, the simplifications in PSDs should be performed carefully, and oversimplification might lead to incorrect particle behavior, as shown by our oversimplified case (one gravel and one sand class), which was indeed much faster than the other two cases but could not capture the correct particle behavior within the context of sand infiltration into the static gravel bed. The simplifications in PSDs are necessary to realize the numerical simulation of infiltration processes with reasonable computational resources and time, but it may lead to an incorrect behavior; therefore, it needs to be addressed properly. Oversimplification should be avoided.

Figure 10.
Frontal (a–c) and top (d–f) perspectives of snapshots of sand infiltration state simulation for experiment 1 considering full PSDs after 15.8 s (a,d), simplified PSDs after 18 s (b,e), and oversimplified PSDs after 40 s (c,f). Note: the particles are colored by their types (sand in red and gravel in blue).
Detailed sand content and porosity profiles are shown in Figure 11. Figure 11a shows the sand content profiles for different PSDs considered in numerical simulations against the experimental data. In the cases with full PSDs and simplified PSDs, the maximum sand content is found in the upper layer, which decreases exponentially with the depth of the gravel bed. It is possible that the full PSD case did not reach the final steady-state infiltration state before 15.8 s of simulation due to computational and time constraints. However, it seems to be approaching the steady-state condition as it could capture the correct infiltration behavior with quite good agreement with the experimental data. On the other hand, the oversimplified PSD case results in the maximum sand content at the bottom of the gravel bed, which remains relatively high along the height of the gravel bed (from the bottom to the top). Please note that the sand content for the oversimplified case is plotted at 40 s. Moreover, by that time, the gravel bed had not reached equilibrium. Although the sand content profile for the oversimplified case does not represent the final infiltration state, it still shows a distinct pattern of percolation behavior, where filling occurs from the bottom to the top. In the original experiment, the adopted case corresponds to bridging behavior. Figure 11b,c show the initial and final porosity profiles for different PSDs considered, respectively. The initially created gravel bed has higher porosity for oversimplified PSDs than simplified and full PSD cases, which eventually resulted in different packing/infiltration processes and quite different final porosities than expected for bridging cases. It has also shown that mono- and poly-disperse particle assemblies have different initial porosities and that PSD plays a crucial role in how the packing is formulated [66]. Due to the simplification of PSDs, not only are the gravel bed characteristics modified but the characteristics of the infiltrating sand are also mutated, which has consequences for the sand infiltration process. Interestingly, the simplified PSD case results in more or less similar initial and final porosity profiles as the full PSD case, indicating that the packing characteristics are not modified significantly and resolved enough to capture the correct infiltration behavior. We observe that oversimplification can lead to wrong infiltration behavior. At the same time, a simplification can still be helpful and give correct results, provided the simplification of PSDs does not result in significant changes in the characteristics of the gravel bed and infiltrating sand (pore size, pore connectivity, and sizes of sediments itself).
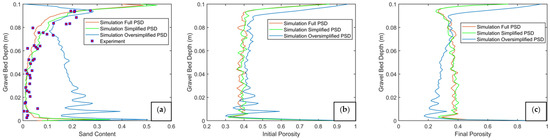
Figure 11.
Sand content (a), initial porosity (b), and final porosity (c) profiles along the depth of the gravel bed considering different particle size distributions (PSDs) for sand and gravel.
Statistical analysis was also performed for the particle size distribution test, similar to the rolling resistance test, with some statistical parameters (MAE, MSE, RMSE, and R), and is summarized in Table 4. Again, only sand content data were available in the experiment. Therefore, the statistical analysis is based on sand content only. The oversimplified PSD case resulted in an incorrect infiltration behavior, demonstrated by high error values and a negative correlation coefficient. A negative correlation coefficient for the oversimplified PSD case also means that the predicted trend is opposite to the one observed in the experiment. Interestingly, the simplified PSD case has a slightly higher correlation coefficient, and MAE, MSE, and RMSE are marginally higher for the full PSD case. Compared to the simplified PSD case reaching a steady state in 18 s, the full PSD case might not have reached the final steady state of infiltration in 15.8 s; therefore, statistically, it seems to be less accurate than the simplified case. Another reason for the full PSD case being statistically less accurate than the simplified PSD case could be the larger DEM time steps and considered materialistic properties in the full PSD case. The full PSD case would show better performance in the statistical analysis if simulated beyond 15.8 s and with further calibration with even smaller DEM time steps and more suitable materialistic properties. Overall, the simplified and full PSD cases resulted in reasonably good agreement with the experimental data, indicating that the simplification of PSDs of sand and gravel could still capture a correct infiltration behavior, but it needs to be carefully handled as oversimplification could entirely modify the gravel bed and infiltrating characteristics, which do not represent the actual system considered for numerical simulations.

Table 4.
Statistical evaluation of different PSDs considered for numerical simulations against the experiment data.
Table 5 summarizes the computational performances for cases considered for the particle size distribution test, with the respective numbers of particles. Please note that sand particles are inserted continuously as the simulation progresses. After every 1 s, 146,799, 133,127, and 40,279 sand particles are poured over the gravel bed for the full, simplified, and oversimplified PSDs, respectively, equivalent to a 0.01 kg/s sand insertion rate. One can see that more sand particles are required to represent the same mass rate when more grain classes (wider PSDs) are considered. The increase in the number of particles also results in extra computational overhead, which slows down the simulations due to the continuous increase in the number of particles. The full PSD case is more vulnerable to the computational speed issue; therefore, the full PSD case was only pursued for 15.8 s of simulation.

Table 5.
Computational performance of the full, simplified, and oversimplified PSD cases in terms of CPU hours and number of particles.
Figure 12 shows the isometric view of the infiltration state of full and simplified PSD cases after 15.8 s and 18 s of simulation duration, respectively. It is evident that both cases result in very similar results concerning the sand infiltration process over the static gravel bed. Despite simplifying the PSDs for sand and gravel with reduced grain classes, the simplified PSD case could capture the correct infiltration behavior with excellent statistical performance, indicating that the basic characteristics of the gravel bed and infiltrating sand remain similar to the full PSD case. As mentioned in the previous section, D15,Gravel and D85,Sand are crucial parameters that govern the infiltration process. The D15,Gravel represents the average pore size of the gravel bed, and D85,Sand represents the larger portion of the infiltrating sand [68,69,70,71]. In order to capture the correct infiltration behavior, these two parameters should not be modified significantly. For the simplified PSD case, the D15,Gravel and D85,Sand is very similar to the full PSD case (see Figure 3), while D15,Gravel and D85,Sand for the full PSD case are 5.09 mm and 0.79 mm, respectively, resulting in the packing ratio D15,Gravel/D85,Sand = 6.44. For simplified PSD cases, D15,Gravel and D85,Sand are 4.58 mm and 0.73 mm, respectively, resulting in the packing ratio D15,Gravel/D85,Sand = 6.14. One can see that the D15,Gravel/D85,Sand ratio is around 6 for both simplified and full PSD cases, which corresponds to the bridging infiltration process as per the threshold (D15,Gravel/D85,Sand < 10.6) suggested by Gibson et al. [38]. On the other hand, the oversimplified PSD case represented the gravel and sand by a binary system and had mono-disperse sand and gravel, with particle sizes of 8 mm and 0.572 mm, respectively. As the case was mono-disperse, having only one size for both sand and gravel, D15,Gravel and D85,Sand could be calculated. Still, the size ratio could be related to the thresholds suggested by Gibson et al. [38]. Due to the oversimplification, the gravel bed and sand characteristics are entirely modified and no longer represent the experimental conditions, demonstrated by the size ratio of DGravel/DSand = 14, which is much higher than the threshold for bridging (D15,Gravel/D85,Sand < 10.6). Therefore, the oversimplified PSD case resulted in a percolation type of infiltration instead of bridging behavior. If the oversimplification of PSDs for gravel and sand is unavoidable due to computational limitations, one could extract the D15,Gravel and D85,Sand from the particle size distribution curve and consider them to represent the binary mixture of the gravel–sand combination. Thus, the size ratio is the same and within the thresholds for different infiltration processes. However, representing the gravel and sand with D15,Gravel and D85,Sand is not appropriate because D85,Sand still represents the larger portion of sand (85% of sand smaller than that size) but D15,Gravel only represents the smaller portion of gravel (15% of gravel smaller than that size). We suggest that simplification is justified as long as the basic characteristics of the gravel bed and infiltrating sand remain similar to PSDs used in the reference experiment (full or exact PSDs). This would not only result in the anticipated infiltration process but also could save significant computational resources.
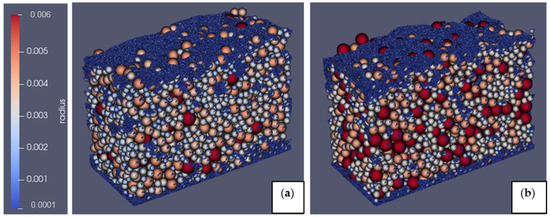
Figure 12.
Isometric view of snapshots of sand infiltration state simulation for experiment 1 considering full PSDs after 15.8 s (a) and simplified PSDs after 18 s (b). Note: the particles are colored by their sizes.
5. Conclusions
This work investigates particle shape effects, which arise due to non-sphericity and irregularities in particle shape. This study also focuses on the effects of particle size distributions (PSDs) on the infiltrating characteristics of sand in a static gravel bed. Particle shape is included implicitly by adding rolling resistance to particles, which indirectly incorporates particle shape effects. The applied Lagrangian particle tracking method (DEM method) is computationally expensive and still limited to a definite number of particles (O~107). Therefore, with the available computational resources, resolving particle shapes for both gravel and sand present in the system is impossible, and including shape effects implicitly seems to be the most efficient way. We tested three different rolling resistance models, namely CDT, EPSD, and EPSD2 models. Separate cases without rolling resistance models (free-rolling) have also been simulated to represent the infiltration process for free-rolling spherical particles. Furthermore, particle size distributions (PSDs) of sand and gravel were simplified to investigate the PSD’s effects on the numerical simulation of sand infiltration process. To do so, the ability of full PSD and simplified versions of PSDs to capture the observed infiltration process were tested in the adapted flume experiment.
We showed that the threshold for bridging and percolation (D15,Gravel/D85,Sand) could help decide the number of grain classes for sand and gravel in the DEM simulations, which not only results in the anticipated infiltration process but also saves significant computational resources. Additionally, the D15,Gravel/D85,Sand ratio can be used to decide whether the rolling friction should be considered for numerical simulations, providing information on scenarios when the shape effect plays a crucial role. Due to computational and time constraints, we could not pursue some cases, especially cases with very small sand sizes (percolations and full PSD cases), until final steady-state infiltration, which can be attempted in future studies. Despite not reaching the steady state/equilibrium for those cases, we could capture the bridging or percolation trend as observed in the original experiment. We intentionally avoided the flowing water effects in this study and focused more on the particle shape and PSD effects, which were either simplified or neglected in previous studies. The process of sand infiltration into the static gravel bed is predominantly gravity-dominated as sand infiltration driven by intra-gravel flow is similar to sand infiltration driven by gravity, as hypnotized by Cui et al. [40] and confirmed by Jaiswal et al. [43]. The findings from this study should also be valid for cases with flowing water, provided the gravel bed remains immobile. In this study, we considered a relatively smaller domain size than the actual flume experiment to simulate a decent number of cases with a reasonable timeframe and with limited computational resources. A more detailed study covering larger domain sizes and an even wider range of gravel and sand compositions would help to confirm our observations. Future studies focusing on these aspects could shed more light on the process of sand infiltration into the static gravel bed. Taken together, the following conclusions can be drawn from the conducted study:
- Rolling resistance models efficiently incorporate effects of non-sphericity and irregularities in particle shape when modeling quasi-static systems such as sand infiltration into a static gravel bed. For the bridging cases (D15,Gravel/D85,Sand < 10.6), rolling resistance models are vital for correct or anticipated infiltration behavior.
- Contrary to the bridging cases, for the percolation cases (D15,Gravel/D85,sand > 15.4), excluding the rolling friction model (free-rolling case) could capture the physically correct percolation type of infiltration, indicating that when pore size becomes significantly larger than infiltrating sand particles, particle shape effects tend to vanish. Shape effects are more important for coarser than finer sand particles. Therefore, the rolling resistance models in modeling percolation should be avoided.
- A comparison of different rolling resistance models shows that all the considered models (CDT, EPSD, and EPSD2) are able to capture particle shape effects wherever the shape effects seem to be vital. The EPSD model performs marginally better than the other two models. Applying these models, we can implicitly consider the effects of particle shape by adding artificial resistance to particle rotation. These models can help obtain the correct infiltration behavior for bridging cases, but the inclusion of rolling resistance can also lead to non-physical and undesirable results for percolation cases. Therefore, it should be used carefully depending on the relative sand–gravel size.
- The DEM method is computationally expensive and limited to a definite number of particles with the currently available computational resources, architecture, and solution algorithms. This usually requires the particle size distributions (PSDs) for sand and gravel to be simplified to represent the required volume or mass of sediments by a lower number of particles. Simplification is necessary to realize the numerical simulations, but oversimplification could entirely modify the characteristics of gravel beds and infiltrating sand, resulting in completely different infiltration behaviors than anticipated.
- A sufficient number of gravel and sand classes (4–5 grain classes) could be a good compromise between the accuracy and realizability of numerical simulations with a decent domain size, which can capture the bulk behavior of sand and gravel beds. Simplified cases (with four grain classes for gravel and five for sand) could capture the correct bridging behavior and perform very well in statistical evaluation against the experimental data. For this purpose, D15,Gravel/D85,Sand could be considered as a measure of the gravel bed and infiltrating sand characteristics. If the D15,Gravel/D85,Sand remain similar to the exact/full PSDs for sand and gravel, then the simplification is justified and should not lead to any non-physical behavior concerning the infiltration process being investigated.
Author Contributions
A.J. (Conceptualization, Investigation, Data Curation, and Writing—Original Draft), M.D.B. (Supervision, Writing Review and Editing), N.R. (Resources and Writing—Review and Editing), and P.R. (Supervision). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
We would like to thank the Leibniz Supercomputing Centre (LRZ) for providing the computational resources required for our study. This study was conducted as part of a PhD research project at TUM with the KAS scholarship. We are very thankful to Konrad-Adenauer-Stiftung (KAS) for making this possible. We would also like to thank Roser Casas Mulet and Subhojit Kadia, both from TUM, for their valuable suggestions. We acknowledge the support of Martin Ohlerich from LRZ for guiding the corresponding author in understanding the workflow and architecture of the supercomputing facility.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ock, G.; Gaeuman, D.; McSloy, J.; Kondolf, G.M. Ecological functions of restored gravel bars, the Trinity River, California. Ecol. Eng. 2015, 83, 49–60. [Google Scholar] [CrossRef]
- Hauer, F.R.; Locke, H.; Dreitz, V.J.; Hebblewhite, M.; Lowe, W.H.; Muhlfeld, C.C.; Nelson, C.R.; Proctor, M.F.; Rood, S.B. Gravel-bed river floodplains are the ecological nexus of glaciated mountain landscapes. Sci. Adv. 2016, 2, e1600026. [Google Scholar] [CrossRef]
- Casas-Mulet, R.; Pander, J.; Prietzel, M.; Geist, J. The HydroEcoSedimentary tool: An integrated approach to characterise interstitial hydro-sedimentary and associated ecological processes. River Res. Appl. 2021, 37, 988–1002. [Google Scholar] [CrossRef]
- Greig, S.M.; Sear, D.A.; Carling, P.A. A review of factors influencing the availability of dissolved oxygen to incubating salmonid embryos. Hydrol. Process. 2007, 21, 323–334. [Google Scholar] [CrossRef]
- Wood, P.J.; Armitage, P.D. Biological Effects of Fine Sediment in the Lotic Environment. Environ. Manag. 1997, 21, 203–217. [Google Scholar] [CrossRef]
- Walling, D.; Owens, P.; Carter, J.; Leeks, G.; Lewis, S.; Meharg, A.; Wright, J. Storage of sediment-associated nutrients and contaminants in river channel and floodplain systems. Appl. Geochem. 2003, 18, 195–220. [Google Scholar] [CrossRef]
- Jones, J.I.; Collins, A.L.; Naden, P.S.; Sear, D.A. The relationship between fine sediment and macrophytes in rivers. River Res. Appl. 2012, 28, 1006–1018. [Google Scholar] [CrossRef]
- Wooster, J.K.; Dusterhoff, S.R.; Cui, Y.; Sklar, L.S.; Dietrich, W.E.; Malko, M. Sediment supply and relative size distribution effects on fine sediment infiltration into immobile gravels. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- East, A.E.; Pess, G.R.; Bountry, J.A.; Magirl, C.S.; Ritchie, A.C.; Logan, J.B.; Randle, T.J.; Mastin, M.C.; Minear, J.T.; Duda, J.J.; et al. Large-scale dam removal on the Elwha River, Washington, USA: River channel and floodplain geomorphic change. Geomorphology 2015, 228, 765–786. [Google Scholar] [CrossRef]
- Bednarek, A.T. Undamming rivers: A review of the ecological impacts of dam removal. Environ. Manag. 2001, 27, 803–814. [Google Scholar] [CrossRef]
- Born, S.M.; Genskow, K.D.; Filbert, T.L.; Hernandez-Mora, N.; Keefer, M.L.; White, K.A. Socioeconomic and Institutional Dimensions of Dam Removals: The Wisconsin Experience. Environ. Manag. 1998, 22, 359–370. [Google Scholar] [CrossRef]
- Cui, Y.; Parker, G.; Braudrick, C.; Dietrich, W.E.; Cluer, B. Dam Removal Express Assessment Models (DREAM). J. Hydraul. Res. 2006, 44, 291–307. [Google Scholar] [CrossRef]
- Cui, Y.; Wilcox, A.C. Numerical modeling of sediment transport upon dam removal: Application to Marmot Dam in Sandy River, Oregon. In Sedimentation Engineering, ASCE Manual; Oregon: Reston, VA, USA, 2005; Volume 54. [Google Scholar]
- Doyle, M.W.; Stanley, E.H.; Harbor, J.M. Channel adjustments following two dam removals in Wisconsin. Water Resour. Res. 2003, 39, 1011. [Google Scholar] [CrossRef]
- Pollard, A.I.; Reed, T. Benthic invertebrate assemblage change following dam removal in a Wisconsin stream. Hydrobiologia 2004, 513, 51–58. [Google Scholar] [CrossRef]
- Stanley, E.H.; Luebke, M.A.; Doyle, M.W.; Marshall, D.W.I. Short-Term Changes in Channel Form and Macroinvertebrate Communities Following Low-Head Dam Removal. J. N. Am. Benthol. Soc. 2002, 21, 172–187. [Google Scholar] [CrossRef]
- Minshall, G.W.; Royer, T.V.; Robinson, C.T. Response of the Cache Creek macroinvertebrates during the first 10 years following disturbance by the 1988 Yellowstone wildfires. Can. J. Fish. Aquat. Sci. 2001, 58, 1077–1088. [Google Scholar] [CrossRef]
- Vieira, N.K.M.; Clements, W.H.; Guevara, L.S.; Jacobs, B.F. Resistance and resilience of stream insect communities to repeated hydrologic disturbances after a wildfire. Freshw. Biol. 2004, 49, 1243–1259. [Google Scholar] [CrossRef]
- Lisle, T.E. Sediment transport and resulting deposition in spawning gravels, north coastal California. Water Resour. Res. 1989, 25, 1303–1319. [Google Scholar] [CrossRef]
- Swanson, F.J.; Dyrness, C.T. Impact of clear-cutting and road construction on soil erosion by landslides in the western Cascade Range, Oregon. Geology 1975, 3, 393. [Google Scholar] [CrossRef]
- Parker, G.; Cui, Y.; Imran, J.; Dietrich, W.E. Flooding in the lower Ok Tedi, Papua New Guinea due to the disposal of mine tailings and its amelioration. In Proceedings of the Recent Trends of Floods and Their Preventive Measures, Hokkaido River Disaster Prevention Res. Res. Cent., Sapporo, Japan, 20–21 June 1996. [Google Scholar]
- Yu, A.B.; Standish, N. Estimation of the porosity of particle mixtures by a linear-mixture packing model. Ind. Eng. Chem. Res. 1991, 30, 1372–1385. [Google Scholar] [CrossRef]
- Yu, A.B.; Standish, N. Limitation of proposed mathematical models for the porosity estimation of nonspherical particle mixtures. Ind. Eng. Chem. Res. 1993, 32, 2179–2182. [Google Scholar] [CrossRef]
- Yu, A.B.; Zou, R.P.; Standish, N. Modifying the Linear Packing Model for Predicting the Porosity of Nonspherical Particle Mixtures. Ind. Eng. Chem. Res. 1996, 35, 3730–3741. [Google Scholar] [CrossRef]
- Lauck, T. A Simulation Model for the Infiltration of Sediment into Spawning Gravel. Master’s Thesis, Humboldt State University, Arcata, CA, USA, 1991. [Google Scholar]
- Herrero, A.; Berni, C. Sand infiltration into a gravel bed: A mathematical model. Water Resour. Res. 2016, 52, 8956–8969. [Google Scholar] [CrossRef]
- Shen, E.; Liu, G.; Jia, Y.; Dan, C.; Abd Elbasit, M.A.; Liu, C.; Gu, J.; Shi, H. Effects of raindrop impact on the resistance characteristics of sheet flow. J. Hydrol. 2021, 592, 125767. [Google Scholar] [CrossRef]
- Einstein, H.A. Deposition of Suspended Particles in a Gravel Bed. J. Hydr. Div. 1968, 94, 1197–1206. [Google Scholar] [CrossRef]
- Herrero, A.; Berni, C.; Camenen, B.; Thollet, F. Laboratory Analysis on silt Infiltration into a Gravel bed. Modélisation Physique de L’infiltration Dans un lit de Graviers. 2015. Available online: https://hal.science/hal-01362697 (accessed on 27 May 2024).
- NCASI. Factors Affecting Changes in the Percent of Fine Sediment in Gravel Bedded Channels; Technical Bulletin No. 0354; NCASI: Research Triangle Park, NC, USA, 1981. [Google Scholar]
- Diplas, P.; Parker, G. Deposition and removal of fines in gravel-bed streams. Dyn. Gravel-Bed Rivers 1992, 313–329. [Google Scholar]
- Evans, E.; Wilcox, A.C. Fine sediment infiltration dynamics in a gravel-bed river following a sediment pulse. River Res. Applic. 2014, 30, 372–384. [Google Scholar] [CrossRef]
- Lunt, I.A.; Bridge, J.S. Formation and preservation of open-framework gravel strata in unidirectional flows. Sedimentology 2007, 54, 71–87. [Google Scholar] [CrossRef]
- Beschta, R.L.; Jackson, W.L. The Intrusion of Fine Sediments into a Stable Gravel Bed. J. Fish. Res. Bd. Can. 1979, 36, 204–210. [Google Scholar] [CrossRef]
- Carling, P.A. Deposition of Fine and Coarse Sand in an Open-Work Gravel Bed. Can. J. Fish. Aquat. Sci. 1984, 41, 263–270. [Google Scholar] [CrossRef]
- Frostick, L.E.; Lucas, P.M.; Reid, I. The infiltration of fine matrices into coarse-grained alluvial sediments and its implications for stratigraphical interpretation. J. Geol. Soc. 1984, 141, 955–965. [Google Scholar] [CrossRef]
- Schälchli, U. The clogging of coarse gravel river beds by fine sediment. Hydrobiologia 1992, 235–236, 189–197. [Google Scholar] [CrossRef]
- Gibson, S.; Abraham, D.; Heath, R.; Schoellhamer, D. Vertical gradational variability of fines deposited in a gravel framework. Sedimentology 2009, 56, 661–676. [Google Scholar] [CrossRef]
- Gibson, S.; Abraham, D.; Heath, R.; Schoellhamer, D. Bridging Process Threshold for Sediment Infiltrating into a Coarse Substrate. J. Geotech. Geoenviron. Eng. 2010, 136, 402–406. [Google Scholar] [CrossRef]
- Cui, Y.; Wooster, J.K.; Baker, P.F.; Dusterhoff, S.R.; Sklar, L.S.; Dietrich, W.E. Theory of Fine Sediment Infiltration into Immobile Gravel Bed. J. Hydraul. Eng. 2008, 134, 1421–1429. [Google Scholar] [CrossRef]
- Bui, V.H.; Bui, M.D.; Rutschmann, P. Combination of Discrete Element Method and Artificial Neural Network for Predicting Porosity of Gravel-Bed River. Water 2019, 11, 1461. [Google Scholar] [CrossRef]
- Bui, V.H.; Bui, M.D.; Rutschmann, P. Advanced Numerical Modeling of Sediment Transport in Gravel-Bed Rivers. Water 2019, 11, 550. [Google Scholar] [CrossRef]
- Jaiswal, A.; Bui, M.D.; Rutschmann, P. On the process of fine sediment infiltration into static gravel bed: A CFD–DEM modelling perspective. River Res. Appl. 2024, 40, 29–48. [Google Scholar] [CrossRef]
- Elmsahli, H.S.; Sinka, I.C. A discrete element study of the effect of particle shape on packing density of fine and cohesive powders. Comput. Part. Mech. 2021, 8, 183–200. [Google Scholar] [CrossRef]
- Soltanbeigi, B.; Papanicolopulos, S.A.; Ooi, J.Y. An insight into the micro-mechanism of the directional constant torque model in quasi-static flow. In Proceedings of the CFDEM® Project User Group Meeting and Workshop, Linz, Austria, 14–15 March 2016. [Google Scholar]
- Guo, Y.; Yang, Y.; Yu, X. Influence of particle shape on the erodibility of non-cohesive soil: Insights from coupled CFD–DEM simulations. Particuology 2018, 39, 12–24. [Google Scholar] [CrossRef]
- Fukumoto, Y.; Sakaguchi, H.; Murakami, A. The role of rolling friction in granular packing. Granul. Matter 2013, 15, 175–182. [Google Scholar] [CrossRef]
- Favier, J.F.; Abbaspour-Fard, M.H.; Kremmer, M.; Raji, A.O. Shape representation of axi-symmetrical, non-spherical particles in discrete element simulation using multi-element model particles. Eng. Comput. 1999, 16, 467–480. [Google Scholar] [CrossRef]
- Favier, J.F.; Abbaspour-Fard, M.H.; Kremmer, M. Modeling Nonspherical Particles Using Multisphere Discrete Elements. J. Eng. Mech. 2001, 127, 971–977. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, W.; Hou, J.; You, Z. Review on physical and chemical factors affecting fines migration in porous media. Water Res. 2022, 214, 118172. [Google Scholar] [CrossRef]
- You, Z.; Osipov, Y.; Bedrikovetsky, P.; Kuzmina, L. Asymptotic model for deep bed filtration. Chem. Eng. J. 2014, 258, 374–385. [Google Scholar] [CrossRef]
- Badalyan, A.; You, Z.; Aji, K.; Bedrikovetsky, P.; Carageorgos, T.; Zeinijahromi, A. Size exclusion deep bed filtration: Experimental and modelling uncertainties. Rev. Sci. Instrum. 2014, 85, 15111. [Google Scholar] [CrossRef]
- Yuan, H.; You, Z.; Shapiro, A.; Bedrikovetsky, P. Improved population balance model for straining-dominant deep bed filtration using network calculations. Chem. Eng. J. 2013, 226, 227–237. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics, 1st ed.; with Corrections; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Iwashita, K.; Oda, M. Rolling Resistance at Contacts in Simulation of Shear Band Development by DEM. J. Eng. Mech. 1998, 124, 285–292. [Google Scholar] [CrossRef]
- Bardet, J.P.; Huang, Q. Numerical modeling of micropolar effects in idealized granular materials. Am. Soc. Mech. Eng. Mater. Div. (Publ.) 1992, 37, 85–92. [Google Scholar]
- Bardet, J.P. Observations on the effects of particle rotations on the failure of idealized granular materials. Mech. Mater. 1994, 18, 159–182. [Google Scholar] [CrossRef]
- Oda, M.; Konishi, J.; Nemat-Nasser, S. Experimental micromechanical evaluation of strength of granular materials: Effects of particle rolling. Mech. Mater. 1982, 1, 269–283. [Google Scholar] [CrossRef]
- Calvetti, F.; Combe, G.; Lanier, J. Experimental micromechanical analysis of a 2D granular material: Relation between structure evolution and loading path. Mech. Cohes.-Frict. Mater. 1997, 2, 121–163. [Google Scholar] [CrossRef]
- Misra, A.; Jiang, H. Measured kinematic fields in the biaxial shear of granular materials. Comput. Geotech. 1997, 20, 267–285. [Google Scholar] [CrossRef]
- Ai, J.; Chen, J.-F.; Rotter, J.M.; Ooi, J.Y. Assessment of rolling resistance models in discrete element simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- Bérard, A.; Patience, G.S.; Blais, B. Experimental methods in chemical engineering: Unresolved CFD-DEM. Can. J. Chem. Eng. 2020, 98, 424–440. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD-DEM. Prog. Comput. Fluid Dyn. Int. J. 2012, 12, 140. [Google Scholar] [CrossRef]
- Latham, J.P.; Munjiza, A.; Lu, Y. On the prediction of void porosity and packing of rock particulates. Powder Technol. 2002, 125, 10–27. [Google Scholar] [CrossRef]
- Iseya, F.; Ikeda, H. Pulsations in Bedload Transport Rates Induced by a Longitudinal Sediment Sorting: A Flume Study using Sand and Gravel Mixtures. Geogr. Ann. Ser. A-Phys. Geogr. 1987, 69, 15–27. [Google Scholar] [CrossRef]
- Honjo, Y.; Veneziano, D. Improved filter criterion for cohesionless soils. J. Geotech. Eng. 1989, 115, 75–94. [Google Scholar] [CrossRef]
- Indraratna, B.; Vafai, F. Analytical Model for Particle Migration within Base Soil-Filter System. J. Geotech. Geoenviron. Eng. 1997, 123, 100–109. [Google Scholar] [CrossRef]
- Sherard, J.L.; Dunnigan, L.P. Filters and leakage control in embankment dams. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1986, 23, 202. [Google Scholar]
- Indraratna, B.; Locke, M.R. Design methods for granular filters—Critical review. Proc. Inst. Civ. Eng.-Geotech. Eng. 1999, 137, 137–147. [Google Scholar] [CrossRef]
- Twenhofel, W.H. The Rounding of Sand Grains. J. Sediment. Res. 1945, 15, 59–71. [Google Scholar] [CrossRef]
- Novák-Szabó, T.; Sipos, A.Á.; Shaw, S.; Bertoni, D.; Pozzebon, A.; Grottoli, E.; Sarti, G.; Ciavola, P.; Domokos, G.; Jerolmack, D.J. Universal characteristics of particle shape evolution by bed-load chipping. Sci. Adv. 2018, 4, eaao4946. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).