Inversion Method for Monitoring Daily Variations in Terrestrial Water Storage Changes in the Yellow River Basin Based on GNSS
Abstract
1. Introduction
2. Materials
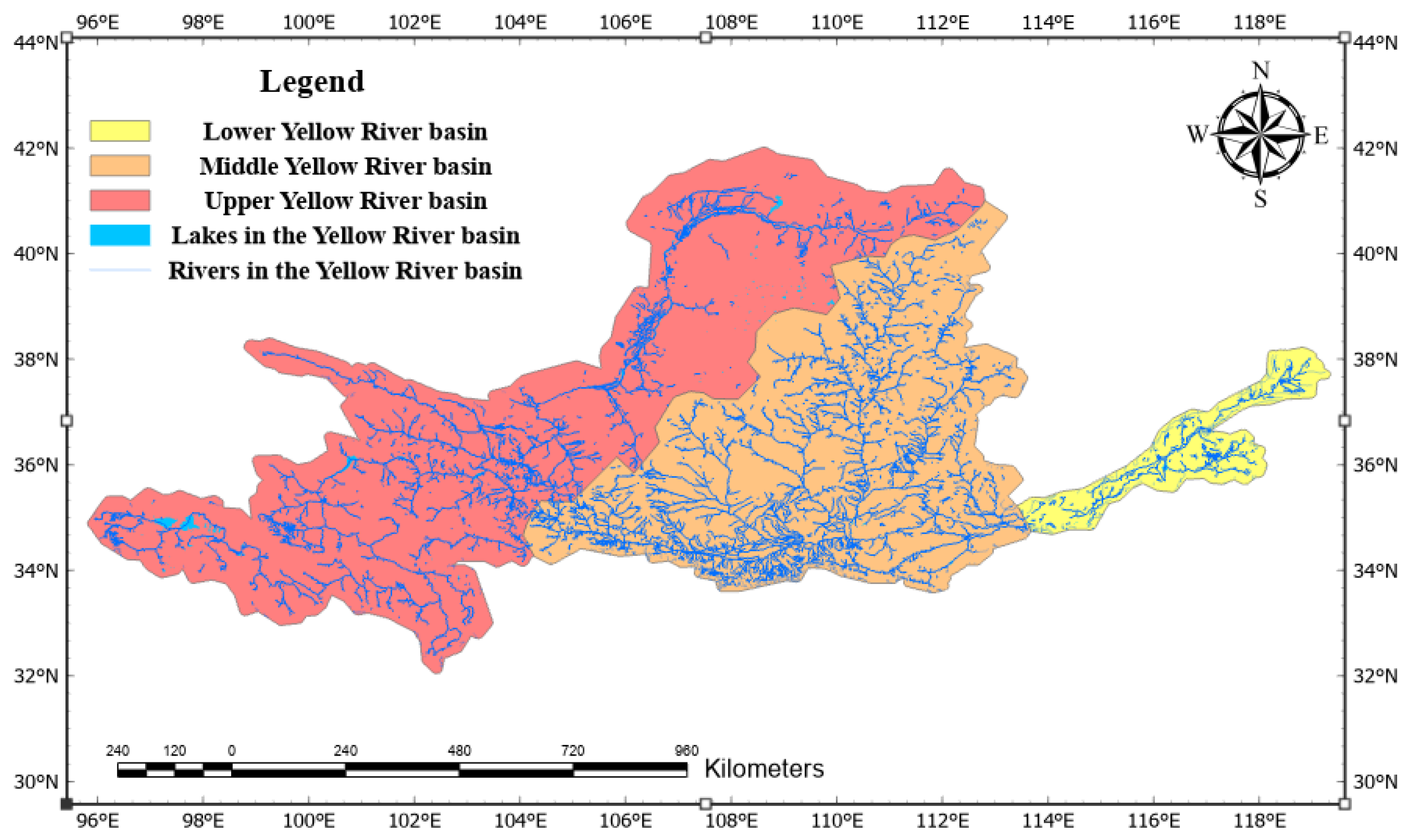
2.1. Overview of the Study Area
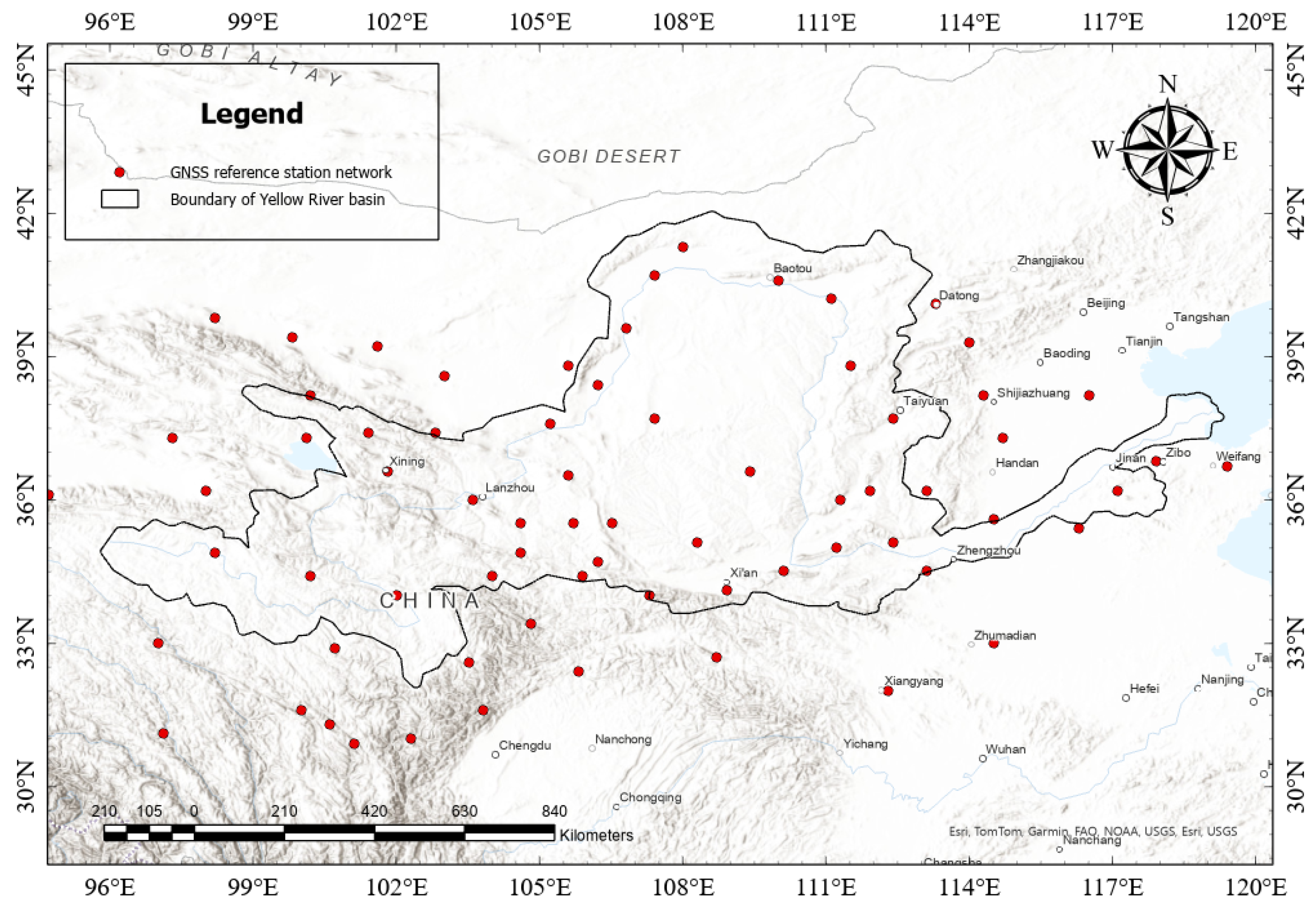
2.2. Selection of Experimental Data
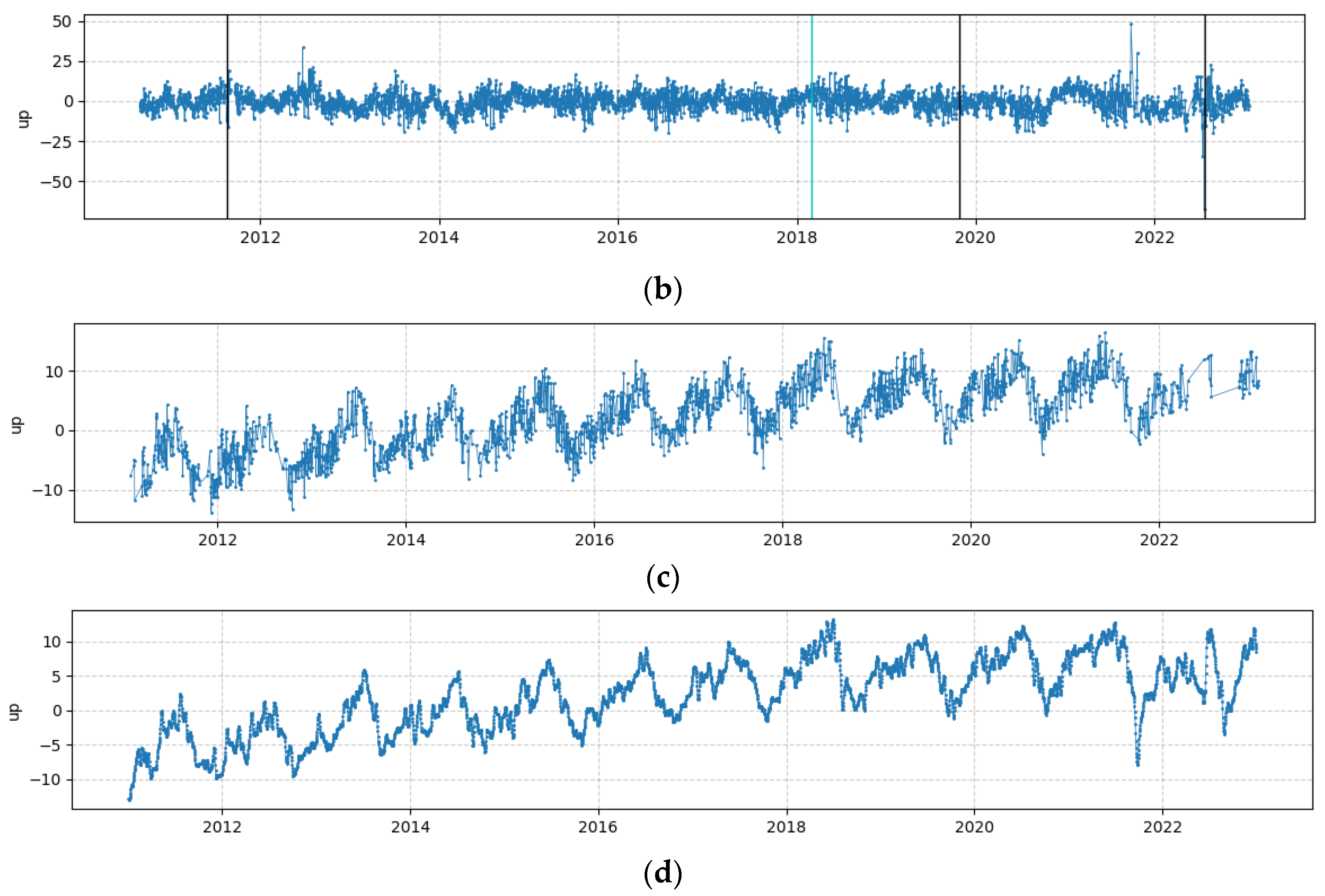
2.3. Preprocessing of Experimental Data
3. Methods
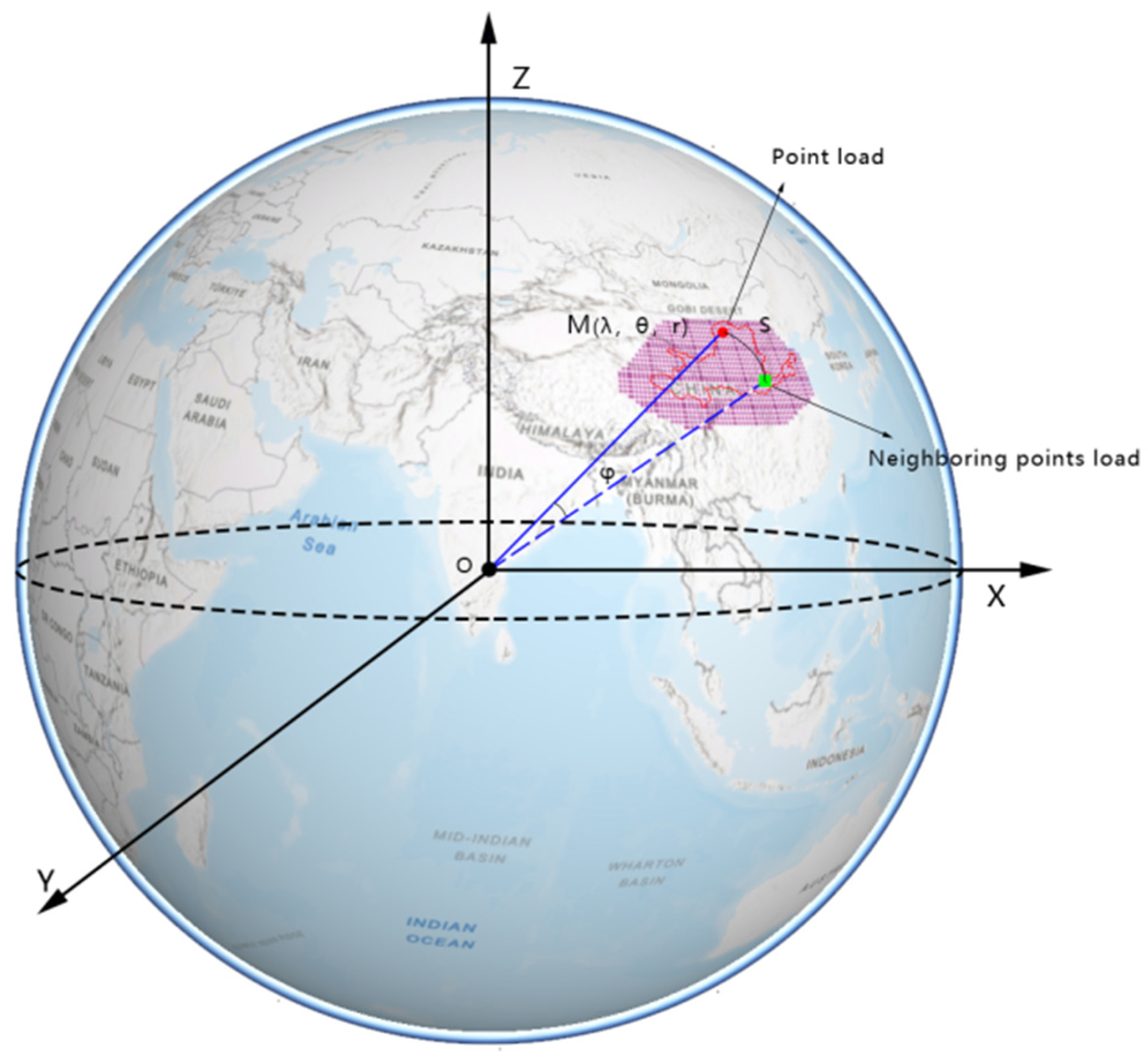
3.1. Load Green’s Function Theory
3.2. Method for Solving for the Equivalent Water Height
3.3. Key Issues in Inverting the EWH
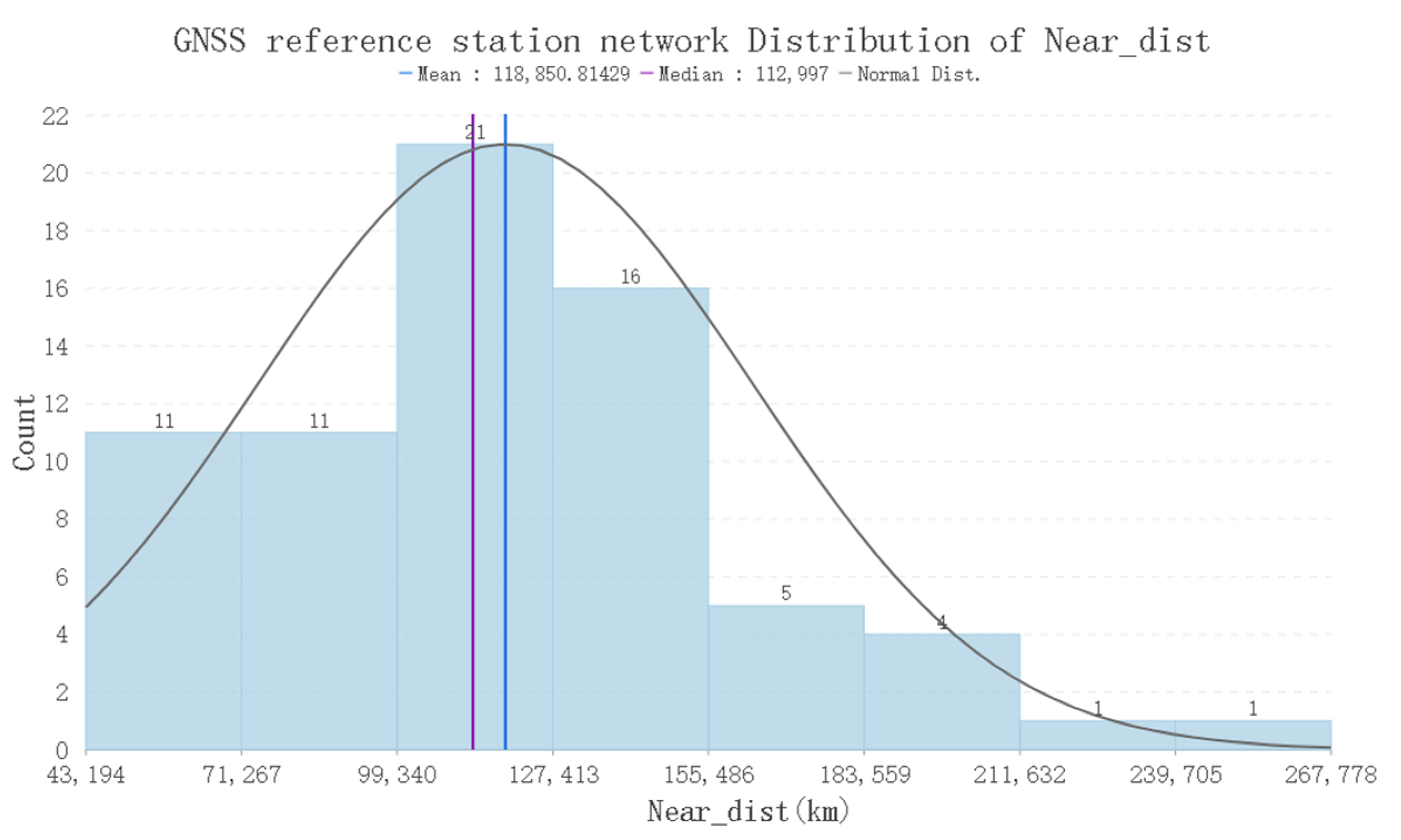
3.3.1. Determination of Green’s Function Design Matrix
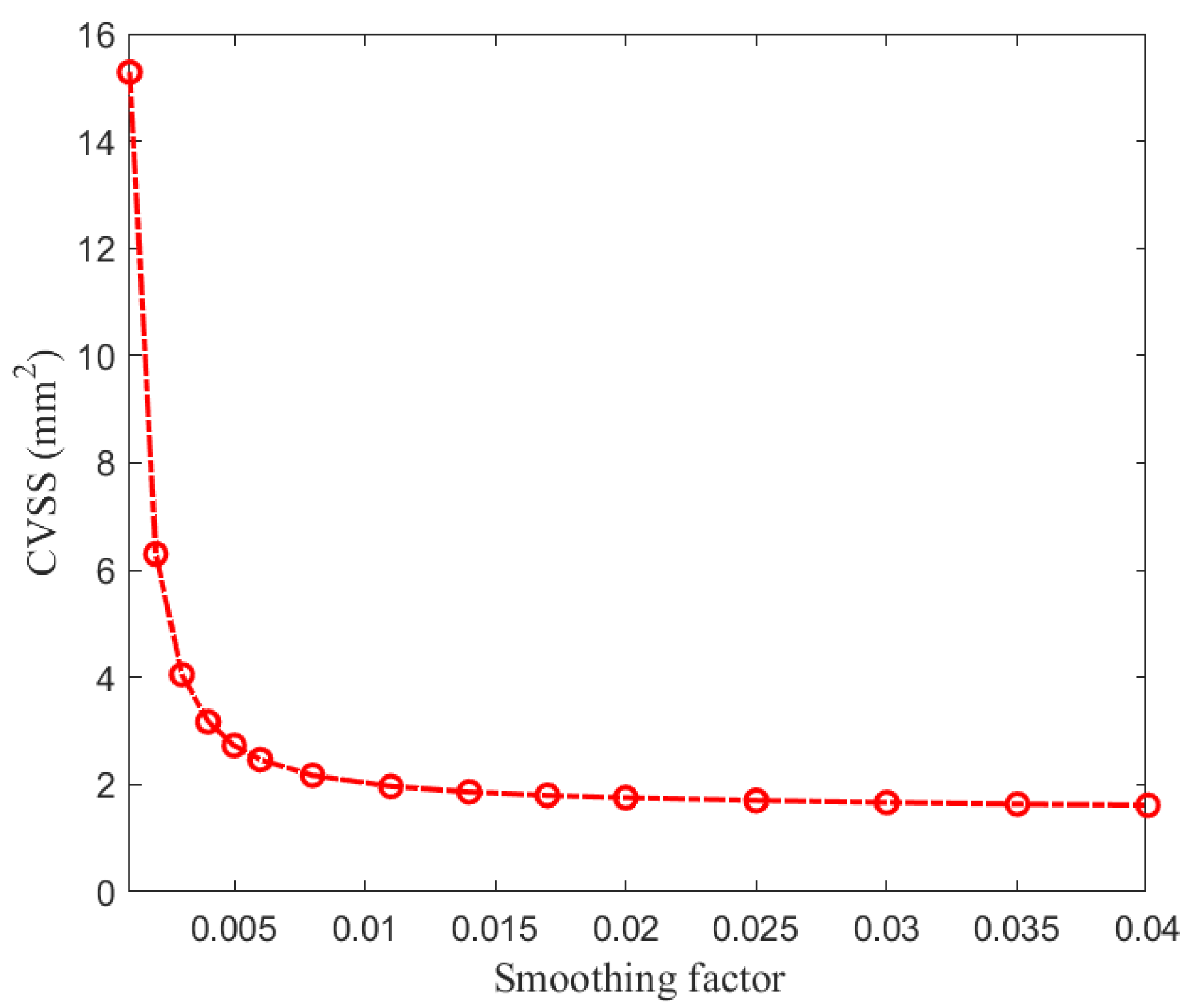
3.3.2. Determination of Regularized Smoothing Matrix and Smoothing Factor
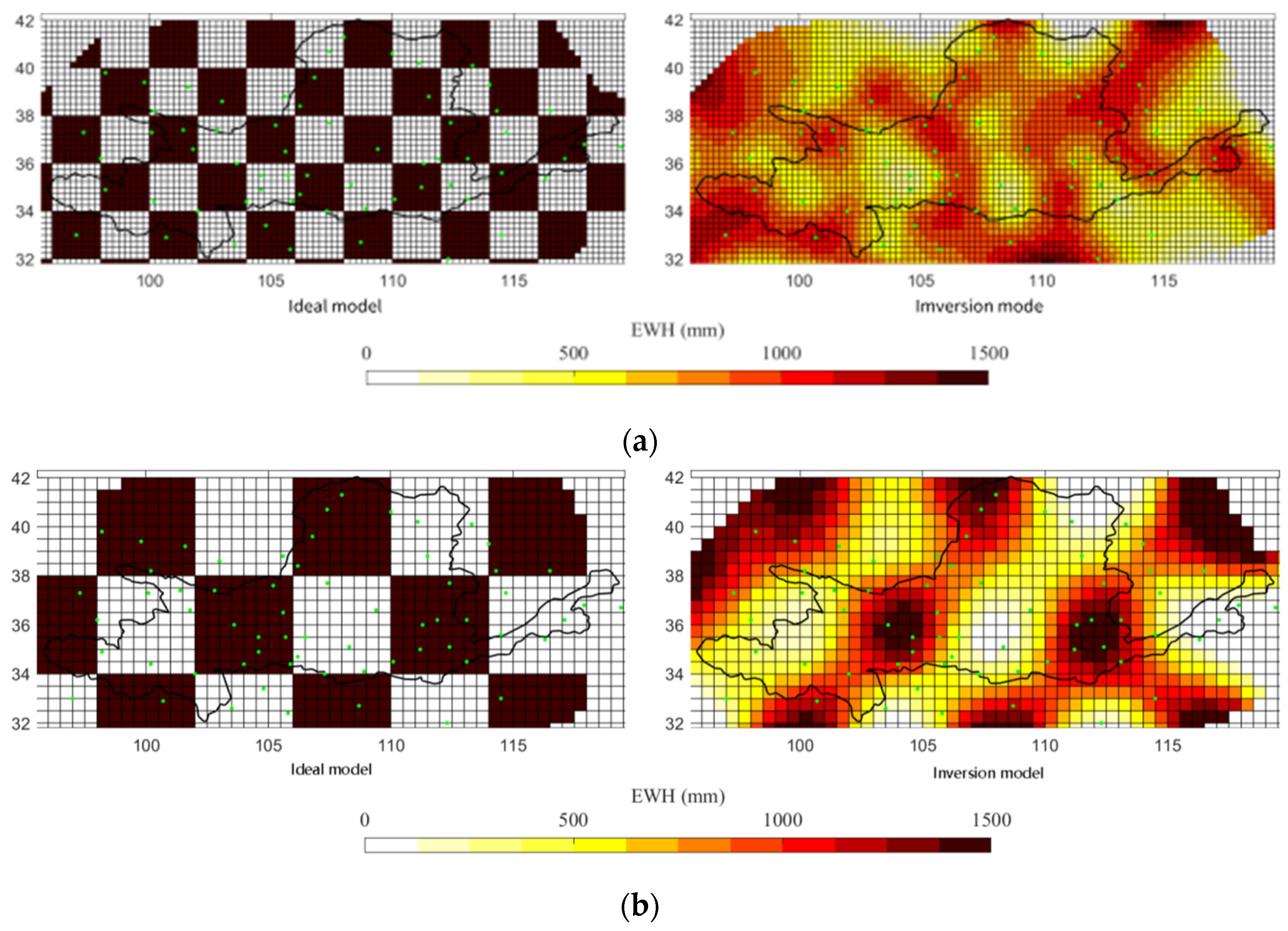
3.3.3. Determination of EWH Resolution
3.4. Methods of Verifying the Inversion Results
4. Results
4.1. Experiments on Key Issues of Inversion
4.1.1. Determination of Vertical Displacement Response Coefficients of Load Green’s Function
4.1.2. Determination of Regularization Smoothing Matrix and Smoothing Factor
4.1.3. Determination of EWH Resolution
4.2. Verification of Inversion Results
4.2.1. PCC Correlation Verification
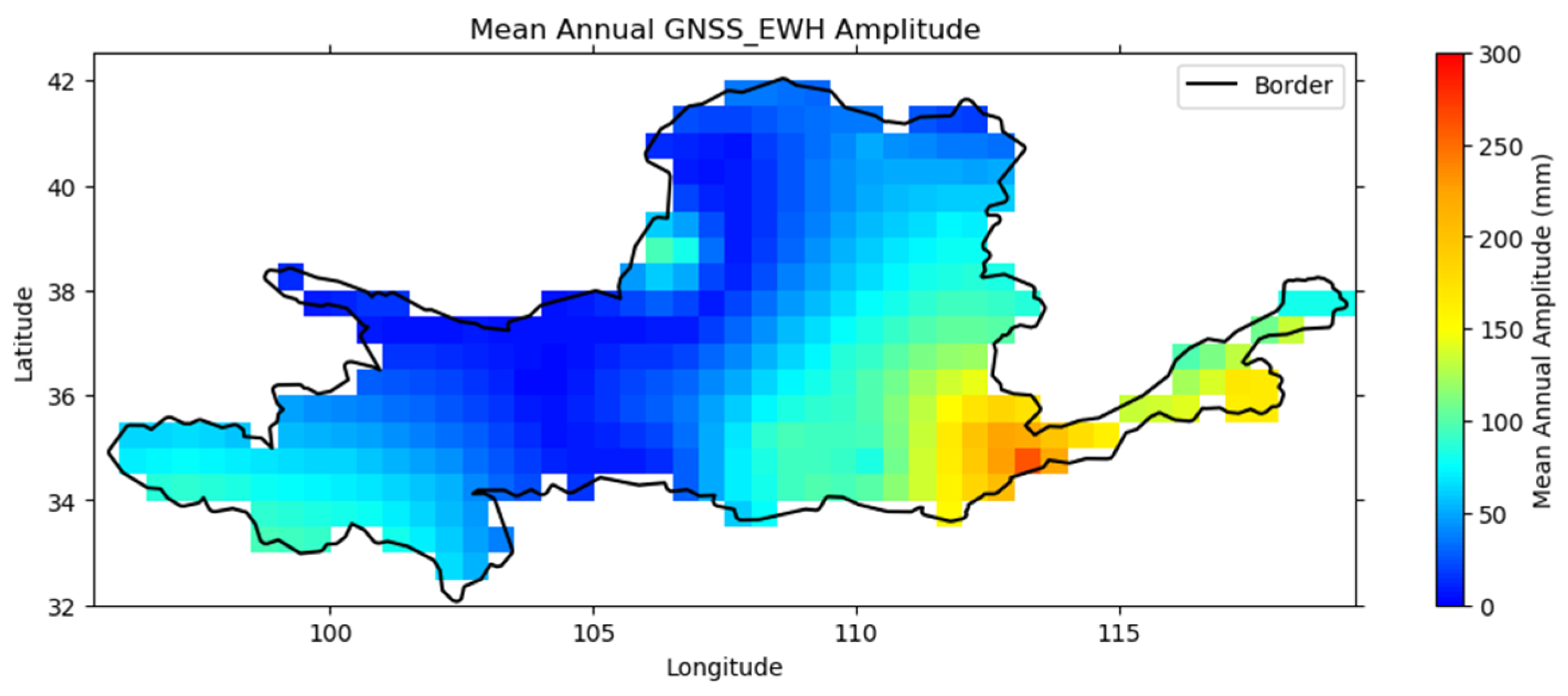
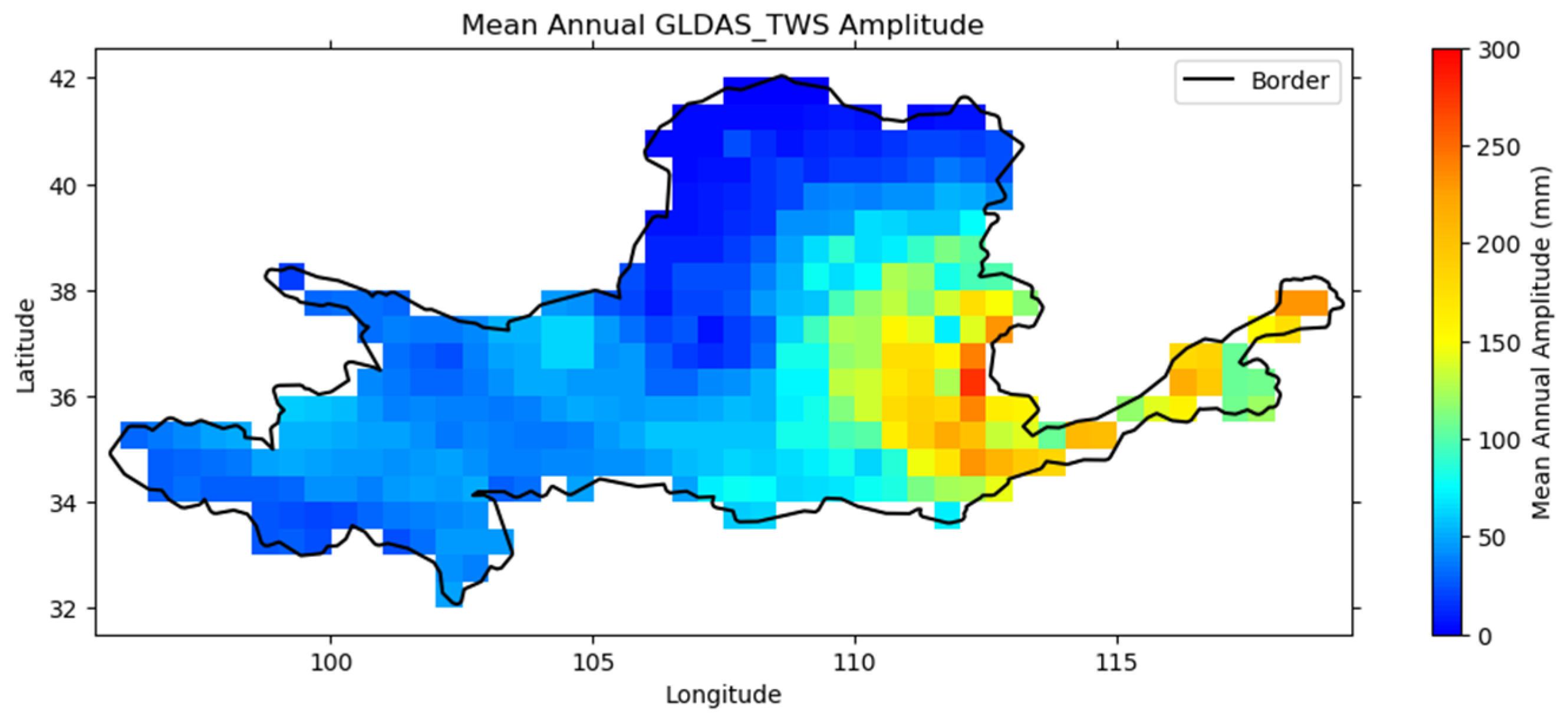
4.2.2. Verification of Spatial Distribution Characteristics of the GNSS_EWH
- (1)
- Verification of spatial distribution of correlation
- (2)
- Verification of Spatial Distribution Characteristics of Amplitudes
- (3)
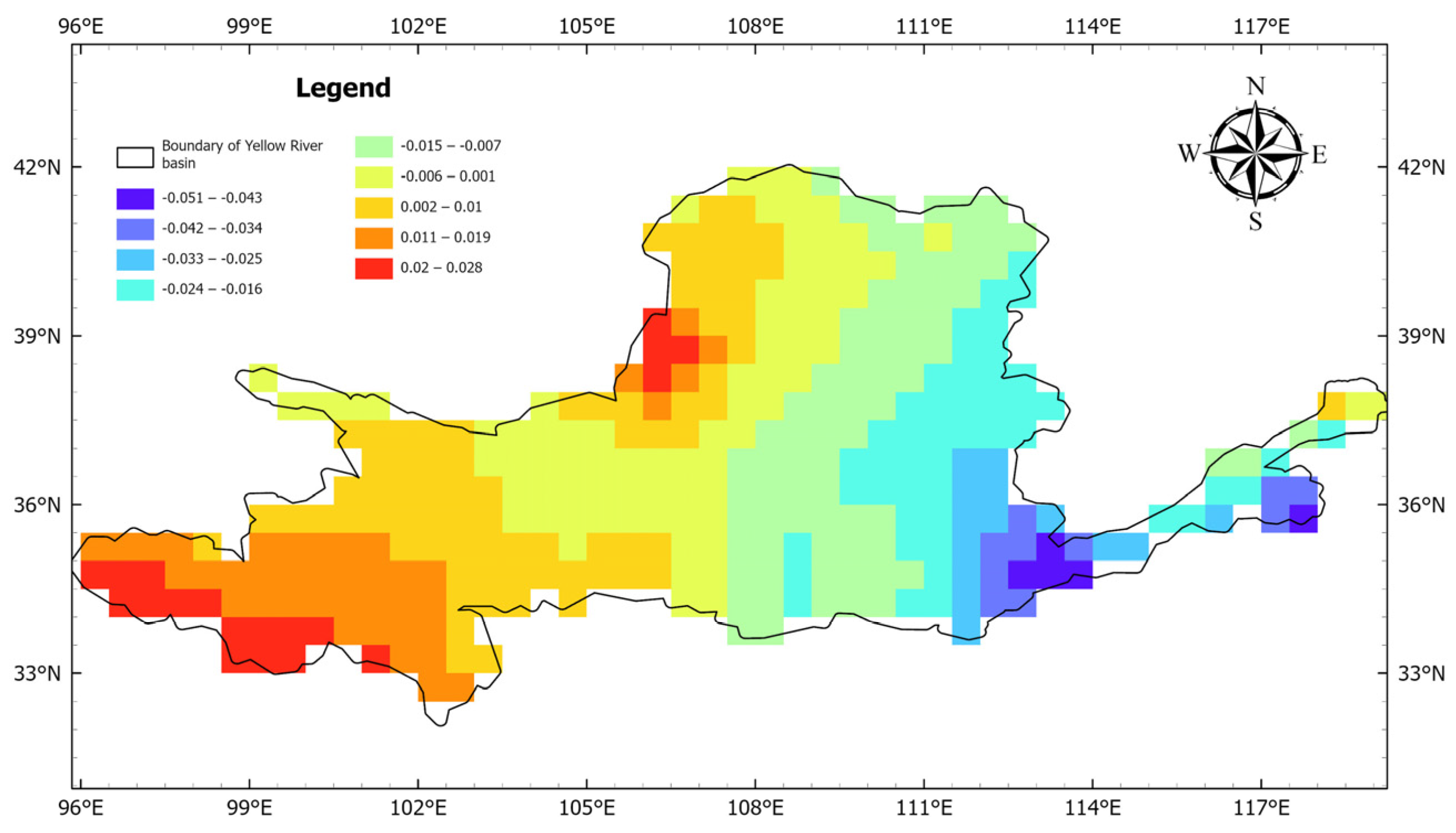
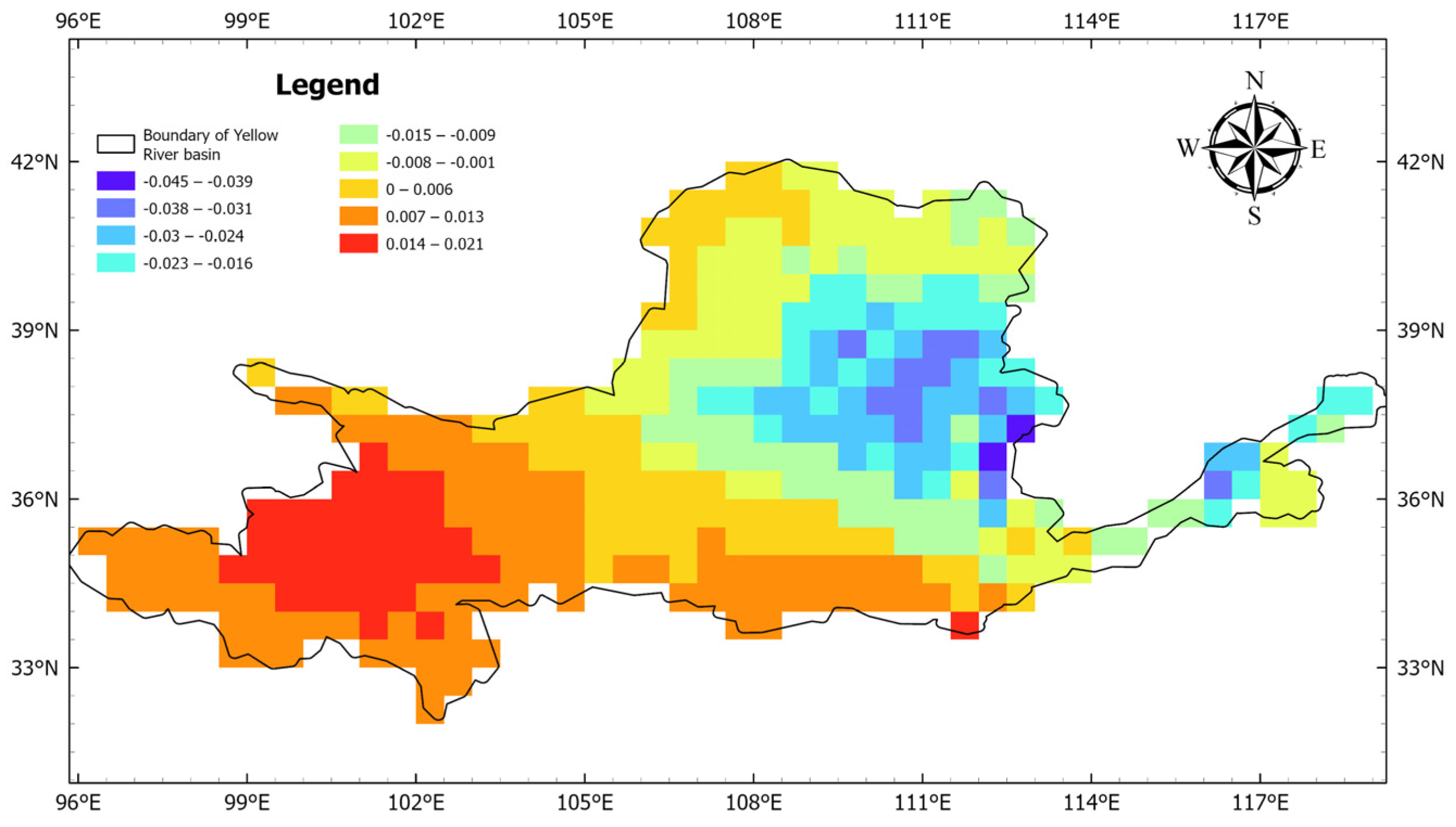
- Verification of Spatial Distribution Characteristics of the Rate of Change
5. Discussion
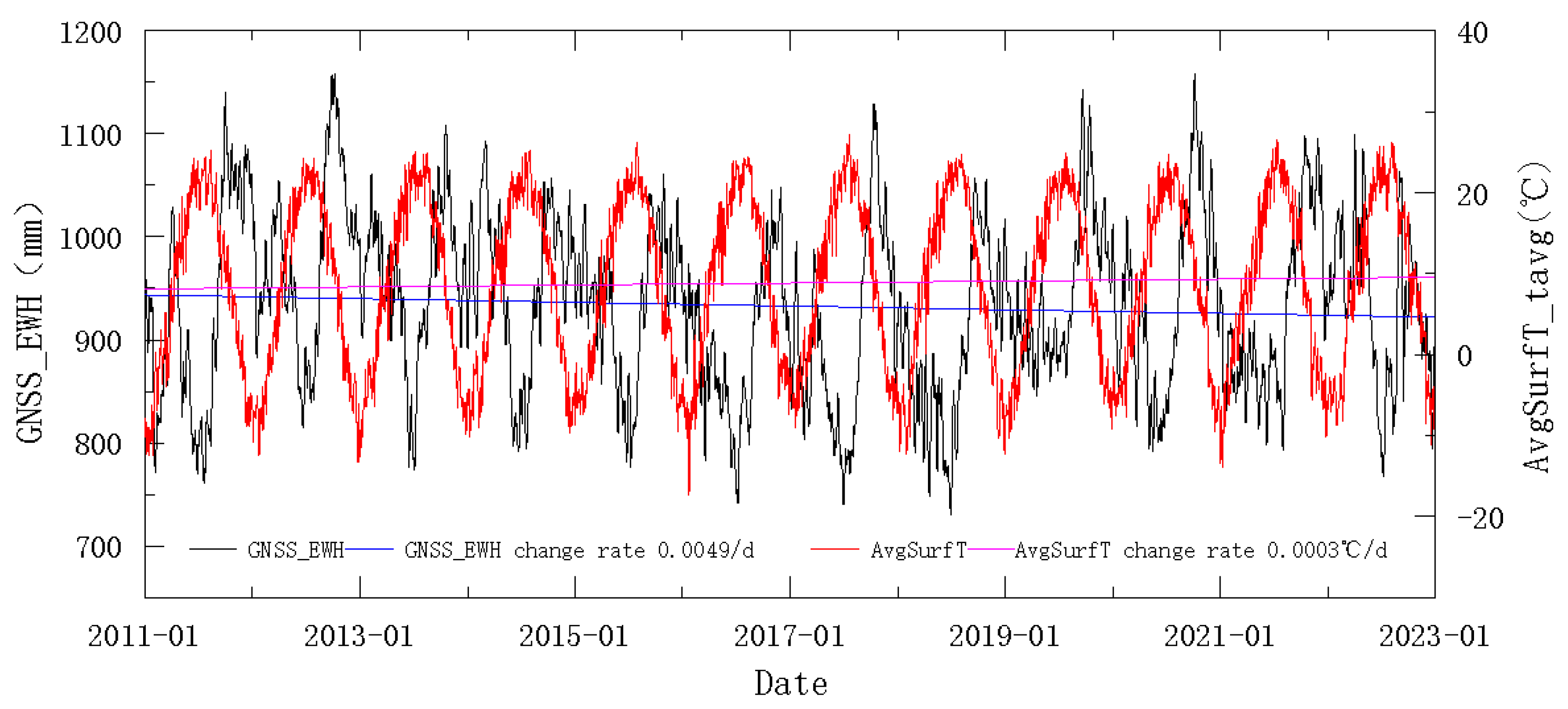
5.1. Trends and Periodicity Analysis of Water Storage Changes in the Yellow River Basin
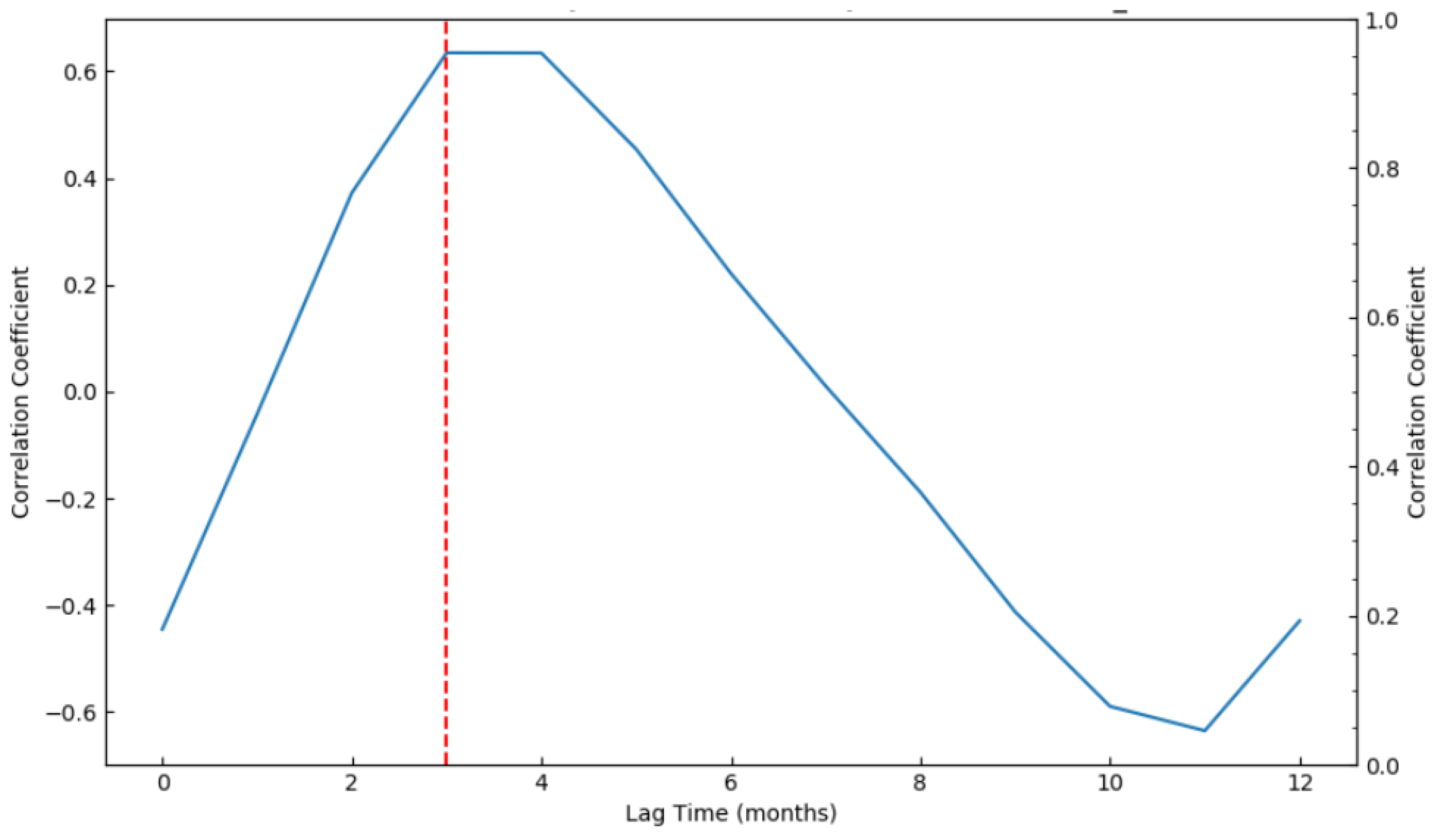
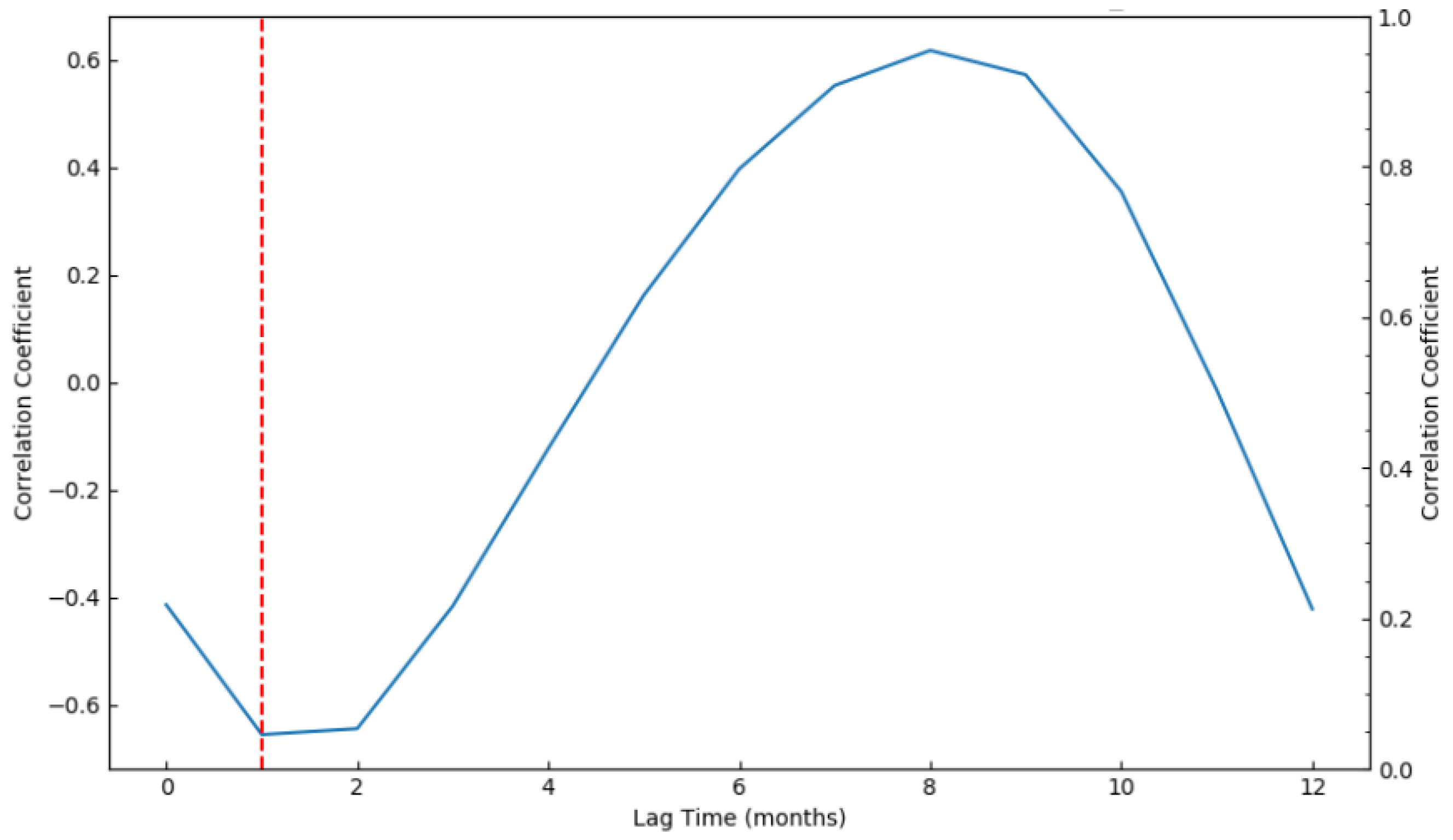
5.2. Attribution Analysis of Water Storage Changes in the Yellow River Basin
6. Conclusions
- (1)
- In the Yellow River Basin, where GNSS stations are unevenly distributed, the proposed method can effectively derive daily water storage products with a spatial resolution of 0.5°. The inverse distance weighted smoothing method designed in this study takes into account the density of the GNSS stations near the grid points and the distance between the grid points and the GNSS stations, and it adjusts the smoothing factor to emphasize the influences of near-field signals on far-field signals. This method enabled the inversion of the water storage changes in the Yellow River Basin during the past 12 years using vertical displacement data from the unevenly distributed GNSS stations. Experimental validation confirmed the reliability of the results.
- (2)
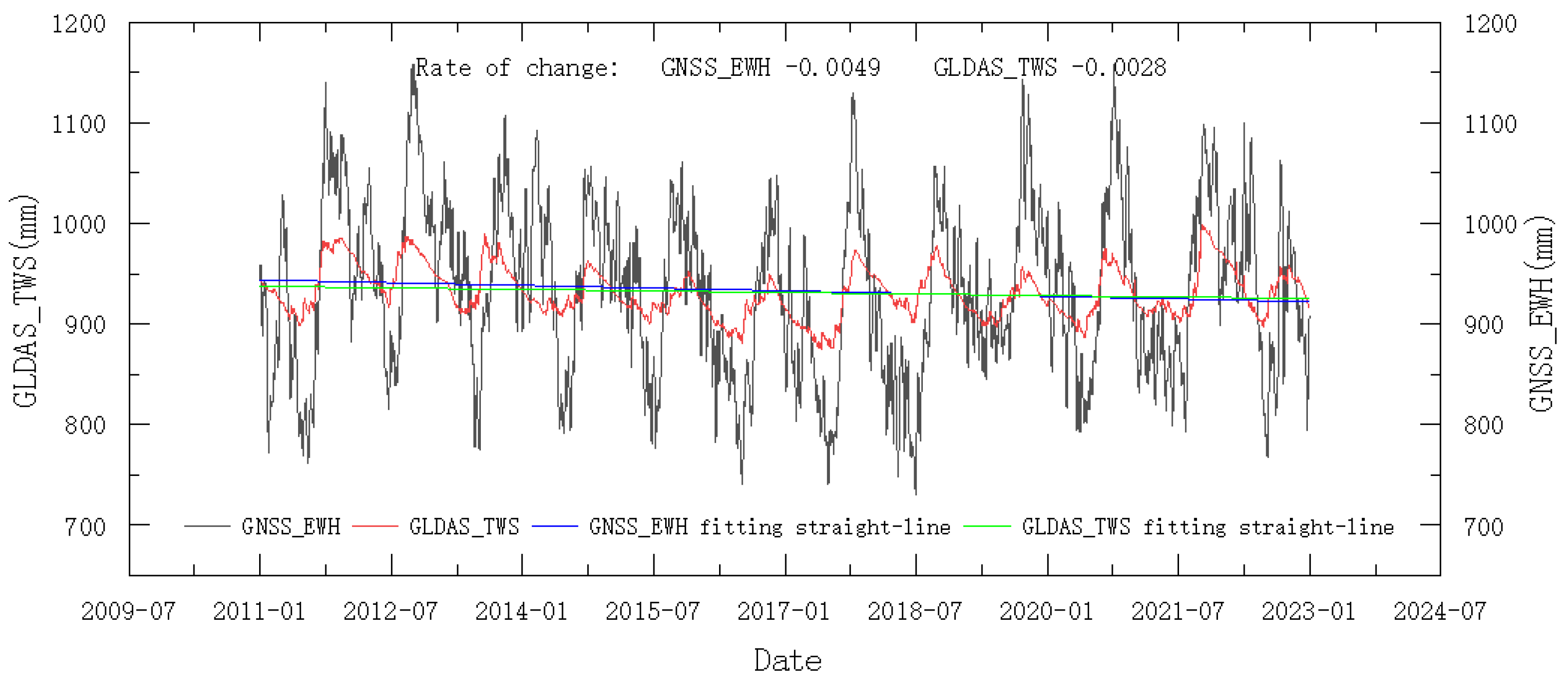
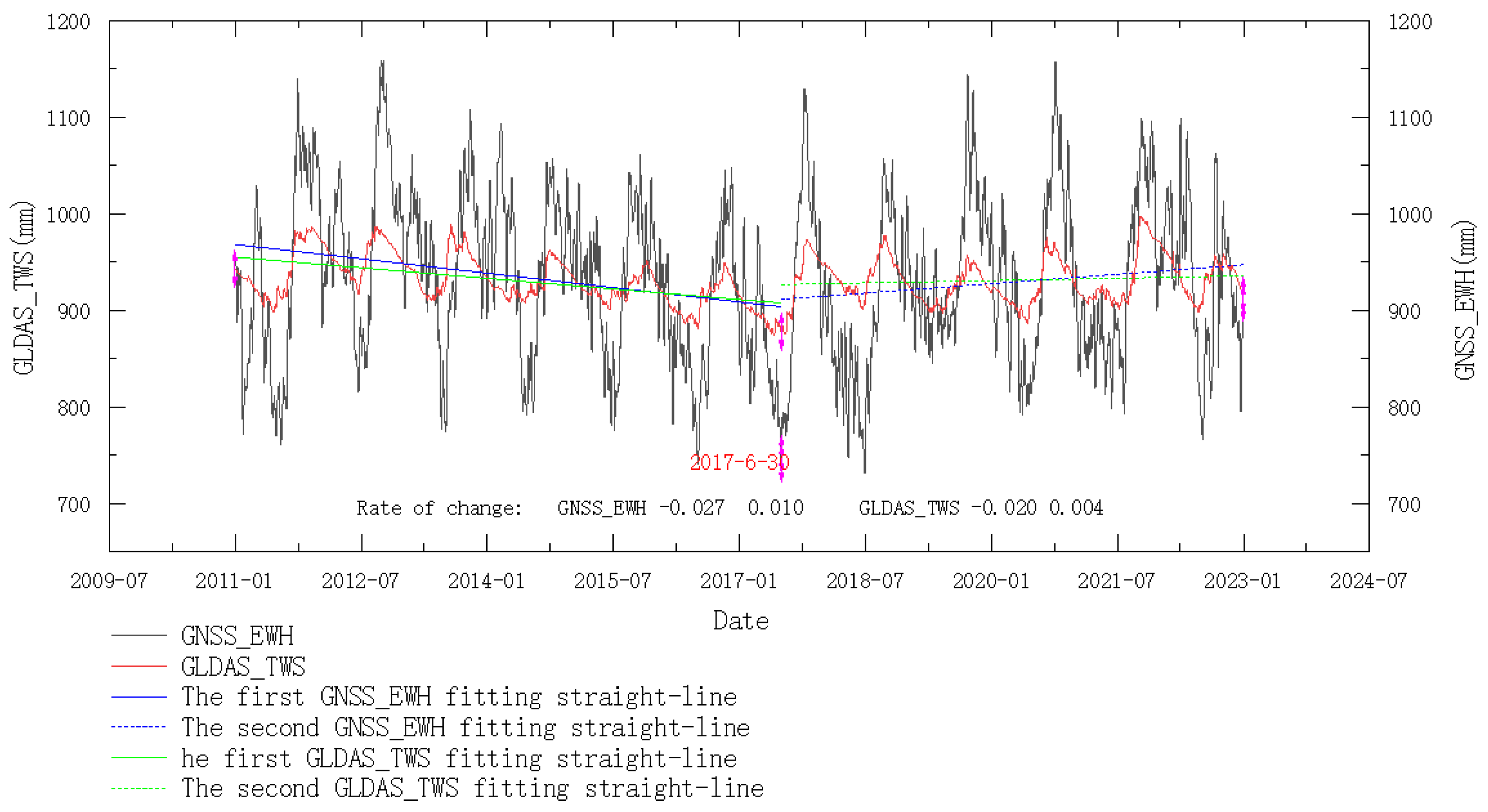
- Compared with water storage products derived from GRACE, the spatial resolution of the water storage products for the Yellow River Basin estimated in this study did not improve, but the temporal resolution was significantly improved from monthly to daily. The analysis of the water storage products estimated in this study revealed that the TWS in the Yellow River Basin exhibited an overall decreasing trend, and it was correlated with the changes in rainfall, evapotranspiration, and surface temperature. The trend analysis of the GNSS_EWH revealed that the water storage in the Yellow River Basin decreased at a rate of 0.027 mm/day from 2011 to 2017 and increased at a rate of 0.010 mm/day from 2017 to 2022, with an overall rate of decrease of 0.0049 mm/day during the last 12 years. Moreover, the map of the annual values in the Yellow River Basin showed that the water storage decreased in the lower-middle and lower reaches and increased in the upper and upper-middle reaches over the past 12 years. The correlation analysis between the estimated water storage in the Yellow River Basin and the rainfall, evapotranspiration, and surface temperature data from GLDAS indicates that there were strong correlations, suggesting that these factors were significant drivers of the water storage changes in the Yellow River Basin.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Wang, Z.; Yang, H.; Zhao, Y. Study of the temporal and spatial patterns of drought in the Yellow River basin based on SPEI. Sci. China Earth Sci. 2018, 61, 317–331. [Google Scholar] [CrossRef]
- Shen, Y.; Yan, H.; Peng, P.; Feng, W.; Zhang, Z.; Song, Y.; Bai, X. Boundary-Included Enhanced Water Storage Changes Inferred by GPS in the Pacific Rim of the Western United States. Remote Sens. 2020, 12, 2429. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J. Geophys. Res. Solid Earth 2009, 114, B05404. [Google Scholar] [CrossRef]
- Chen, J.; Wilson, C.; Tapley, B.; Scanlon, B.; Güntner, A. Long-term groundwater storage change in Victoria, Australia from satellite gravity and in situ observations. Glob. Planet. Chang. 2016, 139, 56–65. [Google Scholar] [CrossRef]
- Ni, S.N.; Chen, J.L.; Li, J.; Chen, C.; Liang, Q. Terrestrial Water Storage Change in the Yangtze and Yellow River Basins from GRACE Time-Variable Gravity Measurements. J. Geod. Geodyn. 2014, 34, 49–55. [Google Scholar]
- Ding, Y.; Huang, D.; Jiang, Z.; Luo, C.; Tang, W. The Periods of Terrestrial Water Storage Changes of China’s Four Basins Derived from GRACE. J. Geod. Geodyn. 2018, 38, 603–608. [Google Scholar]
- Xie, J.; Xu, Y.-P.; Wang, Y.; Gu, H.; Wang, F.; Pan, S. Influences of climatic variability and human activities on terrestrial water storage variations across the Yellow River basin in the recent decade. J. Hydrol. 2019, 579, 124218. [Google Scholar] [CrossRef]
- Zhao, Y.; Shen, Q.; Feng, W.; Wang, H.; Gao, F.; Lai, W.; Liu, T. Changes and Spatio-Temporal Characteristics of Terrestrial Water Storage Variation in China’s Seven Main River Basins during 2002–2018. J. Geod. Geodyn. 2022, 8, 796–801. [Google Scholar]
- Xie, X.; Xing, M.; Wang, L.; Xu, G.; Wen, H. Using GRACE/GRACE-FO Gravity Satellite to Detect the Water Storage Capacity and the Possibility of Extreme Climate in the Yellow River Basin. J. Geod. Geodyn. 2022, 42, 1269–1275. [Google Scholar]
- Gyawali, B.; Ahmed, M.; Murgulet, D.; Wiese, D.N. Filling Temporal Gaps within and between GRACE and GRACE-FO Terrestrial Water Storage Records: An Innovative Approach. Remote Sens. 2022, 14, 1565. [Google Scholar] [CrossRef]
- Wu, X.; Heflin, M.B.; Ivins, E.R.; Argus, D.F.; Webb, F.H. Large-scale global surface mass variations inferred from GPS measurements of load-induced deformation. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Bevis, M.; Alsdorf, D.; Kendrick, E.; Fortes, L.P.; Forsberg, B.; Smalley, R.; Becker, J. Seasonal fluctuations in the mass of the Amazon River system and Earth’s elastic response. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Heki, K. Seasonal modulation of interseismic strain buildup in northeastern Japan driven by snow loads. Science 2001, 293, 89–92. [Google Scholar] [CrossRef] [PubMed]
- White, A.M.; Gardner, W.P.; Borsa, A.A.; Argus, D.F.; Martens, H.R. A Review of GNSS/GPS in Hydrogeodesy: Hydrologic Loading Applications and Their Implications for Water Resource Research. Water Resour. Res. 2022, 58, e2022WR032078. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.L. Climate-driven deformation of the solid Earth from GRACE and GPS. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Wahr, J.; Khan, S.A.; van Dam, T.; Liu, L.; van Angelen, J.H.; Broeke, M.R.v.D.; Meertens, C.M. The use of GPS horizontals for loading studies, with applications to northern California and southeast Greenland. J. Geophys. Res. Solid Earth 2013, 118, 1795–1806. [Google Scholar] [CrossRef]
- Argus, D.F.; Fu, Y.; Landerer, F.W. Seasonal variation in total water storage in California inferred from GPS observations of vertical land motion. Geophys. Res. Lett. 2014, 41, 1971–1980. [Google Scholar] [CrossRef]
- Heki, K. Dense GPS array as a new sensor of seasonal changes of surface loads. Geophys. Monogr. Ser. 2004, 150, 177–196. [Google Scholar] [CrossRef]
- Jiang, Z.; Hsu, Y.-J.; Yuan, L.; Huang, D. Monitoring time-varying terrestrial water storage changes using daily GNSS measurements in Yunnan, southwest China. Remote Sens Environ. 2021, 254, 112249. [Google Scholar] [CrossRef]
- Jiang, Z.; Hsu, Y.-J.; Yuan, L.; Feng, W.; Yang, X.; Tang, M. GNSS2TWS: An open-source MATLAB2021a-based tool for inferring daily terrestrial water storage changes using GNSS vertical data. GPS Solut. 2022, 26, 114. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Zhong, B. Review of Inverting GNSS Surface Deformations for Regional Terrestrial Water Storage Changes. Geomat. Inf. Sci. Wuhan. Univ. 2023, 48, 1724–1735. [Google Scholar]
- Zhong, B.; Li, X.; Chen, J.; Li, Q.; Liu, T. Surface Mass Variations from GPS and GRACE/GFO: A Case Study in Southwest China. Remote Sens. 2020, 12, 1835. [Google Scholar] [CrossRef]
- Enzminger, T.L.; Small, E.E.; Borsa, A.A. Accuracy of Snow Water Equivalent Estimated From GPS Vertical Displacements: A Synthetic Loading Case Study for Western U. S. Mountains. Water Resour. Res. 2018, 54, 581–599. [Google Scholar] [CrossRef]
- Ji, G.; Lai, Z.; Yan, D.; Wu, L.; Wang, Z. Spatiotemporal patterns of future meteorological drought in the Yellow River Basin based on SPEI under RCP scenarios. Int. J. Clim. Chang. Strateg. Manag. 2021, 14, 39–53. [Google Scholar] [CrossRef]
- Si, J.; Li, J.; Lu, S.; Qi, X.; Zhang, X.; Bao, W.; Zhang, X.; Zhou, S.; Jin, C.; Qi, L.; et al. Effects of Climate Change on Surface Runoff and Soil Moisture in the Source Region of the Yellow River. Water 2023, 15, 2104. [Google Scholar] [CrossRef]
- Wang, L.; Shu, Z.; Wang, G.; Sun, Z.; Yan, H.; Bao, Z. Analysis of Future Meteorological Drought Changes in the Yellow River Basin under Climate Change. Water 2022, 14, 1896. [Google Scholar] [CrossRef]
- Zhao, Z.-K.; Tian, Y.-S.; Weng, X.-X.; Li, H.-W.; Sun, W.-Y. Temporal and spatial variation characteristics of surface water area in the Yellow River Basin from 1986 to 2021. Ying Yong Sheng Tai Xue Bao 2023, 34, 761–769. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Yan, H.; Yuan, S. L1 regularization for detecting offsets and trend change points in GNSS time series. GPS Solut. 2018, 22, 88. [Google Scholar] [CrossRef]
- Wu, D.; Yan, H.; Shen, Y. TSAnalyzer, a GNSS time series analysis software. GPS Solut. 2017, 21, 1389–1394. [Google Scholar] [CrossRef]
- Liu, N.; Dai, W.; Santerre, R.; Kuang, C. A MATLAB2021a-based Kriged Kalman Filter software for interpolating missing data in GNSS coordinate time series. GPS Solut. 2018, 22. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Q.; Werner, A.D.; Liu, X. GRACE-Based Hydrological Drought Evaluation of the Yangtze River Basin, China. J. Hydrometeorol. 2016, 17, 811–828. [Google Scholar] [CrossRef]
- Yin, P.; Mu, D.; Xu, T. Water Storage Variations Recovered from Global Navigation Satellite System Network Using Spatial Constraints: A Case Study of the Contiguous United States. Remote Sens. 2023, 15, 5753. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On the Solution of Ill-Posed Problems and the Method of Regularization. Russ. Acad. Sci. 1963, 151, 501–504. [Google Scholar]
- Li, C.; Zhong, P.; Jiang, Z.; Tang, M.; Yang, X.; You, X. The influence of different earth models on atmospheric load displacement modeling in Chinese continent. Chin. Geophys. 2023, 66, 973–985. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988; p. 83. [Google Scholar]



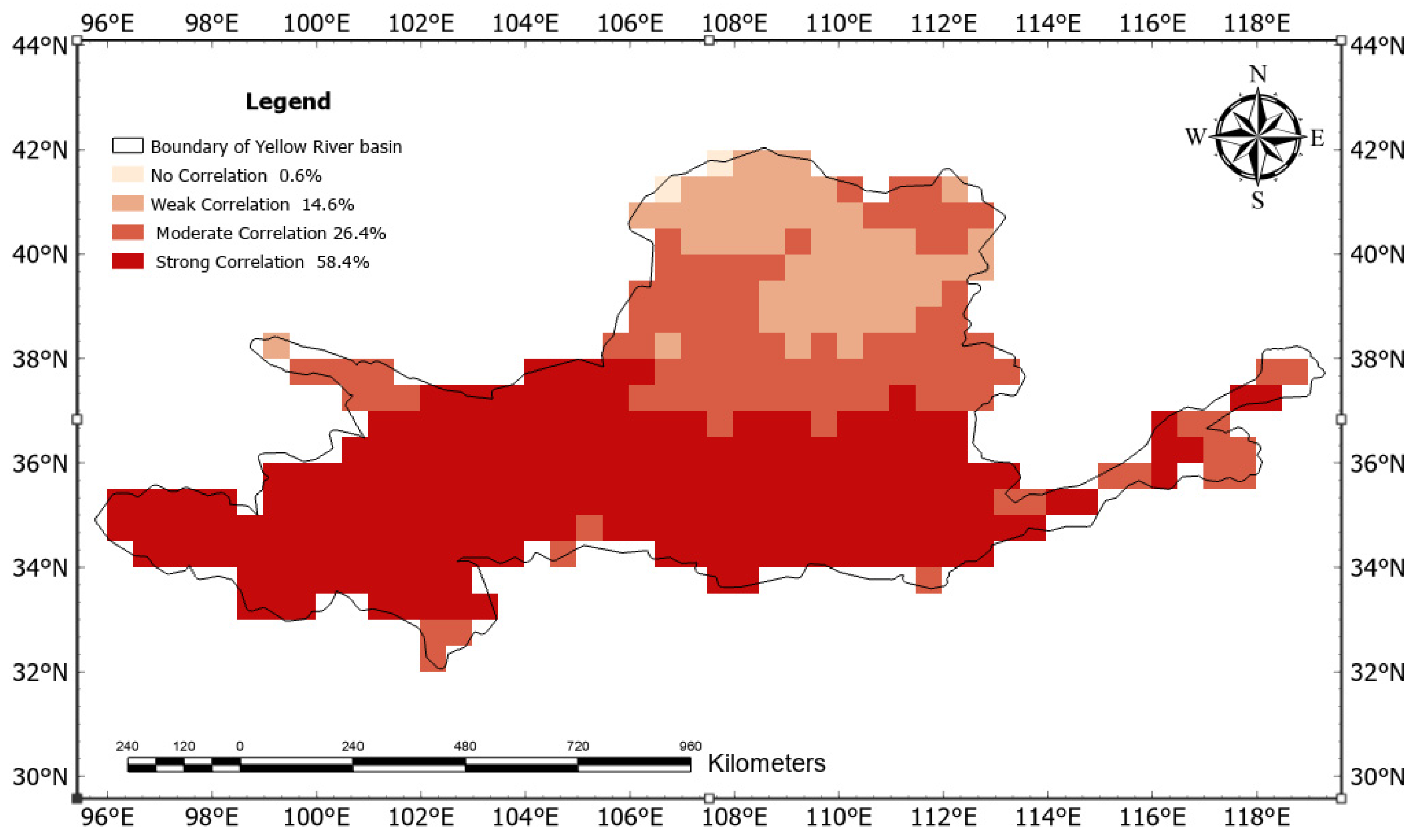
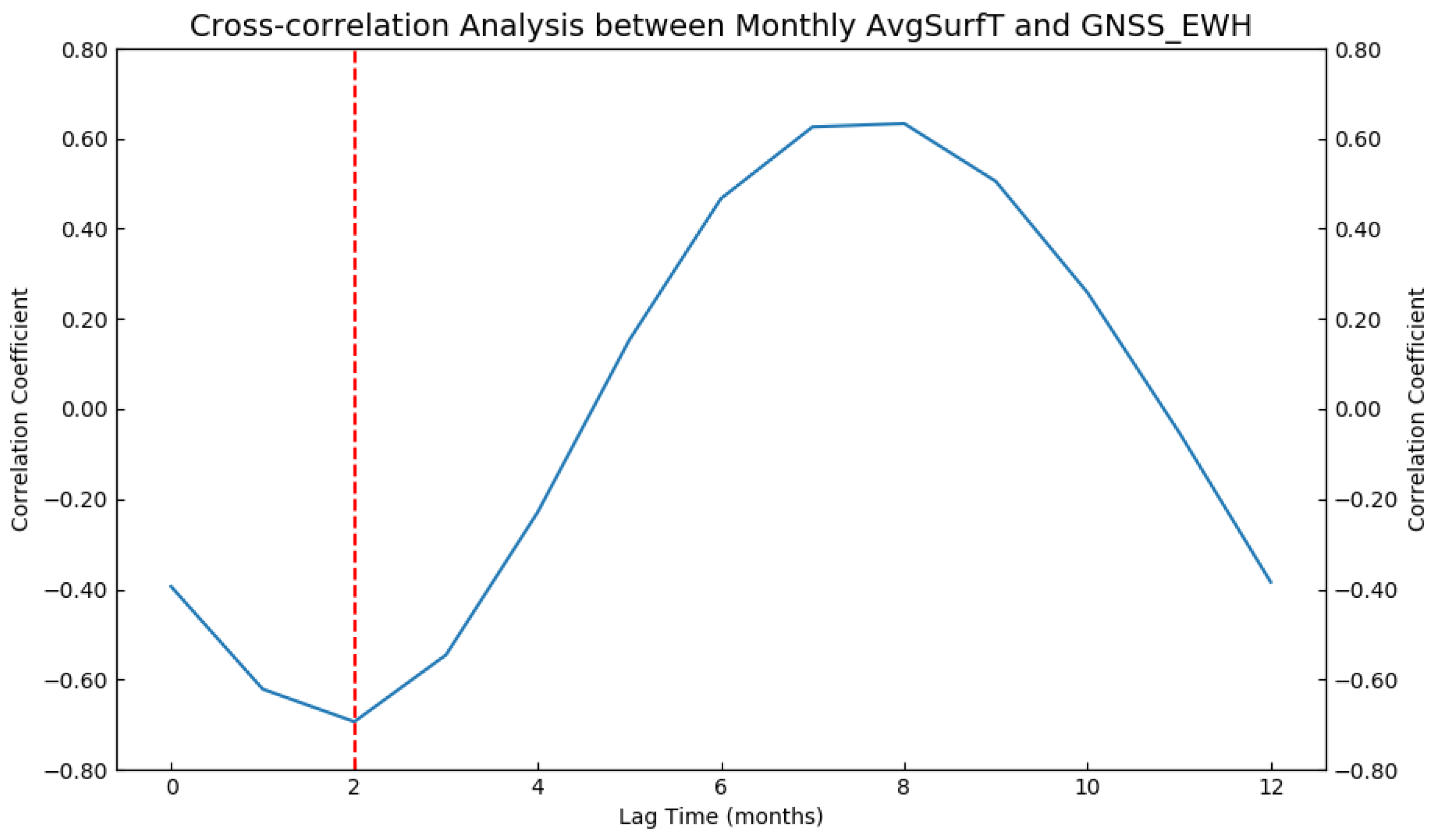
| Degree | No Correlation | Weak Correlation | Moderate Correlation | Strong Correlation |
|---|---|---|---|---|
| PCC | 0–0.1 | 0.1–0.3 | 0.3–0.5 | 0.5–1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Lu, X. Inversion Method for Monitoring Daily Variations in Terrestrial Water Storage Changes in the Yellow River Basin Based on GNSS. Water 2024, 16, 1919. https://doi.org/10.3390/w16131919
Zhang W, Lu X. Inversion Method for Monitoring Daily Variations in Terrestrial Water Storage Changes in the Yellow River Basin Based on GNSS. Water. 2024; 16(13):1919. https://doi.org/10.3390/w16131919
Chicago/Turabian StyleZhang, Wenqing, and Xiaoping Lu. 2024. "Inversion Method for Monitoring Daily Variations in Terrestrial Water Storage Changes in the Yellow River Basin Based on GNSS" Water 16, no. 13: 1919. https://doi.org/10.3390/w16131919
APA StyleZhang, W., & Lu, X. (2024). Inversion Method for Monitoring Daily Variations in Terrestrial Water Storage Changes in the Yellow River Basin Based on GNSS. Water, 16(13), 1919. https://doi.org/10.3390/w16131919




