Comprehensive Safety Analysis of Ultimate Bearing Capacity Considering Hydraulic Fracture for Guxian High RCC Gravity Dam
Abstract
1. Introduction
2. Methodology
2.1. Comparative Analysis Using the Three Design Criteria
2.2. The Ultimate Bearing Capacity Investigation
2.2.1. Numerical Modeling
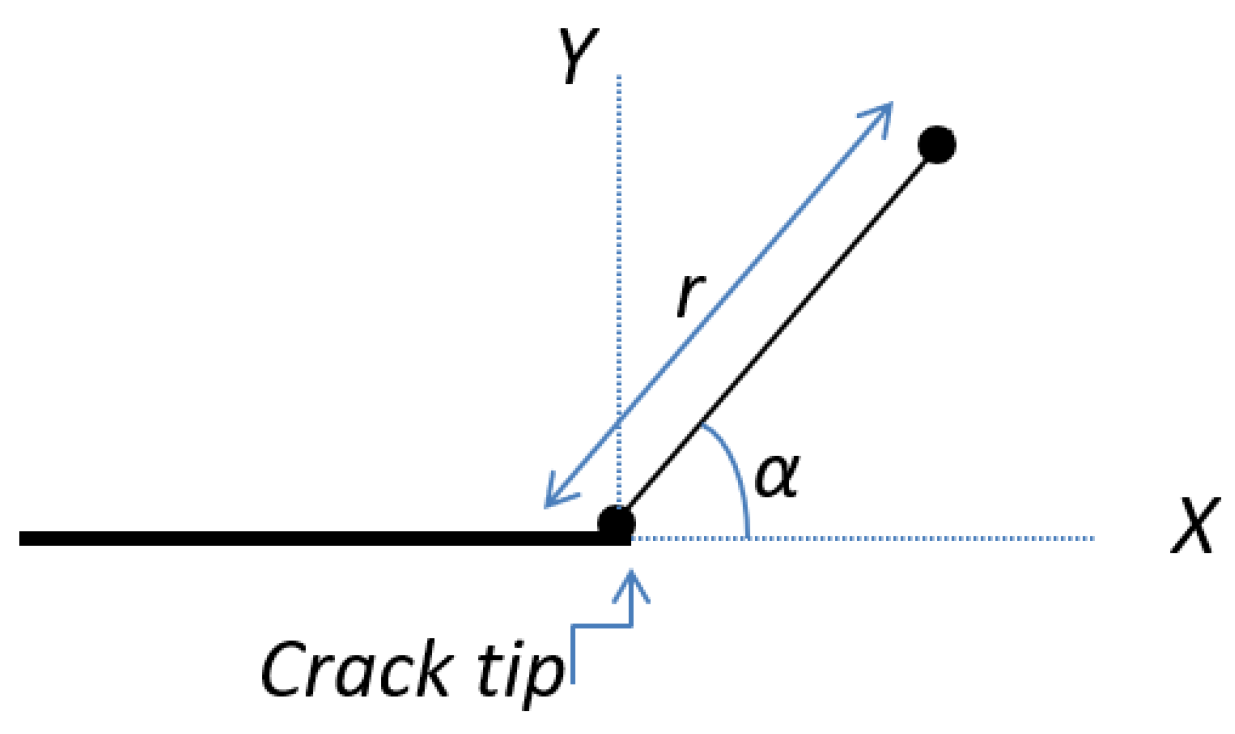
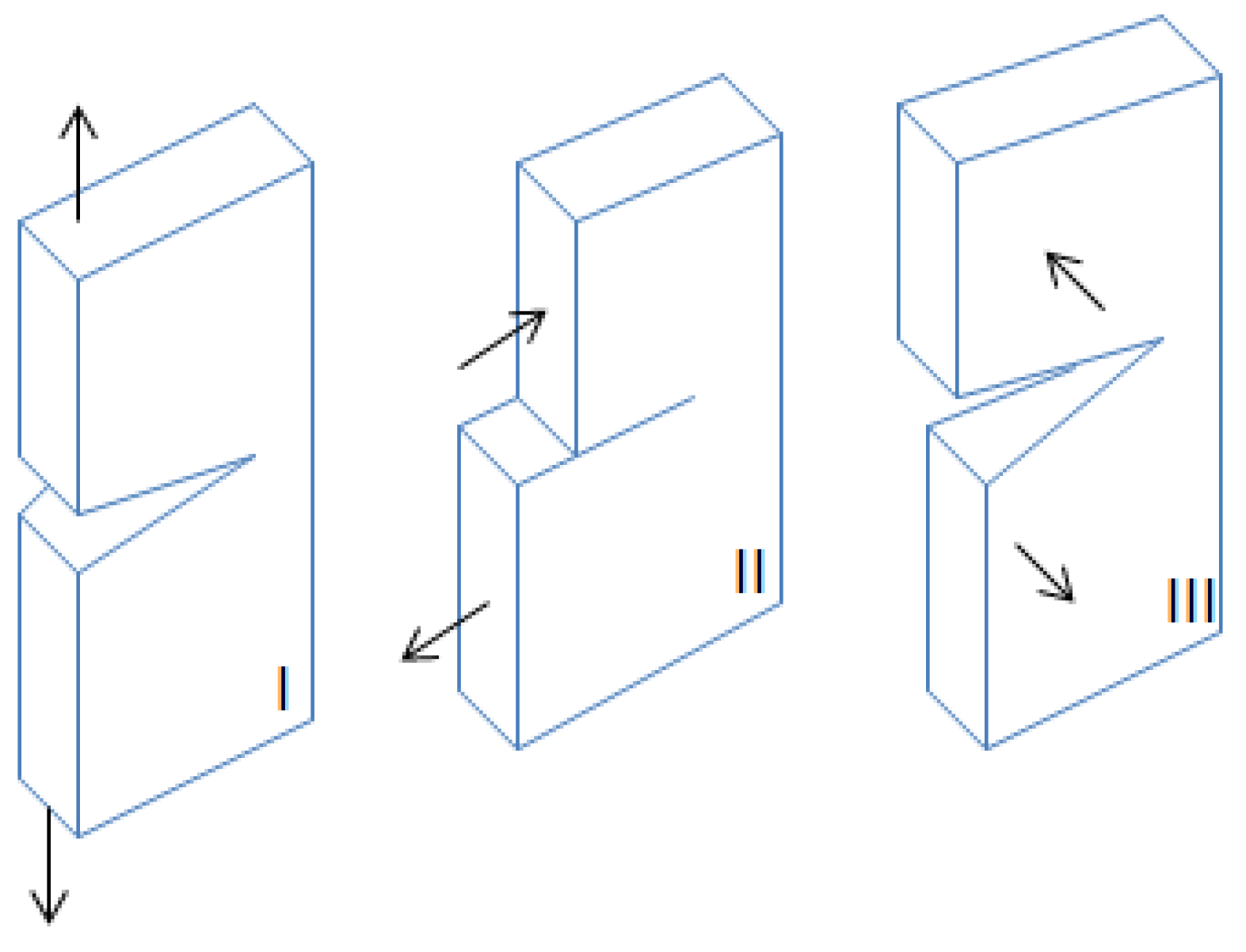
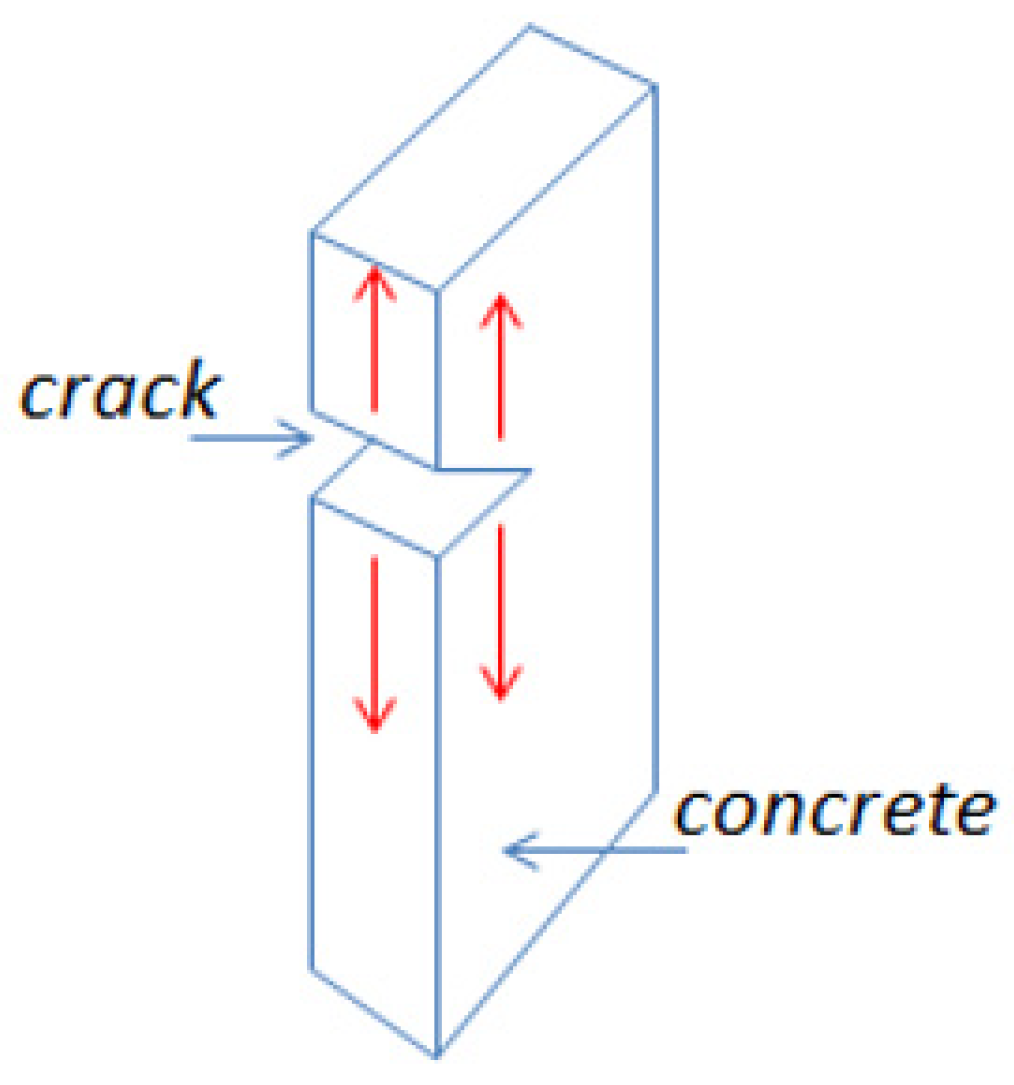
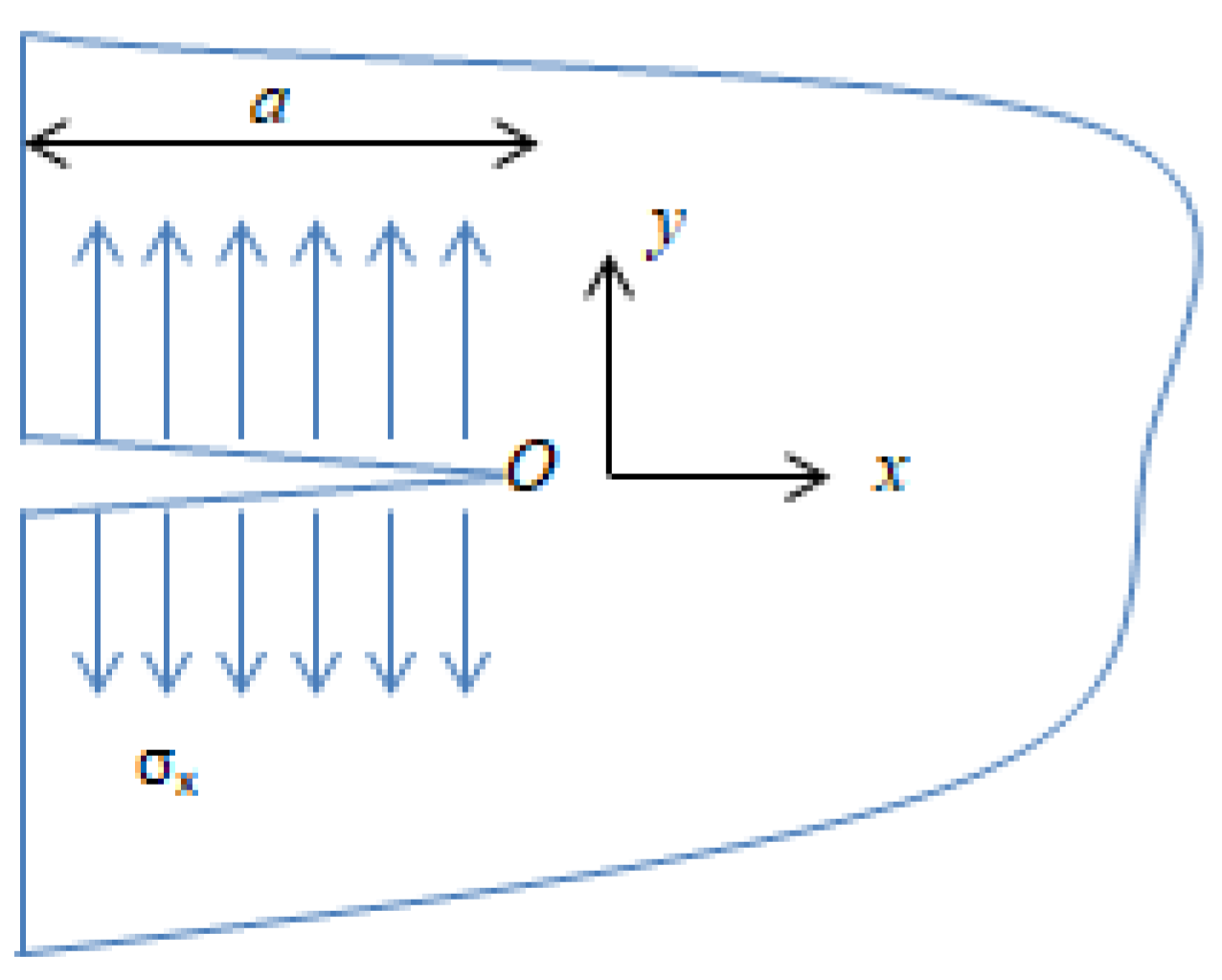
2.2.2. Mathematical Modeling [Fracture Mechanics Modeling]
3. Analysis Procedures
3.1. Comparative Study of Different Design Criteria
3.2. Assessing the Design Regulations’ Resistance to Hydraulic Fracture
3.3. Evaluation of the Ultimate Bearing Capacity
3.3.1. Numerical Modeling (FEM Model)
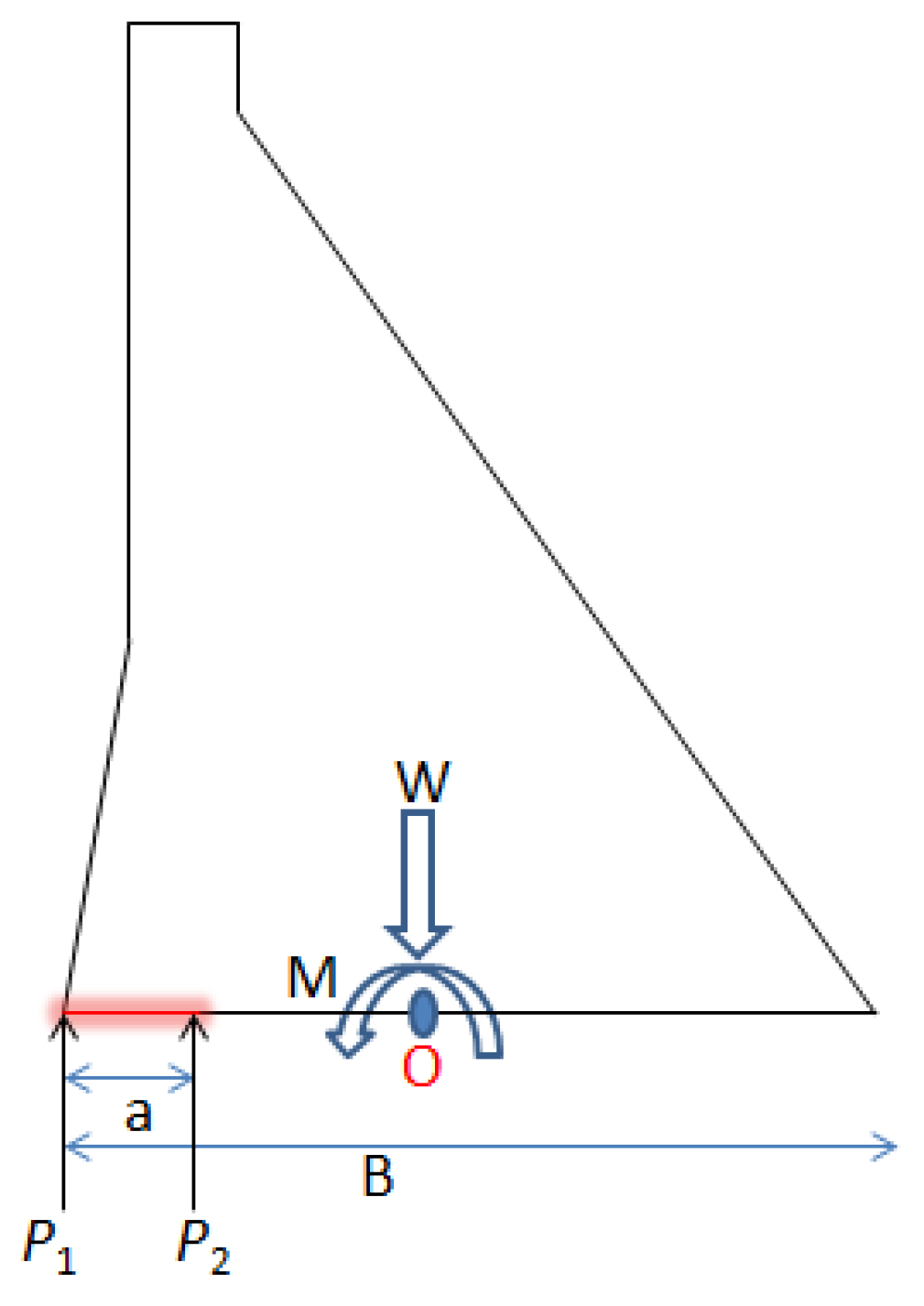
3.3.2. Hydraulic Fracture Evaluation Model (Mathematical Model)
4. Numerical Model Verification
5. Results and Discussion
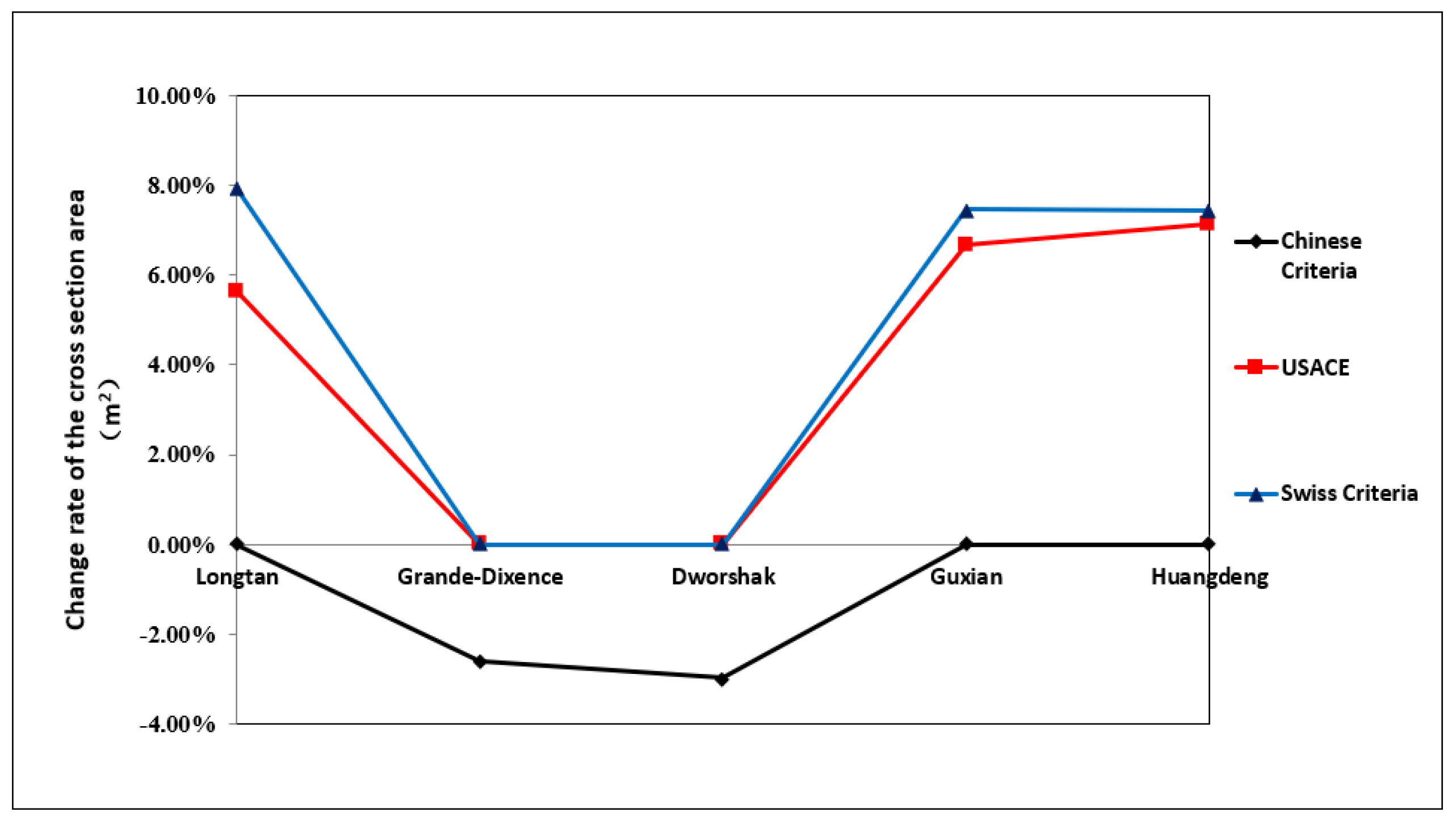
5.1. Comparative Study of Different Design Criteria
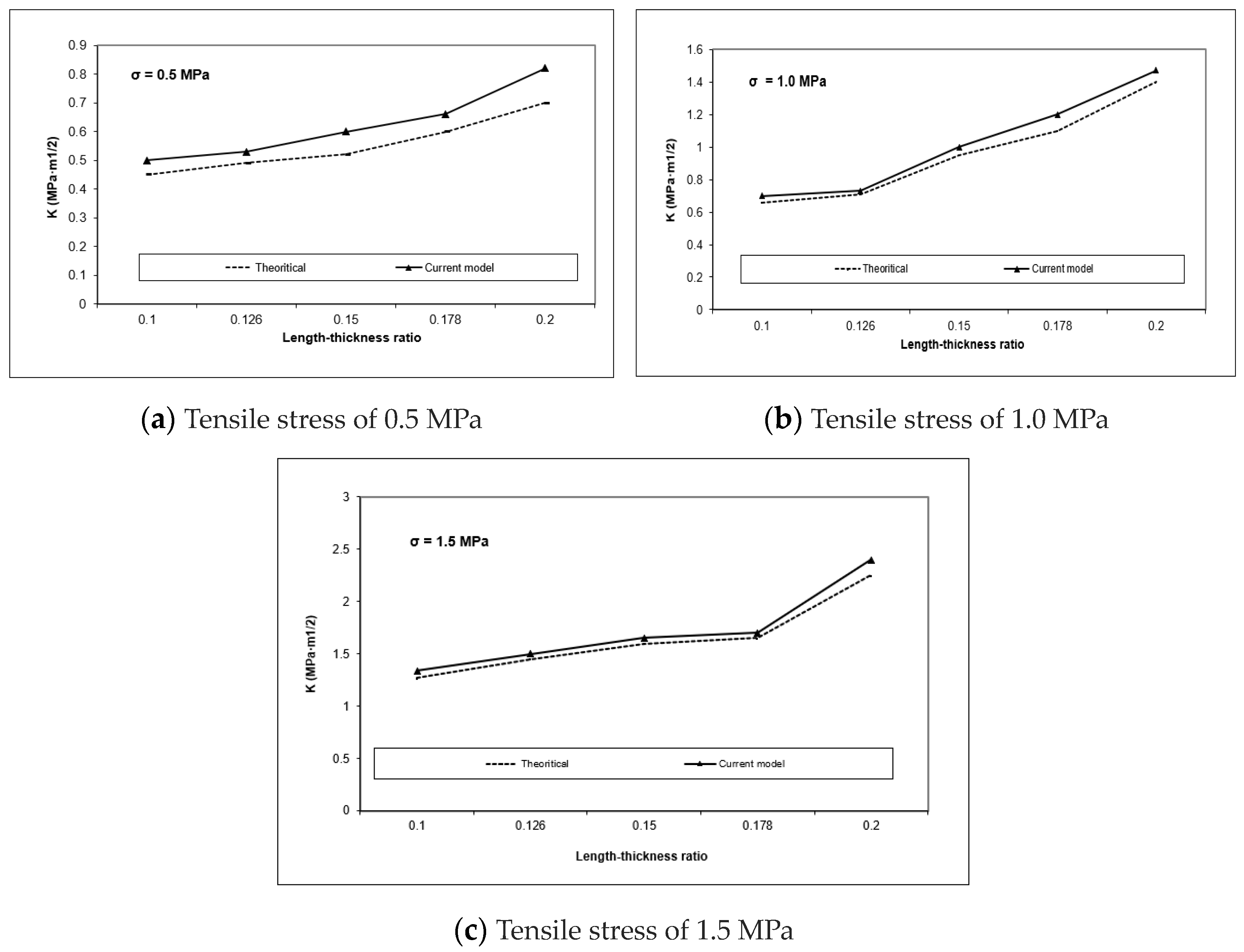
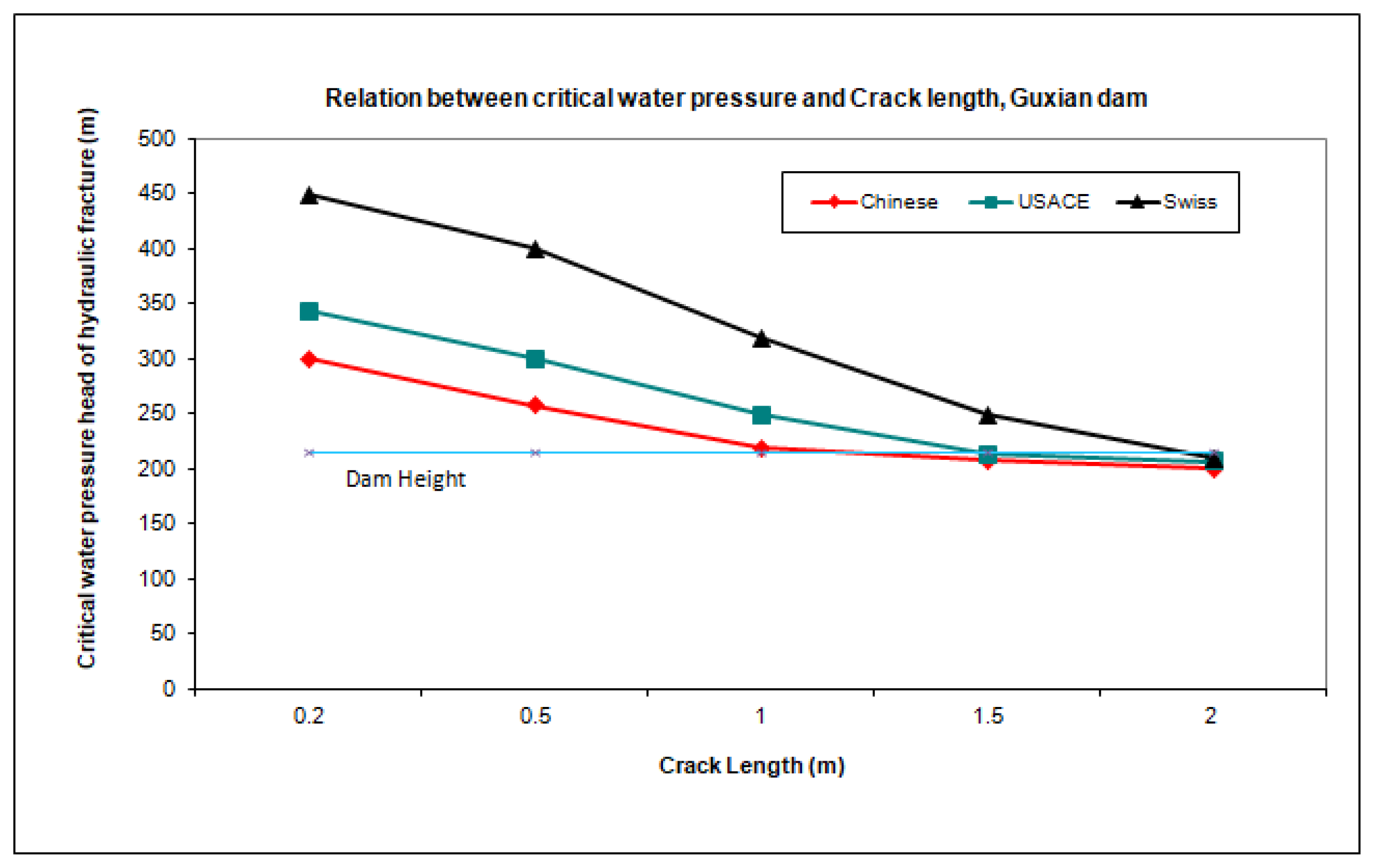
5.2. Assessing the Design Regulations’ Resistance to Hydraulic Fracture
5.3. Evaluation of the Ultimate Bearing Capacity
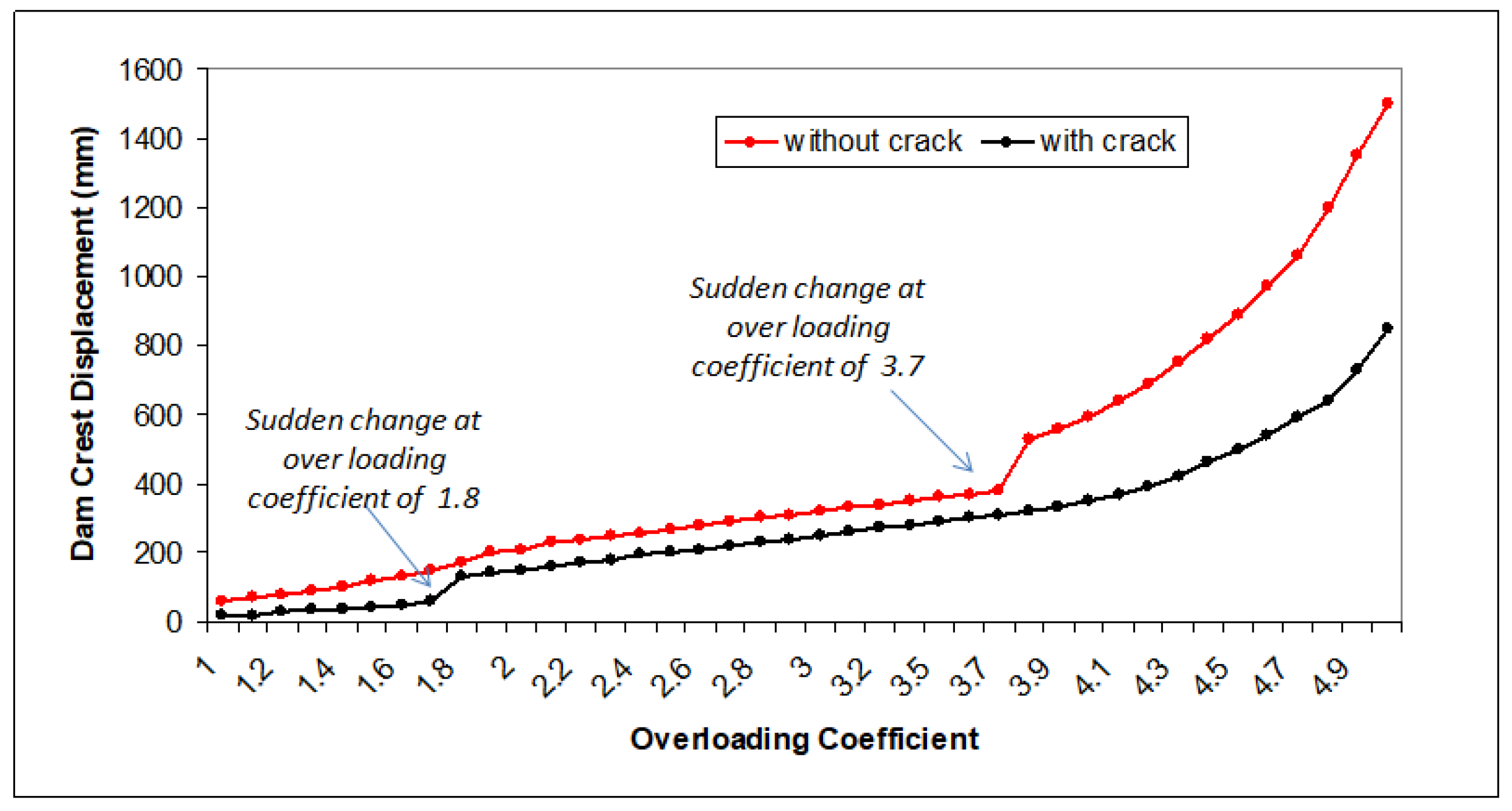
5.3.1. Safety Assessment Using Overloading Method with and without Considering Crack
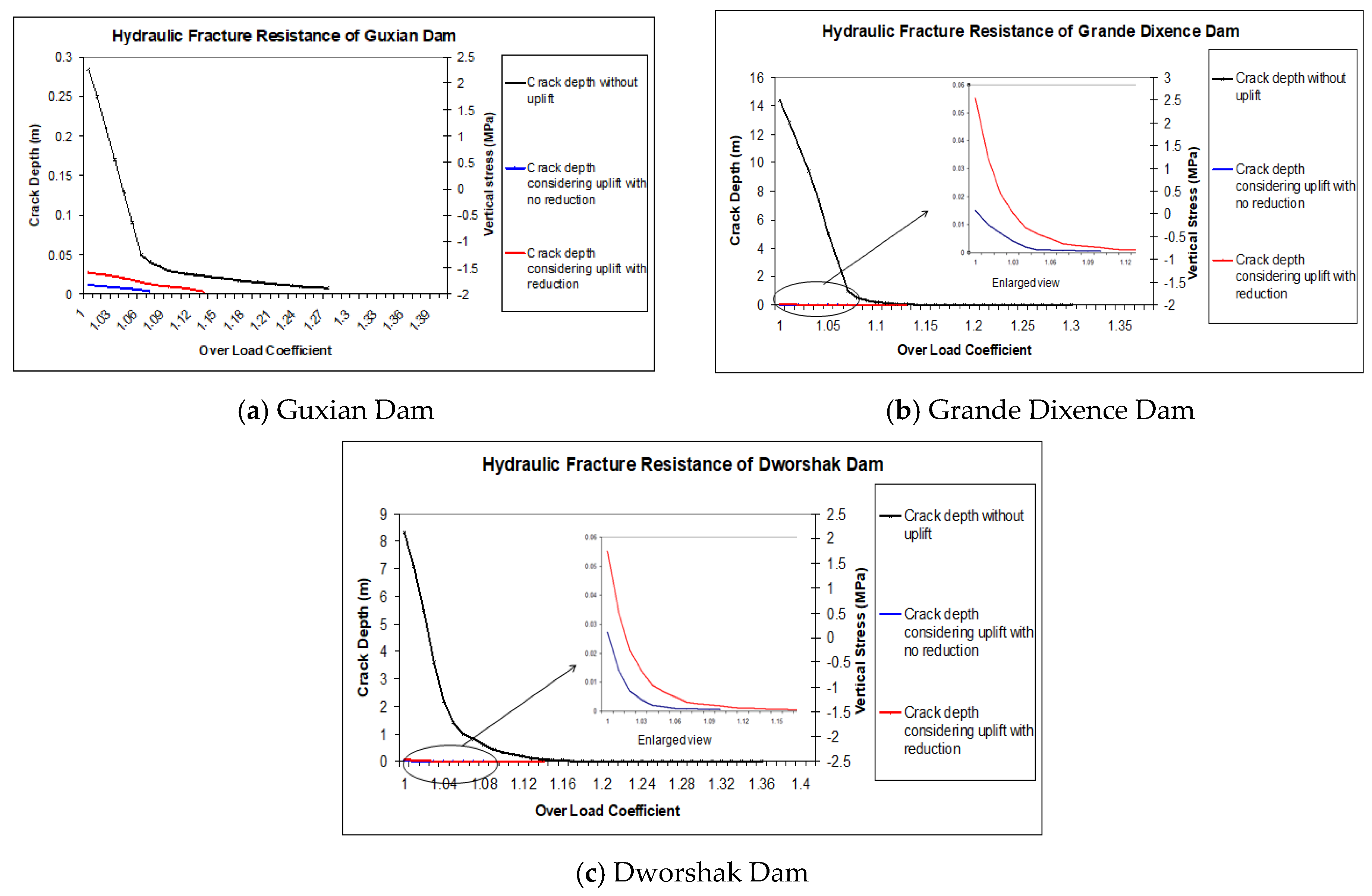
5.3.2. Investigation of Guxian Dam Resistance to Hydraulic Fracture Mathematically
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chinese SL 319-2018; Design Specification for Concrete Gravity Dams. China Water and Power Press: Beijing, China, 2018.
- Swiss Federal Office of Energy (SFOE). Directive on the Safety of Water Retaining Facilities; Part C1, Supervision of Dams section, Federal Department of the Environment, Transport, Energy and Communications (DETEC); Version 2.0; Swiss Federal Office of Energy, Supervision of Dams Section: Bern, Switzerland, 2017. [Google Scholar]
- USBR (United States Bureau of Reclamation). Design of Gravity Dams-Design Manual for Concrete Gravity Dam; A Water Resources Technical Publication; USBR: Denver, CO, USA, 1976. [Google Scholar]
- Federal Energy Regulatory Commission. Engineering Guidelines for the Evaluation of Hydropower Projects; Federal Energy Regulatory Commission: Washington, DC, USA, 1999. [Google Scholar]
- USACE (USA Army of Corps Engineering). Stability Analysis of Concrete Structures, Engineering Manual EM 1110-2-2000; US Army Corps of Engineers: Washington, DC, USA, 2005.
- ANCOLD. Guidelines on Design Criteria for Concrete Gravity Dams; Australian National Committee on Large Dams: Hobart, Australia, 2013. [Google Scholar]
- Al-Shadeedi, M.; Hamdi, E. Comparison of the Structural Stability of Concrete Gravity Dams using USACE and USBR Standards. ARPN J. Eng. Appl. Sci. 2017, 12, 1580–1592. [Google Scholar]
- Goldgruber, M.; Zenz, G. Analysis of Structural Safety of Gravity Dams; Institute of Hydraulic Engineering and Water Resources Management: Graz, Austria, 2012. [Google Scholar]
- Wang, Y.; Jia, J. Experimental study on the influence of hydraulic fracturing on high concrete gravity dams. Eng. Struct. 2017, 132, 508–517. [Google Scholar] [CrossRef]
- Li, W.; Wu, W.; Zhang, J. Numerical Stability Analysis of the Dam Foundation Under Complex Geological Conditions at Great Depth: A Case Study of Kala Hydropower Station, China. Orig. Res. Front. Phys. 2022, 9, 808840. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, X.; Nie, Y.; Tian, Y. Influence of High Water Pressure on Static and Dynamic Compressive Strength of Concrete. Adv. Civ. Eng. 2020, 2020, 8814626. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, X.; Zhou, J.; Nie, Y. Investigation on the influence of high-pressure water environment on fracture performance of concrete. Constr. Build. Mater. 2022, 341, 127907. [Google Scholar] [CrossRef]
- Feng, L.M.; Peakau, O.A.; Zhang, C.H. Cracking analysis of arch dams by 3D boundary element method. J. Struct. Eng. 1996, 122, 691–699. [Google Scholar] [CrossRef]
- Vallejo, S.A.N. Hydraulic Engineering Failure of Large Dams. Master’s Thesis, Graz University of Technology, Graz, Austria, 2016. [Google Scholar]
- Schöberl, P. Crack sanitation at Zillergrundl arch dam. In Proceedings of the Symposium on Repair and Upgrading of Dams; COLD: Stockholm, Sweden, 1996. [Google Scholar]
- Lin, P.; Guan, J.; Peng, H.; Shi, J. Horizontal cracking and crack repair analysis of a super high arch dam based on fracture toughness. Eng. Fail. Anal. 2019, 97, 72–90. [Google Scholar] [CrossRef]
- Liang, W.H.; Qiao, C.X.; Tu, C.L. A summarized study on cracks in Zhexi concrete buttress dam. Shuili Xuebao/J. Hydraul Eng. 1982, 6, 1–10. (In Chinese) [Google Scholar]
- Zhang, H.; Shen, Z.; Xu, L.; Gan, L.; Ma, Z.; Wu, Q.; Liu, D. Experimental investigation on hydraulic fracturing in cement mortar with tensile stress. Eng. Fract. Mech. 2022, 259, 108058. [Google Scholar] [CrossRef]
- Liu, Z.G.; Zhou, Z.B.; Yuan, L.W. Calculation of vertical crack propagation on the upstream face of the Zhexi single buttress dam. J. Hydraul. Eng. 1990, 5, 29–36. [Google Scholar]
- Wang, L.C.; Wu, S.Y. Self-healing mechanism of concrete cracks induced by splitting tensile loading. J. Hydraul. Eng. 2019, 50, 787–797. [Google Scholar]
- Song, Z.P.; Li, N.; Chen, F.X. Three dimensional nonlinear seismic stability analysis of abutment jointed rock mass of high arch dam. Chin. J. Geotech. Eng. 2004, 26, 361–366. [Google Scholar]
- McDonald, J.E.; Curtis, N.F. Repaired and Rehabilitation of Dams; Technical Report, REMR-CS-63; US Army Corps of Engineers, Engineer Research and Development Center: Washington, DC, USA, 1999.
- Brühwiler, E.; Saouma, V.E. Water fracture interaction in concrete-part I: Fracture properties. ACI Mater. J. 1995, 92, 296–303. [Google Scholar]
- Zhao, W.; Fang, T.; Chen, X.; Sun, L. Experimental study on hydraulic fracture behavior of concrete with wedge-splitting testing. Sci. Eng. Compos. Mater. 2023, 30, 20220182. [Google Scholar] [CrossRef]
- Barani, O.R.; Majidaie, S.; Mosallanejad, M. Numerical modeling of water pressure in propagating concrete cracks. J. Eng. Mech. 2016, 142, 04016011. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, B.; Connell, L.D.; Han, Y.; Jeffrey, R.G. A model for hydraulic fracture growth across multiple elastic layers. J. Pet. Sci. Eng. 2018, 167, 918–928. [Google Scholar] [CrossRef]
- Li, Y.; Zhong, H.; Pang, L.; Hu, Z. Influence of the water pressure distribution along crack faces on seismic fracture modeling of a dam-reservoir-foundation system. Eng. Anal. Bound. Elem. 2019, 101, 252–269. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, G.; Yu, X. Seismic cracking analysis of concrete gravity dams with initial cracks using the extended finite element method. Eng. Struct. 2013, 56, 528–543. [Google Scholar] [CrossRef]
- Parvathi, I.S.; Mahesh, M.; Kamal, D.V.V.R. Critical crack lengths of concrete gravity dam by using fracture mechanics. Mater. Today Proc. 2021, 38, 3149–3159. [Google Scholar] [CrossRef]
- Parvathi, I.S.; Mahesh, M.; Kamal, D.V.V.R. XFEM Method for Crack Propagation in Concrete Gravity Dams. J. Inst. Eng. India Ser. A 2022, 103, 677–687. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, Q.; Xia, X.; Wang, L.; Liu, X. Analysis of hydraulic fracturing in concrete dam considering fluid–structure interaction using XFEM-FVM model. Eng. Fail. Anal. 2015, 57, 399–412. [Google Scholar] [CrossRef]
- Gan, L.; Zhang, K.; Zhang, H.; Tian, Z. Coupling analysis of hydraulic fracturing computation base on element-free method. Clust. Comput. 2017, 20, 3213–3224. [Google Scholar] [CrossRef]
- Wang, C.H. Introduction to Fracture Mechanics; DSTO-GD-0103; DSTO Aeronautical and Maritime Research Laboratory: Canberra, Australia, 1996. [Google Scholar]
- Anderson, T.L. Fracture Mechanics, Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Ji, E.; Fu, Z.; Chen, S.; Zhu, J.; Geng, Z. Numerical Simulation of Hydraulic Fracturing in Earth and Rockfill Dam Using Extended Finite Element Method. Adv. Civ. Eng. 2018, 2018, 1782686. [Google Scholar] [CrossRef]
- Deng, H.; Yan, B.; Zhang, X.; Zhu, Y. A new enrichment scheme for the interfacial crack modeling using the XFEM. Theor. Appl. Fract. Mech. 2022, 122, 103595. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, B.; Chen, J.; Li, J.; Wang, M. Shaking Table Test and Numerical Simulation Study of the Reinforcement Strengthening of a Dam. Buildings 2022, 12, 1955. [Google Scholar] [CrossRef]
- Mlakar, P.F. Nonlinear Response of Concrete Gravity Dams to Strong Earthquake-Induced Ground Motion; Technical Report SL-88-7; US Army of Corps: Washington, DC, USA, 1987.
- Clerc, B.; Manso, P.; De Cesare, G. Heightening of Very High Gravity Dams: The Case Study of the Grande Dixence, Numerical Analysis of Dams. Lect. Notes Civ. Eng. 2021, 91, 775–792. [Google Scholar] [CrossRef]
- Pirtz, D. Creep Characteristics of Mass Concrete for DWORSHAK Dam; Structural Engineering Laboratory, Structures and Materials Research Department of Civil Engineering, University of California: Berkeley, CA, USA, 1968. [Google Scholar]
- ACI. Report on Roller-Compacted Mass Concrete, ACI 2017.5R-11; American Concrete Institute: Farmington Hills, MI, USA, 2011. [Google Scholar]
- Zhou, B.; Chai, J.; Wang, J.; Zhou, H.; Wen, L. An XFEM-Based Analysis of Concrete Face Cracking in Rockfill Dams. Math. Probl. Eng. 2021, 2021, 6640668. [Google Scholar] [CrossRef]
- Fang, T.R. Elementary Fracture Mechanics; Science Press: Beijing, China, 2006. [Google Scholar]
- Chinese Aeronautical Establishment. Stress Intensity Factors Handbook; Science Press: Beijing, China, 1981. [Google Scholar]
- Yu, X.Z. Fracture Mechanics of Concrete. Water Power 1988, 2, 49–53. [Google Scholar]
- Wu, Z.M.; Zhao, G.F.; Xi, S.L. Fracture toughness of large concrete specimen. J. Hydraul. Eng. 1997, 6, 67–76. [Google Scholar]
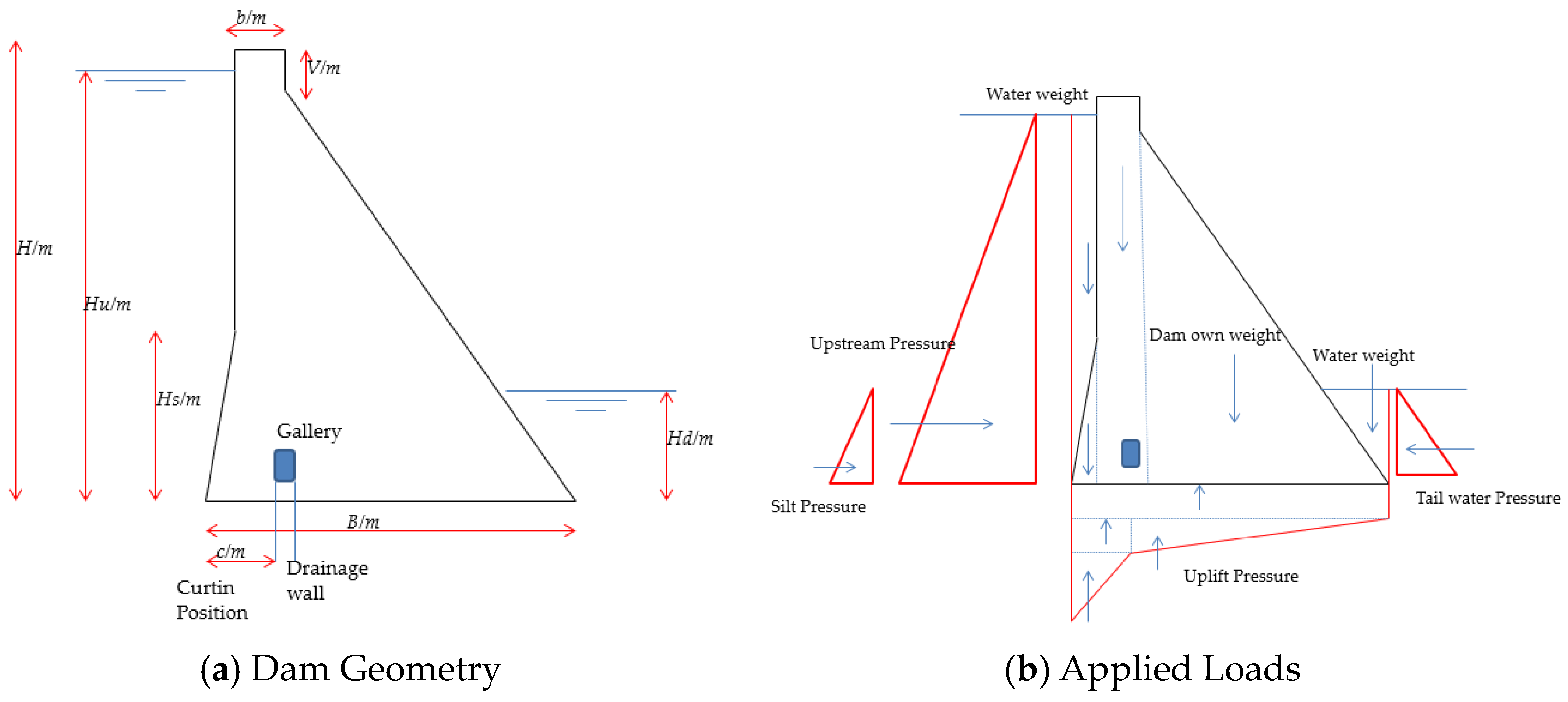



| Parameter/Dam | Guxian | Longtan | Huangdeng | Dworshak | Grande Dixence |
|---|---|---|---|---|---|
| Dam crest width (b/m) | 15 | 18 | 16 | 8.3 | 15 |
| Dam height (H/m) | 215 | 216.5 | 203 | 219 | 284 |
| Height of the slope (Hs/m) | 50 | 63 | 60 | 0 | 0 |
| Slope ratio | 0.3 | 0.25 | 0.3 | 0 | 0 |
| Vertical distance of the dam crest (V/m) | 20 | 26 | 17 | 8 | 15 |
| Downstream slope ratio | 0.8 | 0.73 | 0.73 | 0.8 | 0.81 |
| Dam bottom width (B/m) | 172.35 | 160.77 | 165 | 177.1 | 232.89 |
| Upstream water level (Hu/m) | 215 | 216.5 | 203 | 219 | 284 |
| Downstream water level (Hd/m) | 25 | 25 | 25 | 25 | 25 |
| Concrete bulk density (N/m3) | 24,000 | 24,000 | 24,000 | 24,000 | 24,000 |
| Water density (N/m3) | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 |
| Uplift pressure reduction factor | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 |
| Curtain position (c/m) | 13 | 20 | 20 | 20 | 20 |
| Area of cross-section (m2) | 17,497.13 | 15,146.87 | 15,971 | 19,626.1 | 33,566.21 |
| Chinese Criteria | ||
|---|---|---|
| Safety Factor Using Friction Equation | Shear Resistance Stability | Stress Calculations |
K > 1.10 for usual loading combination | . K′ > 3 for usual loading combination | |
| USACE (US Army Corps of Engineers) CRITERIA | ||
| Overturning Stability | Sliding Stability | Stress Calculations |
The resultant remains within the middle third to maintain compressive stresses. | Minimum FS =2 for usual loading combination | |
| SFOE (Swiss Federal Office of Energy) CRITERIA | ||
| Uplift Stability | Sliding Stability | Stress Calculations |
| Dam | Material | Elastic Properties | Damage for Crack | Plastic Properties | ||
|---|---|---|---|---|---|---|
| Elastic Modulus GPa | Poisson Ratio | Max Principal StressMPa | Friction Angle° | Yield StressMPa | ||
| Longtan | Dam body | 25 | 0.167 | 2.4 | 53 | 1.51 |
| Foundation | 28 | 0.2 | 2.5 | 52 | 1.68 | |
| Huangdeng | Dam body | 26 | 0.167 | 2.4 | 51 | 1.56 |
| Foundation | 29 | 0.2 | 2.5 | 52 | 1.67 | |
| Grande Dixence | Dam body | 35 | 0.2 | 3.5 | 56 | 2.77 |
| Foundation | 32 | 0.2 | 3.5 | 57 | 2.82 | |
| Dworshak | Dam body | 38 | 0.2 | 3.2 | 55 | 2.64 |
| Foundation | 31 | 0.2 | 3.2 | 57 | 2.78 | |
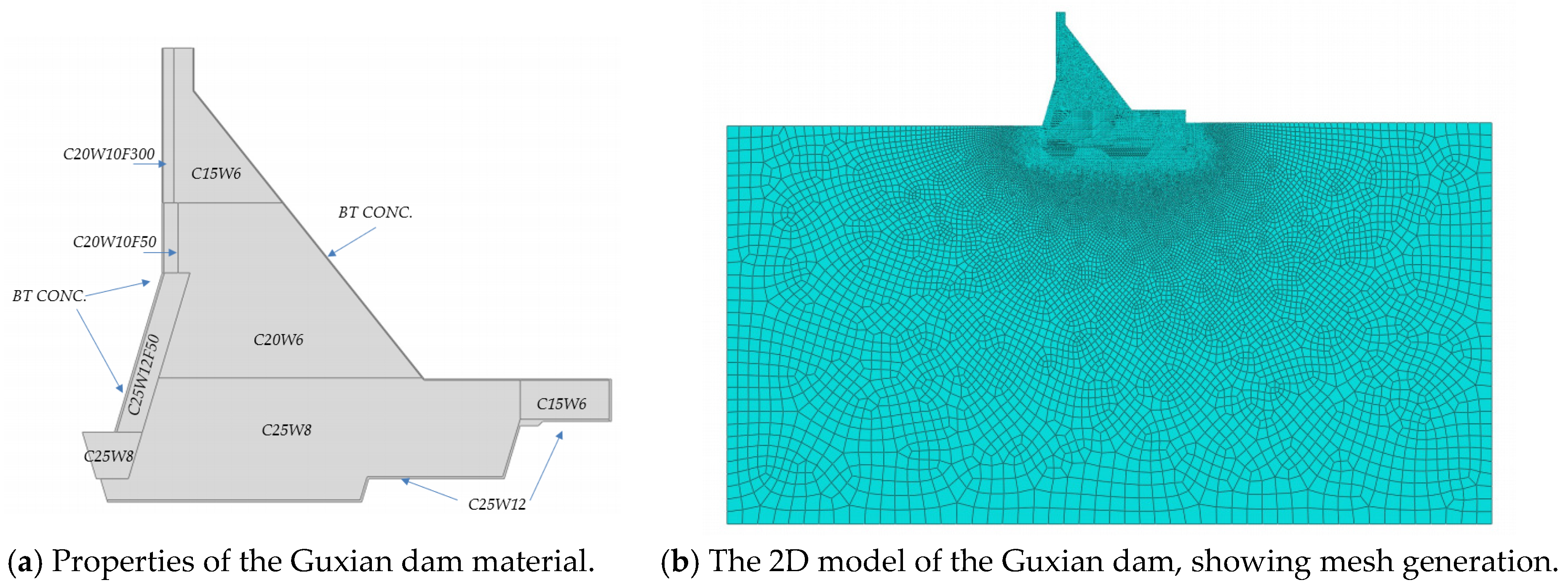
| Guxian | C15W6 | 22 | 0.167 | 9.1 | 50.7 | 1.78 |
| BT CONCRETE | 39 | 0.167 | 2.2 | 59.6 | 4.49 | |
| C20W6 | 25.5 | 0.167 | 1.1 | 51.3 | 2.48 | |
| C25W8 | 28 | 0.167 | 2.35 | 51.7 | 2.52 | |
| Foundation | 32 | 0.2 | 2.3 | 50.7 | 1.80 | |
| Parameter | Guxian | Grande Dixence | Dworshak | Dam Geometric Dimensions |
|---|---|---|---|---|
| D1 (m) | 15 | 15 | 8.3 |  |
| D2 (m) | 20 | 15 | 8 | |
| D3 (m) | 165 | 284 | 219 | |
| D4 (m) | 50 | 0 | 0 | |
| λ1 (slope ratio) | 0.8 | 0.81 | 0.8 | |
| λ2 (slope ratio) | 0.3 | 0 | 0 | |
| h1 (m) | 215 | 284 | 219 | |
| h2 (m) | 25 | 25 | 25 | |
| B (m) | 172.35 | 232.89 | 177.1 | |
| γwat (N/m3) | 10,000 | 10,000 | 10,000 | |
| γcon (N/m3) | 24,000 | 24,000 | 24,000 | |
| ft (Pa) | 1,380,000 | 1,570,000 | 1,710,000 | |
| α | 0.5 | 0.5 | 0.5 |
| Parameter | Chinese Criteria (Original) | USACE Criteria (Modified) | SWISS Criteria (Modified) |
|---|---|---|---|
| Crest width (m) | 15 | 15 | 15 |
| Dam height (m) | 215 | 215 | 215 |
| Slope height (m) | 50 | 50 | 50 |
| Slope ratio | 0.3 | 0.3 | 0.3 |
| Crest vertical distance (m) | 20 | 10 | 19.5 |
| Downstream slope ratio | 0.8 | 0.72 | 0.8 |
| Dam bottom width (m) | 172.35 | 177.6 | 186.4 |
| Area of cross-section (m2) | 17,497.13 | 18,729 | 18,888.1 |
| Parameter/ Criteria | Longtan | Huangdeng | Grande Dixence | Dworshak | ||
|---|---|---|---|---|---|---|
| USACE | SWISS | USACE | SWISS | Chinese | Chinese | |
| Crest width (m) | 18 | 18 | 16 | 16 | 15 | 8.3 |
| Dam height (m) | 216.5 | 216.5 | 203 | 203 | 284 | 219 |
| Slope height (m) | 63 | 63 | 60 | 60 | 0 | 0 |
| Slope ratio | 0.25 | 0.25 | 0.3 | 0.3 | 0 | 0 |
| Crest vertical distance (m) | 19 | 16 | 17 | 17 | 15 | 11.5 |
| Downstream slope ratio | 0.73 | 0.73 | 0.73 | 0.73 | 0.81 | 0.8 |
| Dam bottom width (m) | 165.88 | 168.07 | 172.96 | 180.8 | 225.6 | 174.3 |
| Area of cross-section (m2) | 16,053.89 | 16,453.57 | 17,197.64 | 17,256.9 | 32,691 | 19,040.2 |
| Dam/Method of Calculation | Overloading without Crack | Overloading with Crack |
|---|---|---|
| Longtan | 3.5 | 1.5 |
| Huangdeng | 3.6 | 1.6 |
| Guxian | 3.7 | 1.8 |
| Dworshak | 4.2 | 2.3 |
| Grande Dixence | 4.5 | 2.7 |
| Dam | Crack Initiation Overload Coefficient | Crack Depth (m) | Ultimate Overload Coefficient | Maximum Dam Heel Stress (MPa) |
|---|---|---|---|---|
| Grande Dixence | 1.02 | 14.36 | 1.33 | −1.5 |
| Dworshak | 1.01 | 8.316 | 1.37 | −1.69 |
| Guxian | 1.0 | 0.284 | 1.27 | −1.33 |
| Dam | Crack Initiation Overload Coefficient | Crack Depth (m) | Ultimate Overload Coefficient | Maximum Dam Heel Stress (MPa) |
|---|---|---|---|---|
| Grande Dixence | 1.00 | 0.015 | 1.092 | −1.48 |
| Dworshak | 1.00 | 0.027 | 1.119 | −1.62 |
| Guxian | 1.00 | 0.012 | 1.051 | −1.31 |
| Dam | Crack Initiation Overload Coefficient | Crack Depth (m) | Ultimate Overload Coefficient | Maximum Dam Heel Stress (MPa) |
|---|---|---|---|---|
| Grande Dixence | 1.00 | 0.055 | 1.197 | −1.54 |
| Dworshak | 1.00 | 0.085 | 1.21 | −1.54 |
| Guxian | 1.00 | 0.028 | 1.14 | −1.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramadan, M.; Jia, J.; Zhao, L.; Li, X.; Wu, Y. Comprehensive Safety Analysis of Ultimate Bearing Capacity Considering Hydraulic Fracture for Guxian High RCC Gravity Dam. Water 2024, 16, 1912. https://doi.org/10.3390/w16131912
Ramadan M, Jia J, Zhao L, Li X, Wu Y. Comprehensive Safety Analysis of Ultimate Bearing Capacity Considering Hydraulic Fracture for Guxian High RCC Gravity Dam. Water. 2024; 16(13):1912. https://doi.org/10.3390/w16131912
Chicago/Turabian StyleRamadan, Mohamed, Jinsheng Jia, Lei Zhao, Xu Li, and Yangfeng Wu. 2024. "Comprehensive Safety Analysis of Ultimate Bearing Capacity Considering Hydraulic Fracture for Guxian High RCC Gravity Dam" Water 16, no. 13: 1912. https://doi.org/10.3390/w16131912
APA StyleRamadan, M., Jia, J., Zhao, L., Li, X., & Wu, Y. (2024). Comprehensive Safety Analysis of Ultimate Bearing Capacity Considering Hydraulic Fracture for Guxian High RCC Gravity Dam. Water, 16(13), 1912. https://doi.org/10.3390/w16131912








