Characteristics and Mechanism of Downflow in Front of a Cylindrical Pier with Clear-Water Local Scour
Abstract
1. Introduction
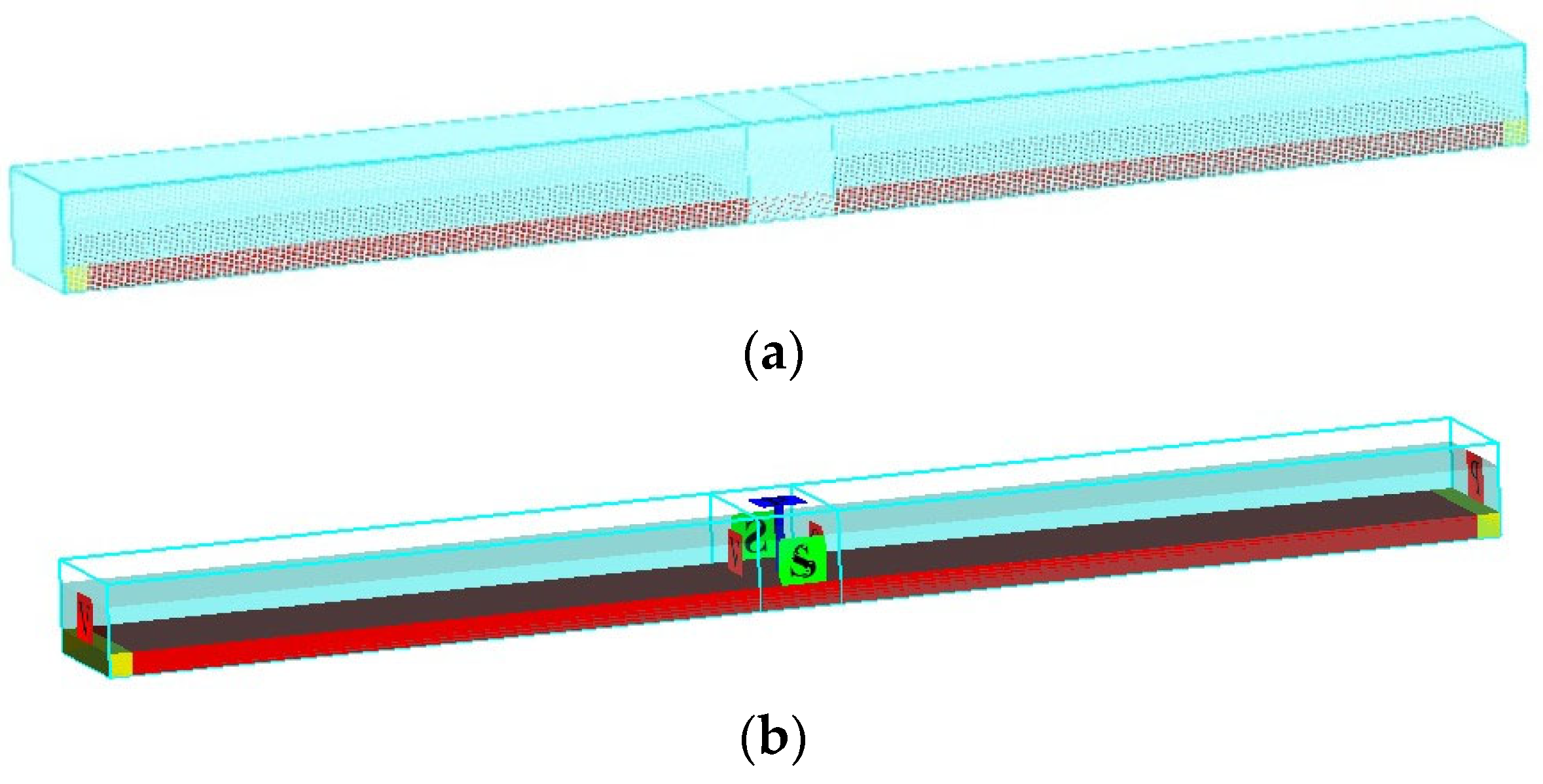
2. Materials and Methods
3. Results and Discussion
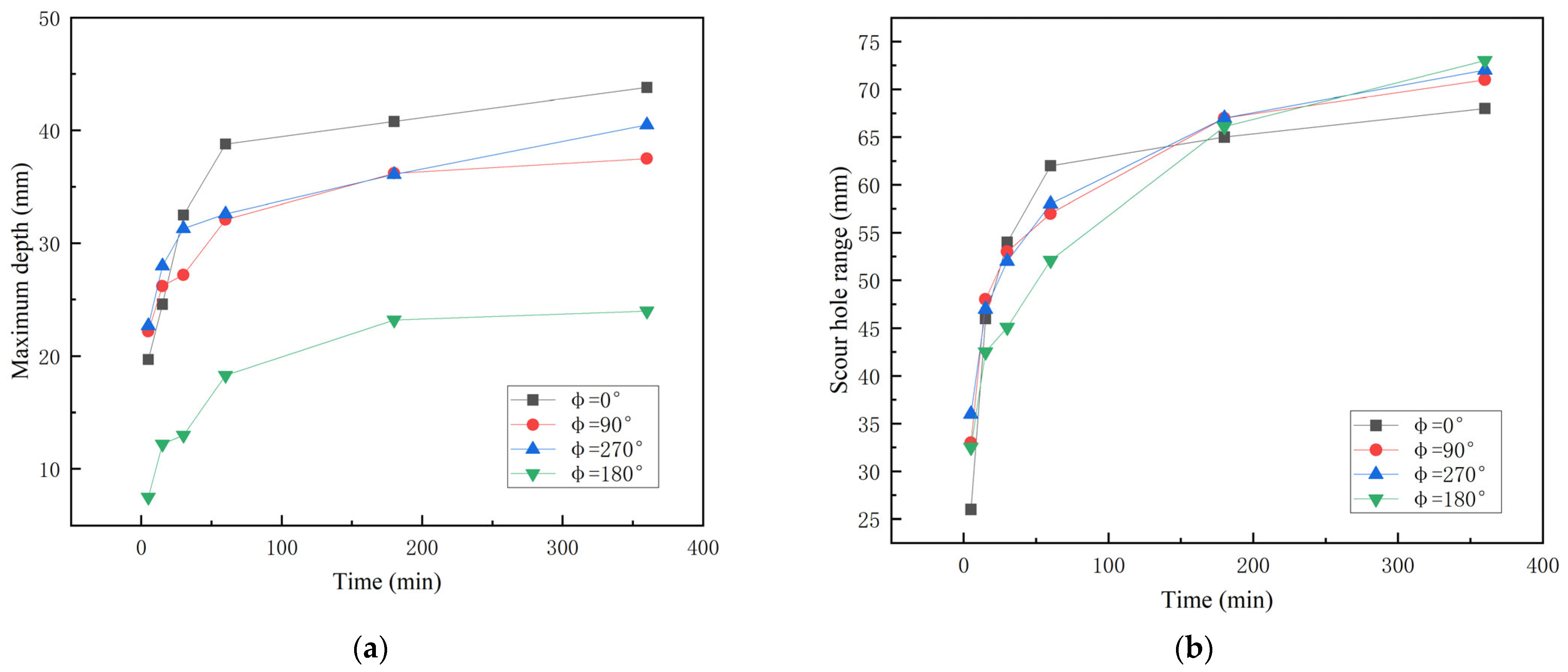
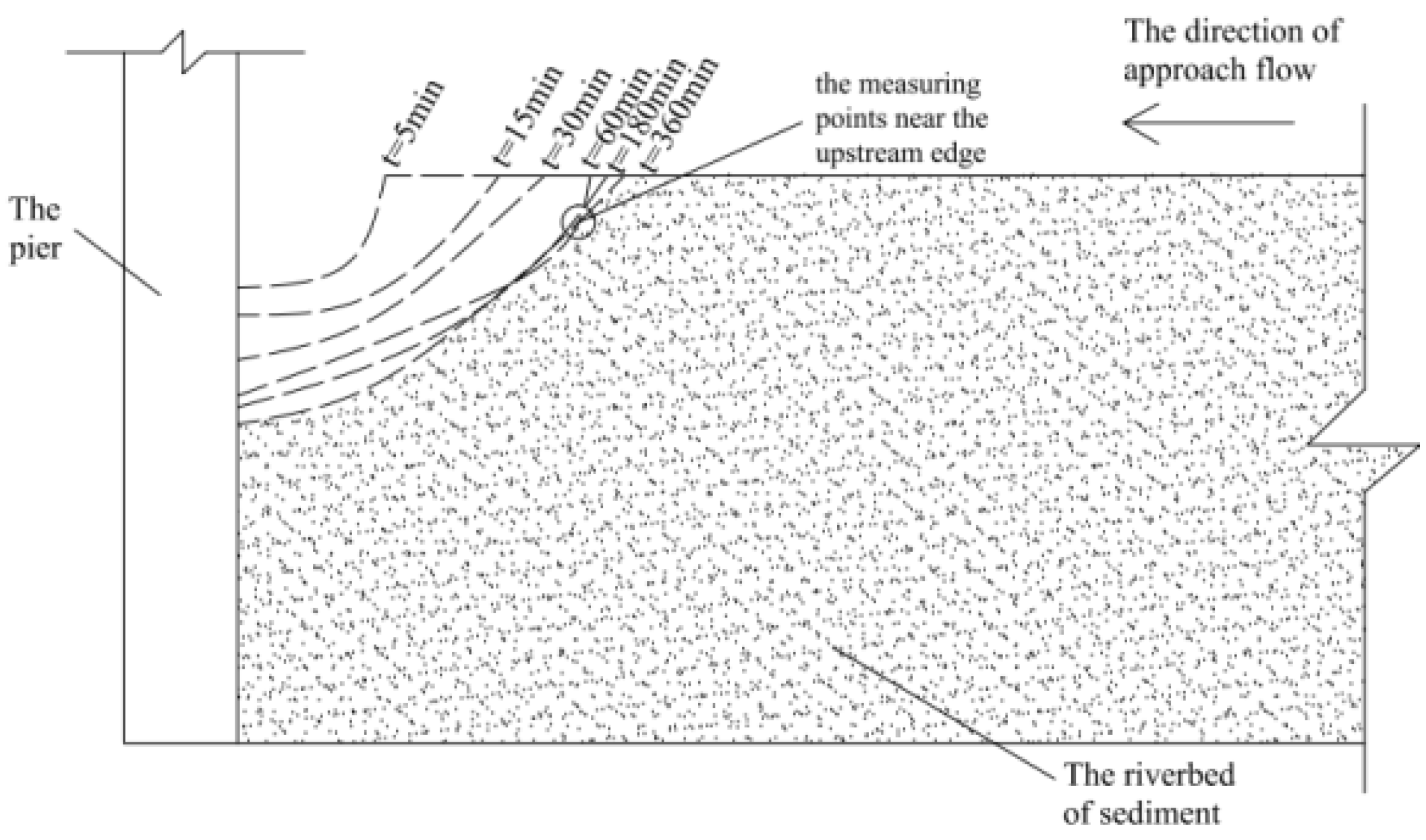
3.1. Result Analysis
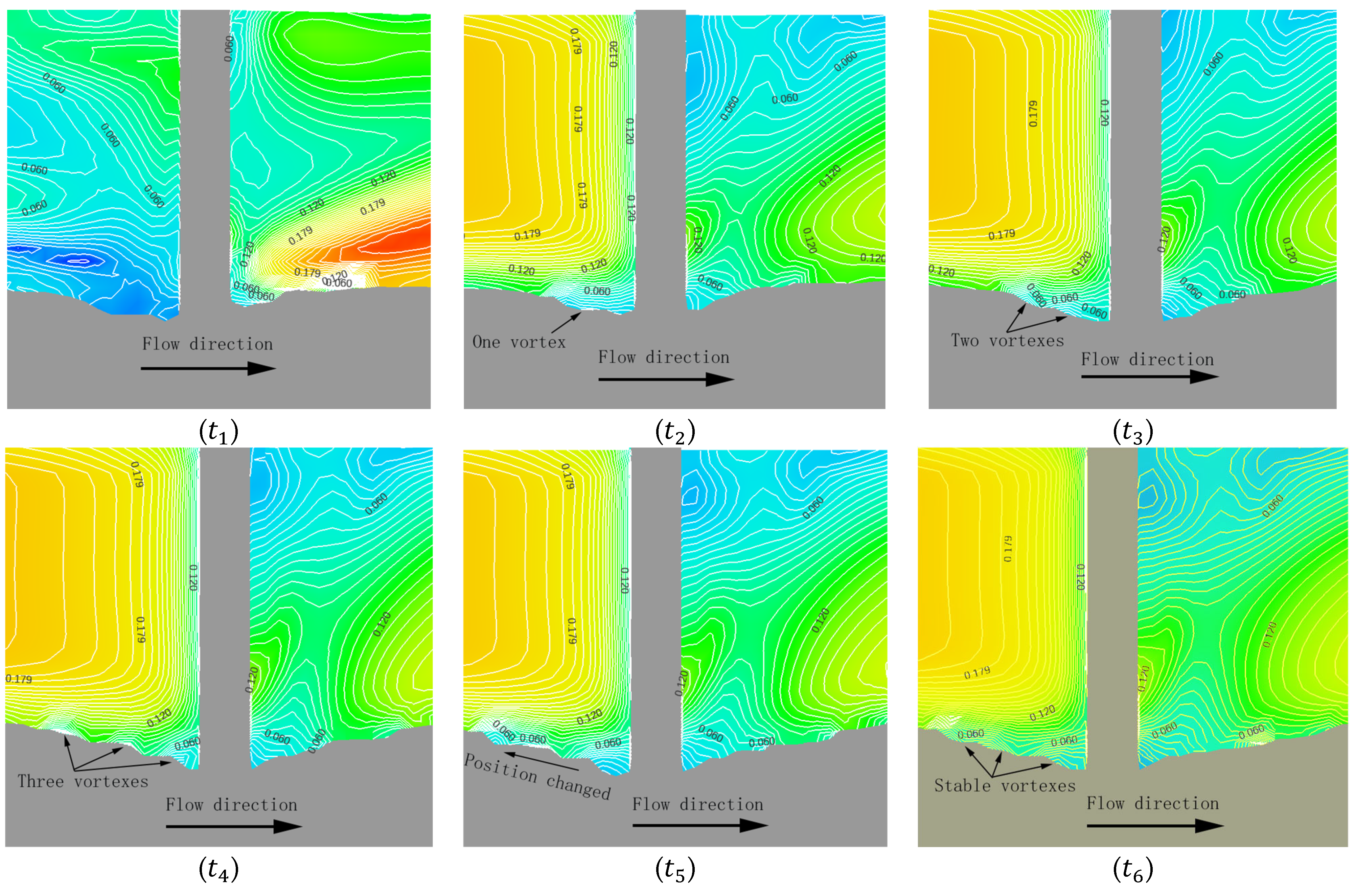
3.2. The Rigorous Interaction between the Downflow and the Horseshoe Vortex System
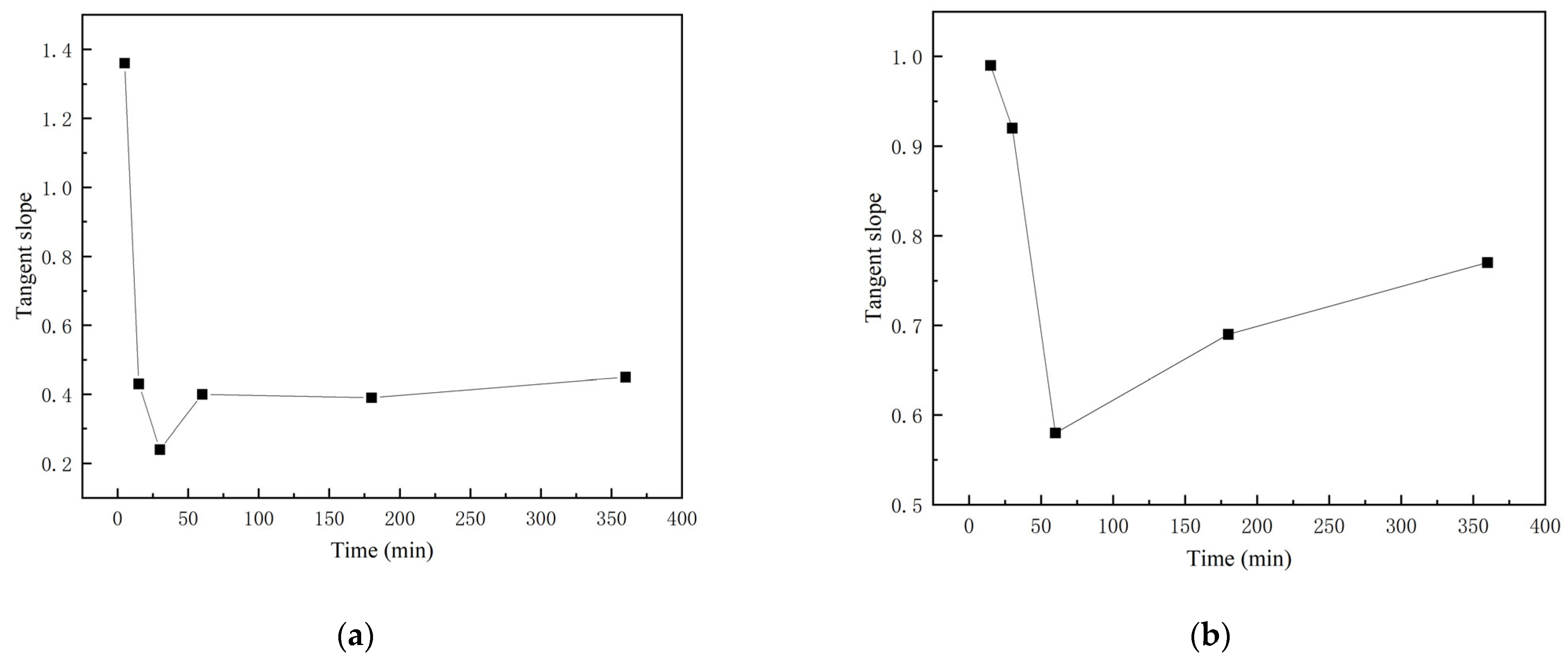
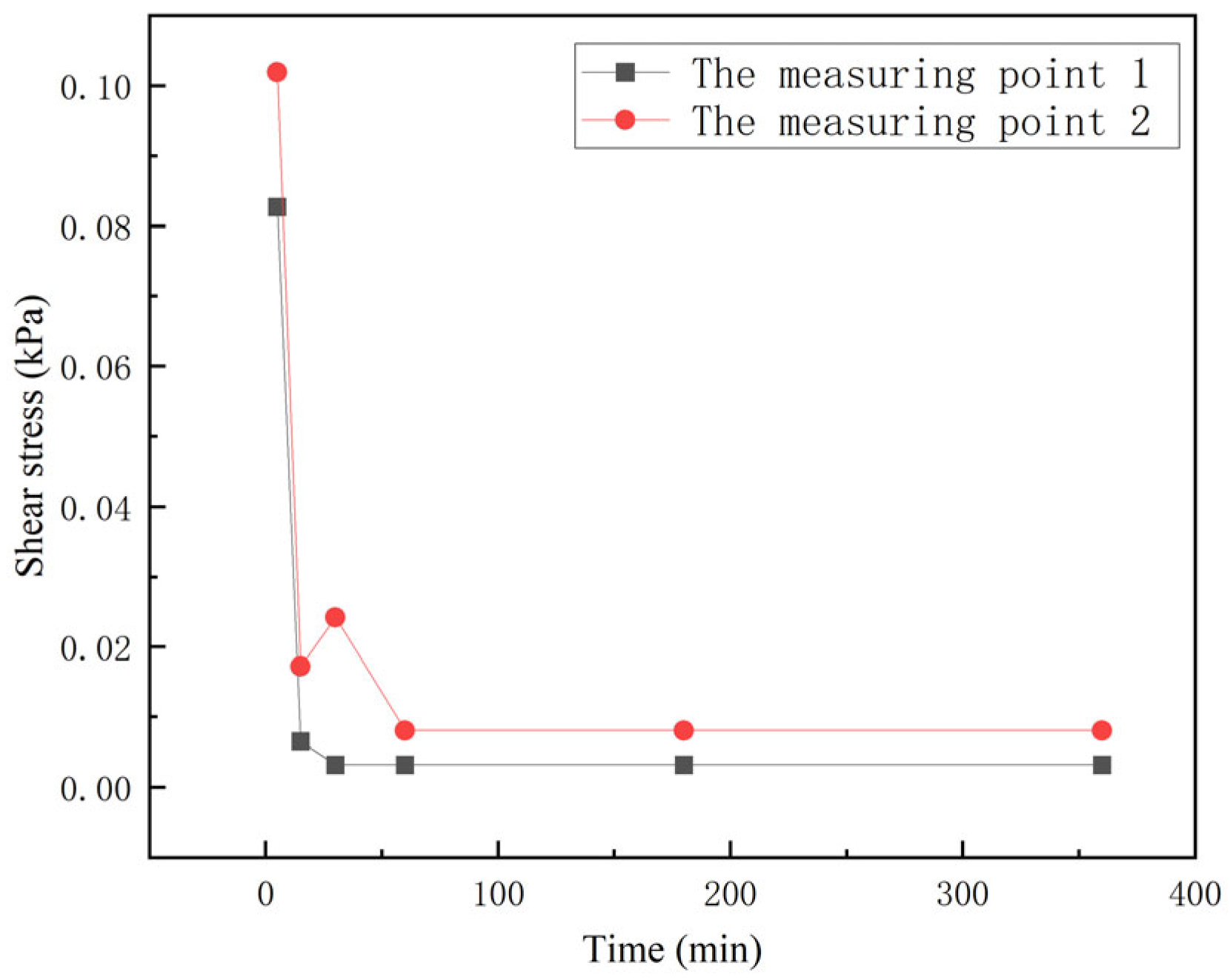
3.3. The Stress State and the Tangent Slope
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols
| Z | Scour depth |
| Zmax | Maximum scour depth |
| Z1 | Scour depth at measuring point 1 |
| Z2 | Scour depth at measuring point 2 |
| k | Tangent slope |
| k1 | Tangent slope at measuring point 1 |
| k2 | Tangent slope at measuring point 2 |
| p | Pressure stress |
| pD | Dynamic water pressure stress |
| pH | Hydrostatic pressure stress |
| p1 | Pressure stress at measuring point 1 |
| p2 | Pressure stress at measuring point 2 |
| Shear stress | |
| Shear stress at measuring point 1 | |
| Shear stress at measuring point 2. | |
| D | Pier diameter |
| d50 | Median diameter of the sediment |
| V | Flow velocity |
| VC | Critical flow velocity of the sediment |
| H | Flow depth |
| ts | Thickness of the sand layer |
| RD | Reynolds number of the pier ) |
| Molecular kinematic viscosity | |
| t | Time factor |
| t1–t6 | A set of six measured time points |
References
- Hunt, D. Monitoring Scour Critical Bridges; The National Academies Press: Washington, DC, USA; Transportation Research Board: Washington, DC, USA, 2009. [Google Scholar] [CrossRef]
- Al-Mussawi, W.; Kais, H. Three-dimensional numerical simulation of local scour around circular bridge pier using Flow-3D software. IOP Conf. Ser. Mater. Sci. Eng. 2020, 745, 012150. [Google Scholar] [CrossRef]
- Wang, C.; Yu, X.; Liang, F. A review of bridge scour: Mechanism, estimation, monitoring and countermeasures. Nat. Hazards 2017, 87, 1881–1906. [Google Scholar] [CrossRef]
- Fang, S.-L. Experiment study on the influence of local scour pit on flow field around piers. Port Waterw. Eng. 2009, 11, 143–152. [Google Scholar] [CrossRef]
- Ranjbar Zahedani, M. Introducing, Examining and Optimising Flow Diversion Structure as an Innovative Countermeasure against Local Scour around Bridge Piers. Ph.D. Thesis, University of Technology Sydney, Ultimo, Australia, 2021. [Google Scholar]
- Melville, B.W.; Raudkivi, A. Flow characteristics in local scour at bridge piers. J. Hydraul. Res. 1977, 15, 373–380. [Google Scholar] [CrossRef]
- Dargahi, B. The turbulent flow field around a circular cylinder. Exp. Fluids 1989, 8, 1–12. [Google Scholar] [CrossRef]
- Raudkivi, A.; Ettema, R. ClearWater Scour at Cylindrical Piers. J. Hydraul. Eng.-Asce 1983, 109, 338–350. [Google Scholar] [CrossRef]
- Mercuri, M.; Pathirage, M.; Gregori, A.; Cusatis, G. Influence of self-weight on size effect of quasi-brittle materials: Generalized analytical formulation and application to the failure of irregular masonry arches. Int. J. Fract. 2023, 246, 117–144. [Google Scholar] [CrossRef]
- Melville, B.W. Live-bed scour at bridge piers. J. Hydraul. Eng. 1984, 110, 1234–1247. [Google Scholar] [CrossRef]
- Benedict, S.T.; Caldwell, A.W. A Pier-Scour Database: 2427 Field and Laboratory Measurements of Pier Scour; 2327-638X; US Geological Survey: Reston, VA, USA, 2014.
- Fakhimjoo, M.; Ardeshir, A.; Behzadian, K.; Karami, H. Experimental investigation and flow analysis of clear-water scour around pier and abutment in proximity. Water Sci. Eng. 2023, 16, 94–105. [Google Scholar] [CrossRef]
- Rahman, M.; Haque, A. Local scour estimation at bridge site: Modification and application of lacey formula. Int. J. Sediment Res. 2003, 18, 333–339. [Google Scholar]
- Baker, C.J. The position of points of maximum and minimum shear stress upstream of cylinders mounted normal to flat plates. J. Wind Eng. Ind. Aerodyn. 1985, 18, 263–274. [Google Scholar] [CrossRef]
- Briaud, J.L.; Ting, F.; Chen, H.; Gudavalli, R.; Perugu, S.; Wei, G. SRICOS: Prediction of scour rate in cohesive soils at bridge piers. J. Geotech. Geoenviron. Eng. 1999, 125, 237–246. [Google Scholar] [CrossRef]
- Devenport, W.; Simpson, R. Time-dependent and time-averaged turbulence structure near the nose of a wing-body junction. J. Fluid Mech. 1990, 210, 23–55. [Google Scholar] [CrossRef]
- Apsilidis, N.; Diplas, P.; Dancey, C.; Vlachos, P.; Raben, S. Local Scour at Bridge Piers: The Role of Reynolds Number on Horseshoe Vortex Dynamics. In Proceedings of the International Conference on Scour and Erosion, San Francisco, CA, USA, 7–10 November 2010; pp. 86–94. [Google Scholar] [CrossRef]
- Guan, D.; Chiew, Y.-M.; Wei, M.; Hsieh, S.-C. Characterization of horseshoe vortex in a developing scour hole at a cylindrical bridge pier. Int. J. Sediment Res. 2019, 34, 118–124. [Google Scholar] [CrossRef]
- Kwan, T.F. A Study of Abutment Scour; University of Auckland New Zealand: Auckland, New Zealand, 1984. [Google Scholar]
- Shafii, I.; Zhang, Z.; Briaud, J.L. Measurement of Hydrodynamic Forces on Gravel Particles in the Erosion Function Apparatus. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2018; pp. 519–524. [Google Scholar]
- Sun, Z.; Dong, H.; Sun, Y.; Li, Z. New formula for scour depth at piles based on energy equilibrium. Ocean Eng. 2023, 287, 115725. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef]
- Ahmed, F.; Rajaratnam, N. Flow around bridge piers. J. Hydraul. Eng. 1998, 124, 288–300. [Google Scholar] [CrossRef]
- Zarrati, A.R.; Nazariha, M.; Mashahir, M. Reduction of Local Scour in the Vicinity of Bridge Pier Groups Using Collars and Riprap. J. Hydraul. Eng.-Asce 2006, 132, 154–162. [Google Scholar] [CrossRef]
- Cheng, L.-Y.; Mou, X.-Y.; Wen, H.; Hao, L.-Z. Experimental research on protection of ring-wing pier against local scour. Adv. Sci. Technol. Water Resour. 2012, 32, 14–18. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, Z.; Cheng, Y.Z.; Ge, Y.B. Numerical simulation on reducing the local scour around a vertical pile by using a protective pile. Chin. J. Hydrodyn. 2019, 34, 122–130. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.; Fredsoe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Khosronejad, A.; Flora, K.; Kang, S. Effect of Inlet Turbulent Boundary Conditions on Scour Predictions of Coupled LES and Morphodynamics in a Field-Scale River: Bankfull Flow Conditions. J. Hydraul. Eng. 2020, 146, 04020020. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, B.; Qi, J. 3D numerical investigation of bridge pier-scour development using a dynamic-mesh updating technique. South-North Water Transf. 2017, 15, 132–137. [Google Scholar] [CrossRef]
- Yu, P.; Zhu, L. Numerical simulation of local scour around bridge piers using novel inlet turbulent boundary conditions. Ocean Eng. 2020, 218, 108166. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, G.; Ettema, R. Detached Eddy Simulation Investigation of Turbulence at a Circular Pier with Scour Hole. J. Hydraul. Eng.-Asce 2009, 135, 888–901. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Melville, B.; Ball, J. Three-dimensional analysis of coherent turbulent flow structure around a single circular bridge pier. Environ. Fluid Mech. 2014, 14, 821–847. [Google Scholar] [CrossRef]
- Pasiok, R.; Stilger-Szydło, E. Sediment particles and turbulent flow simulation around bridge piers. Arch. Civ. Mech. Eng. 2010, 10, 67–79. [Google Scholar] [CrossRef]
- Guo, J.; Gu, S.P.; Zhang, H.X.; Liao, Q.X. Comparison of calculation methods for cylindrical piers under scouring conditions. Zhejiang Univ. Technol. 2019, 47, 637–641. [Google Scholar]
- Aghaee, Y.; Hakimzadeh, H. Three Dimensional Numerical Modeling of Flow around Bridge Piers Using LES and RANS. In Proceedings of the River Flow, Braunschweig, Germany, 8–10 September 2010; pp. 211–218. [Google Scholar]


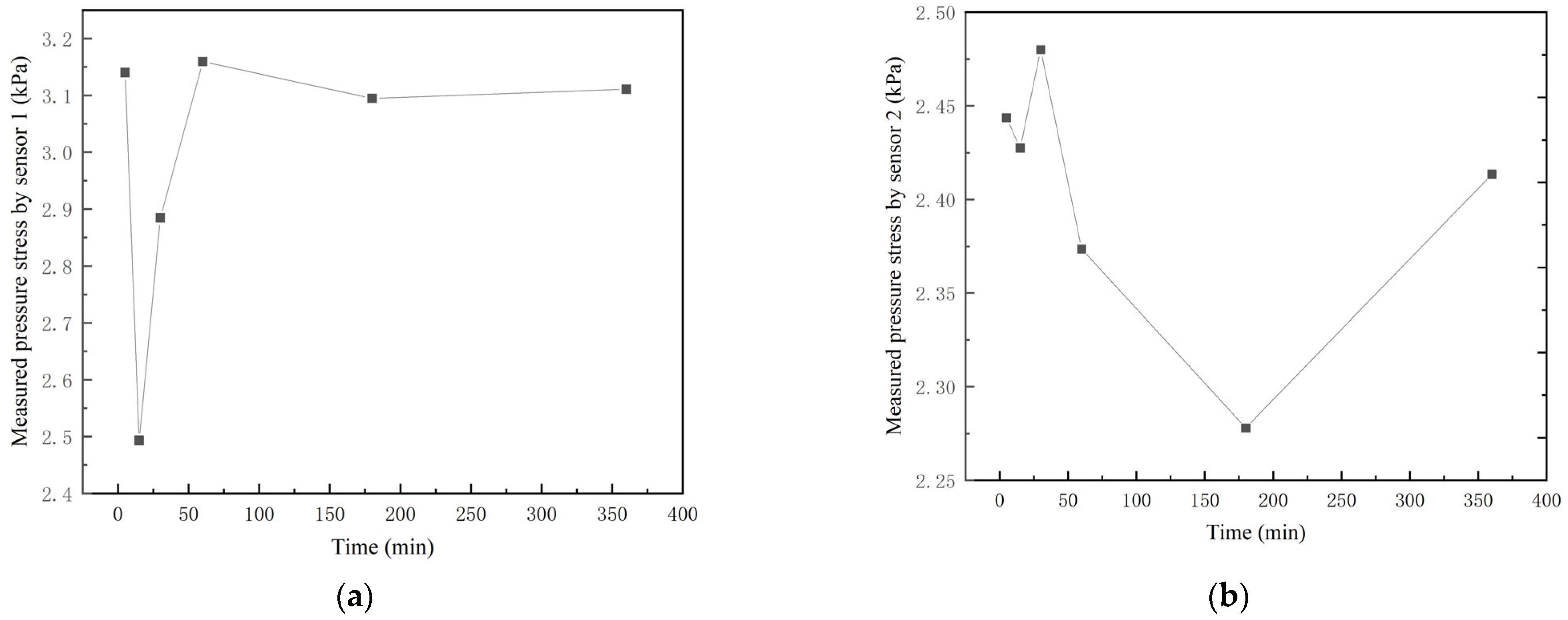
| Time (min) | Pressure Stress of Sensors (kPa) | Hydrostatic Pressure Values (kPa) | ||
|---|---|---|---|---|
| Measuring Point 1 | Measuring Point 2 | Measuring Point 1 | Measuring Point 2 | |
| 5 | 3.14 | 2.44 | 2.15 | 2.00 |
| 15 | 2.49 | 2.43 | 2.23 | 2.07 |
| 30 | 2.88 | 2.47 | 2.27 | 2.13 |
| 60 | 3.16 | 2.37 | 2.31 | 2.23 |
| 180 | 3.10 | 2.28 | 2.35 | 2.25 |
| 360 | 3.11 | 2.41 | 2.39 | 2.26 |
| Experimentally Observed Data | Simulated Data | ||||
|---|---|---|---|---|---|
| Maximum Scour Depth (mm) | Pressure Stress (kPa) | Maximum Scour Depth (mm) | Pressure Stress (kPa) | ||
| Measuring Point 1 | Measuring Point 2 | Measuring Point 1 | Measuring Point 2 | ||
| 19.7 | 3.14 | 2.44 | 19.5 | 3.09 | 2.33 |
| 24.6 | 2.49 | 2.43 | 24.6 | 2.52 | 2.48 |
| 32.5 | 2.88 | 2.47 | 32.0 | 2.63 | 2.35 |
| 38.8 | 3.16 | 2.37 | 38.6 | 3.18 | 2.22 |
| 40.8 | 3.10 | 2.28 | 40.3 | 3.01 | 2.41 |
| 43.8 | 3.11 | 2.41 | 43.0 | 3.21 | 2.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wei, S.; Zhu, D.; Wang, J.; Duan, H. Characteristics and Mechanism of Downflow in Front of a Cylindrical Pier with Clear-Water Local Scour. Water 2024, 16, 1863. https://doi.org/10.3390/w16131863
Wang W, Wei S, Zhu D, Wang J, Duan H. Characteristics and Mechanism of Downflow in Front of a Cylindrical Pier with Clear-Water Local Scour. Water. 2024; 16(13):1863. https://doi.org/10.3390/w16131863
Chicago/Turabian StyleWang, Weizheng, Song Wei, Dayong Zhu, Jun Wang, and Haipeng Duan. 2024. "Characteristics and Mechanism of Downflow in Front of a Cylindrical Pier with Clear-Water Local Scour" Water 16, no. 13: 1863. https://doi.org/10.3390/w16131863
APA StyleWang, W., Wei, S., Zhu, D., Wang, J., & Duan, H. (2024). Characteristics and Mechanism of Downflow in Front of a Cylindrical Pier with Clear-Water Local Scour. Water, 16(13), 1863. https://doi.org/10.3390/w16131863






