Research on Internal Flow and Pressure Fluctuation Characteristics of Centrifugal Pumps as Turbines with Different Blade Wrap Angles
Abstract
1. Introduction
2. Entropy Production Theory
3. Geometric Model and Numerical Schemes
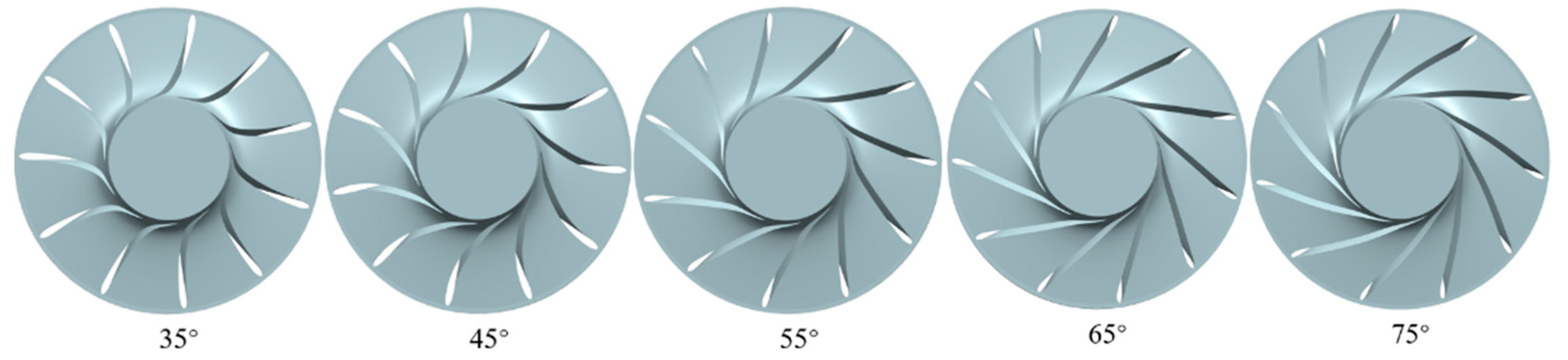
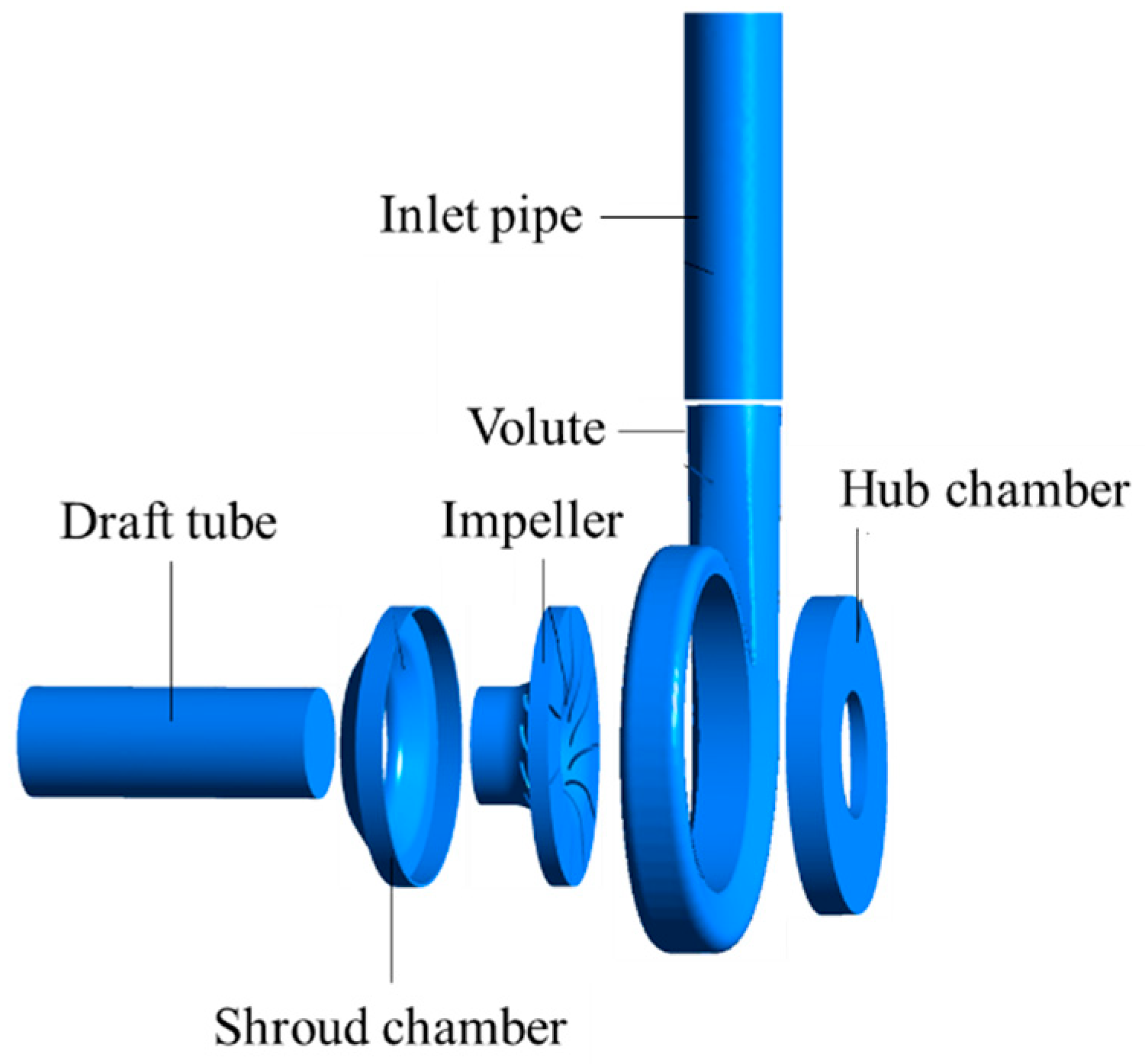
3.1. Pump-Turbine Model and Parameters
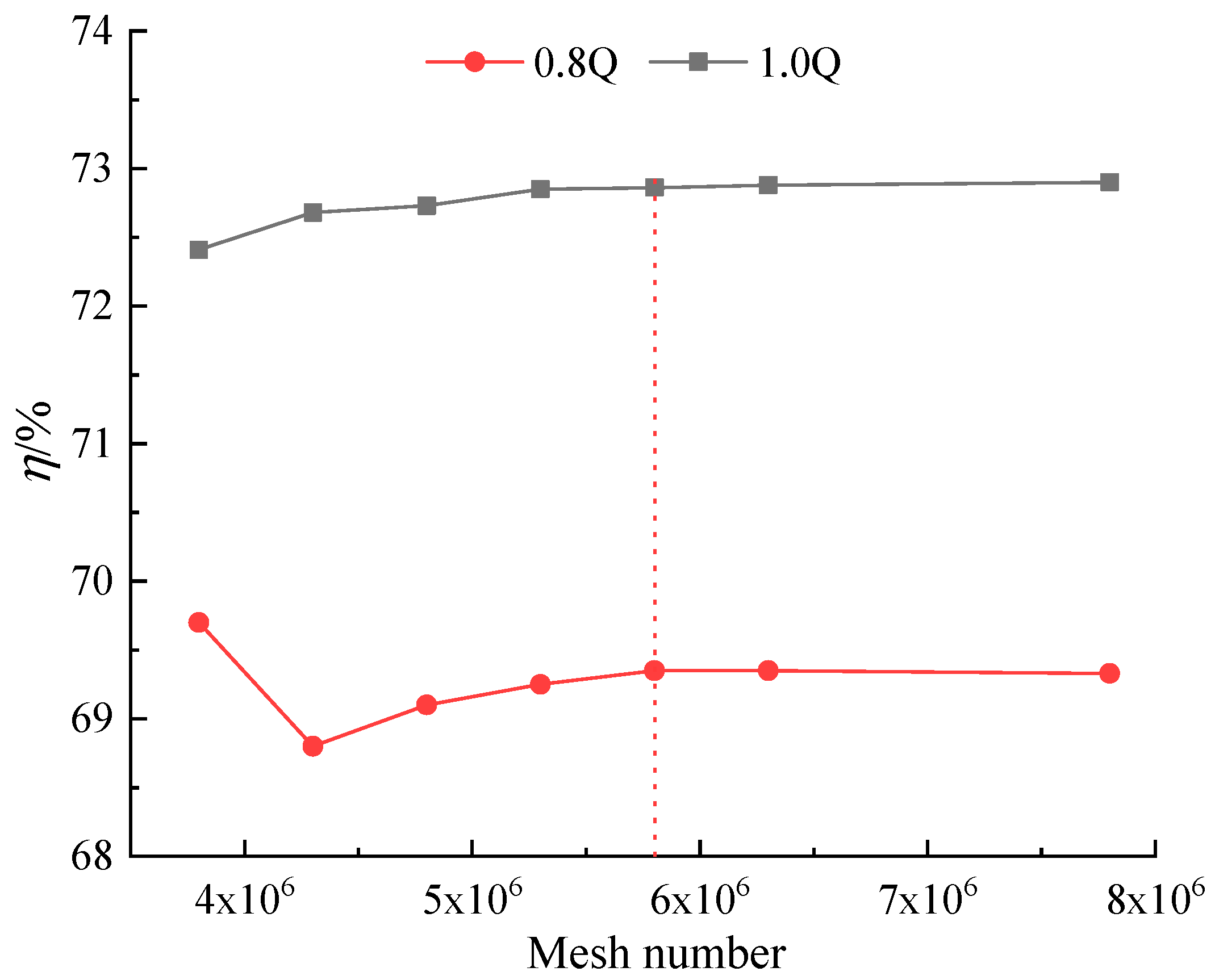
3.2. Mesh Generation and Independence Verification
3.3. Numerical Setting
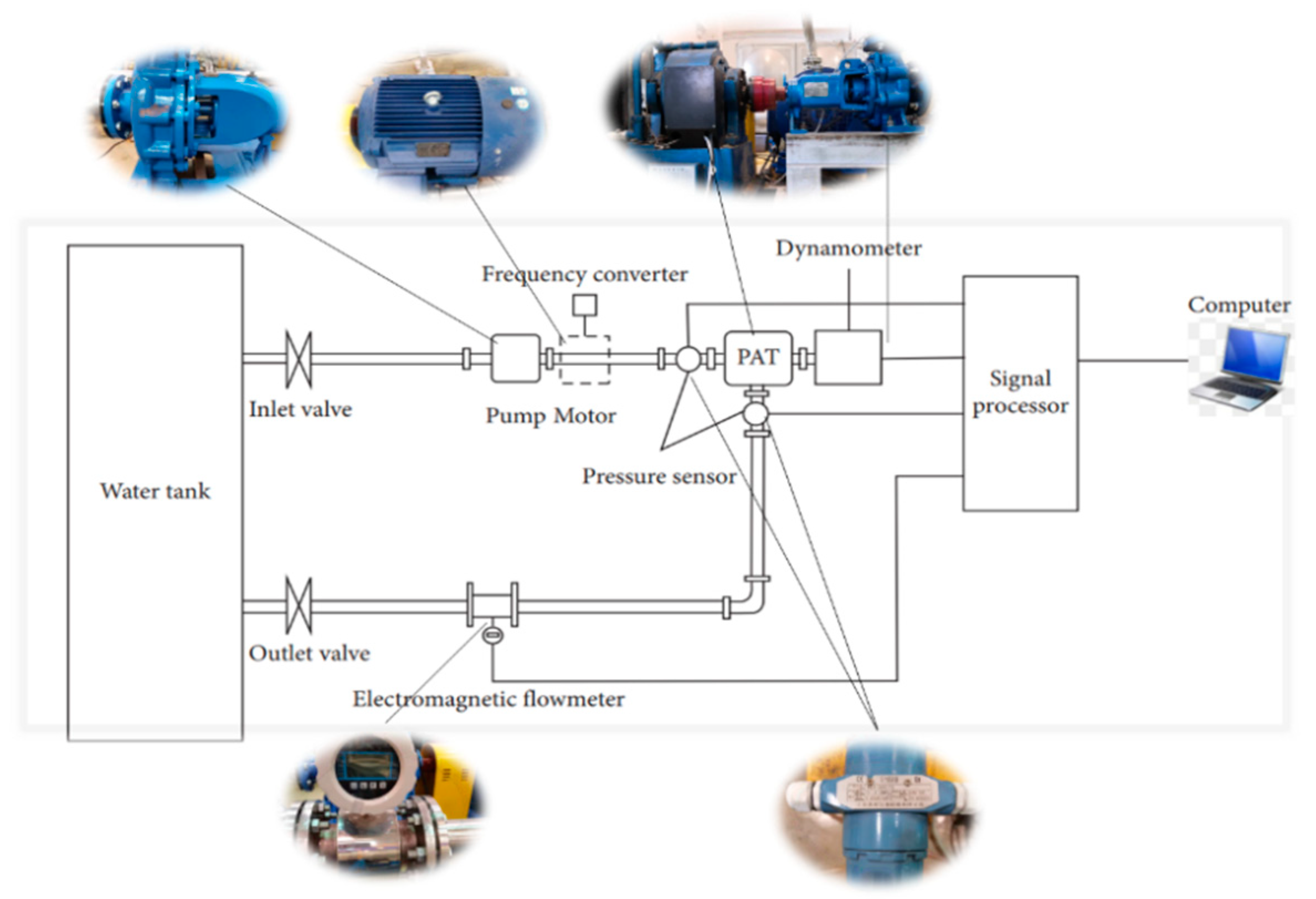
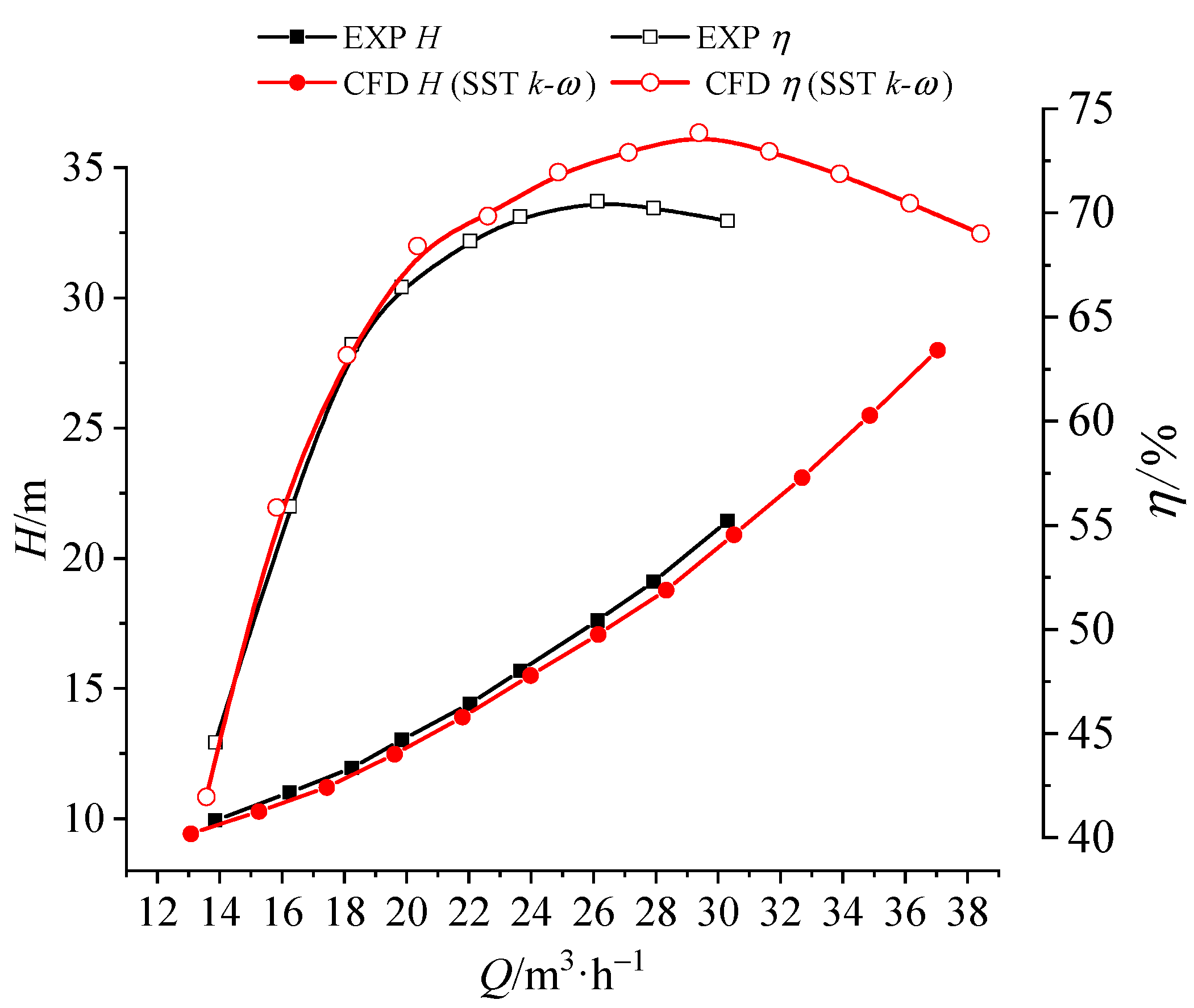
3.4. Verification of Computational Results through Experimental Studies
4. Results and Discussion
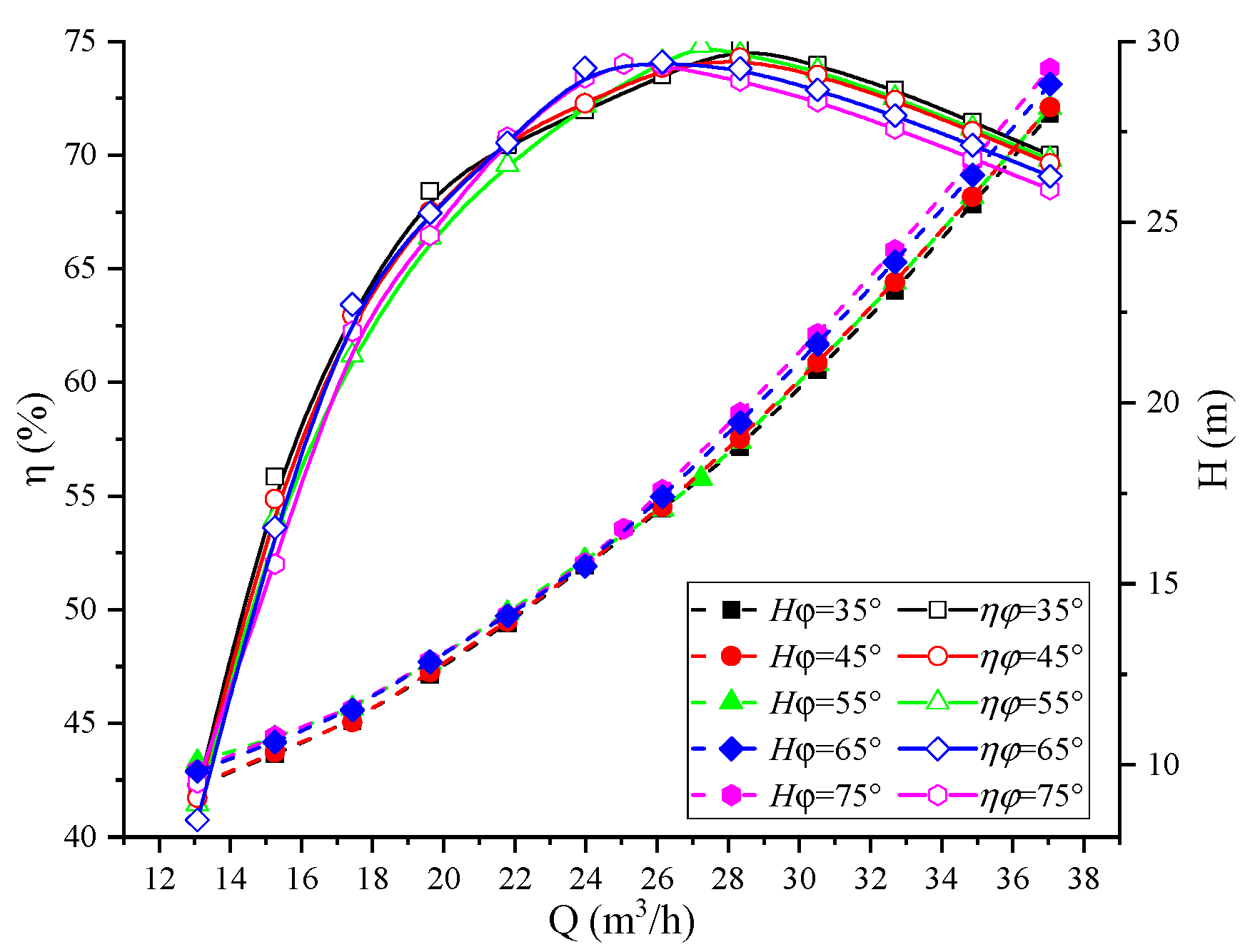
4.1. Analysis of Performance Curves
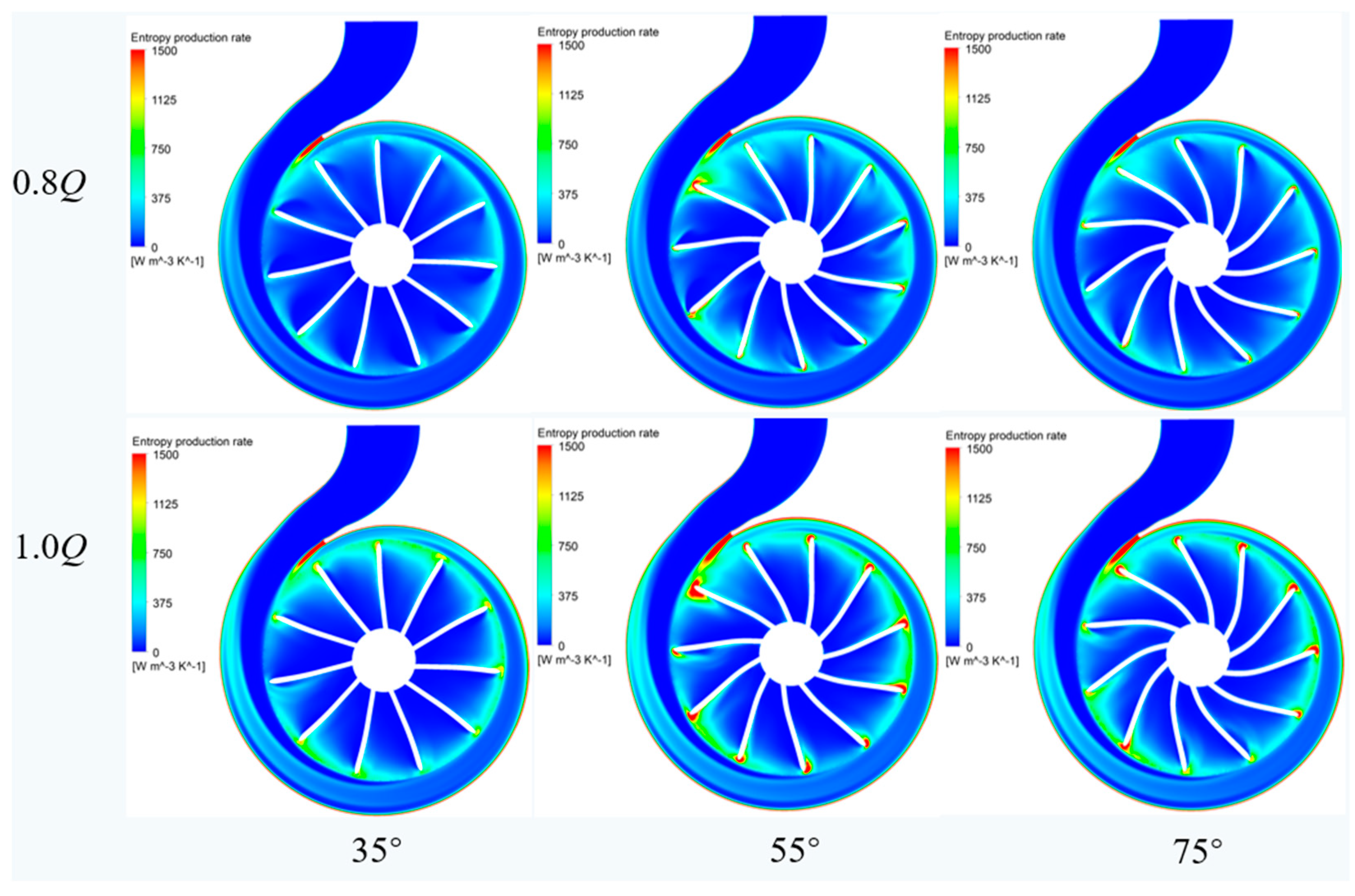
4.2. Entropy Production Analysis
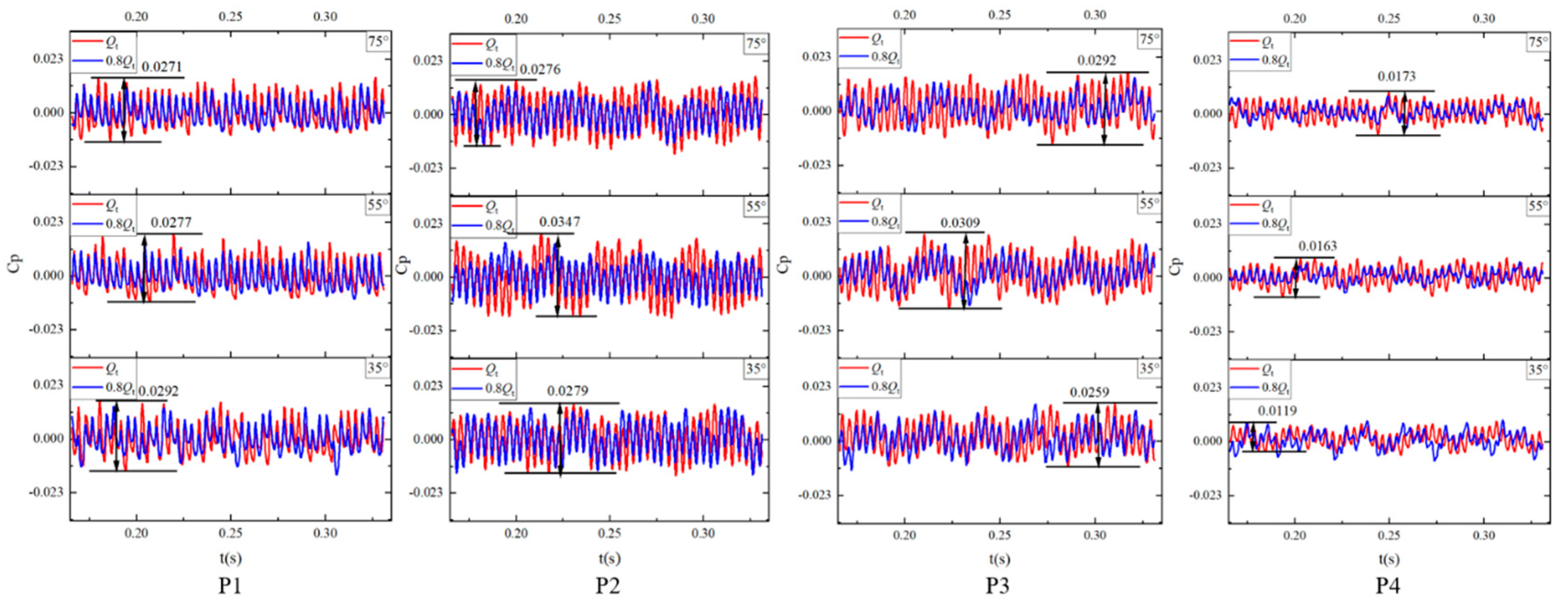
4.3. Transient Characteristics of Pressure Pulsation
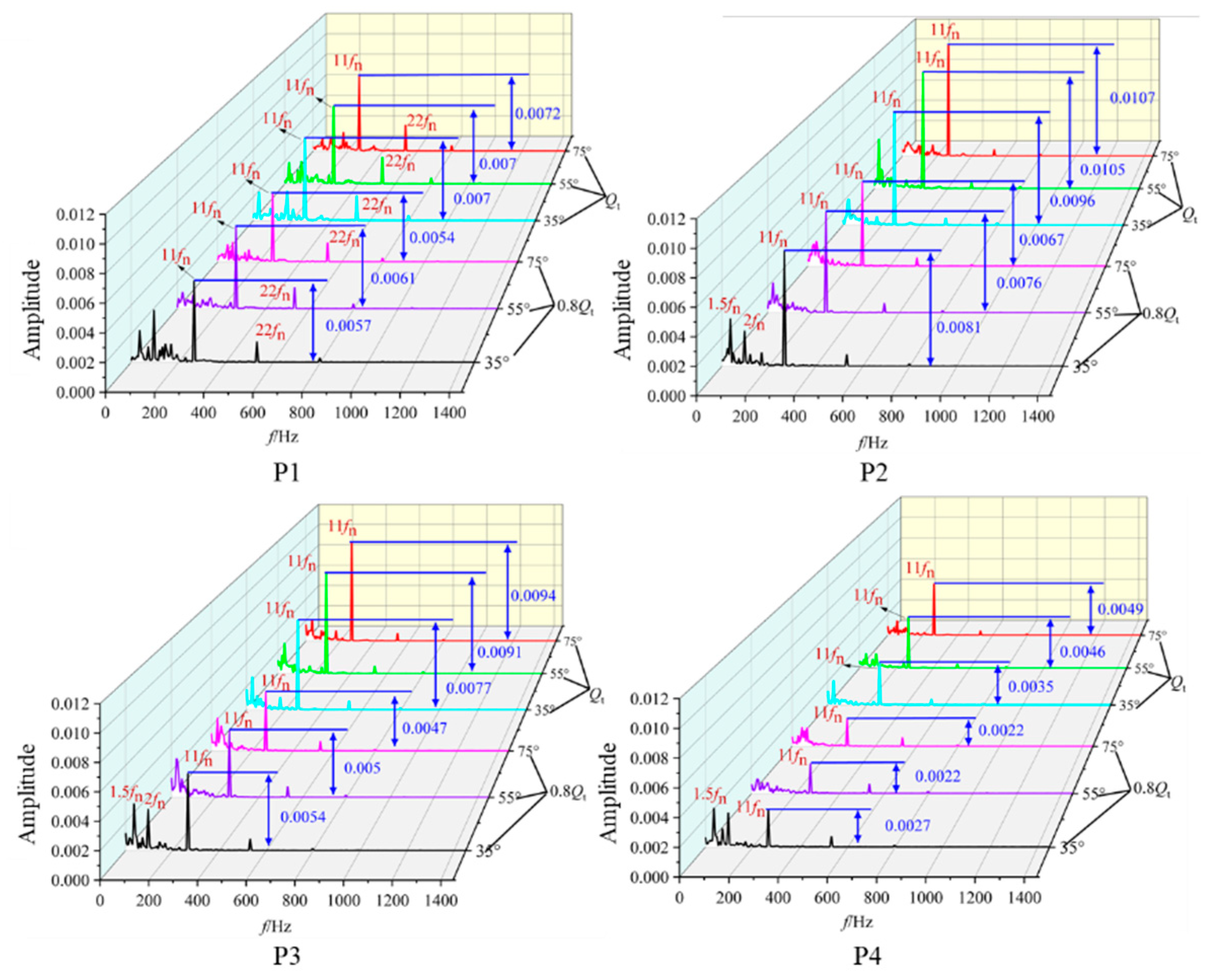
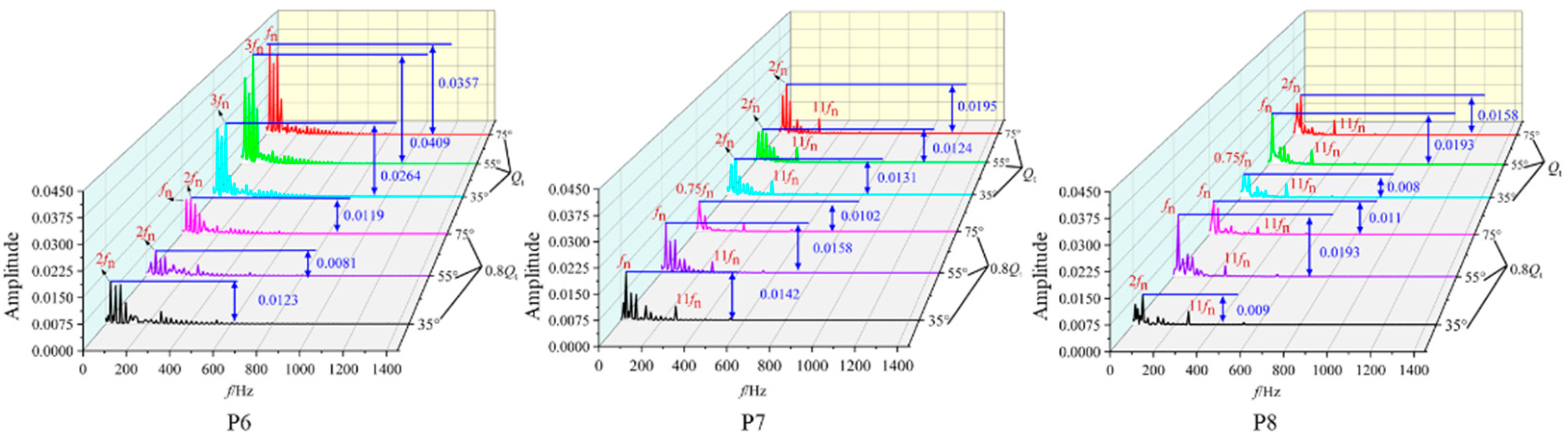
4.3.1. Circumferential Pressure Pulsation Characteristics of the Volute
4.3.2. Radial Pressure Pulsation Characteristics of the Impeller
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, Y.; Kong, F.; Yang, S.; Chen, K.; Dai, T. Effect of blade wrap angle in hydraulic turbine with forward-curved blades. Int. J. Hydrog. Energy 2017, 42, 18709–18717. [Google Scholar] [CrossRef]
- Williams, A.A.; Amiee, B.A. The Turbine Performance of Centrifugal Pumps: A Comparison of Prediction Methods. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 208, 59–66. [Google Scholar] [CrossRef]
- Zhou, L.; Hang, J.; Bai, L.; Krzemianowski, Z.; El-Emam, M.; Yasser, E.; Agarwal, R. Application of entropy production theory for energy losses and other investigation in pumps and turbines: A review. Appl. Energy 2022, 318, 119211. [Google Scholar] [CrossRef]
- Jain, S.V.; Patel, R.N. Investigations on pump running in turbine mode: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 2014, 30, 841–868. [Google Scholar] [CrossRef]
- Yang, S.; Liu, H.; Kong, F.; Dai, C.; Dong, L. Experimental, numerical, and theoretical research on impeller diameter influencing centrifugal pump-as-turbine. J. Energy Eng. 2013, 139, 299–307. [Google Scholar] [CrossRef]
- Yang, S.; Liu, H.; Kong, F.; Xia, B.; Tan, L. Effects of the radial gap between impeller tips and volute tongue influencing the performance and pressure pulsations of pump as turbine. J. Fluids Eng. 2014, 136, 054501. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Theoretical, numerical and experimental investigation of centrifugal pumps in reverse operation. Exp. Therm. Fluid Sci. 2008, 32, 1620–1627. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, Z.; Ran, J.; Li, H. Multi-objective parameter optimization of turbine impeller based on RBF neural network and NSGA-II genetic algorithm. Energy Rep. 2021, 7, 584–593. [Google Scholar] [CrossRef]
- Singh, P.; Nestmann, F. An optimization routine on a prediction and selection model for the turbine operation of centrifugal pumps. Exp. Therm. Fluid Sci. 2010, 34, 152–164. [Google Scholar] [CrossRef]
- Shi, F.X.; Yang, J.H.; Wang, X.H. Analysis on the effect of variable guide vane numbers on the performance of pump as turbine. Adv. Mech. Eng. 2018, 10, 1687814018780796. [Google Scholar] [CrossRef]
- Zhang, D.; Qi, B.; Zhao, R.; Zhang, Q. Optimization design of hydraulic model for seawater desalination energy recovery turbine. J. Drain. Irrig. Mach. Eng. 2021, 39, 649–654. [Google Scholar]
- Jain, S.V.; Swarnkar, A.; Motwani, K.H.; Patel, R.N. Effects of impeller diameter and rotational speed on performance of pump running in turbine mode. Energy Convers. Manag. 2015, 89, 808–824. [Google Scholar] [CrossRef]
- Binama, M.; Su, W.; Cai, W.; Li, X.; Muhirwa, A.; Li, B.; Bisengimana, E. Blade trailing edge position influencing pump as turbine (PAT) pressure field under part-load conditions. Renew. Energy 2019, 136, 33–47. [Google Scholar] [CrossRef]
- Wang, T.; Wang, C.; Kong, F.; Gou, Q.; Yang, S. Theoretical, experimental, and numerical study of special impeller used in turbine mode of centrifugal pump as turbine. Energy 2017, 130, 473–485. [Google Scholar] [CrossRef]
- Wang, T.; Kong, F.; Xia, B.; Bai, Y.; Wang, C. The method for determining blade inlet angle of special impeller using in turbine mode of centrifugal pump as turbine. Renew. Energy 2017, 109, 518–528. [Google Scholar] [CrossRef]
- Qi, B.; Zhang, D.; Geng, L.; Zhao, R.; van Esch, B.P.M. Numerical and experimental investigations on inflow loss in the energy recovery turbines with back-curved and front-curved impeller based on the entropy generation theory. Energy 2022, 239, 122426. [Google Scholar] [CrossRef]
- Wang, T.; Kong, F.; Liu, Y.; Wei, Q. Numerical simulation and validation of effects of blade inlet angle on performance of pump-as-turbine. Trans. Chin. Soc. Agric. Eng. 2017, 33, 98–104. [Google Scholar]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Qi, B.; Bai, X.; Li, Y.; Wang, X.; Zhang, X.; Zhang, D. Research on the influence mechanism of internal flow characteristics on energy conversion in radial energy recovery turbines under multiple conditions. Energy 2024, 296, 131191. [Google Scholar] [CrossRef]
- Qi, B.; Zhang, D.; Li, Y.; Shen, X.; van Esch, B.P.M. A comparative study on the reducing flow rate design method for a desalination energy recovery pump as turbine. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 441. [Google Scholar] [CrossRef]









| Component | Parameters | Value |
|---|---|---|
| Blade of PAT | impeller input diameter D1 (mm) | 160 |
| inlet width b1 (mm) | 8 | |
| blade leading-edge angle βb2 (°) | 90 | |
| blade trailing-edge angle βb1 (°) | 30 | |
| blade wrap angle φ (°) | 35 | |
| number of blades Z | 11 | |
| impeller outlet diameter D2 | 67.2 | |
| Volute | volute base circle D3 | 176 |
| volute outlet width b3 | 20 |
| Instrument | Type | Measured Parameters | Range | Accuracy |
|---|---|---|---|---|
| Battery-powered flowmeter | MEX-LDE | volume flow Q (m3/h) | 0–120 | ±0.5% |
| Pressure transmitter | MEX-3051TG | inlet and outlet pressure P (MPa) | 0–1.6 | ±0.05% |
| Eddy current dynamometer | CWF11D | torque M (N·m) | 0–35 | ±0.4% |
| Speed sensor | rotate speed n (r/min) | 0–10,000 | ±1 r/min | |
| Micro-dynamic pressure sensor | SCYG314 | pressure pulsation P (Pa) | 0–0.8 MPa | ±0.5% |
| Blade Wrap Angle (°) | ηmax (%) | 0.97ηmax (%) | Qmin (m3/h) | Qmax (m3/h) | Best Efficiency Range (m3/h) |
|---|---|---|---|---|---|
| 35 | 74.85 | 72.6 | 23.7 | 33.09 | 9.39 |
| 45 | 74.29 | 72.06 | 22.43 | 33.21 | 10.78 |
| 55 | 74.81 | 72.57 | 24.48 | 32.58 | 8.1 |
| 65 | 74.1 | 71.88 | 22.69 | 32.38 | 9.69 |
| 75 | 74.01 | 71.79 | 22.67 | 31.56 | 8.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; An, W.; Ke, E.; Ma, Y.; Geng, L.; Yang, G.; Zhang, D. Research on Internal Flow and Pressure Fluctuation Characteristics of Centrifugal Pumps as Turbines with Different Blade Wrap Angles. Water 2024, 16, 1861. https://doi.org/10.3390/w16131861
Xu H, An W, Ke E, Ma Y, Geng L, Yang G, Zhang D. Research on Internal Flow and Pressure Fluctuation Characteristics of Centrifugal Pumps as Turbines with Different Blade Wrap Angles. Water. 2024; 16(13):1861. https://doi.org/10.3390/w16131861
Chicago/Turabian StyleXu, Haibo, Weizheng An, Erqinhu Ke, Yingyi Ma, Linlin Geng, Gang Yang, and Desheng Zhang. 2024. "Research on Internal Flow and Pressure Fluctuation Characteristics of Centrifugal Pumps as Turbines with Different Blade Wrap Angles" Water 16, no. 13: 1861. https://doi.org/10.3390/w16131861
APA StyleXu, H., An, W., Ke, E., Ma, Y., Geng, L., Yang, G., & Zhang, D. (2024). Research on Internal Flow and Pressure Fluctuation Characteristics of Centrifugal Pumps as Turbines with Different Blade Wrap Angles. Water, 16(13), 1861. https://doi.org/10.3390/w16131861







