Prediction of Settling Velocity of Microplastics by Multiple Machine-Learning Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. Particle Preparation
2.2. Experimental Design
2.3. Data Collection
2.4. Training and Testing Subsets
2.5. Formula Calculation
3. Artificial Intelligence Model
3.1. Machine-Learning Model
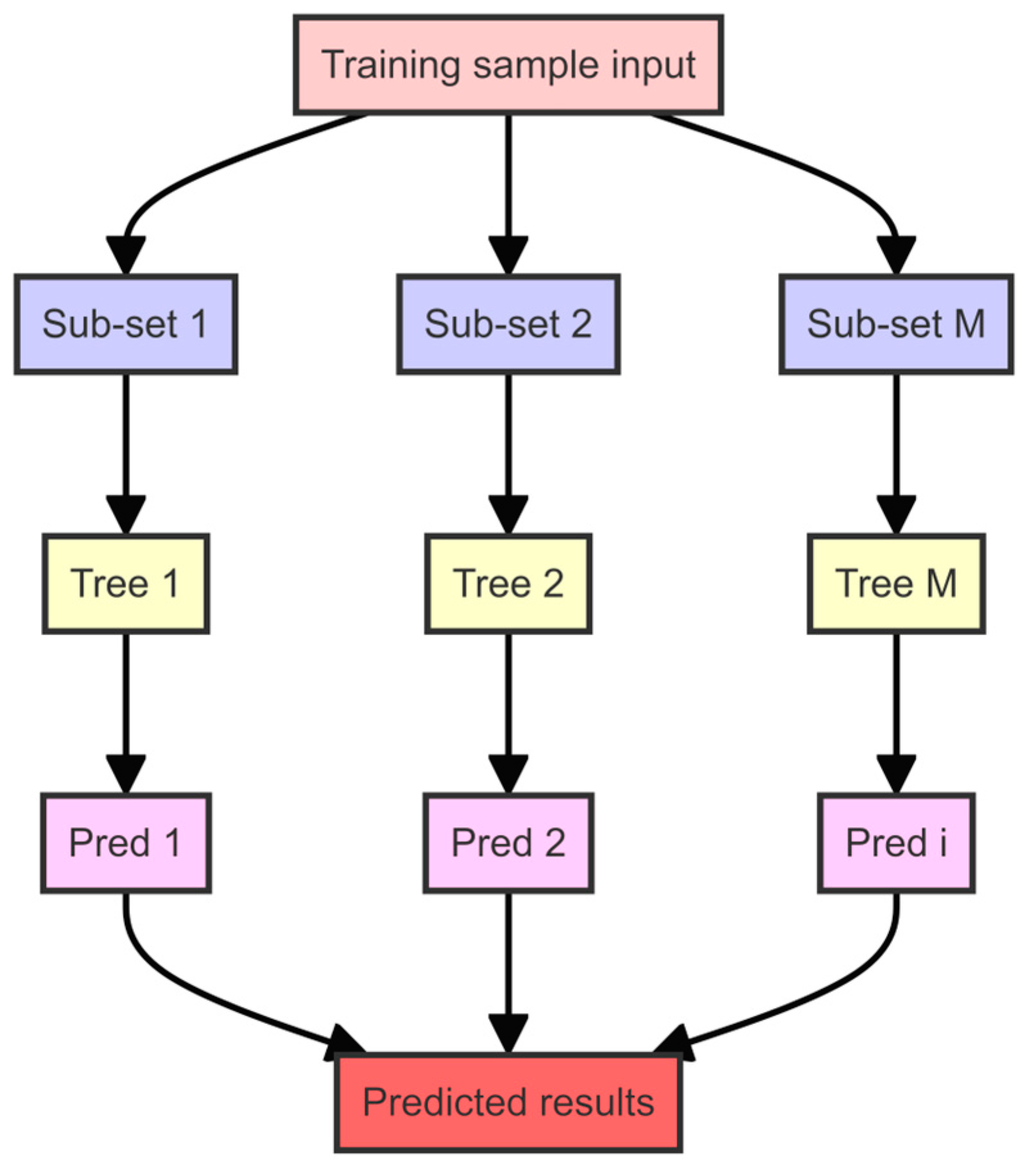
3.1.1. Random Forest
3.1.2. Linear Regression
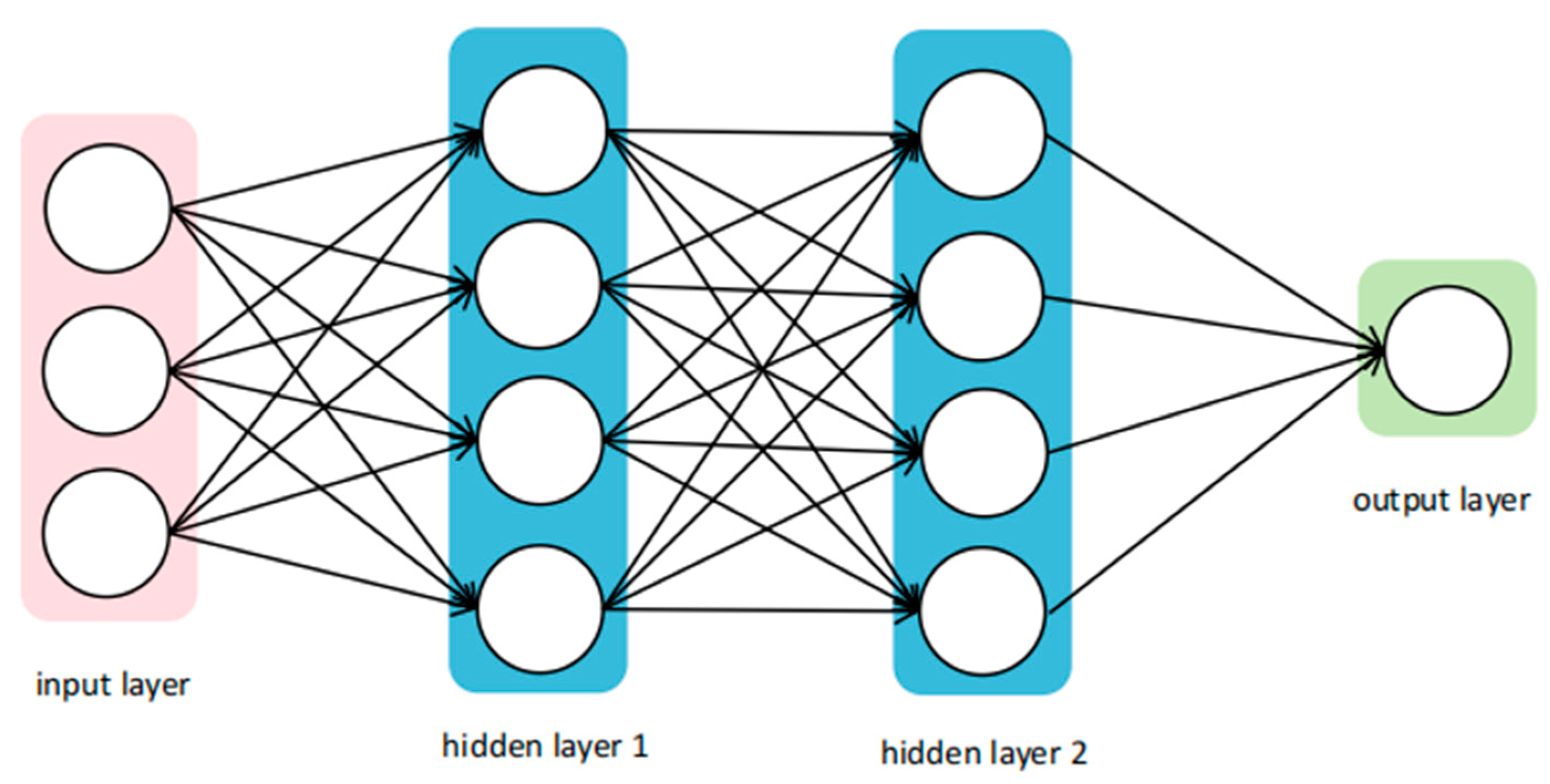
3.1.3. BPNN
3.2. Model Development
3.2.1. Random Forest Algorithm
3.2.2. Linear Regression Algorithm
3.2.3. BPNN
3.3. Modeling for the Regular Models
3.4. Evaluation of the Model
3.4.1. Mean Absolute Error (MAE)
3.4.2. Root Mean Square Error (RMSE)
3.4.3. Coefficient of Determination (R2)
4. Results and Discussion
4.1. Results
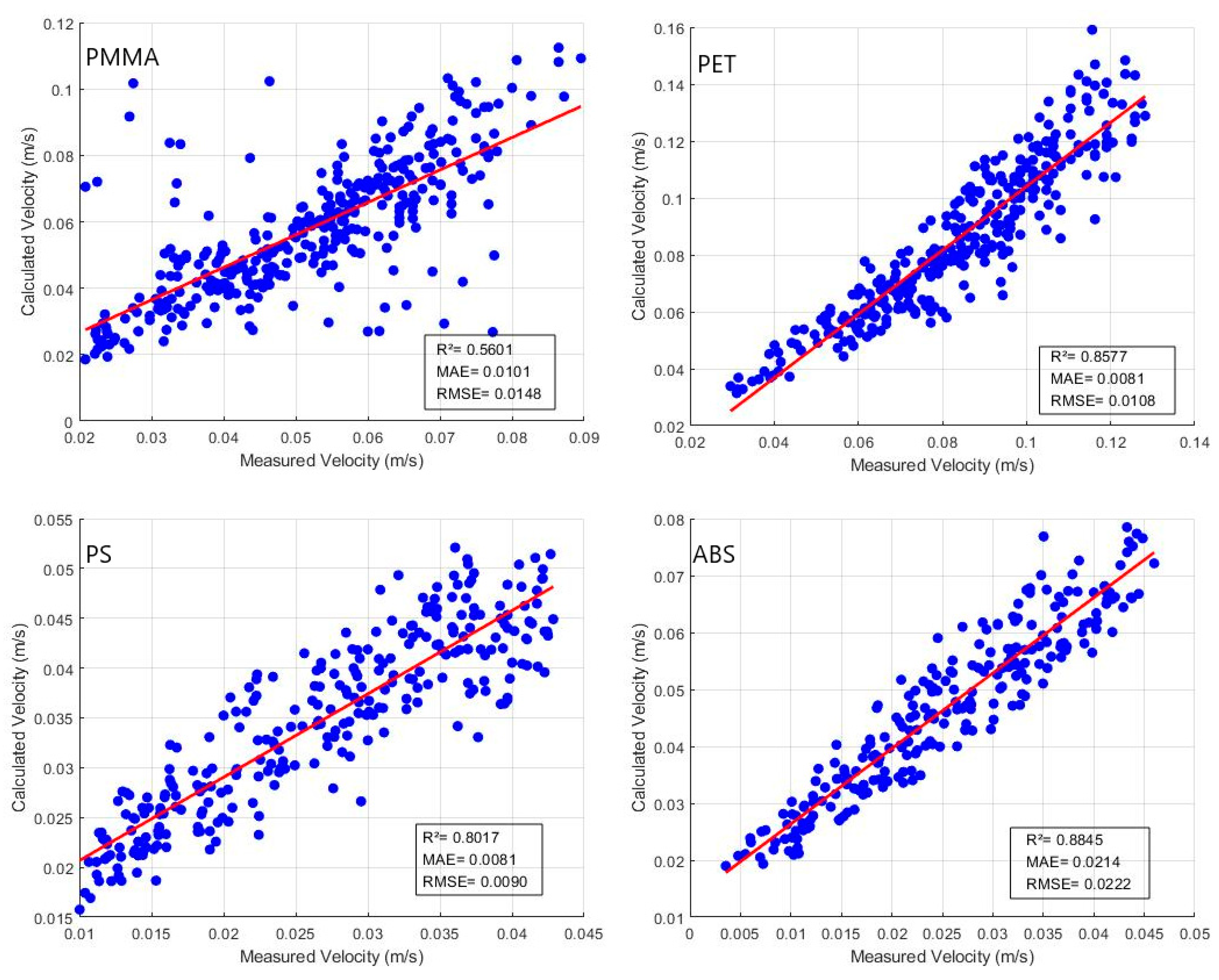
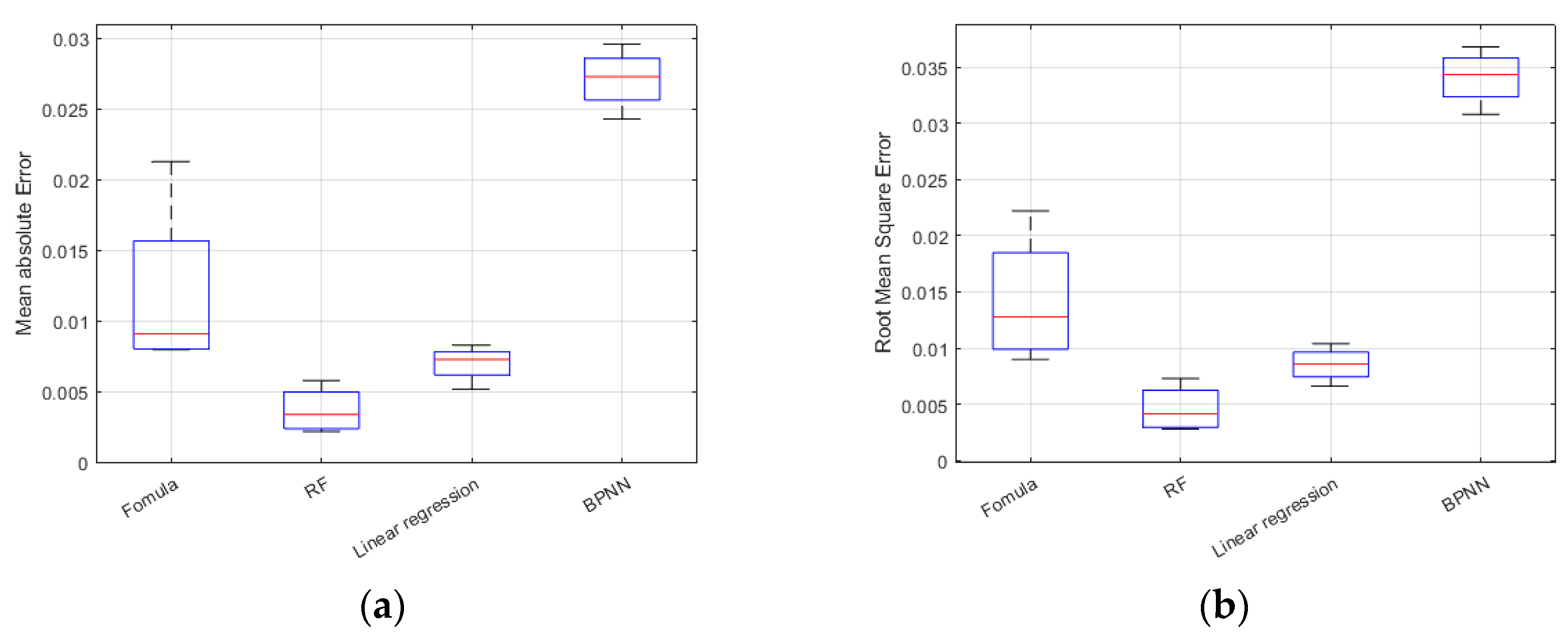
4.1.1. Formula Calculation Results Analysis
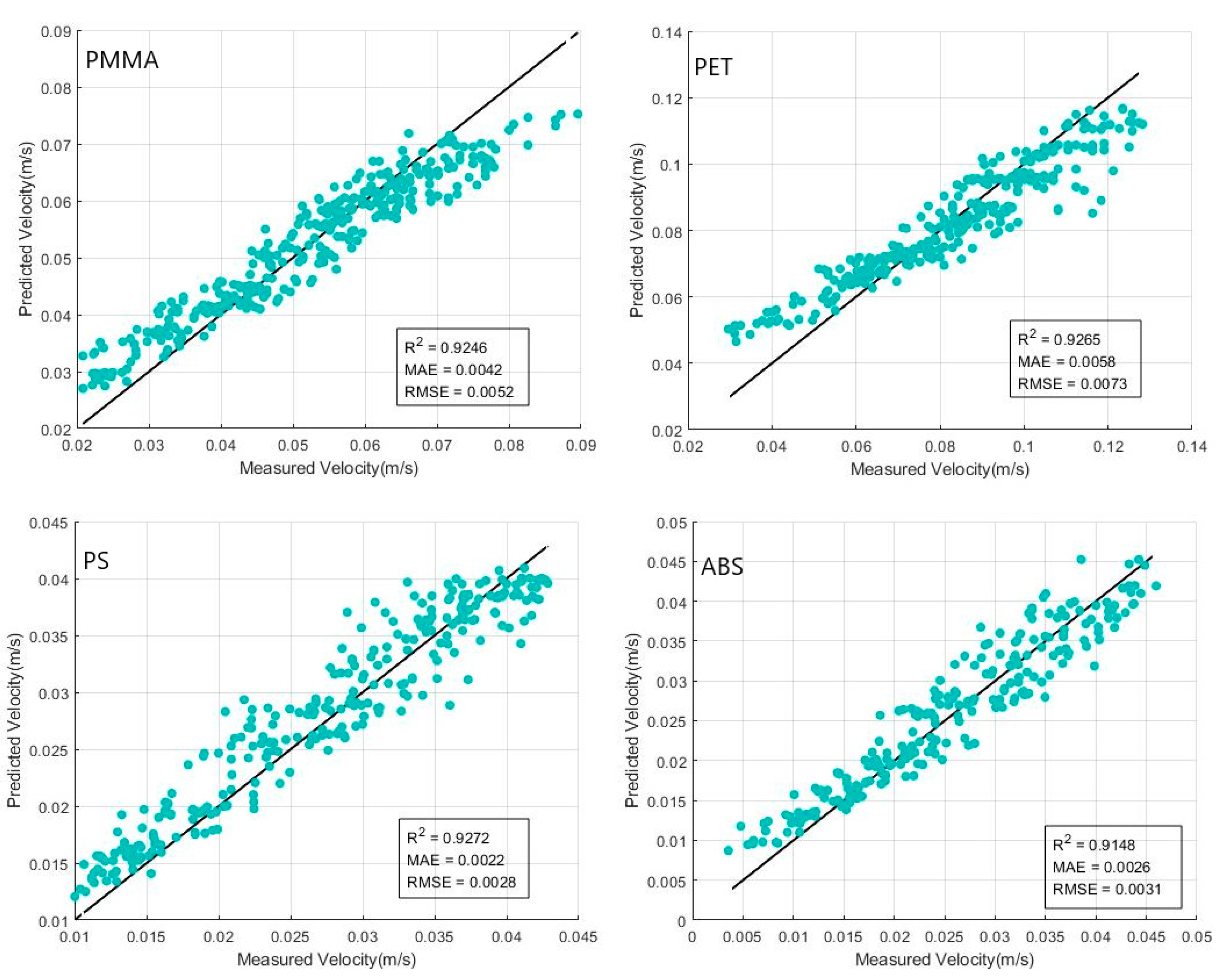
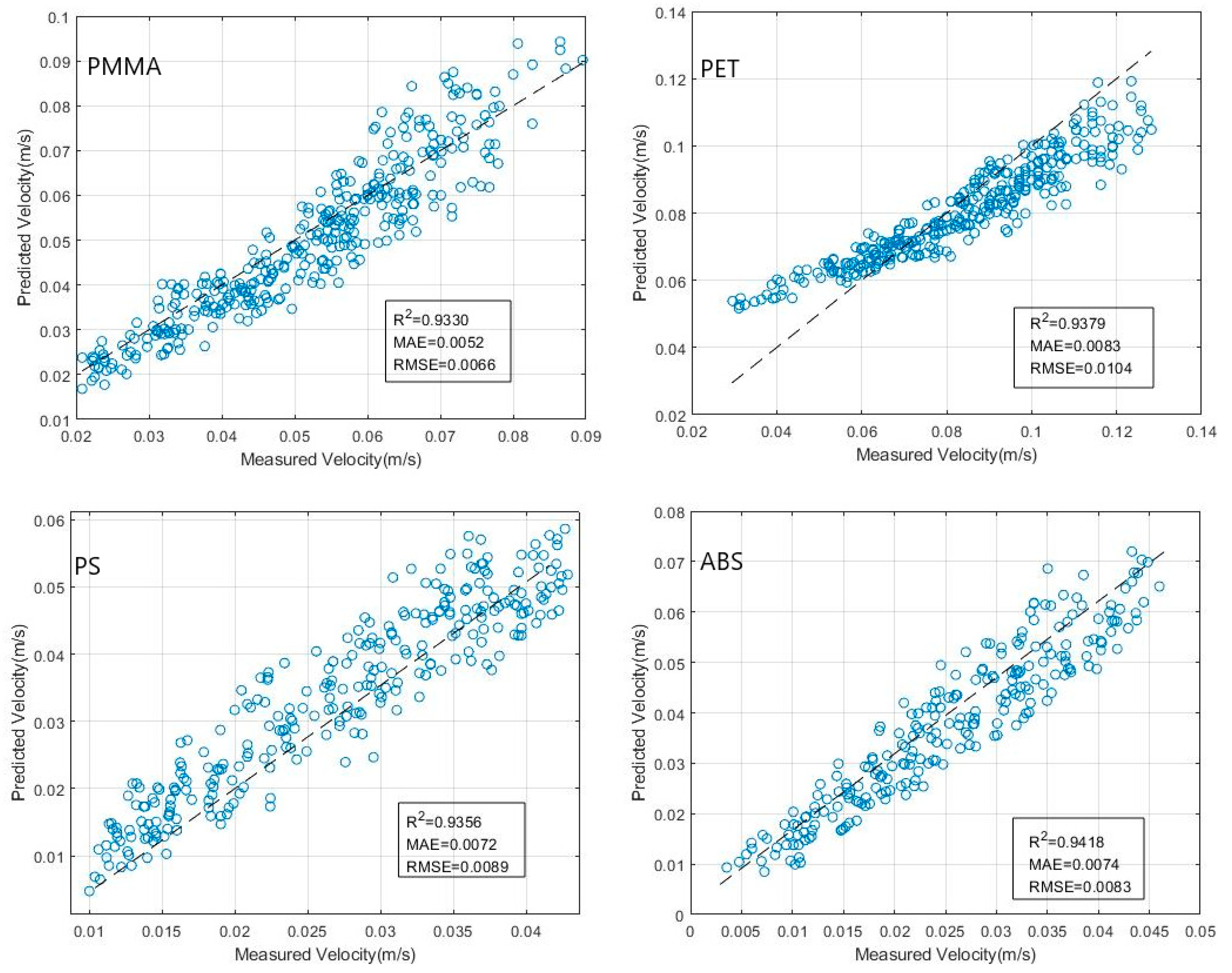
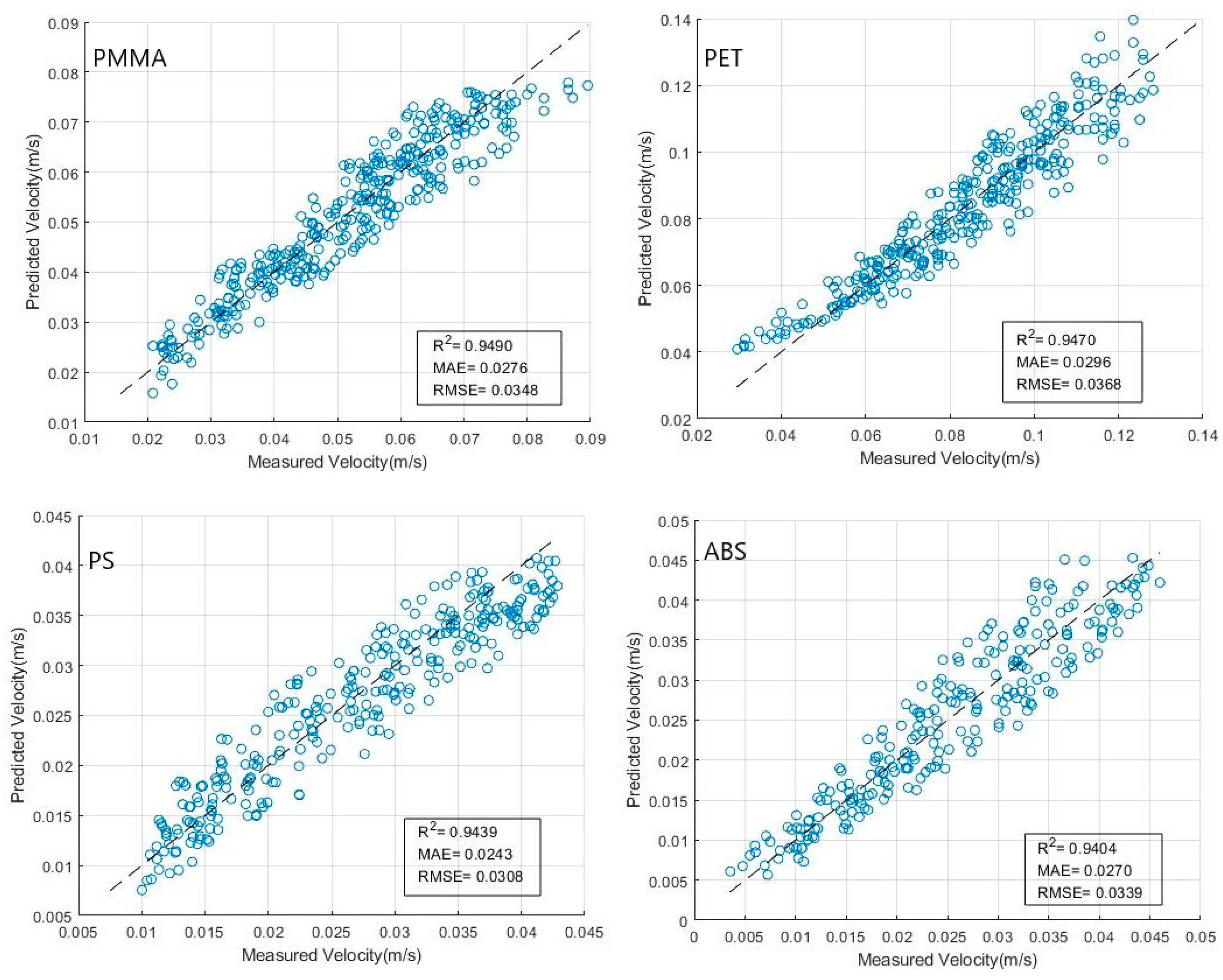
4.1.2. Machine-Learning Prediction Results Analysis
4.2. Discussion
4.3. Parameter Importance Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barnes, D.K.A.; Galgani, F.; Thompson, R.C.; Barlaz, M. Accumulation and fragmentation of plastic debris in global environments. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2009, 364, 1985–1998. [Google Scholar] [CrossRef] [PubMed]
- Reed, S.; Clark, M.; Thompson, R.; Hughes, K.A. Microplastics in marine sediments near Rothera Research Station, Antarctica. Mar. Pollut. Bull. 2018, 133, 460–463. [Google Scholar] [CrossRef]
- La Daana, K.K.; Johansson, C.; Frias, J.P.G.L.; Gardfeldt, K.; Thompson, R.C.; O’Connor, I. Deep sea sediments of the Arctic Central Basin: A potential sink for microplastics. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2019, 145, 137–142. [Google Scholar] [CrossRef]
- Khatmullina, L.; Isachenko, I. Settling velocity of microplastic particles of regular shapes. Mar. Pollut. Bull. 2017, 114, 871–880. [Google Scholar] [CrossRef] [PubMed]
- Avio, C.G.; Gorbi, S.; Milan, M.; Benedetti, M.; Fattorini, D.; D’Errico, G.; Pauletto, M.; Bargelloni, L.; Regoli, F. Pollutants bioavailability and toxicological risk from microplastics to marine mussels. Environ. Pollut. 2015, 198, 211–222. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, G.; Zhang, W. A new model for the terminal settling velocity of microplastics. Mar. Pollut. Bull. 2022, 176, 113449. [Google Scholar] [CrossRef] [PubMed]
- Mason, R.A.; Kukulka, T.; Cohen, J.H. Effects of particle buoyancy, release location, and diel vertical migration on exposure of marine organisms to microplastics in Delaware Bay. Estuar. Coast. Shelf Sci. 2022, 275, 107990. [Google Scholar] [CrossRef]
- Critchell, K.; Lambrechts, J. Modelling accumulation of marine plastics in the coastal zone; what are the dominant physical processes? Estuar. Coast. Shelf Sci. 2016, 171, 111–122. [Google Scholar] [CrossRef]
- Ballent, A.; Purser, A.; de Jesus Mendes, P.; Pando, S.; Thomsen, L. Physical transport properties of marine microplastic pollution. Biogeosciences Discuss. 2012, 9, 18755–18798. [Google Scholar] [CrossRef]
- Kowalski, N.; Reichardt, A.M.; Waniek, J.J. Sinking rates of microplastics and potential implications of their alteration by physical, biological, and chemical factors. Mar. Pollut. Bull. 2016, 109, 310–319. [Google Scholar] [CrossRef]
- Chubarenko, I.; Bagaev, A.; Zobkov, M.; Esiukova, E. On some physical and dynamical properties of microplastic particles in marine environment. Mar. Pollut. Bull. 2016, 108, 105–112. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Baxter, S.L.; Xu, J.; Xu, J.; Zhou, X.; Zhang, K. The practical implementation of artificial intelligence technologies in medicine. Nat. Med. 2019, 25, 30–36. [Google Scholar] [CrossRef] [PubMed]
- Abkenar, S.B.; Mahdipour, E.; Jameii, S.M.; Kashani, M.H. A hybrid classification method for Twitter spam detection based on differential evolution and random forest. Concurr. Comput. Pract. Exp. 2021, 33, e6381. [Google Scholar] [CrossRef]
- Liang, G.; Fan, W.; Luo, H.; Zhu, X. The emerging roles of artificial intelligence in cancer drug development and precision therapy. Biomed. Pharmacother. 2020, 128, 110255. [Google Scholar] [CrossRef] [PubMed]
- Liou, J.-L.; Liao, K.-C.; Wen, H.-T.; Wu, H.-Y. A study on nitrogen oxide emission prediction in Taichung thermal power plant using artificial intelligence (AI) model. Int. J. Hydrogen Energy 2024, 63, 1–9. [Google Scholar] [CrossRef]
- El-Mahdy, M.E.-S.; Mousa, F.A.; Morsy, F.I.; Kamel, A.F.; El-Tantawi, A. Flood classification and prediction in South Sudan using artificial intelligence models under a changing climate. Alex. Eng. J. 2024, 97, 127–141. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, L.; Shi, J. Performance prediction of a supercritical CO2 Brayton cycle integrated with wind farm-based molten salt energy storage: Artificial intelligence (AI) approach. Case Stud. Therm. Eng. 2023, 51, 103533. [Google Scholar] [CrossRef]
- Han, X.; Zhu, J.; Li, H.; Xu, W.; Feng, J.; Hao, L.; Wei, H. Deep learning-based dispersion prediction model for hazardous chemical leaks using transfer learning. Process. Saf. Environ. Prot. 2024, 188, 363–373. [Google Scholar] [CrossRef]
- Xiao, L.; Shi, G.; Song, W. Machine learning predictions on the compressive stress–strain response of lattice-based metamaterials. Int. J. Solids Struct. 2024, 300, 112893. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, Y.; Sekula, P.; Ding, L. Machine learning in construction: From shallow to deep learning. Dev. Built Environ. 2021, 6, 100045. [Google Scholar] [CrossRef]
- Rooki, R.; Ardejani, F.D.; Moradzadeh, A.; Kelessidis, V.; Nourozi, M. Prediction of terminal velocity of solid spheres falling through Newtonian and non-Newtonian pseudoplastic power law fluid using artificial neural network. Int. J. Miner. Process. 2012, 110–111, 53–61. [Google Scholar] [CrossRef]
- Agwu, O.E.; Akpabio, J.U.; Dosunmu, A. Artificial neural network model for predicting drill cuttings settling velocity. Petroleum 2020, 6, 340–352. [Google Scholar] [CrossRef]
- Goldstein, E.B.; Coco, G. A machine learning approach for the prediction of settling velocity. Water Resour. Res. 2014, 50, 3595–3601. [Google Scholar] [CrossRef]
- Van Melkebeke, M.; Janssen, C.; De Meester, S. Characteristics and sinking behavior of typical microplastics including the potential effect of biofouling: Implications for remediation. Environ. Sci. Technol. 2020, 54, 8668–8680. [Google Scholar] [CrossRef] [PubMed]
- Francalanci, S.; Paris, E.; Solari, L. On the prediction of settling velocity for plastic particles of different shapes. Environ. Pollut. 2021, 290, 118068. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.G.; Strom, K.B.; Keyvani, A. Floc properties and settling velocity of San Jacinto estuary mud under variable shear and salinity conditions. Cont. Shelf Res. 2010, 30, 2067–2081. [Google Scholar] [CrossRef]
- Corey, A.T.; Albertson, M.L.; Fults, J.L.; Rollins, R.L.; Gardner, R.A.; Klinger, B.; Bock, R.O. Influence of Shape on the Fall Velocity of Sand Grains. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 1949. [Google Scholar]
- Hazzab, A.; Terfous, A.; Ghenaim, A. Measurement and modeling of the settling velocity of isometric particles. Powder Technol. 2008, 184, 105–113. [Google Scholar] [CrossRef]
- Wang, Z.; Dou, M.; Ren, P.; Sun, B.; Jia, R.; Zhou, Y. Settling velocity of irregularly shaped microplastics under steady and dynamic flow conditions. Environ. Sci. Pollut. Res. 2021, 28, 62116–62132. [Google Scholar] [CrossRef]



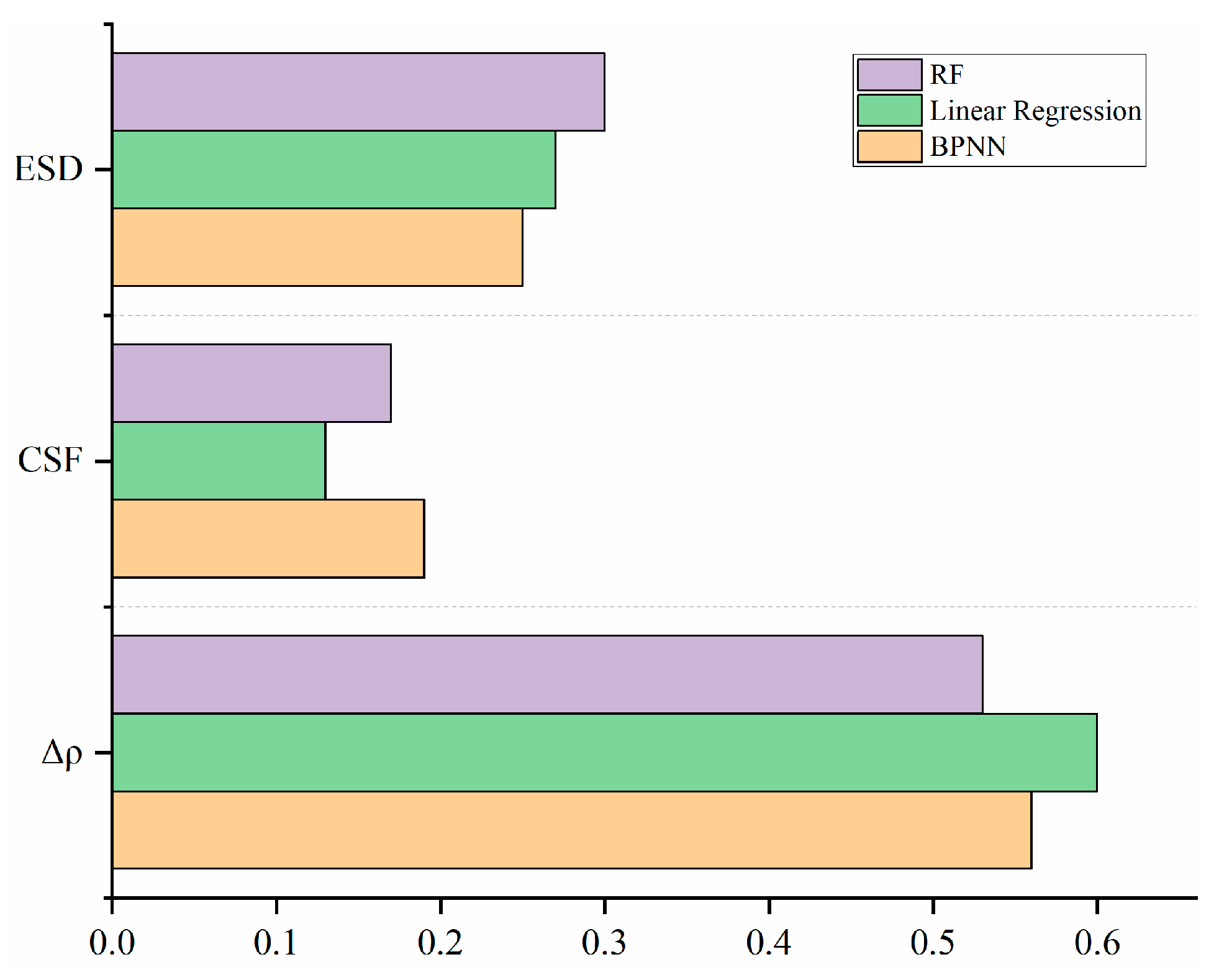
| Mps | Quantity | ESD (mm) | (g/cm3) | csf | ||||
|---|---|---|---|---|---|---|---|---|
| Particle | Maximum | Minimum | Average Values | Maximum | Minimum | Average Values | ||
| PS | 286 | 3.81 | 1.28 | 2.53 | 1.05 | 0.99 | 0.56 | 0.82 |
| ABS | 238 | 4.06 | 0.72 | 2.23 | 1.10 | 0.99 | 0.64 | 0.88 |
| PMMA | 340 | 4.66 | 0.81 | 2.33 | 1.19 | 0.98 | 0.39 | 0.74 |
| PET | 319 | 4.40 | 0.64 | 2.24 | 1.39 | 0.99 | 0.57 | 0.82 |
| Mps | Quantity | ESD | (m/s) | ||
|---|---|---|---|---|---|
| Particle | (mm) | Maximum | Minimum | Average Values | |
| PS | 286 | 1.28–3.81 | 0.0428 | 0.0100 | 0.0270 |
| ABS | 238 | 0.72–4.06 | 0.0459 | 0.0035 | 0.0254 |
| PMMA | 340 | 0.81–4.66 | 0.0895 | 0.0208 | 0.0520 |
| PET | 319 | 0.64–4.40 | 0.1282 | 0.0296 | 0.0838 |
| Mps | Quantity | ESD | csf | ||
|---|---|---|---|---|---|
| Particle | (mm) | (g/cm3) | (m/s) | ||
| PS | 286 | 1.28–3.81 | 1.05 | 0.56–0.98 | 0.0100–0.0428 |
| ABS | 238 | 0.72–4.06 | 1.10 | 0.64–0.99 | 0.0035–0.0459 |
| PMMA | 340 | 0.81–4.66 | 1.19 | 0.39–0.98 | 0.0208–0.0895 |
| PET | 319 | 0.64–4.40 | 1.39 | 0.57–0.99 | 0.0296–0.1282 |
| Source | Particle Materials | Shape | Data Points | Equivalent Spherical Diameter [mm] | Ρ (g/cm3) | CSF | (m/s) |
|---|---|---|---|---|---|---|---|
| Yu et al. [6] | PET | Fragment | 95 | 0.56–2.79 | 1.39 | 0.06–0.34 | 0.019–0.07 |
| PVC | Nodular, fiber | 134 | 0.61–3.55 | 1.14–1.56 | 0.34–0.48 | 0.02–0.06 | |
| PCL | Cylinder, sphere | 37 | 1.03–2.02 | 1.131 | 0.95 | 0.03–0.06 | |
| Fish line | \ | 241 | 0.20–1.57 | 1.13–1.168 | 0.16–0.99 | 0.003–0.05 | |
| PMMA | \ | 73 | 0.48–2.30 | 1.19 | 0.60 | 0.009–0.05 | |
| POM | \ | 68 | 0.55–2.25 | 1.42 | 0.11 | 0.01–0.04 | |
| PS | Fragment, pellet, cylinder | 51 | 0.50–2.12 | 1.05–1.055 | 0.04–1.00 | 0.004–0.02 | |
| Van Melkebeke et al. [24] | PET | Fragment | 20 | 1.37–2.80 | 1.37 | 0.07~0.83 | 0.01–0.10 |
| PVC | Fiber | 20 | 0.64–1.61 | 1.43 | 0.02~0.16 | 0.007–0.02 | |
| PE | Film | 20 | 1.25–2.13 | 0.95–1.01 | 0.01~0.06 | 0.004–0.02 | |
| Francalanci et al. [25] | PVC | Pellet | 38 | 1.68–4.94 | 1.084–1.25 | 0.25–0.85 | 0.069–0.156 |
| PET | Pellet, fragment | 70 | 2.3–5.44 | 1.10–1.37 | 0.10~0.79 | 0.022–0.177 | |
| ABS | Pellet | 30 | 2.41–2.89 | 1.04 | 0.65 | 0.03–0.0467 | |
| PS | Pellet | 30 | 3.31–4.14 | 1.03 | 0.80 | 0.034–0.057 |
| Model | Main Parameter Setting |
|---|---|
| RF | The minimum number of leaf node samples: 1–30 Decision trees: 10–100 Maximum tree depth = 3 |
| Linear regression | Function: fillm |
| BPNN | Hidden layers: 2 Neurons in first layer: 20 Neurons in second layer: 10 Maximum epochs N = 2000 Learning rate = |
| Mps | Quantity | (m/s) | ||
|---|---|---|---|---|
| Particle | Maximum | Minimum | Average Values | |
| PMMA | 340 | 0.112 | 0.019 | 0.058 |
| PET | 319 | 0.159 | 0.031 | 0.086 |
| PS | 286 | 0.052 | 0.016 | 0.035 |
| ABS | 238 | 0.078 | 0.019 | 0.047 |
| Mps | Quantity | R2 | MAE | RMSE |
|---|---|---|---|---|
| Particle | ||||
| PMMA | 340 | 0.5601 | 0.0101 | 0.0147 |
| PET | 319 | 0.8577 | 0.0081 | 0.0108 |
| PS | 286 | 0.8017 | 0.0080 | 0.0089 |
| ABS | 238 | 0.8845 | 0.0213 | 0.0222 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, Z.; Cao, L.; Gao, Y.; Hou, Y.; Wu, D.; Huo, Z.; Zhao, X. Prediction of Settling Velocity of Microplastics by Multiple Machine-Learning Methods. Water 2024, 16, 1850. https://doi.org/10.3390/w16131850
Leng Z, Cao L, Gao Y, Hou Y, Wu D, Huo Z, Zhao X. Prediction of Settling Velocity of Microplastics by Multiple Machine-Learning Methods. Water. 2024; 16(13):1850. https://doi.org/10.3390/w16131850
Chicago/Turabian StyleLeng, Zequan, Lu Cao, Yun Gao, Yadong Hou, Di Wu, Zhongyan Huo, and Xizeng Zhao. 2024. "Prediction of Settling Velocity of Microplastics by Multiple Machine-Learning Methods" Water 16, no. 13: 1850. https://doi.org/10.3390/w16131850
APA StyleLeng, Z., Cao, L., Gao, Y., Hou, Y., Wu, D., Huo, Z., & Zhao, X. (2024). Prediction of Settling Velocity of Microplastics by Multiple Machine-Learning Methods. Water, 16(13), 1850. https://doi.org/10.3390/w16131850







