Abstract
Advances in convolutional neural networks (CNNs) provide novel and alternative solutions for water quality management. This paper evaluates state-of-the-art optimization strategies available in PyTorch to date using AlexNet, a simple yet powerful CNN model. We assessed twelve optimization algorithms: Adadelta, Adagrad, Adam, AdamW, Adamax, ASGD, LBFGS, NAdam, RAdam, RMSprop, Rprop, and SGD under default conditions. The AlexNet model, pre-trained and coupled with a Multiple Linear Regression (MLR) model, was used to estimate the quantity black pixels (suspended solids) randomly distributed on a white background image, representing total suspended solids in liquid samples. Simulated images were used instead of real samples to maintain a controlled environment and eliminate variables that could introduce noise and optical aberrations, ensuring a more precise evaluation of the optimization algorithms. The performance of the CNN was evaluated using the accuracy, precision, recall, specificity, and F_Score metrics. Meanwhile, MLR was evaluated with the coefficient of determination (), mean absolute and mean square errors. The results indicate that the top five optimizers are Adagrad, Rprop, Adamax, SGD, and ASGD, with accuracy rates of 100% for each optimizer, and values of 0.996, 0.959, 0.971, 0.966, and 0.966, respectively. Instead, the three worst performing optimizers were Adam, AdamW, and NAdam with accuracy rates of 22.2%, 11.1% and 11.1%, and values of 0.000, 0.148, and 0.000, respectively. These findings demonstrate the significant impact of optimization algorithms on CNN performance and provide valuable insights for selecting suitable optimizers to water quality assessment, filling existing gaps in the literature. This motivates further research to test the best optimizer models using real data to validate the findings and enhance their practical applicability, explaining how the optimizers can be used with real data.
1. Introduction
Water quality is an essential aspect of public health and environmental sustainability. The presence of contaminants, such as total suspended solids (TSS), significantly impacts the potability and safety of the water supply, posing substantial challenges to effective monitoring and maintenance [1]. Water quality also has important consequences for aquatic ecosystems and biodiversity. Turbidity, a key indicator of water quality, is influenced by the concentration of TSS. High turbidity levels can interfere with aquatic habitats, affect species that depend on water for their survival, and contribute to the degradation of river and marine ecosystems [2]. Ensuring water quality is therefore essential not only to protect human health but also to preserve the integrity and functioning of aquatic ecosystems [3].
TSS are related to the accumulation of organic and inorganic matter, feed residues, and aquatic microorganisms. They are defined as the amount of mass present in a water column (mg/L) [4]. Meanwhile, turbidity is the degree of loss of water transparency due to TSS [5]. Both tend to increase almost proportionally [6]. There are different methods to calculate and monitor them. Method 180.1 by the U.S. EPA, known as nephelometry, is based on comparing the intensity of light scattered by a reference sample and the sample being measured. The measurement ranges between 0 and 40 NTU (nephelometric turbidity units) and, to achieve higher values, the samples must be diluted in water and the measurement rescaled [7]. This method is the most commonly used and is implemented in the majority of commercial turbidimeters, utilizing a light source and a sensor detector, but it has several limitations. Inexpensive turbidimeters often have limited detection ranges and can be influenced by colored dissolved substances or air bubbles, leading to inaccurate readings. Additionally, these turbidimeters typically require multiple data records for comparison, which can be time-consuming and less efficient in dynamic environments [8,9,10]
Recent techniques for turbidity measurement have been developed, such as the method implemented by Zhou and Zhang, which presents a new approach based on ultraviolet–visible near-infrared (UV-VIS-NIR) absorption measurements, achieving a coefficient of determination of 0.99 [11]. Additionally, Goblirsch et al. implemented fluorescence spectroscopy for turbidity estimation, achieving a sensitive detection of 0.2 NTU [12]. However, both methods are expensive. Zhue et al. introduced a method using two NIR digital cameras for turbidity measurement, but it requires two data records for estimation and is also expensive [13]. Cheng et al. proposed a method based on the scattering of light, which effectively eliminates difficult-to-remove air bubbles in the water channel with high accuracy, but it requires a constant calibration process to work effectively [14].
Advancements in image processing have introduced new methods for assessing turbidity. Digital image processing techniques analyze the gray levels in water images to estimate turbidity levels. For instance, studies have demonstrated how image pixels correlate with water turbidity [15,16,17]. These methods, however, also face challenges such as sensitivity to lighting conditions and image quality.
Convolutional neural networks (CNNs) offer a promising alternative for turbidity measurement. CNNs replicate the human visual cortex, making them highly effective for image analysis tasks such as classification and detection [18,19]. CNNs are mathematical algorithms that replicate how humans learn and mimic the mammalian visual cortex using computational blocks and multiple layers of artificial neurons to approximate any continuous function [20]. CNNs are particularly advantageous in this context because they can handle the complex patterns and high-dimensional data typical in image analysis tasks. They offer robust feature extraction capabilities that traditional methods might miss. This makes CNNs suitable for analyzing images of water samples where suspended solids need to be identified and quantified accurately.
Multiple linear regression (MLR) is another technique that has been used to model and predict water quality parameters. MLR can be particularly useful when the relationship between the predictors (input variables) and the response variable (output) is linear. It is simpler and computationally less intensive compared to CNNs. However, MLR may not capture complex patterns and interactions in the data as effectively as CNNs. Combining CNNs with MLR can use the strengths of both methods, providing a robust framework for turbidity and TSS estimation.
For measuring the performance of a CNN coupled with MLR, there exists a loss function where the parameter weights are adjusted to reduce the discrepancy between the model’s predictions and the known data. During the training process, these weights are iteratively updated by optimization algorithms to minimize the loss function [21,22]. The optimization algorithms produce a fast fit with low memory costs, avoid overfitting, and prevent the model from settling in the local minima of the loss function. The selection of an optimizer depends on the nature of the database used.
Typically, two commonly used optimizers for TSS and turbidity measurement are Adam and SGD. For the Adam algorithm, Feizi et al. achieved a turbidity estimation accuracy of 97.5%, though only after a large number of epochs, specifically between 150 and 200 [17]. Nazemi et al. also implemented a CNN to classify turbid water samples, achieving 98.42% accuracy for color images and 94.34% for grayscale images [23]. On the other hand, Haciefendioglu et al. only reached 87% accuracy [24], while Li et al. achieved a mean square error of 0.92 [25]. Additionally, an SGD algorithm has also been implemented in turbidity and TSS tasks. Wan et al. reached an R-squared of 0.931 [26], and Lopez-Betancur et al. achieved 98.24% accuracy for turbidity, and a 97.20% for TSS estimation [27].
Despite obtaining acceptable results, Adam and SGD may not be generalized solutions due to their sensitivity to data distribution and variability. This is related to the nature of the applied database and the specific characteristics of these optimizers [28]. The selection of an optimizer for the evaluation of TSS and turbidity should be based on the potential of the CNNs to be trained and the characteristics of the database to be used. It should also provide a foundation for the development of more efficient and accessible water quality monitoring methods. This can have a significant impact on water resource management and the protection of aquatic ecosystems.
For this purpose, a comparison of twelve different optimization algorithms available in PyTorch was conducted to identify the most effective ones for estimating suspended solids in liquid samples using a pre-trained AlexNet model. Computationally generated binary images were used for this comparison [29]. This methodology was adopted to maintain a controlled environment and eliminate variables that could introduce noise and optical aberrations. In this way, we ensure that the optimization algorithms focus on the nature of the database, which consists of black points (suspended solids) on a white background, analogous to liquid samples with suspended solids as referred as referred in articles [15,16,17,27]. The aim of this research is to identify the most suitable optimizer based on the nature of the database and to provide additional information about the performance of each optimizer.
2. Materials and Methods
This section describes the different algorithm optimizers evaluated for the classification task using computationally generated binary images with black points (simulating suspended solids) on a white background image.
2.1. CNN and Multiple Linear Regression (MLR) Used
Therefore, since the goal is to analyze optimization algorithms, a simple CNN like AlexNet is used to isolate and evaluate the performance of each optimized algorithm in the task of measuring suspended solids. AlexNet is based on convolutional and fully connected layers, exhibits a suitable representation capacity to capture discriminative features present in such visually simple images. Additionally, its computational efficiency and ease of transfer of pre-trained weights make it an attractive option for this specific binary classification problem. Furthermore, AlexNet has been widely studied and benchmarked in various image classification tasks, making it a well-understood and reliable choice for this research [30].
Any CNN involves two main steps: feature extraction and classification. The classification step uses neurons to process inputs (features) and compute a response (output) or logits, which are then usually normalized using a SoftMax function to determine the probabilities of classes. The trained CNN’s output vector can be seen as a decoded version of the input image because the model extracts hidden information from the sample. Although the CNN can accurately classify certain liquid samples, it faces challenges when dealing with images containing intermediate levels of samples. However, by utilizing the feature vectors (CNN output vectors) to train a multiple linear regression (MLR) model, it is possible to predict the values for any sample. The key is to train the CNN with classes that encompass the desired dynamic range of the samples. In a multiple linear regression model, multiple independent variables are used to predict a single dependent variable. Specifically, in this context, the feature vectors obtained from the CNN serve as the independent variables, while the number of black pixels values represents the dependent variables. This MLR approach allows us to approximate new black pixel values based on the logits vector obtained from unknown images or images not used in the training process, providing a valuable tool for sample analysis and prediction [27]. The general sequence described is shown in Figure 1.

Figure 1.
Model performance sequence used.
2.2. Optimization Algorithms Evaluated
Optimization algorithms play a critical role in the training of convolutional neural networks (CNNs) by minimizing the loss function and improving the model’s performance. These algorithms adjust the weights of the neural network to reduce the error between predicted and actual outcomes. In this study, we evaluate twelve different optimization algorithms available in PyTorch to identify the most effective ones for estimating suspended solids in liquid samples using a pre-trained AlexNet model. The evaluated algorithms include Adadelta, Adagrad, Adam, AdamW, Adamax, ASGD, LBFGS, NAdam, RAdam, RMSprop, Rprop, and SGD. Each algorithm has unique characteristics and advantages, which are briefly described below.
2.2.1. Adadelta
The method adjusts dynamically over time, relying solely on first-order information, and incurs minimal computational overhead compared to basic stochastic gradient descent [31]. The main advantages of this method include: no manual adjustment of the learning rate; insensitivity to hyperparameters; minimal computational requirements, and robustness to large gradients, noise, and choice of architecture.
2.2.2. Adagrad
This optimizer incorporates data observed in earlier iterations, adapting subgradient methods to the geometry of the data. This method is based on a diagonal approximation of the matrix obtained from the products of subgradients. In essence, the adaptation enhances the effectiveness of the method on certain types of data with sparse gradients compared to previous methods [32].
2.2.3. Adam
This method focuses on efficient optimization using information from first- and second-order gradients without requiring a large amount of memory. Learning rates are adaptively adjusted for different parameters based on these moment estimates. This can be useful in situations where memory resources are limited or when efficient optimization is sought using low-order gradient information [33]. The advantages of this optimizer include its ability to adapt to changes in gradient scale, automatically control step sizes during optimization to enhance convergence, and its effectiveness in situations with sparse gradients.
2.2.4. AdamW
This method improves the regularization of the Adam optimization algorithm by separating weight decay from gradient-based updates. It shows that decoupling weight decay simplifies hyperparameter optimization, as it makes the optimal configurations for learning rate and weight decay factor much more independent of one another [34].
2.2.5. Adamax
Adamax, a variant of Adam, utilizes second-order gradient information and applies a different infinity norm to compute adaptive learning rates. Adamax is preferred in situations where gradients demonstrate a wide range of magnitudes [33].
2.2.6. ASGD
Average Stochastic Gradient Descent is based on averaging gradients over time to smooth the optimization process and improve convergence, particularly in situations where gradients may be noisy or problem conditions are complex [35].
2.2.7. LBFGS
Limited Memory Broyden Fletcher Goldfarb Shanno is an optimization algorithm based on Matlab’s minFunc. It relies on an efficient approximation of the inverse of the Hessian matrix (which describes how gradients change with respect to model parameters). Instead of storing and manipulating the entire matrix, it employs only a low-memory approximation of previous gradients. This makes it particularly suitable for optimization problems in high-dimensional spaces or with limited memory resources [36].
2.2.8. NAdam
Nesterov-accelerated Adam is based on replacing the momentum component of Adam with the Nesterov’s accelerated gradient (NAG) algorithm. The NAdam algorithm employs first- and second-order information to adjust the learning rate adaptively and determine the direction of the step. This allows it to perform better in scenarios with steep valleys or when there is high curvature in the loss function. Consequently, this leads to improved convergence speed in non-convex problems and enhances the quality of learning for models [37].
2.2.9. RAdam
The Rectified Adam algorithm recognizes that, due to the limited number of samples in the early stages of model training, the adaptive learning rate in the Adam model exhibits an undesirably large variance. This can lead the model to converge towards suboptimal local minima. Therefore, RAdam not only rectifies this variance of the adaptive learning rate but also compares favorably with the warmup heuristic [38].
2.2.10. RMSprop
The operation of RMSprop is based on maintaining a weighted average of the squares of previous gradients. This allows it to be applied in situations where it is not advisable for the learning rate to be constant, such as when dealing with loss functions that have different scales, variable curvature, slow convergence, and oscillation cycles, among others [39].
2.2.11. Rprop
The resilient propagation algorithm performs a direct adaptation of the weight step based on local gradient information, according to the behavior of the sequence of signs of the partial derivatives. What is most interesting is that this algorithm is not affected by the behavior of the gradient, which is very useful for situations where the gradient is highly volatile or difficult to interpret [40].
2.2.12. SGD
Stochastic Gradient Descent uses training data samples in a stochastic manner, which means it employs small, randomly selected data subsets in each iteration, making it computationally more efficient. Furthermore, the use of small random subsets is highly beneficial when working with large datasets. However, its primary advantage can also lead to it being a noisier and less stable algorithm [41].
A summary of the main characteristics of these algorithms and their relationship with the dataset is described in Table 1.

Table 1.
Characteristics of optimization algorithms, coupled with the features of the dataset, to optimize the performance of each optimizer in practical applications.
2.3. Database
The dataset was created by randomly adding black pixels to white images, resulting in binary images. Nine classes were created based on the number of black pixels in a white image. These nine classes represent the number of black pixels and are labeled as 0, 6272, 12,544, 18,816, 25,088, 31,360, 37,632, 43,904, and 50,176 (See Figure 2). The images were created with dimensions of 224 × 224 pixels, corresponding to the input layer of the CNN used.

Figure 2.
Classes used for training process (note: the gray frame around the image for the class with 0 black pixels is purely illustrative, framing the size and highlighting that it is a completely white image; the images used for training do not include it).
A total of 9000 images from nine different classes were generated. Out of these, 7200 images were randomly selected for the training process (800 images per class), while the remaining 1800 images were allocated to the validation dataset (200 images per class). Additionally, 8000 new images for eight additional classes with intermediate pixel concentrations were generated to test the different optimization algorithms. These intermediate classes included images with black pixel amount between the main classes, specifically designed to validate the generalization capability of the model, and these were not utilized in training the CNN (See Figure 3).

Figure 3.
Additional classes used to validate the optimization algorithms.
Each image was carefully inspected to ensure it adhered to the specified class definitions. The generation process was automated to maintain consistency and prevent human error. Furthermore, the distribution of black pixels in each image was random to simulate various real-world conditions where suspended solids might not be evenly distributed.
The training process was developed and implemented using a workstation with the specifications described in the orange part of Table 2. Optimization algorithms and AlexNet CNN were extracted from the PyTorch torchvision package. For the training of the CNN, the algorithm executed a total of 50 epochs with 5-fold cross-validation for each optimization algorithm listed in Table 1. The cross-validation technique was used to ensure the robustness of our findings, and statistical tests were applied to compare the performance of different optimization algorithms.

Table 2.
Computer specifications and hyperparameters used in the training process.
The epoch number was selected by analyzing the loss of training according to previous executions of the training process. The network was trained with the default momentum settings for the optimization algorithms that required this hyperparameter. The batch size was set to 40 to balance computational efficiency and training stability. The hyperparameters used in the experiment are listed in the blue part of Table 2.
Data augmentation techniques, such as random rotations and flips, were applied to the training images to improve the model’s robustness and generalization capability. The validation set was strictly used to evaluate the performance of the trained models, ensuring an unbiased assessment of their predictive accuracy.
2.4. Evaluation Metrics
The performance of the proposed method was evaluated for a classification task based on the confusion matrix, which has four important elements: TP for true positives, TN for true negatives, FP for false positives, and FN for false negatives. These elements of the confusion matrix are used to calculate the following performance metrics for evaluating the classifier, as listed in the blue part of Table 3: accuracy, precision, recall, specificity, and F-score [27].

Table 3.
Performance metrics used for classification task and MLR evaluation.
Additionally, for evaluate the performance of the MLR, whose task is to estimate the correct measured value of black pixels, the following metrics used are listed in the orange part of Table 3: coefficient of determination, mean absolute error, and mean square error, where y_predicted is defined as the predicted value, y_true as the true value, and y_mean as the average of the y data [20].
3. Results
This research evaluated state-of-the-art optimization algorithms aimed at classifying and estimating the number of black points on a white background image, which is related to suspended solids in liquid samples. The goal for classification was to assess their accuracy, precision, recall, specificity, and F-Score. The training time taken by each optimizer is listed in Table 4.

Table 4.
Training time for each optimizer.
The performance metrics were evaluated using an additional validation dataset (See Figure 3), which consisted of eight classes with 1000 images in each class. This dataset included intermediate classes, which were not used in the training process. The performance metrics are presented in Table 5. The confusion matrix of the best performing optimization algorithms is presented in Figure 4.

Table 5.
Performance metrics of the AlexNet CNN for each optimization algorithm.

Figure 4.
Confusion matrix for the best optimization algorithms.
The classification task was evaluated according to the following accuracy categories: Excellent (0.90–1.00), Good (0.80–0.89), Moderate (0.70–0.79), and Poor (below 0.70) [42,43]. The models Adagrad, Rprop, Adamax, SGD, ASGD, and Adadelta achieved 100% classification accuracy. RAdam also archived excellent accuracy. This achievement may be attributed to the dataset used, which consists of a structured database storing information about the presence or absence of objects, such as suspended solids. The structured nature of the database allows for efficient gradient-based optimization for algorithms such as SGD, ASGD, Rprop, and Adadelta [44,45]. Furthermore, it is plausible that many of these objects may be absent for the majority of entries in the database, resulting in a sparse representation of the data. This sparse representation is suitable for algorithms like Adagrad and Adamax [46]. However, these results are only for the classification task and are not definitive for the estimation of the number of black points on a white background image, which is related to suspended solids. For the estimation task, the aim was to assess their coefficient of determination, mean absolute error, and mean square error. The results are listed in Table 6. The models that achieved 100% accuracy demonstrated excellent performance in the estimation task. Additionally, two more models (LBFGS and RAdam) are added that, despite not achieving 100% accuracy, show good and moderate coefficients of determination, respectively.

Table 6.
MLR performance metrics of the AlexNet CNN for each optimization algorithm.
In addition, the predicted data for each optimization algorithm are shown in Table 7. The true data represent the number of black pixels in the images that were created. An error bar plot comparing the best models in terms of classification accuracy is shown in Figure 5, and for the regression coefficient of determination in Figure 6.

Table 7.
Mean values ± standard deviation of the black pixels estimated by CNN + MLR for each optimizer.
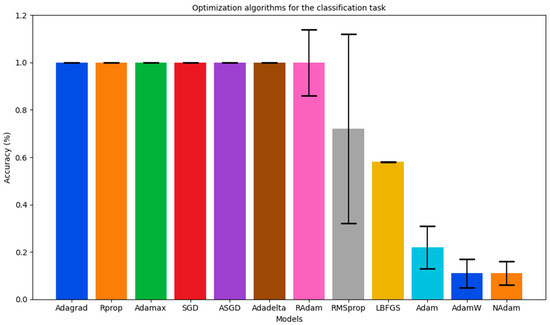
Figure 5.
Optimization algorithms for classification task using accuracy metric.
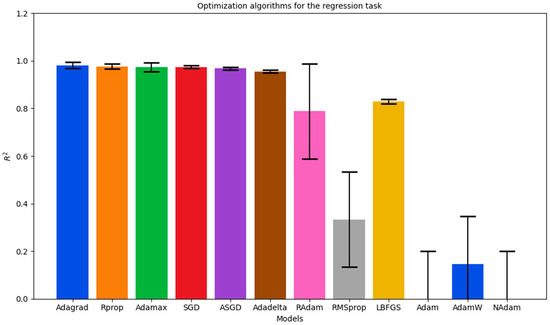
Figure 6.
Optimization algorithms for classification task using coefficient of determination (R2).
4. Discussion
The results obtained in our research show significant variability in the performance of the optimization algorithms used for the estimation of suspended solids. In particular, the Adagrad, Rprop, Adamax, SGD, and ASGD algorithms proved to be the most effective, achieving 100% accuracy in the classification task and high coefficients of determination (R2) in the estimation task. The top five optimization algorithms do not require momentum to function (See Table 1 listed in Section 2); they have their own default optimization strategies. Remember that momentum is an optional feature that can improve the convergence and stability of optimization algorithms. However, momentum can sometimes lead to overshooting the minimum in the loss surface, leading to slower convergence, or becoming stuck in local minima [47].
SGD has emerged as a standard method for optimizing various types of deep neural networks, primarily because of its capacity to escape local minima like ASGD (verifiable with the best training times in Table 4) [48,49], and its efficiency for large-scale datasets, making it ideal for linear classification problems related to our database’s nature [50]. Additionally, in recent works, SGD has proven to be an excellent optimizing algorithm for suspended solids and turbidity estimation using CNN, presenting value of 0.931 [26], accuracy of 98.24% and 97.20% for TSS and turbidity, respectively [27], accuracy of 94% for turbidity task [51].
Adamax and Rprop are known for their robustness against noisy gradients and abrupt fluctuations. This allowed them to maintain consistent performance even in the presence of variability in the images. Adamax, due to its adaptive ability, also works well with low-resolution images [52]. Rprop, in particular, performs well when gradients are very noisy or have abrupt fluctuations, as it focuses only on the sign of the gradient and not its magnitude [53].
The structure of the dataset, consisting of binary images with uniformly distributed black pixels, favors algorithms that handle sparse and high-dimensional data well. For example, Adagrad adapts the learning rate for each parameter individually based on the history of gradients for that parameter. When a feature is infrequent in the dataset, Adagrad assigns a higher learning rate to that parameter, allowing the algorithm to make larger updates for these infrequent features. Adagrad is particularly effective at handling sparse and high-dimensional features, such as those found in black and white pixel images. This can result in faster convergence and excellent performance, as shown in this study [54,55].
In the literature, ADAM optimizers have reached in turbidity task: 0.89 of AUC (good discrimination between classes) [56], mean square error less than 0.05 [57], value of 0.80 [58], accuracy of 88.45% [59] and 87% [24]. These values are lower than those that SGD has been able to provide, as seen in the present study. In the case of Adam, it is important to note that it could achieve better performance if the initial hyperparameters are adjusted according to the observed training trends. However, this research aimed to analyze each optimizer with its default hyperparameters to determine which ones adapt best to datasets with suspended particles. The use of default hyperparameters may have benefited certain algorithms that are well-suited to these initial settings, while others might require fine-tuning to achieve optimal performance.
In this study, computationally generated images were used, where black pixels represent suspended solids in a liquid sample. This methodology was adopted to maintain a controlled environment and eliminate variables that could introduce noise and optical aberrations. The relationship between the number of black pixels and turbidity or suspended solids values is based on previous studies that have demonstrated the feasibility of using computer vision techniques to estimate these parameters. A relevant work that establishes a relationship between pixel values and turbidity is presented by Berrocal et al. [60], and by Gang Dou et al. [61]. Additionally, this relationship is more detectable through digital image processing techniques, such as those presented by Karnawat and Patil [62]. In image processing, various features, including the gray levels in the images, are related to the image pixels, and are used to detect the degree of water turbidity, as defined by Feizi et al. [17].
However, all the simulated suspended solids in this study have the same dimensions, which may not reflect real-world conditions where suspended solids vary in size and color. The system’s performance on real samples, where suspended solids have different sizes and colors, remains to be tested. Furthermore, overlapping effects in real applications have not been considered in this study. In practice, suspended solids can overlap, which could affect the accuracy of turbidity estimation. A possible solution might be to consider turbidity not as a single image but as a combination of images gathered at different times, allowing for a more comprehensive analysis.
This study provides a comprehensive comparison of multiple optimization algorithms in the estimation of suspended solids, filling a gap in the existing literature. The results indicate that algorithms such as Adagrad and Rprop are highly effective for this task, which can guide future research and practical applications in water quality monitoring. Additionally, by using default hyperparameter settings, we demonstrate that it is possible to obtain accurate results without the need for complex adjustments, facilitating implementation in practical environments.
In conclusion, our findings not only highlight the importance of selecting the appropriate optimization algorithm based on the nature of the dataset but also provide a foundation for the development of more efficient and accessible water quality monitoring methods. This can have a significant impact on water resource management and the protection of aquatic ecosystems.
In future research, we hope to extend our approach to real data to further validate our findings and improve their practical applicability. Additionally, addressing the limitations identified in this study, such as varying sizes and colors of suspended solids and overlapping effects, will be critical in enhancing the system’s robustness and reliability in real-world applications.
5. Conclusions
In this paper, a performance comparison of twelve optimization algorithms was conducted on an AlexNet CNN and an MLR to estimate the quantity of black points (suspended solids) distributed randomly on a white background image, which simulates the total suspended solids in liquid samples. The goal was to assess the effectiveness of different optimizers on image classification and multiple linear regression related to suspended solids in liquid samples. Therefore, AlexNet and the MLR were trained with nine classes from 0 to 50,176 black pixels per image and validated with eight additional extra classes (not used in the training process) ranging from 3136 to 47,040 black pixels per image.
The results demonstrated that the performance of each optimizer is influenced by the characteristics of our dataset. The three worst optimizers performances were shown to be Adam, AdamW, and NAdam. And the top five best optimizer performances were by Adagrad, Rprop, Adamax, SGD, and ASGD. The Adagrad optimizer was chosen as the first option because it attained a coefficient of determination ( 0.982), largely owing to its adaptive learning rate for each parameter and its ability to manage sparse and high-dimensional features.
As future work, the top five optimizers could be tested for performance in the top CNN models to date and the different regression models to achieve better method performance. Additionally, it is expected that this research study will be helpful in improving the development of new turbidimeters based on CNN implementations.
Author Contributions
Conceptualization, D.L.-B., E.G.-R. and C.G.-M.; methodology, D.L.-B., E.G.-R., C.G.-M. and S.G.J.; software, C.G.-M.; validation, T.S.-A., M.M.R., E.O.-T. and S.G.J.; formal analysis, D.L.-B., M.M.R., E.O.-T. and C.G.-M.; investigation, D.L.-B.; resources, T.S.-A. and E.G.-R.; data curation, D.L.-B. and C.G.-M.; writing—original draft preparation, D.L.-B. and C.G.-M.; writing—review and editing, D.L.-B., E.G.-R. and C.G.-M.; visualization, T.S.-A., E.G.-R. and S.G.J.; supervision, E.G.-R. and C.G.-M.; project administration, E.G.-R., T.S.-A. and C.G.-M.; funding acquisition, M.M.R. and E.O.-T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The first author thanks CONAHCYT for its support in the scholarship Estancias Posdoctorales México 2022 (1) (CVU: 637281).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Boyd, C.E. Suspended Solids, Color, Turbidity, and Light. In Water Quality: An Introduction; Boyd, C.E., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 119–133. ISBN 978-3-030-23335-8. [Google Scholar]
- Lopez-Betancur, D.; Moreno, I.; Guerrero-Mendez, C.; Gómez-Meléndez, D.; Macias, P.M.d.J.; Olvera-Olvera, C. Effects of Colored Light on Growth and Nutritional Composition of Tilapia, and Biofloc as a Food Source. Appl. Sci. 2020, 10, 362. [Google Scholar] [CrossRef]
- Sun, F.; Mu, Y.; Leung, K.M.Y.; Su, H.; Wu, F.; Chang, H. China Is Establishing Its Water Quality Standards for Enhancing Protection of Aquatic Life in Freshwater Ecosystems. Environ. Sci. Policy 2021, 124, 413–422. [Google Scholar] [CrossRef]
- Qin, S.; Cai, X.; Ma, L. A Novel Light Fluctuation Spectrum Method for In-Line Particle Sizing. Front. Energy 2012, 6, 89–97. [Google Scholar] [CrossRef]
- Lin, X.; Wu, M.; Shao, X.; Li, G.; Hong, Y. Water Turbidity Dynamics Using Random Forest in the Yangtze River Delta Region, China. Sci. Total Environ. 2023, 903, 166511. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Cao, Y.; Gui, H.; Liu, J.; Lu, L.; Cao, H.; Yu, T.; You, H. The Design of Rapid Turbidity Measurement System Based on Single Photon Detection Techniques. Opt. Laser Technol. 2015, 73, 44–49. [Google Scholar] [CrossRef]
- O’Dell, J.W. Determination of turbidity by nephelometry. In Methods for the Determination of Metals in Environmental Samples; Elsevier: Amsterdam, The Netherlands, 1996; pp. 378–387. ISBN 978-0-8155-1398-8. [Google Scholar]
- Bright, C.; Mager, S.; Horton, S. Response of Nephelometric Turbidity to Hydrodynamic Particle Size of Fine Suspended Sediment. Int. J. Sediment Res. 2020, 35, 444–454. [Google Scholar] [CrossRef]
- Vu, C.T.; Zahrani, A.A.; Duan, L.; Wu, T. A Glass-Fiber-Optic Turbidity Sensor for Real-Time In Situ Water Quality Monitoring. Sensors 2023, 23, 7271. [Google Scholar] [CrossRef]
- Chu, C.-H.; Lin, Y.-X.; Liu, C.-K.; Lai, M.-C. Development of Innovative Online Modularized Device for Turbidity Monitoring. Sensors 2023, 23, 3073. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, J. Simultaneous Measurement of Chemical Oxygen Demand and Turbidity in Water Based on Broad Optical Spectra Using Backpropagation Neural Network. Chemom. Intell. Lab. Syst. 2023, 237, 104830. [Google Scholar] [CrossRef]
- Goblirsch, T.; Mayer, T.; Penzel, S.; Rudolph, M.; Borsdorf, H. In Situ Water Quality Monitoring Using an Optical Multiparameter Sensor Probe. Sensors 2023, 23, 9545. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Cao, P.; Liu, S.; Zheng, Y.; Huang, C. Development of a New Method for Turbidity Measurement Using Two NIR Digital Cameras. ACS Omega 2020, 5, 5421–5428. [Google Scholar] [CrossRef]
- Chen, K.; Wang, X.; Wang, C. High-Precision Monitoring System for Turbidity of Drinking Water by Using Scattering Method. IEEE Sens. J. 2023, 23, 29525–29535. [Google Scholar] [CrossRef]
- Hakiki, R.; Zevi, Y.; Muntalif, B.S.; Purnama, I. Edge detection technique for simultaneous measurement of total suspended solids and turbidity. Int. J. Geomate 2023, 25, 74–82. [Google Scholar] [CrossRef]
- Montassar, I.; Benazza-Benyahia, A. Water Turbidity Estimation in Water Sampled Images. In Proceedings of the 2020 5th International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Sousse, Tunisia, 2–5 September 2020; pp. 1–5. [Google Scholar]
- Feizi, H.; Sattari, M.T.; Mosaferi, M.; Apaydin, H. An Image-Based Deep Learning Model for Water Turbidity Estimation in Laboratory Conditions. Int. J. Environ. Sci. Technol. 2023, 20, 149–160. [Google Scholar] [CrossRef]
- Parra, L.; Ahmad, A.; Sendra, S.; Lloret, J.; Lorenz, P. Combination of Machine Learning and RGB Sensors to Quantify and Classify Water Turbidity. Chemosensors 2024, 12, 34. [Google Scholar] [CrossRef]
- Liu, K.; Liang, Y. Enhancement Method for Non-Uniform Scattering Images of Turbid Underwater Based on Neural Network. Image Vis. Comput. 2023, 138, 104813. [Google Scholar] [CrossRef]
- Guerrero-Mendez, C.; Saucedo-Anaya, T.; Moreno, I.; Araiza-Esquivel, M.; Olvera-Olvera, C.; Lopez-Betancur, D. Digital Holographic Interferometry without Phase Unwrapping by a Convolutional Neural Network for Concentration Measurements in Liquid Samples. Appl. Sci. 2020, 10, 4974. [Google Scholar] [CrossRef]
- Jiang, W.; Liang, Y.; Jiang, Z.; Xu, D.; Zhou, L. ABNGrad: Adaptive Step Size Gradient Descent for Optimizing Neural Networks. Appl. Intell. 2024, 54, 2361–2378. [Google Scholar] [CrossRef]
- Rivera, M.M.; Guerrero-Mendez, C.; Lopez-Betancur, D.; Saucedo-Anaya, T. Dynamical Sphere Regrouping Particle Swarm Optimization: A Proposed Algorithm for Dealing with PSO Premature Convergence in Large-Scale Global Optimization. Mathematics 2023, 11, 4339. [Google Scholar] [CrossRef]
- Nazemi Ashani, Z.; Zainuddin, M.F.; Che Ilias, I.S.; Ng, K.Y. A Combined Computer Vision and Convolution Neural Network Approach to Classify Turbid Water Samples in Accordance with National Water Quality Standards. Arab. J. Sci. Eng. 2024, 49, 3503–3516. [Google Scholar] [CrossRef]
- Hacıefendioğlu, K.; Baki, O.T.; Başağa, H.B.; Mete, B. Deep Learning-Based Total Suspended Solids Concentration Classification of Stream Water Surface Images Captured by Mobile Phone. Env. Monit. Assess 2023, 195, 1498. [Google Scholar] [CrossRef]
- Li, Y.; Kong, B.; Yu, W.; Zhu, X. An Attention-Based CNN-LSTM Method for Effluent Wastewater Quality Prediction. Appl. Sci. 2023, 13, 7011. [Google Scholar] [CrossRef]
- Wan, S.; Yeh, M.-L.; Ma, H.-L.; Chou, T.-Y. The Robust Study of Deep Learning Recursive Neural Network for Predicting of Turbidity of Water. Water 2022, 14, 761. [Google Scholar] [CrossRef]
- Lopez-Betancur, D.; Moreno, I.; Guerrero-Mendez, C.; Saucedo-Anaya, T.; González, E.; Bautista-Capetillo, C.; González-Trinidad, J. Convolutional Neural Network for Measurement of Suspended Solids and Turbidity. Appl. Sci. 2022, 12, 6079. [Google Scholar] [CrossRef]
- Martinez, F.; Montiel, H.; Martinez, F. Comparative Study of Optimization Algorithms on Convolutional Network for Autonomous Driving. IJECE 2022, 12, 6363. [Google Scholar] [CrossRef]
- Torch.Optim—PyTorch 2.3 Documentation. Available online: https://pytorch.org/docs/stable/optim.html (accessed on 6 May 2024).
- Maeda-Gutiérrez, V.; Galván-Tejada, C.E.; Zanella-Calzada, L.A.; Celaya-Padilla, J.M.; Galván-Tejada, J.I.; Gamboa-Rosales, H.; Luna-García, H.; Magallanes-Quintanar, R.; Guerrero Méndez, C.A.; Olvera-Olvera, C.A. Comparison of Convolutional Neural Network Architectures for Classification of Tomato Plant Diseases. Appl. Sci. 2020, 10, 1245. [Google Scholar] [CrossRef]
- Zeiler, M.D. Adadelta: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2019, arXiv:1711.05101. [Google Scholar]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent Advances in Stochastic Gradient Descent in Deep Learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- minFunc—Unconstrained Differentiable Multivariate Optimization in Matlab. Available online: https://www.cs.ubc.ca/~schmidtm/Software/minFunc.html (accessed on 2 October 2023).
- Dozat, T. Incorporating Nesterov Momentum into Adam. 2016. Available online: https://openreview.net/forum?id=OM0jvwB8jIp57ZJjtNEZ (accessed on 2 October 2023).
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the Variance of the Adaptive Learning Rate and Beyond. arXiv 2019, arXiv:1908.03265. [Google Scholar]
- Graves, A. Generating Sequences With Recurrent Neural Networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993. [Google Scholar]
- Hassan, E.; Shams, M.Y.; Hikal, N.A.; Elmougy, S. The Effect of Choosing Optimizer Algorithms to Improve Computer Vision Tasks: A Comparative Study. Multimed. Tools Appl. 2023, 82, 16591–16633. [Google Scholar] [CrossRef]
- Evenson, K.R.; Wen, F.; Herring, A.; Di, C.; LaMonte, M. Calibrating Physical Activity Intensity for Hip-Worn Accelerometry in Women Age 60 to 91 Years: The Women’s Health Initiative OPACH Calibration Study. Prev. Med. Rep. 2015, 2, 750–756. [Google Scholar] [CrossRef]
- Altinkurt, E.; Avci, O.; Muftuoglu, O.; Ugurlu, A.; Cebeci, Z.; Ozbilen, K.T. Logistic Regression Model Using Scheimpflug-Placido Cornea Topographer Parameters to Diagnose Keratoconus. J. Ophthalmol. 2021, 2021, 5528927. [Google Scholar] [CrossRef]
- Notsawo, P.J.T. Stochastic Average Gradient: A Simple Empirical Investigation. arXiv 2023, arXiv:2310.12771. [Google Scholar]
- Mehmood, F.; Ahmad, S.; Whangbo, T.K. An Efficient Optimization Technique for Training Deep Neural Networks. Mathematics 2023, 11, 1360. [Google Scholar] [CrossRef]
- Sorour, S.E.; Wafa, A.A.; Abohany, A.A.; Hussien, R.M. A Deep Learning System for Detecting Cardiomegaly Disease Based on CXR Image. Int. J. Intell. Syst. 2024, 2024, 8997093. [Google Scholar] [CrossRef]
- Adadb: Adaptive Diff-Batch Optimization Technique for Gradient Descent | IEEE Journals & Magazine | IEEE Xplore. Available online: https://ieeexplore.ieee.org/abstract/document/9481902 (accessed on 27 May 2024).
- Shi, H.; Yang, N.; Tang, H.; Yang, X. aSGD: Stochastic Gradient Descent with Adaptive Batch Size for Every Parameter. Mathematics 2022, 10, 863. [Google Scholar] [CrossRef]
- Naseer, I.; Akram, S.; Masood, T.; Jaffar, A.; Khan, M.A.; Mosavi, A. Performance Analysis of State-of-the-Art CNN Architectures for LUNA16. Sensors 2022, 22, 4426. [Google Scholar] [CrossRef]
- Drogkoula, M.; Kokkinos, K.; Samaras, N. A Comprehensive Survey of Machine Learning Methodologies with Emphasis in Water Resources Management. Appl. Sci. 2023, 13, 12147. [Google Scholar] [CrossRef]
- Zhou, L.; Xiao, Y.; Chen, W. Imaging Through Turbid Media with Vague Concentrations Based on Cosine Similarity and Convolutional Neural Network. IEEE Photonics J. 2019, 11, 1–15. [Google Scholar] [CrossRef]
- Mishra, N.K.; Dutta, M.; Singh, S.K. Multiscale Parallel Deep CNN (mpdCNN) Architecture for the Real Low-Resolution Face Recognition for Surveillance. Image Vis. Comput. 2021, 115, 104290. [Google Scholar] [CrossRef]
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Differential Evolution Optimization for Resilient Stacked Sparse Autoencoder and Its Applications on Bearing Fault Diagnosis. Meas. Sci. Technol. 2018, 29, 125002. [Google Scholar] [CrossRef]
- Opałka, S.; Stasiak, B.; Szajerman, D.; Wojciechowski, A. Multi-Channel Convolutional Neural Networks Architecture Feeding for Effective EEG Mental Tasks Classification. Sensors 2018, 18, 3451. [Google Scholar] [CrossRef]
- Yang, J.; Bagavathiannan, M.; Wang, Y.; Chen, Y.; Yu, J. A Comparative Evaluation of Convolutional Neural Networks, Training Image Sizes, and Deep Learning Optimizers for Weed Detection in Alfalfa. Weed Technol. 2022, 36, 512–522. [Google Scholar] [CrossRef]
- Krishnan, G.; Joshi, R.; O’Connor, T.; Javidi, B. Optical Signal Detection in Turbid Water Using Multidimensional Integral Imaging with Deep Learning. Opt. Express 2021, 29, 35691. [Google Scholar] [CrossRef]
- Song, C.; Zhang, H. Study on Turbidity Prediction Method of Reservoirs Based on Long Short Term Memory Neural Network. Ecol. Model. 2020, 432, 109210. [Google Scholar] [CrossRef]
- Keller, S.; Maier, P.M.; Riese, F.M.; Norra, S.; Holbach, A.; Börsig, N.; Wilhelms, A.; Moldaenke, C.; Zaake, A.; Hinz, S. Hyperspectral Data and Machine Learning for Estimating CDOM, Chlorophyll a, Diatoms, Green Algae and Turbidity. Int. J. Environ. Res. Public Health 2018, 15, 1881. [Google Scholar] [CrossRef]
- Kumar, L.; Afzal, M.S.; Ahmad, A. Prediction of Water Turbidity in a Marine Environment Using Machine Learning: A Case Study of Hong Kong. Reg. Stud. Mar. Sci. 2022, 52, 102260. [Google Scholar] [CrossRef]
- Berrocal, E.; Sedarsky, D.L.; Paciaroni, M.E.; Meglinski, I.V.; Linne, M.A. Laser Light Scattering in Turbid Media Part I: Experimental and Simulated Results for the Spatial Intensity Distribution. Opt. Express 2007, 15, 10649. [Google Scholar] [CrossRef] [PubMed]
- Dou, G.; Chen, R.; Han, C.; Liu, Z.; Liu, J. Research on Water-Level Recognition Method Based on Image Processing and Convolutional Neural Networks. Water 2022, 14, 1890. [Google Scholar] [CrossRef]
- Karnawat, V.; Patil, S.L. Turbidity Detection Using Image Processing. In Proceedings of the 2016 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 29–30 April 2016; pp. 1086–1089. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).