Physical Model Test of Deformation Self-Adaptive Mechanism of Landslide Mass

Abstract

Reservoir impoundment induces a large amount of cumulative deformation of landslide body, leading to damage to the geological environment. Due to many yearly cycles of reservoir water fluctuation, the cumulative deformation of landslides tends to be stable, showing a self-adaptive deformation phenomenon. The study of the self-adaptive deformation mechanism is very important for evaluating landslide stability and achieving the safe operation of hydropower stations. To study the mechanism of self-adaptive deformation, two sets of physical models were used to monitor the groundwater, earth pressure, and cumulative deformation of landslide under periodic fluctuations of the reservoir water level. The results showed that the soil consolidation compaction, release of sliding stress, and increase in permeability are the three main factors of the self-adaptive deformation of landslide accumulation. The overall permeability decreased first and then increased, the front permeability increased greatly, and the middle and rear permeability decreased. The main factors that affected the permeability change were deformation and seepage force.

1. Introduction

Since the beginning of the 21st century, China has built a large number of hydropower stations, such as the Three Gorges Hydropower Station, the Xiluodu Hydropower Station on the Jinsha River, the Xiangjiaba Dam Hydropower Station, and the Jinping Cascade Hydropower Station on the Yalong River. A large number of reservoirs must inevitably be built in hydropower construction, and the water levels of reservoirs rise and fall, which can induce significant bank slope deformation and instability [1,2]. According to an investigation in 2003, there were 4664 landslides and ancient landslides in the Three Gorges Reservoir area, including 2619 wading landslides [3]. The reservoir area was divided into three stages of water storage in 2003, 2006, and 2008. In October 2010, the experimental water storage of the Three Gorges project reached 175 m. Since the impoundment of the Three Gorges Reservoir, 674 landslides have resulted in significant deformation, and there have been a total of eight large-scale landslides sliding into the river [4]. According to the statistics, during the hydrologic period of the Three Gorges Reservoir, 75.5% of the landslide deformation occurred in the period of water storage and 24.5% occurred in the normal operation period [5]. However, 75.7% of the landslide deformation occurred in the reservoir water level decline and stability stage during the normal operation period. During the five periods from 2009 to 2013, the deformation of the landslides varied from 9 to 29, and the deformation caused by most landslide accumulation decreased year by year. Thus, the deformation caused by landslides is closely related to the rise and fall of the reservoir water level. However, the amount of landslide deformation has decreased year by year under the action of long-term cyclic variations of the reservoir water. After the rise and fall of the circulating water level, the deformation caused by landslides gradually decreases, and the stability of the landslides is gradually improved, which shows the self-adaptation phenomenon of deformation, that is, self-repair and self-stability occur.

At present, there are few systematic studies on the self-adaptive mechanism of the deformation of landslide accumulation, and most of them are focused on the strength regeneration of slip zone soils [6,7,8,9]. Li carried out consolidation and shear tests on the slip zone soil of the Sanmashan landslide and Outang landslide and verified that the strength regeneration of the slip zone soil resulted from the rise and fall of the reservoir water level [10]. Furthermore, the strength regeneration mechanism of the slip zone soil was analyzed [11,12,13]. It was also found that the fluctuation of the reservoir water level may increase the permeability of the fluctuating zone of the water level of the landslide body. As a result, the seepage force decreases, and landslide stability is improved. However, this was not confirmed by experiments but based on the previous literature. Yan divided the long-term deformation evolution trend of reservoir landslides into five categories and pointed out that the reason a slow creep landslide gradually stabilizes is that the front sliding bed is gentle, there is a slight difference between static and dynamic frictional resistances of the sliding surface, and the sliding belt is thick [14]. In recent years, some scholars have noted that the spatial variability of landslide permeability has a greater impact on landslide stability [15,16]. However, over the long geological history, due to the changes in the natural environment or human engineering activities, the permeability of a landslide also changes with time, i.e., there is time variability of the permeability [17,18,19]. Ivoke et al. investigated the hydraulic conductivity of highly expansive Yazoo clay at different wet–dry cycles [20]. It was concluded that with the increase in dry–wet cycles, the permeability coefficient increased gradually [21]. The measured groundwater level data was used to quantitatively calculate the permeability changes of the Xigouwan landslide [22]. It was concluded that after the first water level rise and fall in 2008, the permeability coefficient increased by a multiple of 1.5–3. The increase in the permeability coefficient is the main mechanism through which some landslides with better permeability gradually reach deformation self-adaptation.

Determining the deformation self-adaptive mechanism of landslide accumulation and how its permeability changes with the rise and fall of the reservoir water level is a scientific problem that needs to be studied in depth and solved urgently. The physical model test of a landslide can not only reveal the mechanism and variation characteristics of landslides induced by reservoir water but can also be used to directly observe the change in the seepage field and permeability of a landslide. Therefore, physical model tests of landslide accumulation deformation induced by periodic fluctuations of reservoir water levels were carried out in this study to determine the variation characteristics of the groundwater dynamics and the seepage fields of landslides under long-term fluctuations of reservoir water levels. Furthermore, the self-adaptive mechanism of landslide deformation was revealed.

2. Test Protocol

The landslide body in the Three Gorges Reservoir area is most widely composed of a soil–rock mixture, which is significantly affected by the reservoir water, and the landslide is primarily of a hydrodynamic pressure type. Therefore, the model test used a soil–rock mixture as the landslide body material to simulate the hydrodynamic pressure-type landslide.

2.1. Principle of Experiment

The similarity rule is the theoretical basis of landslide physical simulation tests. Based on the similarity rule, similar materials were selected, and the landslide model was constructed. Finally, the results or conclusions obtained from the physical simulations were applied to the prototype landslide to perform the overall evaluation. For the similarity theory of the landslide model, the main reference theories were the π theorem and three principles of similarity. Similarity analysis was carried out using dimensional and equation analysis methods [23,24].

(1)

Geometric similarity

Based on the size of the landslide in the Three Gorges Reservoir area and the laboratory test conditions, the geometric similarity ratio L* = N1 = 100.

(2)

Hydrodynamic characteristics similarity

This study mainly simulated the rise and fall of the reservoir water level. The field reservoir water level rose and fell by 30 m. Based on the proportion of the reservoir water level fluctuation zone in the whole slope body, the indoor simulation rose and fell by 30 cm, and the hydrodynamic similarity ratio was determined to be N2 = 100.

(3)

Material similarity

Material similarity was one of the key factors to ensure the effectiveness of the model. The most important factors for the deformation of reservoir landslides are the softening effect and hydrodynamic pressure effect. Considering the purpose of this experiment, the weight, strength, and permeability coefficient of the landslide body were taken as the main similarity parameters, with a similarity ratio of about 1.

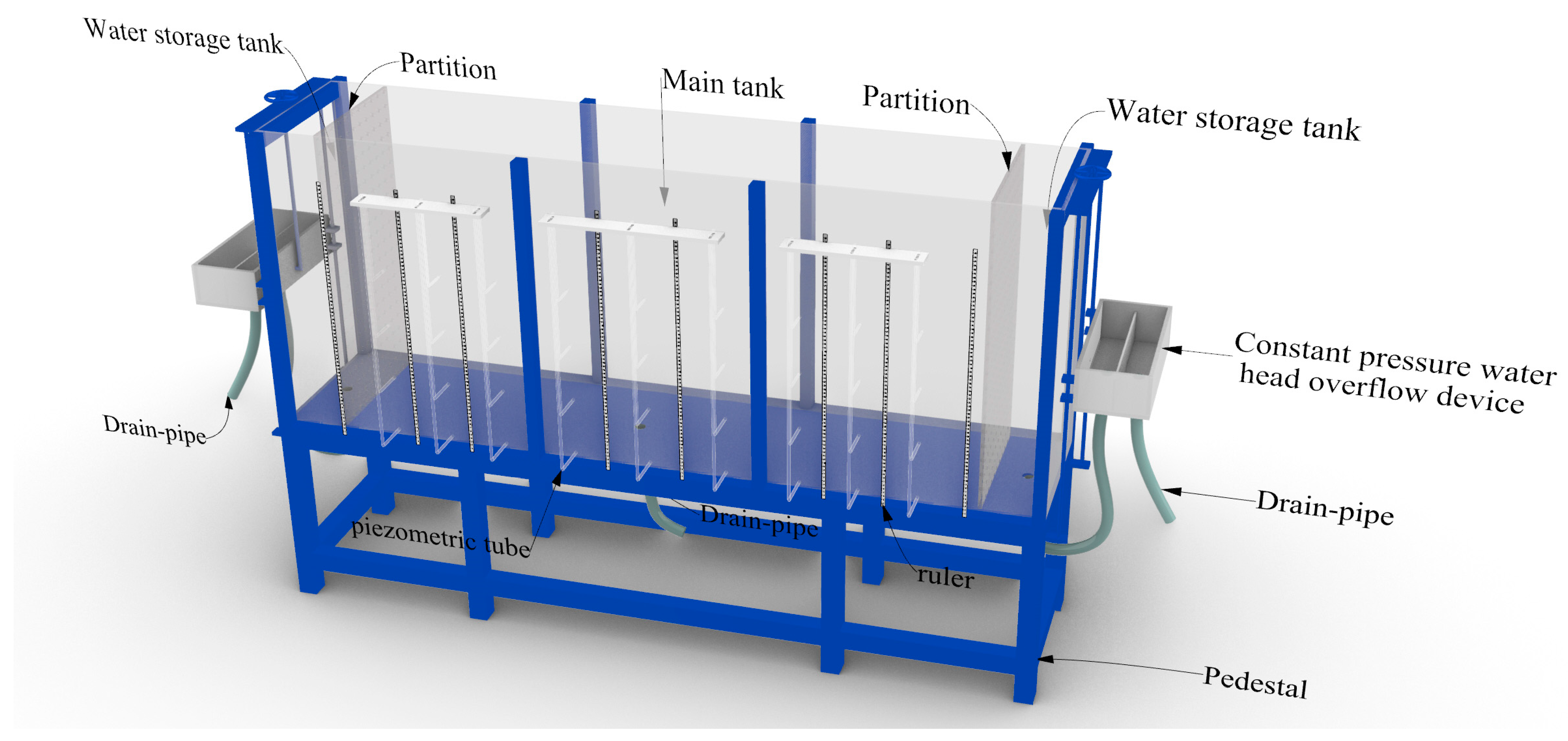
2.2. Test Model Box

The model box was made of a toughened glass material and a stainless steel frame. The model device consisted of a main tank, water storage tank, constant pressure water head overflow device, pedestal, and reinforcing bracket. The model box was 2.02 m long, 0.42 m wide, and 0.8 m high, and the net length of the main groove was 1.68 m. The test set is shown in Figure 1.

2.3. Physical Model and Parameters

A typical section of the Wadingi landslide accumulation in the Three Gorges Reservoir area was selected for this experiment, as shown in Figure 2. The sliding bed was bedrock, and the model was made of solid bricks and mortar. The landslide body was a mixture of earth and stone, and the samples in the model were composed of clay, sand, and crushed stone. The grain gradation was based on the material composition of the Shiliushubao landslide, and the initial mass moisture content was set to 15%.

The slip surface of Model 1 (Figure 2a) was set as a broken line. The slip surface was paved with mortar, and clay sealed the trailing edge up to 60 cm. The angle between the landslide surface and the horizontal plane was 30°, the trailing edge of the slide body was 0.8 m high, the leading edge was 0.1 m high, and the leading edge was in direct contact with the partition. The trailing edge of the sliding body was a platform with a length of 0.47 m at a horizontal distance of 1.21 m from the slope, with a volume of 0.152 m³. One reservoir water level monitor, labeled #1, and seven pore water pressure gauges, labeled #2–#8 from the leading edge to the trailing edge, were installed. Seven earth pressure gauges were installed, which were close to the pore water pressure gauges, and they were labeled s1–s7 from the leading edge to the trailing edge.

In Model 2 (Figure 2b), the slip surface was 0.7 m high at the trailing edge, 0.1 m high at the leading edge, and 0.1 m from the partition. The leading edge of the sliding body was 45° steep, the horizontal length was 1.58 m, and the volume was about 0.095 m³. One reservoir water level monitor, labeled #1, and seven pore water pressure gauges, labeled #1–#8, from the leading edge to the trailing edge, were installed. No earth pressure gauges were installed.

2.4. Working Conditions

The model test simulated the rise and fall of the reservoir water level. The back edge water head was set with a constant water head and the front edge water level changed periodically many times. The water level variation conditions are shown in

Table 1. Water level fluctuation conditions.

Condition No.	Gravel Particle Content above 2 mm	Trailing Edge Water Head (cm)	Leading Edge Starting Water Level (cm)	Rise and Fall of Reservoir Water Level (cm)	Rate of Rise and Fall
Model 1	53%	62	10	10–40–10	The rate of rise and fall of the reservoir water level was 10 cm/5 min in the 1st to the 6th cycle and 30 cm/time in the 7th and 8th cycles
Model 2	76%	67	10	10–50–10	To increase the hydraulic gradient, the rate of water level rise and fall was 40 cm/time

.

3. Test Results

3.1. Variation Characteristics of Seepage Field and Permeability

3.1.1. Variation Characteristics of Seepage Field

The tests showed that the rise and fall of the reservoir water level mainly affected the middle front of the landslide. When the reservoir water level rose from a low to a high level, the reservoir water infiltrated from the outside to the inside of the landslide body. The seepage field in the landslide body was high outside and low inside and had a concave inward shape until it became smooth after stabilization. When the reservoir’s water level dropped from high to low, the groundwater was discharged from the landslide. The seepage field in the landslide was high inside and low outside.

After the reservoir water level rose and fell repeatedly many times, the seepage field in the slope body also showed some subtle changes. For example, with the same rise rate of the reservoir water level, after periodically rising and falling many times, the degree of concavity and the amount of hysteresis of the infiltration line at the front of the slope were reduced (Figure 3), indicating that the permeability of the front changed.

During the test, it was also observed that the soil particles in the pores and voids of the slope were affected by the rising and storage of reservoir water and the soaking by the groundwater. The cohesion was weakened, which caused particles to break away from the original mother body and be suspended in the voids. When the reservoir’s water level fell, the fine soil particles moved out of the slope with the flow. After many reservoir water level fluctuations cycles, many seepage channels formed in the slope. The amount of seepage increased after the formation of seepage channels. As the seepage channels discharged the internal groundwater, the groundwater carried a large number of fine particles from the channel continuously. With rising reservoir water levels, the channel’s fine particles also moved to the inside slope with the seepage, but the movement distance was short.

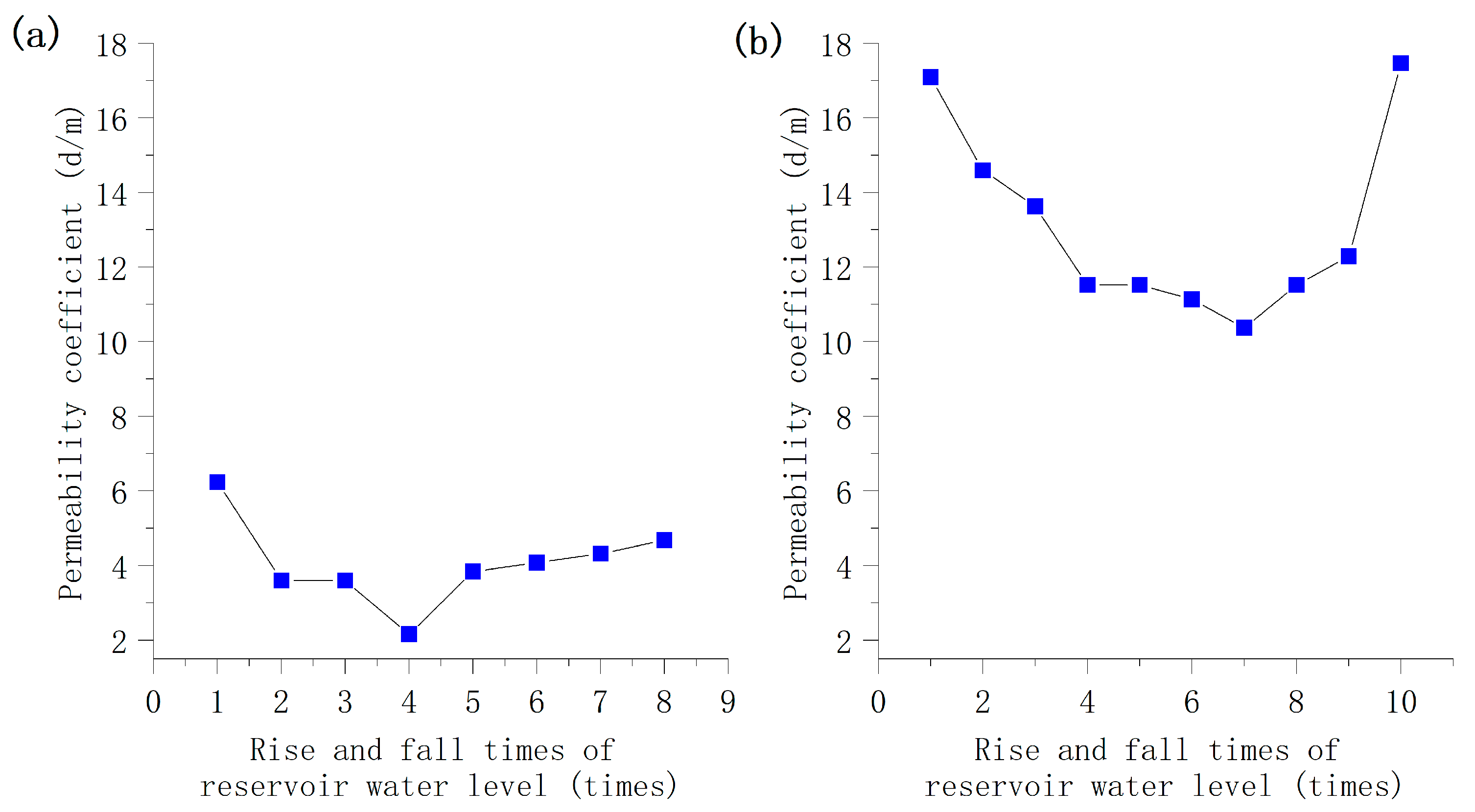
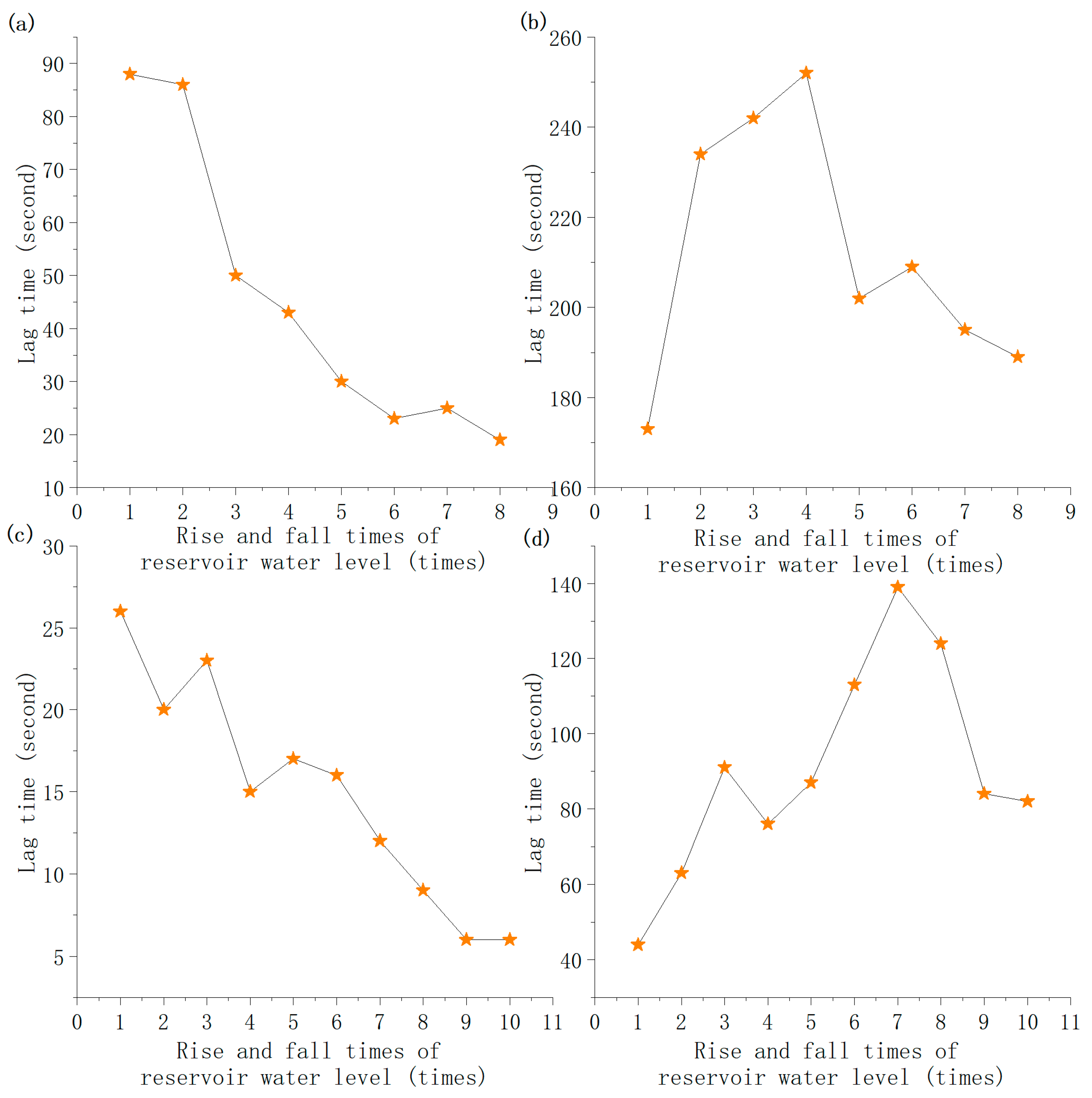
3.1.2. Quantitative Analysis of Permeability Change

Based on the seepage data analysis, the seepage trend was that with the increase in the number of cycles of the water level rising and falling, the seepage decreased first and then increased. Based on the amount of seepage, the permeability coefficient of the whole slope could be calculated by the indoor constant head test formula [25]:

$$\mathrm{k}=\frac{\mathrm{Q}\times \mathrm{L}}{\mathrm{A}\times △\mathrm{h}}$$

where k is the permeability coefficient (cm/s); Q is the stable seepage discharge (cm³/s); L is the length of the seepage path (cm); A is the permeated cross-section (cm²); and Δh is the water head difference (cm). Figure 4 shows the variations of the permeability coefficient.

As shown in Figure 4, with the increase in the number of cycles of the water level rising and falling, the permeability coefficients of the two models decreased sharply first, then slowly, and then gradually increased. The permeability coefficient of Model 1 reached a minimum of 2.16 m/d after the fourth cycle, and the total decrease was about 65%. In comparison, Model 2 reached a minimum of 10.37 m/d after the seventh cycle, and the total decrease was about 39%. The permeability of Model 2 was significantly greater than that of Model 1, and the degrees of permeability decrease and increase of Model 2 were lower than those of Model 1, which was mainly related to the particle size distribution of Model 2. After many cycles, the permeability would likely exceed the maximum permeability before the reservoir water level fluctuations occurred.

3.1.3. Qualitative Analysis of Permeability Change

The permeability change could be analyzed by the response time of the pore water pressure within the slope to the change in the reservoir water level. Because the test was conducted with a model, the size and distances were limited. The distances between the pore water pressure sensors were short. To obtain accurate response times between several sensors, Model 1 used data monitoring points #1, #4, and #7, while Model 2 used data monitoring points #1, #4, and #8 for analysis. There were four inflection points in the process of the water level rising and falling. The starting point of the high pore water pressure was chosen as the analysis point, and the lag time corresponding to each analysis point was analyzed statistically, as shown in Figure 5.

The lag time refers to the difference between when the reservoir water level rises to the top and when the pore water pressure rises to the top. According to Figure 5, the initial lag time of monitoring point #4 in Model 1 was 88 s. The lag time decreased gradually with the increase in reservoir water fluctuations, and the lag time of the eighth cycle decreased to 19 s. The initial lag time of monitoring point #7 was 173 s. With the increase in reservoir water level fluctuations, the lag time first increased sharply and then the oscillations decreased. The longest lag time of this monitoring point was 252 s in the 4th cycle, and, in the 10th cycle, the lag time was reduced to 189 s. After increasing the water decline rate, the lag time reduction increased. The initial lag time of monitoring point #4 in Model 2 was 26 s. With the increase in the number of reservoir water fluctuations, the oscillations of the lag time decreased, the total time showed a decreasing trend, and the lag time for the 10th cycle was reduced to 6 s. The first cycle lag time of monitoring point #8 was 44 s. With the increase in reservoir water fluctuations, the lag time increased sharply first and then decreased gradually. It could be seen that the lag time of the pore water pressure within the front was gradually reduced, with a maximum reduction of 97%, and the response speed became faster. The response time of the pore water pressure buried in the middle and at the rear edge of the reservoir increased first and then decreased. It continued to decrease after the continuous rise and fall of the reservoir water level. This showed that the front permeability increased gradually, the middle and back permeability decreased sharply first, and then the oscillations increased gradually. The overall comprehensive permeability also decreased first, then increased, and finally tended to be stable after a long period of reservoir water level rising and falling. When the rate of reservoir water decline increased, the lag time decreased, and the permeability increased.

3.2. Characteristics of Deformation and Stability

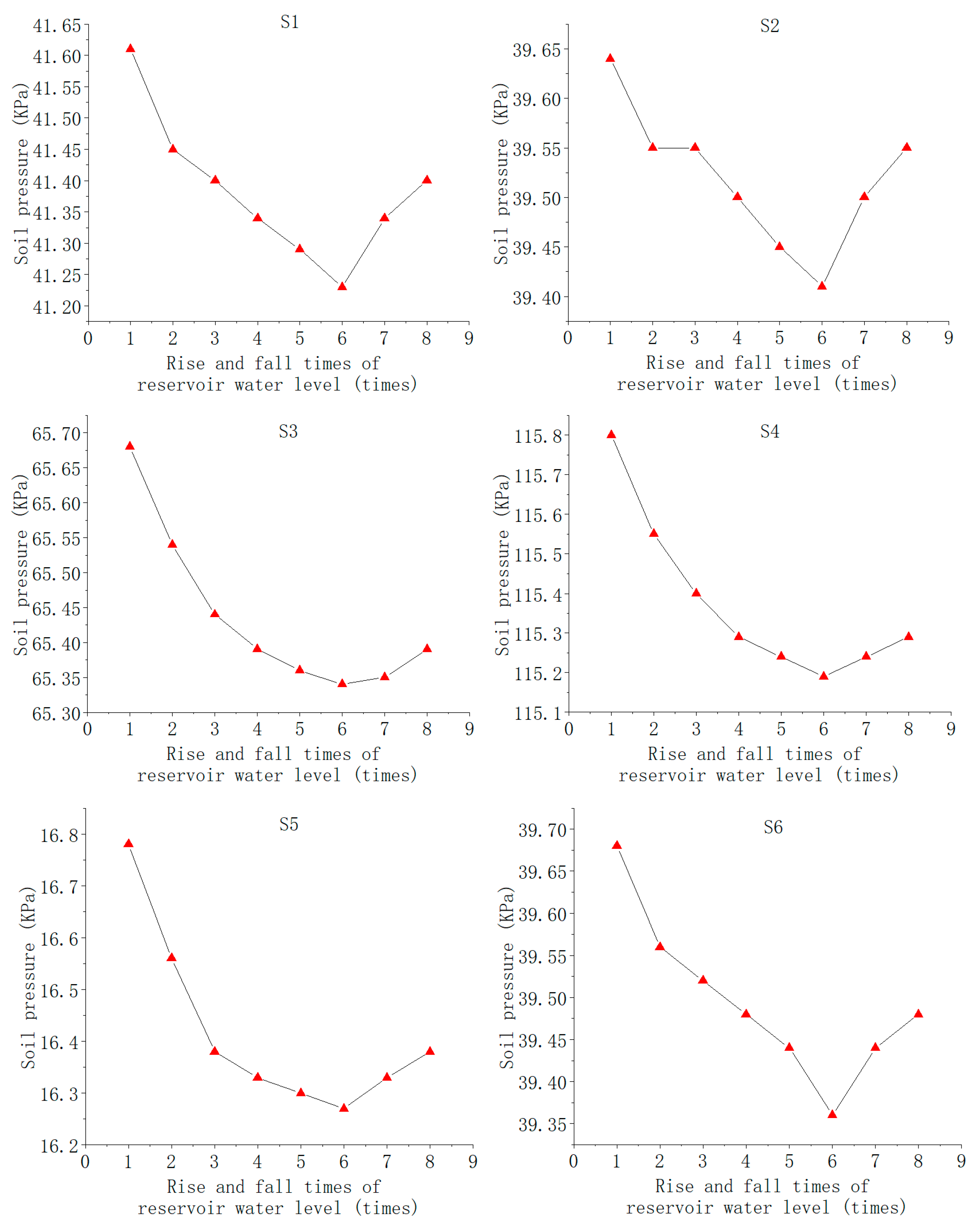
3.2.1. Changes in Earth Pressure

According to the data on earth pressure collected from Model 1, the earth pressure of S1–S6 rose and fell with the rise and fall of the reservoir water level. The earth pressure was the greatest at a high and lowest at a low water level, and the maximum variation was 1.6 kPa. The earth pressure of S7 was the lowest and varied irregularly, mostly between 2 and 5 kPa, while that of S4 was the greatest, varying between 114.8 and 115.8 kPa.

The maximum earth pressures at each high water level for pressure sensors S1–S6 are shown in Figure 6. In the first six reservoir water level cycles, the highest pressure values of pressure gauges S1–S6 decreased sharply and gradually with the increase in the number of reservoir water level cycles. However, in the seventh cycle, due to the increase in the drawdown rate of the reservoir water level, the earth pressure’s decreasing trend quickly reversed, and the pressure began to increase. This showed that the earth pressure decreased and the overall stability of the slope increased after the model was subjected to multiple water level fluctuations. However, the increase in the rise and fall rate of the reservoir water level could affect the internal stress of the landslide, and the stability could change accordingly.

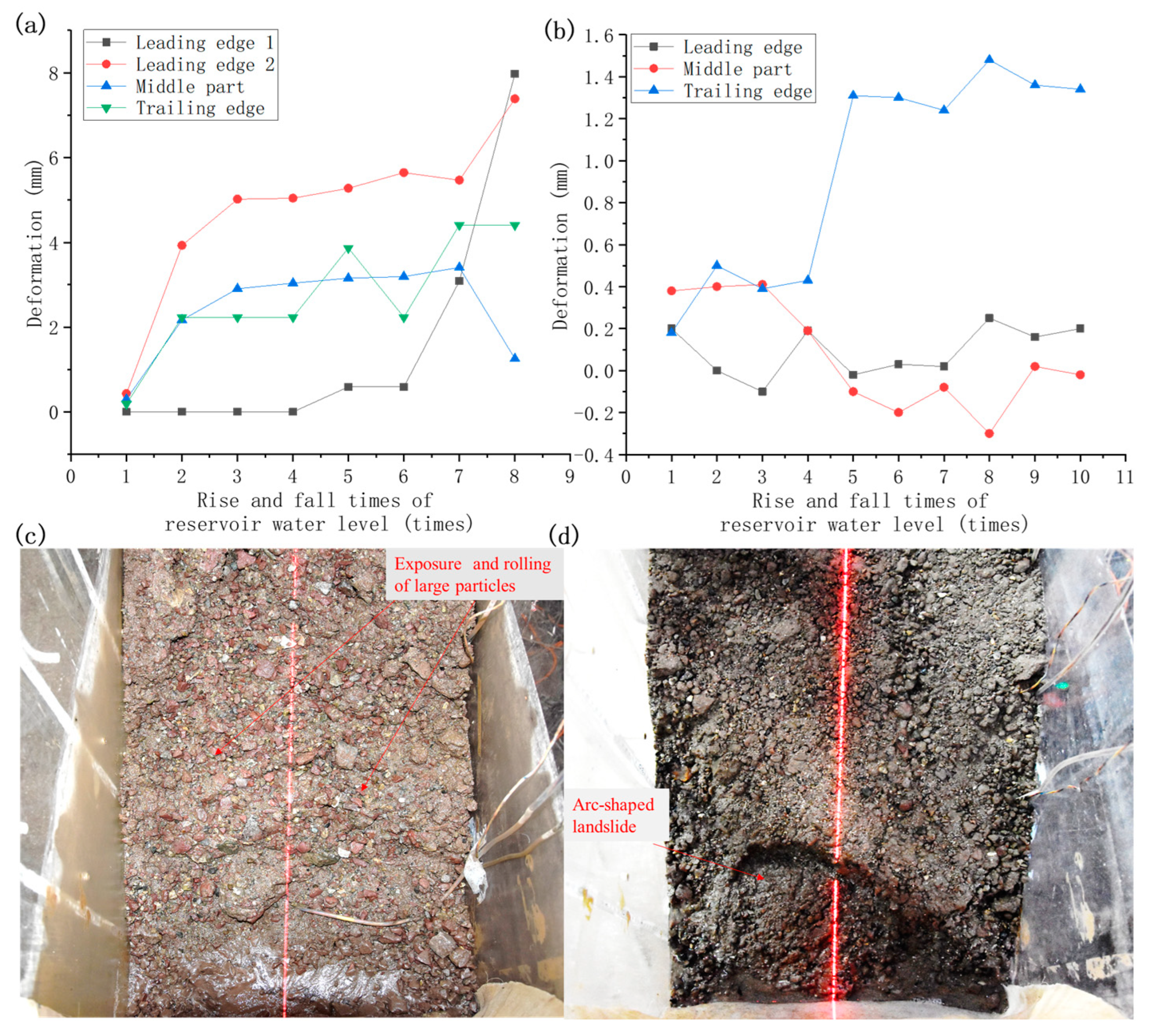
3.2.2. Changes in Surface Displacement

The typical deformation photographs and the curves of surface displacements of the typical positions on the profile lines of the two models with the number of rise and fall cycles are shown in Figure 7. During the experiment, it was observed that the leading edge deformation of Model 1 was very small, and tiny particles on the surface of Model 1 were lost during the first three reservoir water level fluctuation cycles. Subsequently, during the fourth–seventh water level fluctuation cycles, the front particle loss increased, the large particles were exposed, and the surface was shaped like steps. In the seventh cycle, deformation cracks occurred on the back surface, and the deformation increased, which may have been related to the increase in the rate of water level decline. The entire model did not produce large deformations, with no apparent collapse of the leading edge, characterized mainly by the loss of small particles and the exposure of large particles until destabilized rolling occurred (Figure 7c). The deformation of the leading edge was the greatest, at about 10 mm. The deformation of the middle part was about 1–3 mm and that of the trailing edge was about 3–5 mm (Figure 7a).

In Model 2, during the first drawdown of the reservoir, concentrated flow appeared on the right side of the leading edge, resulting in a significant loss of particles on the right side and small deformation. During the fourth reservoir water level decline, the left side of the front also had a large amount of particle loss due to the concentrated water flow and then it had a small collapse in the fifth and sixth cycles. During the eighth reservoir water level decline, a regular arc-shaped landslide occurred at the leading edge (Figure 7d). In the following two cycles of reservoir water fluctuations, the leading edge deformation gradually expanded and moved forward, and the leading edge slope deformation became slower. According to the deformation photographs, the overall displacement was about 20 mm forward, and the leading edge extended 100 mm forward because of the bank collapse. According to the displacement monitoring curve, the deformation of the back part was only in the range of 1–2 mm (Figure 7b).

In summary, according to the photographs and the surface displacement curves, the deformation of the middle and rear parts of the slope was small and was mainly due to the settlement caused by the collapsibility. The deformation of the leading edge of Model 2 was greater than that of Model 1, mainly due to the smaller clay content of Model 2 and the smaller cohesion of the soil mass, but the overall stability was good.

4. Discussion

4.1. Mechanism Analysis of Permeability Change

Based on the experimental observation and data analysis, the permeability of the landslide mass changed, decreasing first and then increasing. We know that particle size distribution and compactness are the main factors affecting soil permeability. When the permeability of the landslide mass changes, the above two factors must change. The permeability of the landslide mass was affected by the deformation and the seepage force mainly due to the rise and fall of the reservoir water level, as shown in Figure 8.

4.1.1. Effect of Deformation

The influence of deformation on the permeability was mainly compaction, front bank collapse, and internal deformation.

(1) The influence of compaction persisted for a long time, but it mainly greatly influenced the early stage of reservoir water level rising and falling. In particular, when the reservoir water level rose for the first time, the soil was soaked in water, the soil became soft, and the porosity was reduced by the weight of the soil and the upper part. When the reservoir water level dropped, the groundwater level in the slope body dropped, the effective stress increased, and compression deformation occurred. As a result of the compaction, the porosity of the soil mass decreased, and the original stable seepage was destroyed, which was the main reason for the decrease in the seepage flow in the early stage and the decrease in permeability first.

(2) The front bank collapse increased the permeability of the landslide mass. The front edge was eroded by the reservoir water and washed away by the waves. The fine particles in the surface layer were carried into the reservoir water as runoff. The front edge underwent small-scale bank collapse to different degrees, the original structure was destroyed, and the material structure became loose. As a result, the leading edge permeability increased (Figure 8a,c).

(3) Internal deformation caused the permeability of the landslide mass to decrease first and then increase. If there was a stable seepage passage in the slope, the internal deformation destroyed the seepage passage first and caused local seepage clogging, causing the permeability to decrease. Due to various factors, deformation and displacement of different degrees occurred inside the slope body, and deformation cracks appeared on the ground. These damaged the original material structure of the slope body, reduced the compactness, and made the structure looser. As a result, the permeability of the whole slope body was enhanced. Therefore, seepage channels re-formed in the slope after a period of seepage, resulting in a gradual increase in the permeability throughout the slope (Figure 8a,b).

4.1.2. Effect of Seepage Force

The influence of the seepage force on the permeability was mainly seepage action and the rate of water level rise and fall.

(1) The seepage action was divided into seepage potential erosion and clogging. Seepage potential erosion was caused by some fine particles in the saturated zone flowing out of the slope through the pore channels between coarse particles, which increased the void size and the number of voids in the slope, resulting in pipeline seepage and enhanced permeability [26,27,28]. During the experiment, especially in the early stage of the reservoir water level rising and falling, the seepage water was turbid, and the discharged water mostly contained particles smaller than 2 mm (Figure 8c,d). By comparing Figure 8a with Figure 8c, we can see that there are fewer fine particles and more coarse particles in Figure 8a at the same location, which indicates that the front edge of the model was eroded by seepage after many cycles of the water level rising and falling. Seepage clogging was the deposition of fine particles in the process of moving forward with the flow of water, mainly manifested by the accumulation and clogging of fine particles in the front of the slope with the flow of water, thus reducing the seepage flow.

(2) The rate of rise and fall of the reservoir water level affected the permeability. When the rate of water level decline increased, there was a larger hydraulic gradient in the slope, that is, the seepage force increased, which accelerated the flow of small particles in the slope and increased the role of seepage potential erosion, increasing the permeability. During the model test, it was observed that when the rate of water level decline was increased, the discharged water was turbid, the number of discharged fine particles increased, and the particle size increased. It can be seen that increasing the rate of reservoir water level decline affected the permeability, generally increasing the permeability.

4.2. Mechanism Analysis of Deformation Self-Adaptation

According to the monitoring data of the soil pressure and surface displacement, the deformation of the landslide model gradually slowed and became stable. There were three main reasons for the self-adaptation of the deformation: consolidation compaction, the release of sliding stress, and the increase in permeability, as shown in Figure 9.

(1)

Consolidation and compaction

Consolidation compaction was the main reason for the self-adaptation of landslide deformation. The reservoir’s water level rose and fell for the first time, which caused the sliding body in the water level fluctuation zone to be soaked by water. The water content suddenly increased, which led to the settlement and deformation of the landslide accumulation. Because of the long-term gravity action of the overlying soil, the soil in the fluctuating zone of water level was compressed, the porosity decreased, and the density and shear strength increased. When the reservoir’s water level rose and fell many times, some minerals in the soil were dissolved in the water. Dry and wet cycles occurred in the rock and soil, forming chemical precipitates, which caused the loose and deformed soil–rock mixture to undergo cementation. Under the coupling action of compression and consolidation, the strength was regenerated, the shear strength gradually increased, and the stability was gradually improved. After many cycles of rising and falling water levels, deformation occurred in the vertical direction in the landslide model, creating 10–20 mm of settlement. In addition, there was consolidation and compaction in the sliding direction, mainly due to differential deformation in the sliding direction, that is, small deformation at the leading edge and large deformation at the middle and rear, which resulted in extrusion and compaction. Thus, the shear strength could also be increased.

(2)

Increased permeability

After a long period of reservoir water level rise and fall, the front permeability increased, and the middle and rear permeabilities decreased, that is, the middle and rear groundwater levels dropped and the front groundwater level increased. For a hydrodynamic landslide, the total hydraulic gradient in the slope decreased, the total seepage force decreased, the sliding force decreased, deformation gradually weakened, and the stability increased. The earth pressure data obtained in the test verified that the general trend of the earth pressure change was that the earth pressure decreased with the increase in the number of cycles of the water level rising and falling. However, the increase in permeability may not be conducive to the stability of the landslide for the buoyancy weight loss landslide.

(3)

Release of sliding stress

The release of sliding stress was an important reason for the landslide deformation reaching self-adaptation. According to Figure 9, the landslide body had different degrees of deformation caused by external factors, such as rising and falling water levels. The deformation mainly manifested as front bank collapse, internal cracks, creep displacement of the landslide body, and settlement deformation. After many periods of creep displacement and settlement, the landslide body dropped 10–20 mm in the vertical direction and moved forward by about 20 mm in the horizontal direction. The position and the center of gravity of the landslide body dropped, the gravitational potential energy decreased, and the downward momentum was released. The landslide body was originally a single unit. However, because of the internal cracks, it could become divided into multiple blocks. If the blocks did not make contact or if the contact was not close, it could result in limited sliding thrust transmission, and the sliding force would be weakened. With the multi-stage bank collapse of the leading edge, the slope of the leading edge became gentle, which caused the leading edge to extend at least 100 mm forward, and the anti-sliding force arm and moment increased. Therefore, the small deformation gradually released the sliding stress so that the sliding force gradually decreased and the stability gradually improved.

5. Conclusions

Based on large-scale physical model tests, the self-adaptive deformation mechanism of landslide accumulation under the action of reservoir water level fluctuations was studied by monitoring seepage, pore water pressure, earth pressure, and surface displacement. The following conclusions were drawn:

(1)

Due to the rise of the impounded water level and the subsequent 12 years of operation during which the reservoir water level rose and fell, the permeability of the landslide accumulation in the Three Gorges Reservoir area changed. The permeability first decreased and then increased, and the permeability of the leading edge increased greatly. The main factors affecting the permeability change were collapsible compaction, seepage, front bank collapse, internal deformation, and the rate of reservoir water level rise and fall.

(2)

When the landslide underwent small deformation, the permeability of the slope above the groundwater level increased. However, the seepage channels of the slope below the groundwater level may have been blocked. After many cycles of the reservoir water level rising and falling, new and relatively stable seepage channels (pipeline seepage) formed in the slope, composing the network seepage.

(3)

The model test results showed that the landslide mass deformation was self-adaptive. The main reasons for the self-adaptive characteristics were as follows: (1) the long-term consolidation compaction caused the shear strength of the landslide body to increase gradually; (2) the small deformation caused the sliding stress to release, and the sliding force decreased; and (3) the permeability increased and caused the seepage force to decrease. The interactions of these three factors improved the stability of the landslide.