Abstract
In the design of offshore engineering foundations, a critical consideration involves determining the peak shear strength of marine soft clay sediment. To enhance the accuracy of estimating this value, a database containing 729 direct shear tests on marine soft clay sediment was established. Employing a machine learning approach, the Particle Swarm Optimization algorithm (PSO) was integrated with the Adaptive Boosting Algorithm (ADA) and Back Propagation Artificial Neural Network (BPANN). This novel methodology represents the initial effort to employ such a model for predicting the peak shear strength of the soil. To validate the proposed approach, four conventional machine learning algorithms were also developed as references, including PSO-optimized BPANN, Support Vector Machine (SVM), BPANN, and ADA-BPANN. The study results show that the PSO-BPANN model, which has undergone optimization via Particle Swarm Optimization (PSO), has prediction accuracy and efficiency in determining the peak shear performance of marine soft clay sediments that surpass that offered by traditional machine learning models. Additionally, a sensitivity analysis conducted with this innovative model highlights the notable impact of factors such as normal stress, initial soil density, the number of drying–wetting cycles, and average soil particle size on the peak shear strength of this type of sediment, while the impact of initial soil moisture content and temperature is comparatively minor. Finally, an analytical formula derived from the novel algorithm allows for precise estimation of the peak shear strength of marine soft clay sediment, catering to individuals lacking a background in machine learning.
1. Introduction
Marine soft clay sediment is a commonly employed foundation material in various offshore engineering projects, including embankments and breakwaters [1,2,3,4]. Consequently, the mechanical properties of marine soft clay sediment, particularly its peak shear strength, play a pivotal role in ensuring the stability of ocean engineering structures [5,6,7]. The decline in the peak shear strength of marine soft clay sediment can lead to instability and potential damage to foundations or even the entire offshore engineering application [8,9,10]. This underscores the significance of accurately assessing the peak shear strength of marine soft clay sediment for the operational safety of engineering infrastructures [11,12,13,14].
Throughout the operational phase, the marine soft clay sediment foundation is unavoidably subjected to diverse environmental factors within the ocean, which can exert a substantial influence on its peak shear strength [15,16,17]. For instance, in offshore regions, the climate is changeful, such as alternating periods of rainfall and shine. These changes can induce drying–wetting cycles in the marine soft clay sediment, causing frequent expansion and shrinkage, which can reduce the clay peak shear strength [18,19,20]. Furthermore, the thermal reactions resulting from the climatic changes can cause temperature variations, which can either strengthen or weaken the mechanical properties of the soil [21,22,23]. Additionally, inherent properties of the marine soft clay sediment, such as soil density, moisture content, and other factors, can also have an impact on its peak shear strength [10,24,25,26]. Considering the prediction of the peak shear strength of marine soft clay sediment, the impact of both external and internal influencing factors cannot be overlooked [27,28,29].
To precisely evaluate the peak shear strength of marine soft clay sediment, researchers have designed specialized testing equipment capable of simulating the unique service conditions within these environments [30,31,32,33]. Notably, Chao and Fowmes [33] introduced a custom apparatus capable of quantifying the peak shear strength of soil or the soil-geosynthetics interface under varying temperature conditions during drying–wetting cycles. By utilizing these custom test devices, the peak shear resistance of marine soft clay sediment in practical offshore engineering environments can be assessed. However, there are several limitations associated with laboratory test approaches. Firstly, developing bespoke apparatuses can be costly and requires specialized mechanical and design knowledge, which may not be readily available to every environmental or construction engineering researcher. Secondly, operating the custom apparatuses typically requires the continuous involvement of a skilled practitioner, which can be labor intensive. Thirdly, the process of simulating the real offshore engineering environment, including reaching temperature equilibrium or conducting drying–wetting cycles, can be time consuming [34,35,36]. Developing precise predictive models that accurately estimate the peak shear strength of marine soft clay sediments under real-world conditions have the potential to significantly address the aforementioned challenges.
As previously mentioned, the peak shear strength of marine soft clay sediments is influenced by a diverse array of variables exhibiting intricate interaction mechanisms [37,38,39]. The intricate nature of this problem poses significant challenges in establishing direct empirical equations through conventional statistical methods, thereby making it challenging to accurately replicate the nonlinear relationship between these influences [40,41]. This relationship is crucial for precise estimation of peak shear strength [42,43,44]. This underscores the pressing need for reliable approaches capable of providing accurate and efficient estimation of the peak shear strength of marine soft clay sediment [45,46].
The scientific community has shown significant interest in machine learning techniques, leading to their widespread application in marine engineering. This widespread adoption is primarily attributed to the techniques’ remarkable capacity to precisely capture the intricate and non-linear relationships among various factors [47]. Notably, Cavalcante et al. [42] utilized machine learning approaches to estimate rock tensile strength, demonstrating the powerful predictive capacity of machine learning techniques in such applications. Likewise, in the domain of predicting soil peak shear strength, efforts have been made to leverage machine learning models for precise estimations. Khodkari et al. [47,48,49,50,51] utilized Genetic Algorithm (GA) optimized Artificial Neural Networks (ANNs) to evaluate soil shear strength based on the inherent characteristics of the soil. Meanwhile, Chao et al. [51] applied a hybrid Support Vector Machine (SVM) model to assess soil shear strength, and Xu et al. [52] developed a Particle Swarm Optimization (PSO) optimized Support Vector Machine (SVM) model for the same purpose. Despite these advancements, existing research on machine learning models for soil peak shear strength exhibits certain deficiencies that necessitate further refinement [53,54]. Firstly, soil shear strength modeling often ignores the effects of environmental factors such as dry and wet cycles and temperature, thus limiting its ability to assess the peak shear strength of marine soft clay sediments under real-world conditions of use [55,56]. Secondly, prior studies predominantly relied on basic and overly simplified machine learning algorithms, ignoring the potential for greater advanced algorithms, including technology sets such as the ADA combined with BPANN, for precise estimation of peak shear strength in soil [57,58,59].
The predictive performance of machine learning algorithms is significantly influenced by a subset of parameters referred to as hyperparameters [60,61,62]. Prior to modeling, the hyperparameters of the machine learning model must be optimized by employing appropriate optimization algorithms. This step is crucial as it can significantly improve the predictive performance of the models [63,64,65]. Extensive research in the literature supports this claim, with various academic researchers acknowledging the notable advancements achieved through the employment of optimization algorithms [66,67,68]. In general, the machine learning models without combining optimization algorithms are inefficient, with slow convergence speed, overtraining, or are prone to converging to local optima, and often pose a convergence problem. More importantly, there is subjectivity in the artificially determining of initial model parameters, which causes low predictive accuracy. Hence, the optimized algorithms, such as Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) have been applied by some researchers to optimize the initial parameters of machine learning models for evaluating the properties of geotechnical materials, and an increase in both predictive accuracy and convergence speed of the constructed machine learning models after combining optimization algorithms has been demonstrated. For instance, Chao et al. [33] applied PSO and Genetic Algorithm (GA) to optimize the performance of BPANN and Support Vector Machine (SVM) algorithms when assessing the peak shear strength for the soil-geosynthetics interface. Nevertheless, there is a lack of reports on how optimization algorithms can be used to improve the predictive performance of machine learning algorithms when estimating the peak shear strength of marine soft clay sediments.
In this study, we introduced an innovative PSO-tuned ADABPANN algorithm to predict the peak shear strength of marine soft clay sediment using a database derived from 729 laboratory tests. This marks the first application of the PSO-tuned ADABPANN algorithm in forecasting soil peak shear strength. Simultaneously, five distinct traditional machine learning models, including PSO-tuned BPANN and SVM models, BPANN, and ADABPANN algorithms, were established to assess the applicability of the newly proposed model. Utilizing the PSO-optimized ADABPANN model, susceptibility analysis was conducted, leading to the formulation of an analytical formula for precise predictions of the peak shear strength of marine soft clay sediment, catering to practitioners lacking machine learning expertise. The proposed PSO-tuned ADABPANN model demonstrates accurate and efficient estimation of the peak shear strength for marine soft clay sediment, serving as a pivotal element in advancing the design and operational safety of foundations.
2. Machine Learning Algorithms
This paper employed three types of machine learning algorithms: BPANN, SVM, and Adaptive Boosting Algorithm-Back Propagation Artificial Neural Network (ADABPANN), alongside the optimization algorithm Particle Swarm Optimization (PSO). The basic explanation and fundamental specifications of these algorithms are outlined below.
2.1. BPANN
The BPANN model, as a general structure, consists of input, hidden, and output layers [69,70,71]. The number of neurons in the input and output layers is directly correlated with the number of input and output variables, respectively. In this study, this amounts to 6 and 1. The determination of the number of hidden layer neurons (9) was achieved through an exhaustive enumeration method, as illustrated in Figure 1. Furthermore, the BPANN model employs HTSTF as the activation function and the Levenberg–Marquardt Backpropagation Algorithm (LMBA) as the training algorithm for the network.
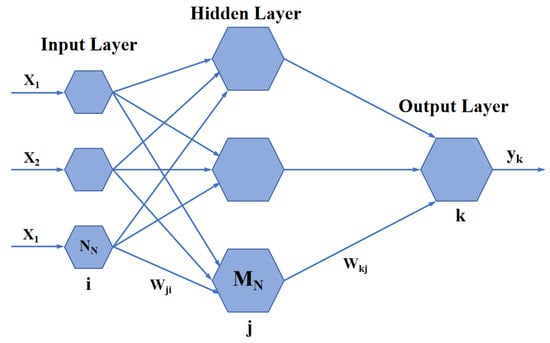
Figure 1.
The typical structure of BPANN.
2.2. SVM
SVM has the capability to perform regression operations with limited sample data [72,73,74,75]. Furthermore, SVM can utilize kernel functions to project specimens from a low-dimensional space to a high-dimensional space, thus effectively transforming a nonlinear problem into a linear one [76].
2.3. ADA-BPANN
ADA-BPANN is a resilient ensemble machine learning algorithm that utilizes BPANN models with identical structures. This integration is based on the principles of bootstrap aggregating theory, which enhances its overall performance and robustness [75,77]. In this study, the specifications of the BPANN models align with the previously mentioned BPANN model. The ADA-BPANN algorithm offers advantages such as straightforward operation, cost-effective computation, superior predictive accuracy, and generalization capability [78,79].
The detailed configurations of the constructed models are illustrated in Table 1.

Table 1.
Configurations of the employed algorithms.
2.4. PSO
PSO is a heuristic optimization algorithm that simulates natural evolution principles to guide the optimization of a population [80]. Specifically, PSO is inspired by bird predation behavior, where particles within the population serve as potential solutions. Through the continuous adjustment of particle motion velocities, PSO strives to identify the optimal solution for the given problem [81,82].
3. Hyperparameters Optimization
In the study, PSO was employed to optimize the hyperparameters the machine learning algorithms proposed, utilizing RMSE (Root-Mean-Square Error) as the fitness metric. (Equation (1)). Given the commonality of PSO optimization processes and the availability of detailed introductions by many researchers, this study does not provide an in-depth explanation of the optimization procedures. The specific optimizing procedure is presented in Figure 2.
where n denotes number of samples, denotes observed value, signifies the predicted value.
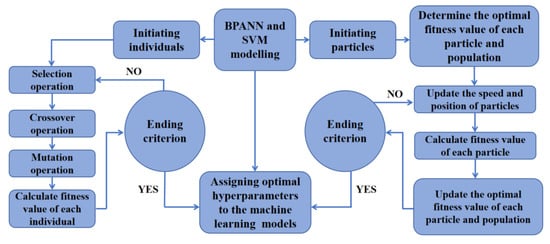
Figure 2.
The flow chart of PSO optimizing.
The parameters that control PSO are summarized in Table 2, while Table 3 presents the optimization hyperparameter and the corresponding ranges for optimization.

Table 2.
The control variables for the optimization algorithm.

Table 3.
The optimization hyperparameters.
4. Methodology
4.1. Laboratory Tests
The physical experiments were conducted using a custom-designed temperature-controlled direct shear apparatus, which consists of several main components, including a temperature-controlled system, a drying–wetting cycles-controlled system, a normal pressure loading system, and a shear pressure loading system. The internal large interface shear system is placed inside the temperature chamber. The upper shear box has a square cross-sectional area of 300 mm by 300 mm and a thickness of 150 mm. The temperature-controlled system is capable of adjusting the temperature of the soil sample by utilizing a heating device located beneath the bottom shear box. The temperature can be adjusted within a range of 30 °C to 140 °C, with a high level of precision, maintaining control within 0.2 °C. Additionally, the drying–wetting cycles-controlled system can regulate the moisture status of the soil sample, allowing for controlled submersion in water or drying cycles. The normal pressure and shear pressure systems are capable of measuring the peak shear strength for soil in diverse normal pressure (0 kPa~400 kPa), with the maximum shear displacement being 100 mm.
The standard testing protocol is as follows: (1) Gently place the marine soft clay sediment sample into the upper and bottom shear boxes and compact it lightly. (2) Activate the temperature-controlled system to stabilize the soil sample temperature for the entire test duration. (3) Initiate the drying–wetting cycles-controlled system to subject the clay sample to cycles. Wetting cycles involve fully submerging the soil sample in water for 0.5 h, constituting one wetting cycle. During drying cycles, maintain the soil sample in a dry-state (soil samples were removed from water and dried using the ambient temperature chamber) for 0.5 h, constituting one drying cycle. One drying–wetting cycle comprises one wetting cycle and one drying cycle. (4) After a predetermined number of drying–wetting cycles, begin the undrained shearing procedure with a shear rate of 1 mm/minute and a maximum shearing displacement of 100 mm. (5) Derive the peak shear strength for marine soft clay sediment under specific temperatures during distinct drying–wetting cycles based on the test data. In the present study, the peak shear strength of marine soft clay sediment with varying mean soil particle sizes, initial density, and initial moisture content was measured under different temperatures, numbers of drying–wetting cycles, and normal pressure. The experimental condition involved unconsolidated undrained shearing. The properties of the marine soft clay sediment sample are listed in Table 4, and the test plan is detailed in Table 5. A total of 729 sets of tests were conducted.

Table 4.
The basic parameters of soil sample.

Table 5.
The test plan.
4.2. Database Creation and Data Processing
Using the above test data, a database containing 729 datasets was created for machine learning modeling. Within these datasets, 583 groups (80%) were randomly chosen for training datasets for constructing the machine learning algorithm. Meanwhile, 146 groups (20%) were randomly chosen as test datasets to evaluate the predictive ability of the proposed machine learning algorithm. Each data group consisted of six variables, namely initial soil density (D), initial soil moisture content (M), initial mean soil particle size (S), temperature (T), drying–wetting cycle number (C), and normal pressure (N), serving as input parameters. The output variable was determined as the peak shear strength of the marine soft clay sediment sample (H). Table 6 shows the statistics of the input and output variables in the database. Figure 3 shows the distribution of the input parameter data in the database, where the x-axis represents the count of data groups associated with the value of a particular input variable, and the y-axis represents the value of the input parameter. Also, the correlation between the input parameters was investigated, with the Pearson’s correlation matrix being illustrated in Figure 4. According to Figure 4, The correlation coefficients between the input parameters (initial density, initial moisture content, mean soil particle size, temperature, number of drying–wetting cycles, and normal pressure) are 0. This indicates that the input parameters are independent of each other and they do not have a correlation.

Table 6.
The statistics.
Figure 3.
Data distributions for the database. (a) Initial soil density; (b) initial moisture content; (c) mean soil particle size; (d) number of drying–wetting cycles; (e) normal stress; (f) temperature.
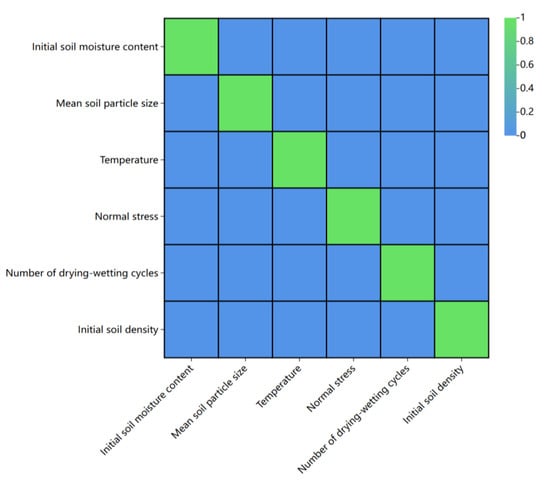
Figure 4.
Pearson correlation coefficients graph.
In this study, a machine learning model was constructed using Matlab. Before starting the machine learning modeling, the dimensions of the input and output variables were normalized to improve the predictive accuracy and effectiveness of the machine learning algorithm. The normalization formula is as follows (2).
where and represent normalized and initial data, respectively, and denote the minimum and maximum data, respectively.
4.3. Approaches for Evaluating Performance
The predictive accuracy of the constructed machine learning algorithm is evaluated by three parameters:
- (i)
- RMSE: The definition of RMSE is expressed in Equation (1), representing the standard error between the estimated and measured values. A lower RMSE value indicates higher accuracy in the model.
- (ii)
- Correlation coefficient (R2): The definition of R2 is expressed in Equation (3), which is the associated degree between the change of forecasted and observed value. R2 value is in the range of [−1, 1], with −1 and 1 representing the absolutely negative and positive correlations, respectively [82,83].
- (iii)
- Mean absolute percentage error (MAPE): MAPE is defined in Equation (4) as a dimensionless parameter. A smaller MAPE value indicates a more accurate model, with a value of 0 indicating a perfect prediction.
5. Predicting Performance
5.1. Results for Hyperparameter Optimization
The process of optimizing hyperparameters for ADABPANN, BPANN, and SVM models using PSO approach is depicted in Figure 5.
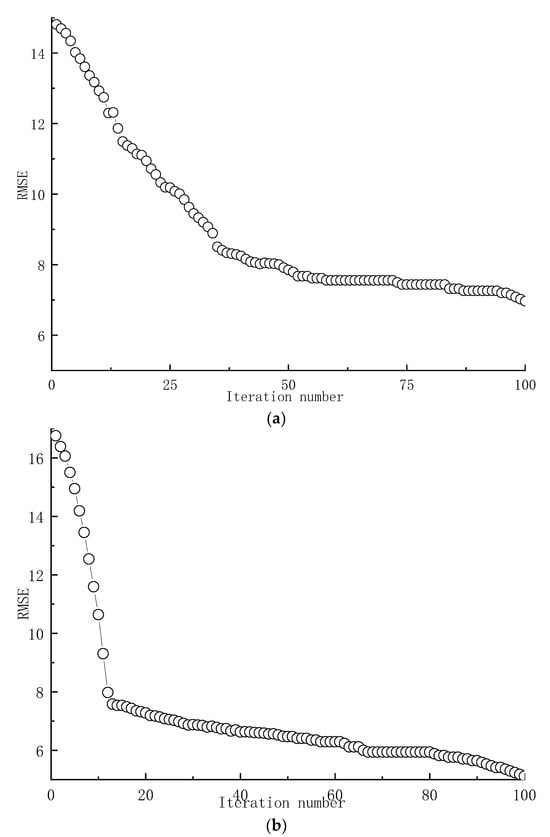
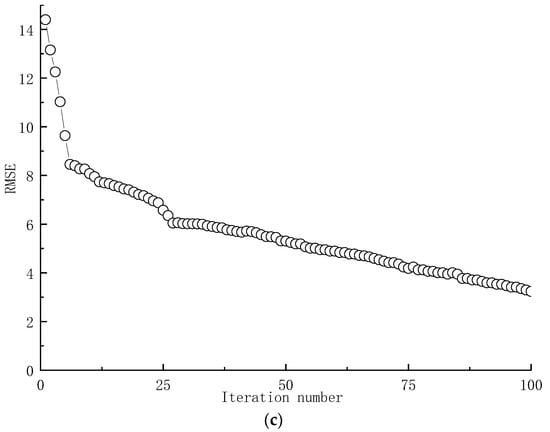
Figure 5.
Optimization processes by PSO. (a) BPANN; (b) SVM; (c) ADABPANN.
As depicted in Figure 5, for ADABPANN, BPANN, and SVM, the RMSE value gradually decreases with the increase in the iteration number during the PSO process. Comparing the optimized RMSE value to the value before optimization reveals a relatively significant decrease. Specifically, after optimization using PSO, the RMSE of ADABPANN, BPANN, and SVM decreases from 14.5 to 3.1, 16.9 to 5, and 14.7 to 6.9, respectively. This indicates the pronounced improvement effect of PSO on predictive accuracy.
5.2. Predicting Performance
The predictive performance of the machine learning models developed for evaluating the drilling and measuring datasets is illustrated in Figure 6, Figure 7 and Figure 8.
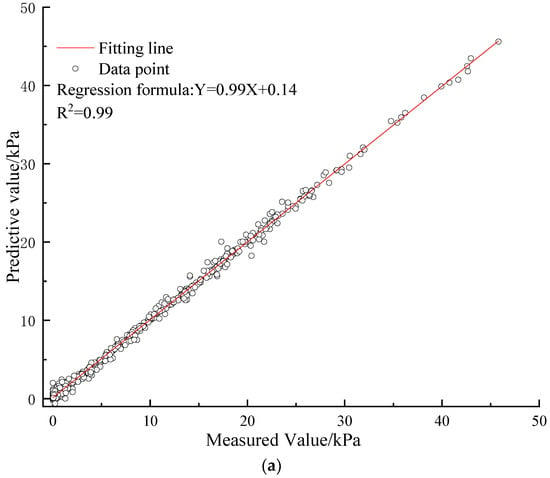
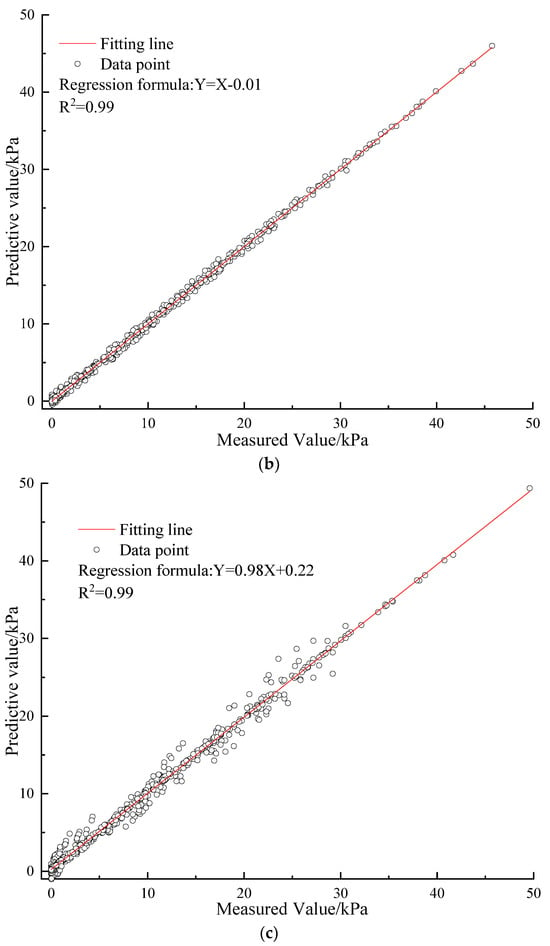
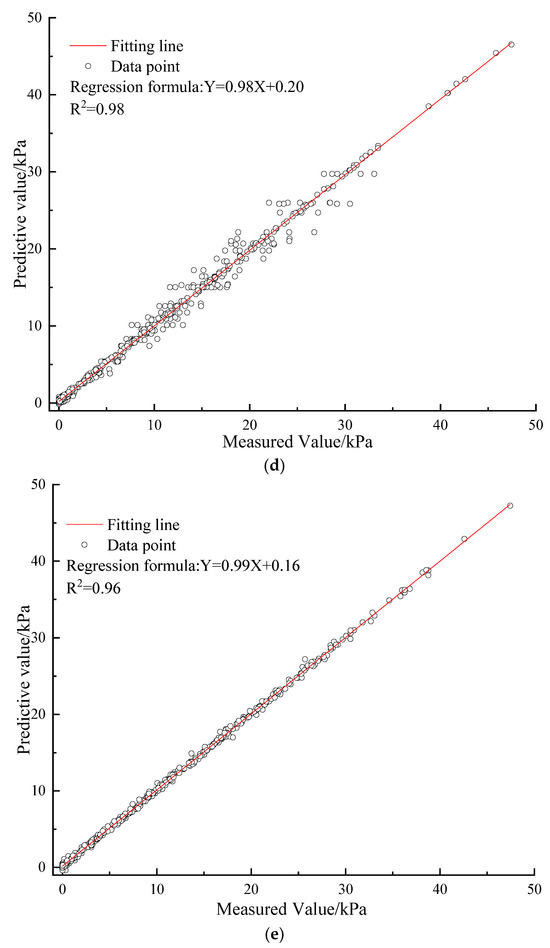
Figure 6.
The R value for the algorithms in training datasets. (a) BPANN; (b) SVM; (c) PSO−BPANN; (d) PSO−SVM; (e) PSO−ADABPANN.
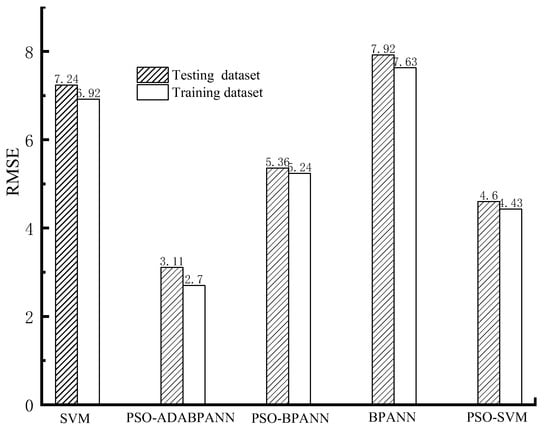
Figure 7.
The RMSE values of the models.
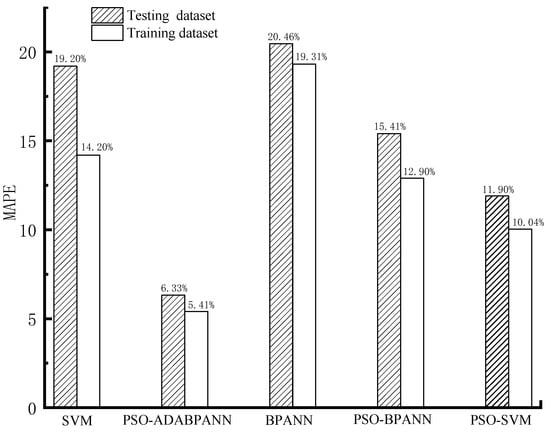
Figure 8.
The MAPE values of the models.
When evaluated with the training datasets, as depicted in Figure 6, Figure 7 and Figure 8, the PSO-tuned ADABPANN model exhibits superior predictive performance compared to the other four algorithms. It is noteworthy that the model has the highest predictive accuracy with the lowest RMSE value of 2.7, the smallest MAPE value of 5.41%, and the highest R2 value of 0.99. The PSO-tuned SVM model follows closely in performance. In contrast, the predictive capabilities of the PSO-tuned BPANN model, SVM model, and BPANN model appear relatively inferior.
As depicted in Figure 7, Figure 8 and Figure 9, the PSO-tuned ADABPANN model consistently outperforms the other four machine learning models in terms of prediction performance when assessed with the test dataset. Notably, the PSO-tuned ADABPANN model shows the best prediction accuracy with the lowest RMSE value of 3.11, the smallest MAPE value of 6.33%, and the highest R2 value of 0.99. Among the rest of the machine learning models, the PSO-tuned SVM model performs relatively well. In summary, the PSO-tuned ADABPANN model demonstrates superior performance in evaluating both training and testing datasets compared to the PSO-tuned SVM model and BPANN model. Specifically, the PSO-tuned ADABPANN model excels in forecasting the peak shear strength for marine soft clay sediment with higher precision and efficiency. Notably, within the same machine learning algorithm, the models combined using the PSO algorithm outperform individual machine learning models, exhibiting higher predictive accuracy.
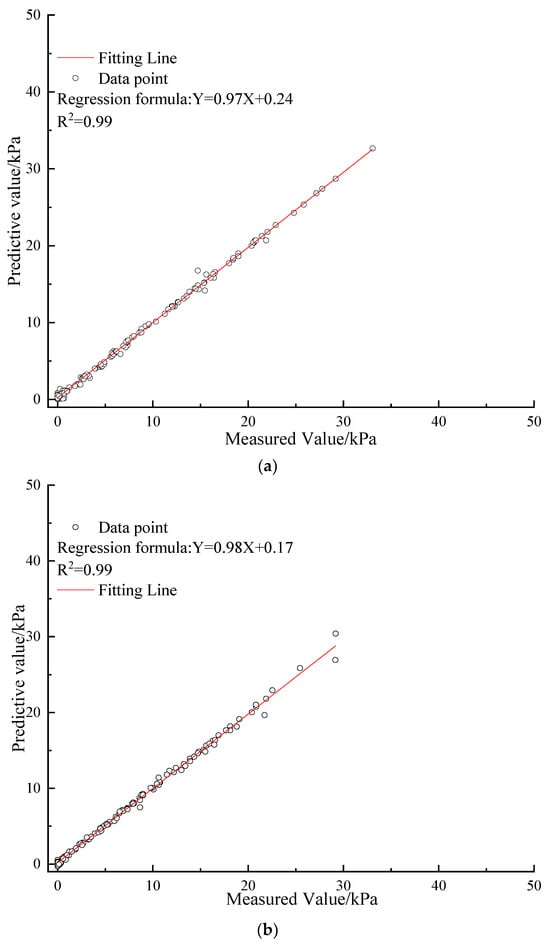
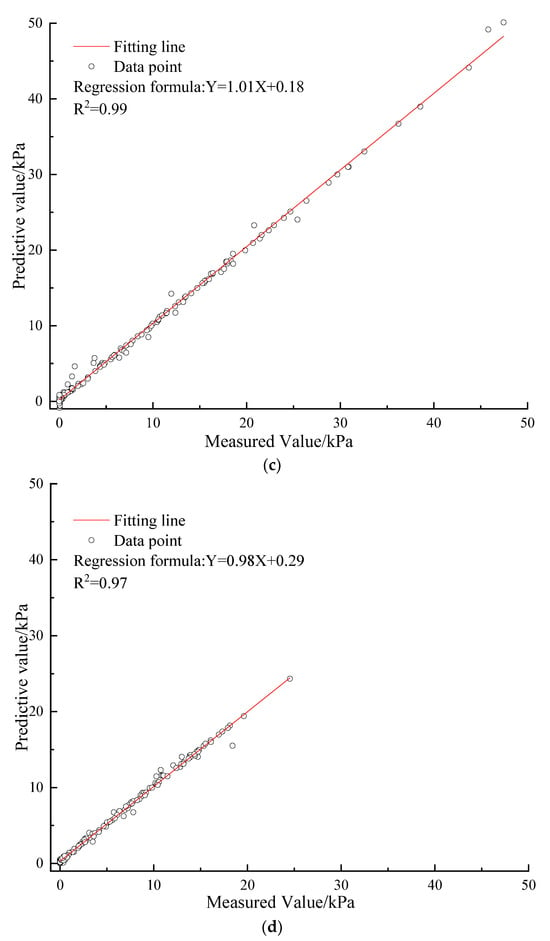
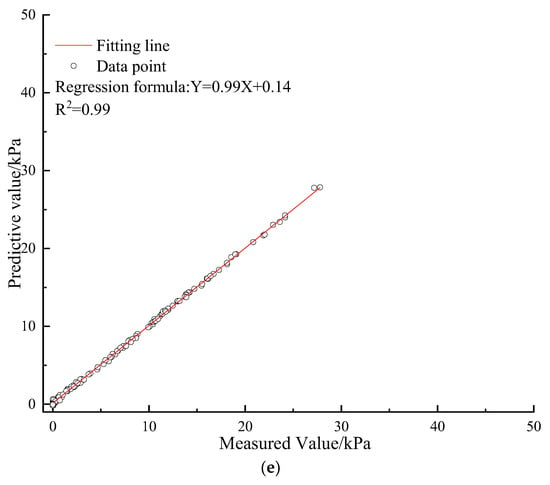
Figure 9.
The R2 value for the algorithms in testing datasets. (a) BPANN; (b) SVM; (c) PSO-BPANN; (d) PSO-SVM; (e) PSO-ADABPANN.
5.3. Sensitivity Analysis
In this comprehensive section, the meticulously crafted PSO-tuned ADABPANN model is utilized to conduct a rigorous sensitivity analysis. The purpose of this analysis is to scrutinize the relative importance of various input parameters in predicting the peak shear strength of marine soft clay sediments. By doing so, we aim to gain a deeper understanding of how these parameters influence the overall prediction accuracy and to identify any potential areas of improvement for future model iterations. The ADABPANN algorithm, composed of multiple BPANN models will be discussed. The relative importance of the input variables is assessed using the Garson’s algorithm as defined in Equation (5). Determining the relative importance of input variables in the BPANN algorithm using the Gasson algorithm serves as a surrogate measure for assessing the significance of these parameters in the ADABPANN model. As shown in Figure 10, this surrogate metric allows us to gain insight into the impact of various input factors on the overall predictive performance of the ADABPANN model. By analyzing these findings, we can identify potential areas for optimization and refinement, further enhancing the accuracy and reliability of the model [84,85].
where signifies the relative significance for input variables, and , represents the connectivity weight for the hidden-input and hidden-output layers (N, M represents the input and output variable numbers, respectively).
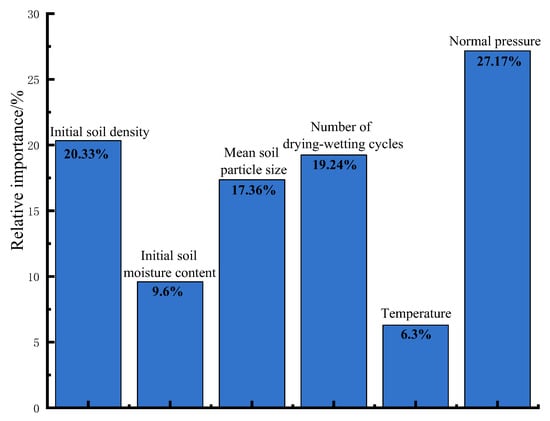
Figure 10.
Relative significance for the input variables.
As illustrated in Figure 10, normal stress is identified as having the highest impact on the peak shear resistance of marine soft clay sediment, with a relative significance of 27.17%. It is closely followed by initial soil density, the drying–wetting cycle number, and mean soil particle size, accounting for 20.33%, 19.24%, and 17.36%, respectively. Conversely, the influence of initial soil moisture content and temperature on peak shear strength is relatively small, contributing 9.6% and 6.3%, respectively. For a detailed understanding of the mechanism, please refer to the “Discussion” section.
6. Establishment of an Analytical Formula
The above analysis suggests that the constructed PSO-tuned ADABPANN model can offer accurate estimations of the peak shear strength for marine soft clay sediment. However, due to the intricacies of machine learning modeling, applying these models might pose a challenge for individuals without a background in machine learning. To address this limitation, this section proposes an analytical formula for forecasting the peak shear strength of marine soft clay sediment by utilizing the built PSO-tuned ADABPANN model. As previously mentioned, the ADABPANN model consists of a set of BPANN models, and the output values of the BPANN models can be calculated from the connection weights and biases of the nodes in the model using Equation (6). Therefore, the estimation of the PSO-ADABPANN model can be obtained from Equation (6) by using the average connection weights and biases calculated for the BPANN models that make up the ADABPANN algorithm, as detailed in Table 7 [86,87,88,89,90].

Table 7.
Connected weights and biases for the constructed PSO-ADABPANN algorithm.
Utilizing Equation (6), the analytical formula for estimating the peak shear strength for marine soft clay sediment is derived and presented in Equation (7).
where and denote the highest and lowest data for the peak shear strength in the database, respectively, and .
Among Equation (8):
Among Equation (9):
where denotes the connection weights between the i-th hidden layer junction and the output layer junction of the constructed PSO-ADABPANN algorithm, as detailed in Table 7.
In Equation (10):
where denotes the biases for the j-th hidden layer node; denotes the connected weight between the j-th input layer junction and the i-th hidden layer junction; denotes the i-th uni-formalized input variable.
7. Validation of the Predicting Performance with the Physical Tests
In order to assess the feasibility of the suggested analytical formulation and machine learning model, we compared the peak shear strengths of marine soft clay sediments predicted using the analytical formulation with the peak shear strengths acquired from physical tests. The overall process is outlined as follows: (1) Conduct large direct shear experiments on marine soft clay sediment with varying properties under different test conditions using the bespoke apparatus. The basic parameters of the marine soft clay sediment sample and the test plan are listed in Table 8 and Table 9, respectively, totaling 32 sets of tests. (2) Estimate the peak shear strength of marine soft clay sediment based on the soil sample properties and test conditions using Equation (7). (3) Compare the peak shear strength obtained from the analytical equation and machine learning model, with the results illustrated in Figure 11 [91,92,93,94,95].

Table 8.
The fundamental parameters of the validation soil sample.

Table 9.
The validation test plan.
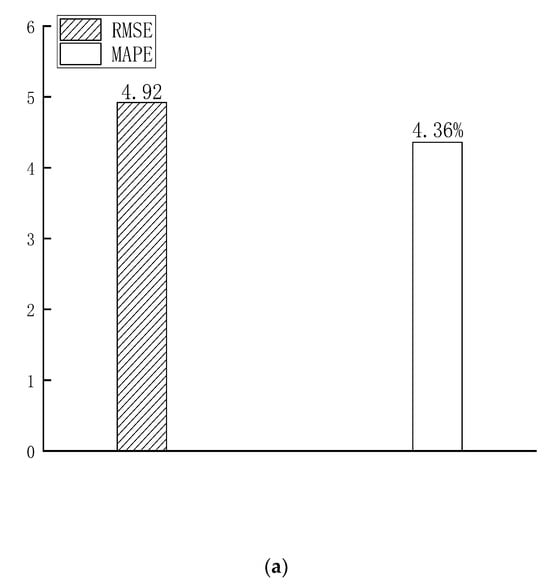
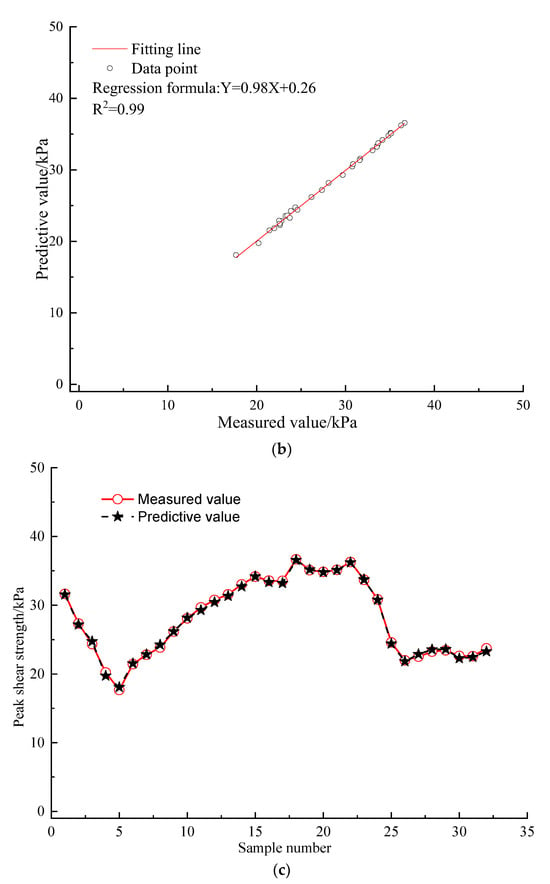
Figure 11.
The validation results. (a) The MAPE and RMSE; (b) the R2 values; (c) the predicted and measured value.
As shown in Figure 11, the peak shear strengths of marine soft clay sediments predicted using the analytical equations are very close to the peak shear strengths obtained from laboratory tests [96,97,98]. Specifically, the RMSE, MAPE, and R2 values are 4.92, 4.36%, and 0.99, respectively. These results indicate that the prediction accuracy of the constructed analytical equations and machine learning model is satisfactory.
8. Discussion
The sensitivity analysis indicates a substantial impact of the drying–wetting cycle number on the peak shear strength of marine soft clay sediment used as foundations, with a notable relative significance of 19.24%. This influence is attributed to the expansion and shrinkage properties of marine soft clay sediment during the absorption and expulsion of water, respectively. The frequent alternation of soil expansion and shrinkage during drying–wetting cycles leads to volume variations, inducing the generation of cracks within the marine soft clay sediment. This damage to the structure consequently decreases the peak shear strength. Moreover, a larger drying–wetting cycle number is observed to cause more significant damage to the soil structure, resulting in a larger decreasing magnitude in the peak shear strength compared to a smaller number of cycles. Therefore, the drying–wetting cycle number exhibits a relatively high importance in determining the peak shear strength of marine soft clay sediment. It is essential to note that in this study, the relative significance of the initial soil moisture content for the peak shear strength is relatively small, at 9.6%. This is attributed to the requirement that marine soft clay sediment samples undergo drying–wetting cycles before conducting large direct shear tests. Consequently, the moisture content of the soil samples tends to converge to a similar level after the drying–wetting cycles, diminishing the impact of initial moisture content on the peak shear strength. Furthermore, the low relative significance of temperature, at 6.3%, can be explained by the moderate temperature range (20–60 °C) adopted in this research. This temperature range is not extreme enough to induce freezing or melting of the soil, which would significantly alter the soil structure and result in a large variation in peak shear strength.
Two critical aspects of this research warrant further improvement. (1) In actual offshore engineering sites, the environment of marine soft clay sediment is intricate, and the environmental factors affecting marine soft clay sediment extend beyond just drying–wetting cycles and temperature. Therefore, future research should strive to determine the peak shear resistance of marine soft clay sediment under the influence of various environmental loadings, including leachate erosion, to augment the current database. These enhancements will establish a robust foundation for the advancement of machine learning models, enabling more precise assessments of the peak shear strength of marine soft clay sediments in real-world offshore engineering applications. (2) In practical offshore engineering, the stress environment experienced by marine soft clay sediment is complex, involving factors such as triaxial shear stress, among others. Therefore, conducting tests to measure the peak shear strength of marine soft clay sediment under various stress conditions, including triaxial shearing and axial shearing, would be valuable. Based on these test results, existing databases can be extended to create more accurate machine learning models capable of predicting the peak shear performance of marine soft clay sediments in real stress environments.
9. Conclusions
This study has established a comprehensive database comprising 729 large-scale direct shear tests, providing a robust foundation for developing a novel PSO-tuned ADABPANN model aimed at predicting the peak shear strength of marine soft clay sediment. The constructed model takes into account essential input parameters, including initial soil density, initial soil moisture content, mean soil particle size, number of drying–wetting cycles, temperature, and normal pressure. It is noteworthy that this marks the first application of the PSO-tuned ADABPANN model for estimating soil peak shear resistance. In order to authenticate and contrast the predictive performance of the proposed innovative algorithms, traditional machine learning models such as PSO-optimized BPANN and SVM were also developed. In addition, a sensitivity analysis based on the PSO-optimized ADABPANN algorithm was conducted to evaluate the relative importance of the input parameters on the peak shear strength of marine soft clay sediments. In addition, an analytical expression was devised to facilitate precise evaluation of peak shear strengths for organizations lacking expertise in machine learning techniques.
The current study confirms the efficacy of the proposed PSO-optimized ADABPANN algorithm in efficiently and accurately evaluating the peak shear performance of marine soft clay sediments, which outperforms conventional machine learning algorithms. Notably, this study observed superior optimization and efficiency when PSO was employed. Sensitivity analyses showed that normal stress, initial soil density, average soil grain size and number of wet and dry cycles had a significant effect on the peak shear strength of marine soft clay sediments, whereas the initial soil moisture content and temperature had relatively minor effects.
In conclusion, accurately estimating the peak shear strength of marine soft clay sediments poses significant challenges due to the presence of numerous influencing factors and intricate interaction mechanisms. Nevertheless, the introduction of the novel PSO-adjusted ADABPANN model successfully addresses these challenges, providing a reliable method for accurate and efficient prediction of peak shear strength. The model provides a solid foundation for future developments in foundation design, thereby improving the overall performance and effectiveness of offshore infrastructure.
Author Contributions
Conceptualization, Z.X. and X.F.; investigation, H.W. and Z.L.; resources, S.H. and Z.L.; data curation, Z.X. and Z.L.; writing—original draft, S.H. and Z.L.; writing—review and editing, Z.L., H.W., and Z.X.; visualization, P.T., K.T., and Y.W.; software, Z.L., S.H., and H.W.; supervision, X.F.; funding acquisition, Z.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
In this paper, all data, models, and code used during the study appear in the submitted article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Narani, S.S.; Abbaspour, M.; Hosseini, S.M.M.; Aflaki, E.; Nejad, F.M. Sustainable reuse of Waste Tire Textile Fibers (WTTFs) as reinforcement materials for expansive soils: With a special focus on landfill liners/covers. J. Clean. Prod. 2020, 247, 119151. [Google Scholar] [CrossRef]
- Xie, H.; Wang, Q.; Wu, J.; Chen, Y. Analytical model for methane migration through fractured unsaturated landfill cover soil. Eng. Geol. 2019, 255, 69–79. [Google Scholar] [CrossRef]
- Chao, Z.; Shi, D.; Zheng, J. Experimental research on temperature–Dependent dynamic interface interaction between marine coral sand and polymer layer. Ocean. Eng. 2024, 297, 117100. [Google Scholar] [CrossRef]
- Cui, J.; Jin, Y.; Jing, Y. Elastoplastic Solution of Cylindrical Cavity Expansion in Unsaturated Offshore Island Soil Considering Anisotropy. J. Mar. Sci. Eng. 2024, 12, 308. [Google Scholar] [CrossRef]
- Ladd, C.C.; Foott, R. New design procedure for stability of soft clays. J. Geotech. Eng. 1974, 100, 763–786. [Google Scholar]
- Ladd, C.C. Stability evaluation during staged construction. J. Geotech. Eng. 1991, 117, 540–615. [Google Scholar] [CrossRef]
- Stamatopoulos, C.A. Constitutive modeling of earthquake-induced slides on clays along slip surfaces. Landslides 2009, 6, 191–207. [Google Scholar] [CrossRef]
- Cortellazzo, G.; Russo, L.E.; Busana, S.; Carbone, L.; Favaretti, M.; Hangen, H. Field trial of a reinforced landfill cover system: Performance and failure. Geotext. Geomembr. 2022, 50, 655–667. [Google Scholar] [CrossRef]
- Liu, M.; Lu, H.; Deng, Q.; Ji, S.; Qin, L.; Wan, Y. Shear strength, water permeability and microstructure of modified municipal sludge based on industrial solid waste containing calcium used as landfill cover materials. Waste. Manag. 2022, 145, 20–28. [Google Scholar] [CrossRef]
- Chao, Z.; Wang, H.; Hu, S.; Wang, M.; Xu, S.; Zhang, W. Permeability and porosity of light-weight concrete with plastic waste aggregate: Experimental study and machine learning modelling. Constr. Build. Mater. 2024, 411, 134465. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, J.; Feng, S. The era of low-permeability sites remediation and corresponding technologies: A review. Chemosphere 2023, 313, 137264. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Sun, Z.; Ren, X.; Zhang, J.; Yu, J.; Zhang, W. An improved Smoothed Particle Hydrodynamics (SPH) method for modelling the cracking processes of teeth and its applications. J. Mech. Behav. Biomed. 2022, 136, 105518. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Ren, X.; Zhang, J. Simulating the chemical-mechanical-damage coupling problems of cement-based materials using an improved smoothed particle hydrodynamics method. Case Stud. Constr. Mat. 2023, 18, e02018. [Google Scholar] [CrossRef]
- Yu, S.; Sun, Z.; Yu, J. An improved meshless method for modeling the mesoscale cracking processes of concrete containing random aggregates and initial defects. Constr. Build. Mater. 2023, 363, 129770. [Google Scholar] [CrossRef]
- He, J.; Feng, X.; Zhou, L.; Zhou, L.; Zhang, L. The effect of leachate seepage on the mechanical properties and microstructure of solidified sludge when used as a landfill temporary cover material. Waste. Manag. 2021, 130, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.J.; Chang, J.Y.; Shi, H.; Zheng, Q.T.; Guo, X.Y.; Zhang, X. L Failure of an unfilled landfill cell due to an adjacent steep slope and a high groundwater level: A case study. Eng. Geol. 2019, 262, 105320. [Google Scholar] [CrossRef]
- Mukherjee, K.; Mishra, A.K. An assessment of the mechanical performance of a novel sand bentonite-glass fiber composite for the avoidance of catastrophic landfill failure. Constr. Build. Mater. 2022, 348, 128644. [Google Scholar] [CrossRef]
- Wanare, R.; Shetty, R.; Jayanthi, P.N.V. Investigation to Quantify Suction Characteristics of Marine Soil during Drying and Wetting Cycles. Geotech. Test. J. 2021, 44, 112–129. [Google Scholar] [CrossRef]
- Akatsuka, T.; Mitamura, O. Response of denitrification rate associated with wetting and drying cycles in a littoral wetland area of Lake Biwa, Japan. Limnology 2011, 12, 127–135. [Google Scholar] [CrossRef]
- Chen, F.; Chen, W.; Wang, H.; Yang, J.; Tong, S. On Mechanical Properties of Ferronickel Slag Powder Cement Soil Under Coupled Effects of Marine Environment and Wetting-Drying Cycles. SSRN 2023, 4427764. [Google Scholar]
- Lin, H.; Gong, X.; Zeng, Y. Experimental study on the effect of temperature on HDPE geomembrane/geotextile interface shear characteristics. Geotext. Geomembr. 2023, 52, 394–407. [Google Scholar] [CrossRef]
- Lin, H.; Huang, W.; Wang, L. Transport of Organic Contaminants in Composite Vertical Cut-Off Wall with Defective HDPE Geomembrane. Polymers 2023, 15, 3031. [Google Scholar] [CrossRef]
- Shi, D.; Niu, J.; Zhang, J. Effects of particle breakage on the mechanical characteristics of geogrid-reinforced granular soils under triaxial shear: A DEM investigation. Geomech. Energy. Environ. 2023, 34, 100446. [Google Scholar] [CrossRef]
- Akbarimehr, D.; Eslami, A.; Aflaki, E. Geotechnical behaviour of clay soil mixed with rubber waste. J. Clean. Prod. 2020, 271, 122632. [Google Scholar] [CrossRef]
- Chang, I.; Cho, G.C. Shear strength behavior and parameters of microbial gellan gum-treated soils: From sand to clay. Acta. Geotech. 2019, 14, 361–375. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. Influence of the grain-size distribution curve of quartz sand on the small strain shear modulus G max. J. Geotech. Geoenviron. 2009, 135, 1404–1418. [Google Scholar] [CrossRef]
- Payan, M.; Khoshghalb, A.; Senetakis, K. Effect of particle shape and validity of Gmax models for sand: A critical review and a new expression. Comput. Geotech. 2016, 72, 28–41. [Google Scholar] [CrossRef]
- Payan, M.; Senetakis, K.; Khoshghalb, A. Effect of gradation and particle shape on small-strain Young’s modulus and Poisson’s ratio of sands. Int. J. Geomech. 2017, 17, 04016120. [Google Scholar] [CrossRef]
- Dong, Y. Reseeding of particles in the material point method for soil–structure interactions. Comput. Geotech. 2020, 127, 103716. [Google Scholar] [CrossRef]
- Cekerevac, C.; Laloui, L. Experimental study of thermal effects on the mechanical behaviour of a clay. Int. J. Numer. Anal Ment. 2004, 28, 209–228. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, Z.; Xu, X.; Du, H. Volumetric calculation method and temperature characteristics of frozen soil in mechanical testing. Col. Reg. Sci. Technol. 2013, 85, 225–231. [Google Scholar] [CrossRef]
- Stoltz, G.; Cuisinier, O.; Masrouri, F. Weathering of a lime-treated clayey soil by drying and wetting cycles. Eng. Geol. 2014, 181, 281–289. [Google Scholar] [CrossRef]
- Chao, Z.; Fowmes, G. Modified stress and temperature-controlled direct shear apparatus on soil-geosynthetics interfaces. Geotext. Geomembr. 2021, 49, 825–841. [Google Scholar] [CrossRef]
- Chao, Z.; Gong, B.; Yue, W.; Xu, X.; Shi, D.; Yang, C.; Hu, T. Experimental study on stress-dependent gas permeability and porosity of artificially cracked cement mortar. Constr. Build. Mater. 2022, 359, 129290. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Randolph, M.F. Investigation of impact forces on pipeline by submarine landslide using material point method. Ocean. Eng. 2017, 146, 21–28. [Google Scholar] [CrossRef]
- Ren, P.; Chen, Z.L.; Li, L.; Gong, W.; Li, J. Dynamic shakedown behaviors of flexible pavement overlying saturated ground under moving traffic load considering effect of pavement roughness. Comput. Geotech. 2024, 168, 106134. [Google Scholar] [CrossRef]
- Wang, P.; Yin, Z.Y.; Hicher, P.Y. Micro-mechanical analysis of one-dimensional compression of clay with DEM. Int. J. Numeranal. Met. 2023, 47, 2706–2724. [Google Scholar] [CrossRef]
- Wang, P.; Yin, Z.Y.; Wang, Z.Y. Micromechanical investigation of particle-size effect of granular materials in biaxial test with the role of particle breakage. J. Eng. Mech-ASCE 2022, 148, 04021133. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Wang, P.; Zhang, F. Effect of particle shape on the progressive failure of shield tunnel face in granular soils by coupled FDM-DEM method. Tunn. Undergr. Space Technol. 2020, 100, 103394. [Google Scholar] [CrossRef]
- Wan, D.; Wang, M.; Zhu, Z. A coupled model of asymmetric GIMP and tetrahedron CPDI based on the penalty contact algorithm for simulating dynamic rock splitting. Int. J. Rock. Mech. Min. 2023, 170, 105483. [Google Scholar] [CrossRef]
- Shu, Y.; Zhu, Z.; Wang, M. Parameter calibration of the tensile-shear interactive damage constitutive model for sandstone failure. J. Rock. Mech. Geotech. 2024, 16, 1153–1174. [Google Scholar] [CrossRef]
- Cavalcante, A.L.B.; Mascarenhas, P.V.S. Efficient approach in modeling the shear strength of unsaturated soil using soil water retention curve. Acta. Geotech. 2021, 16, 3177–3186. [Google Scholar] [CrossRef]
- Yavari, N.; Tang, A.M.; Pereira, J.M.; Hassen, G. Effect of temperature on the shear strength of soils and the soil–structure interface. Can. Geotech. J. 2016, 53, 1186–1194. [Google Scholar] [CrossRef]
- Schjønning, P.; Lamandé, M.; Keller, T.; Labouriau, R. Subsoil shear strength—Measurements and prediction models based on readily available soil properties. Soil. Till. Res. 2020, 200, 104638. [Google Scholar] [CrossRef]
- Cui, P.; Zhou, J.; Gao, R. Prediction of the permeability tensor of marine clayey sediment during cyclic loading and unloading of confinement pressure using physical tests and machine learning techniques. Water 2024, 16, 1102. [Google Scholar] [CrossRef]
- Song, S.; Wang, P.; Yin, Z. Micromechanical modeling of hollow cylinder torsional shear test on sand using discrete element method. J. Rock. Mech. Geotech. 2024, in press. [Google Scholar] [CrossRef]
- Chao, Z.; Fowmes, G.; Dassanayake, S.M. Comparative study of hybrid artificial intelligence approaches for predicting peak shear strength along soil-geocomposite drainage layer interfaces. Int. J. Geosynth. Ground Eng. 2021, 7, 60. [Google Scholar] [CrossRef]
- Khodkari, N.; Hamidian, P.; Khodkari, H. Predicting the small strain shear modulus of sands and sand-fines binary mixtures using machine learning algorithms. Transp. Geotech. 2024, 44, 101172. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Keawsawasvong, S.; Jearsiripongkul, T. Data-driven prediction of stability of rock tunnel heading: An application of machine learning models. Infrastructures 2022, 7, 148. [Google Scholar] [CrossRef]
- Tran, D.T.; Onjaipurn, T.; Kumar, D.R. An eXtreme Gradient Boosting prediction of uplift capacity factors for 3D rectangular anchors in natural clays. Earth. Sci. Inform. 2024, 17, 2027–2041. [Google Scholar] [CrossRef]
- Chao, Z.; Ma, G.; He, K.; Wang, M. Investigating low-permeability sandstone based on physical experiments and predictive modeling. Uudergr. Space 2021, 6, 364–378. [Google Scholar] [CrossRef]
- Xu, C.; Liu, X.; Wang, E.; Wang, S. Calibration of the microparameters of rock specimens by using various machine learning algorithms. Int. J. Geomech. 2021, 21, 04021060. [Google Scholar] [CrossRef]
- Wang, P.; Xu, C.; Yin, Z.Y. A DEM-based Generic Modeling Framework for Hydrate-Bearing Sediments. Comput. Geotech. 2024, 171, 106287. [Google Scholar] [CrossRef]
- Wang, F.; Ding, C.; Pan, H. A mesostructure-informed cohesion-based numerical method for fracture behavior of slate with foliation structure. Int. J. Rock. Mech. Min. 2022, 160, 105252. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Randolph, M.F. Quantification of impact forces on fixed mudmats from submarine landslides using the material point method. Appl. Ocean. Res. 2020, 102, 102227. [Google Scholar] [CrossRef]
- Gan, L.; Xu, W.; Zhang, Z. Macro-microscopic experimental and numerical simulation study of fiber-mixed concrete under the salt–freezing effect. J. Build. Eng. 2024, 82, 108371. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Shi, D. Determination of Safety Monitoring Indices for Roller-Compacted Concrete Dams Considering Seepage–Stress Coupling Effects. Mathematics 2023, 11, 3224. [Google Scholar] [CrossRef]
- Wan, D.; Wang, M.; Zhu, Z. Coupled GIMP and CPDI material point method in modelling blast-induced three-dimensional rock fracture. Int. J. Min. Sci. Technol. 2022, 32, 1097–1114. [Google Scholar] [CrossRef]
- Shiuly, A.; Hazra, T.; Sau, D.; Maji, D. Performance and optimisation study of waste plastic aggregate based sustainable concrete–A machine learning approach. Cleaner. Waste. Syst. 2022, 2, 100014. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Liang, X.; Li, Y. New wind speed forecasting approaches using fast ensemble empirical model decomposition, genetic algorithm, Mind Evolutionary Algorithm and Artificial Neural Networks. Renew. Energy 2015, 83, 1066–1075. [Google Scholar] [CrossRef]
- Wang, H.; Shen, J. An improved model combining evolutionary algorithm and neural networks for PV maximum power point tracking. IEEE Access 2018, 7, 2823–2827. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, D.; Huang, H. A phase-field-based multi-physics coupling numerical method and its application in soil–water inrush accident of shield tunnel. Tunn. Undergr. Space Technol. 2023, 140, 105233. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, M.; Shen, W. Fluid-solid-phase multi-field coupling modeling method for hydraulic fracture of saturated brittle porous materials. Eng. Fract. Mech. 2023, 286, 109231. [Google Scholar] [CrossRef]
- Xu, J.; Gong, J.; Li, Y. Surf-riding and broaching prediction of ship sailing in regular waves by LSTM based on the data of ship motion and encounter wave. Ocean. Eng. 2024, 297, 117010. [Google Scholar] [CrossRef]
- Iqtidar, A.; Bahadur Khan, N.; Kashif-ur-Rehman, S.; Faisal Javed, M.; Aslam, F.; Alyousef, R.; Mosavi, A. Prediction of compressive strength of rice husk ash concrete through different machine learning processes. Crystals 2021, 11, 352. [Google Scholar] [CrossRef]
- Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting concrete compressive strength using hybrid ensembling of surrogate machine learning models. Cement. Concrete. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
- Shao, W.; Li, Q.; Zhang, W.; Shi, D.; Li, H. Numerical modeling of chloride diffusion in cement-based materials considering calcium leaching and external sulfate attack. Constr. Build. Mater. 2023, 401, 132913. [Google Scholar] [CrossRef]
- Gholami, V.; Booij, M.J.; Tehrani, E.N.; Hadian, M.A. Spatial soil erosion estimation using an artificial neural network (ANN) and field plot data. Catena 2018, 163, 210–218. [Google Scholar] [CrossRef]
- Moayedi, H.; Jahed, A.D. Optimizing an ANN model with ICA for estimating bearing capacity of driven pile in cohesionless soil. Eng. Comput 2018, 34, 347–356. [Google Scholar] [CrossRef]
- Yusof, M.F.; Azamathulla, H.M.; Abdullah, R. Prediction of soil erodibility factor for Peninsular Malaysia soil series using ANN. Neural Comput. Appl. 2014, 24, 383–389. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Shao, W.; Qin, F.; Shi, D.; Soomro, M.A. Horizontal bearing characteristic and seismic fragility analysis of CFRP composite pipe piles subject to chloride corrosion. Comput. Geotech. 2024, 166, 105977. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, D.; Shen, Z.; Zhang, J.; Zhao, S.; Gan, L.; Tang, P. Influence of chopped basalt fibers on the fracture performance of concrete subjected to calcium leaching. Theor. Appl. Fract. Mec. 2023, 125, 103934. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kohestani, V.R.; Hassanlourad, M.; Ardakani, A. Evaluation of liquefaction potential based on CPT data using random forest. Nat. Hazards 2015, 79, 1079–1089. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, H.; Liang, F.; Li, L. Numerical investigation on lateral monotonic and cyclic responses of scoured rigid monopile based on an integrated bounding surface model. Comput. Geotech. 2024, 166, 105997. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Hogg, R.V.; McKean, J.W.; Craig, A.T. Introduction to Mathematical Statistics; Pearson Education: Bangalore, India, 2013. [Google Scholar]
- Garson, G.D. A comparison of neural network and expert systems algorithms with common multivariate procedures for analysis of social science data. Soc. Sci. Comput. Rev. 1991, 9, 399–434. [Google Scholar] [CrossRef]
- Goh, A.T.C. Back-propagation neural networks for modeling complex systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Kulhawy, F.H.; Chua, C.G. Bayesian neural network analysis of undrained side resistance of drilled shafts. J. Geotech. Geoenviron. 2005, 131, 84–93. [Google Scholar] [CrossRef]
- Shao, W.; He, X.; Shi, D.; Zhu, W. Prediction of Crack Width in RC Piles Exposed to Local Corrosion in Chloride Environment. Materials 2023, 16, 6403. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Ku, Q.; Li, C.; Wang, H.; Dong, Y.; Cheng, Z. Single-particle crushing behaviour of carbonate sands studied by X-ray microtomography and a combined finite–discrete element method. Acta. Geotech. 2022, 17, 3195–3209. [Google Scholar] [CrossRef]
- Fan, N.; Jiang, J.; Nian, T.; Dong, Y.; Guo, L.; Fu, C.; Tian, Z.; Guo, X. Impact action of submarine slides on pipelines: A review of the state-of-the-art since 2008. Ocean. Eng. 2023, 286, 115532. [Google Scholar] [CrossRef]
- Shi, D.; Chen, X.; Shao, W. Modeling of bidirectional chloride convection-diffusion for corrosion initiation life prediction of RC square piles under drying-wetting cycle. Appl. Ocean Res. 2023, 141, 103789. [Google Scholar] [CrossRef]
- Zhang, Y.; Zang, W.; Zheng, J.; Cappietti, L.; Zhang, J.; Zheng, Y.; Fernandez-Rodriguez, E. The influence of waves propagating with the current on the wake of a tidal stream turbine. Appl. Energy 2021, 290, 116729. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Zheng, J.; Zheng, Y.; Zhang, J.; Liu, Z.; Fernandez-Rodriguez, E. Research of the array spacing effect on wake interaction of tidal stream turbines. Ocean. Eng. 2023, 276, 114227. [Google Scholar] [CrossRef]
- Zhao, G.; Wu, T.; Ren, G.; Zhu, Z.; Gao, Y.; Shi, M.; Ding, S.; Fan, H. Reusing waste coal gangue to improve the dispersivity and mechanical properties of dispersive soil. J. Clean. Prod. 2023, 404, 136993. [Google Scholar] [CrossRef]
- Zhao, G.; Zhu, Z.; Ren, G.; Wu, T.; Ju, P.; Ding, S.; Shi, M.; Fan, H. Utilization of recycled concrete powder in modification of the dispersive soil: A potential way to improve the engineering properties. Constr. Build. Mater. 2023, 389, 131626. [Google Scholar] [CrossRef]
- Hou, Z.; Liu, Y.; Han, Z.; Tang, M.; Gong, X.; Su, D.; Wang, L. Experimental Study of the Bearing Characteristics of a Novel Energy-Saving and Environmentally Friendly Pile: Drilling with Prestressed Concrete Pipe Cased Piles. Int. J. Geomech. 2024, 24, 04024035. [Google Scholar] [CrossRef]
- Chao, Z.; Li, Z.; Dong, Y.; Shi, D.; Zheng, J. Estimating compressive strength of coral sand aggregate concrete in marine environment by combining physical experiments and machine learning-based techniques. Ocean. Eng. 2024, 308, 118320. [Google Scholar] [CrossRef]
- Rao, P.; Feng, W.; Ouyang, P. Formation of plasma channel under high-voltage electric pulse and simulation of rock-breaking process. Phys. Scr. 2023, 99, 015604. [Google Scholar] [CrossRef]
- Zheng, Z.; Xu, H.; Zhang, K.; Feng, G.; Zhang, Q.; Zhao, Y. Intermittent disturbance mechanical behavior and fractional deterioration mechanical model of rock under complex true triaxial stress paths. Int. J. Min. Sci. Technol. 2024, 34, 117–136. [Google Scholar] [CrossRef]
- Zheng, Z.; Deng, B.; Li, S.; Zheng, H. Disturbance mechanical behaviors and anisotropic fracturing mechanisms of rock under novel three-stage true triaxial static-dynamic coupling loading. Rock. Mech. Rock Eng. 2023, 57, 2445–2468. [Google Scholar] [CrossRef]
- Li, T.; Zhu, Z.; Wu, T.; Ren, G.; Zhao, G. A potential way for improving the dispersivity and mechanical properties of dispersive soil using calcined coal gangue, J. Mater Res. Technol. 2024, 29, 3049–3062. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).