Abstract
Taking the Jiefangzha irrigation area of the Inner Mongolia Autonomous Region as the research area, the response relationships between the backscattering coefficient and radar frequency, radar incidence angle, root-mean-square height, correlation length, and soil water content under different conditions were simulated using advanced integral equations. The backscattering characteristics of exposed surfaces in cold and dry irrigation areas were discussed, and the reasons for the different effects were analyzed. Based on this, surface roughness models and statistical regression moisture inversion models were constructed through co-polarized backscatter coefficients and combined surface roughness. The correlation between the inverted surface roughness values and the measured values was R2 = 0.7569. The correlation between the soil moisture simulation values and the measured values was R2 = 0.8501, with an RMSE of 0.04. The findings showed a strong correlation between the values from the regression simulation and the measured data, indicating that the model can be applied to soil moisture inversion and has a good inversion accuracy. Compared with previous studies in the same area, the inversion model proposed in this paper has a higher accuracy and is more suitable for the inversion of soil moisture in the Jiefangzha irrigation area. These findings can support research on the water cycle and water environment assessment in the region.
1. Introduction
Soil water is a key driver of energy exchange between the surface and atmosphere, which has been widely used in ecological environment monitoring, climate change perception, water resources allocation, and public health management. In actual production, to guide farmland cultivation, irrigation, and the drainage of farmland or dynamically monitor the spatio-temporal changes caused by disasters such as floods and landslides, the required soil moisture data must have the sufficient time and spatial accuracy to meet real needs. As the most reliable way to obtain soil water products, passive microwave remote sensing has the technical advantages of a short revisit period, solid physical foundation, and no cloud interference; therefore, it has been developed rapidly [1].
In agricultural research, soil moisture conditions have become a restricting factor for crop growth and development. Especially in arid and semi-arid areas, the accurate estimation of soil moisture plays an important role in crop growth estimation, water-saving irrigation, drought prediction, and salinization control [2,3]. Located in the middle and upper reaches of the Yellow River in Central and Western China, the Hetao irrigation area of Inner Mongolia is a typical arid and semi-arid area, which is characterized by scarce rainfall, high evaporation, and a serious water deficit [4]. Soil salinization is the main problem that troubles the development of agricultural production in the irrigation area. The degree of salinization in irrigated areas will change with changes in the soil water, so the accurate monitoring of soil water information has very important practical significance for salinization control and crop growth protection [5].
As the main means of active microwave remote sensing to monitor soil moisture, synthetic-aperture radar (SAR) is highly sensitive to soil moisture (especially in the C-band). Soil moisture determines the soil’s dielectric properties, to which radar backscattering is closely related; that is, soil moisture exerts an indirect effect on radar backscattering information through affecting the soil’s dielectric properties. Based on the above relationship, a quantitative inversion model between radar backscattering and soil water content can be established. However, there is a complex interaction between radar electromagnetic waves and the surface. In addition to the soil’s dielectric constant (soil moisture), radar system parameters (radar frequency, incidence angle, polarization mode, and so on), surface roughness (root mean square height, surface correlation length, and so on), and other factors will affect radar backscattering [6]. Therefore, how to eliminate the influence of many factors and use radar remote sensing images to achieve large-scale, rapid, and accurate long-term dynamic monitoring of soil moisture has been the focus of research [7].
Ground fluctuation can be characterized by surface roughness, which plays an important role in the backscattering coefficient. Soil is a random rough surface, and the backscattering coefficient is related to the surface roughness, so it is necessary to establish a suitable surface roughness model to accurately obtain the backscattering coefficient of the surface object information, then lay a foundation for the accurate inversion of the surface object information using microwave remote sensing images. Surface roughness and its models are usually described using the root-mean-square height (S) and correlation length (L). The root-mean-square height describes the surface roughness in the vertical direction, while the correlation length describes the surface roughness in the horizontal direction. Surface roughness models are closely related to soil water retrieval models by remote sensing. Through considering surface roughness, the accuracy and practicability of inversion models can be significantly improved. Surface roughness is an important factor that cannot be ignored in theoretical analysis, model parameterization, data fusion, or error correction. In practical applications, a comprehensive consideration of surface roughness can provide more scientific and reliable data support for agricultural management, water resource utilization, and ecological protection. (1) In microwave remote sensing, the surface roughness directly affects the backscattering coefficient. Rough surfaces lead to more complex scattering patterns, which change the strength and polarization characteristics of the microwave signal. The inversion models of common microwave sensors, such as synthetic-aperture radar (SAR), must consider the effect of roughness. In optical remote sensing, surface roughness affects the reflectivity of the surface and changes the received spectral signal. Rough surfaces will lead to a stronger scattering effect, such that the reflection spectrum under the same humidity conditions is different under a different roughness [8]. (2) Adding surface roughness parameters to the inversion model can adjust the model output to make it closer to the actual situation. For example, surface roughness data are used to correct the radar backscattering coefficient, resulting in more accurate soil moisture estimates. Through sensitivity analysis, the influence of roughness on the inversion results can be quantified, in order to optimize the model parameters and reduce inversion errors [9]. (3) Through introducing a surface roughness model, the inversion errors caused by changes in roughness can be corrected and the reliability of the inversion results can be improved. With field measurements and experimental data, the inversion model with surface roughness parameters can be verified to ensure its accuracy and stability. The scattering behavior of electromagnetic waves on a rough surface is significantly affected by the surface microstructure. Roughness will affect the scattering coefficient, thereby changing the signal intensity and polarization characteristics received by the remote sensor. Considering the surface roughness, the soil moisture inversion accuracy of microwave remote sensing is significantly improved. The necessity of a surface roughness model for the remote sensing retrieval of soil water models is influenced by the fact that it significantly affects the reflection and scattering characteristics of electromagnetic waves, and thus directly affects the accuracy of the inversion results. A large number of academic studies have shown that surface roughness is the key factor affecting the accuracy of soil moisture retrieval by remote sensing [10]. Ignoring this factor will lead to significant inversion errors and reduce the practicality and reliability of the model [11,12].
How to overcome the influence of surface roughness and other factors on microwave radiation has become an important problem in the study of the microwave remote sensing retrieval of soil water information. Through radar imaging technology, active microwaves can be used to obtain the surface backscattering coefficient and then establish the relationship between it, the soil moisture, and the soil dielectric constant, before finally achieving the purpose of soil moisture inversion research based on the backscattering coefficient. Active microwave remote sensing uses a variety of processing methods, such as multi-polarization, multi-frequency, or multi-incidence angle radar data, to obtain accurate soil water information [13,14]. To date, many studies have utilized the relationships between surface parameters and field-measured data to develop empirical or semi-empirical models based on known data. Scholars from both domestic and foreign institutions have put forth a number of empirical, semi-empirical, and theoretical models that build upon research on the backscattering properties of bare surfaces in order to remove the impact of surface roughness on soil moisture retrieval using synthetic-aperture radar (SAR). Through examining the connection between soil moisture and radar backscattering, empirical models for soil moisture retrieval have been established. Among them, models that are linear and exponential are frequently used. When Ulaby et al. [15] first claimed that bare soil backscattering largely depends on the surface roughness and soil dielectric constant, they reached this conclusion using a simple linear formula to estimate the soil moisture content on bare surfaces. However, this relationship usually applies only to areas with a low surface roughness. Geng et al. [16] conducted a study in agricultural areas using C-band SAR data and discovered a substantial link between radar backscattering coefficients in horizontal polarization mode and surface soil wetness. Yu et al. [17] pointed out that, under specific radar wavelengths, incidence angles, and vegetation (sparse) conditions, soil moisture on relatively flat surfaces can be directly related to backscattering coefficients through an exponential empirical relationship. For this reason, empirical models lack a comparable theoretical foundation and require significant amounts of relevant field-measured data, even if they are easy to use and have fewer parameters, producing strong results for particular study areas. The models’ construction is dependent on certain research fields, restricting their capacity for generalization and adaptation. Over the years, both domestic and foreign scholars have proposed a variety of microwave scattering models to systematically explore the relationship between backscattering coefficients and soil moisture. These models include the integral equation model (IEM) [18], advanced integral equation model (AIEM) [19], Oh model [20], Shi model [21], and Dubois model [22,23]. Through the study of the backscattering characteristics of bare and vegetation-covered surfaces, surface roughness has been identified as an important factor affecting backscattering and has a significant impact on soil moisture retrieval. A common solution is to use combined roughness to combine root-mean square-height (S) and correlation length (L) together, reducing the number of parameters in the soil moisture retrieval model. Zribi et al. [24] proposed a combined roughness parameter, ZS = S2/L, and, using the differences between incidence angles, they eliminated the influence of combined roughness parameters and quantitatively retrieved the surface soil moisture. Based on the combined roughness parameter ZS = S2/L, Ding et al. [25] established an empirical model for soil moisture retrieval on smooth surfaces and combined it with RADARSAT-2 remote sensing imagery to quantitatively retrieve the surface soil moisture in the Weihe Kuqa River Delta. Based on an analysis of simulated data from the AIEM model, Yu et al. [17,26] and Chen et al. [5] each established empirical models using combined roughness parameters and used these empirical models to quantitatively retrieve the soil moisture at the Zhangye Grassland Experimental Station in Gansu Province, achieving satisfactory results. We believe that combined roughness parameters are still useful for retrieving soil moisture information, even though they simplify the retrieval model and reduce the number of model parameters.
Accurate soil water simulation is of great significance for water-saving irrigation, crop yield estimation, the optimal allocation of agricultural water resources, and ecological environment restoration [27]. As a result, a specific farmland in the Jiefangzha Irrigation District of the Inner Mongolia Autonomous Region was chosen as the study region. Using simulated data from the advanced integrated equation model (AIEM), this study directly examines the response relationships of the backscattering coefficients of bare soil surfaces in arid regions with the radar incidence angle, radar frequency, soil moisture, root-mean-square height, and correlation length. Using data from the RADARSAT-2 SAR satellite, a new model for retrieving soil moisture was information developed based on these response relationships. It is of constructive significance to analyze the backscattering characteristics and retrieve the soil moisture in the Hetao irrigation area by combining the physical AIEM with SAR data.
2. Study Area and Work Overview
2.1. Study Area
The study area is situated in Hangjinhou Banner, in the Inner Mongolia Autonomous Region’s Jiefangzha Irrigation District on the Hetao Plain [28], with geographic coordinates ranging from 40°46′ to 40°59′ north (latitude) and 106°43′ to 107°15′ east (longitude); see Figure 1 and [29] for the geographical location of the Jiefangzha irrigation area. The terrain of the irrigation district is characterized by a plateau, with lower elevation in the northeast and higher elevation in the southwest, at an altitude of approximately 1033–1055 m, with slopes ranging from 1.25% to 2%. The area experiences severe cold and little snow in winter, as well as hot and dry conditions in summer [30], typical of a temperate plateau and continental climate. The average annual temperature ranges from 6.3 to 7.7 °C, with low precipitation of 100–250 mm and evaporation of around 2400 mm, and a frost-free period of 120–150 days per year. The Hetao Irrigation District spans more than 1.053 million hectares and is roughly 270 km from east to west and 40–75 km from north to south. The Jiefangzha Irrigation District is situated in the western portion of Inner Mongolia’s Hetao Irrigation District [31]; it shares borders with the Yongji Irrigation District to the east, the Yellow River to the south, the Yin Mountains to the north, and the Ulan Buh Desert to the west. The controlled area of the irrigation district is 220,000 hectares, with the existing irrigation area covering 140,000 hectares and the drainage area covering 170,000 hectares. The complex soil–water–salt environment system in the Jiefangzha Irrigation District makes it an ideal experimental area [32,33].
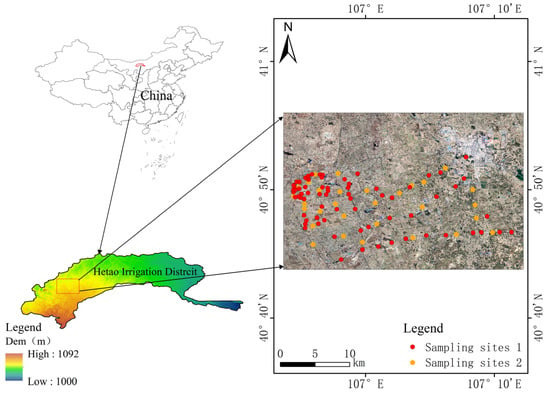
Figure 1.
Spatial location of the study area.
2.2. Radar Data Acquisition and Processing
RADARSAT-2 is the successor to RADARSAT-1 and is characterized by its short revisit cycle and ability to acquire fine polarization data. Among its products, the single look complex (SLC) slant range product stands out in particular, because it effectively fixes issues with satellite reception while preserving the optimal phase and amplitude information of focused SAR data and the best resolution of each beam mode. Due to these features, RADARSAT-2 demonstrates great potential for surface monitoring, as it is unaffected by weather, illumination, or cloud cover and provides reliable, high-quality SAR data for various fields, such as hydrology and meteorology [34].
This study makes use of remote sensing imagery from RADARSAT-2, which is outfitted with a C-band synthetic-aperture radar (SAR) device. A single scene with a 30.42° incidence angle, 25 km × 25 km swath size, and ground resolution of 8 m was obtained from the RADAR-SAT-2 fine polarization SLC format radar imagery data. ‘H’ stands for horizontal polarization and ‘V’ for vertical polarization in the SLC format of the imaging data. When the radar image was overpassed on 11 April 2016, Hangjinhou Banner’s surface was covered in bare soil ahead of the spring irrigation season.
The SARscape module of ENVI 5.3 software was used to process the RADARSAT-2 image, and the backscattering coefficient was obtained. The processing steps were as follows: (1) focusing processing, (2) multi-view processing, (3) spot filtering, (4) geocoding and radiometric calibration, (5) geometric correction, and (6) feature extraction. We used the output ROIs of the ASCII function to output the required sampling point backscattering coefficients into a text document for use.
2.3. Ground Measurement Data
The ground experiment included soil collection, soil bulk density measurement, surface roughness measurement, and the GPS positioning of sampling points. The soil bulk density was calculated using a soil corer.
2.3.1. Soil Moisture
One hundred sampling points were set up in farmlands with different moisture contents within the study area (see Figure 1). The data collection period was from 11 April to 14 April 2016. At this time, the bare surface of the irrigation area was not covered by vegetation before spring irrigation, so the influence of vegetation did not need to be considered during water retrieval. In this sampling process, there was no field irrigation in the test area. The first 10 days of surface data collection (1–10 April 2016) were all sunny, except for 2 April 2016, when it was cloudy. The four days of weather for the ground data collection were as follows: 11 April, cloudy; 12 April, sunny; 13 April, sunny; and 14 April, cloudy. In the large area of bare farmland within the ditch management zone, soil samples were collected from a 10 cm layer. Three soil samples were uniformly taken at each sampling point to eliminate sampling representativeness errors. Using a handheld GPS receiver, the sampling spots’ WGS84 coordinates were determined. The primary procedures included weighing the soil while it was wet, weighing it after drying, and figuring out how much moisture was in the soil. The volumetric soil moisture content was determined using conversion formulae (see Formula (1)), because this is a crucial quantity in RADARSAT-2 soil moisture retrieval tests. Information on the soil moisture content and backscattering coefficient in the test area is shown in Table 1.
where is the soil mass density; is the pure water density, which is 1 at a normal temperature and pressure; is the mass water content; and is the volume water content.

Table 1.
Measurement information table.
2.3.2. Determination of Soil Particle Composition
The dielectric constant can be affected differently by different types of soil. Relevant research has demonstrated that the actual part of the dielectric constant decreases with a decreasing sand content when adjusting the soil moisture content. Thus, the soil composition component must be taken into account when retrieving soil moisture content utilizing microwave remote sensing data. Soil samples were collected for the experiment, naturally dried, pulverized, and sieved. A Helos/BR laser particle size analyzer was then used to measure the composition of the soil particles. For every soil sample that was analyzed, the laser particle size analyzer produced a detection report. The percentages of sand and clay in the soil were calculated from these reports, accounting for the silt (0.002–0.02), sand (0.02–2), and clay (<0.002) categorization criteria. The percentages of the various sand and clay contents are displayed in Table 2. We measured the bulk density of the soil samples with a ring cutter measuring 100 cm3.

Table 2.
Percentage of sand and clay.
2.3.3. Soil Parameter Composition Determination
The characteristics of radar backscattering are not only related to the parameters of the radar satellite itself, but also to the dielectric constant and surface roughness. Three variables are used to quantify surface roughness in microwave scattering models: the root- mean-square height (S), correlation length (L), and autocorrelation function. These models typically represent rough surfaces as static and randomly distributed. This frequently did not produce satisfying results, since early studies of mixed-roughness inversion models only included correlation length (L) or root-mean-square height (S) in the model computations. In order to represent surface roughness, researchers have combined correlation length and root-mean-square height. For example, Shi et al. [35] used the wavenumber (k), root-mean-square-height (S), and roughness spectrum (W) to form SR = (kS)2W, Oh et al. [36] used S/L, and Zribi et al. [37] proposed combined roughness by merging the root-mean-square height and correlation length into one parameter: ZS = S2/L. The combined parameters that they used achieved good results and have become widely used in soil moisture retrieval studies. In this study, the present combined roughness was used for inversion modeling.
Using a constructed roughness plate that was one meter long and had centimeter gridlines, the surface roughness was measured in both the east–west and north–south directions. The sample points’ surface roughness was determined by taking the average value of the measurements. A picture of the roughness plate when measuring the surface roughness is shown in the reference [38]. The step method of the surface roughness measurement is as follows: (1) The profile plate (with the centimeter grid) is inserted vertically into the surface to ensure that the surface of the plate is perpendicular to the surface and stable. (2) From one end of the profile plate, the surface height is recorded at certain intervals (e.g., per centimeter) along the length of the profile plate. The spacing of the recording points should be consistent with the spacing of the grid to ensure uniform data. (3) A height-measuring tool is used to measure the surface height of each point and record it. (4) The above measurement steps are repeated at different locations to obtain more comprehensive surface roughness data. This method is simple and easy to use, can effectively reflect small height changes in the surface, and is suitable for the roughness measurements of various surface types.
3. Investigation and Application of the Advanced Integral Equation Model (AIEM)
3.1. Advanced Integral Equation Model (AIEM)
Due to the random distribution and complex geometric features of the Earth’s natural surfaces, it is not feasible to simulate all scattering situations through models. Therefore, researchers often interpret radar data using theoretical, empirical, or semi-empirical models to obtain useful information. The integral equation model (IEM) has attracted widespread attention and emphasis from researchers, as it is based on rigorous electromagnetic theory [39]. However, it has been discovered that the IEM’s treatment of Fresnel model reflection coefficients under various roughness circumstances is very simplistic, and that the model is unable to adequately define actual surface roughness when applied to real surface conditions. This can occasionally result in substantial discrepancies between the measured values and the IEM’s simulated values.
The advanced integral equation model (AIEM), proposed by Wu et al. [40] and Fung et al. [41], is an improvement upon the IEM. Compared to other models, it can more realistically replicate a wide range of surface roughness and accurately capture radar backscatter coefficient information from the Earth’s surface radiation; it is widely used in the analysis and modeling of microwave radiation and surface scattering. It is expressed as follows:
where pq represents the polarization mode, s represents the surface root-mean-square height, and k represents the wave number; , , Wn(−2kx,0) is the surface roughness power spectrum, and fpq and Fpq are functions related to the Fresnel reflection coefficient. According to [42,43], the Fresnel reflection coefficient depends on the moisture content of the soil.
In response to the shortcomings of the IEM, two improvements have been made:
- (1)
- Improvement of surface autocorrelation function:
Based on extensive ground truth data, it is known that, under smooth surface conditions, the surface autocorrelation function follows an exponential function, while under rough surface conditions, it reflects a Gaussian correlation function. Since real surface conditions typically lie between smooth and rough, the form of the surface autocorrelation function should also lie between exponential and Gaussian functions, and it should be continuous [44]. However, when simulating surface scattering characteristics, the IEM produces discontinuous surface autocorrelation functions, leading to certain errors in the results. This necessitates the development of a continuous correlation function model to describe these surface conditions. Therefore, in the improved integral equation model, the generalized power-law spectral density function proposed by Li et al. and its corresponding surface autocorrelation function are adopted to achieve continuity in describing roughness.
- (2)
- Improvement of Fresnel reflection coefficients:
Fresnel reflection coefficients vary with surface roughness, but the IEM simply categorizes roughness into smooth and rough conditions, lacking expression for moderate roughness conditions. Consequently, Fresnel reflection coefficients also lack continuity in this regard.
The AIEM addresses these two issues in the IEM, significantly reducing the discrepancy between the model simulation values and actual measurements, and enabling better simulation of rough surface scattering. Therefore, we adopted the AIEM to simulate surface scattering data.
3.2. Simulation of Bare Surface Backscattering Characteristics Using the AIEM
When radar acquires the backscattering coefficient of the Earth’s surface, it is influenced by various factors, such as soil parameters (soil moisture, bulk density, and particle composition, etc.), surface roughness parameters (root-mean-square height and correlation length, etc.), and radar parameters (frequency, incidence angle, and polarization, etc.).
We analyzed the variation trends of the backscattering coefficient with respect to these parameters, as well as the reasons behind these variations, through simulating the backscattering coefficient under five parameters—incidence angle, soil moisture, correlation length, root-mean-square height, and radar frequency—using the AIEM. This established the groundwork for creating a simulated database of the bare surface backscattering properties. The relationship between these parameters’ variations and the backscattering coefficient’s response was investigated experimentally using the method of controlling variables, which involved changing each of the five parameters’ values separately while keeping the other variables constant.
3.2.1. The Influence of Radar Frequency Variation on the Backscattering Coefficient
The other variables were kept unchanged (parameters: incidence angle of 30°, root-mean-square height of 0.8 cm, correlation length of 23 cm, and soil moisture of 0.22, etc.), the radar frequency variable was changed, and the effect of frequency change on the backscattering coefficient was studied. Using the output values from the AIEM, we plotted the changes in the backscattering coefficient with frequency variation, as shown in Figure 2. An analysis of the response of the backscattering coefficient to frequency variation revealed that, within a certain range, the backscattering coefficient for the same polarization increased with an increasing frequency. Radar signals at higher frequencies have shorter wavelengths, allowing them to better detect the microstructure of the Earth’s surface or target objects. This situation increases the probability of various scattering effects because of the more complex interaction between the radar signal and the Earth’s surface or target items. Multiple scattering increases the scattering intensity in different directions, thereby increasing the backscattering coefficient.
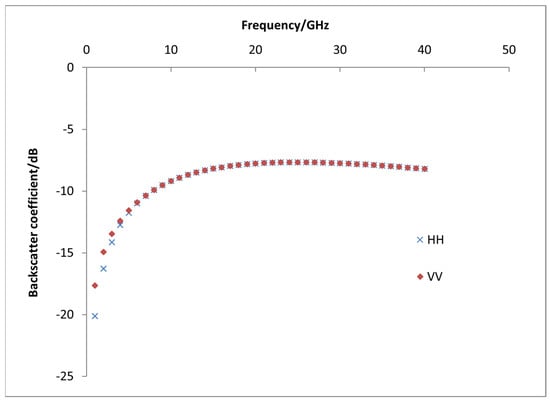
Figure 2.
Frequency response: backscattering coefficient response graph.
3.2.2. Impact of Changing Radar Incidence Angle on the Backscattering Coefficient
The backscattering coefficient is a quantity that describes the intensity of radar signals scattered by ground objects, whereas the radar incidence angle is the angle between the radar beam and the vertical line to the ground surface. The backscattering coefficient and the radar incidence angle are closely correlated. Maintaining the other variables unchanged (parameters: radar frequency of 5.4, root-mean-square height of 0.8 cm, correlation length of 23 cm, and soil moisture of 0.22, etc.), changing the incidence angle variable, and investigating the influence of changes in the incident angle on the backscattering coefficient, we showed the changes in the backscattering coefficient with incidence angle variation using the AIEM’s output data, as illustrated in Figure 3. The backscattering coefficient for the same polarization increased with a decreasing radar incidence angle within a particular range, according to an analysis of the backscattering coefficient’s reaction to incidence angle changes. This was due to the fact that, when the incidence angle dropped, the radar beam moved in a direction that was closer to being perpendicular to the ground. This caused further multiple reflections of the radar waves between the radar and the ground, increasing the number of scattering events. Additionally, it became more susceptible to the influence of terrain undulations and ground roughness, as well as being more prone to interact with surface features such as vegetation. As a result, the backscattering coefficient continuously rose as the radar echo intensity progressively rose.
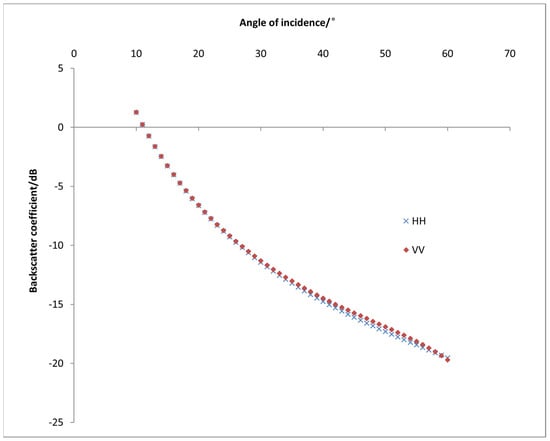
Figure 3.
Response of the backscattering coefficient to the angle change.
3.2.3. The Effect of Root-Mean-Square Height on the Backscattering Coefficient
There is a substantial correlation between the backscattering coefficient and the root-mean-square (RMS) height. The interaction between radar waves and the ground surface can be impacted by the roughness of the soil surface, which can, therefore, change the backscattering coefficient’s numerical value. Keeping the other variables unchanged (parameters: radar frequency of 5.4, incidence angle of 30°, correlation length of 23 cm, and soil moisture of 0.22, etc.), the root-mean-square height variable was changed and the influence of the root-mean-square height on the backscattering coefficient was studied. The variation in the backscattering coefficient with changes in the RMS height was plotted using the AIEM’s output values. More surface roughness is typically indicated by a greater RMS height of the soil surface, suggesting that more scattering events happen when radar waves interact with the soil surface. Therefore, a greater RMS height typically leads to a higher backscattering coefficient, indicating more radar waves scattered in the backward direction, resulting in a stronger backscattering signal, as shown in Figure 4. However, after reaching a certain threshold, the backscattering coefficient reached a peak value. This phenomenon necessitates more research and study, as it may be related to variations in the soil surface roughness causing changes in the scattering properties. Higher RMS values have less of an impact on the backscattering coefficient, and it is possible to examine the backscattering coefficient corresponding to two different RMS values.
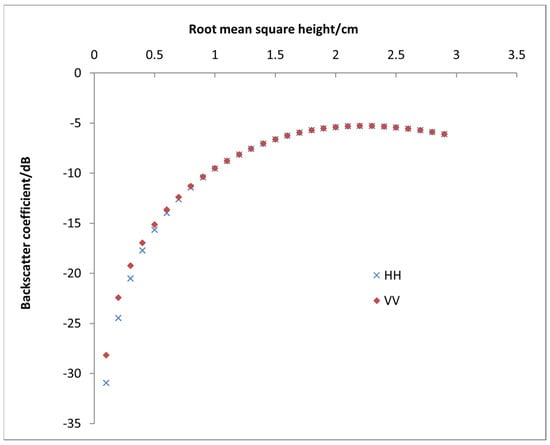
Figure 4.
Response of the backscattering coefficient when the root-mean-square height changes.
Saturation effect: on situations where the soil roughness is relatively high, when the RMS height reaches a certain threshold, the roughness of the soil surface may have reached a saturation state, where further increases in roughness may not significantly increase the number of multiple scattering events. Instead, there may be phenomena of mutual masking or interference between some scattering events, leading to a decrease in the backscattering coefficient.
Reduced multiple scattering: as the RMS height rises to a certain point, the average route length between multiple scattering events may become shorter as a result of the increased roughness of the soil surface. However, additional multiple scattering events may still occur. As a result, the backscattering coefficient may drop as a result of a decrease in the scattering components from longer distances in the backscattering signal.
Phase compensation effect: in situations where the soil’s surface roughness is relatively high, there are phase differences between scattering centers at different positions. When the RMS height increases to a certain extent, the phase compensation effect may come into play, causing interference in certain directions of the scattering signal, thereby reducing the backscattering coefficient.
3.2.4. The Backscattering Coefficient Is Significantly Influenced by the Correlation Length
In radar remote sensing, the correlation length refers to the scale size of surface feature variations in the horizontal direction. This is commonly used to describe the roughness of the terrain or the extent of surface undulations. A larger correlation length indicates that the variations in surface features are larger in the horizontal direction, implying a lower surface roughness. Conversely, a smaller correlation length indicates smaller variations in surface features in the horizontal direction, implying a higher surface roughness. The correlation length and the backscattering coefficient have a specific relationship.
Maintaining the other variables unchanged (parameters: radar frequency of 5.4, incidence angle of 30°, root-mean-square height length of 0.8 cm, and soil water content of 0.22, etc.), the correlation length variable was changed and the influence of the correlation length change on the backscattering coefficient was studied. Figure 5 illustrates the creation of a plot of the backscattering coefficient’s variation with correlation length modification based on the AIEM’s output data. Examining the backscattering coefficient’s reaction to variations in the correlation length, it can be seen that, within a specific range, the backscattering coefficient for the same polarization decreased with an increasing correlation length. When the correlation length was large, the variations in surface features in the horizontal direction were also large, indicating a lower surface roughness and relatively flat terrain. In such cases, there was relatively less interaction between the radar beam and the surface, resulting in a relatively smaller backscattering coefficient.
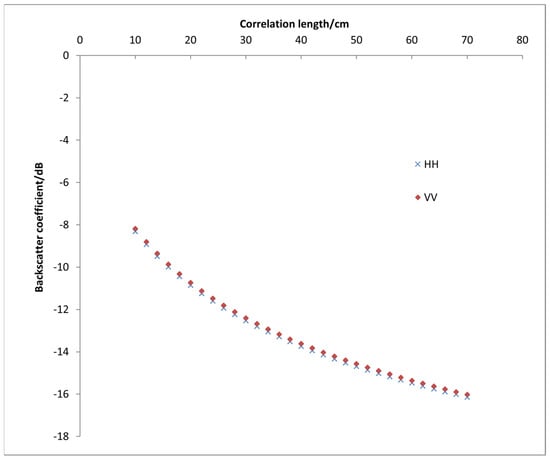
Figure 5.
Reaction of the backscattering coefficient to variations in the correlation length.
3.2.5. The Effect of Moisture in the Soil on the Backscattering Coefficient
As soil moisture is one of the key variables controlling surface scattering characteristics, there is a close relationship between soil moisture and the backscattering coefficient. Keeping the other variables unchanged (parameters: radar frequency of 5.4, incidence angle of 30°, root-mean-square height of 0.8 cm, and correlation length of 23 cm, etc.), the soil water variable was changed and the influence of soil water changes on the backscattering coefficient was studied. Figure 6 illustrates the creation of a plot of the backscattering coefficient’s fluctuation with changes in the soil moisture based on the AIEM’s output data. For the same polarization, the backscattering coefficient showed a monotonically increasing connection with the soil moisture, according to studies of the coefficient’s reaction to variations in soil moisture. The backscattering coefficient progressively saturated with an increasing soil moisture; a 10% increase in moisture corresponded to only a 1 dB rise in the backscattering coefficient. Therefore, SAR images are more sensitive to soils with a lower moisture content, while their sensitivity is reduced in areas with a higher moisture content. In high-moisture soil conditions, there will inevitably be some inversion errors, which are determined by the mechanism of radar scattering. This relationship holds for other polarization modes as well. As the soil’s moisture content increases, its dielectric constant increases almost linearly, and its conductivity also increases. The dielectric constant directly affects the reflection of electromagnetic energy by objects. A higher dielectric constant leads to stronger echo intensity and, consequently, to larger backscattering coefficients.
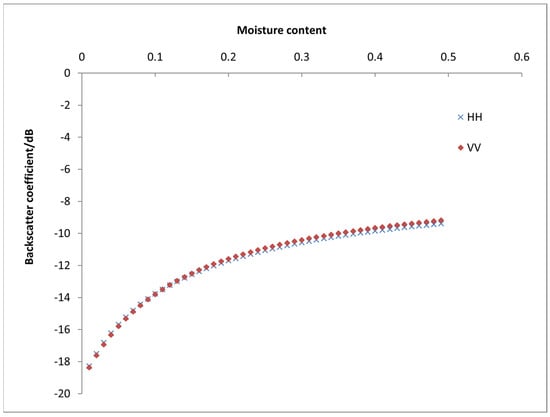
Figure 6.
Response of the backscattering coefficient to changes in soil moisture.
It is clear from the aforementioned analysis that the surface characteristics significantly affect the backscattering coefficient of the bare soil surfaces in the research region. Strong regularities in the backscattering properties of the bare soil surfaces in the study region can be used to create a model that explains the connection between surface attributes and the backscattering coefficient. Consequently, variables such as soil moisture and the surface roughness of exposed soil surfaces can be reversed using this approach.
3.3. AIEM Validation
Through varying the values of variables, including the radar frequency, radar incidence angle, soil moisture, root-mean-square height, and correlation length, through in the AIEM, we discovered that these variables significantly affect the backscattering coefficient. To evaluate the model’s simulation results, in this experiment, we compared the measured backscattering coefficients of the sampling points on the RADATSAT-2 radar images in Hangjinhou Banner with the simulated values from the AIEM, as shown in Figure 7 and Figure 8. We noticed that the correlation coefficients were rather strong and that the trend lines of the scatter plots of the measured and simulated backscattering coefficients in the figures had slopes of close to 1. This suggests that the measured backscattering coefficients can be accurately simulated by the backscattering coefficients computed using the AIEM.
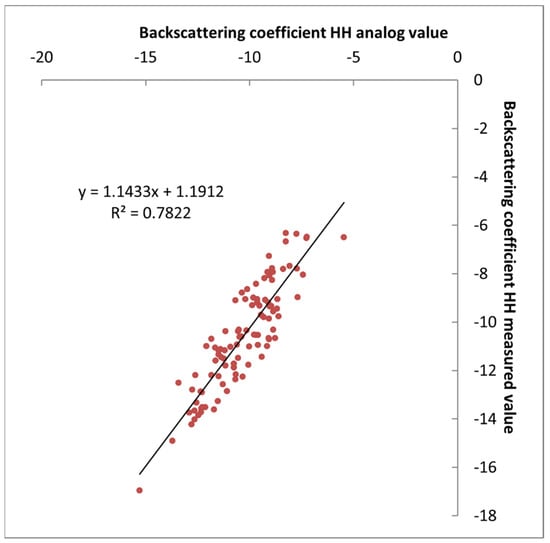
Figure 7.
Backscattering coefficient HH comparison.
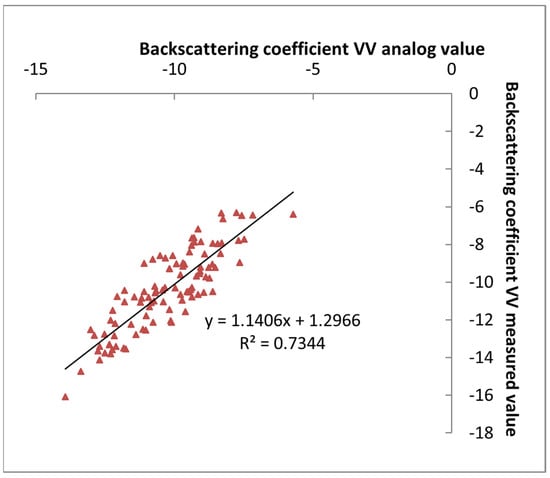
Figure 8.
Backscattering coefficient VV comparison.
4. Soil Water Retrieval
The most popular theoretical backscattering coefficient model for resolving soil moisture on sparsely vegetated and bare soil surfaces is the AIEM [11]. The backscattering coefficient of bare soil can be viewed as a function of the soil moisture (MV) content and surface roughness (root-mean-square height (S) and correlation length (L)) when the radar system parameters are fixed.
It is acknowledged that determining the link between these factors and the radar backscattering coefficient, as well as obtaining the roughness parameters, is required in order to invert the soil moisture content. The analysis would become more complex if the relationships between the backscattering coefficient, correlation length (L), and root-mean-square height (S) were examined independently. Here, we represent the surface roughness using composite roughness (ZS = S2/L) in order to simplify the parameters. Consequently, as a function of ZS and MV, the backscattering coefficient model can be simplified:
Thus, in order to invert the soil moisture content, we can create an empirical model based on the backscattering coefficient, soil roughness, and soil moisture.
4.1. Establishment of Soil Water Inversion Model Based on the AIEM Model
4.1.1. Establishment of Surface Roughness Model
The empirical regression equation model was established with simulated values of the co-polarized backscattering coefficient (HH and VV) as independent variables and measured values of the combined roughness (ZS) as dependent variables. As shown in Figure 9, 70 randomly chosen field sample points out of 100 were used to construct the model and determine its parameters. Figure 9 shows that the backscattering coefficient has an exponential relationship with the total roughness, as expressed by the following formula:
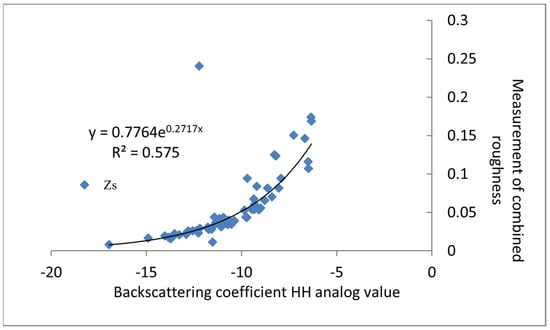
Figure 9.
Combined roughness (ZS) inversion.
The remaining 30 sampling points were substituted into the equation above to obtain simulated values for th combined roughness. Through an analysis of the correlation between the measured and simulated values of the combined roughness, an R-squared value of 0.7569 was obtained, indicating a good correlation between the regression equation model’s inferred values and the actual observed values, as depicted in Figure 10.
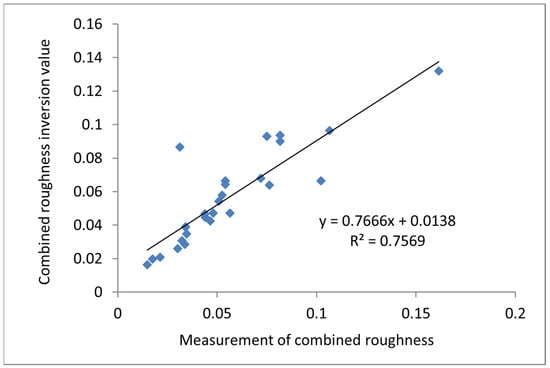
Figure 10.
Correlation between the inversion value of the empirical model and the measured values of soil roughness.
4.1.2. The Soil Water Content Model Was Established Based on AIEM Simulation Data
Several studies have derived different mathematical relationships by analyzing simulated data from the AIEM. In this study, [34,35,39,45] were consulted, and considering Equation (5), along with the response relationships between the simulated backscattering coefficients from the AIEM [46] and soil moisture [47], root-mean-square height, and correlation length (as discussed in Section 3.2), the relationship between the soil moisture content [48] and backscattering coefficients, as well as the combined soil roughness, can be represented as follows:
where A, B, C, and D are the relevant parameters, represents the value of the backscattering coefficient HH, represents the value of the backscattering coefficient VV, and ZS represents the soil composite roughness.
We selected 70 points out of 100 sampling points to establish the empirical regression equation model and obtain the model parameters. The formula is as follows:
The remaining 30 sampling points were substituted into Equation (8) to obtain the simulated values of the statistical regression moisture inversion model. As can be seen in Figure 11, a strong correlation was found between the regression equation model’s inversion values and the actual observed values through an analysis of the correlation between the measured moisture content and the simulated values of the empirical regression moisture model, yielding an R2 value of 0.8501 and an RMSE of 0.04.
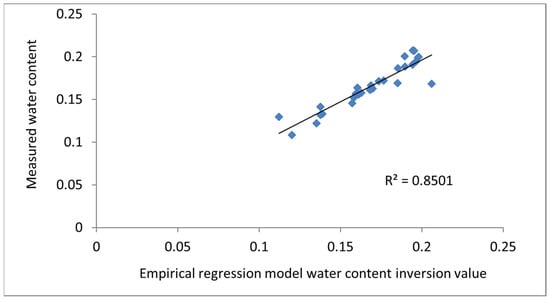
Figure 11.
Correlation between water content inversion values and measured values.
4.2. Soil Water Retrieval
For soil moisture retrieval in this experiment, the combined roughness inversion formula and soil moisture inversion formula were utilized [49]. Using the ENVI software, the experiment divided the distribution of soil moisture in the research region into four categories: 0–0.1, 0.1–0.2, 0.2–0.3, and >0.3. The study area’s soil moisture distribution map was acquired, as shown in Figure 12, which illustrates that the study area’s soil moisture content was generally low, with most places having a soil moisture content of less than 20%. Therefore, this can be combined with the spring irrigation system to adjust the amount of water in the first irrigation, in order to guide agricultural production. Upon comparison, it was found that the soil moisture variation observed by Wang et al. [21] in their study region (employing combined roughness for quantitative retrieval) and the soil moisture retrieval carried out in this work showed a similar tendency. Overall, the study’s empirical soil moisture retrieval model can reliably determine the study area’s soil moisture content. Therefore, this empirical model has a certain applicability in similar work in arid regions.
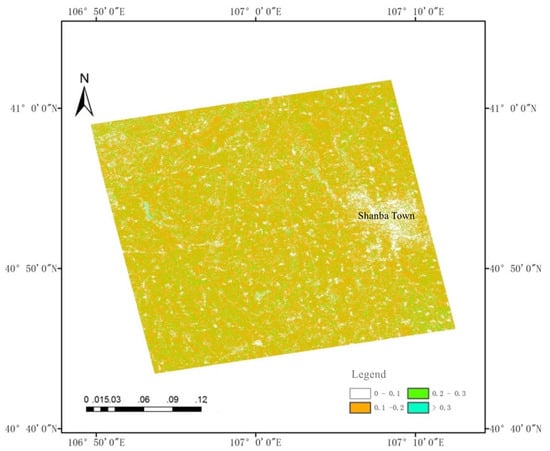
Figure 12.
Soil water content classification chart.
5. Discussion
The analysis revealed that variations in the radar frequency, incidence angle, soil moisture content, root-mean-square height, and correlation length significantly affect the backscattering coefficient. The obtained relationships between these five parameters and the backscattering coefficient were consistent with the findings of previous studies by Wang et al. [38] (April, farmland), Yang et al. [50] (July, desert), Yang et al. [46] (July, desert), and Zhen et al. [35] (July, sand dunes). Differences in soil texture, climatic conditions [51], topographic environment, measurement methods for soil moisture content, and variations in custom-made surface roughness measurement plates among the study areas might lead to slight discrepancies in the observed data or image data, possibly causing minor differences in the variation patterns. Geographically, the extremely arid conditions and fragile ecological environment of the Ordos Plateau region studied by Yang et al. [50] are characterized by desertification and scarce soil moisture, resulting in distinct differences in surface type, surface moisture, soil particle size, and roughness, which can influence the backscattering coefficient in radar images. Temporally, variations in soil moisture and surface roughness due to seasonal changes can affect the impact of soil on radar image backscattering coefficients. Therefore, seasonal variations in soil properties should be considered when interpreting and analyzing radar images to better understand and explain their characteristics. Additionally, differences in field sampling methods, such as using different custom-made surface roughness measurement plates, may yield varying results depending on factors such as plate size, shape, surface treatment, material, and manufacturing process.
In the soil moisture retrieval section, the R2 value obtained in this study was 0.8501. This can be compared with the accuracy of the soil moisture retrieval models proposed by Zhen et al. [35] in a sand dune study area (R2 = 0.906) and Wang et al. [52] based on the Sentinel-1 microwave modeling of soil moisture at the oasis scale (R2 = 0.76; however, the error of soil moisture content between the simulated value and measured value was more than 4%, and the inversion accuracy was low, which may have been caused by systematic error and accidental error). Additionally, Han et al. [53] used ASAR C-band polarimetric radar data and an improved particle swarm algorithm to retrieve the soil moisture in the Heihe River Basin, which showed a good correlation with the measured data (R2 = 0.7786); Meanwhile, Kong et al. [31] built a soil water inversion model with the Feng sandy beach area as the research area; according to the measured data, the model’s inversion results had a good correlation with the measured values (R2 = 0.8541), and the root-mean-square error was 0.06. In comparison with the aforementioned models, the accuracy of the proposed retrieval model in this study was relatively high. Geographical location, time, and variations in experimental techniques were the primary causes of the discrepancies in accuracy throughout the investigations. Nonetheless, models developed in many research fields might offer insightful information specific to those fields. Additionally, all retrieval models establish a connection between soil moisture and radar backscattering coefficients, eliminating the need for manual surface roughness assessment and allowing for more effective soil moisture retrieval. This differs from Wang et al.’s retrieval model, which still retains parameters for combined roughness [38].
The AIEM also has some specific limitations, assumptions, and potential uncertainties in simulating farmland soil moisture; these factors need to be considered during the development and application of the model in order to ensure the reliability and accuracy of its results: (1) Limitations. a: Data acquisition and quality. Soil moisture data can have a low spatial and temporal resolution, which can cause models to fail to accurately capture local changes and short-term dynamics. Obtaining high-quality, long-time-series soil moisture data can be difficult, especially in resource-limited or remote areas. b: Complex environmental factors. The soil moisture in farmland is affected by many factors, such as rainfall, evaporation, plant root activity, and soil type. These complex interactions can be difficult to fully incorporate into models. Changes in soil moisture are often non-linear, and simple linear models may not be sufficient to capture this complexity. c: Model applicability. The AIEM may perform well in specific farmland or climate conditions, but this model may not perform well in different geographical locations or climate conditions. The adaptability of the model at different scales (from plots to regions) may be limited, requiring specific adjustments for different scales. (2) The assumptions of the AIEM. a: Models generally assume that the training data and the prediction data have the same distribution. However, the soil water distribution may be significantly different from season to season, year to year, or region to region. b: It is assumed that the soil water measurement points are independent. However, in practice, soil water has a spatial correlation, and ignoring this correlation may lead to model errors. c: It is assumed that the soil and environmental conditions remain unchanged during the application of the model, but there may be changes in reality, such as climate change, changes in irrigation management practices, and so on. Therefore, special attention should be paid to climate change and irrigation during and before the sampling time in the test area. (3) Potential uncertainties. a: Climate and weather conditions (e.g., natural conditions such as rainfall, temperature, wind speed, and humidity) have a direct impact on soil moisture, but these conditions are highly uncertain and difficult to predict accurately. b: The soil’s physical and chemical properties (such as soil texture, organic matter content, porosity, and so on) may vary significantly at different locations and depths, increasing the uncertainty of the model predictions. c: Field management practices (such as irrigation, fertilization, tillage, and so on) have important effects on soil moisture, but these factors can have a high variability and uncertainty. d: The parameters and structure selected by the model may have a significant impact on the results. Different model structures or parameter choices can lead to significantly different predictions. Through discussing the limitations, assumptions, and potential uncertainties of the AIEM mentioned above, in order to improve the reliability and practicability of the model when simulating farmland soil water, researchers and practitioners should improve measures in the following four aspects, so as to better cope with the limitations and uncertainties of the AIEM when simulating farmland soil water and improve the accuracy and application value of model prediction: (1) Improve data acquisition, data quality, and coverage through high-resolution sensor networks and long-term monitoring. (2) Consider multivariable and non-linear relationships and introduce more complex model structures, such as deep learning and hybrid models, to better capture the complex dynamics of soil water. (3) Strengthen model validation through extensively verifying the model under different climate and soil conditions, in order to ensure its generalizability. (4) Combine external information, meteorological forecasting, remote sensing data, and management practice information to reduce the impact of uncertainties on model prediction.
6. Conclusions
In this work, we extracted the backscattering coefficient from RADARSAT-2 SAR imagery of the Hetao Irrigation District in Bayannur City, Inner Mongolia Autonomous Region. The study used the simulation database of the AIEM to examine the backscattering properties of bare soil under various radar frequencies, incidence angles, soil moisture levels, root-mean-square heights, and correlation lengths through analysis and modeling of the pertinent data. Based on the AIEM model, an empirical model suitable for soil water inversion in the study area was established and verified, and the quantitative inversion of soil water in the study area was carried out by combining RADARSAT-2 SAR imagery. The following are the study’s primary conclusions:
- When the radar frequency and incidence angle are increased, the backscattering coefficient of bare soil rises; it then steadily falls with an increasing incidence angle, rises with an increasing root-mean-square height up to a certain threshold, falls with an increasing correlation length, and rises with an increasing soil moisture content. There is a strong regularity in the backscattering properties of bare soil in the studied area.
- The response link between each parameter and the radar backscattering coefficient was discovered by a mechanism analysis utilizing the AIEM. Based on this, surface roughness and statistical regression moisture retrieval models were constructed using co-polarized backscattering coefficients and combined surface roughness. Using field data for verification, the correlation between the retrieved surface roughness and measured values was R2 = 0.7569. R2 = 0.8501 and an RMSE of 0.04 were the correlation coefficients between the simulated and measured levels of soil moisture. The model showed a high degree of accuracy in retrieval.
- Using the empirical moisture retrieval model, quantitative soil moisture retrieval was carried out for the research region in conjunction with RADARSAT-2 SAR data in the HH and VV polarizations. The findings show that the research area’s soil moisture content is generally low, with most places having a soil moisture content of less than 20%. In the studied area, the empirical model works well for quantitative soil moisture retrieval.
However, the model and methods employed in this study are only applicable to land surfaces with sparse vegetation. This is due to the fact that vegetation cover on the ground can both scatter and absorb microwave signals that are released by radar, complicating the link between microwave signals and soil moisture. Thus, the difficulty of predicting soil moisture retrieval models will unavoidably depend on the density of vegetation cover on the land surface; this is an issue that must be further researched and addressed in the development of remote sensing soil moisture retrieval research in the future.
Author Contributions
Formal analysis, writing—original draft, writing—review and editing, C.Y.; data curation, funding acquisition, methodology, software, supervision, validation, writing—original draft, writing—review and editing, Q.L.; writing—review and editing, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52069020).
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
Thanks to the anonymous reviewers, academic editors and editors for their comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, G. Study on Water and Salt Transport and Salt Redistribution among Different Land Types in Hetao Irrigation District. Ph.D. Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2021. [Google Scholar] [CrossRef]
- Zhang, M. Surface Soil Moisture Retrieval in Wheat Covered Area Using Multi-temporal SAR and Optical Satellite Data. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2021. [Google Scholar] [CrossRef]
- Shi, Z.; Liang, Z.; Yang, Y.; Guo, Y. Status and Prospect of Agricultural Remote Sensing. Trans. Chin. Soc. Agric. Mach. 2015, 46, 247–260. [Google Scholar] [CrossRef]
- Gu, Z.; Zhu, T.; Jiao, X.; Xu, J.; Qi, Z. Evaluating the Neural Network Ensemble Method in Predicting Soil Moisture in Agricultural Fields. Agronomy 2021, 11, 1521. [Google Scholar] [CrossRef]
- Chen, J.; Jia, Y.; Yu, F. Soil moisture inversion by radar with dual-polarization. Trans. Chin. Soc. Agric. Eng. 2013, 29, 109–115+298. [Google Scholar] [CrossRef]
- Wang, C. Based on Ensemble Kalman Filtering and HYDRUS-1D Model Study on Assimilation of Soil Moisture Remote Sensing Data. Master’s Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2023. [Google Scholar] [CrossRef]
- Das, B.; Rathore, P.; Roy, D.; Chakraborty, D.; Bhattacharya, B.K.; Mandal, D.; Jatav, R.; Sethi, D.; Mukherjee, J.; Sehgal, V.K.; et al. Ensemble surface soil moisture estimates at farm-scale combining satellite-based optical-thermal-microwave remote sensing observations. Agric. For. Meteorol. 2023, 339, 109567. [Google Scholar] [CrossRef]
- Zhang, L.; Lei, Z.; Wang, L.; Meng, Q.; Zeng, J. Retrieval of soil moisture based on Gaofen-3 (GF-3) satellite synthetic aperture radar data over agricultural fields. J. Zhejiang Univ. (Agric. Life Sci.) 2024, 50, 209–220. [Google Scholar] [CrossRef]
- Deng, X.; Wang, H. Recent advances on algorithms and applications of soil moisture retrieval from microwave remote sensing. J. Zhejiang Univ. (Agric. Life Sci.) 2022, 48, 289–302. [Google Scholar] [CrossRef]
- Wang, S. Development of surface roughness and soil moisture retrieval algorithm using passive microwave remote sensing data. Acta Geodaet. Cartogr. Sin. 2021, 50, 1419. [Google Scholar] [CrossRef]
- Jagdhuber, T.; Hajnsek, I.; Bronstert, A.; Papathanassiou, K.P. Soil Moisture Estimation Under Low Vegetation Cover Using a Multi-Angular Polarimetric Decomposition. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2201–2215. [Google Scholar] [CrossRef]
- Bourgeau-Chavez, L.L.; Leblon, B.; Charbonneau, F.; Buckley, J.R. Evaluation of polarimetric Radarsat-2 SAR data for development of soil moisture retrieval algorithms over a chronosequence of black spruce boreal forests. Remote Sens. Environ. 2013, 132, 71–85. [Google Scholar] [CrossRef]
- Yin, C.; Liu, Q.; Wang, C.; Wang, F. Inversion of soil moisture by surface spectral measurement combined with active microwave remote sensing. Southwest China J. Agric. Sci. 2022, 35, 2595–2602. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Batlivala, A.P.P. Optimum Radar Parameters for Mapping Soil Moisture. IEEE Trans. Geosci. Electron. 1976, 14, 81–93. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Batlivala, P.P.; Dobson, M.C. Microwave Backscatter Dependence on Surface Roughness, Soil Moisture, and Soil Texture: Part I—Bare Soil. IEEE Trans. Geosci. Electron. 1978, 16, 286–295. [Google Scholar] [CrossRef]
- Geng, H.; Gwyn, Q.H.J.; Brisco, B.; Boisvert, J.; Brown, R.J. Mapping of Soil Moisture from C-Band Radar Images. Can. J. Remote Sens. 2014, 22, 117–126. [Google Scholar] [CrossRef]
- Yu, F.; Zhao, Y. A New Method for Soil Moisture Inversion by Synthetic Aperture Radar. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 317–321. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Chen, K.S.; Tzong-Dar, W.; Leung, T.; Qin, L.; Jiancheng, S.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’Neill, P.E.; Engman, E.T. Estimation of Bare Surface Soil Moisture and Surface Roughness Parameter Using L-band SAR Image Data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- Dubois, P.C.; van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef]
- Ma, T.; Han, L.; Liu, Q. Retrieving the Soil Moisture in Bare Farmland Areas Using a Modified Dubois Model. Front. Earth Sci. 2021, 9, 735958. [Google Scholar] [CrossRef]
- Zribi, M.; Dechambre, M. A new empirical model to inverse soil moisture and roughness using two radar configurations. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 2223–2225. [Google Scholar]
- Ding, J.; Yao, Y. Evaluation of Soil Moisture Contents Under Sparse Vegetation Coverage Conditions Using Microwave Remote Sensing Technology in Arid Region. Sci. Geogr. Sin. 2013, 33, 837–843. [Google Scholar] [CrossRef]
- Yu, F.; Li, H.; Zhang, C.; Wan, Z.; Liu, J.; Zhao, Y. A New Approach for Surface Soil Moisture Retrieving Using Two-polarized Microwave Remote Sensing Data. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 225–228. [Google Scholar] [CrossRef]
- Li, J.; Mao, X.; Shang, S.; Steenhuis, T. Modeling Regional Soil Water Balance in Farmland of the Middle Reaches of Heihe River Basin. Water 2017, 9, 847. [Google Scholar] [CrossRef]
- Zeng, L.; Liu, Q.; Jing, L.; Lan, L.; Feng, J. Using Generalized Regression Neural Network to Retrieve Bare Surface Soil Moisture From Radarsat-2 Backscatter Observations, Regardless of Roughness Effect. Front. Earth Sci. 2021, 9, 657206. [Google Scholar] [CrossRef]
- Li, Z.; Chen, F.; Wen, X.; Gao, H.; Tong, W. Effexts of climate change on soil salinity in Hetao irrigation area. J. China Agric. Univ. 2013, 18, 61–68. [Google Scholar]
- Feng, X.; Liu, Q. Regional Soil Salinity Monitoring Based on Multi-source Collaborative Remote Sensing Data. Trans. Chin. Soc. Agric. Mach. 2018, 49, 127–133. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Q.; Ma, T. Inversely Calculating the Roughness of Bare Soil Surface in Cold-arid Irrigation Regions Using the SAR Method. J. Irrig. Drain. 2017, 36, 74–80. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Q.; Qu, Z.; Wang, L.; Li, X.; Wang, Y. Inversion and verification of salinity soil moisture using microwave radar. Trans. Chin. Soc. Agric. Eng. 2017, 33, 108–114. [Google Scholar] [CrossRef]
- Sun, Y.; Qu, Z.; Liu, Q. Monitoring of Nitrogen and Phosphorus in Farmland Topsoil Based on Multi-source Data of Ground Spectrum Combined with SAR. J. Irrig. Drain. 2020, 39, 120–127. [Google Scholar] [CrossRef]
- Zhen, P. Research on Soil Moisture Retrieval Using Microwave Remote Sensing Data Based on Roughness Parameter in Blown-Sand Region. Master’s Thesis, Chang’an University, Xi’an China, 2016. [Google Scholar]
- Zhen, P. The Inversion of Soil Moisture of Sandy Beach by Aiem on Calibrated Roughness. Yunnan Geol. 2016, 35, 114–117. [Google Scholar]
- Oh, Y. Quantitative Retrieval of Soil Moisture Content and Surface Roughness from Multipolarized Radar Observations of Bare Soil Surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 596–601. [Google Scholar] [CrossRef]
- Zribi, M. Surface soil moisture estimation from the synergistic use of the (multi-incidence and multi-resolution) active microwave ERS Wind Scatterometer and SAR data. Remote Sens. Environ. 2003, 86, 30–41. [Google Scholar] [CrossRef]
- Wang, X. Study on Soil Dielectric Properties and Multisource Remote Sensing Moisture Inversion in Salinization Irrigated Area. Master’s Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2017. [Google Scholar]
- Kong, J.; Zhen, P.; Li, J.; Yang, X.; Yang, J.; Wu, Z. Retrival for Soil Moistur Using Microwave Remote Sensing Data Based on a New Combined Roughness Parameter. Geogr. Geo-Inf. Sci. 2016, 32, 34–38. [Google Scholar]
- Tzong-Dar, W.; Kun-Shan, C. A reappraisal of the validity of the IEM model for backscattering from rough surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 743–753. [Google Scholar] [CrossRef]
- Fung, A.K.; Chen, K.S. An Update on the IEM Surface Backscattering Model. IEEE Geosci. Remote Sens. Lett. 2004, 1, 75–77. [Google Scholar] [CrossRef]
- Yang, J.; Deng, Q.; Li, S.; Zhang, L.; Chen, Q.; Sun, G.; Sun, Z. Synergistic Inversionof Soil in Vegetation Covered Areas of the Lower Yellow River Based on Optical and SAR Remote Sensing. Yellow River 2023, 45, 106–110. [Google Scholar] [CrossRef]
- Guo, W.; Ma, M.; Sun, P. Research on the soil water content inversion based on Sentinel-1A data and BP neural network. China Rural Water Hydropower 2023, 65, 89–94. [Google Scholar] [CrossRef]
- Zheng, L. Research on Bare Surface Soil Moisture Inversion Based on the Microwave Remote Sensing. Master’s Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2014. [Google Scholar]
- Jiang, L. Research on Soil Moisture Retreval Base on Sentinel Data. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2020. [Google Scholar] [CrossRef]
- Liu, F. Inversion of Soil Moisture Based on Dual-Polarization RADARSAT-2 Data. Master’s Thesis, Chang’an University, Xi’an, China, 2018. [Google Scholar]
- Han, G. Soil Surface Moistur Inversion Research on Salt-Affected Soils by Polarimetric Radar in Arid Areas. Ph.D. Thesis, Xinjiang University, Urumqi, China, 2013. [Google Scholar]
- Yang, T. Application of Soil Moisture Monitoring in Wheat Field Using Radar and Optical Remote Sensing Data. Master’s Thesis, East China Normal University, Shanghai, China, 2018. [Google Scholar]
- Han, L.; Wang, C.; Yu, T.; Gu, X.; Liu, Q. High-Precision Soil Moisture Mapping Based on Multi-Model Coupling and Background Knowledge, Over Vegetated Areas Using Chinese GF-3 and GF-1 Satellite Data. Remote Sens. 2020, 12, 2123. [Google Scholar] [CrossRef]
- Yang, L.; Liu, F.; Li, Y.; Liu, J.; Li, G.; Jin, M. Simulation of backscattering characteristics of bare surface based on the AIEM model in arid areas. J. Lanzhou Univ. (Nat. Sci.) 2019, 55, 176–182. [Google Scholar] [CrossRef]
- Wang, F.; Li, R.; Wang, S.; Wang, H.; Shi, Y.; Zhang, Y.; Zhao, J.; Yang, J. Seasonal Drought Dynamics and the Time-Lag Effect in the MU Us Sandy Land (China) Under the Lens of Climate Change. Land 2024, 13, 307. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Chen, W.; Yang, A. Microwave modeling of soil moisture in Oasis regional scale based on Sentinel-1 radar images. J. Infrared Millim. Waves 2017, 36, 120–126. [Google Scholar] [CrossRef]
- Han, L.; Qin, X.; Chen, L. Inversion of soil moistre on bare surface by dual polarization SAR data. Eng. Surv. Mapp. 2018, 27, 7–12. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).