Novel Ensemble Learning Approach for Predicting COD and TN: Model Development and Implementation
Abstract
1. Introduction
2. Model Development and Data Preparation
2.1. Ensemble Model
2.2. Exploratory Data Analysis (EDA)
2.3. Data Preprocessing
2.4. Feature Engineering
2.5. Hyperparameter Tuning
2.6. Evaluation Metrics
3. Materials and Methods
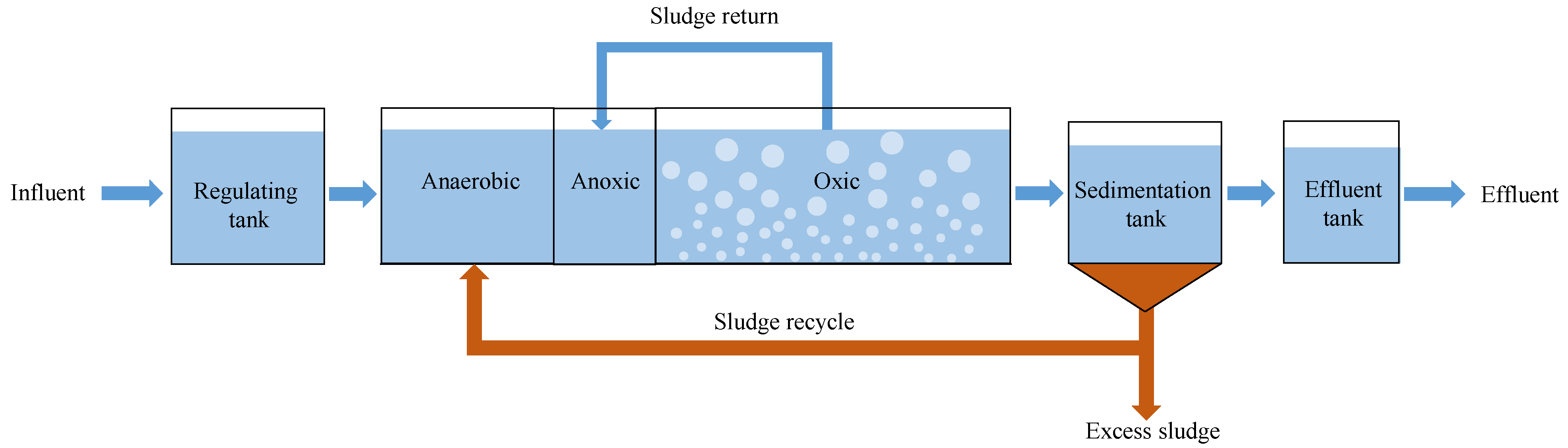
3.1. A2O Process
3.2. Analytical Methods
4. Results and Discussion
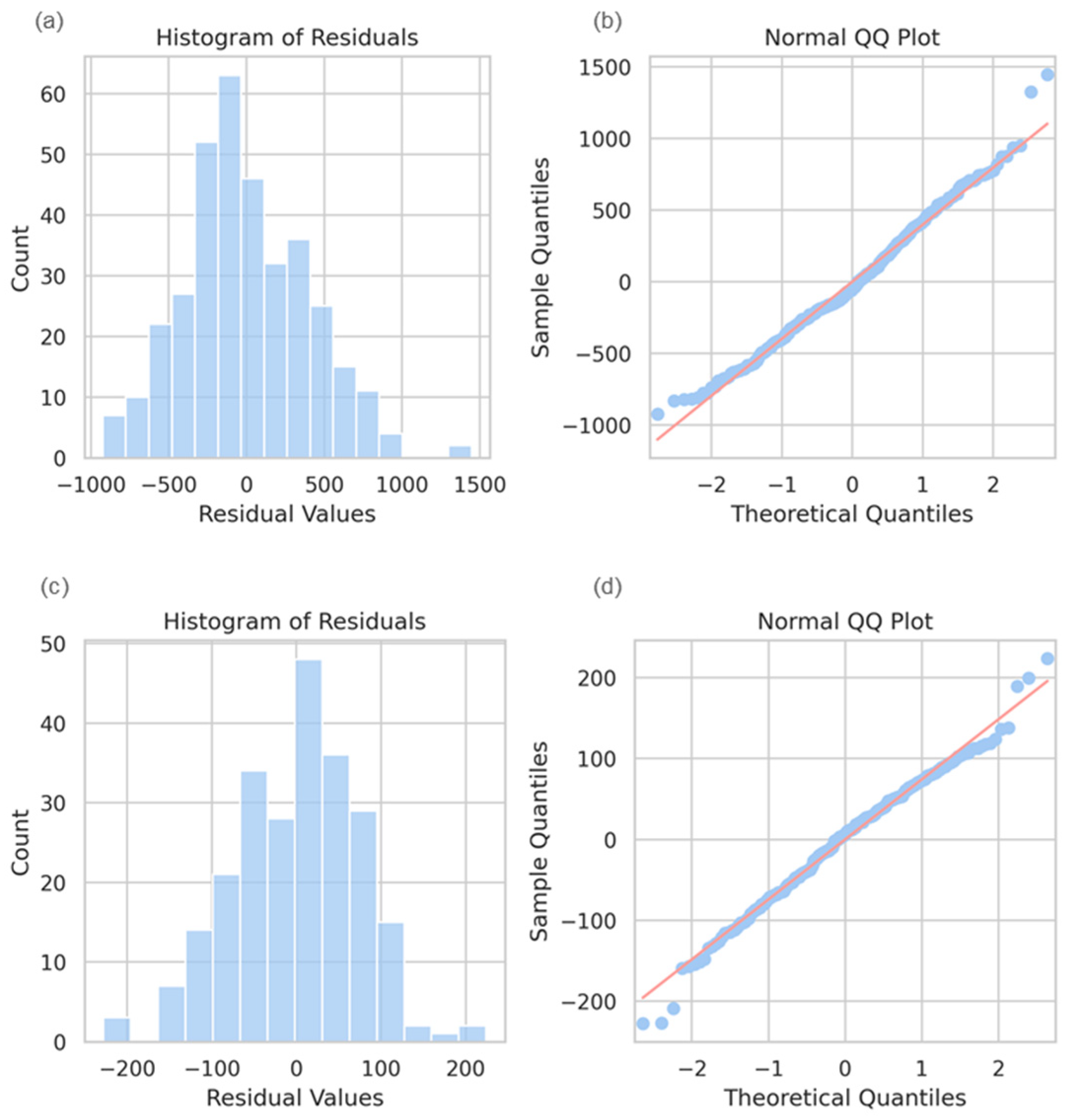
4.1. Applicability of Various Regression Models
4.1.1. Multiple Linear Regression (MLR) Model
4.1.2. Multilayer Perceptron Model (MLP)
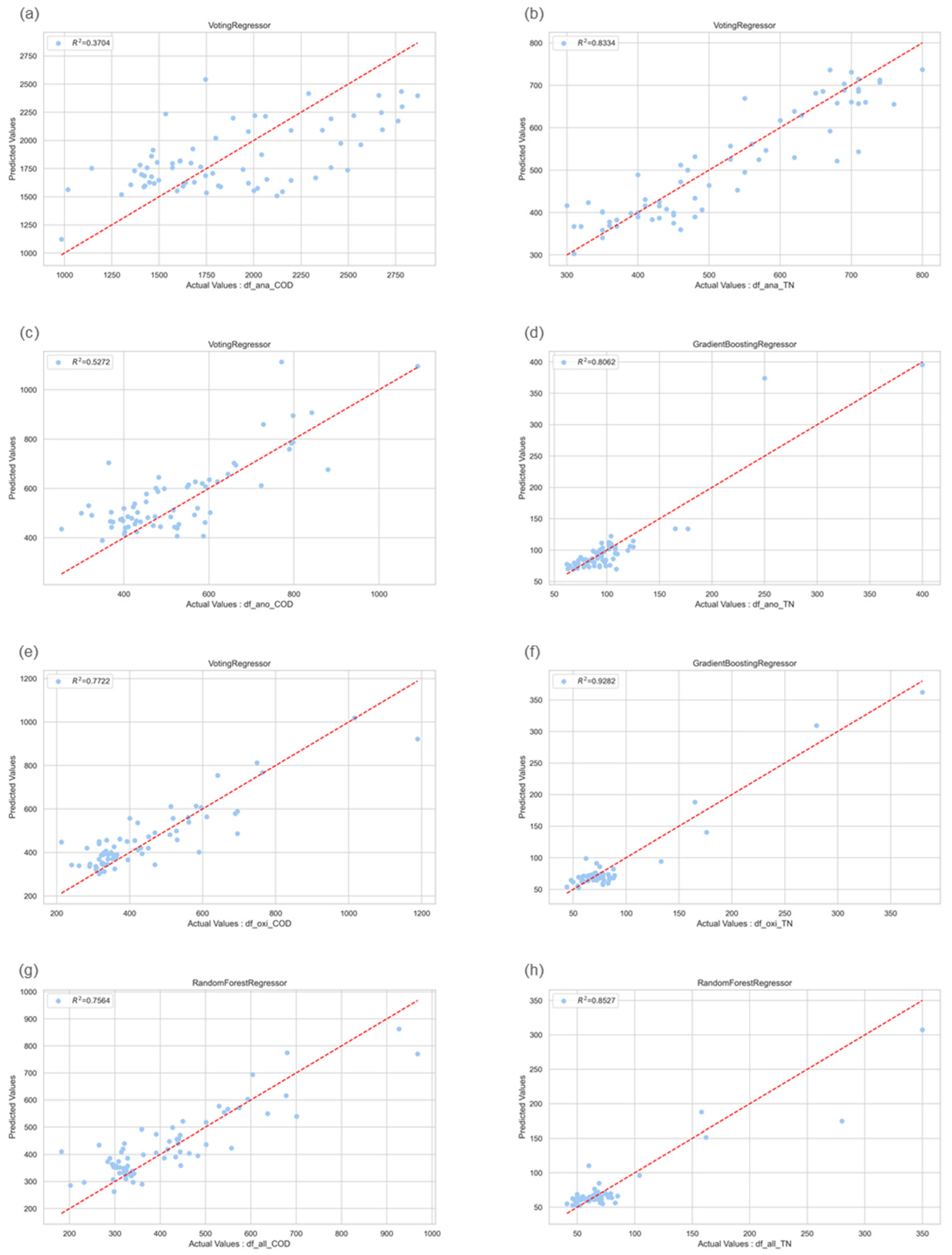
4.2. Prediction of COD and TN Using Ensemble Model
4.3. Predicting COD and TN Removal Efficiencies Based on the C/N Ratio
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wongburi, P.; Park, J.K. Big Data Analytics from a Wastewater Treatment Plant. Sustainability 2021, 13, 12383. [Google Scholar] [CrossRef]
- Maiza, M.; Beltrán, S.; Westling, K.; Carlsson, B.; Mulas, M.; Bergström, P.; Hyyryläinen, S.; Gorka, U. DIAMOND: AdvanceD data management and InformAtics for the optimuM operatiON anD control of WWTPs. In Proceedings of the ICA 2013, Narbonne, France, 18–20 September 2013. [Google Scholar]
- Siegrist, R.L. Introduction to Decentralized Infrastructure for Wastewater Treatment and Water Reclamation. In Decentralized Water Reclamation Engineering: A Curriculum Workbook; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–37. [Google Scholar]
- Aghdam, E.; Mohandes, S.R.; Manu, P.; Cheung, C.; Yunusa-Kaltungo, A.; Zayed, T. Predicting quality parameters of wastewater treatment plants using artificial intelligence techniques. J. Clean. Prod. 2023, 405, 137019. [Google Scholar] [CrossRef]
- Häck, M.; Köhne, M. Estimation of was tewater process parameters using neural networks. Water Sci. Technol. 1996, 33, 101–115. [Google Scholar] [CrossRef]
- Haimi, H.; Mulas, M.; Corona, F.; Vahala, R. Data-derived soft-sensors for biological wastewater treatment plants: An overview. Environ. Model. Softw. 2013, 47, 88–107. [Google Scholar] [CrossRef]
- Pai, T.-Y. Gray and Neural Network Prediction of Effluent from the Wastewater Treatment Plant of Industrial Park Using Influent Quality. Environ. Eng. Sci. 2008, 25, 757–766. [Google Scholar] [CrossRef]
- Fan, R.; Wang, S.; Chen, H. A COD measurement method with turbidity compensation based on a variable radial basis function neural network. Anal. Methods 2023, 15, 5360–5368. [Google Scholar] [CrossRef] [PubMed]
- Akbar, M.A.; Sharif, O.; Selvaganapathy, P.R.; Kruse, P. Identification and Quantification of Aqueous Disinfectants Using an Array of Carbon Nanotube-Based Chemiresistors. ACS Appl. Eng. Mater. 2023, 1, 3040–3052. [Google Scholar] [CrossRef] [PubMed]
- Civelekoglu, G.; Yigit, N.O.; Diamadopoulos, E.; Kitis, M. Modelling of COD removal in a biological wastewater treatment plant using adaptive neuro-fuzzy inference system and artificial neural network. Water Sci. Technol. 2009, 60, 1475–1487. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhou, P.; Xie, Y.; Chai, T. Improved model-free adaptive predictive control method for direct data-driven control of a wastewater treatment process with high performance. J. Process Control 2022, 110, 11–23. [Google Scholar] [CrossRef]
- Jafar, R.; Awad, A.; Jafar, K.; Shahrour, I. Predicting Effluent Quality in Full-Scale Wastewater Treatment Plants Using Shallow and Deep Artificial Neural Networks. Sustainability 2022, 14, 15598. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on typical tabular data? Adv. Neural Inf. Process. Syst. 2022, 35, 507–520. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Schapire, R.E. The Strength of Weak Learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Erdebilli, B.; Devrim-İçtenbaş, B. Ensemble Voting Regression Based on Machine Learning for Predicting Medical Waste: A Case from Turkey. Mathematics 2022, 10, 2466. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate imputation by chained equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Yeo, I.K.; Johnson, R.A. A new family of power transformations to improve normality or symmetry. Biometrika 2000, 87, 954–959. [Google Scholar] [CrossRef]
- Grotenhuis, M.t.; Thijs, P. Dummy variables and their interactions in regression analysis: Examples from research on body mass index. arXiv 2015, arXiv:1511.05728. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Nadiri, A.A.; Shokri, S.; Tsai, F.T.-C.; Moghaddam, A.A. Prediction of effluent quality parameters of a wastewater treatment plant using a supervised committee fuzzy logic model. J. Clean. Prod. 2018, 180, 539–549. [Google Scholar] [CrossRef]
- Khair, U.; Fahmi, H.; Al Hakim, S.; Rahim, R. Forecasting error calculation with mean absolute deviation and mean absolute percentage error. J. Phys. Conf. Ser. 2017, 930, 012002. [Google Scholar] [CrossRef]
- Güçlü, D.; Dursun, S. Amelioration of carbon removal prediction for an activated sludge process using an artificial neural network (ANN). CLEAN–Soil Air Water 2008, 36, 781–787. [Google Scholar] [CrossRef]
- Nasr, M.S.; Moustafa, M.A.; Seif, H.A.; El Kobrosy, G. Application of Artificial Neural Network (ANN) for the prediction of EL-AGAMY wastewater treatment plant performance-EGYPT. Alex. Eng. J. 2012, 51, 37–43. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Xue, T.; Li, B.; Dai, X.; Peng, Y. Treating low carbon/nitrogen (C/N) wastewater in simultaneous nitrification-endogenous denitrification and phosphorous removal (SNDPR) systems by strengthening anaerobic intracellular carbon storage. Water Res. 2015, 77, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.-C.; Lu, Y.-Z.; Xu, L.-R. Effects of the carbon/nitrogen (C/N) ratio on a system coupling simultaneous nitrification and denitrification (SND) and denitrifying phosphorus removal (DPR). Environ. Technol. 2021, 42, 3048–3054. [Google Scholar] [CrossRef] [PubMed]
- Lai, T.M.; Dang, H.V.; Nguyen, D.D.; Yim, S.; Hur, J. Wastewater treatment using a modified A2O process based on fiber polypropylene media. J. Environ. Sci. Health Part A 2011, 46, 1068–1074. [Google Scholar] [CrossRef] [PubMed]
- Lim, E.-T.; Jeong, G.-T.; Bhang, S.-H.; Park, S.-H.; Park, D.-H. Evaluation of pilot-scale modified A2O processes for the removal of nitrogen compounds from sewage. Bioresour. Technol. 2009, 100, 6149–6154. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Guo, L.; Sun, M.; Zhao, Y.; Gao, M.; She, Z. Effects of hydraulic retention time (HRT) on denitrification using waste activated sludge thermal hydrolysis liquid and acidogenic liquid as carbon sources. Bioresour. Technol. 2017, 224, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhang, Y.; Yang, M.; Kamagata, Y. Effects of hydraulic retention time on nitrification activities and population dynamics of a conventional activated sludge system. Front. Environ. Sci. Eng. 2013, 7, 43–48. [Google Scholar] [CrossRef]
- Mohan, T.K.; Nancharaiah, Y.; Venugopalan, V.; Sai, P.S. Effect of C/N ratio on denitrification of high-strength nitrate wastewater in anoxic granular sludge sequencing batch reactors. Ecol. Eng. 2016, 91, 441–448. [Google Scholar] [CrossRef]



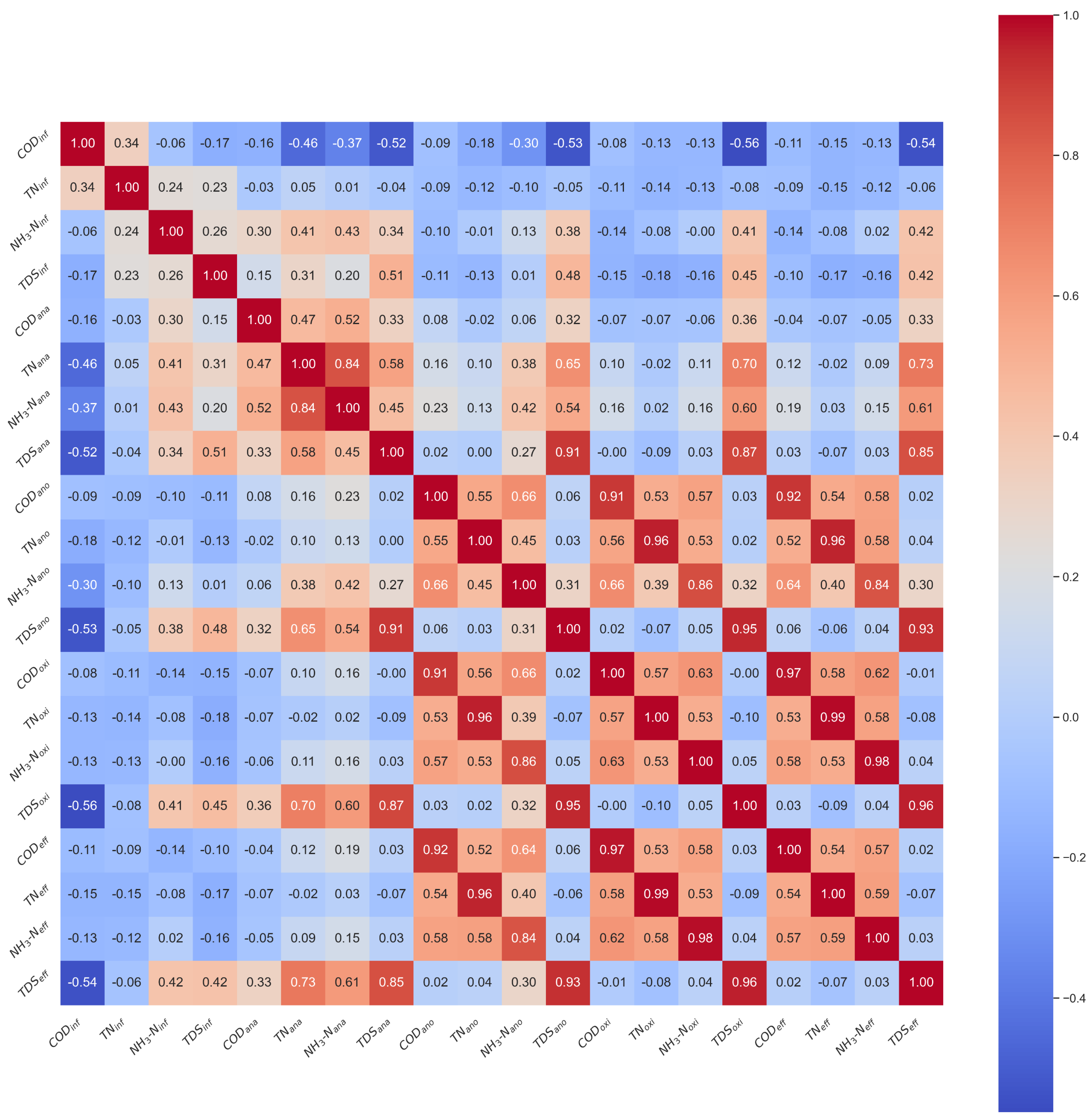






| Parameter | COD | NH3-N | TN | TDS | |
|---|---|---|---|---|---|
| Anaerobic | CODana | 1.0000 | |||
| NH3-Nana | 0.5336 * | 1.0000 | |||
| TNana | 0.4913 | 0.8433 | 1.0000 | ||
| TDSana | 0.3761 | 0.4504 | 0.5764 | 1.0000 | |
| Anoxic | CODano | 1.0000 | |||
| NH3-Nano | 0.6555 | 1.0000 | |||
| TNano | 0.5493 | 0.4512 | 1.0000 | ||
| TDSano | 0.0471 | 0.3045 | 0.0212 | 1.0000 | |
| Oxic | CODoxi | 1.0000 | |||
| NH3-Noxi | 0.5749 | 1.0000 | |||
| TNoxi | 0.5357 | 0.5860 | 1.0000 | ||
| TDSoxi | 0.0150 | 0.0263 | −0.0666 | 1.0000 | |
| Parameter | # of 0 | Parameter | # of 0 |
|---|---|---|---|
| CODinf * | 0 | NH3-Nano | 0 |
| NH3-Ninf | 0 | TNano | 0 |
| TDSinf | 0 | TDSano | 112 |
| Tinf | 0 | CODoxi | 0 |
| TNinf | 0 | NH3-Noxi | 0 |
| pHinf | 0 | TNoxi | 0 |
| CODana | 0 | TDSoxi | 112 |
| NH3-Nana | 0 | CODeff | 0 |
| TNana | 0 | NH3-Neff | 0 |
| TDSana | 112 | TNeff | 0 |
| CODano | 0 | TDSeff | 112 |
| Parameter | Count | Mean | Std | Min | 25% | 50% | 75% | Max | |
|---|---|---|---|---|---|---|---|---|---|
| Influent | COD | 352 | 6087.0 | 1170.3 | 2390.0 | 5290.0 | 5980.0 | 6792.5 | 9780.0 |
| NH3-N | 352 | 305.0 | 88.4 | 104.0 | 235.0 | 305.0 | 370.0 | 554.0 | |
| TDS | 352 | 6638.5 | 1353.7 | 3540.0 | 5820.0 | 6565.0 | 7420.0 | 12,800.0 | |
| Temp. | 352 | 35.8 | 4.7 | 18.0 | 33.0 | 36.1 | 39.0 | 46.6 | |
| TN | 352 | 707.6 | 124.4 | 360.0 | 610.0 | 700.0 | 800.0 | 1120.0 | |
| pH | 352 | 7.3 | 0.5 | 5.8 | 7.2 | 7.3 | 7.4 | 10.3 | |
| Anaerobic | COD | 352 | 1857.6 | 472.2 | 863.0 | 1497.3 | 1780.0 | 2152.8 | 3294.0 |
| NH3-N | 352 | 267.0 | 115.2 | 76.0 | 166.0 | 249.5 | 369.3 | 570.0 | |
| TN | 352 | 517.1 | 147.2 | 180.0 | 400.0 | 490.0 | 660.0 | 840.0 | |
| TDS | 352 | 5058.4 | 3571.7 | 0.0 | 0.0 | 6700.0 | 7662.5 | 10,900.0 | |
| Anoxic | COD | 352 | 558.3 | 189.7 | 66.0 | 421.8 | 524.5 | 642.3 | 1338.0 |
| NH3-N | 352 | 59.9 | 63.5 | 12.0 | 27.0 | 37.0 | 64.0 | 360.0 | |
| TN | 352 | 99.2 | 44.7 | 58.0 | 81.0 | 93.0 | 102.0 | 430.0 | |
| TDS | 352 | 4773.7 | 3376.2 | 0.0 | 0.0 | 6210.0 | 7342.5 | 9600.0 | |
| Oxic | COD | 352 | 457.4 | 184.5 | 149.0 | 329.8 | 398.5 | 552.0 | 1261.0 |
| NH3-N | 352 | 24.8 | 54.1 | 3.0 | 5.0 | 7.0 | 12.0 | 336.0 | |
| TN | 352 | 78.7 | 44.5 | 44.0 | 64.0 | 70.0 | 76.0 | 400.0 | |
| TDS | 352 | 4582.2 | 3285.7 | 0.0 | 0.0 | 5690.0 | 7280.0 | 9980.0 | |
| Effluent | COD | 352 | 434.3 | 163.4 | 138.0 | 320.0 | 392.5 | 524.3 | 1058.0 |
| NH3-N | 352 | 21.4 | 49.3 | 2.0 | 4.0 | 6.0 | 9.3 | 309.0 | |
| TN | 352 | 73.0 | 43.2 | 40.0 | 60.0 | 65.0 | 70.0 | 390.0 | |
| TDS | 352 | 4422.0 | 3211.8 | 0.0 | 0.0 | 5400.0 | 7172.5 | 9770.0 | |
| Parameters (mg/L) | Influent | Anaerobic Reactor | Anoxic Reactor | Oxic Reactor | Effluent |
|---|---|---|---|---|---|
| COD | 6077.3 ± 1173.0 | 1857.6 ± 472.2 | 558.3 ± 190.0 | 457.4 ± 184.5 | 434.3 ± 163.4 |
| NH3-N | 304.6 ± 88.9 | 267.0 ± 115.2 | 59.9 ± 63.5 | 24.8 ± 54.1 | 21.4 ± 49.3 |
| TDS | 6612.6 ± 1332.3 | 7419.0 ± 1071.8 | 7001.4 ± 1038.4 | 6720.6 ± 1193.0 | 6485.5 ± 1308.0 |
| TP | 19.9 ± 8.5 | - | - | - | - |
| TN | 706.7 ± 124.8 | 517.1 ± 147.2 | 99.2 ± 44.7 | 78.7 ± 44.5 | 73.0 ± 43.2 |
| Sulfate | 978.7 ± 601.1 | - | - | - | - |
| Chloride ion | 869.2 ± 226.0 | - | - | - | - |
| Total salinity | 3528.0 ± 503.3 | - | - | - | - |
| Volatile phenol | 85.1 ± 30.3 | - | - | - | - |
| Temp. (°C) | 35.9 ± 4.7 | - | - | - | - |
| pH | 7.3 ± 0.5 | - | - | - | - |
| MLSS | - | - | 4212.7 ± 1038.4 | 4097.4 ± 409.5 | - |
| Dep. Variable | Intercept & Independent Variables | Coefficient | Standard Error | t-Value | P > |t| | R2 (Adj.) | F-Statistics (Prob.) | Breusch–Pagan (Prob.) | VIF |
|---|---|---|---|---|---|---|---|---|---|
| CODana | Interceptana | 648.6080 | 184.5770 | 3.5140 | 0.001 | 0.3050 (0.2990) | 52.00 (1.88 × 10−19) | 9.2257 (0.0099) | 10.5067 |
| NH3-Nana | 1.6232 | 0.2630 | 6.1710 | 0.000 | |||||
| TDSana | 0.1074 | 0.0280 | 3.7840 | 0.000 | |||||
| TNana | Interceptana | 226.3749 | 10.3800 | 21.8090 | 0.000 | 0.7510 (0.7490) | 468.40 (1.49 × 10−99) | 8.3245 (0.0155) | |
| NH3-Nana | 0.9651 | 0.0430 | 22.5470 | 0.000 | |||||
| TDSana | 0.0065 | 0.0010 | 4.7390 | 0.000 |
| Process | Features | Target | Model | R2 | MAE | MAPE | MSE | RMSE |
|---|---|---|---|---|---|---|---|---|
| Anaerobic | TDSana NH3-Nana | COD | Multilayer Perceptron | −0.0281 | 306.8756 | 0.1864 | 1.478 × 105 | 384.4962 |
| TN | Multilayer Perceptron | 0.6096 | 82.2764 | 0.1858 | 9.667 × 103 | 98.3218 |
| Process | Features | Target | Model | R2 | MAE | MAPE | MSE | RMSE |
|---|---|---|---|---|---|---|---|---|
| Anaerobic | pHinf Tempinf NH3-Nana TDSana | COD | Random Forest Regressor | 0.3611 | 314.0597 | 0.1730 | 139,249.0139 | 373.1608 |
| Gradient Boosting Regressor | 0.3667 | 307.3038 | 0.1692 | 138,028.2257 | 371.5215 | |||
| XGB Regressor | 0.2808 | 320.7301 | 0.1768 | 156,761.5667 | 395.9313 | |||
| Voting Regressor | 0.3704 | 314.8617 | 0.1714 | 137,239.0012 | 370.4578 | |||
| TN | Random Forest Regressor | 0.7972 | 48.2324 | 0.0971 | 3996.0776 | 63.2145 | ||
| Gradient Boosting Regressor | 0.8033 | 47.4283 | 0.0952 | 3876.5724 | 62.2621 | |||
| XGB Regressor | 0.7982 | 49.5103 | 0.1017 | 3976.5846 | 63.0602 | |||
| Voting Regressor | 0.8334 | 43.4740 | 0.0870 | 3282.3695 | 57.2920 | |||
| Anoxic | pHinf Tempinf NH3-Nano TDSano | COD | Random Forest Regressor | 0.5068 | 86.1109 | 0.1833 | 12,174.7390 | 110.3392 |
| Gradient Boosting Regressor | 0.4807 | 82.7199 | 0.1772 | 12,819.2609 | 113.2222 | |||
| XGB Regressor | 0.4401 | 92.1794 | 0.1995 | 13,822.4896 | 117.5691 | |||
| Voting Regressor | 0.5272 | 82.6990 | 0.1815 | 11,671.4214 | 108.0344 | |||
| TN | Random Forest Regressor | 0.7611 | 13.1522 | 0.1211 | 496.6391 | 22.2854 | ||
| Gradient Boosting Regressor | 0.8062 | 11.8176 | 0.1091 | 402.9547 | 20.0737 | |||
| XGB Regressor | 0.8003 | 11.7854 | 0.1084 | 415.2215 | 20.3770 | |||
| Voting Regressor | 0.8010 | 11.7671 | 0.1015 | 413.6942 | 20.3395 | |||
| Oxic | pHinf Tempinf NH3-Noxi TDSoxi | COD | Random Forest Regressor | 0.7375 | 60.6232 | 0.1552 | 7892.0438 | 88.8372 |
| Gradient Boosting Regressor | 0.7611 | 63.0409 | 0.1607 | 7184.0118 | 84.7586 | |||
| XGB Regressor | 0.7264 | 67.8336 | 0.1701 | 8225.6465 | 90.6953 | |||
| Voting Regressor | 0.7722 | 60.1776 | 0.1523 | 6849.8258 | 82.7637 | |||
| TN | Random Forest Regressor | 0.8633 | 10.7976 | 0.1291 | 325.6551 | 18.0459 | ||
| Gradient Boosting Regressor | 0.9282 | 9.7993 | 0.1229 | 170.9395 | 13.0744 | |||
| XGB Regressor | 0.8887 | 10.8189 | 0.1370 | 265.1009 | 16.2819 | |||
| Voting Regressor | 0.9005 | 10.5414 | 0.1265 | 237.0049 | 15.3950 | |||
| Oxic with all data * | pHinf Tempinf NH3-Ninf TDSinf NH3-Nana TDSana NH3-Nano TDSano NH3-Noxi TDSoxi | COD | Random Forest Regressor | 0.7564 | 54.4847 | 0.1502 | 5328.1426 | 72.9941 |
| Gradient Boosting Regressor | 0.7399 | 58.7900 | 0.1525 | 5690.3028 | 75.4341 | |||
| XGB Regressor | 0.7280 | 58.2190 | 0.1582 | 5950.2342 | 77.1378 | |||
| Voting Regressor | 0.7350 | 57.6162 | 0.1545 | 5796.6046 | 76.1354 | |||
| TN | Random Forest Regressor | 0.8527 | 9.8803 | 0.1250 | 317.1213 | 17.8079 | ||
| Gradient Boosting Regressor | 0.7609 | 11.1788 | 0.1391 | 514.7406 | 22.6879 | |||
| XGB Regressor | 0.7805 | 11.3402 | 0.1261 | 472.6688 | 21.7409 | |||
| Voting Regressor | 0.8477 | 10.2401 | 0.1237 | 328.0104 | 18.1111 |
| Parameter | Process | R2 | Calculated C/N | Measured Removal Efficiency (%) | Calculated Removal Efficiency (%) |
|---|---|---|---|---|---|
| COD | Anaerobic | 0.9387 | 2.2~8.3 (3.7) * | 0.24~0.86 (0.68) | 0.23~0.86 (0.68) |
| Anoxic | 0.9396 | 2.7~10.9 (5.8) | 0.18~0.94 (0.68) | 0.17~0.85 (0.69) | |
| Oxic | 0.6971 | 2.4~14.8 (6.2) | 0.00~0.55 (0.17) | 0.00~0.45 (0.19) | |
| TN | Anaerobic | 0.5970 | 2.2~8.3 (3.7) | 0.00~0.70 (0.25) | 0.00~0.64 (0.25) |
| Anoxic | 0.9228 | 2.7~10.9 (5.8) | 0.09~0.90 (0.79) | 0.12~0.88 (0.79) | |
| Oxic | 0.7385 | 2.4~14.8 (6.2) | 0.00~0.49 (0.21) | 0.00~0.57 (0.22) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Q.; Kim, J.-Y.; Wang, Y.; Ren, X.; Guo, Y.; Park, J.-H.; Park, S.-G.; Lee, S.-Y.; Zheng, G.; Wang, Y.; et al. Novel Ensemble Learning Approach for Predicting COD and TN: Model Development and Implementation. Water 2024, 16, 1561. https://doi.org/10.3390/w16111561
Cheng Q, Kim J-Y, Wang Y, Ren X, Guo Y, Park J-H, Park S-G, Lee S-Y, Zheng G, Wang Y, et al. Novel Ensemble Learning Approach for Predicting COD and TN: Model Development and Implementation. Water. 2024; 16(11):1561. https://doi.org/10.3390/w16111561
Chicago/Turabian StyleCheng, Qiangqiang, Ji-Yeon Kim, Yu Wang, Xianghao Ren, Yingjie Guo, Jeong-Hyun Park, Sung-Gwan Park, Sang-Youp Lee, Guili Zheng, Yawei Wang, and et al. 2024. "Novel Ensemble Learning Approach for Predicting COD and TN: Model Development and Implementation" Water 16, no. 11: 1561. https://doi.org/10.3390/w16111561
APA StyleCheng, Q., Kim, J.-Y., Wang, Y., Ren, X., Guo, Y., Park, J.-H., Park, S.-G., Lee, S.-Y., Zheng, G., Wang, Y., Lee, Y.-J., & Hwang, M.-H. (2024). Novel Ensemble Learning Approach for Predicting COD and TN: Model Development and Implementation. Water, 16(11), 1561. https://doi.org/10.3390/w16111561







