Abstract
In slopes where a mixture of coarse and fine particles is present, the infiltration of rainfall can cause the migration of fine particles. This migration alters the hydraulic properties of the soil and has implications for slope stability. In this study, the slope under investigation is a tailings dam composed of loosely consolidated soil with a wide particle size distribution. Due to rainfall infiltration, fine particles tend to migrate within the voids of the coarse particle framework, leading to changes in hydraulic properties and inducing slope instability. The classical internal erosion constitutive model, known as the Cividini and Gioda erosion criterion, is commonly used to predict the behavior and effects of fine particle erosion in geotechnical engineering. However, certain parameters in this erosion criterion equation, such as long-term density, are challenging to obtain through experiments. To investigate the coupled evolution of seepage and erosion within landfill slopes under the influence of rainfall infiltration and to understand the mechanisms of slope instability, this research assumes the erosion of fine particle suspension and adopts the Worman and Olafsdottir erosion criterion to establish a coupled model of unsaturated seepage and internal erosion. The developed model simulates the coupled response of seepage and erosion in unsaturated landfill slopes under three different rainfall intensities. It is then combined with the infinite slope model to quantitatively analyze the impact of fine particle migration on soil permeability and slope stability. The numerical simulations provide the following findings: The Worman and Olafsdottir erosion criterion, unlike the Cividini and Gioda erosion criterion, only requires the determination of the soil’s gradation curve to estimate the erosion rate. Internal erosion primarily occurs within the leading edge of moisture penetration, accelerating the advancement of the wetting front and reducing slope stability. When the rainfall intensity is lower than the saturated permeability coefficient, the influence of internal erosion can be disregarded. However, under rainfall intensities equal to or greater than the saturated permeability coefficient, considering internal erosion results in a difference in the depth of the wetting front of up to 34.2 cm after 6 h in the R2 scenario. The safety factor without considering internal erosion is 1.12, whereas considering internal erosion yields safety factors between 1.08 and 1.09. In the R3 scenario, the difference in the depth of the wetting front reaches 53.8 cm after 6 h, with a safety factor of 1.12 without considering internal erosion and safety factors between 1.06 and 1.07 when considering internal erosion.
1. Introduction
In this article, the slope under study is located in Yunnan Province, China. The slope was formed by directly stacking externally transported waste soil, and it has been in place for over 16 years. The soil used for filling was not treated, resulting in a heterogeneous overall state of the slope. Even after the long duration of the fill, certain parts of the slope have not fully consolidated. The fill material is a mixture of coarse and fine particles, and the soil exhibits geometries that are susceptible to seepage-induced internal erosion [1,2,3]. Under the infiltration of rainfall, particles in these broadly graded or gap-graded soils may be separated from the soil structure by interstitial water flow and follow the water flow into the pores formed by the coarse matrix [4]. The process of soil fine particle migration will inevitably change the local particle size distribution of content in the soil, leading to localized changes in the hydraulic and mechanical properties of the soil within the slope [5,6] and affecting the transient stability of the slope [7]. Field-scale observations and controlled laboratory experiments suggest that rainfall infiltration prompts the movement of fine particles from the upper region’s slope and surface towards its base, a process facilitated by seepage-induced internal erosion [8,9].
In the theoretical research of internal erosion, in order to describe the whole process of migration and its related hydraulic mechanical behavior in unsaturated soils during rainfall infiltration, Lei [10] proposed a coupled seepage erosion deformation equation and used it to study the effect of skeleton deformation on rainfall infiltration in unsaturated soil columns. Zhang [11] studied the interaction between soil seepage and internal erosion, established a coupled model of unsaturated seepage and internal erosion, and investigated the influence of erosion parameters onhydraulic properties. Li [12] studied the hydrodynamic envelope of soil erosion due to internal instability induced by seepage with reference to the theory of one-dimensional upward and downward seepage and the laboratory stress gradient paths. Jiang [5] investigated the fine particle migration in the dam and the slope failure mode and proposed a coupled model of the fine particle migration equations, the unsaturated seepage equations, and the equations for local stability analysis. Bi [13] proposed a method to characterize the variation in soil gradation during internal erosion. This method utilized fundamental dimensional equations to describe the migration of macroscopic fine particles and additional dimensional equations to control the variation in soil gradation. By employing this approach, it became possible to capture the particle size distribution features for particles of any size during the internal erosion process. Ma [14] derived a set of coupled governing equations for five phases (soil skeleton, erodible fine particles, fluidized particles, water, and air) in porous media based on the continuum mixture theory. The Smoothed Particle Hydrodynamics (SPH) method was employed to describe the influence of porous media saturation and erosion on the shear strength of the porous media. Jiang [15] reformulated the mass conservation equation to account for different types of internal erosion, considering the erosion of suspended particles in pore channels and general erosion. This equation incorporated the pore size distribution and hydraulic gradient, enabling an effective assessment of the mass of eroded particles in the soil. In this study, the general erosion assumption for suspended particles was adopted, and Jiang’s mass conservation equation for internal erosion was employed to evaluate the mass of eroded particles.
In the research of erosion criteria, the likelihood of internal erosion is influenced by a variety of factors, including geometric aspects (such as the distribution of grain and pore sizes, as well as the shapes of grains and pores), hydraulic variables (including the hydraulic gradient, seepage direction, velocity of pore fluids), and mechanical factors (like the degree of compaction and applied stresses) [16,17,18]. Based on laboratory tests, physical modeling tests, and field observations, scholars have proposed various erosion laws, most of which are empirical relationships that relate erosion rates to water flow characteristics (i.e., seepage rates, hydraulic gradients), porosity, particle density, and empirical erosion coefficients [19,20,21]. However, these empirical equations are not based on physical derivations and therefore have their limitations. For instance, the formula introduced by Cividini and Gioda [22] establishes a linear correlation between the rate of internal erosion and that of seepage. However, obtaining some variables in this equation through experimental means proves challenging, including the long-term density that is linked to the hydraulic gradient at the beginning of internal erosion. Worman and Olafsdottir [23] selected seepage stress as a parameter instead of seepage velocity and used moment balance techniques to derive an erosion rate equation. This equation demonstrates a nonlinear correlation between the internal erosion rate and the seepage velocity and hydraulic gradient. Additionally, the parameters within this erosion constitutive equation are relatively easier to obtain compared to the erosion criteria proposed by Cividini and Gioda. Hence, this study conducted a comparative analysis between the erosion criteria proposed by Worman and Olafsdottir and those proposed by Cividini and Gioda.
In the context of traditional slope stability research, Zhang [24] discusses the differences between the calculation methods of shallow slope safety factors derived from the infinite slope model (ISM) and the Bishop method. Nitzsche [25], utilizing a finite element model of sloping regions, considers the special deformation mechanisms within shear zones and establishes a connection between shear strain on slip surfaces and the evolution of slope stability, proposing a numerical algorithm for calculating safety factors. Dowon [26] presents a theoretical framework for the analysis of infinite rock slope, specifically addressing weakened rock masses due to weathering and other geological processes. The consequences resulting from the assumption of the complete fracture of rock masses, eliminating tensile strength, are investigated through precise solutions obtained using statics and kinematics. Novel approaches to slope stability prediction often involve the integration of machine learning and deep learning methods. Guo [27], based on a physics-based Fast Shallow Landslide Assessment Model (FSLAM), captures the impact of rainfall on the probability of slope failure and evaluates rainfall-induced landslide disasters using 123 landslide cases triggered in Wenzhou City, southeastern China, as an example. Nie [28] proposes a new slope stability analysis method combining the scaled boundary finite element method (SBFEM), the strength reduction method (SRM), and a grid refinement algorithm based on a quadtree structure. Li [29] presents an intelligent slope stability prediction method based on an improved pelican optimization algorithm (IPOA) and optimized random forest algorithm (RF), applied to the Lala Copper Mine in Sichuan Province. The results demonstrate the reliability and effectiveness of the prediction model based on the improved IPOA and RF algorithms, with an accuracy rate of up to 90.4%, providing a solid technical foundation for predicting slope instability in geotechnical engineering. In this study, traditional infinite slope stability calculation formulas are employed for stability analysis, while future research can explore in-depth studies of slope stability in interdisciplinary fields such as machine learning and artificial intelligence.
The realization of rainfall boundaries in numerical simulation usually requires the dynamic conversion of pressure boundaries and flow boundaries [30,31], especially under heavy rainfall conditions. It is generally believed that when the surface soil is not saturated, the actual rainfall infiltration rate is the rainfall intensity, and the rainfall boundary is the flow boundary. In contrast, when the slope is saturated, the rainfall is divided into two parts, one part of which infiltrates into the interior of the soil body, and the other part of which is retained on the soil surface to form slope runoff, and the actual infiltration rate on the soil surface is controlled by the depth of the runoff because the depth of ponding water will be dynamically varied, and so the rainfall boundary is actually a non-constant pressure boundary [32]. Therefore, in order to accurately describe the infiltration flux and address the complexities of rainfall boundaries, the diffusion wave approximation equation, based on Wang’s research findings [32], is utilized to compute the dynamic ponding depth. This approach allows for the depiction of the dynamic conversion between flow boundaries and pressure boundaries.
This study employs the erosion criteria proposed by Worman and Olafsdottir and determines the internal erosion parameters through experimental methods. A comparative analysis is conducted, contrasting these criteria with those proposed by Cividini and Gioda. By incorporating the mass conservation equation for internal erosion, an internal erosion model is developed. To accurately describe the boundaries of rainfall, the diffusion wave equation is introduced to transform the traditional rainfall boundary, enabling the dynamic conversion between flow boundaries and pressure boundaries. Finally, a numerical analysis is conducted using an infinite slope model constructed based on field conditions, considering different rainfall intensities. The aim is to explore the effects of considering or neglecting internal erosion on soil permeability and slope stability.
2. Integrated Model for Unsaturated Flow and Internal Erosion
2.1. Governing Equations for Surface Flow
The diffusive wave approximation equation is widely used to describe the slope runoff process [33,34] (variation in water depth on a slope). Since the water depth of slope runoff is extremely shallow, its vertical slope water depth can be approximated as the vertical water depth between the water surface and the slope [34], so its mass conservation equation is as follows.
where = timing of rainfall ; = depth of water on vertically oriented slopes ; = mean flow velocity in the depth direction of the water flow ; = rainfall intensity ; indicates infiltration flux .
Its momentum conservation equation considers the balance between the friction term and the gravity-driven term and combined with Manning’s formula [35], yields
where = Manning’s coefficient of friction ; = slope elevation ; = slope ratio; ; = flow rate of slope runoff ; it can be expressed as the product of runoff flow rate and head
Substituting Equation (3) into Equation (1), the approximate equation for the diffusion wave is given by the following:
2.2. Fundamental Equations for Subsurface Flow and Erosion Dynamics
Soil is viewed as an amalgam of solid and liquid elements, incorporating a fixed soil skeleton, a fluid particulate phase that can move, and water. This configuration allows for the free movement of fine particles, dislodged by erosion, within the soil matrix alongside the water. The movable fine particles, denoted as , and the stationary soil matrix, represented by , signify the densities of these two distinct phases. Hence, two separate continuity equations are formulated to account for each phase [15]:
where = flux vector of fine particles transported by percolation ; indicates the rate of mass transfer from the skeletal phase to the mobile phase; it is also known as the erosion rate .
For fine particles uniformly distributed within the soil skeleton, it is assumed that the flux occurs over the entire surface at and that the fine particle migration movement occurs within the soil medium itself and includes pore water:
where = flow rate per cross-sectional area of soil medium ; = porosity; indicates seepage rate .
Thus, the fine particle flux, i.e., the mass passing through the entire unit area, including soil particles and the pore cross-section, per unit time, can be expressed as
During rainfall infiltration, fine particle migration movement occurs throughout the soil matrix, and according to Equations (5) and (8), the continuity equation for fine particles can be expressed as follows:
For the skeleton part of the soil [20], based on the relationship between erosion rate and porosity, the change in porosity during erosion can be expressed as follows:
The classical equations for describing the variable saturated seepage of groundwater are the Richards equation and the two-phase flow equation. Because the Richards equation has the advantages of its simple form and clear physical meaning of parameters, the Richards equation is chosen to describe the variable saturated flow in soil in this paper [33]:
Equation (10) is the partial differential equation describing the saturated unsaturated seepage in a geotechnical body with pore water pressure as the independent variable, where denotes the Hamiltonian operator (math.); = pore water pressure ; = specific volume of water ; = effective saturation; = saturated permeability coefficient ; = relative permeability coefficient; = density of water ; = gravitational acceleration ; = location in spatial coordinates ; = water storage rate .
2.3. Constitutive Laws for Internal Erosion
To accurately assess the equation of the dynamics of internal erosion, the equation delineating this process is instrumental. Worman and Olafsdottir [23] pinpointed seepage stress, which is intrinsically linked to the hydraulic gradient, as the principal mechanism propelling the displacement of fines. Opting for seepage stress over seepage velocity and their formulation of the erosion rate equation, derived through the moment balance technique, elucidates the dependency of seepage stress on several factors, including seepage velocity, the hydraulic gradient, and the specifics of pore size and distribution. This equation uncovers a nonlinear dependency linking the internal erosion rate with both seepage velocity and the hydraulic gradient. Moreover, it reveals the critical role played by the distribution of pore sizes, along with seepage velocity, in influencing the erosion rate. The formula for calculating the internal erosion rate is presented as follows:
where = porosity, = porosity ratio = , = specific density of particles, = hydraulic gradient, = particle size with 85% passage rate, = harmonized mean of particle diameter volume distribution, = kinematic viscosity, and = moveable area. In this study, we use Equations (12)–(15) to model internal erosion rates.
The erosion criteria used in this study include a comparison between the Worman and Olafsdottir erosion criterion and the Cividini and Gioda erosion criterion [22]. The erosion rate in the Cividini and Gioda erosion criterion can be expressed as follows:
where is the erosion rate coefficient, represents the current density of erodible fine particles in the soil, and represents the long-term density of fine particles, which can be expressed as follows:
where is the critical hydraulic gradient at the onset of erosion, represents the erodible fine particle content corresponding to , and is a parameter in the erosion criterion. The critical hydraulic gradient value in the erosion criterion is referenced from the Sterpi experiment [21], and it is set as .
2.4. Hydraulic Properties of Partially Saturated Soils
In this study, the van Genuchten–Mualem model [36,37] was used to calculate the Soil–Water Characteristic Curve (SWCC) saturation, infiltration function, and specific water capacity of unsaturated soils. The van Genuchten–Mualem model is expressed as
where = volumetric moisture content; = saturated moisture content; = residual moisture content; = pressure head ; , , denote empirical constants, Mualem figures [37] .
To account for the impact of internal erosion on hydraulic characteristics, the coefficient of saturated permeability is characterized as a function of porosity, following the principles of the Kozeny–Carman equation [38]:
where and correspond to the initial porosity and initial permeability coefficient, respectively.
2.5. Slope Stability Analysis
Infinite slope stability analysis serves as a tool for evaluating the stability of soil slopes subjected to rainfall, considering that slope failures induced by rainfall infiltration tend to be superficial. The safety factor for a potential slip surface located at depth as depicted in Figure 1 is calculated as follows [39]:
where = slope angle; = soil capacity ; = effective cohesion ; = effective friction angle; = slip depth (Figure 1); = pore water pressure head ; = bulk weight of water ; is the angle indicating the rate of increase in shear strength related to substrate suction force, and the value depends on the substrate suction, generally about one-third to two-thirds of . Here, is assumed to be 12°.
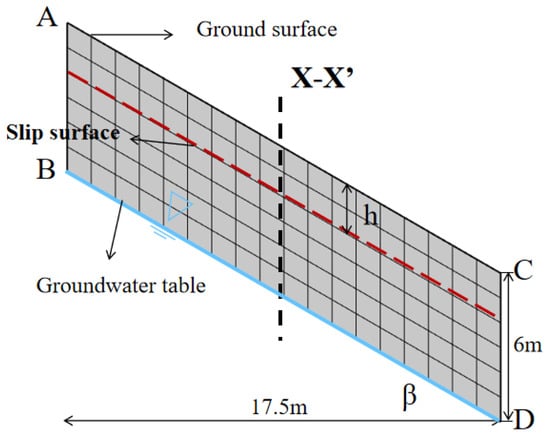
Figure 1.
A finite element model of the illustrative example.
The effective cohesion and the effective friction angle are affected by the porosity and can be found by the following relation [40]:
where , denote the initial cohesion and the initial internal friction angle, respectively.
3. Finite Element and Soil Parameters
3.1. Finite Element Modeling and Boundary Conditions
A finite element model for an infinite slope, set at a 30° angle, as shown in Figure 1, was developed using a representative soil material reflective of actual site conditions. This model comprises 4060 quadrilateral elements alongside 302 boundary elements, with the soil layer maintaining a depth of 6 m. Within the context of rainfall infiltration, AC delineates the infiltration boundary, whereas AB and CD represent impermeable boundaries, and BD signifies the boundary of a constant water table. For the purposes of stability analysis, AC is treated as an unconstrained boundary, AB and CD function as roller-supported boundaries, and BD is considered a fixed constraint boundary. Porosity alterations are attributed solely to internal erosion, starting from a homogeneous porosity across the field. The SWCC and the permeability function are illustrated in Figure 2, with additional hydraulic parameters detailed in Table 1.
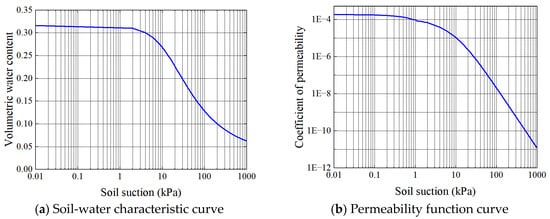
Figure 2.
The SWCC and permeability function of the residual soil.

Table 1.
Soil hydraulic parameters used in the study.
The infiltration rate across the slope surface AC is specified as [30]
where = infiltration rate; = auxiliary smoothing functions (Figure 3); indicates the thickness of the semi-permeable layer; = rain intensity. The specified boundary condition for infiltration flux indicates that the infiltration rate matches the rainfall intensity along the flow boundary when the pore water pressure on the slope surface AC is negative. Conversely, when the pore water pressure on AC becomes positive, the infiltration flux transitions to a pressure infiltration boundary, wherein the depth of ponding is determined using the diffusion wave equation. This setup facilitates the bi-directional dynamic transition between the rainfall flux boundary and the pressure boundary, governed by Equations (4) and (26).
Figure 3.
Function and .
3.2. Soil Grading Test
The test soil was taken from the slope of a tailing pond fill, and the composition of the fill was mainly clay, gravel, stones, gravel, etc., with uneven composition; among them, the content of gravel, stones, etc. was about 15–20%, and partially 30–70%, and the diameter of the blocks was generally 3–10 cm. According to the basic situation of the test soil material, and the requirements of the fill material for the later indoor geotechnical test, the maximum sieve diameter of the sieve test was chosen to be 60 mm, and the particles exceeding 60 mm were counted individually, and the minimum sieve diameter was 2 mm. The maximum sieve diameter was 60 mm, and the particles exceeding 60 mm were counted separately, and the minimum sieve diameter was 2 mm. This sieve test used a sieve machine to sieve the stacked bulk, so as to determine the particle size composition and distribution characteristics of the bulk soil material. The apertures of the sifter and sieve mesh are shown in Figure 4.

Figure 4.
Geotechnical sifter and screen aperture in a coarse-grained soil chamber.
After the particle size sieving of the test soil material, the particle size distribution characteristics of the soil material were obtained, as shown in Figure 4 and Figure 5, where the gradation curves are shown in Figure 6. This soil has a coefficient of homogeneity, Cu, of 85.52 greater than 20 and is considered to be internally unstable [3].

Figure 5.
Characteristics of particle size distribution of bulk soil material.
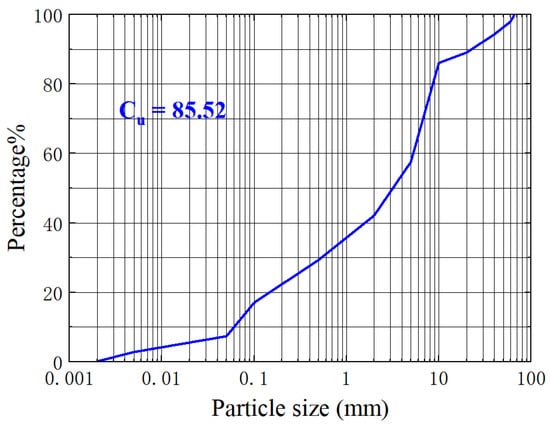
Figure 6.
Soil Gradation Curve.
4. An Analysis of the Results
To comprehensively consider varying intensities of rainfall, we established three different rainfall intensities for constant rainfall infiltration: , slightly below the saturated permeability coefficient; , slightly above the saturated permeability coefficient; and , significantly higher than the saturated permeability coefficient. By comparing the infiltration results with and without considering internal erosion, we analyzed the impact of internal erosion on slope permeability and stability. Additionally, we compared the Worman and Olafsdottir erosion criterion with the Cividini and Gioda erosion criterion to assess the applicability and accuracy of the Worman and Olafsdottir criterion.
As depicted in Figure 7a, when the rainfall intensity is below the saturation coefficient, there is no significant difference between considering and neglecting internal erosion. However, when the rainfall intensity exceeds the saturated infiltration coefficient, as shown in Figure 7b, the depth of the wetting front is greater when internal erosion is considered after 2 h of rainfall. As infiltration progresses, the difference in the depth of the wetting front between considering and neglecting internal erosion reaches 12.6 cm at the 5th hour and 34.2 cm at the 6th hour. Under the R3 rainfall intensity condition, as illustrated in Figure 7c, the disparity between coupled analysis and uncoupled analysis becomes more pronounced. After 6 h of rainfall, the difference in the depth of the wetting front between considering and neglecting internal erosion reaches 53.8 cm. This indicates that when the rainfall intensity surpasses the saturated permeability coefficient, internal erosion enhances the soil’s permeability, accelerating the flow and infiltration of rainwater within the soil and causing the soil to reach an unstable state more rapidly.
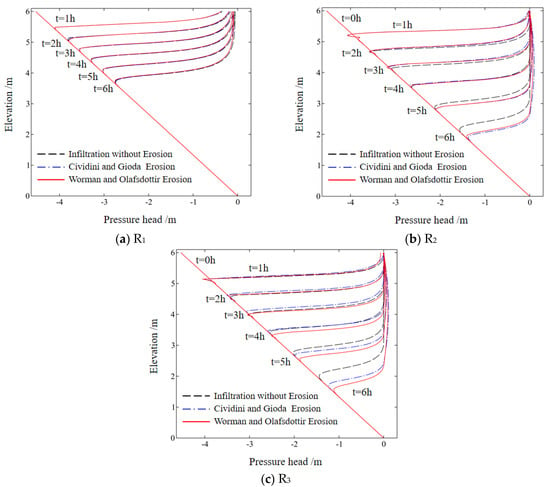
Figure 7.
Changes in pore water pressure profiles along the cross-section X–X′ illustrated in Figure 1.
Furthermore, the results obtained using the Worman and Olafsdottir erosion criterion are similar to those obtained using the Cividini and Gioda erosion criterion. In the R3 scenario after 6 h of rainfall, the depth of the wetting front calculated using the Worman and Olafsdottir erosion criterion is greater than that calculated using the Cividini and Gioda erosion criterion. Conversely, in the R2 scenario, the opposite is observed. This discrepancy arises from the different erosion principles followed by the two criteria. The erosion rate in the Worman and Olafsdottir criterion is a nonlinear function of the hydraulic gradient J, as shown in Equations (13)–(15), while the erosion rate in the Cividini and Gioda criterion is a linear function of the hydraulic gradient J. Consequently, the subsequent variations in the porosity and local density of fine particles also exhibit characteristics of nonlinear and linear distributions, respectively.
Figure 8 demonstrates the variation in the effective bulk density of the soil along the X−X’ cross-section, located at the midpoint of the slope, under three different rainfall scenarios. The effective bulk density is a combination of the dry density of the soil and the density of the pore water. Due to internal erosion, some fine particles flow with the pore water, resulting in a decrease in the local density of fine particles and, consequently, a reduction in the effective bulk density of the soil. Hence, during the process of rainfall infiltration, the effective bulk density initially increases rapidly as rainwater enters the soil pores. However, as a significant amount of pore water infiltrates the soil, it continuously erodes and carries away fine particles, leading to a decrease in the effective bulk density.
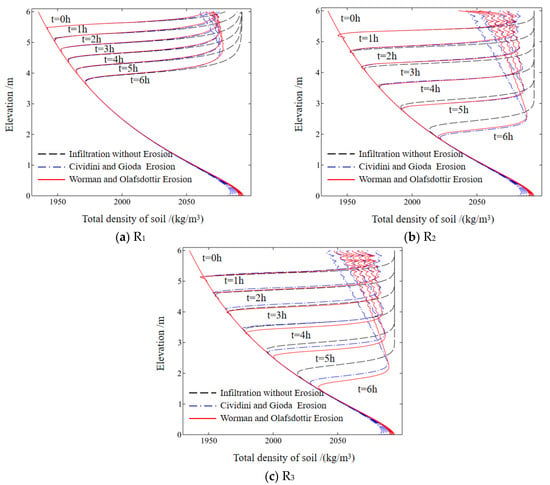
Figure 8.
Temporal variation in effective bulk density along X–X′ cross-section for soil density.
Furthermore, the graph clearly illustrates that internal erosion primarily affects the surface layer of the slope. Changes in surface soil density occur almost simultaneously with the progress of the wetting front. Additionally, fine particles near the groundwater level also experience slight erosion. This is mainly because as the flow velocity approaches saturation, it becomes sufficient to displace the fine particles, aligning with the erosion principles outlined in Equations (12)–(15). Figure 9, Figure 10 and Figure 11 further depict the variations in the porosity and local density of fine particles at different time intervals under the three different rainfall intensities.
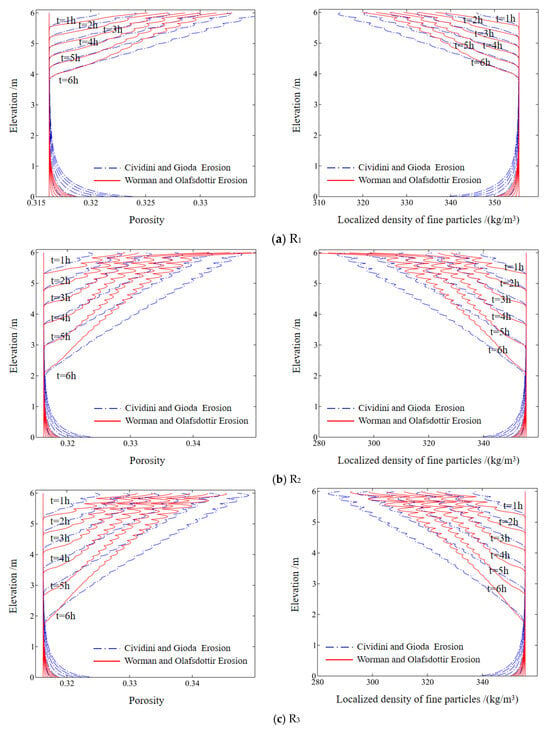
Figure 9.
Temporal variation in the porosity and local density of fine particles along the X–X′ cross-section.
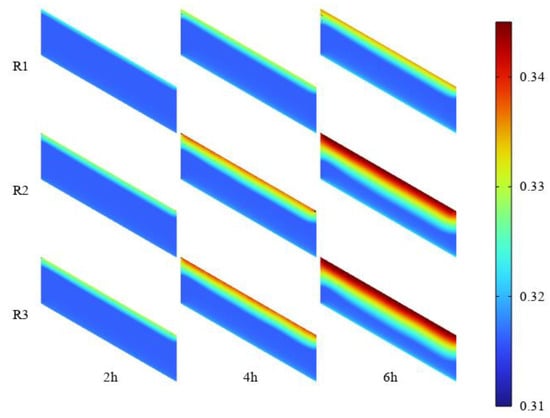
Figure 10.
Porosity changes in rainfall stages under three different rainfall intensities.
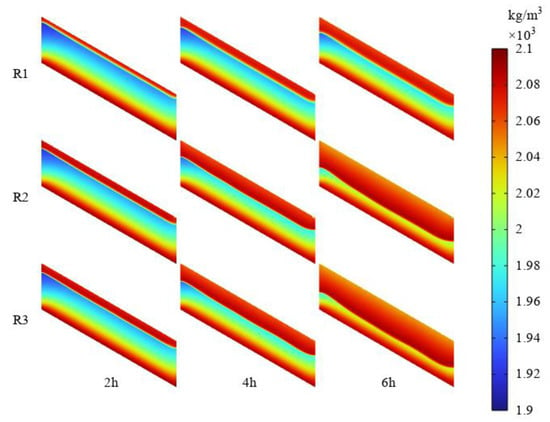
Figure 11.
Variation in effective bulk density during rainfall stages at three different rainfall intensities.
On the left side of Figure 9, we observe the temporal variation in porosity along the X−X’ cross-section at the midpoint of the slope for the three different rainfall scenarios. The right side displays the corresponding temporal variation in the local density of fine particles along the same cross-section. As a result of fine particle erosion, the porosity of the surface layer of the soil progressively increases. After 6 h of rainfall, the porosity of the surface layer reaches 0.335, 0.347, and 0.348 for the three rainfall scenarios, respectively. Conversely, the local density of fine particles in the surface layer continuously decreases. After 6 h of rainfall, the local density of fine particles in the surface layer reaches 341.8 kg/m3, 286.7 kg/m3, and 283.1 kg/m3 for the three scenarios, respectively. The negative correlation between the porosity and local density of fine particles aligns with the erosion concept. Furthermore, the erosion rate in the Worman and Olafsdottir erosion criterion follows a nonlinear function of the hydraulic gradient J, which explains the nonlinear characteristics observed in the variations in the porosity and local density of fine particles.
The hydraulic gradient plays a crucial role in influencing the rate of internal erosion. Figure 12 depicts the curves of the hydraulic gradient during different time intervals under the three rainfall scenarios. In the unsaturated zone, the hydraulic gradients all exceed 0.48, with significantly high gradients near the wetting front surpassing 10. As the soil in the wetting front region becomes saturated, the hydraulic gradient noticeably decreases but remains greater than 1.0.
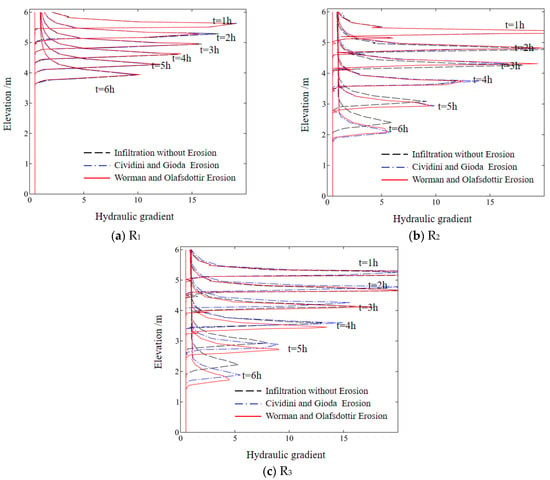
Figure 12.
Hydraulic gradients along cross-section X–X′.
Figure 13 presents a comparative analysis of safety factors with and without considering internal erosion during different time intervals under the three rainfall scenarios. The results demonstrate that when the rainfall intensity is below the saturated permeability coefficient, there is no significant difference in the safety factors between the two cases. However, as depicted in Figure 13b, when the rainfall intensity exceeds the saturated permeability coefficient, the safety factors exhibit variations with increasing rainfall duration. At 6 h, the safety factor without considering internal erosion is 1.12, while the safety factors under the Cividini and Gioda erosion criterion and the Worman and Olafsdottir erosion criterion are 1.08 and 1.09, respectively. In the case of the R3 rainfall scenario, as illustrated in Figure 13c, the impact of internal erosion further amplifies this disparity. After 6 h of rainfall, the safety factor without considering internal erosion is 1.11, while the safety factors under the Cividini and Gioda erosion criterion and the Worman and Olafsdottir erosion criterion are 1.07 and 1.06, respectively. These findings indicate that as rainfall duration increases, intense rainfall infiltration accelerates internal erosion, consequently affecting the slope’s overall stability.
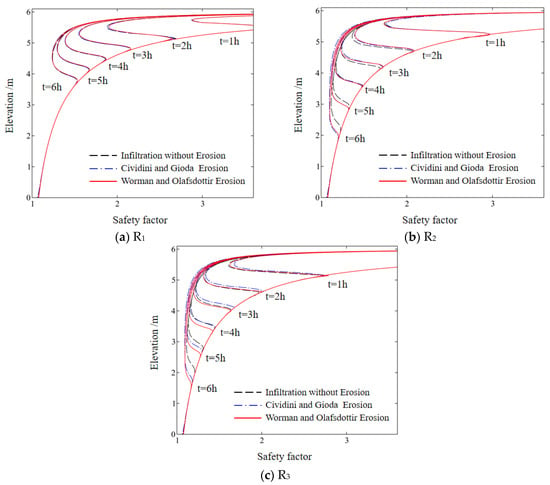
Figure 13.
Safety factor along cross-section X–X′.
5. Conclusions
This study focuses on erosion by fine particle suspension and utilizes the Worman and Olafsdottir erosion criterion, comparing it with the Cividini and Gioda erosion criterion. The objective is to establish a coupled model of unsaturated seepage and internal erosion, simulating the response of seepage and erosion in unsaturated fill slopes under three different rainfall intensities. By employing an infinite slope model, this study quantitatively analyzes the impact of fine particle migration on soil permeability and slope stability. The numerical simulation results yield the following key findings:
- (1)
- The Worman and Olafsdottir erosion criterion demonstrates good applicability and accuracy, requiring only the determination of the soil mass grading curve, in contrast to the Cividini and Gioda erosion criterion.
- (2)
- When the rainfall intensity reaches or exceeds the saturated permeability coefficient, the influence of internal erosion on soil permeability becomes significant. Under rainfall condition R2, the depth difference in the wetting front between considering and not considering internal erosion reaches 34.2 cm after 6 h. Under rainfall condition R3, the depth difference in the wetting front reaches 53.8 cm after 6 h. Conversely, if the rainfall intensity remains below this threshold, the impact of internal erosion on soil permeability can be negligible.
- (3)
- When the rainfall intensity reaches or exceeds the saturated permeability coefficient, the influence of internal erosion on slope stability cannot be ignored. Internal erosion accelerates instability. Under rainfall condition R2, the safety factor without considering internal erosion is 1.12, while the safety factor considering internal erosion ranges from 1.08 to 1.09. Under rainfall condition R3, the safety factor without considering internal erosion is 1.12, while the safety factor considering internal erosion ranges from 1.06 to 1.07. Conversely, if the rainfall intensity remains below this threshold, the impact of internal erosion on slope stability can be negligible.
However, this study has certain limitations. While it provides an effective erosion criterion for slope seepage erosion under rainfall, each erosion criterion has its own limitations. Further research is necessary to assess the applicability of different erosion criteria and investigate the long-term effects of internal erosion in various slope environments. Nevertheless, the results highlight the crucial role of internal erosion in modifying slope stability, particularly when intense rainfall surpasses the soil’s saturated permeability capacity. This understanding contributes to enhanced risk assessment and mitigation strategies for slope-related hazards. Future research can build upon these findings to develop more accurate erosion criteria and explore the application of hybrid models in different geotechnical engineering contexts, thereby advancing slope stability analysis and design methods.
Author Contributions
Methodology, K.H.; Data curation, H.S.; Writing—original draft, Q.C.; Writing—review & editing, X.N. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (Grant No. 51964023) and the Yunnan Provincial Foundation Human Training Program (Grant No. KKSY201521064).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The author, Qunzhi Cheng, was employed by the company Yunnan Yarong Mining Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Lei, X.; Zhang, W.; Chen, X.; Ming, L. Influence of Internal Erosion on Rainfall-Induced Instability of Layered Deposited-Soil Slopes. Mathematics 2023, 11, 4348. [Google Scholar] [CrossRef]
- Zhen, J.; Yang, X.; Wang, B. Study on the destruction of backfilled loess slopes by short-term extreme rainfall erosion. Bull. Eng. Geol. Environ. 2023, 82, 406. [Google Scholar] [CrossRef]
- Li, S.; Russell, A.R.; Muir Wood, D. Internal erosion of a gap-graded soil and influences on the critical state. Acta Geotech. 2024. [Google Scholar] [CrossRef]
- Yang, J.; Yin, Z.Y.; Laouafa, F. Modeling coupled erosion and filtration of fine particles in granular media. Acta Geotech. 2019, 14, 1615–1627. [Google Scholar] [CrossRef]
- Jiang, X.; Zhanyuan, Z.; Chen, H.; Deng, M.; Niu, Z.; Deng, H.; Zuyin, Z. Natural dam failure in slope failure mode triggered by seepage. Geomat. Nat. Hazards Risk 2020, 11, 698–723. [Google Scholar] [CrossRef]
- Li, Z.; Luo, X.; Bi, J. Numerical modelling of internal erosion process in gravel soils based on the percolation analytical method. Environ. Earth Sci. 2020, 79, 358. [Google Scholar] [CrossRef]
- Scheuermann, A.; Mühlhaus, H.B. Infiltration instabilities in granular materials: Theory and experiments. Acta Geotech. 2015, 10, 289. [Google Scholar] [CrossRef]
- Crosta, G.; di Prisco, C. On slope instability induced by seepage erosion. Can. Geotech. J. 1999, 36, 1056–1073. [Google Scholar] [CrossRef]
- Hu, M.; Wang, N.; Meng, Q. Study on the erosion process of loose gravel soil on slope and its characteristics. Geotechnics 2005, 11, 31–35. [Google Scholar]
- Lei, X.-Q.; Yang, Z.-J.; He, S.-M.; Liu, E.-L.; Wong, H.; Li, X.-P. Hydro-mechanical analysis of rainfall-induced fines migration process within unsaturated soils. J. Mt. Sci. 2017, 14, 2603–2619. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, F.; Zhang, H. Influences of internal erosion on infiltration and slope stability. Bull. Eng. Geol. Environ. 2019, 78, 1815–1827. [Google Scholar] [CrossRef]
- Li, M.; Fannin, R.J. Internal erosion: Critical hydraulic gradient in one-dimensional vertical seepage and its relation to soil gradation. Can. Geotech. J. 2022, 59, 769–772. [Google Scholar] [CrossRef]
- Bi, J.; Zhang, H.; Luo, X.; Shen, H.; Li, Z. Modeling of internal erosion using particle size as an extra dimension. Comput. Geotech. 2021, 133, 104021. [Google Scholar] [CrossRef]
- Ma, G.; Bui, H.H.; Lian, Y.; Tran, K.M.; Nguyen, G.D. A five-phase approach, SPH framework and applications for predictions of seepage-induced internal erosion and failure in unsaturated/saturated porous media. Comput. Methods Appl. Mech. Eng. 2022, 401, 115614. [Google Scholar] [CrossRef]
- Jiang, X.; Wörman, A.; Chen, X.; Zhu, Z.; Zou, Z.; Xiao, W.; Li, P.; Liu, G.; Kang, D. Internal erosion of debris-flow deposits triggered by seepage. Eng. Geol. 2023, 314, 107015. [Google Scholar] [CrossRef]
- Kenney, T.C.; Chahal, R.; Chiu, E.; Ofoegbu, G.I.; Omange, G.N.; Ume, C.A. Controlling constriction sizes of granular filters. Can. Geotech. J. 1985, 22, 32–43. [Google Scholar] [CrossRef]
- Wan, C.F.; Fell, R. Assessing the potential of internal instability and suffusion in embankment dams and their foundations. J. Geotech. Geoenviron. Eng. 2008, 134, 401–407. [Google Scholar] [CrossRef]
- Chang, D.S.; Zhang, L.M. Extended internal stability criteria for soils under seepage. Soils Found. 2013, 53, 569–583. [Google Scholar] [CrossRef]
- Vardoulakis, I.; Stavropoulou, M.; Papanastasiou, P. Hydro-mechanical aspects of the sand production problem. Transport. Porous. Med. 1996, 22, 225–244. [Google Scholar] [CrossRef]
- Papamichos, E.; Vardoulakis, I. Sand erosion with a porosity diffusion law. Comput. Geotech. 2005, 32, 47–58. [Google Scholar] [CrossRef]
- Sterpi, D. Effects of the erosion and transport of fine particles due to seepage flow. Int. J. Geomech. 2003, 3, 111–122. [Google Scholar] [CrossRef]
- Cividini, A.; Gioda, G. Finite-element approach to the erosion and transport of fine particles in granular soils. Int. J. Geomech. 2004, 4, 191–198. [Google Scholar] [CrossRef]
- Wörman, A.; Olafsdottir, R. Erosion in a granular medium interface. J. Hydraul. Res. 2010, 30, 639–655. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J. A comparative study between infinite slope model and Bishop’s method for the shallow slope stability evaluation. Eur. J. Environ. Civ. Eng. 2021, 25, 1503–1520. [Google Scholar] [CrossRef]
- Nitzsche, K.; Herle, I. Strain-dependent slope stability. Acta Geotech. 2020, 15, 3111–3119. [Google Scholar] [CrossRef]
- Park, D. Implications of infinite rock slope analysis: Tension cut-off and graphical interpretation. Comput. Geotech. 2024, 172, 106410. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, B.; He, J.; Xu, C.; Zeng, T.; Zhu, Y. Hazard assessment for regional typhoon-triggered landslides by using physically-based model—A case study from southeastern China. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2023, 17, 740–754. [Google Scholar] [CrossRef]
- Nie, X.; Chen, K.; Zou, D.; Kong, X.; Liu, J.; Qu, Y. Slope stability analysis based on SBFEM and multistage polytree-based refinement algorithms. Comput. Geotech. 2022, 149, 104861. [Google Scholar] [CrossRef]
- Li, M.; Li, K.; Qin, Q.; Yue, R. Slope stability prediction based on IPOARF algorithm: A case study of Lala Copper Mine, Sichuan, China. Expert. Syst. Appl. 2023, 229, 120595. [Google Scholar] [CrossRef]
- Nian, G.Q.; Chen, Z.H.; Zhang, L.F.; Bao, M.; Zhou, Z.H. Treatment of two boundary conditions for rainfall infiltration in slope and its application. Rock. Soil. Mech. 2020, 41, 4105–4115. [Google Scholar]
- Chui, M.F.T.; Freyberg, L.D. Implementing Hydrologic Boundary Conditions in a Multiphysics Model. J. Hydrol. Eng. 2009, 14, 1374–1377. [Google Scholar] [CrossRef]
- Wang, X.; Dong, M.; Kong, M. Improvement of rainfall boundary treatment based on diffusion wave approximation equation. Geotechnics 2023, 44, 1761–1770. [Google Scholar]
- Zhu, Y.; Ishikawa, T.; Subramanian, S.S.; Luo, B. Simultaneous analysis of slope instabilities on a small catchment-scale using coupled surface and subsurface flows. Eng. Geol. 2020, 275, 105750. [Google Scholar] [CrossRef]
- Weill, S.; Mouche, E.; Patin, J. A generalized Richards equation for surface/subsurface flow modelling. J. Hydrol. 2008, 366, 9–20. [Google Scholar] [CrossRef]
- Tian, D.; Liu, D. A new integrated surface and subsurface flows model and its verification. Appl. Math. Model. 2011, 35, 3574–3586. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil. Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Wan, R.G.; Wang, J.; Liu, Y.N. Prediction of volumetric sand production using a coupled geomechanics-hydrodynamic erosion model. J. Canad Pet. Technol. 2006, 45, 34–40. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).