Abstract
Reference crop evapotranspiration (ET0) is a key factor in ecohydrological processes. Studying the variation trend of ET0 in arid river valleys and its influencing factors is not only helpful to understanding the response of dry and hot river valleys to hydrological processes under the background of climate change but also has important guiding significance for the efficient allocation of soil and water resources and the stable maintenance of the ecosystem in this area. Based on the daily meteorological data of three representative meteorological stations in the middle Dry-hot Valley of the Jinsha River from 1988 to 2019, the ET0 variation and its influencing factors in the middle Dry-hot Valley of the Jinsha River are analyzed by quantitative and qualitative methods. The results showed that (1) the ET0 in the middle and middle of the Dry-hot Valley of Jinsha River showed a significant fluctuating trend (Z > 1.98), and the linear change rates were examined in Huaping, Yuanmou, and Panzhihua. (2) Grey correlation analysis and principal component analysis mutually verify that daily mean temperature is the most influential meteorological factor. (3) The sensitivity of ET0 to the change in meteorological factors in the middle section and its sub-sections is as follows: daily average temperature, daily relative humidity, daily average wind speed, and sunshine hours. ET0 is the most sensitive to the change in daily average temperature, followed by the strengthening of daily average wind speed and the reduction in daily relative humidity, and the sensitivity of ET0 to the change in sunshine hours is the least. (4) Among the regions, the meteorological factors that contributed the most to the increase in ET0 in Huaping, Panzhihua, and Yuanmou were daily average wind speed (6.086%), daily average wind speed (8.468%) and daily average temperature (3.869%), respectively. The meteorological factors that contributed the least were sunshine hours.
1. Introduction
Evapotranspiration (ET) is an essential component of the water cycle and a key process in plant physiology [1]. It represents the total water vapor flux from vegetation and the Earth’s surface to the atmosphere, primarily consisting of transpiration (T), soil evaporation (Es), and canopy interception (Ec), reflecting the movement of water among soil, vegetation, and the atmosphere [2]. Extensive research indicates that transpiration plays a critical role in the global water cycle and water resource management. Approximately two-thirds of the water evaporated into the atmosphere annually is attributed to transpiration, with this proportion potentially higher in arid regions. Furthermore, studies have shown a close relationship between extreme hydrological events such as droughts and floods and ET [3].
At present, there are various methods for calculating ET, and many scholars at home and abroad have also made certain discussions on the applicability of different estimation methods in the study area [4,5,6,7]. Based on the Food and Agriculture Organization of the United Nations (FAO)’s Penman–Monteith model [8], the mainstream model was developed, which comprehensively considers the changes in crop physiological characteristics and meteorological factors and therefore has high calculation accuracy and a wide application range. The reference crop evapotranspiration (ET0) in this model is regarded as the theoretical upper limit of actual vegetation transpiration. It plays a key role in monitoring the change in meteorological factors and the dry and wet state of climate [9]. Therefore, an in-depth understanding of ET0 trends and their potential causes is essential to effectively manage regional water resources, develop agricultural irrigation systems, and accurately predict climate change.
According to the latest report of the Intergovernmental Panel on Climate Change (IPCC) of the United Nations [10], the global average temperature has risen by 1.1 °C compared with that before the industrial revolution, which confirms that the global climate is experiencing a warming trend, and this global warming trend has an important impact on ET0 and its related meteorological elements [11]. As a key indicator for estimating vegetation transpiration and agricultural water management, the change trend of ET0 reflects the change in crop water demand under future climate change. Therefore, it is of great significance to study the change trend of ET0 and its influencing factors, which can provide a scientific basis for water resources management and coping with climate change.
In recent years, the analysis of the relationship between the change trend of ET0 and meteorological factors has become a hot topic for many researchers at home and abroad, and some achievements have been made. For example, Matteo Ippolito et al. [12] used sensitivity analysis to identify the influencing factors of ET0 changes in Sichibi Island, Italy, and determined that the main influencing factors were daily minimum temperature and daily maximum temperature. Ippolito et al. [13] adopted the fuzzy cluster analysis method and found that the main factor affecting the change in ET0 in the Fars province of Iran was temperature. Lv Xiaorong et al. [14] used the principal component analysis method to find that the main factor affecting the change in ET0 in Hubei Province was the annual mean temperature. By using the correlation analysis method, Yan et al. [15] found that daily relative humidity, daily average wind speed, sunshine duration, and daily average temperature were the dominant factors affecting the change in ET0 in Guangxi Province. Although a variety of methods have been applied to relevant studies, these research methods are often limited to specific analytical means. Considering the numerous and interwoven factors affecting ET0 and the complex interactions among meteorological factors, the application of a single method may be difficult to fully reveal the influence mechanism. Therefore, the comprehensive application of multiple analysis methods to quantitatively study the impact of meteorological factors on ET0 and explore the sensitivity of ET0 to changes in different meteorological factors are crucial for understanding the response of the hydrological cycle to climate change [16]. More importantly, the current research on the trend of ET0 change and its influencing factors in specific regions is still relatively limited, especially in the fragile ecosystem areas, such as the Dry-hot Valley of the Jinsha River; the relevant research is still in the stage of few, so in-depth research on this region will help to understand the mechanism of ET0 change more comprehensively. And provide a scientific basis for taking effective countermeasures in the future.
2. Materials and Methods
2.1. Study Area
The middle section of the Jinsha River’s Dry-hot Valley is located in the upper reaches of the Yangtze River. It features a hot climate, distinct dry and wet seasons, uneven precipitation distribution, and intense evaporation, making it one of the typical ecologically fragile areas in China [17]. The regions of Panzhihua, Yuanmou, and Huaping in this area are significant production areas for off-season fruits and vegetables in China (Figure 1). However, the scarcity of water resources has consistently been a critical limiting factor for its agricultural development. In order to address this issue, it is crucial to reveal the trends in ET0 in the middle section of the Jinsha River’s Dry-hot Valley, unravel the complex relationship between ET0 and meteorological factors, and understand the response mechanism of ET0 under changing meteorological conditions. The aim is to provide a scientific theoretical basis for the rational allocation of irrigation water and the enhancement of water resource utilization in the middle section of the Jinsha River’s Dry-hot Valley.
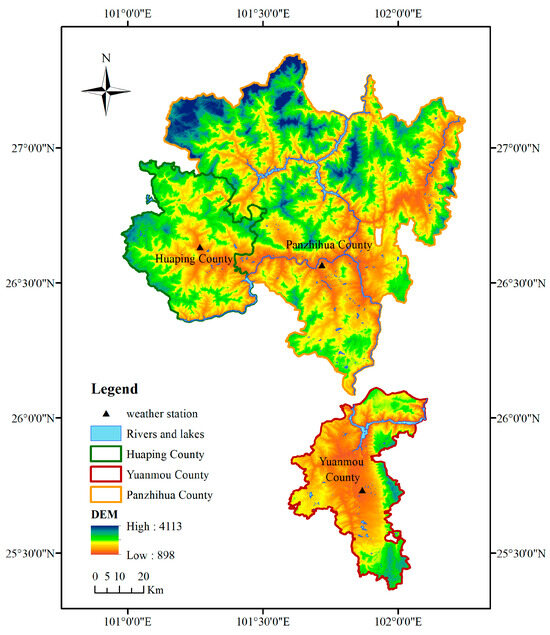
Figure 1.
Summary map of the study area.
2.2. Data
The data used in this study were obtained from the China Meteorological Data Network (https://data.cma.cn/, accessed on 15 January 2024), covering three meteorological stations in Panzhihua, Yuanmou, and Huaping during the period of 1988–2019 for day-by-day meteorological element data. The selected meteorological elements include daily relative humidity (RH), sunshine hours (n), daily average temperature (Tmean), daily maximum temperature (Tmax), daily minimum temperature (Tmin), average wind speed (u), etc.
2.3. Methods
2.3.1. Potential Evapotranspiration Calculation
When calculating ET0, many factors need to be considered, including surface type, temperature, and humidity. Due to the complex influence of these factors, the calculation results of ET0 may fluctuate, and the Penman–Monteith formula has practical characteristics which are suitable for climate types in different regions, is simple to operate, and can provide relatively accurate calculation results [8]. Its expression is
where ET0 is the reference crop evaporation amount (mm); Rn is the net radiation [MJ/(m2·d)]; G is the soil heat flux [MJ/(m2·d)]; γ is the hygroscopic constant; T is the average daily temperature (°C); U2 is 2 m wind speed (m/s); es and ea are saturated vapor pressure and actual vapor pressure (kPa), respectively. Δ is the slope of the saturation water vapor pressure curve (kPa/°C). In addition to the meteorological data collected above, other input variables required by Penman–Monteith formula are obtained by deducing and calculating basic meteorological data. For specific methods, please refer to the relevant literature [2].
2.3.2. Climate Propensity Rate and ET0 Propensity Rate
Generally, it is represented by the tilt rate of a linear equation [18]. The calculation formula is
where x is the factor value; a is a constant term; b is the regression coefficient; i is the year of the time series. The climatic factors and tendency rate are 10b.
2.3.3. Principal Component Analysis
Principal component analysis is a statistical analysis method that converts multiple variables into a few uncorrelated comprehensive variables by dimensionality reduction. Its mathematical model is as follows: for k observed variables X1… Xk, a data matrix of n observed samples [19].
Synthesize k predictors into p new variables (synthetic variables):
The model satisfies the following: (1) Fi and Fj are not correlated (i ≠ j, i, j = 1, 2, …, p); (2) Variance of F1 > variance of F2 > variance of F3, and so on; (3) In the model F1 is called the first principal component, F2 is the second principal component, and so on.
2.3.4. Grey Relational Degree Analysis
Gray relational analysis is a new theory and method put forward by Deng [20]; its core is to measure the degree of correlation between factors by comparing the development trend of factor curves. Different from traditional methods, it does not require a large sample size and does not rely on typical distribution laws. Grey relational degree analysis transforms the development trend curve of factors into a grey series, calculates the relational degree, and reveals the main influencing factors and their influencing degree in the development of the system. Grey correlation degree is defined as follows: Let the system main behavior sequence X0 = (x0(1), x0(2),…, x0(n)), related behavior sequence X0 = (x0(1), x0(2),…, x0(n)) and then for ε ∈ (0, 1).
γ(X0, Xi) is called the grey correlation degree of X0 and Xi, where ε is called the resolution coefficient; its role is to improve the significance of the difference between the grey correlation coefficients, ε ∈ (0, 1); the experience value is generally ε = 0.5.
2.3.5. Path Analysis
Path analysis is a multivariate statistical analysis method. The independent variable xi(I = 1, 2, …, n) The simple correlation coefficient with the dependent variable y is divided into the direct effect of xi on y (direct path coefficient) and xi. Through the indirect effect of other independent variables on y (indirect path coefficient), the relative importance of each factor is directly compared, which makes the analysis results more consistent with the actual situation [21].
The dependent variable y receives multiple factors (x1, x2, …, xn), and then the multiple regression equation can be applied:
According to the principle of path analysis, the equation of using a correlation coefficient to solve the path coefficient is as follows:
where rij is the correlation coefficient between xi and xj; riy is the simple correlation coefficient between xi and y; bi is a direct path coefficient, which reflects the direct effect of independent variable xi on dependent variable y. rijbj is the indirect path coefficient, which reflects the indirect effect of independent variable xi on dependent variable y through xj.
2.3.6. Sensitivity Analysis
This study uses the sensitivity coefficient defined by McCuen [22] to determine the sensitivity of potential evapotranspiration changes to meteorological elements:
where ET0 is potential evapotranspiration (mm/d); Sx is the sensitivity coefficient of potential evapotranspiration with respect to meteorological factor x, dimensionless quantity.
2.3.7. Contribution Rate Analysis
By multiplying the sensitivity coefficient of the meteorological factor with the relative change rate of the meteorological factor for many years, the change in ET0 caused by the meteorological factor is obtained, that is, the contribution of the factor to the change in ET0. If the contribution rate is positive (negative), it indicates that the factor causes the increase (decrease) of ET0, and if the absolute contribution rate is large (small), it indicates that the meteorological factor has a large (small) influence on ET0. The contribution rate is calculated as follows [23,24,25,26]:
3. Results
3.1. Analysis of PET Changes
Table 1 and Figure 2 are the results of the annual ET0 dynamic process in the middle and subsections of the Jinsha River Dry-hot Valley. There are significant differences in the annual average ET0 value, stability, propensity rate, and correlation, showing obvious geographical differences and trends. In the past 32 years, ET0 in the middle of the dry and hot valley of Jinsha River and in the subregions of Panzhihua, Yuanmou, and Huaping showed a significant upward trend (Z > 1.98), with an increase rate of 38.336, 47.696 mm, 16.257 mm and 51.055 mm per 10 years, respectively. The growth rate was shown as Huaping > Yuanmou > Panzhihua. The annual average ET0 in the Panzhihua area is about 1462.731 mm, which is relatively slightly lower than that in the middle part of the Jinsha River Dry-hot Valley (1495.522 mm) and Huaping (1415.706 mm) but significantly lower than that in Yuanmou area (1608.128 mm). In the middle part of the Jinsha River Dry-hot Valley, the maximum value of annual ET0 reached 1681.433 mm, and the minimum value was 1337.500 mm, with the maximum value occurring in 2012 and the minimum value in 1990. On the other hand, in the Panzhihua area, the annual ET0 is as follows: the maximum value is 1604.900 mm, the minimum value is 1279.200 mm, the maximum value occurs in 2019, while the minimum value occurs in 2002, and the standard deviation is 85.135 mm. For the Yuanmou area, the data of the annual ET0 show that the maximum value is 1905.300 mm, the minimum value is 1397.700 mm, with the maximum value occurring in 2012 and the minimum value in 2008, and presenting a significance level of 0.135 ** in terms of correlation. Finally, in the Huaping area, the annual ET0 was 1594.000 mm as the maximum value and 1268.200 mm as the minimum value, with the maximum value occurring in 2004 and the minimum value occurring in 1990. The discrete coefficient of Yuanmou is 7.030%, with the worst stability, followed by Huaping and Panzhihua, with increased stability of fluctuation changes. Overall, the data indicate that the annual ET0 values in the middle part of the Jinsha River Dry-hot Valley and its different subsections generally show an upward trend; however, the magnitude of the change, the significance of the change trend, and the level of correlation among the regions are somewhat different.

Table 1.
Interannual trends of ET0 in the middle part of the Jinsha River Dry-hot Valley and its subsections.
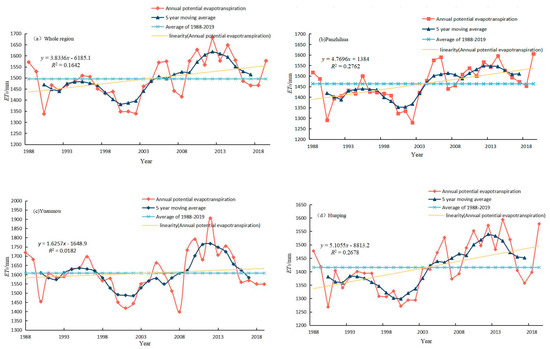
Figure 2.
Process of interannual variation in ET0 in the middle region of the Jinsha River Dry-hot Valley and its segments, 1988–2019.
3.2. Principal Component Analysis of Meteorological Factors
ET0 size is affected by complex factors, and various meteorological factors are interrelated and affect each other. The six meteorological factors Tmean, Tmax, Tmin, RH, n, and u affecting the change in ET0 were subjected to principal component analysis, and the results were as follows. Table 2 shows KMO > 0.6, indicating that there is a correlation between the variables, in line with the requirements of principal component analysis, and through Bartlett’s test, p < 0.05 is significant and can be carried out the principal component analysis. The first three principal components were extracted, and their cumulative variance explained accounted for 94.97%, of which the first principal component accounted for 70.09% (expression: F1 = 0.156u − 0.208RH + 0.158n + 0.229Tmean + 0.203Tmin + 0.227Tmax), and the variables with larger absolute values of loadings were Tmean, Tmin, and Tmax, mainly reflecting the effect of temperature. The second principal component accounts for 14.53% (expression: F2 = −0.78u + 0.246RH + 0.651n + 0.113Tmean + 0.002Tmin + 0.197Tmax), mainly reflecting the effect of wind speed, the component loadings of the largest meteorological factors is u. The third principal component accounts for 10.36% (expression: F3 = −0.358u + 0.477RH − 0.714n + 0.353Tmean + 0.776Tmin + 0.127Tmax), mainly reflecting the influence of radiation, and the largest meteorological factor of component loadings is n. Overall, the principal component analysis reveals the relationship between ET0 and meteorological factors more deeply, and the change in ET0 is mainly affected by temperature and less affected by humidity.

Table 2.
Results of principal component loading of meteorological factors.
3.3. Cluster Analysis and Gray Correlation Analysis of Meteorological Factor Systems
Systematic cluster analysis is the process of combining the most similar objects based on the degree of closeness between observations or variables, categorizing observations in an aggregation-by-aggregation fashion until finally, all samples are clustered into one class [27]. As Table 3 shown, the cluster analysis divides the six meteorological elements into four classes, and Tmen, Tmax, and Tmin are categorized as Type I according to the role of temperature on the change in ET0; n and u are Type II and Type III, respectively, reflecting the influence of radiation and wind speed; and RH is Type IV, reflecting the influence of humidity on the change in ET0. The gray correlation method takes ET0 as the reference series, and the six meteorological indicators as the comparison series, and the correlation degree is calculated and ranked; the higher the ranking, the greater the influence of meteorological indicators on ET0, and vice versa, the lesser the influence on ET0. The correlation degree of ET0 and meteorological indicators is ranked as follows: Tmean > Tmax > Tmin > n > u > RH, the influence of Tmean on ET0 is the greatest, with 0.809, and the influence of RH on ET0 is the least, with 0.643. Tmean, Tmax, Tmin, and n are thermal factors, u is the dynamic factor, and RH is the humidity factor. The gray correlation results verified that the first principal component loadings of the largest meteorological factors, Tmean, Tmin, and Tmax, were closely related to ET0. Considering the results of cluster analysis and gray correlation degree analysis, in order to simplify the problem and eliminate the repeated correlation factors, a total of four meteorological factors, Tmean, RH, n, and u, were selected as the key factors to carry out the subsequent pathway analysis [16].

Table 3.
Results of grey correlation degree analysis and clustering analysis of meteorological factors.
3.4. Flux Analysis of ET0 by Meteorological Factors
According to the results of the systematic cluster analysis and gray correlation analysis of meteorological factors, four meteorological factors, RH, u, Tmean, n, were identified for the pathway analysis, and the results were as follows. The results are shown in Table 4. Changes in ET0 were correlated with all four meteorological factors in the table (p < 0.01), but there were differences in the direct and indirect effects of each meteorological factor on ET0. The pathway coefficients reflect the magnitude of the direct effect of meteorological factors on the changes in ET0, and the order is as follows: Tmean > u > RH > n, except for the negative value of RH, all other values are positive, which indicates that RH is inversely related to the changes in ET0 and that u, Tmean, and n are in a positive direction to ET0, i.e., with the decrease in RH, the trend of ET0 is to increase, and with the increase in u, Tmean, and n, the trend of ET0 is to increase. The factor that has the largest direct effect on ET0 is RH, and the smallest effect is n. The indirect pathway coefficient reflects the indirect effect of other meteorological factors on ET0 changes through a certain meteorological factor, and the ranking is RH > u > Tmean > n, with RH as the main factor indirectly affecting ET0 changes and n as the least indirectly affecting factor. The correlation coefficients represent the combined effects, and the ranking is Tmean > u > RH > n. Tmean has the greatest effect on ET0 changes, n has the least effect, and the increase in Tmean, u, n, and the decrease in RH contribute to the increase in ET0 changes.

Table 4.
Flux analysis of meteorological factors on ET0.
3.5. Analysis of the Contribution of Meteorological Factors to Changes in ET0 and Sensitivity of ET0 to Changes in Meteorological Factors
As Table 5 shows, the sensitivity of ET0 to changes in meteorological factors in the middle part of the Jinsha River Dry-hot Valley and its subsections is ranked as Tmean, RH, u, n; and the contribution rate of meteorological variables to ET0 is ranked as u, RH, Tmean, n. The influence of meteorological variables with a high degree of sensitivity on ET0 is different from the order of their contribution rate to ET0. When the changes in these meteorological variables with a high degree of sensitivity are not significant for many years, it may lead to their lower contribution rate to ET0. When these highly sensitive meteorological variables do not change significantly over the years, it may lead to their lower contribution to ET0. In the middle part of the Jinsha River Dry-hot Valley, Tmean increases by 5.820% over the years, and the increase in temperature causes an increase in ET0, with a positive contribution rate of 2.981%; ET0has a low sensitivity to n, and the increase in n by 4.872% over the years causes an increase in ET0, with a positive contribution rate of 0.488%; RH changes inversely with ET0 because the relative rate of change in RH over the years is −9.999%, and the decrease in RH causes an increase in ET0, with a positive contribution rate of 4.12%; and the decrease in RH causes an increase in ET0, with a positive contribution rate of 4.12%, with a positive contribution of 4.126%; although ET0 is relatively insensitive to changes in u, the multi-year changes in u are significant, with a multi-year relative rate of change of 21.475% causing an increase in ET0 with a positive contribution of 5.519%, and an increase in u is the main factor causing an increase in ET0 in the middle Jinsha River Dry-hot Valley region.

Table 5.
Contributions of meteorological variables to ET0 in the middle and subsections of the Jinsha River Dry-hot Valley.
In each segment, the meteorological factors with the largest contribution to the increase in ET0 in Huaping, Panzhihua, and Yuanmou were u (6.086%), u (8.468%), and Tmean (3.869%), respectively. The meteorological factor with the smallest contribution rate is n. The ordering of the contribution rate of meteorological factors in Huaping is u, RH, Tmean, n; the ordering of the contribution rate of meteorological factors in Panzhihua is u, RH, Tmean, n; the ordering of the contribution rate of meteorological factors in Yuanmou is Tmean, RH, u, n; the ordering of the sensitivity of ET0 to the changes in meteorological factors in each segment is consistent with the ordering of the sensitivity of the changes in meteorological factors is Tmean, RH, u, and n. Due to the difference in changes in the various meteorological factors over the years, the caused inconsistency in the contribution and ranking of ET0 changes.
4. Discussion
The Jinshajiang River Dry-hot Valley has a very harsh climate due to its special geographic location and unique topography and geomorphology, which makes it one of the most fragile ecological environments in China. The ET0 in the middle and subsections of the Jinshajiang River Dry-hot Valley showed a significant fluctuating upward trend from 1988–2019 (p < 0.05), which was consistent with the results of Liu Qinsuan et al. [28] This is consistent with the results of the ET0 study on the Yunnan–Guizhou Plateau, but it should be noted that there are also other studies showing a decreasing trend in ET0 [29,30,31,32]. However, it should be noted that other studies have also shown a downward trend in ET0, indicating that ET0 changes in different regions are different; that is, ET0 changes are geographically specific. The linear change rate of ET0 in the whole region is 38.336 mm every 10 years, and the change rate of Huaping is the most obvious, which is 51.055 mm every 10 years. The correlation between meteorological factors and ET0 was calculated as Tmean, Tmax, Tmin, n, u, RH, which indicated that ET0 was strongly correlated with Tmean, Tmax, and Tmin and was verified with the results of principal component analysis, which was consistent with the conclusion of Ma Yali et al. [10] The study of Hexi Corridor concluded that ET0 had the highest degree of association with temperature. The pathway analysis showed that n, Tmean, u played a positive role in ET0 changes, and RH played an inverse role in ET0 changes, and the increase in n, Tmean, u and the decrease in RH contributed to the increase in ET0 changes, which was consistent with the results of the study on ET0 in the hilly areas of Sichuan and Central China by Feng Yu et al. [26] The conclusion that the flux coefficients of ET0 and RH in the hilly area of central Sichuan are negative, and those of n, Tmean, and u are positive is consistent with the conclusion of Feng Yu et al. The sensitivities of the middle Jinshajiang River Dry-hot Valley and its subsections were ranked as Tmean, RH, u, and n. ET0 was most sensitive to the increase in Tmean, followed by the decrease in RH and the increase in u to increase ET0, and ET0 was the least sensitive to the change in n, which was consistent with the findings of Ni Ningqi et al. [33]. This is consistent with the conclusion that ET0 is the most sensitive to Tmean changes, followed by RH, in the southwestern part of the Yunnan-Guizhou Plateau over the past 56 years. Among the subsections, the meteorological factors with the largest contribution to ET0 increase in Huaping, Panzhihua, and Yuanmou were u (6.086%), u (8.46%), and Tmean (3.869%), and the meteorological factor with the smallest contribution was n. The results of the study are consistent with the findings of Wang Xiao-Jing et al. [34] study, which found that wind speed and temperature had the largest contribution in the ET0 changes over the past 50 years. The contribution rate and the magnitude of multi-year relative change together determine the difference between the sensitivity factors and the main influencing factors. Although ET0 is the most sensitive to the change in Tmean, the multi-year change in Tmean is not significant, which leads to the inconsistency between the contribution rate and the ordering of sensitivity coefficients.
The aim of this study was to investigate the influence of climatic factors on ET0 change in the middle part of the Jinsha River Dry-hot Valley region, focusing on the interrelationships between four meteorological factors such as Tmean, RH, u, and n, and ET0 change; however, in addition to the meteorological factors, a variety of elements such as the subsurface, moisture conditions, land-use practices, and human activities also have a significant impact on the change in ET0 [35]. However, to fully understand the mechanism of ET0 change, it is necessary to explore the effects of various aspects, such as climate change, in greater depth. In this study, principal component analysis (PCA), cluster analysis (CA), and through-trail analysis (TTA) were used to explore the causes of ET0 changes qualitatively, while sensitivity analysis (SA) and contribution rate calculation (CR) were used to quantitatively assess the sensitivity of ET0 to climatic variables and the contribution of ET0 to climatic variables, and at the same time, the changes in ET0 under the coupling of quantitative and qualitative effects were taken into account, which provided a new basis for revealing the response mechanism of ET0 changes to meteorological variables. This provides a new basis for revealing the response mechanism of ET0 changes to meteorological variables [26]. The study is also based on the study of ET0 changes under quantitative and qualitative coupling effects. Given global warming, this study helps to scientifically predict the trend of ET0 change in the middle part of the Jinsha River Dry-hot Valley and provides a scientific basis for the formulation of a rational irrigation water use plan and the improvement in the utilization efficiency of agricultural water resources.
5. Conclusions
(1) The annual ET0 in the middle part of the Jinsha River Dry-hot Valley and its subsections all showed a significant increase (Z > 1.98), with the increase shown as Huaping > Yuanmou > Panzhihua. The annual average ET0 of Panzhihua was about 1462.731 mm, which was slightly lower than that of the middle section of the Jinsha River Dry-hot Valley (1495.522 mm) and Huaping (1415.706 mm) but significantly lower than that of Yuanmou (1608.128 mm). The annual maximum and minimum ET0 values in each region occurred in different years, showing obvious fluctuations. Meanwhile, the Yuanmou area showed a high dispersion coefficient (7.030%) and the worst stability, followed by Huaping and Panzhihua.
(2) The results of the principal component analysis show that the first principal component is temperature, the second principal component is wind speed, and the third principal component is radiation, and the changes in ET0 are mainly affected by temperature and less by humidity. Cluster analysis divided the six meteorological factors into four categories, and the gray correlation values were calculated as follows in descending order: Tmean > Tmax > Tmin > n > u > RH. Gray correlation and principal component analysis verified each other to verify the meteorological factors with the largest loadings of the first principal component.
(3) The sensitivity of ET0 to changes in meteorological factors in the middle part of the Jinsha River Dry-hot Valley and its subsections is ranked as Tmean, RH, u, n. ET0 is most sensitive to the increase in Tmean, followed by the decrease in RH and the increase in u. ET0 is prompted to increase in size, and ET0 is the least sensitive to the change in n. The increase in ET0 in the middle part of the Jinsha River Dry-hot Valley is the most sensitive to the increase in RH and u. In each segment, the meteorological factors with the largest contribution of ET0 increase in Huaping, Panzhihua, and Yuanmou were u (6.086%), u (8.468%), and Tmean (3.869%), respectively. The meteorological factor with the smallest contribution was n.
Author Contributions
Conceptualization, formal analysis, methodology, software, validation, visualization, writing—original draft and writing—review & editing, Z.L. and Y.S.; investigation, Z.H., L.P., D.Q. and G.T.; funding acquisition, project administration, resources and supervision, Z.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was founded by the Natural Ecological Network Project of Yunnan Province (2023-YN-07) and the Science and Technology Innovation Platform Project of China National Forestry and Grassland Administration (2022132108).
Data Availability Statement
The daily series of meteorological data used in this study are available from the National Meteorological Science Centre of China (http://data.cma.cn/ (accessed on 28 April 2023)).
Acknowledgments
The authors acknowledge contributions from all members of the project team.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhou, H.; Tang, J.; Olin, S.; Miller, P. A comprehensive evaluation of hydrological processes in a second-generation dynamic vegetation model. Hydrol. Process. 2024, 38, e15152. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.; Wang, X.; Lu, R.; Liu, L. A review of water movement process in SPAC in the semi-arid and arid regions based on stable isotopes. Sheng T’ai Hsueh Pao Acta Ecol. Sin. 2024, 44, 1360–1373. [Google Scholar]
- Liu, W.; Zhang, B.; Wei, Z. Heterogeneity analysis of main driving factors affecting potential evapotranspiration changes across different climate regions. Sci. Total Environ. 2024, 912, 168991. [Google Scholar] [CrossRef]
- Proutsos, N.D.; Tsiros, I.X.; Nastos, P.; Alexandros, T. A note on some uncertainties associated with Thornthwaite’s aridity index introduced by using different potential evapotranspiration methods. Atmos. Res. 2021, 260, 105727. [Google Scholar] [CrossRef]
- Dong, J.; Xing, L.; Cui, N.; Zhao, L.; Guo, L.; Wang, Z.; Du, T.; Tan, M.; Gong, D. Estimating reference crop evapotranspiration using improved convolutional bidirectional long short-term memory network by multi-head attention mechanism in the four climatic zones of China. Agric. Water Manag. 2024, 292, 108665. [Google Scholar] [CrossRef]
- Tegos, A.; Stefanidis, S.; Cody, J.; Koutsoyiannis, D. On the Sensitivity of Standardized-Precipitation-Evapotranspiration and Aridity Indexes Using Alternative Potential Evapotranspiration Models. Hydrology 2023, 10, 64. [Google Scholar] [CrossRef]
- Bidabadi, M.; Babazadeh, H.; Shiri, J.; Saremi, A. Estimation reference crop evapotranspiration (ET0) using artificial intelligence model in an arid climate with external data. Appl. Water Sci. 2024, 14, 3. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D5109. [Google Scholar]
- Lagos, L.O.; Souto, C.; Lillo-Saavedra, M.; Pérez, A.; Hirzel, J.; Kuschel-Otárola, M.; Holzapfel, E.; Scaff, L. Daily crop evapotranspiration and diurnal dynamics of the surface energy balance of a drip-irrigated blueberry (Vaccinium corymbosum) orchard. Irrig. Sci. 2024, 42, 1–13. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2022: The Physical Science Basis, Contribution of Working. 2022. Available online: https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_FrontMatter.pdf (accessed on 30 March 2024).
- Yao, N.; Jiang, K.; Xie, W.; Zhang, D.; Yang, X.; Yu, Q. Temporal and Spatial Evolution of Drought Disasters in ShanXi Province under Background of Climate Change. Trans. Chin. Soc. Agric. Mach. 2023, 55, 270–281. [Google Scholar]
- Ippolito, M.; Caro, D.; Cannarozzo, M.; Provenzano, G.; Ciraolo, G. Evaluation of daily crop reference evapotranspiration and sensitivity analysis of FAO Penman-Monteith equation using ERA5-Land reanalysis database in Sicily, Italy. Agric. Water Manag. 2024, 295, 108732. [Google Scholar] [CrossRef]
- Abedi-Koupai, J.; Dorafshan, M.; Javadi, A.; Ostad-Ali-Askari, K. Estimating potential reference evapotranspiration using time series models (case study: Synoptic station of Tabriz in northwestern Iran). Appl. Water Sci. 2022, 12, 212. [Google Scholar] [CrossRef]
- Lv, X.; Wang, X. Analysis on spatial-temporal variation of potential evapotranspiration and its influencincfactors in Hubei Province. J. Cent. China Norm. Univ. (Nat. Sci.) 2016, 50, 764–769. [Google Scholar]
- Yan, Y.; Huang, K.; Hu, B.; Wang, S.; Huang, Y. Spatial and temporal variations of reference evapotranspiration and its influencing factors inGuangxi Xiiang River Basin from 1965 to 2018. Chin. J. Ecol. 2020, 39, 1676–1684. [Google Scholar]
- Ma, L.; Niu, Z.; Sun, D. Relationship between changes in spatial and temporal patterns of potential evapotranspiration and meteorological factors in Hexi Corridor. Arid Land Geogr. 2010, 47, 192–202. [Google Scholar]
- Liu, F.; Li, K.; Sun, Y.; Tang, G.; Zhang, C. Effects of climate on vegetaion recovery in Dry-hot Valleys of hengduan moutainous region in southwest China. Resour. Environ. Yangtze Basin 2010, 19, 1386–1391. [Google Scholar]
- Niu, J.; Wang, J.; Peng, J.; Wang, Y.; Hao, L. Change of Potential Evapotranspiration and Its Affecting Factors in Desert-oasis Zone. Arid Zone Res. 2016, 33, 766–772. [Google Scholar]
- Yin, X.; Wei, L.; Zhen, W. Simulation of the relationship between bare-ground submersible evaporation and meteorological elements based on principal component analysis. J. China Hydrol. 2020, 40, 7–13+39. [Google Scholar]
- Sun, J.; Ruan, B.; Jiang, R.; Xu, F. Analysis of grey relation degree of reference crops evapo-transpiration andmeteorological variables in Qingtongxia Irrigation Area. J. China Inst. Water Resour. Hydropower Res. 2006, 3, 232–235. [Google Scholar]
- Yin, Y.; Liu, X. Path analysis and its application. Stat. Educ. 2006, 2, 24–26. [Google Scholar]
- McCuen, R.H. A sensitivity and error analysis of procedures used for estimating evaporation. Water Resour. Bull. 1979, 416, 486–498. [Google Scholar]
- Yun, H.; Wu, S.; Chen, G.; Dai, E. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Climatol. 2010, 101, 19–28. [Google Scholar] [CrossRef]
- Niu, J.; Yang, W.; Wang, J.; Chi, C.; Wu, J.; Zhang, S. Analysis of Change Characteristics and Mutation on Climate in the Main Stream of Tarim River. J. Irrig. Drain. 2017, 36, 106–112. [Google Scholar]
- Ma, Y.; Sun, D.; Zhang, R.; Xu, J.; Wang, X. Driving Factors of Temporal and Spatial Variation of Reference Crop Evapotranspiration in Gansu Province. Chin. J. Agrometeorol. 2022, 43, 881–892. [Google Scholar]
- Ma, Y.; Niu, Z.; Zhang, R.; Sun, D.; Chen, J.; Bai, Z. Temporal and Spatial Evolution and Driving Factors of Potential Evapotranspiration in Shule River Basin. Res. Soil Water Conserv. 2022, 29, 350–357. [Google Scholar]
- Yuan, H.; Juncang, P.; Juan, L.; Yang, F.; Fang, Y.; Cao, Y.; Wang, Y.; Li, X.; Wang, Y.; Deng, B.; et al. GC/MS fingerprinting with hierarchical cluster analysis to determine components in breakable capsules in cigarette filter. Tob. Sci. Technol. 2018, 51, 54–60. [Google Scholar]
- Liu, Q.; Wu, Z.; Cui, N.; Zhu, S.; Zhen, S. Spatial-temporal distribution characteristics and attribution analysis of reference cropevapotranspiration in Yunnan-Kweichow Plateau. J. Drain. Irrig. Mach. Eng. 2022, 40, 302–310. [Google Scholar]
- Zhang, G.; Zhang, D.; Zhao, Y.; Tian, G.; Wei, A. Change of dry and wet surface conditions in Shanxi region under the background of climate warming. Arid Land Geogr. 2020, 43, 281–289. [Google Scholar]
- Ji, X.; Ma, Q.; Yang, S.; Wang, Z. Analysis of potential evapotranspiration variation in Cele County, Xinjiang in the past 56 years. Southwest China J. Agric. Sci. 2019, 32, 416–421. [Google Scholar]
- Zhai, Q.; Ao, X.; Sun, B.; Wang, B. Changes of potential evapotranspiration and ecological water demand in Liaoning Province from 1981 to 2010. Chin. Agric. Sci. Bull. 2014, 30, 228–235. [Google Scholar]
- Feng, Y.; Cui, N.; Wei, X.; Zhao, L.; Wang, J. Temporal-spatial distribution characteristics and causes analysis of reference cropevapotranspiration in hilly area of central Sichuan. J. Nat. Res. 2014, 30, 78–86+339. [Google Scholar]
- Ni, N.; Li, G.; Cui, N.; Jiang, S.; Tang, Q.; Liu, S.; Liao, G.; Wang, L. Sensitivity analysis of reference crop evapotranspiration in recent 56 years in Southwestern China. Jiangsu Agri. Sci. 2019, 47, 298–305. [Google Scholar]
- Wang, X.; Li, Z.; Zhao, C.; Zhang, Z. Spatiotemporal variations of the reference crop evapotranspiration in the arid region of northwest China during 1961–2011. J. Ecol. 2014, 34, 5609–5616. [Google Scholar]
- Wang, Z.; Wang, W.; Li, J. A review of the advances in water source composition and observation methods of evapotranspiration. Hydrol. Eng. Geol. 2021, 48, 1–9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).