Optimization of the Coupling between Water and Energy Consumption in a Smart Integrated Photovoltaic Pumping Station System
Abstract
1. Introduction
2. Materials and Methods
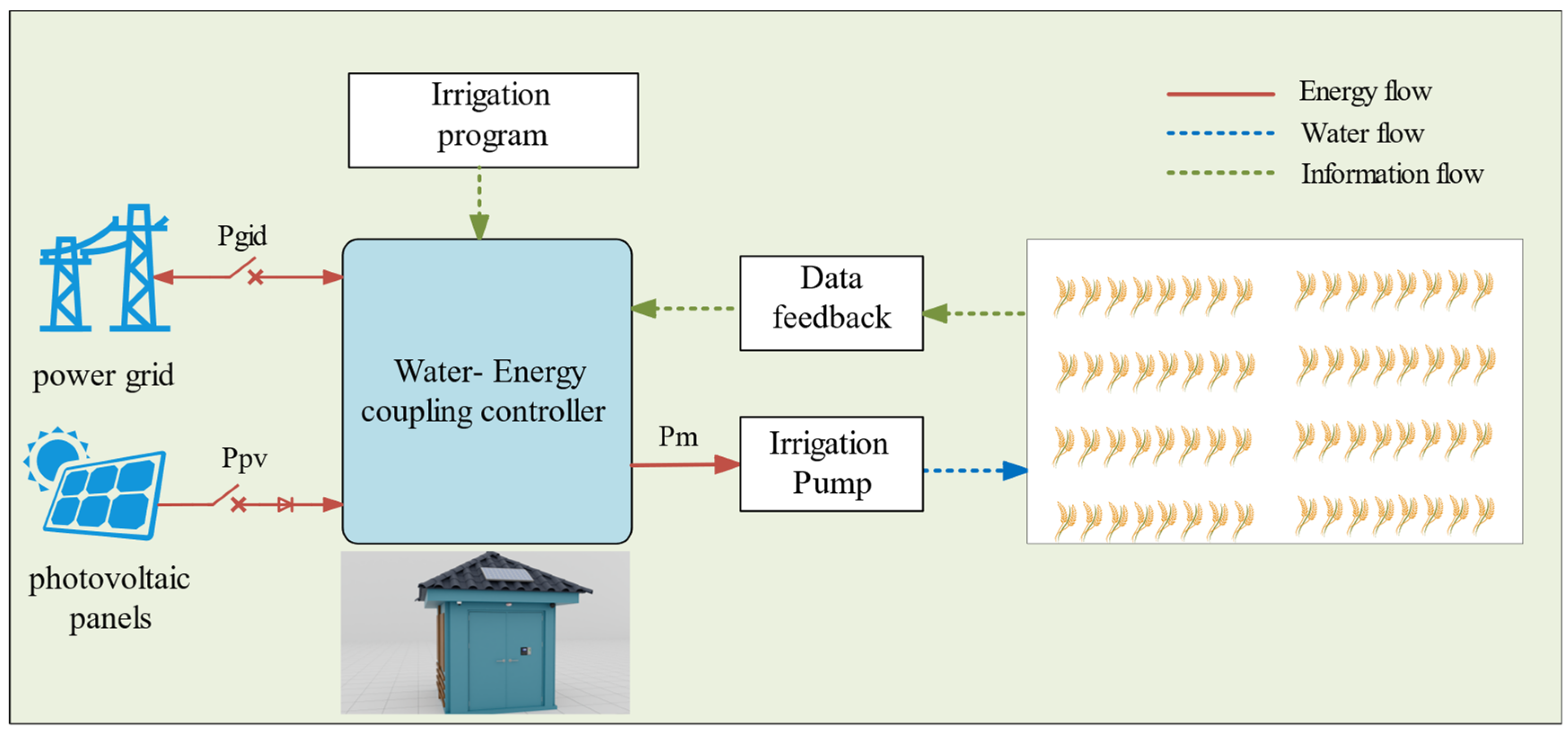
2.1. Description of the System
2.2. Optimization Model
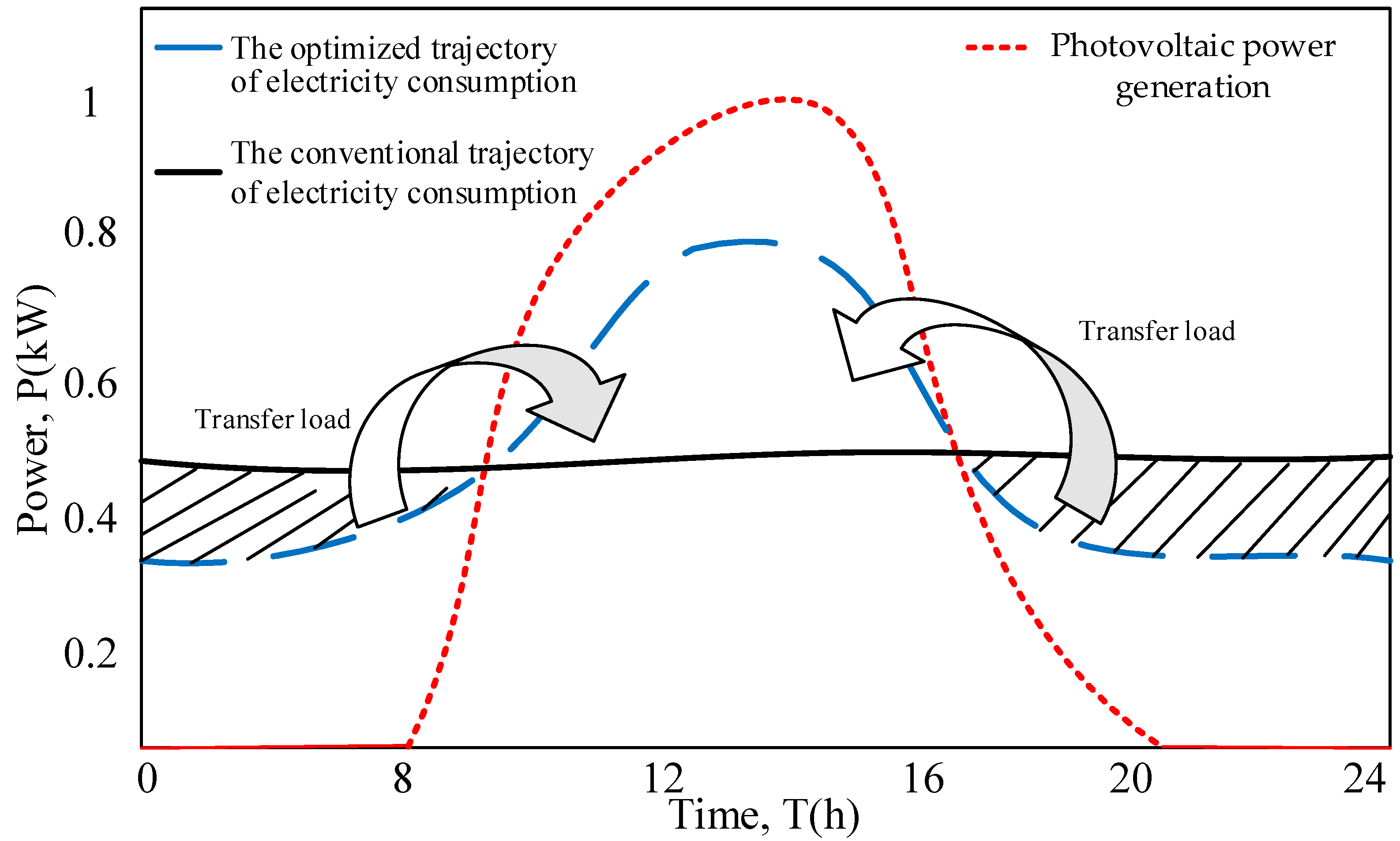
2.2.1. Objective Function
2.2.2. Constraints
- Power balance constraint
- Water demand constraint
- Speed constraint
2.3. Solving Methods
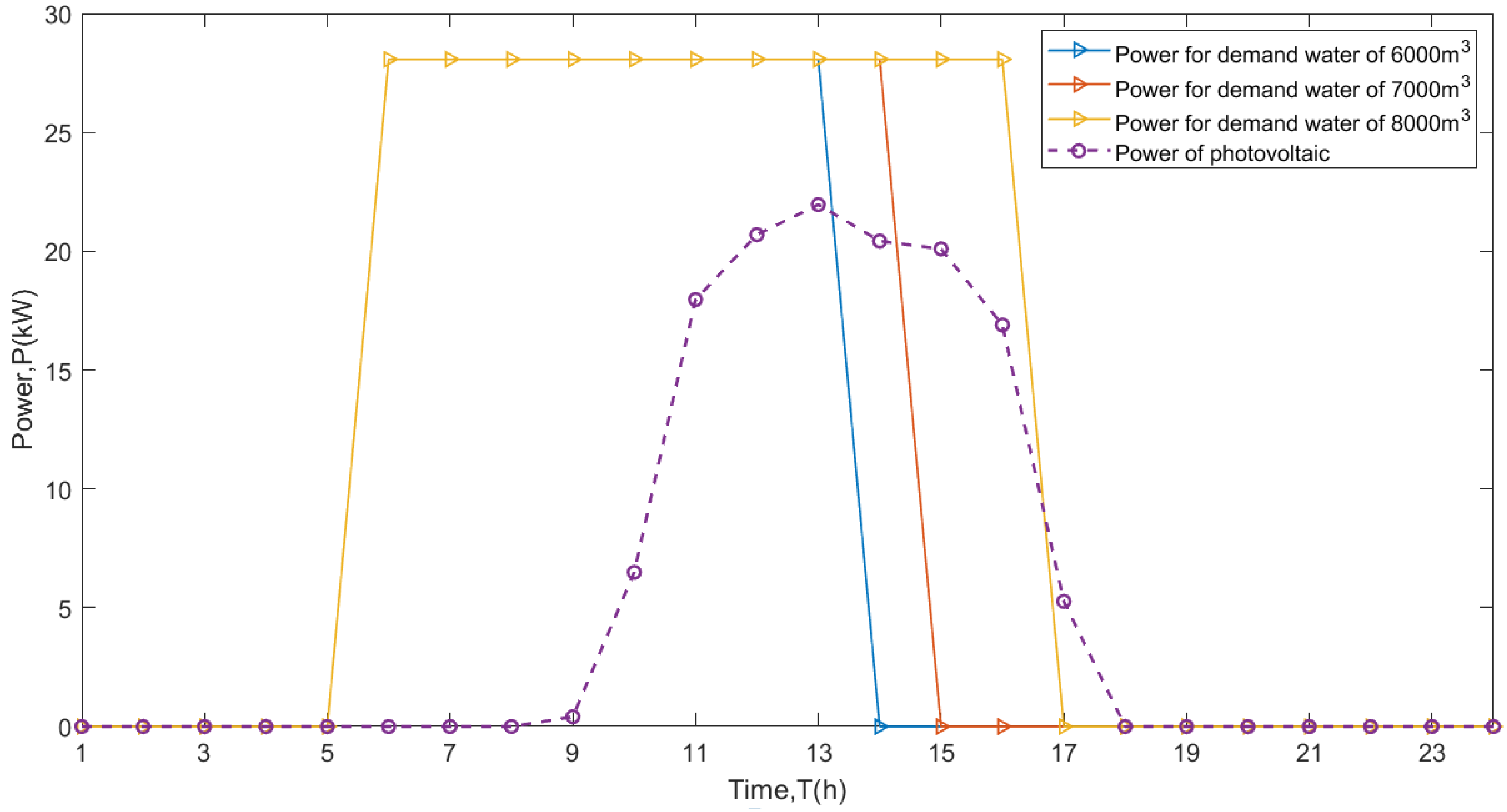
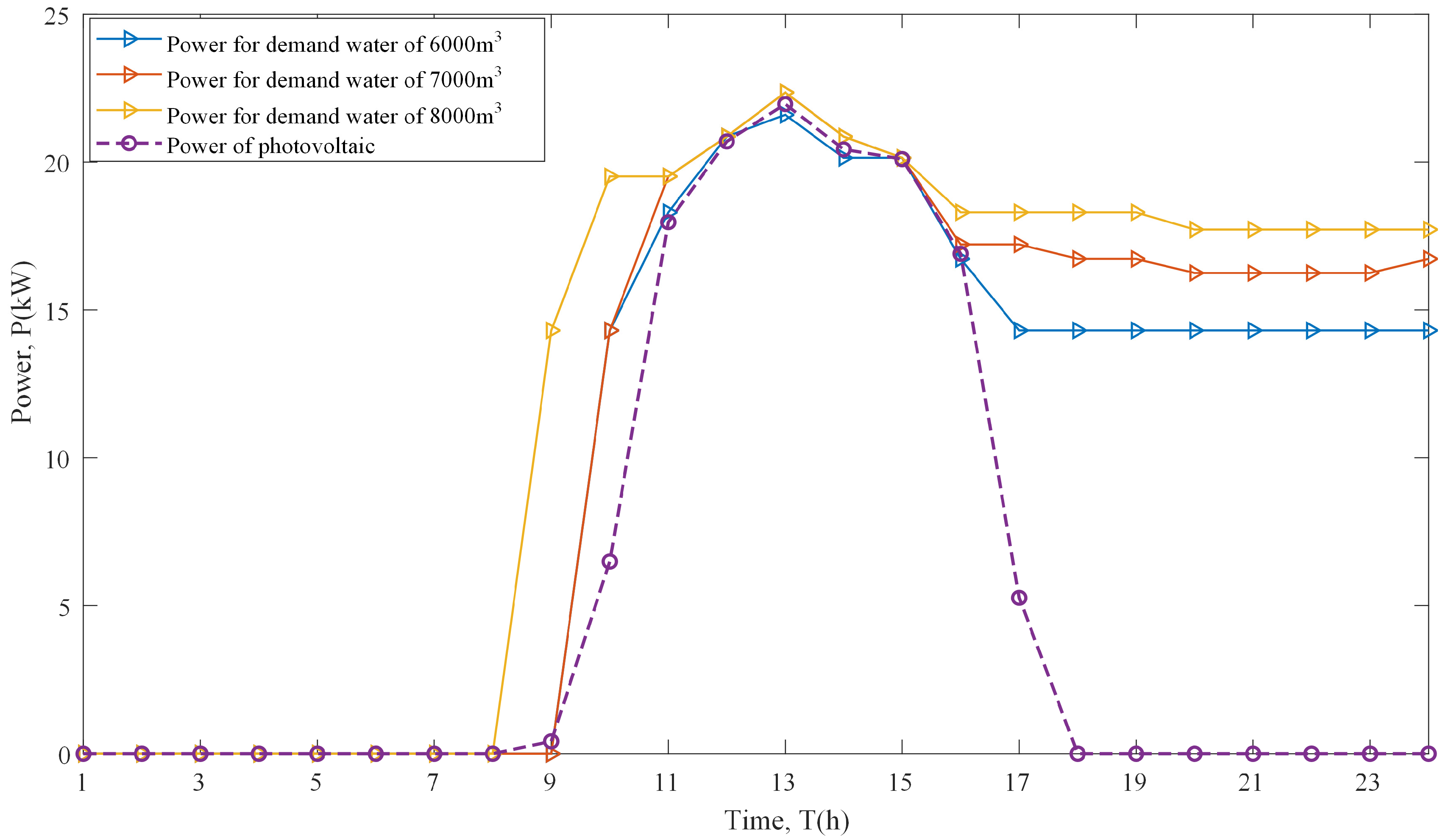
3. Results
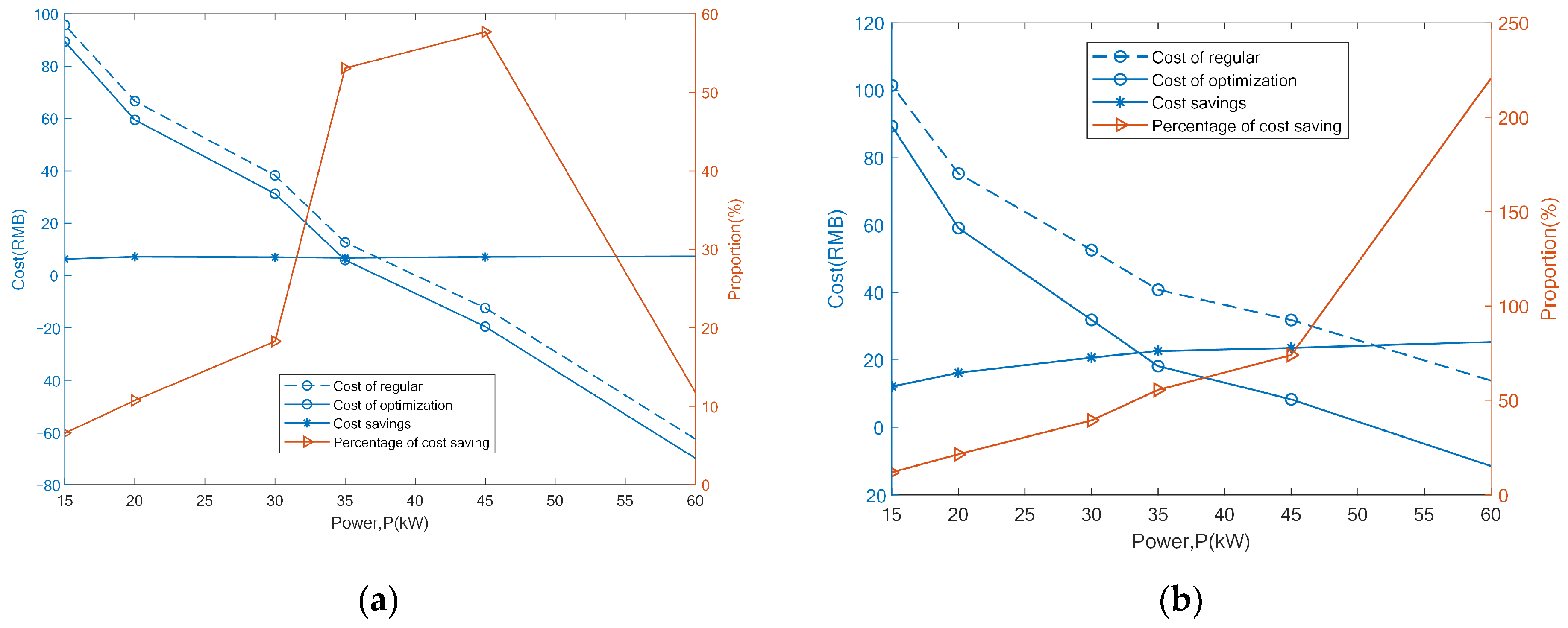
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Jeong, J.; Zhang, X. Model Application for Sustainable Agricultural Water Use. Agronomy 2020, 10, 396. [Google Scholar] [CrossRef]
- Wabela, K.; Hammani, A.; Abdelilah, T.; Tekleab, S.; El-Ayachi, M. Optimization of Irrigation Scheduling for Improved Irrigation Water Management in Bilate Watershed, Rift Valley, Ethiopia. Water 2022, 14, 3960. [Google Scholar] [CrossRef]
- Hu, K.; Raghutla, C.; Chittedi, K.R.; Zhang, R.; Koondhar, M.A. The Effect of Energy Resources on Economic Growth and Carbon Emissions: A Way Forward to Carbon Neutrality in an Emerging Economy. J. Environ. Manag. 2021, 298, 113448. [Google Scholar] [CrossRef]
- Zheng, J.; Duan, H.; Zhou, S.; Wang, S.; Gao, J.; Jiang, K.; Gao, S. Limiting Global Warming to below 1.5 °C from 2 °C: An Energy-System-Based Multi-Model Analysis for China. Energy Econ. 2021, 100, 105355. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Krysanova, V.; Benestad, R.E.; Hov, Ø.; Piniewski, M.; Otto, I.M. Uncertainty in Climate Change Impacts on Water Resources. Environ. Sci. Policy 2018, 79, 1–8. [Google Scholar] [CrossRef]
- Licandeo, F.; Flores, F.; Feijoo, F. Assessing the Impacts of Economy-Wide Emissions Policies in the Water, Energy, and Land Systems Considering Water Scarcity Scenarios. Appl. Energy 2023, 342, 121115. [Google Scholar] [CrossRef]
- Kumar Jha, S.; Ramatshaba, T.S.; Wang, G.; Liang, Y.; Liu, H.; Gao, Y.; Duan, A. Response of Growth, Yield and Water Use Efficiency of Winter Wheat to Different Irrigation Methods and Scheduling in North China Plain. Agric. Water Manag. 2019, 217, 292–302. [Google Scholar] [CrossRef]
- Sahoo, S.R.; Agyeman, B.T.; Debnath, S.; Liu, J. Knowledge-Based Optimal Irrigation Scheduling of Agro-Hydrological Systems. Sustainability 2022, 14, 1304. [Google Scholar] [CrossRef]
- Han, A.; Huang, J.; Wang, X.; Zhu, Z. Efficient Water-Saving Irrigation, Space Efficiency and Agricultural Development—Study Based on Spatial Stochastic Frontier Model. J. Syst. Sci. Complex 2023, 36, 2559–2579. [Google Scholar] [CrossRef]
- Yang, X.; Pu, Y.; Weng, S.; Hou, M.; Wang, Z. Review of Agricultural Water-Saving Policies and Measures in Recent Years–a Case Study of Jiangsu Province, China. Water Supply 2022, 22, 3951–3967. [Google Scholar] [CrossRef]
- Hiremath, D.; Makadia, J.J.; Rudrapur, S. Economic Impact and Decomposition Analysis of Income Change Vis-à-Vis Drip and Conventional Irrigation Technology in Bananas: A Case Study of the South Gujarat Region in India. J. Irrig. Drain. Eng. 2023, 149, 04023029. [Google Scholar] [CrossRef]
- Zhao, R.-H.; He, W.-Q.; Lou, Z.-K.; Nie, W.-B.; Ma, X.-Y. Synchronization Optimization of Pipeline Layout and Pipe Diameter Selection in a Self-Pressurized Drip Irrigation Network System Based on the Genetic Algorithm. Water 2019, 11, 489. [Google Scholar] [CrossRef]
- Hori, K.; Kim, J.; Kawase, R.; Kimura, M.; Matsui, T.; Machimura, T. Local Energy System Design Support Using a Renewable Energy Mix Multi-Objective Optimization Model and a Co-Creative Optimization Process. Renew. Energy 2020, 156, 1278–1291. [Google Scholar] [CrossRef]
- Kumar, C.M.S.; Singh, S.; Gupta, M.K.; Nimdeo, Y.M.; Raushan, R.; Deorankar, A.V.; Kumar, T.M.A.; Rout, P.K.; Chanotiya, C.S.; Pakhale, V.D.; et al. Solar Energy: A Promising Renewable Source for Meeting Energy Demand in Indian Agriculture Applications. Sustain. Energy Technol. Assess. 2023, 55, 102905. [Google Scholar] [CrossRef]
- Tomaszewska, B.; Akkurt, G.G.; Kaczmarczyk, M.; Bujakowski, W.; Keles, N.; Jarma, Y.A.; Baba, A.; Bryjak, M.; Kabay, N. Utilization of Renewable Energy Sources in Desalination of Geothermal Water for Agriculture. Desalination 2021, 513, 115151. [Google Scholar] [CrossRef]
- Chandel, S.S.; Nagaraju Naik, M.; Chandel, R. Review of Solar Photovoltaic Water Pumping System Technology for Irrigation and Community Drinking Water Supplies. Renew. Sustain. Energy Rev. 2015, 49, 1084–1099. [Google Scholar] [CrossRef]
- Taousanidis, N.; Gavros, K. An Analysis of Photovoltaic Irrigation System for Olive Orchards in Greece. IOP Conf. Ser. Mater. Sci. Eng. 2016, 161, 012095. [Google Scholar] [CrossRef]
- Munarto, R.; Faishal, A. Feasibility Study of Photovoltaic Water Pump for Rice Paddy Irrigation. MATEC Web Conf. 2018, 218, 02011. [Google Scholar] [CrossRef]
- Pardo Picazo, M.; Juárez, J.; García-Márquez, D. Energy Consumption Optimization in Irrigation Networks Supplied by a Standalone Direct Pumping Photovoltaic System. Sustainability 2018, 10, 4203. [Google Scholar] [CrossRef]
- Monís, J.I.; López-Luque, R.; Reca, J.; Martínez, J. Multistage Bounded Evolutionary Algorithm to Optimize the Design of Sustainable Photovoltaic (PV) Pumping Irrigation Systems with Storage. Sustainability 2020, 12, 1026. [Google Scholar] [CrossRef]
- Barrueto Guzmán, A.; Barraza Vicencio, R.; Ardila-Rey, J.; Núñez Ahumada, E.; González Araya, A.; Arancibia Moreno, G. A Cost-Effective Methodology for Sizing Solar PV Systems for Existing Irrigation Facilities in Chile. Energies 2018, 11, 1853. [Google Scholar] [CrossRef]
- Koohi-Fayegh, S.; Rosen, M.A. A Review of Energy Storage Types, Applications and Recent Developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Yuan, H.; Ye, H.; Chen, Y.; Deng, W. Research on the Optimal Configuration of Photovoltaic and Energy Storage in Rural Microgrid. Energy Rep. 2022, 8, 1285–1293. [Google Scholar] [CrossRef]
- Lynch, M.Á.; Nolan, S.; Devine, M.T.; O’Malley, M. The Impacts of Demand Response Participation in Capacity Markets. Appl. Energy 2019, 250, 444–451. [Google Scholar] [CrossRef]
- Tan, Z.; Ju, L.; Reed, B.; Rao, R.; Peng, D.; Li, H.; Pan, G. The Optimization Model for Multi-Type Customers Assisting Wind Power Consumptive Considering Uncertainty and Demand Response Based on Robust Stochastic Theory. Energy Convers. Manag. 2015, 105, 1070–1081. [Google Scholar] [CrossRef]
- Zhang, Y.; Harman, M.; Ochoa, G.; Ruhe, G.; Brinkkemper, S. An Empirical Study of Meta- and Hyper-Heuristic Search for Multi-Objective Release Planning. ACM Trans. Softw. Eng. Methodol. 2018, 27, 1–32. [Google Scholar] [CrossRef]
- Al-Shaery, A.M.; Khozium, M.O.; Farooqi, N.S.; Alshehri, S.S.; Al-Kawa, M.A.M.B. Problem Solving in Crowd Management Using Heuristic Approach. IEEE Access 2022, 10, 25422–25434. [Google Scholar] [CrossRef]
- Xu, Z.; Gong, Z.; Cheng, H.; Cheng, J. Optimal Water Allocation Integrated with Water Supply, Replenishment, and Spill in the in-Series Reservoir Based on an Improved Decomposition and Dynamic Programming Aggregation Method. J. Hydroinform. 2023, 25, 989–1003. [Google Scholar] [CrossRef]
- Wu, G.; Pedrycz, W.; Suganthan, P.N.; Mallipeddi, R. A Variable Reduction Strategy for Evolutionary Algorithms Handling Equality Constraints. Appl. Soft Comput. 2015, 37, 774–786. [Google Scholar] [CrossRef]
- Dolgopolik, M.V. A Unifying Theory of Exactness of Linear Penalty Functions II: Parametric Penalty Functions. Optimization 2017, 66, 1577–1622. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, T. Composite Quantization. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 1308–1322. [Google Scholar] [CrossRef] [PubMed]


| Time | Water Demands | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 6000 m3 | 7000 m3 | 8000 m3 | |||||||
| Pump Speed (r/min) | Pump Power (kW) | Water Volume (m3) | Pump Speed (r/min) | Pump Power (kW) | Water Volume (m3) | Pump Speed (r/min) | Pump Power (kW) | Water Volume (m3) | |
| 1–8 | - | - | - | - | - | - | - | - | - |
| 9 | - | - | - | 1102 | 14.30 | 312.01 | 1102 | 14.30 | 312.01 |
| 10 | 1102 | 14.30 | 312.01 | 1182 | 16.86 | 438.35 | 1254 | 19.51 | 531.22 |
| 11 | 1184 | 16.93 | 441.12 | 1208 | 17.79 | 473.41 | 1254 | 19.51 | 531.22 |
| 12 | 1246 | 19.21 | 521.49 | 1264 | 19.90 | 543.22 | 1288 | 20.86 | 571.32 |
| 13 | 1184 | 16.93 | 441.12 | 1236 | 18.83 | 509.15 | 1306 | 21.60 | 591.83 |
| 14 | 1246 | 19.21 | 521.49 | 1264 | 19.90 | 543.22 | 1270 | 20.14 | 550.33 |
| 15 | 1184 | 16.93 | 441.12 | 1136 | 18.83 | 509.15 | 1270 | 20.14 | 550.33 |
| 16 | 1184 | 16.93 | 441.12 | 1182 | 16.86 | 438.35 | 1222 | 18.30 | 491.51 |
| 17 | 1130 | 15.15 | 360.51 | 1158 | 16.05 | 403.95 | 1222 | 18.30 | 491.51 |
| 18 | 1130 | 15.15 | 360.51 | 1158 | 16.05 | 403.95 | 1222 | 18.30 | 491.51 |
| 19 | 1130 | 15.15 | 360.51 | 1158 | 16.05 | 403.95 | 1222 | 18.30 | 491.51 |
| 20 | 1130 | 15.15 | 360.51 | 1158 | 16.05 | 403.95 | 1222 | 18.30 | 491.51 |
| 21 | 1130 | 15.15 | 360.51 | 1158 | 16.05 | 403.95 | 1222 | 18.30 | 491.51 |
| 22 | 1130 | 15.15 | 360.51 | 1158 | 16.05 | 403.95 | 1206 | 17.72 | 470.78 |
| 23 | 1130 | 15.15 | 360.51 | 1158 | 16.05 | 403.95 | 1206 | 17.72 | 470.78 |
| 24 | 1130 | 15.15 | 360.51 | 1158 | 16.05 | 403.95 | 1206 | 17.72 | 470.78 |
| Subtotal | 6003.6 | 6998.5 | 7999.7 | ||||||
| Time | Water Demands | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 6000 m3 | 7000 m3 | 8000 m3 | |||||||
| Pump Speed (r/min) | Pump Power (kW) | Water Volume (m3) | Pump Speed (r/min) | Pump Power (kW) | Water Volume (m3) | Pump Speed (r/min) | Pump Power (kW) | Water Volume (m3) | |
| 1–8 | - | - | - | - | - | - | - | - | - |
| 9 | - | - | - | - | - | - | 1102 | 14.30 | 312.01 |
| 10 | 1102 | 14.30 | 312.01 | 1102 | 14.30 | 312.01 | 1254 | 19.51 | 531.22 |
| 11 | 1222 | 18.30 | 491.51 | 1254 | 19.51 | 531.22 | 1254 | 19.51 | 531.22 |
| 12 | 1288 | 20.86 | 571.32 | 1288 | 20.86 | 571.32 | 1288 | 20.86 | 571.32 |
| 13 | 1306 | 21.60 | 591.83 | 1324 | 22.35 | 611.91 | 1324 | 22.35 | 611.91 |
| 14 | 1270 | 20.14 | 550.33 | 1288 | 20.86 | 571.32 | 1288 | 20.86 | 571.32 |
| 15 | 1270 | 20.14 | 550.33 | 1270 | 20.14 | 550.33 | 1270 | 20.14 | 550.33 |
| 16 | 1178 | 16.73 | 432.77 | 1192 | 17.21 | 452.08 | 1222 | 18.30 | 491.51 |
| 17 | 1102 | 14.30 | 312.01 | 1192 | 17.21 | 452.08 | 1222 | 18.30 | 491.51 |
| 18 | 1102 | 14.30 | 312.01 | 1178 | 16.73 | 432.77 | 1222 | 18.30 | 491.51 |
| 19 | 1102 | 14.30 | 312.01 | 1178 | 16.73 | 432.77 | 1222 | 18.30 | 491.51 |
| 20 | 1102 | 14.30 | 312.01 | 1164 | 16.25 | 412.76 | 1206 | 17.72 | 470.78 |
| 21 | 1102 | 14.30 | 312.01 | 1164 | 16.25 | 412.76 | 1206 | 17.72 | 470.78 |
| 22 | 1102 | 14.30 | 312.01 | 1164 | 16.25 | 412.76 | 1206 | 17.72 | 470.78 |
| 23 | 1102 | 14.30 | 312.01 | 1164 | 16.25 | 412.76 | 1206 | 17.72 | 470.78 |
| 24 | 1102 | 14.30 | 312.01 | 1178 | 16.73 | 432.77 | 1206 | 17.72 | 470.78 |
| Subtotal | 5996.2 | 7001.6 | 7999.3 | ||||||
| Demand Water (m3) | Cost of Conventional Operation Mode | Cost of Optimized Operation Mode | Cost Saving | |||||
|---|---|---|---|---|---|---|---|---|
| Mode 1 (¥) | Mode 2 (¥) | Irrigation Water (m3) | Mode 1 (¥) | Mode 2 (¥) | Irrigation Water (m3) | Mode 1 (%) | Mode 2 (%) | |
| 6000 | 55.43 | 79.94 | 5946.7 | 49.76 | 55.56 | 5996.2 | 10.2 | 30.5 |
| 7000 | 67.31 | 83.84 | 6690 | 63.15 | 64.83 | 7001.6 | 6.2 | 22.7 |
| 8000 | 91.52 | 93.58 | 8176 | 77.10 | 77.18 | 7999.3 | 15.8 | 17.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Chen, X. Optimization of the Coupling between Water and Energy Consumption in a Smart Integrated Photovoltaic Pumping Station System. Water 2024, 16, 1493. https://doi.org/10.3390/w16111493
Xu Z, Chen X. Optimization of the Coupling between Water and Energy Consumption in a Smart Integrated Photovoltaic Pumping Station System. Water. 2024; 16(11):1493. https://doi.org/10.3390/w16111493
Chicago/Turabian StyleXu, Zuping, and Xing Chen. 2024. "Optimization of the Coupling between Water and Energy Consumption in a Smart Integrated Photovoltaic Pumping Station System" Water 16, no. 11: 1493. https://doi.org/10.3390/w16111493
APA StyleXu, Z., & Chen, X. (2024). Optimization of the Coupling between Water and Energy Consumption in a Smart Integrated Photovoltaic Pumping Station System. Water, 16(11), 1493. https://doi.org/10.3390/w16111493





