On the Optimized Management of Activated Distributed Storage Systems: A Novel Approach to Flood Mitigation

Abstract

New flood records are being set across the world as precipitation patterns change due to a warming climate. Despite the presence of longstanding water management infrastructure like levees and reservoirs, this rise in flooding has been met with property damage, loss of life, and hundreds of billions in economic impact, suggesting the need for new solutions. In this work, the authors suggest the active management of distributed networks of ponds, wetlands and retention basins that already exist across watersheds for the mitigation of flood damages. As an example of this approach, we investigate optimal control of the gated outlets of 130 such locations within a small watershed using linear programming, genetic algorithms, and particle swarm optimization, with the objective of reducing downstream flow and maximizing basin storage. When compared with passive operation (i.e., no gated outlets) and a uniformly applied active management scheme designed to store water during heavy rainfall, the optimal control techniques (1) reduce the magnitudes of peak flow events by up to 10%, (2) reduce the duration of flood crests for up to several days, and (3) preserve additional storage across the watershed for future rainfall events when compared with active management. Combined, these findings provide both a better understanding of dynamically controlled distributed storage as a flood fighting technique and a springboard for future work aimed at its use for reducing flood impacts.

1. Introduction

Observed extreme precipitation events have become more frequent across the central United States since the mid-20th century [1]. This trend has been shown to be largely attributable to climate change [2] and, as atmospheric vapor pressure increases with temperatures, is likely to continue [3,4,5]. Unsurprisingly, recent decades have also seen a marked increase in flood events across the American Midwest [6,7,8,9]. Development of floodplains during this period has highlighted the reliance of society on ever-expanding flood infrastructure, namely barrier structures (i.e., levees) and large flood control reservoirs [10]. Though this infrastructure has grown along with the communities that rely on it, the damages associated with catastrophic flooding suggest that additional measures are required [11,12,13].

Riverine flooding is largely a question of available watershed storage combined with the spatiotemporal variability of rainfall, meaning that adding flood storage to a watershed is critical to reduce flood impacts. While this objective could be met through the construction of large reservoirs, past research has indicated that the monetary, ecological, and societal costs of such projects may be too high [14,15,16]. Recent research has examined the use of existing networks of ponds, wetlands, and retention basins for flood control, a method known as “distributed storage”. These studies have shown that storing heavy rainfall in these distributed pond locations can meaningfully reduce downstream flows and delay peak timing within both urban [17,18] and rural [19,20] settings for a variety of rainfall durations, intensities, and recurrence rates. An investigation by [19] was particularly interested in the incremental effect of adding ponds to a watershed, thus increasing basin storage. By evaluating the Soap Creek Watershed, a rural watershed with 130 ponding locations, while only considering randomly selected ponds in groups of 0, 33, 66, 99, and all 130 ponds, they found that flow reductions incrementally increased as storage was added, eventually finding downstream peak flow reductions of up to 43% from a “no ponds” condition. These results align with other investigations of distributed storage networks that have evaluated a variety of conditions. Further examples include a study of an urban 62 km² watershed that found the addition of 100 detention basins offered only a 4% reduction in downstream flows [17]. Ref. [18] found that a system of detention basins in a 14 km² watershed reduced downstream flows by up to 11%. This earlier work showed promise using passive operation or by simply allowing the ponding locations to drain naturally without the use of gated outlets. To further reduce flood impacts, more recent research has evaluated active control of distributed storage networks or implementing gated outlets that allow for more structured control of the network’s storage.

Examples of investigations focused on activated distributed storage are few. Published studies on the topic have found further reduction in streamflows from passive operation across a wide array of storm durations and annual exceedance probabilities, though the magnitude of these reductions was dependent on the spatial and temporal characteristics of a given rainfall event [21,22]. Ref. [21] sought to determine whether activated management via manually operated gated outlets at each ponding location within a distributed network could further reduce downstream flows. Using SCS design storms with recurrence values of 0.2, 0.1, 0.02, and 0.01 applied uniformly across a watershed and three active management operations schemes, they found peak flow reductions of 70% when their results were compared with passive management of the same watershed under identical rainfall. To confirm these findings under realistic rainfall conditions (i.e., spatiotemporal variability of rainfall intensity), [22] used stochastic storm transposition to create over 50,000 years of synthetic rainfall to evaluate active management of the Soap Creek distributed storage network under a variety of rainfall conditions. This study confirmed the findings of those outlined above and found that reductions provided by the storage network were highly dependent on the basin’s spatial scale and rainfall intensity. Refs. [21,22] utilized the Soap Creek Watershed, thus building upon the findings of [19]. This resulted in the Soap Creek distributed storage network being well studied and understood. Among the more nuanced findings of these studies is that uniformly applying reservoir operation plans to many ponds within a watershed may not contain the required flexibility to achieve maximum flood impact reduction [22]. This suggests that a more nuanced operational approach based on optimal control may be required.

Optimum operation of single reservoirs dates back decades, with early studies providing strong evidence that “one size fits all” approaches to reservoir management are not always sufficient to meet the dam’s intended purpose [23,24]. Among these early studies were many that relied on traditional optimization methods, namely stochastic and chance-constrained linear programming [25,26]. However, problems arise when systems of reservoirs, each with unique purposes including hydropower production, water supply, and flood control, lead to complex optimization formulations with high dimensionality. In many cases, this combination of variables can lead to nonlinearity, variables that are time-dependent, or multitarget parameters, all of which can bring the viability of linear programming (LP) into question [27]. To address these challenges, many studies have applied metaheuristic optimization approaches to reservoir operation problems, which use random search for optima using empirical guidelines.

Though many metaheuristic techniques exist, among the most used ones for reservoir operation are evolutionary algorithms (i.e., genetic algorithms) and swarm intelligence (i.e., particle swarm optimization). Evolutionary algorithms are based on the theory of evolution and use a population-based approach, where multiple solutions are combined into one iteration to evolve a new population of potential solutions in the next iteration [28]. This type of metaheuristic optimization is particularly popular for reservoir operation applications due to its relative simplicity and problem independence. Studies using genetic algorithms (GAs) include those of [29] for the derivation of multi-objective operating rule curves and [30], who conducted a study on the Three Gorges Reservoir interested in minimizing lake level decline while maximizing power generation.

Particle swarm optimization (PSO) is a search method that is based on the interactions of individual solutions within a stochastically generated population [31]. The randomly generated “particles” within the population “search” for an optimal solution based upon both personal and global fitness, governed by user-defined exploration parameters. Like GAs, the relative simplicity of PSO makes it ideal for use in multi-objective optimization. As a result, it has been used widely in both reservoir operation and design applications [32,33,34]. In a comparative analysis between GAs and PSO at a single dam, PSO outperformed the GAs in terms of solution accuracy, convergence rate, and run time to reach global optima [34].

While LP, GAs, and PSO have been widely adopted for optimization of reservoir applications, these studies have focused on either single reservoir locations or small networks of large reservoirs. Though many studies of single reservoir systems include a variety of considerations (i.e., hydropower generation, flood control, and water supply), the low number of locations serves to reduce the computational complexity and dimensionality of the resultant optimization problem. Here, the authors propose and compare the use of LP, GAs, and PSO for the determination of hourly, real-time gate operations within a distributed storage network of 130 small ponding locations. To the authors’ knowledge, this work represents a novelty within the literature, as we are not aware of another study investigating optimal control of a network of so many ponds for real-time flood management. The aim of this work is twofold: (1) to identify differences in the distributed storage network response to various optimal control techniques and (2) to determine whether optimal control can meaningfully reduce peak streamflows when compared with passive and uniform active management.

2. Data and Methods

To evaluate the effects of optimized reservoir management within a distributed storage system, we used the Hillslope Link Model (HLM). The HLM was developed at the University of Iowa’s Iowa Flood Center [35], where it has been used for real-time streamflow forecasting within Iowa for more than a decade. It decomposes a watershed into its constituent hillslopes and channel links [36,37]. Using this decomposition, a runoff generation module uses vertically aligned storages within the soil column to represent overland flow, interflow, and baseflow [37,38]. Channel runoff is calculated at each link before being routed downstream via flow aggregation using a nonlinear velocity formulation, which results in a system of ordinary differential equations. This system of equations is evaluated using an asynchronous differential equation solver developed specifically for the HLM [39,40]. The HLM includes a module that simulates gated outlets within a watershed [21]. This module was critical throughout this investigation, as it made active management of a distributed storage system possible within the model’s framework.

For the hydrologic forcing within the model, we employed the Multi-Radar Multi-Sensor (MRMS) rainfall product throughout this study. This product is rain gauge-corrected [41,42] and provides data at 1 km² and 1 h spatiotemporal resolutions for the period from 2016 to the present. Beyond the fine resolution it offers, the MRMS system improves upon other remotely sensed rainfall products by applying local gauge bias correction at a latency of roughly 1.5 h [43].

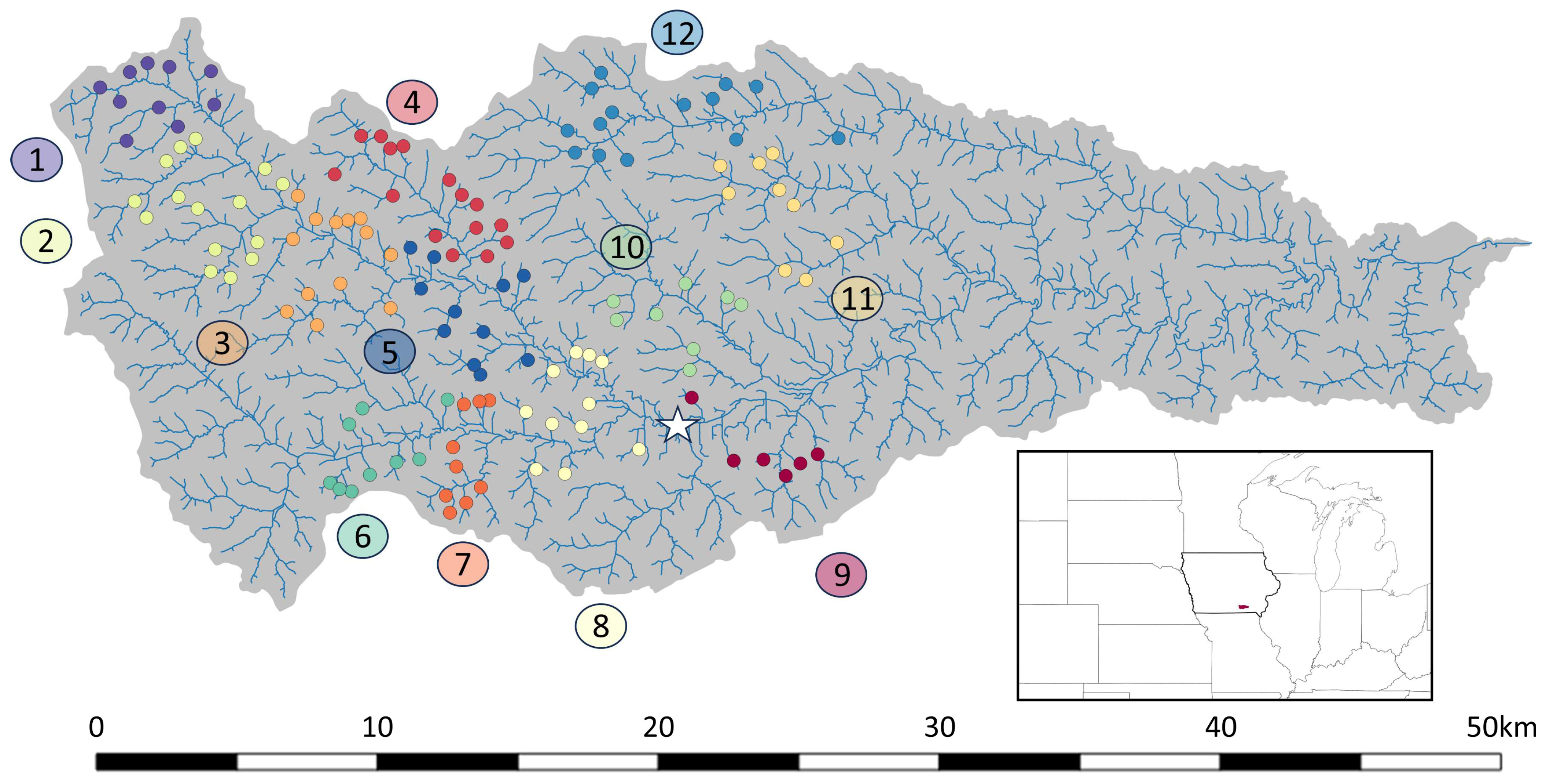
Our use of the distributed storage network in the Soap Creek Watershed, a tributary to the Des Moines River in southeastern Iowa, serves to illustrate dynamic system operation. There are 130 ponds within this watershed, whose storage-to-discharge relationships were established in an earlier study [44], a critical requirement for an evaluation of reservoir response to outlet operations. The watershed and its 130 ponds are shown in Figure 1. Soap Creek makes up a drainage area of roughly 660 km², comprising 2431 hillslope link pairs within the HLM, and it has been the subject of several studies on distributed storage that have established the technique as a viable flood mitigation option [19,21,22]. These earlier studies provide a foundational understanding of basin response to the operation of a distributed storage network, thus offering a proper context for the exploration of distributed storage management using a set of optimization criteria.

To evaluate the effects of operating this distributed storage network using optimal control, we divided the watershed into 12 groups of ponds. The individual characteristics of each group are shown in

Table 1. Descriptions of the pond groups.

Group	Ponds	Drainage Area (km2)	Storage (m3)	Basin Percentage	Threshold (m3/s)
1	10	22.70	767,795	7.49	2.06
2	15	57.34	1,024,788	9.99	3.40
3	13	89.19	676,886	6.60	4.32
4	15	120.21	1,125,380	10.97	5.07
5	11	133.76	719,664	7.02	5.37
6	9	78.82	419,612	4.09	4.04
7	9	92.24	596,797	5.82	4.39
8	11	255.07	726,624	7.09	7.61
9	6	308.41	287,193	2.80	8.43
10	8	39.63	968,499	9.44	2.78
11	9	45.40	1,518,004	14.80	3.00
12	14	54.31	1,423,463	13.88	3.30

. The division of the ponds into these groups was based upon both the proximity of the ponds to each other and each group of ponds sharing a single downstream channel link. The distribution of these pond groups is organized by color in Figure 1, with each group labeled to correspond to those in Table 1. We defined a flow threshold for the subbasin encapsulating each group (12 in total), which each pond group would work cooperatively to not exceed. Since the Soap Creek Watershed is both quite remote and ungauged, there was no historical context for establishing these thresholds. Furthermore, flood impact thresholds (e.g., flood stages) are generally rather arbitrary, often corresponding to the inundation of adjacent infrastructure or some degree of economic damage rather than a universally accepted definition of flooding. The subjective aspect of these levels makes their establishment for a rural basin like Soap Creek challenging. This is due to its dearth of surrounding infrastructure combined with no gauging network to determine at what stage impacts occur. To resolve this, we used the concept of a flood potential index from [45] to establish an initial estimate of the bank full flow values (m³/s) across Soap Creek based upon the drainage area (A, km²) of the location in question, as described in Equation (1):

$$Q_{bankfull}=e^{1.33+0.54\ln \left(\mathrm{A}\right)}$$

(1)

As this study was focused primarily on the dynamic operation of distributed ponding locations toward the reduction of flood impacts, it was important that the rainfall events triggered the specified thresholds at various points within the basin, thus initiating the optimization schemes. Establishing synthetic thresholds (i.e., those not based on the associated stages of critical infrastructure) is subjective and difficult in practice, though the Soap Creek Watershed has been the subject of several published studies that helped the authors pinpoint such thresholds. Ref. [44] used LiDAR data to develop an HEC-HMS model suite of the watershed, complete with soil and landcover data, and used a variety of SCS design storms to assess the effects of passive management of some of the ponds on downstream flows. Ref. [19] conducted a similar study using the HLM and rainfall generated using a Bartlett–Lewis rectangular pulse model. Refs. [21,22] used uniformly applied SCS design storms and stochastically transposed storms, respectively, to assess the effects of active management on downstream locations. Despite using a variety of models and rainfall generation methods, these studies found base flows that varied between dry creek beds in the upper reaches to roughly 10 m³/s near the basin outlet and up to roughly 1000 m³/s at the outlet after a rainfall event associated with roughly a 0.01 recurrence level (a 100year storm). The consistency of these results forms a strong foundation for threshold estimation across the watershed. After an iterative analysis to determine the viability of these results, the authors determined that 10% of the value provided by Equation (1) was sufficient to achieve frequent initiation of the thresholds for this analysis. The resultant reduction in flows from those established in Equation (1) would result in (1) more frequent use of dynamic dam operation and (2) more water being stored in the ponding locations. This established a more conservative operation scheme that was commensurate with protected infrastructure located near the river channel under baseflow conditions.

For our evaluation of optimal control of these groups of ponds, we selected three optimization methods: linear optimization, optimization using genetic algorithms, and particle swarm optimization. These represent a few of the techniques that are currently employed in the study of reservoir operation. For comparison, we also included the results of both a passive operation scheme as well as active operation of the reservoir network using a storage-to-discharge relationship that was established and tested in previous studies on Soap Creek [21,22]. This “guide curve” simply defines the allowable discharge through each gated outlet at various storage thresholds within each ponding location. These provide a good contrast to the optimal control simulations, as passive operation represents a distributed storage network with no outlet control (i.e., water is released from the ponds as fast as the hydraulic features of the system will allow), while the active control scheme dictates rather little water release until high storage utilization is met within each pond. Furthermore, as the passive and active operation schemes only account for the storage within each individual ponding location, the operation of each outlet is conducted without regard for the operations of any nearby ponds or downstream thresholds.

Each optimal control technique utilizes the same objective functions to ensure consistency within this comparative analysis. These functions were applied to each of the 12 ponding groups, and they are defined as follows:

$$\mathit{min}f\left(Q\right)={\sum }_{i=1}^{dams}\frac{\left(S_{pond}-\Delta T{Q}_{out}\right)W_i}{S_{spillway}}$$

(2)

where $S_{pond}$ is the storage (m³) within each ponding location at a given time, $\Delta T$ is the time step (1 h, or 3600 s for our experiment), $Q_{out}$ is the outflow (m³/s) from that pond, $S_{spillway}$ is the pond storage that corresponds to spillway activation, and $dams$ depicts the number of dams within a given group. The variable $W_i$ represents a weighting constant which seeks to ensure that individual ponds within each group are not favored based upon their better efficacy at releasing water, thus lowering that pond’s storage ($S_{pond}$) more quickly (i.e., having a larger outlet conduit or more advantageous storage to discharge relationship). $W_i$ is defined as follows:

$$W_i=1-\left(\frac{S_{pond}}{S_{group}}\right)$$

(3)

where $S_{group}$ is the total storage within a given pond group. The second objective function seeks to maximize the outflow of each pond group, thus maximizing the available storage within each group for future rainfall, as defined in Equation (4):

$$\mathit{max}f\left(Q\right)={\sum }_{i=1}^{dams}{Q}_{out}$$

(4)

These objective functions are constrained by (1) the defined downstream thresholds for each ponding group (Equation (5)) and (2) the physical limitations of each outlet in evacuating water, given a specific pond storage (Equation (6)) [44]:

$$\left({\sum }_{i=1}^{dams}{Q}_{out}\right)+Q_{unreg}+Q_{spillways}\le Q_{thresh}$$

(5)

$$0\le Q_{out}\le Q_{rating}$$

(6)

Unregulated flow ($Q_{unreg}$) is defined as all flow that is not dictated by pond releases (i.e., surface runoff), where $Q_{spillways}$ represents uncontrolled releases from each pond that are not possible to dictate by optimal control and $Q_{thresh}$ indicates the downstream threshold constant of each ponding group (Table 1). Finally, the objective functions were combined into a single, multi-objective function (Equation (7)), and a fitness penalty of 9999 was applied to all solutions that did not satisfy the constraints defined by Equations (5) and (6):

$$\min f\left(Q\right)=-{\sum }_{i=1}^{dams}\frac{\left(S_{pond}-\Delta T{Q}_{out}\right)W}{S_{spillway}}-{\sum }_{i=1}^{dams}{Q}_{out}+penalty$$

(7)

The utilization of genetic and particle swarm techniques requires the definition of further parameters that define how these methods are applied. In our use of a GA, we defined a generational population size of 50, a limit of 2000 generations, a mutation rate of 0.1, and an elitism rate of 0.05. For evaluation of the optimal control via PSO, we defined a swarm size of 100, a maximum of 2000 iterations, an inertial weight of 0.9, and local and global exploration constants of 0.1. The determination of the inertial weight and local and global parameters was based upon a grid search technique that aimed to ensure maximal distribution of flow across the ponds within each group (i.e., avoid scenarios where a single pond was completely open while many others were completely closed). 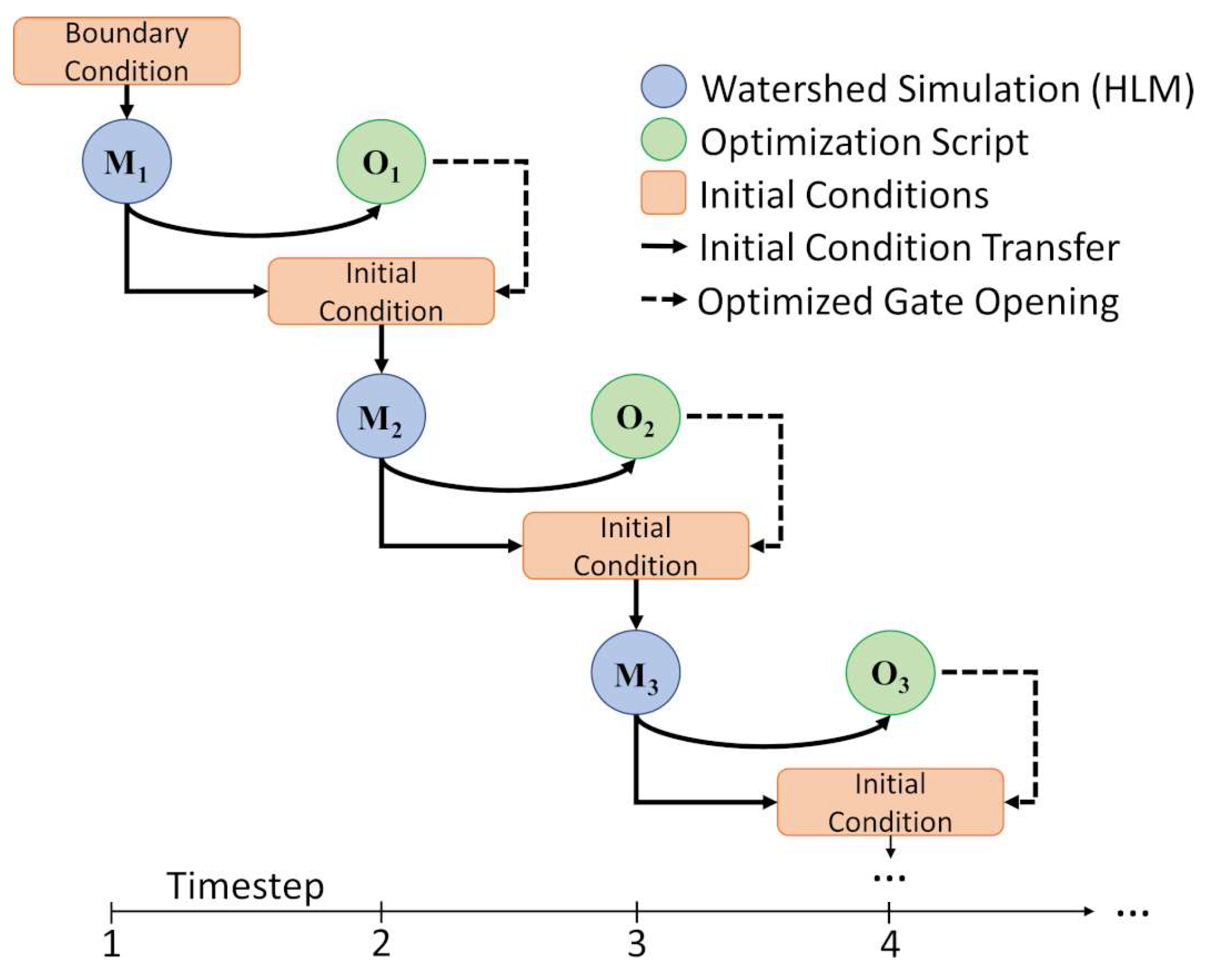The resulting values aligned with a variety of studies and the literature regarding parameter selection [46], substantiating the methods undertaken for this application. We applied each optimization algorithm to the results of the HLM at an hourly timestep. Using the Hillslope Link Model, we simulated the Soap Creek Watershed and passed the results to an external optimization script operated within a high-performance computing cluster. This optimization script evaluated Equations (1)–(7) based on the results of each HLM timestep, and given those values, an optimized set of gate openings was calculated. These optimized results were then combined with the watershed variables (i.e., soil moisture, streamflow, ground surface runoff, evapotranspiration, etc.) by overwriting the gate setting initially calculated by the HLM for each of the 130 ponds. We then used this new packet of values as the initial condition for the next timestep within the HLM, and the process was repeated for the duration of the simulation window. We illustrate this process in Figure 2.

Using MRMS data from two 30 day periods that experienced multiple rainfall events (from 15 August through 15 September 2018 and from 15 May through 15 June 2019), referred to here after as events 1 and 2, respectively, we operated the 130 ponds within the Soap Creek distributed storage network utilizing the HLM and the five operation schemes outlined above (passive, active, and three optimal control schemes). This process was complicated by (1) the short period of record of the MRMS system (dating back to 2016) and (2) a prolonged period of drought across the study area that roughly aligned with the MRMS system’s period of record. As this was a study of a storage network’s response to optimized operation, it was imperative that we used real rainfall events (i.e., those that were spatiotemporally variable). In addition, compounding events, or those that occur in quick succession, are important to evaluate, as this is the only way to fully analyze basin response due to the time required for the ponding locations to drain following each event.

3. Results and Discussion

In this section, we present the major findings from the HLM simulations that evaluated the hydrologic response within the Soap Creek Watershed from using passive, active, and dam operations dictated by various optimal control techniques. We initialized the model with a basin storage utilization of 40% (i.e., all 130 ponds began 40% full), as this was a value determined to be reasonable following modest rainfall [22]. Data from the MRMS system was used as the hydrologic forcing for the HLM, and two 30 day periods were evaluated. These time periods were selected after a review of the MRMS data showed that multiple rainfall events occurred within the Soap Creek Watershed during these times. We specifically outline the flow peaks within each event in

Table 2. Summary of results of activated distributed storage using passive, active, and optimal control at the threshold point of Group 8. Results show peak flows during rainfall events within the specified time windows, reductions achieved from passive (P) and active (A) management using optimal control schemes, and the duration reductions of these methods.

Event	Peak	Date and Time	Flow (m3/s)					Reduction P (%)			Reduction A (%)			Duration Reduction (h)
			P	A	LP	GA	PSO	LP	GA	PSO	LP	GA	PSO	From P	From A
1	1	24 August 2018, 1700	271	261	258	258	258	4.8	4.8	4.8	1.1	1.1	1.1	20	11
	2	29 August 2018, 0700	129	125	120	120	121	7.0	7.0	6.2	4.0	4.0	3.2	24	27
	3	1 September 2018, 0800	37	36	35	33	34	5.4	10.8	8.1	2.8	8.3	5.6	0	0
2	1	19 May 2019, 0700	196	185	181	182	181	7.7	7.1	7.7	2.2	1.6	2.2	24	18
	2	26 May 2019, 1000	132	127	120	119	119	9.1	9.8	9.8	5.5	6.3	6.3	37	45
	3	29 May 2019, 0700	103	100	91	92	91	11.7	10.7	11.7	9.0	8.0	9.0	41	54

.

Hydrographs for the two 30 day events analyzed in this study are shown in Figure 3 at the threshold location of Group 8 (white star in Figure 1). These hydrographs reveal several findings. First, there was a clear reduction offered by active management, both uniform and dynamic, over passive management at the hydrograph peaks (see Table 2 for tabular values from the corresponding peaks labeled in Figure 3). This is indicated by the red line (passive management) emerging from the others and achieving higher peak flows for every event within both windows. Also of note is the reduction from uniform active management (blue line in Figure 3) offered by the three dynamic methods, though it is hard to distinguish between linear, genetic, and particle swarm optimization in these plots. The points in the hydrograph when the dynamic methods achieved their desired downstream thresholds are identifiable when the hydrographs begin to oscillate following each hydrograph peak. These oscillations are a result of the ponds in each group opening and closing their gates to maintain their specified thresholds (in this case, 10% of the result from Equation (1)). These points of oscillation show that while the dynamic methods fell back below their thresholds, passive and uniformly active management were still on the receding limb of each storm peak, showing a reduction in the duration of elevated flows. In short, this work has shown that optimized management of the ponding location outlets (1) reduced the intensity of the flood (i.e., lowered the eventual crest) and (2) reduced the duration of the elevated flows or shortened the time that flooding was occurring.

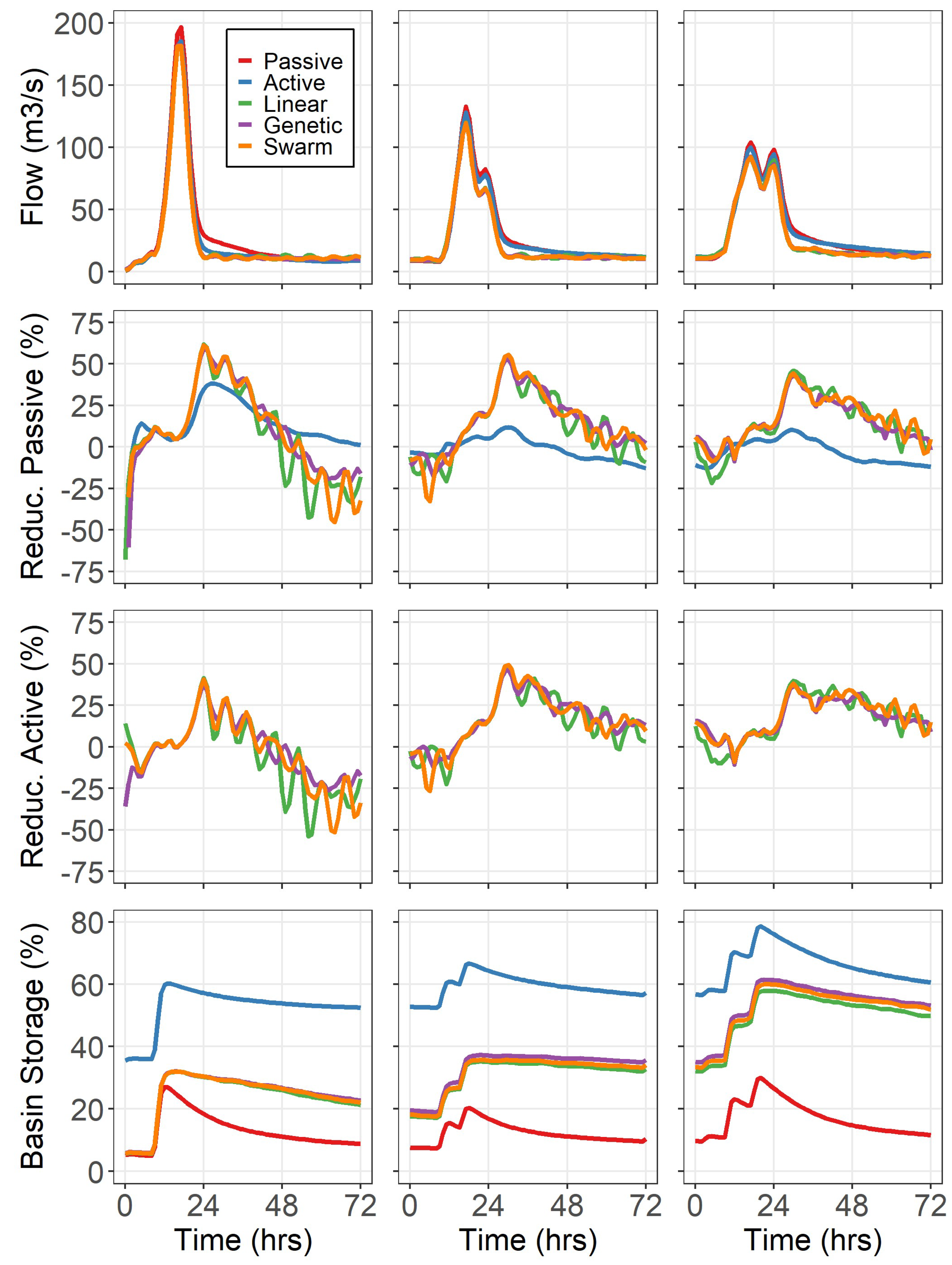
As explained above, Figure 3 does not elucidate the differences between the various dynamic operation methods for either evaluated event, as the individual hydrographs are difficult to distinguish from each other. While the two events are distinct, the results of using optimal control in a distributed storage network were similar between the events. Figure 4 shows the resultant hydrographs for the 72 h period near three major peaks within event 2, labeled in Figure 3. Again, these reflect the flows just downstream of the threshold location for pond group 8, a point that drained 255 km² of Soap Creek (38% of the total watershed area). This is a useful reference point, as threshold locations further downstream (i.e., below pond group 9 or 10) represent much larger drainage areas, with larger portions of the streamflow resulting from uncontrolled releases. This serves to obscure the effects of optimal control of the ponding locations. Note that this location in the watershed benefits both from the operation of the ponds within group 8 and from a compounding thresholding effect from the seven groups upstream of it. Figure 4 shows the peak flow reductions from passive operation offered by active operation at each peak, with additional intensity reductions achieved using optimal control. The algorithms for LP, GA, and PSO performed comparably, with the GA and PSO reducing stream flows from passive and active operation by roughly 10% and 8%, respectively, at the time of maximum flow rates. More notably are the steep recessions provided by optimal control as they attempted to achieve streamflows below the defined flow threshold (7.61 m³/s for group 8). This resulted in additional flow reductions from passive and active operation achieved by the optimal control methods between 40% and 50%. Additionally, reductions in the duration of flows that drastically exceeded the flow threshold by as much as roughly 40 and 55 h when compared with the passive and active operation schemes, respectively, were achieved. The reduction percentages eventually became negative once the flows produced by passive and active management became lower than those of the optimal control methods. In the case of passive operation, this was due to the ponds freely draining their impounded storage, resulting in quick water evacuation, while active operation fell into a lower threshold of releases, resulting in reduced outflows to mitigate downstream flooding. The final major finding of this work is the differentiation in basin storage utilization achieved by the five operation methods. While passive operation quickly evacuated its storage, it did so at the cost of the highest downstream flows, while active operation attempted to mitigate downstream floods by aggressively storing water during most of the simulation. The optimal control schemes pass water when the downstream thresholds allow and store water during heavy rain, resulting in a reduction in flood magnitude and duration, all while maintaining additional storage for future storms when compared with active operation. It should be noted that the intensities of the rainfall events considered in this study were not sufficient to exhaust the storage capacity of any of the 130 ponds in Soap Creek. This resulted in all pond releases occurring through its gated outlets.

We expected all three optimization methods to improve the dam operation for downstream flow reduction when compared with a uniformly applied active operation scheme, as each is designed to find the optimal solution given a set of object functions and constraints. However, as this is the first such study of a large network of small impoundments, we wanted to include a comparative analysis to illustrate any differences in the methods as a reference for future work. While LP, the GA, and PSO all outperformed the passive and active operational methods when comparing resultant flood intensities and durations, there are some noteworthy differences in the application of these techniques. LP was more likely to completely open or close dam conduits than the GA and PSO were, and given adequate time, this resulted in quicker evacuation of the basin storage, thus mildly increasing downstream flows and decreasing overall basin storage utilization when compared with the other two methods (see Figure 4). Conversely, the GA was the most likely of the three to distribute flows across all ponds within the group. This resulted in slightly slower water evacuation, resulting in decreased downstream flows and higher basin storage utilizations. This was due to the ability of the user to control more parameters within the GA and PSO techniques than in LP, thus allowing for more nuanced control of the hourly gate decisions, in this case meaning a tendency for these techniques to favor more uniformly distributed water release among the ponds in each group. While this did roughly double the simulation time from LP to the GA and PSO, the total run times for the metaheuristic examples were to the order of 2.5 min per simulated hour on a high-performance computing cluster, meaning their use for real-time operation is not drawn into question.

4. Conclusions

In this work, we evaluated and compared the effects of operating a distributed storage network using passive and active operation, as well as three optimal control techniques that utilized linear, genetic, and particle swarm optimization. We conducted this work using the Hillslope Link Model for the Soap Creek Watershed in southeastern Iowa, as it has a well-studied distributed storage network of 130 ponding locations. Through comparative analysis, we could evaluate the implications unique to each operational type. We summarize the major findings as follows:

• All three optimal control techniques reduced both the intensity and duration of flooding events at varying spatial scales within Soap Creek.
• In addition to achieving less severe and shorter flood events than active operation, optimal control of the distributed storage network did so while utilizing less storage across the watershed. This reduces the risk of successive rainfall events exceeding storage capacity within the watershed, thus inducing uncontrolled spillway flows.
• While the linear, genetic, and particle swarm optimization techniques performed similarly, it is notable that linear optimization tended to release slightly more water from the pond groups than the particle swarm and genetic optimization techniques. As a result, after successive rainfall events, the metaheuristic approaches tended to have slightly higher basin storage utilization.

The results of this study suggest that optimal control of distributed storage networks offers additional reductions to flood intensity and duration with those already achieved from the addition of active management to passively managed distributed storage networks.

The objective of this work was to ascertain possible benefits from the optimized management of distributed storage networks, and it also provides context for future research. We assumed the availability of land around each ponding location for flood storage, no operation or maintenance costs, and an adopted central operation scheme. The implementation of such a system requires thorough consideration of the economic, legal, and logistical implications of such a network, akin to the construction of any other large-scale infrastructure project. Better understanding of these aspects of activated distributed storage invites a variety of future research. An additional notable limitation to this study is the reliance on calculated thresholds within the watershed. Though these flowrates are quite reasonable given previous studies of Soap Creek, a more realistic analysis would include the known flow values associated with societal and ecological impacts. The combination of these more arbitrary flow rates throughout a watershed could provide a more nuanced understanding of these methods under more realistic circumstances.