1. Introduction
An ultra-high-speed centrifugal pump is an important part of the oil supply system for an aero-engine, which provides high pressure to ensure optimal operating conditions [
1,
2]. However, higher speed places greater demands on the safety of the centrifugal pump system, and the complex transient flow and pressure pulsations at high-speed conditions increase system instability [
3,
4]. It is necessary to investigate the structure stability of the ultra-high-speed centrifugal pump to ensure the normal operation of the aero-engine.
The internal flow analysis of centrifugal pump is one of the main research fields because it can better present flow information and visualize the performance of centrifugal pump. Visser et al. [
5] applied a laser Doppler velocimetry (LDV) measurement system to explore the multiple directional velocities of the relative flow. Their experimental results presented a good agreement with theoretical values for the core ow region. Jafarzadeh et al. [
6] applied three known turbulence models to investigate the head and power coefficients. Jia et al. [
7] researched the pressure distribution of the front casing, back casing, and volute casing according to the numerical calculation and pressure experiment at six different working conditions. The results indicated that the pressure fluctuation was affected by the tongue of the volute. Cui et al. [
8] applied the sliding mesh to investigate the unsteady flow structures for a complex impeller. They found that the main reason for the unstable flow inside the pump was the interaction between the stationary volute and rotating impeller. Zhang et al. [
9,
10,
11] carried out a series of studies and paid more attention to the unsteady flow characteristics. Wei et al. [
12] studied the effect of the gap drainage structure on the steady and transient characteristics according to numerical calculation and experimental verification. They found that a small gap width was good for the pump performance.
Furthermore, with the advancement of numerical computations and experiments, the issue of pressure pulsation is receiving increasing attention. An increasing body of research suggests that elevated levels of pressure pulsation can lead to vibration and noise in centrifugal pumps, thereby exerting adverse effects on the secure and steady operation of these pumps [
13,
14,
15,
16]. Barrio et al. [
17,
18] investigated the relationship between impeller geometric parameters and pressure pulsation characteristics. They found that reducing the impeller–tongue gap led to a corresponding increase in pressure pulsation characteristics. González et al. [
19] found that secondary flow played a main role in the blade-passing frequency. Chalghoum et al. [
20] discovered that the relative position between the volute tongue and impeller resulted in periodic pressure fluctuations. Huang et al. [
21] studied the characteristics of pressure fluctuations in pump mode. The results showed that there were differences in pressure fluctuations at different heights of the bladeless region, with the highest pressure fluctuations near the bottom ring.
Due to the highly coupled nonlinear process of the interaction between fluids and liquids, it is necessary to use fluid–structure interaction methods to solve the problem [
22]. Recently, the study of fluid–structure interaction (FSI) of centrifugal pumps has become a new hot topic in research. The positional variation of the impeller has been found to impact the internal flow field of the pump, subsequently altering the pressure pulsation and pump performance [
23,
24]. Baun et al. [
25] investigated the impeller-to-volute position and tried to find the optimal position for different volutes. Cao et al. [
26] conducted a study on centrifugal pumps under different eccentricity conditions; they observed a degradation in performance with increasing eccentricity. Tao et al. [
27] examined pump performance and pressure pulsation under an eccentric condition. They discovered that considering eccentricity allowed for the capture of multiple frequency components, including the rotation frequency and its multiples. Zhou et al. [
28,
29] focused on the study of the fluid excitation characteristics in centrifugal pump impellers with compound motion. The calculated results were closer to the experimental results when the compound motion was in a certain range. Zhao et al. [
30] determined that eccentricity could influence the head and radial force under cavitation conditions. Li et al. [
31] explored the internal flow fields of mixed-flow pumps with eccentric impellers, identifying increased eccentricity as the primary factor for decreased pump efficiency. From the research in the aforementioned literature, it can be observed that the effect of FSI is crucial for centrifugal pump rotor systems and it should not be neglected. Yuan et al. [
32] simulated impellers with different structures using a single fluid–structure coupling method and found that under the same flow rate, the maximum equivalent force value of the closed impeller was the highest, while the maximum equivalent stress value of the split impeller was the lowest. Shen et al. [
33] considered the fluid–structure coupling effect and analyzed pump rotors with different blade installation angles. They found that under the same flow rate, the axial force increases with the increase in the blade installation angle. At the same flow rate, the maximum deformation equivalent stress increases with the increase in the blade installation angle.
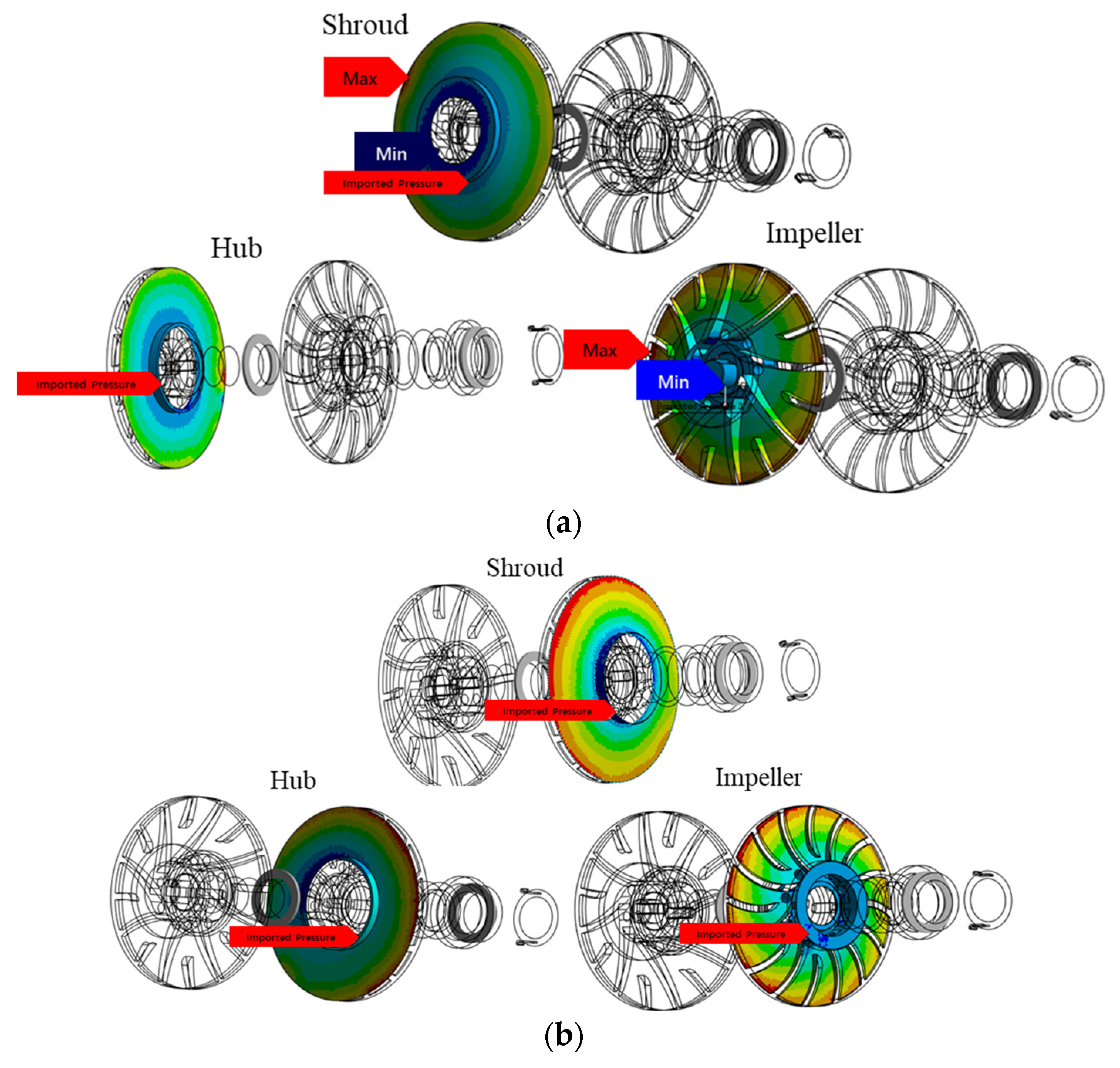
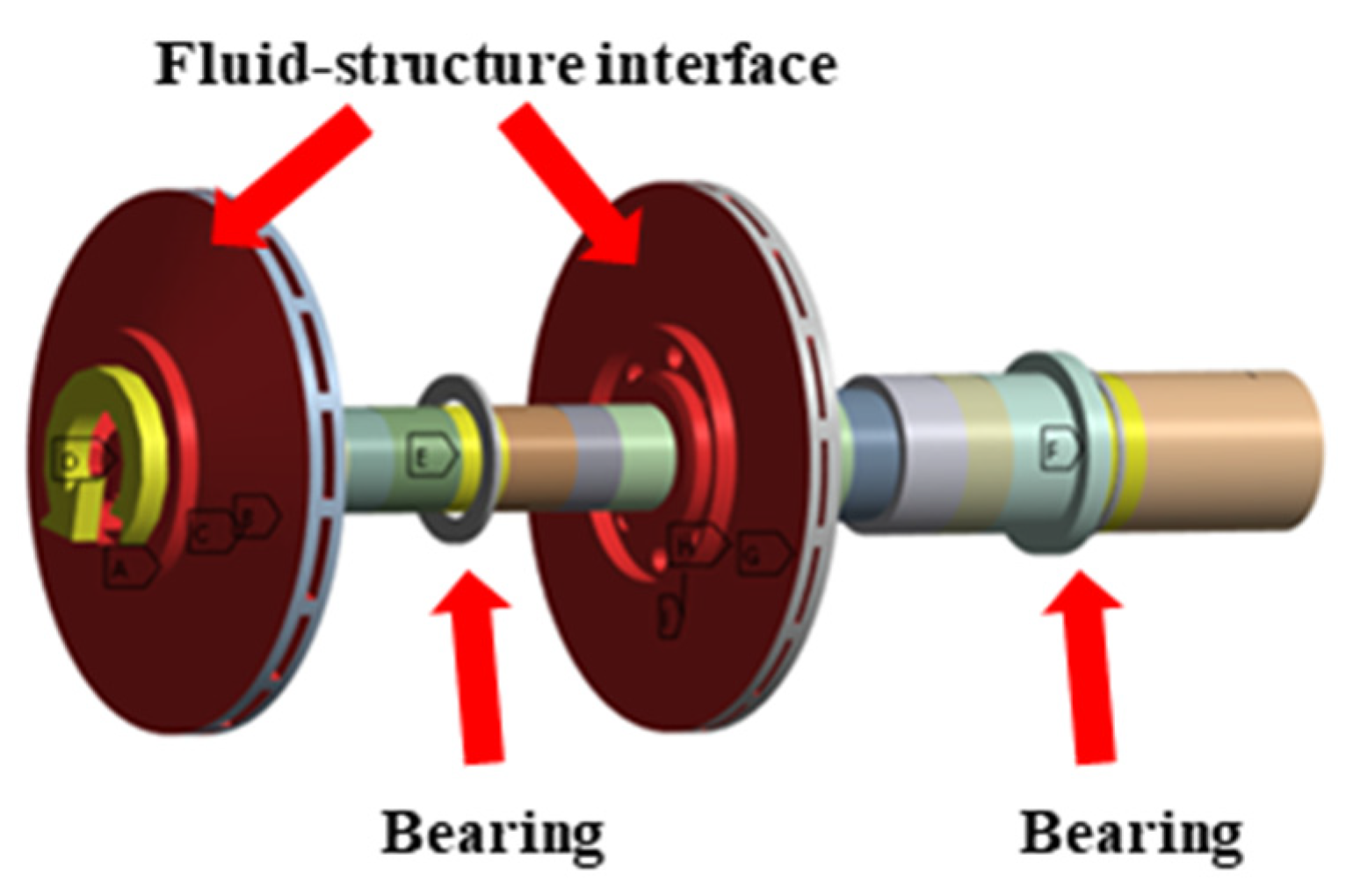
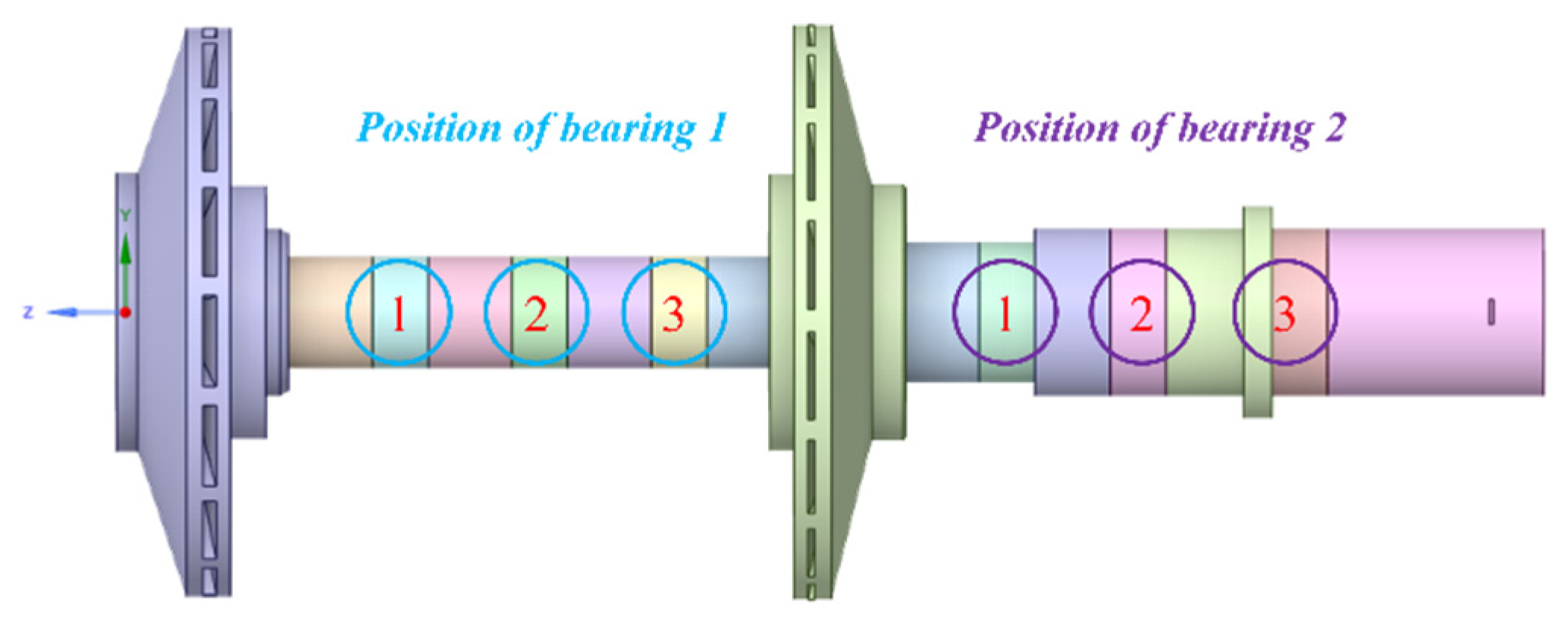
For ultra-high-speed centrifugal pumps, the current research is very limited, and the impact of FSI on the structure characteristics of the rotor system is still an unknown field. Therefore, it is crucial to explore the structure characteristics of the pump rotor system considering FSI. In this paper, a parallel double-stage ultra-high-speed centrifugal pump rotor system model with a rotational speed of 28,000 rpm was regarded as the research object, and the structure characteristics considering the FSI effect were studied for different flow rates, bearing positions, and bearing stiffnesses. The simulation results show good agreement with the experimental results. In addition, the optimal design results were obtained through an orthogonal test and the transient characteristics were further analyzed.
4. Conclusions
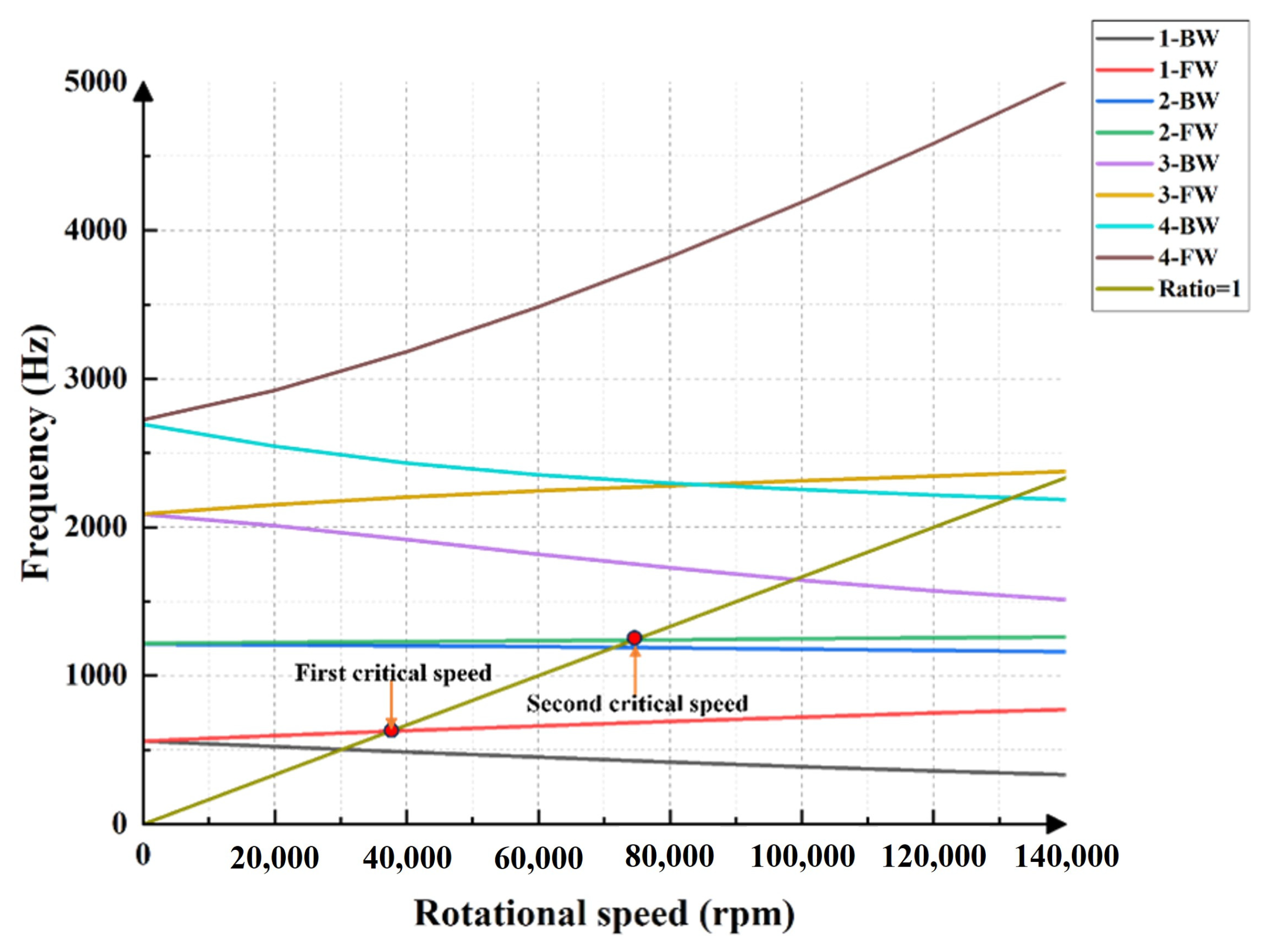
This paper investigates the structural characteristics of a parallel double-stage ultra-high-speed centrifugal pump rotor system considering the FSI. The steady characteristics of the coupled rotor system are analyzed using a Campbell diagram and modal shapes. The accuracy of numerical calculation is verified by the experimental data. The dynamic stress and deformation of the rotor system are obtained. Finally, the orthogonal test is conducted to explore the influence of flow rate, bearing position, and bearing stiffness on the transient structural characteristics of the system. The main conclusions are as follows:
1. The operating speed of the pump system is lower than the first critical speed. The existing cross-support structure meets high-speed stability requirements and there is no resonance in the cantilevered rotor system.
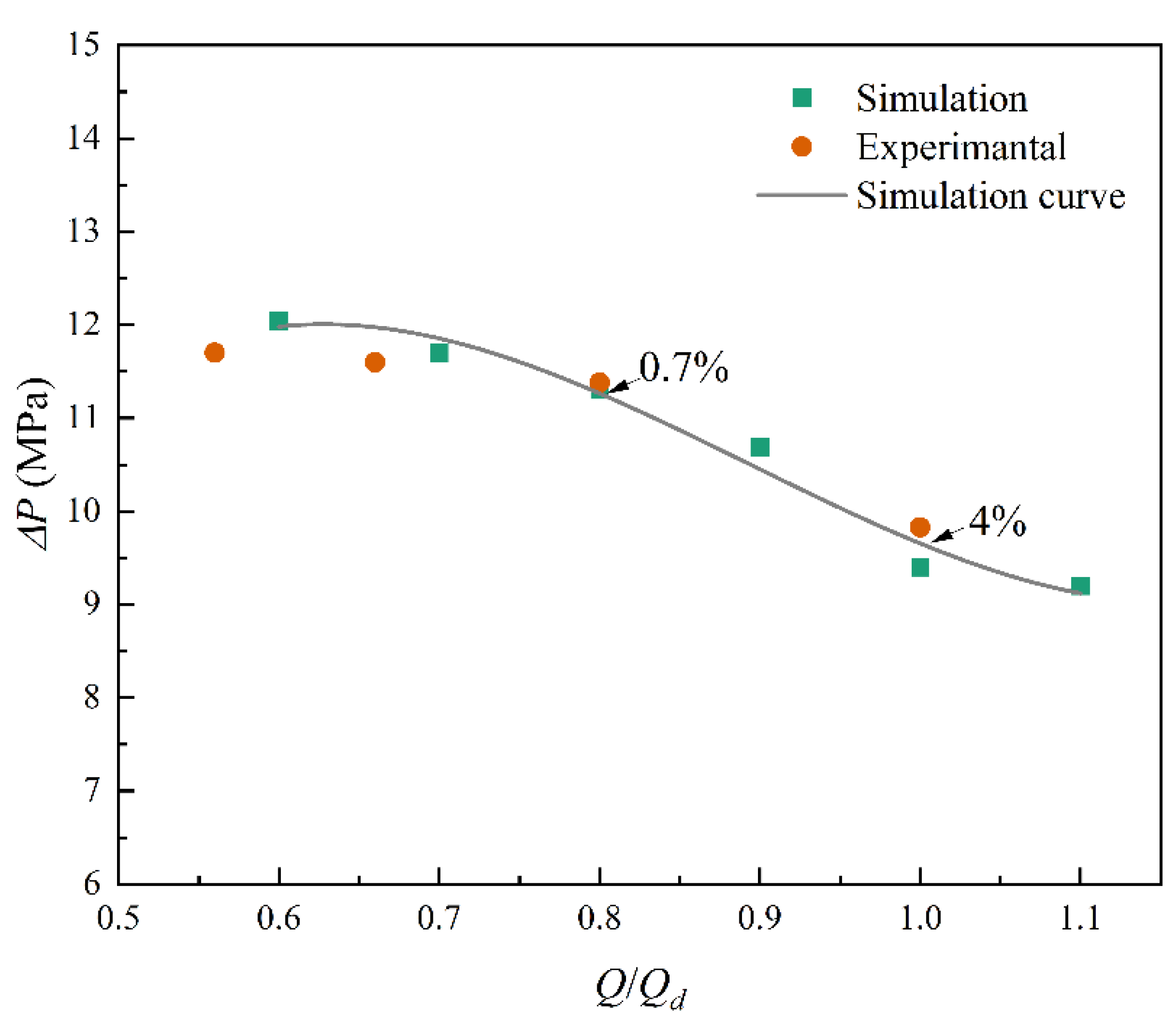
2. Compared with the numerical results and experimental data, the maximum and minimum errors for the head of Pump 2 are 4% and 0.7%, respectively. These small relative errors validate the accuracy of the proposed model.
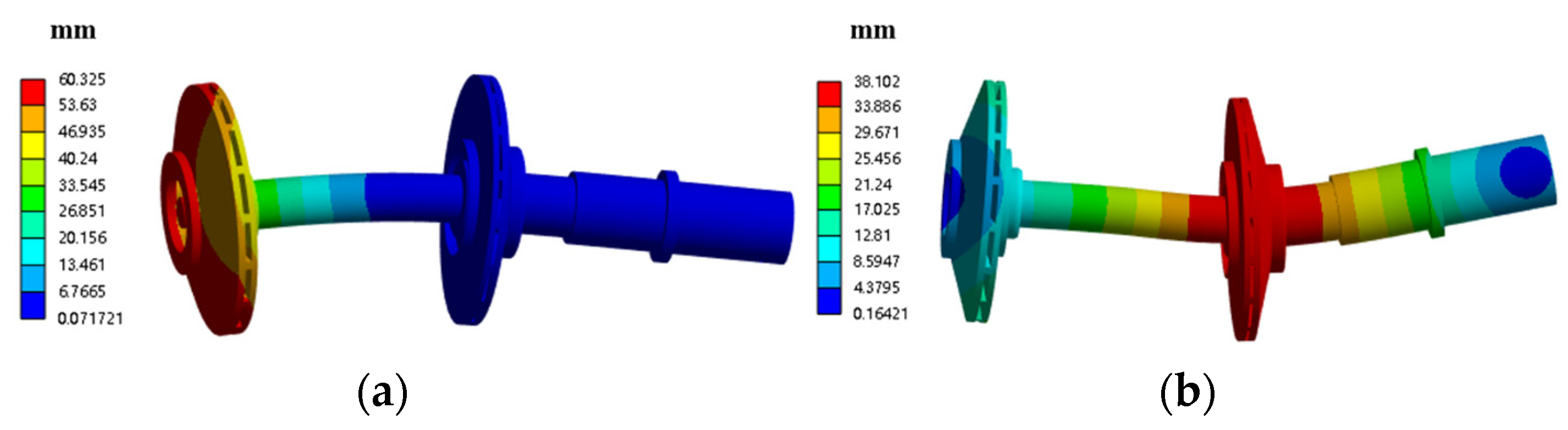
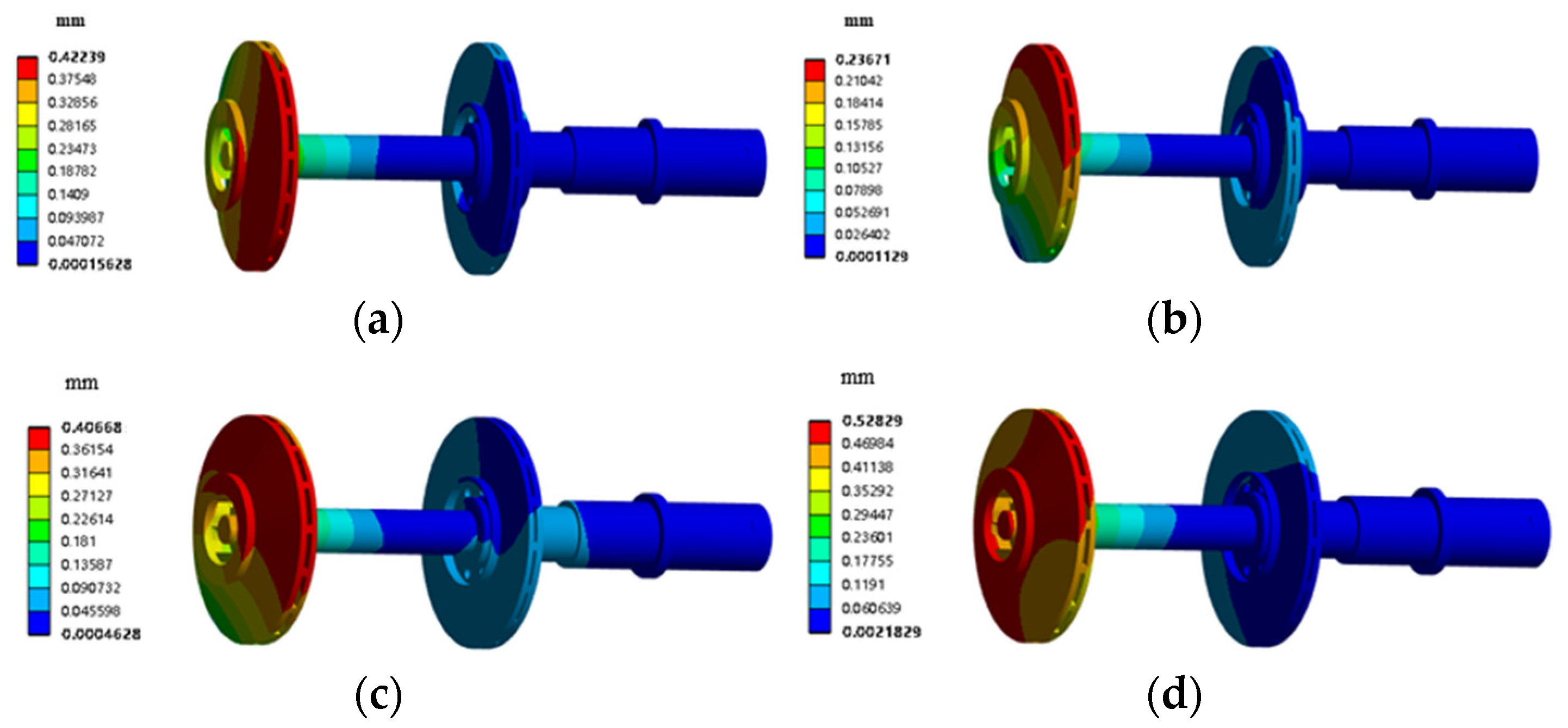
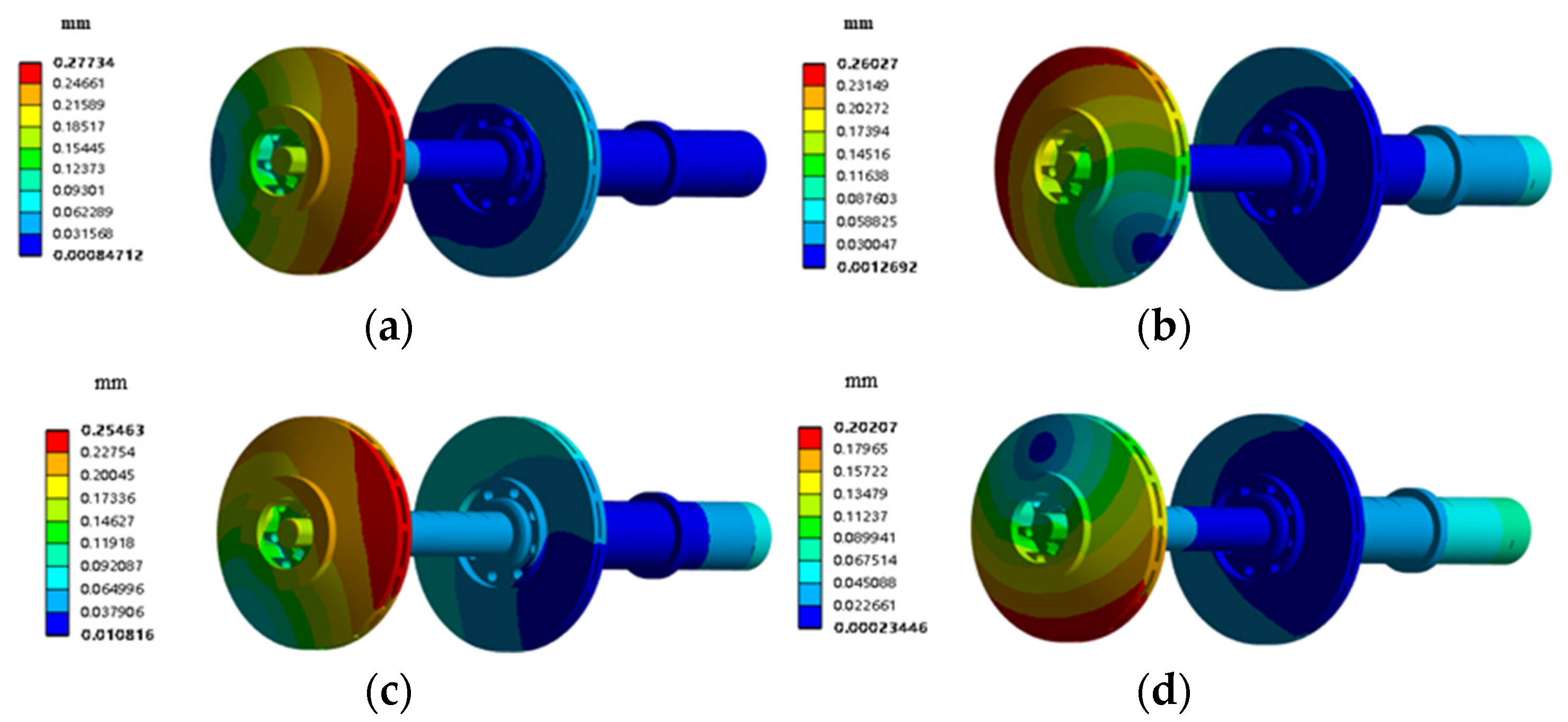
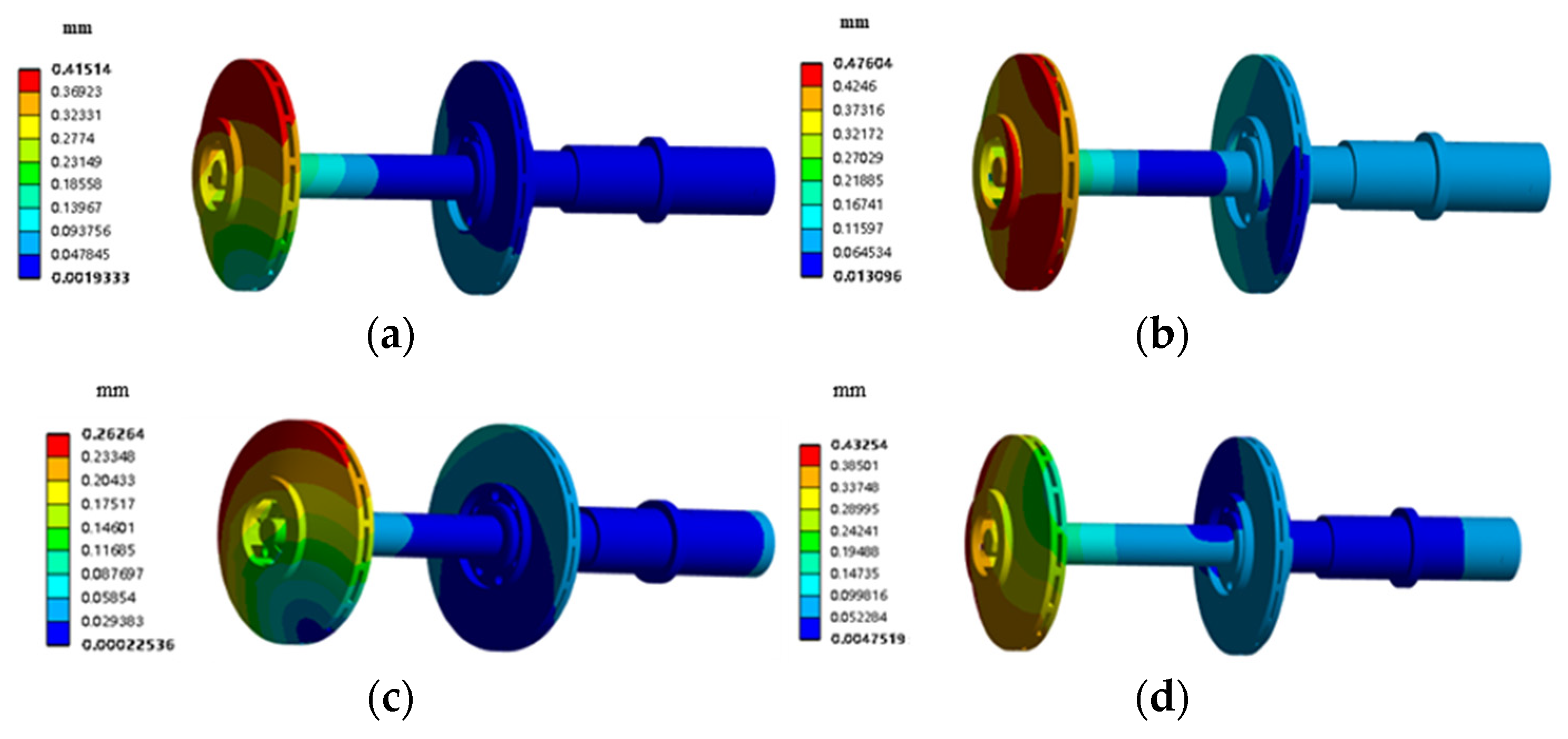
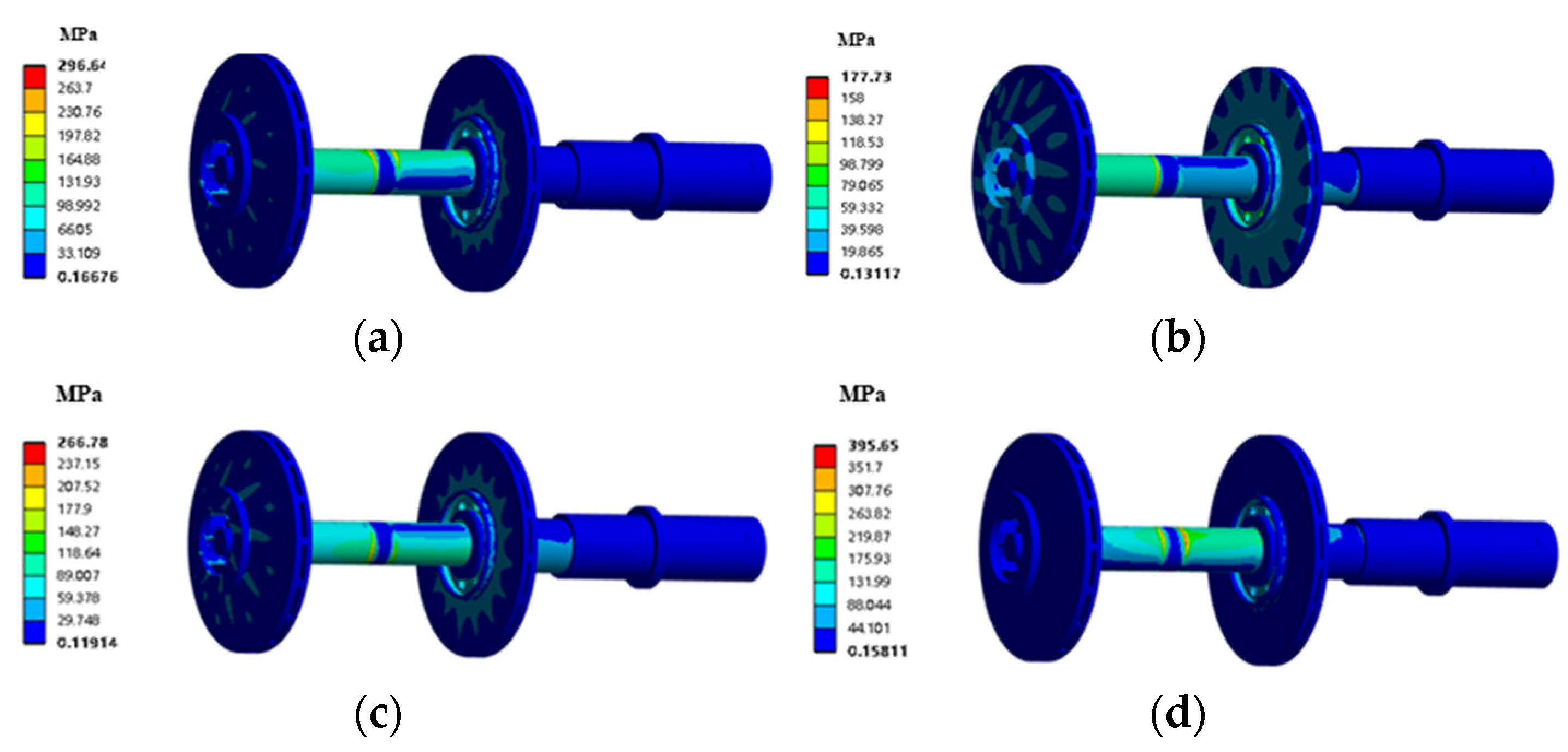
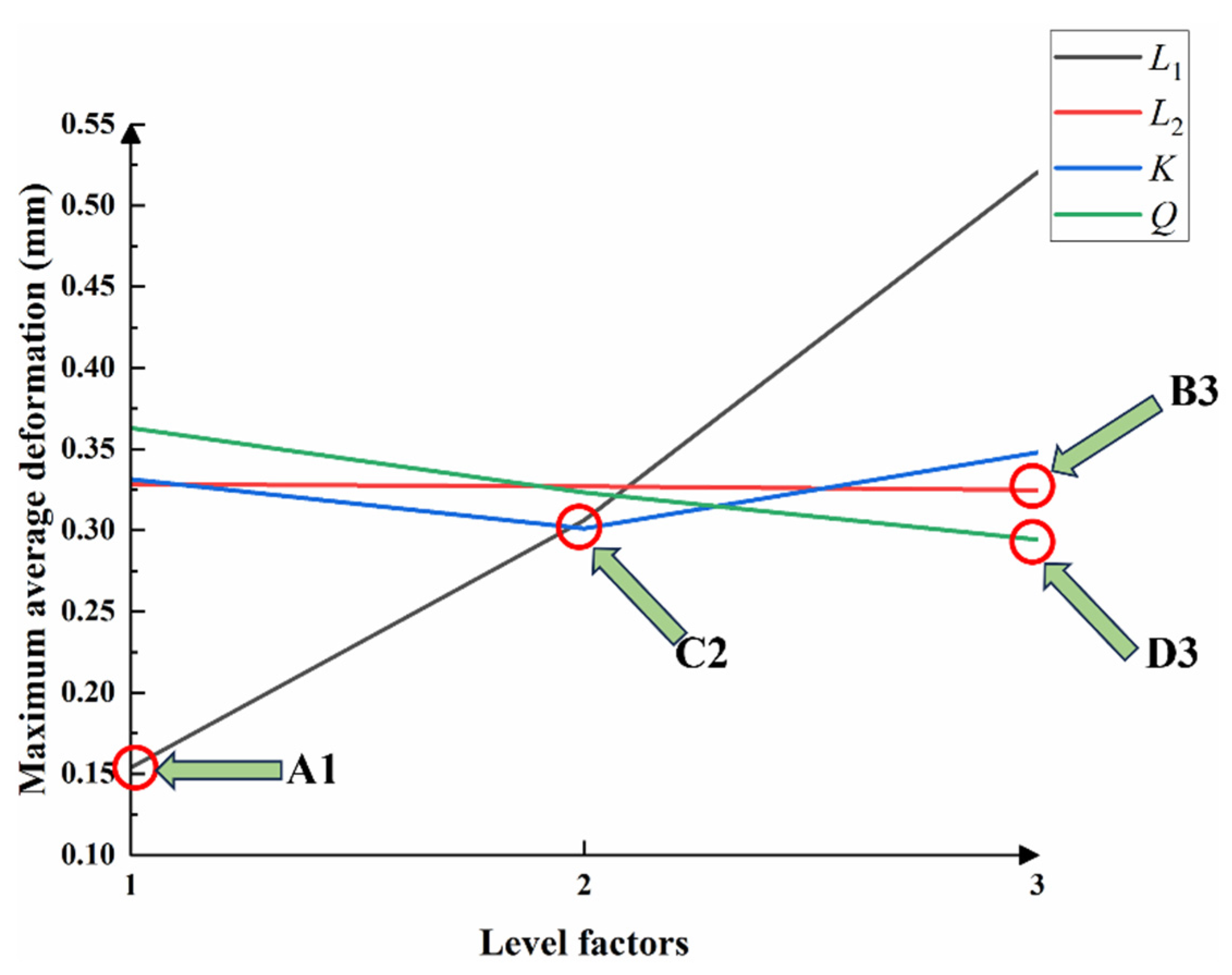
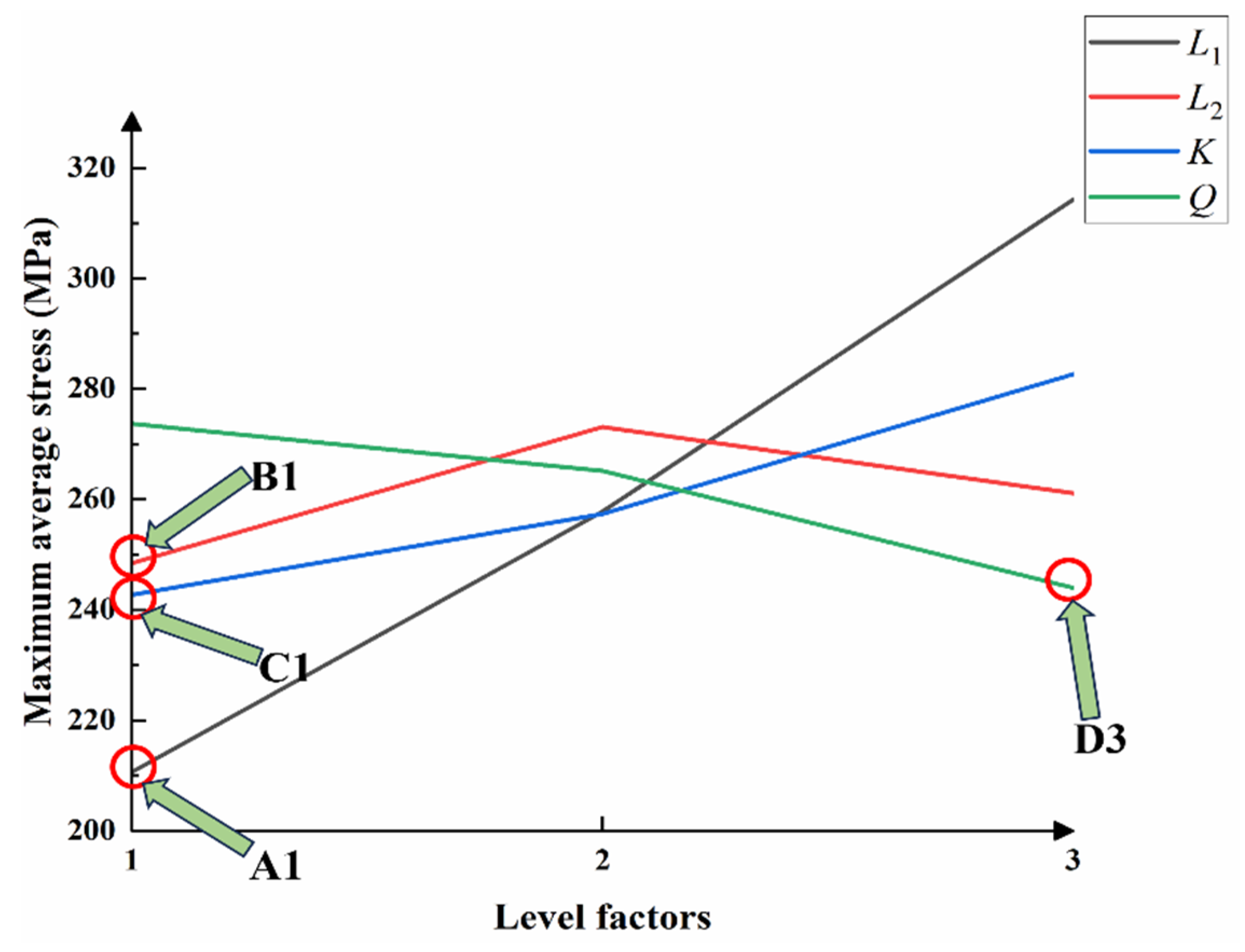
3. The minimum values for maximum average deformation and maximum average stress are less than 0.31 mm and 245 MPa, respectively, under design conditions. Variable flow conditions can lead to an increase in the maximum average deformation and stress.
4. The influence of each factor on the maximum average deformation is in the order of L1 > Q > K > L2. The influence of each factor on the maximum average stress is in the order of L1 > K > Q > L2. L1 has the greatest influence on the maximum average stress and stress of the rotor system. With the increase of L1, the maximum average deformation and maximum average stress increase.