Systemic Risk Analysis of Safety, Progress, and Investment in the Construction of a Water Transfer Project and the Importance of Common Cause Failure

Abstract

Safety, progress, and investment risks are correlated during the construction period of large-scale water transfer projects. However, previous studies have only considered individual risk factors, overlooking the potential systemic risk posed to safety, progress, and investment, as well as any underlying common cause failures. Since traditional risk analysis methods are ill-suited to addressing common cause failure, this paper’s objective was to establish a comprehensive evaluation index framework and to identify the basic events of common cause failure. To do that, we developed a risk analysis method that models common cause failure based on a Bayesian network for assessing that systemic risk. The Henan Section of the Yangtze-to-Huaihe River Water Diversion Project in China was then used as a case study. The results show that a variety of common cause failure events, such as epidemic disease, design alteration, lagged approval process, heavy rain in the flood season, renewal material and failing equipment, construction accidents, and external interference, can significantly impact the safety, progress, and investment systemic risk. Design alteration poses the greatest risk, with renewal material and failing equipment exerting the strongest influence among all common cause failure events. It is also possible to elucidate the predominant causal chains; specifically, the contributing influence of each basic failure event to the systemic risk can be clarified by adjusting their respective initial state. The failure of renewal material and failing equipment was found to significantly increase the safety risk. This study effectively simulated the complex causal relationships and uncertainties of pertinent risk factors, thereby enhancing our understanding of the systemic risk associated with safety, progress, and investment in large-scale water transfer projects.

1. Introduction

In recent years, an increasing level of government investment has been earmarked for the national infrastructure of water resources and hydropower engineering. In this respect, the most representative type of construction is the large-scale water transfer project, which provides an important way to solve the uneven distribution of water resources across time and space [1,2]. The large-scale water transfer project has several key characteristics: a long construction period (more than 5 years), a large amount of invested funds, many involved contributing factors, and wide-ranging social influences. These inevitably lead to differential risks arising in different construction periods of the project, and these risks are dynamic in that they change in their type and also shift in predominance [3,4]. In terms of types, a large-scale water transfer project is faced with safety risks, progress risks, investment risks, credit risks, environmental risks, political risks, and legal risks. In general, however, the main risks affecting large-scale water transfer projects can be subsumed under safety, progress, and investment risks [5,6,7,8].

Extensive research has been conducted on safety, progress, and investment risks [9,10]. To evaluate the safety risks, the LEC or improved LEC method is often used, which gauges risk as the product of three indicator values [11]: the likelihood of an accident or hazardous event (L, likelihood), the frequency of people’s exposure to hazardous environments (E, exposure), and the consequences of an accident occurring (C, consequence). A second approach, called the risk matrix method, can also be used to evaluate those three risks. In this approach, the degree of each risk is determined by jointly considering the probability (P) of several known risk factors and the consequence of risk loss (C). This method is simple and intuitive and less prone to making mistakes [12]. Both methods belong to the class of semi-qualitative and semi-quantitative methods. Concerning a more quantitative approach, the AHP-fuzzy comprehensive risk assessment method can be used to analyze safety risks during the construction period of infrastructure projects [13,14].

As more research on risk analysis is pursued, the relevant risk assessment data are becoming increasingly dependent on various expert evaluation systems [15,16,17]. Furthermore, most studies still focus on a single risk factor (e.g., only consider safety risk or progress risk) pertaining to safety, progress, and investment risks [18], leaving unexamined the potential systemic risk during the construction period and correlations between these three risk categories. Moreover, the risk due to common cause failures in the overall safety, progress, and investment system remain neglected and unaccounted for in such studies. When conducting a risk assessment, the traditional risk analysis method often assumes that the judgment of failure for each risk factor is independent of other risk factors in the system, but this itself is prone to excessive judgment error. Common cause failure (CCF) refers to the failure of two or more elements simultaneously or in a short time interval in the system under the influence of some shared cause [19]. During the construction period of large-scale water transfer projects, two or three risk failures among safety, progress, and investment risks may co-occur due to one causal factor, such as non-compliant construction, human-made operational mistakes, or disturbance to the site environment. Different types of risks or failure events caused by the same hazard sources are thus aptly termed common cause risks or CCFs; these are capable of reducing the system’s overall reliability. Hence, the relative independence assumption of failure probability of each risk in the system is no longer tenable (i.e., invalid) because of the CCF theory [20]. At present, the effect of common cause failure on systemic risk analysis of water projects remains insufficiently explored. Only Serrano-Lombillo et al. [21] and Bowles et al. [22] referred to common cause failure or common cause adjustments in systems of dams, but they didn’t study common cause failure quantitatively or its effect on systemic risk.

Given the complexity of the risk system for large-scale water transfer projects, a fault tree analysis approach is too complicated and cumbersome [23]. Instead, a Bayesian network, rooted in graph theory and the Bayesian probability formula, can clearly and quantitatively express the complex causality and uncertainty between variables. It is, therefore, a key method for capturing and conveying uncertainty so as to robustly infer and analyze the state and probability distribution of each variable by its conditional probability [24]. The main objective of this study was to develop a systemic risk analysis method for safety, progress, and investment considering CCF based on a Bayesian network in the construction of a water transfer project. Here, the Henan Section of the Yangtze-to-Huaihe River Water Diversion Project in China was chosen as a case study. First, a comprehensive evaluation index framework for safety, progress, and investment risks was established. Next, by analyzing these, the basic events of CCF that lead to two or three risk failures among safety, progress, and investment risk categories were identified, with the failure modes of system coupling investigated. Then, in combination with plausible causal relationships between various risk factors, a risk analysis model that explicitly considers CCF for the safety, progress, and investment system during the construction period of this large-scale water transfer project was derived based on the Bayesian network. Further, by adjusting the initial state of CCF events, backward reasoning was carried out to distinguish the prominent causal chains. In this way, the importance of CCF and how basic events of CCF shape the systemic risk posed for safety, progress, and investment was clarified.

2. Study Area

The Henan Section of the Yangtze-to-Huaihe River Water Diversion Project started construction in July 2019 and completed the major test for transferring water in December 2022. This project was primarily designed to supply water to the water-receiving area of China’s Henan Province via the Xifei River. Its main task was to eventually supply water to both urban and rural areas, as well as the local rivers and lakes, to improve the ecological environment. The project is classified as Grade I, indicating it is a large-scale project; its construction sites encompass six counties (districts): Dancheng County and Luyi County in Zhoukou City and Zhecheng County, Suiyang County, Yongcheng County, and Xiayi County in Shangqiu City [25,26]. The layout of this project is shown in Figure 1.

This water project’s construction began in the boundary area between the Henan and Anhui provinces. It diverts water to Henan through a three-stage pumping station from the Qingshui River to the upper reaches of the Shiliang floodgate. Then, the water flows via gravity through the Luxin Canal to the Houchenlou storage reservoir in Luyi County. From there, the water is further diverted to Zhecheng County, Suiyang County, and Xiayi County via a pressurized pumping station and pressure pipeline (Figure 1). The main components of this project include two open channels, three water pipelines, four storage reservoirs, and five pumping stations, along with various ancillary structures (consisting of 148 crossings over rivers, highways, and high-speed railways). The project is divided into seven sections, each featuring different construction tasks. Sections one to four mainly entail river projects, while sections five to seven focus mainly on pipeline projects.

China’s Ministry of Water Resources initially approved a 5-year construction period for this project. However, to meet the provincial government’s requirements, the project must actually be implemented within a 4-year period. Furthermore, the core of the project was completed within 3 years to ensure it meets the water supply conditions, thus maximizing the water conveyance benefit. The total investment in construction amounted to 7.65 billion yuan.

Through the on-site investigation of the project, we collected a large amount of information about on-site construction, including the main construction projects and annual or monthly progress plans and reports. Then, the main issues encountered during its construction so far were summarized. These mainly consisted of (1) significant delays in land acquisition and approval, (2) slow progress in the protection of cultural relics, and (3) slow progress caused by design alterations to the Houchenlou Reservoir in Luyi County and Xincheng Reservoir in Shangqiu City. The adjustments made to the construction period of each construction section can be summarized as follows. (1) The total progress of the fourth construction section was revised in September 2020, not only due to challenges in expropriation and relocation procedures but also the altered design for the storage reservoir of the Houchenlou Reservoir. The resulting delay in construction amounted to 358 days. (2) Completion of the second construction section was partially hindered by an epidemic disease (COVID-19), leading to the pre-flood construction milestones and investment targets not being met on schedule. Adjustments to the annual progress plan were made in February 2020.

From the investigation and summary of the constraints of the investment plan’s implementation, several main reasons for those adjustments were evident. These include (1) the outbreak of epidemic disease (COVID-19); (2) significant design alterations; (3) adjustments in central planning; (4) the impact of land acquisition; (5) complicated changes and evaluation procedures resulting from complex river-crossing engineering; (6) multiple expert argumentations required for justifying changed procedures; and (7) external interference surrounding the construction of the Luxin Canal. Because it involves 46 sewage outlets flanked by many residents, pollution discharge into the river during the water project’s construction period significantly disrupted its implantation and progress and, subsequently, the level of investment.

3. Methodology

3.1. Comprehensive Evaluation Index Framework for Safety, Progress, and Investment Risks

A critical factor to consider in the risk analysis of a safety, progress, and investment system during the construction of a long-distance, large-scale water transfer project is how to devise a comprehensive evaluation index framework for assessing systemic risk. This study delved into risk factors related to safety, progress, and investment; selected indicators for risk assessment based on established principles; and then combined research findings of risk source types with actual situations encountered during the water project’s construction period. Further, by referring to the relevant literature [27,28], norms (Guidelines for hazard identification and risk assessment in the construction of water resources and hydropower engineering in China), and expert knowledge, those risks generally perceived to have minimal impacts were screened out. This led to the development of a comprehensive evaluation index framework for safety, progress, and investment risks, as depicted in Figure 2.

This paper established a three-level index framework for the safety, progress, and investment systemic risk evaluation. Specifically, it consists of three first-level indicators, 10 second-level indicators, and 33 third-level indicators. Within this framework (Figure 2), various safety risks were further categorized into personnel risk, material and equipment risk, and site risk during the construction period. Progress risk can be decomposed into social and environmental risk, technical material and equipment risk, and organizational management risk. Similarly, investment risk is divided among social and political risks, natural environmental risks, design management risks, and financial and economic risks.

3.2. Analysis of CCF for Safety, Progress, and Investment of Large-Scale Water Diversion Projects during the Construction Period

3.2.1. CCF Model

As noted before, CCF denotes the concurrent failure of two or more risk factors due to a shared cause. In considering CCF, the basic events in systemic risk comprise CCFs and independent failures; Figure 3 illustrates the correlation between these two types of failure for the three risk factors: safety (S), progress (P), and investment (I). The risk failure rate λ can be determined with simulation tests or using expert experience. Specifically, λ has two components: the failure rate resulting from independent failure (λ₁) and that from CCF in various stages (λ₂, λ₃), which can be summed accordingly [29,30]:

λ = λ₁ + λ₂ + λ₃

(1)

Here, λ₁ is the independent failure, such as λ_S, λ_P, and λ_I (the yellow part) in Figure 3; λ₂ is the failure rate of second-stage CCF, whereby two risk factors falter in tandem from a shared cause, such as λ_SP, λ_PI, and λ_SI (the white part); likewise, λ₃ is the failure rate of third-stage CCF, whereby three risk factors fail simultaneously due to a common cause, for instance λ_SPI (the blue part).

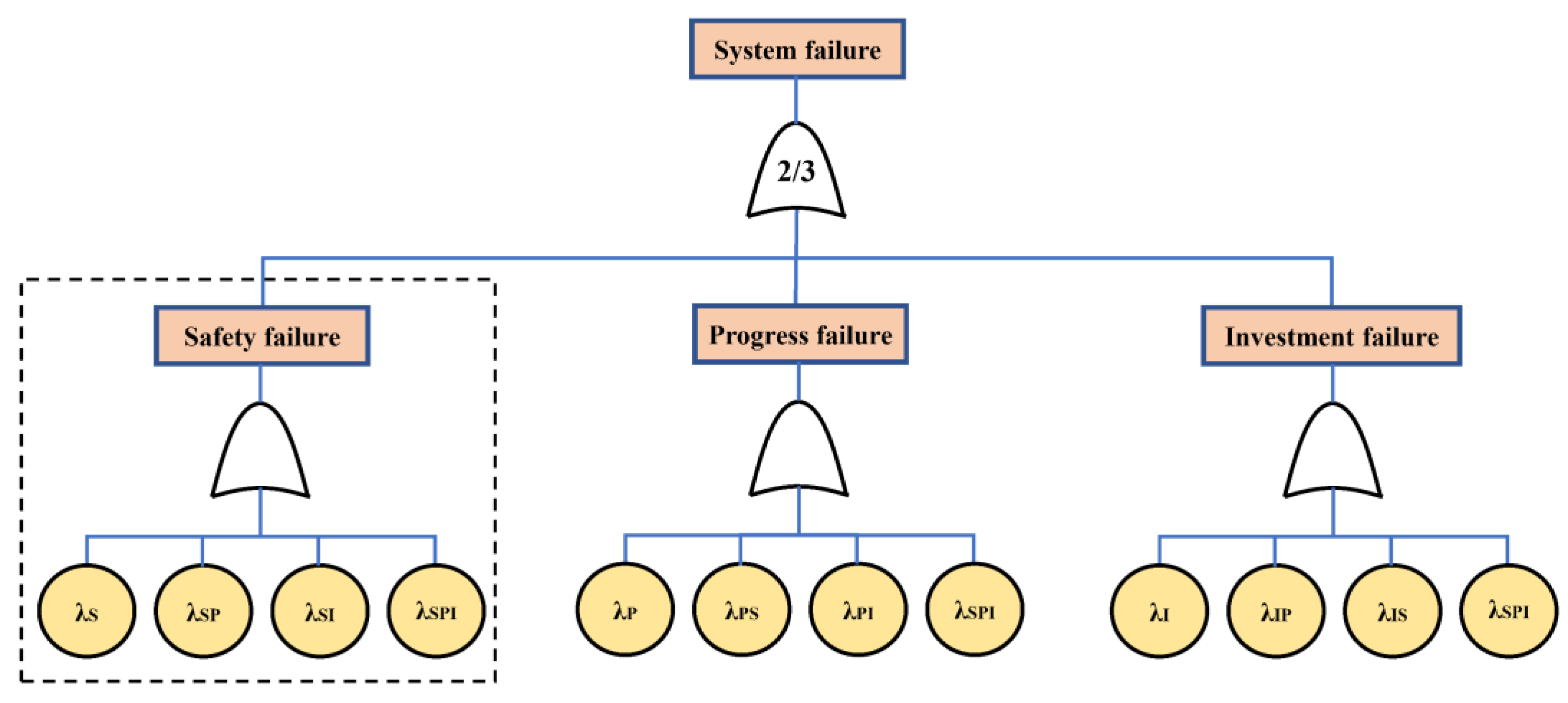
The fault tree model for the 2/3 voting system (a system that has three units does not fail as long as two units do not fail) is presented in Figure 4. Figure 4a shows that the three risk categories—safety, progress, and investment—share the same function and structure when ignoring any CCF. Figure 4b depicts a scenario that considers CCFs. It can be easily seen that basic events in the fault tree are composed of independent failures and CCFs. CCF can be considered as a distinct basic event, requiring the establishment of a corresponding event module.

3.2.2. Considering CCF in the Safety, Progress, and Investment Risk Analysis of the Water Project’s Construction Period

A simplified tree model for safety, progress, and investment CCF is illustrated in Figure 5. In this simplified model, the three components of the system are assumed to be independent of each other. This means that the failure of one component does not affect the failure probability of any other component. These components are the following:

(1) The probability of a single failure of the safety part is denoted by λ_S;

(2) The occurrence probability of a safety and progress CCF is denoted by λ_SP;

(3) The occurrence probability of a safety and investment CCF is denoted by λ_SI;

(4) The occurrence probability of CCF of safety, progress, and investment is denoted by λ_SPI.

Hence, the summed probability of safety failure λ_AFAIL can be expressed as follows:

λ_AFAIL = λ_S + λ_SP + λ_SI + λ_SPI

(2)

The sum of the failure probabilities of the safety, progress, and investment system can then be expressed as follows:

λ_SYSTEMFAIL = λ_Sλ_P + λ_Pλ_I + λ_Sλ_I + λ_SP + λ_PI + λ_SPI

(3)

The minimum cut-off sets of the fault tree in Figure 5 are as follows: {λ_S, λ_P}, {λ_P, λ_I}, {λ_S, λ_I}, {λ_SP}, {λ_SI}, {λ_PI}, {λ_SPI}.

However, if CCF is not taken into account, the probability of failure for the safety, progress, and investment system is obtained as follows:

λ_SYSTEM = λ_Sλ_P + λ_Sλ_I + λ_Pλ_I

(4)

3.3. Risk Analysis of the Safety, Progress, and Investment System in the Water Project’s Construction Based on a Bayesian Network

When faced with a system that has many indicators, traditional fault tree analysis can become highly complex and challenging. In such cases, the Bayesian network method may offer an alternative approach for a robust risk analysis.

3.3.1. Bayesian Network Theory

A Bayesian network is based on the conditional probability formula, which expresses the relationship between prior probability and posterior probability, using the prior probability to deduce the probability of future accidents. Bayesian networks are widely used in risk analysis and uncertainty analysis. Events B1, B2, …, Bn are a set of incompatible complete events; B_i is a discrete variable, and p(B_i) > 0; and A is an arbitrary event. The theoretical basis formula for any Bayesian network is as follows:

$$p\left(B_i|A\right)=\frac{p\left(B_i\right)p\left(A|B_i\right)}{{\displaystyle \sum _{i=1}^{n}p\left(B_i\right)p\left(A|B_i\right)}}$$

(5)

where p(B) is the prior probability, p(B|A) is the posterior probability, and p(A|B) is the likelihood function.

3.3.2. Structure and Construction of a Bayesian Network

A Bayesian network is a highly effective graphical decision-making tool that is widely used for reasoning and data analysis in complex problems involving uncertainty. In recent years, the Bayesian network approach has been increasingly applied in the field of risk analysis to better address various uncertainties and complex issues [31,32]. In this vein, we propose such an approach, one integrated with a comprehensive evaluation index framework for safety, progress, and investment risks, to analyze the systemic risk associated with the construction phase of large-scale water transfer projects. This approach aims to effectively integrate multiple sources of information by considering their correlations. Moreover, empirical data are utilized to estimate the parameters of the network’s structure, thereby reducing the subjectivity of parameter determination.

Bayesian networks are composed of Directed Acyclic Graphs (DAGs) and Conditional Probability Tables (CPTs). A DAG is established based on the relationships between states of each variable, conforming to graph theory principles. A DAG comprises nodes and directed line segments, with the nodes denoting random variables; two nodes are connected by a single arrow, which indicates a direct causal relationship from the parent node A to the child node C [33,34]. The directed line segments signify the correlation and causality between nodes, as illustrated in Figure 6 for a simple Bayesian network. Each variable is categorized into different states, and for the link between two variables (the ‘cause’ [parent variable] and the ‘effect’ [child variable]), the use of CPTs is needed to quantify the strength of their relationship. The values of CPTs can be derived from a suite of sources, including literature research, historical data, field monitoring data, expert opinion scores, and random sampling or by employing the likelihood weighting algorithm proposed by Korb and Nicholson [35] to calculate an approximate solution for the posterior probability. Bayesian networks have three main types of nodes: target, decision, and state nodes. For instance, the safety, progress, and investment systemic risk was the target node in this paper.

3.3.3. Implementation of Bayesian Networks

This study used the Netica software by Norsys Software Corp. (https://www.norsys.com/netica.html, accessed on 8 May 2024) to build a Bayesian network to facilitate inferential analysis. Netica is a highly practical and efficient software tool specifically designed for Bayesian network analysis. It enables swift probabilistic reasoning and is capable of detecting and learning from probabilistic relationships in the data.

4. Results

4.1. Construction of a Safety, Progress, and Investment Systemic Risk Model That Considers CCF

The fault tree model developed here is able to address CCF arising within the safety, progress, and investment system. According to the summarized information in Section 2 (the last two paragraphs), in accounting for various risk failure forms, a total of seven CCF basic events (

Table 1. The basic events of common cause failure and their failure probability.

No.	Basic Event	Safety Risk	Progress Risk	Investment Risk	Symbol	Probability
1	Epidemic disease	√	√	√	G1	0.0004
2	Design alteration	×	√	√	G2	0.0306
3	Lagged approval process	×	√	√	G3	0.0071
4	Heavy rain in the flood season	√	√	×	G4	0.0055
5	Renewal material and failing equipment	√	√	√	G5	0.0015
6	Construction accidents	√	√	√	G6	0.0002
7	External interference	×	√	√	G7	0.0033

) were included to ensure a comprehensive failure rate analysis. Table 1 shows which risk factors fail simultaneously as a result of one CCF event.

By applying the methodology described by Yazdi et al. [36], the risk fault tree model for the safety, progress, and investment system in the water project’s construction period was created by incorporating the basic events of CCF. This model, shown in Figure 7, enabled the identification of risk coupling modes within that system. In Figure 7, the basic event symbol (each indicated by a green annotation) corresponds to the CCF basic events listed in Table 1.

4.2. Systemic Risk Analysis of Safety, Progress, and Investment during the Construction Period

4.2.1. Risk Analysis of CCF Basic Events Associated with the Safety, Progress, and Investment System

The failure probability values of CCF basic events (column 7 in Table 1) were determined using the collected information about the on-site construction of the Yangtze-to-Huaihe River Water Diversion Project (i.e., its Henan section). The failure probability of G1 was determined using the probability of an epidemic disease happening and the proportion of project delays it causes during the construction period. The probability of design alteration occurrence can be calculated using the design alteration rate, which is the ratio of the total cost of design change to the dynamic cost. For G2, its failure probability was determined using the design change that occurred during the construction period of the water diversion project. The probability of delay in the approval of resettlement work was obtained by calculating the changed cost of construction land acquisition and resettlement compensation to the total cost of resettlement. The failure probability of G3 was determined using changes in the resettlement process during the construction period of the project, while that of G4 was simply the ratio of heavy rain days to the total number of days [37]. For G5, its failure probability was related to material update equipment failure, which was calculated using the material update rate and equipment failure rate, the latter determined this way: [downtime waiting time + maintenance time] / total planned use time, as formulated by Luo et al. [38]. The failure probability of G6, which was associated with construction accidents, was obtained from the ratio of these to the total number of people during a statistical period, as per Koc and Gurgun [39], and two reports (i.e., The 2017 National Bureau of Statistics Report on the Development of the Construction Industry in the 40 Years of Reform and Opening Up and the National Construction Safety Production Situation Analysis Report).

External interference in construction refers to the influence of the Luxin Canal. Since the project has 46 sewage outlets along its length, with many residents on either side of the river, much sewage has been discharged during the construction period, which can threaten the water quality safety of the project. Construction interference can have a pronounced impact on the progress aspects of the water project and subsequently affect investment levels. However, while it chiefly affects the start time of subprojects, it does not substantially alter the overall progress. The probability of external interference (G7) in construction was calculated by measuring the increase in design change investment—for engineering treatments applied to the Luxin Canal and Baigou River crossing—as a proportion of total annual investment.

4.2.2. Coupling Failure Mode Analysis of the Safety, Progress, and Investment System in the Construction Period When Considering CCF

This coupling analysis was also based on the collected information about the on-site construction of this project. As before, the safety, progress, and investment systemic risk categories were assumed to be independent of each other. These components of CCF can be defined as follows:

Individual failure of safety, denoted by λ_S, represents the summed failure probability of all other events except G1, G4, G5, and G6 in the safety failure scheme in Figure 7. Individual failure of progress, denoted by λ_P, represents the summed failure probability of all other events except G1 to G7 in the progress failure scheme in Figure 7. Individual failure of the investment part, denoted by λ_I, represents the summed failure probability of all other events except G1, G2, G3, G5, G6, and G7 in the investment failure scheme in Figure 7. Failure of safety and progress, denoted by λ_SP, is the probability of G4 in Figure 7. Failure of safety and investment has a zero probability. Failure of progress and investment, denoted by λ_PI, is the summed probability of G2, G3, and G7 in Figure 7. Failure of safety, progress, and investment, denoted by λ_SPI, is the summed probability of G1, G5, and G6 in Figure 7.

It is evident from Equation (3) and Figure 7 that the fault tree analysis method is overly complex and burdensome. Hence, for inferential analysis, this paper instead applies the Bayesian network method, since it enables a clearer depiction of the causal logical relationships between each event.

4.3. Bayesian Network-Based Risk Analysis of the Safety, Progress, and Investment System during the Construction of a Large-Scale Water Diversion Project

4.3.1. Building the Bayesian Network for the Systemic Risk Analysis of Safety, Progress, and Investment

The assembly of this Bayesian network to incorporate CCF was based on literature analysis, expert interviews, and field investigation results. The parent and child nodes in the network’s structure were determined by incorporating the comprehensive evaluation index framework of the safety, progress, and investment system, along with its CCF basic events. The resulting Bayesian network, as presented in Figure 8, was then utilized to analyze the causal relationships between various risk factors. Moreover, the outcome of this Bayesian network was then expressed as a probability distribution for each sub-variable.

In this case study, to analyze the safety, progress, and investment systemic risk during the construction period of the water diversion project, various data sources were utilized. These included the comprehensive evaluation index framework for safety, progress, and investment systemic risk; safety accident data; the rectification data of hidden safety dangers; and expert experience. The analytic hierarchy process-fuzzy comprehensive evaluation method and the LEC method were employed to assess the systemic risk, yielding the failure probability for each factor in each index layer. Within the proposed Bayesian network, the identified main risk source factors (node variables) associated with safety, progress, and investment risks were interconnected. Each node in the network indicated a driving factor of risk. According to the field survey data and a given node’s state, each variable (node) was discretized into two states: success and failure.

Here, the decision node represented the basic events of CCF, with its prior probability derived from the risk analysis performed in Section 4.2.1. The intermediate nodes corresponded to the criterion layer and index layer within the comprehensive evaluation index framework. The prior probability and CPT of each node were then determined by using the risk analysis of the safety, progress, and investment system during the water project’s construction period. The target nodes encompassed the systemic risk arising from safety risk, progress risk, and investment risk, for which the conditional probability distribution is determined by applying the concept of a 2/3 voting system, as described in Section 3.2.1. As an example, the resulting CPT for the safety risk category is shown in

Table 2. The conditional probability table of safety risk.

Personnel Risk (S1)	Material and Equipment Risks (S2)	Site Risk (S3)	Safety Risk (S)
success	success	success	success
success	success	failure	success
success	failure	success	success
success	failure	failure	failure
failure	success	success	success
failure	success	failure	failure
failure	failure	success	failure
failure	failure	failure	failure

.

4.3.2. Backward Reasoning and Inferring the Dominant Causal Chains

According to the reverse reasoning algorithm of Bayesian network theory, the target node “safety, progress, and investment systemic risk” can be set to a 100% failure rate. This means that when the failure of that systemic risk occurs, the key risk factors in the Bayesian network could be analyzed. The most significant risk of CCF was G2 (design change), with a failure probability of 62.1%. Both G1 (epidemic disease) and G4 (heavy rain in the flood season) were ranked the next highest, with failure probabilities of 60.7% and 39.5%, respectively. The occurrence of one or more of these three events leads to the failure probability of the safety, progress, and investment systemic risk becoming higher.

Likewise, by setting the target node “safety, progress, and investment systemic risk” to a 100% failure rate, the causal chains can be inferred to detect the dominant ones. After analyzing here, G2 (design change) emerged as the major source of failure for the safety, progress, and investment system. This failure (G2) will cause the nodes in the causal chain to falter, such that G2→P21→P2→P→ safety, progress, and investment system failure and G2→I31→I3→I→ safety, progress, and investment system failure. These two chain factors are thus vital to the project’s progress lag management; hence, they should be the primary focus when managing the progress of this case study’s water diversion project.

4.3.3. Response of Target Variables to Different Scenarios Associated with CCF Events

According to the established Bayesian network, when the state of a certain node is modified or its probability distribution is adjusted, it becomes possible to infer how the probabilities of other nodes change in each state. Hence, one can analyze the magnitude of change in the probability of different states for a given target variable in response to different scenarios. In this section, the response of each target variable to various CCF scenarios is examined using the results in

Table 3. The magnitude of change in probabilities obtained for the response of target variables to different scenarios associated with CCF events.

Failure of Different Scenarios	Target Variables
	Safety Risk (S)	Progress Risk (P)	Investment Risk (I)
Epidemic disease (G1)	0.193	0.005	0
Design alteration (G2)	0	0.002	0
Lagged approval process (G3)	0	0.004	0
Heavy rain in the flood season (G4)	0.002	0.003	0
Renewal material and failing equipment (G5)	0.203	0.011	0.001
Construction accidents (G6)	0.113	0.007	0.001
External interference (G7)	0	0.005	0

.

Compared with the normal state (i.e., the current situation), the failure of G5, which concerns renewal material and failing equipment, will significantly impact the safety risk. Additionally, the failure of G1, which is linked to epidemic disease, and G6, which is associated with construction accidents, will also have serious consequences for the safety risk. In terms of progress risk, the failure of G5 will have a major impact on it, followed by G6. Finally, failures in both G5 and G6 will affect the investment risk. Evidently, when CCF events happen, the failure of renewal material and failing equipment exert a substantial influence on safety, progress, and investment risks. This is because the failure of renewal material and failing equipment is a recognized fundamental factor in the failure of the safety, progress, and investment system (see Table 1). In comparison to the effect of G5, although G1 and G6 also contribute to the failure of safety, progress, and investment, according to probability analysis based on the Bayesian network used, these two factors have a relatively weak impact on the failure of the safety, progress, and investment system of the water project’s construction phase. Unlike G5, G1, and G6, as described above, G2, G3, G4, and G7 only contribute to the failure of two target variables in this case study. Therefore, the basic event of material renewal and failing equipment should be paid more attention to, and adequate preparations should be made for production factors such as materials and equipment during the construction phase of this water transfer project. It is necessary to strengthen the monitoring, warning, and forecasting of important risk factors, formulate a detailed risk response plan, and implement dynamic risk management.

5. Discussion

The systemic risk of safety, progress, and investment is critical to the construction period of water transfer projects. He et al. [40] analyzed the systemic risk of the Henan Section of the Yangtze-to-Huaihe River Water Diversion Project without considering CCF. They only evaluated which risk factors were the highest and how they ranked, but they could not further observe the effect of each risk factor or CCF events on the systemic risks. Moreover, the study by He et al. [40] found that some common factors have different evaluation results. For example, the evaluation results of P15 are inconsistent with those of I22 in Figure 2. Thus, it is critical to further study the CCF model and CCF events in terms of the safety, progress, and investment system in the future.

Most studies about common cause failure mainly focus on power and mechanical systems. Zuo et al. [41] applied the CCF theory to the hydraulic system balance circuit and studied the effect of CCF events on hydraulic systems in a Bayesian network. Little attention has been paid to the effects of CCF or CCF basic events on the systemic risk of a water project. To the best of our knowledge, this is the first study that solves those problems.

Bayesian network is an effective method to analyze the reliability and risk level of a water project. It can overcome the shortcomings of fault trees and other methods and realize bidirectional reasoning accurately and efficiently. The model and results in this paper are, to a certain degree, consistent with the actual situations encountered during the water project’s construction period. However, in practical application, the Bayesian network model established based on field monitoring data and expert experience may have certain discrepancies with the actual situation. So, it is necessary to further verify and optimize the network with more field monitoring data to improve the fitting degree as much as possible. The parametric learning and structural adaptability of Bayesian networks provide a way to solve this problem.

The risk analysis method proposed in this paper is also applicable to other water projects. This study provided theoretical and technical references to improve the reliability of the systemic risk and reduce the occurrence of risk events during the construction period for a water project.

6. Conclusions

Traditional risk analysis of large-scale water transfer projects during their construction overlooks an in-depth consideration of the safety, progress, and investment systemic risk, as well as the role of CCF. These shortcomings were the impetus for this comprehensive study, which proposes an approach for rigorously analyzing safety, progress, and investment systems by directly considering CCF during the construction period of water transfer projects that is based on Bayesian probability network theory. Through the examination of the Henan Section of the Yangtze-to-Huaihe River Water Diversion Project as a case study, several key findings emerged:

(1) Through the identification of the coupling failure modes within the safety, progress, and investment system, we determined the CCF basic events during the construction period of this water diversion project in China. The common cause events for safety and progress failures include heavy rainfall in the flood season (G4). Crucially and interestingly, no common cause events were identified for either safety or investment failure. Additionally, common cause events for progress and investment failures include design alteration (G2), lagged approval process (G3), and external interference (G7). Those events for safety, progress, and investment failures include epidemic disease (G1), renewal material and failing equipment (G5), and construction accidents (G6).

(2) Utilizing a Bayesian network approach, we built a model that integrates the comprehensive evaluation index framework for safety, progress, and investment systemic risk with the basic events related to CCFs. This assembled model enables the simulation of both the strength and uncertainty of causal relationships between the variables, enhancing our awareness of how node variables change within overall safety, progress, and investment systemic risk.

(3) By applying the backward reasoning of the Bayesian network, this study obtained the greatest risk-posing CCF event (design change) and the underlying causal chain when the “safety, progress, and investment systemic risk” is considered a complete failure. Moreover, this work highlighted those CCF events that warrant targeted management and control. By adjusting the probability distribution of CCF basic events, inferential results for target nodes can be reliably obtained. Through probability analysis using a Bayesian network, our work shows that the failure of renewal material and failing equipment as a CCF basic event significantly impacts safety, progress, and investment systemic risk.