Enhancing Oil–Water Flow Prediction in Heterogeneous Porous Media Using Machine Learning
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations of Two-Phase Flow in a Heterogeneous Porous Medium
2.2. Reference Methods
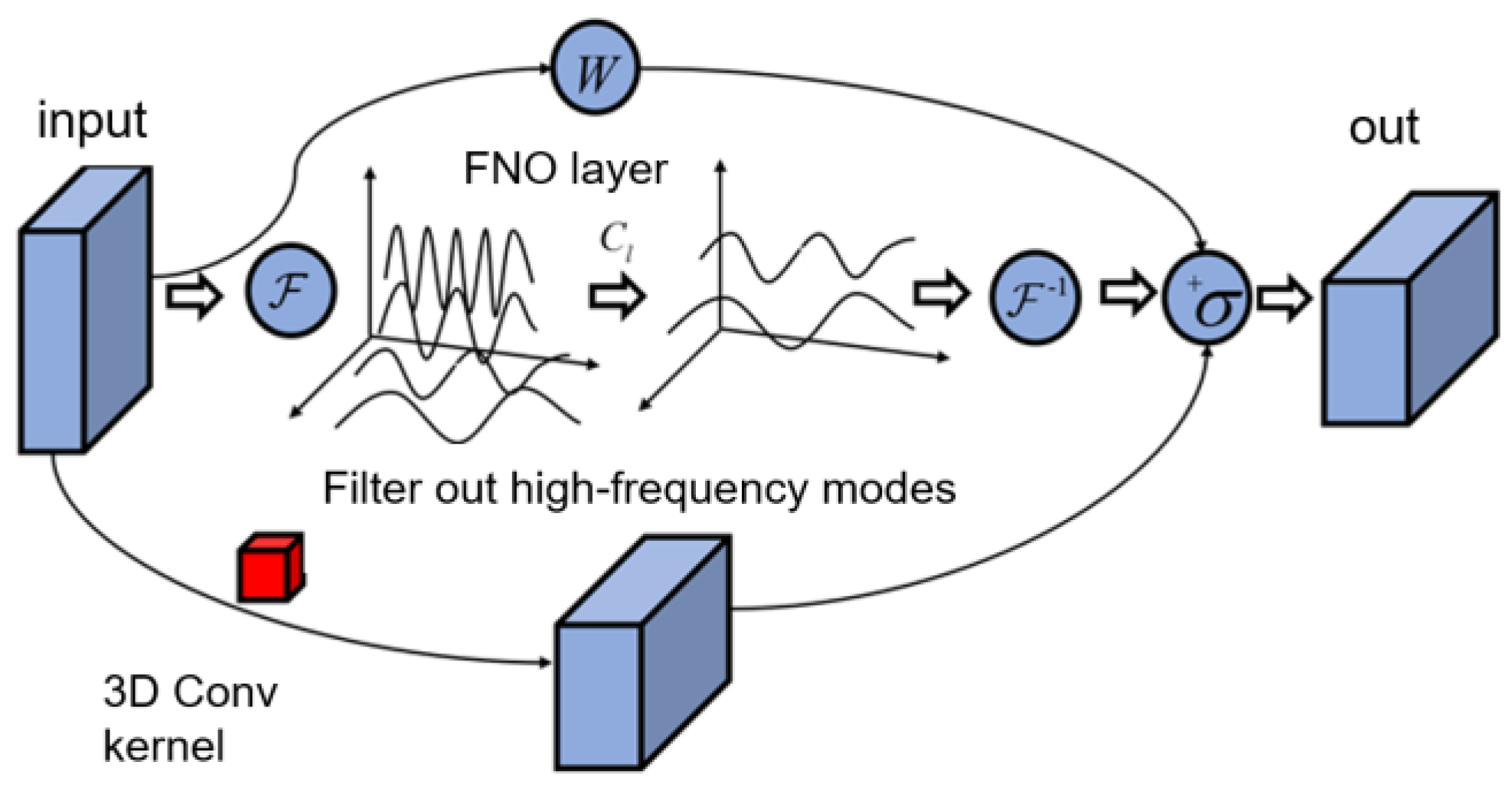
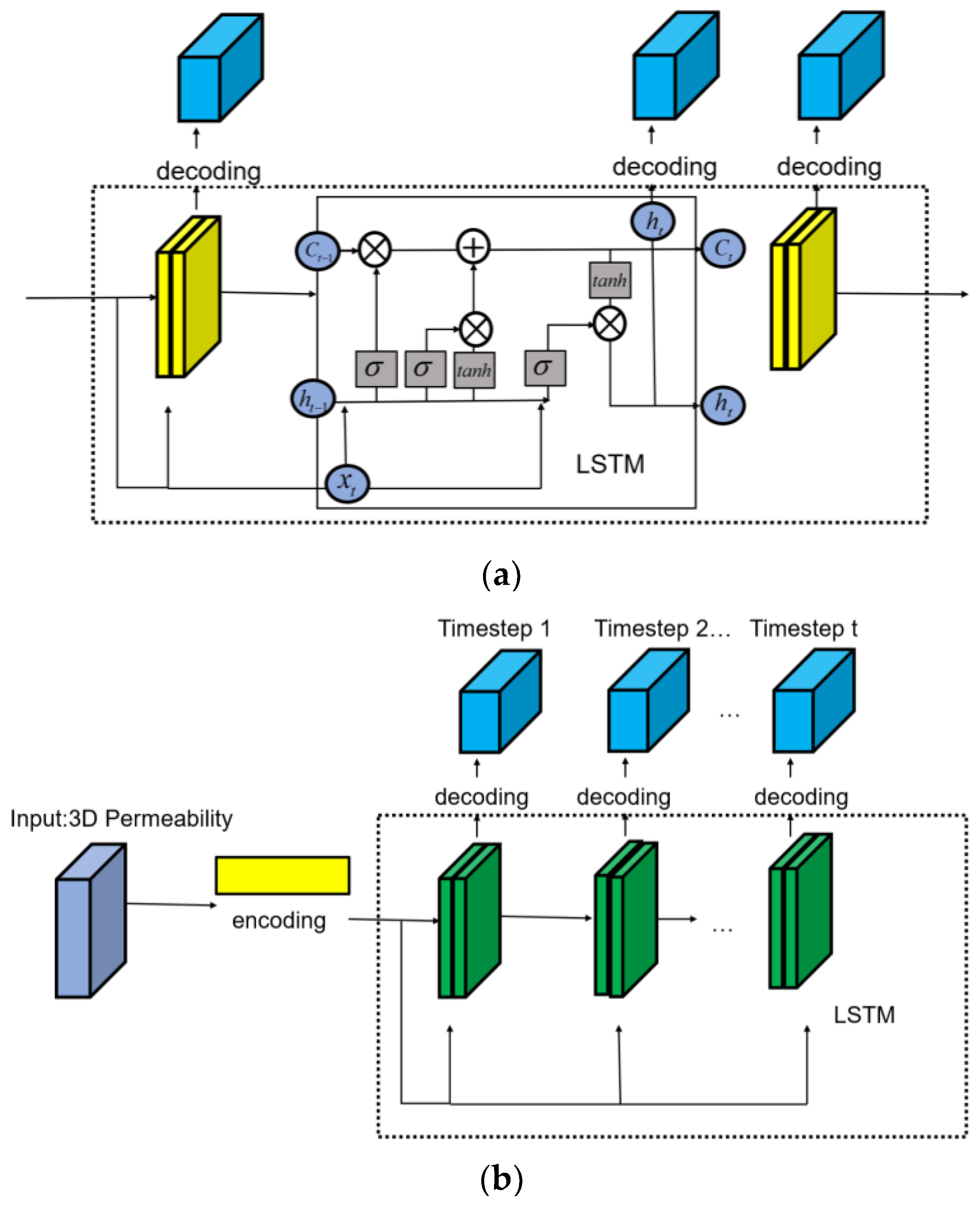
2.3. Convolutional Long Short-Term Memory-Fourier Neural Operator
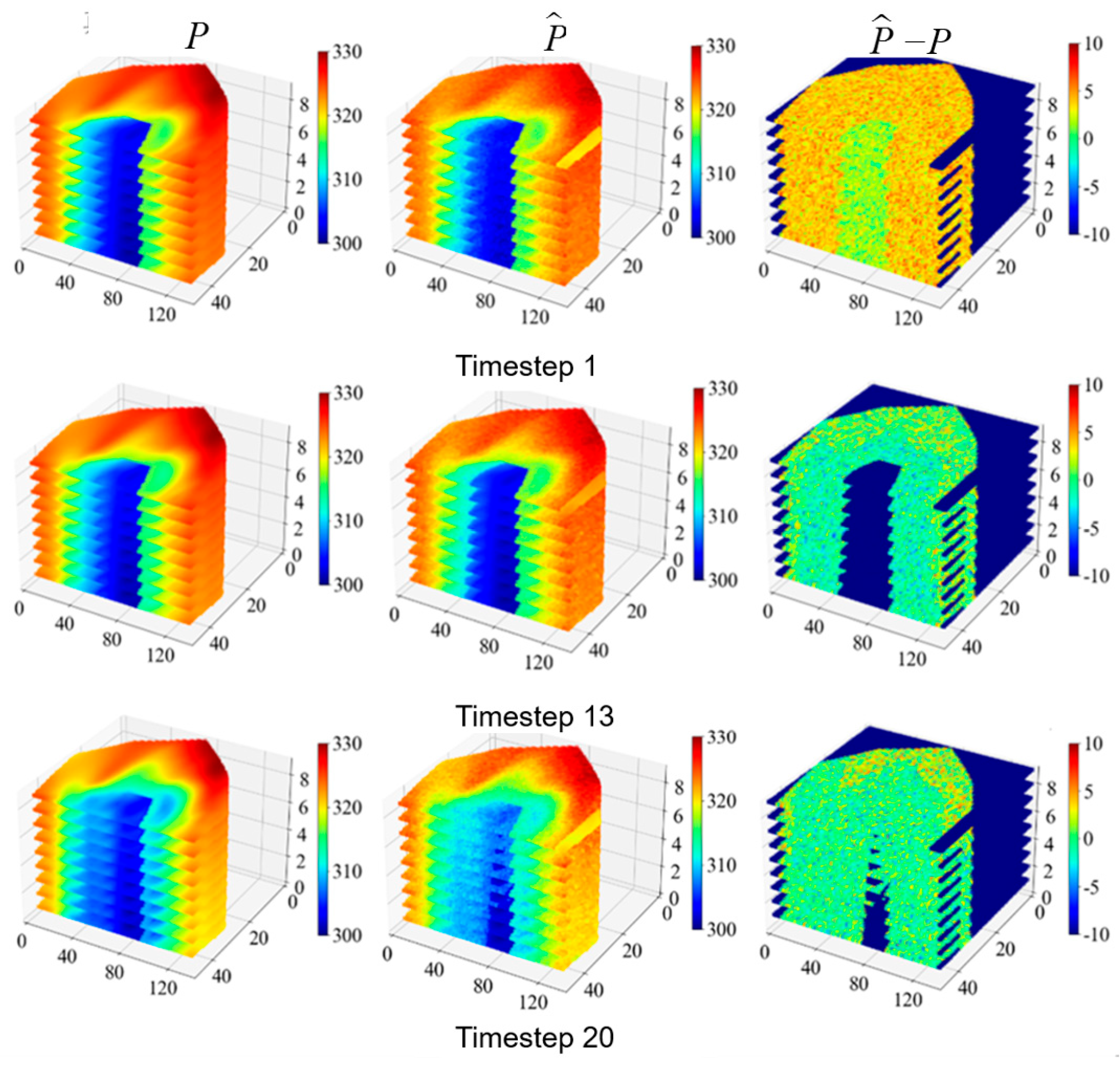
3. Case Study
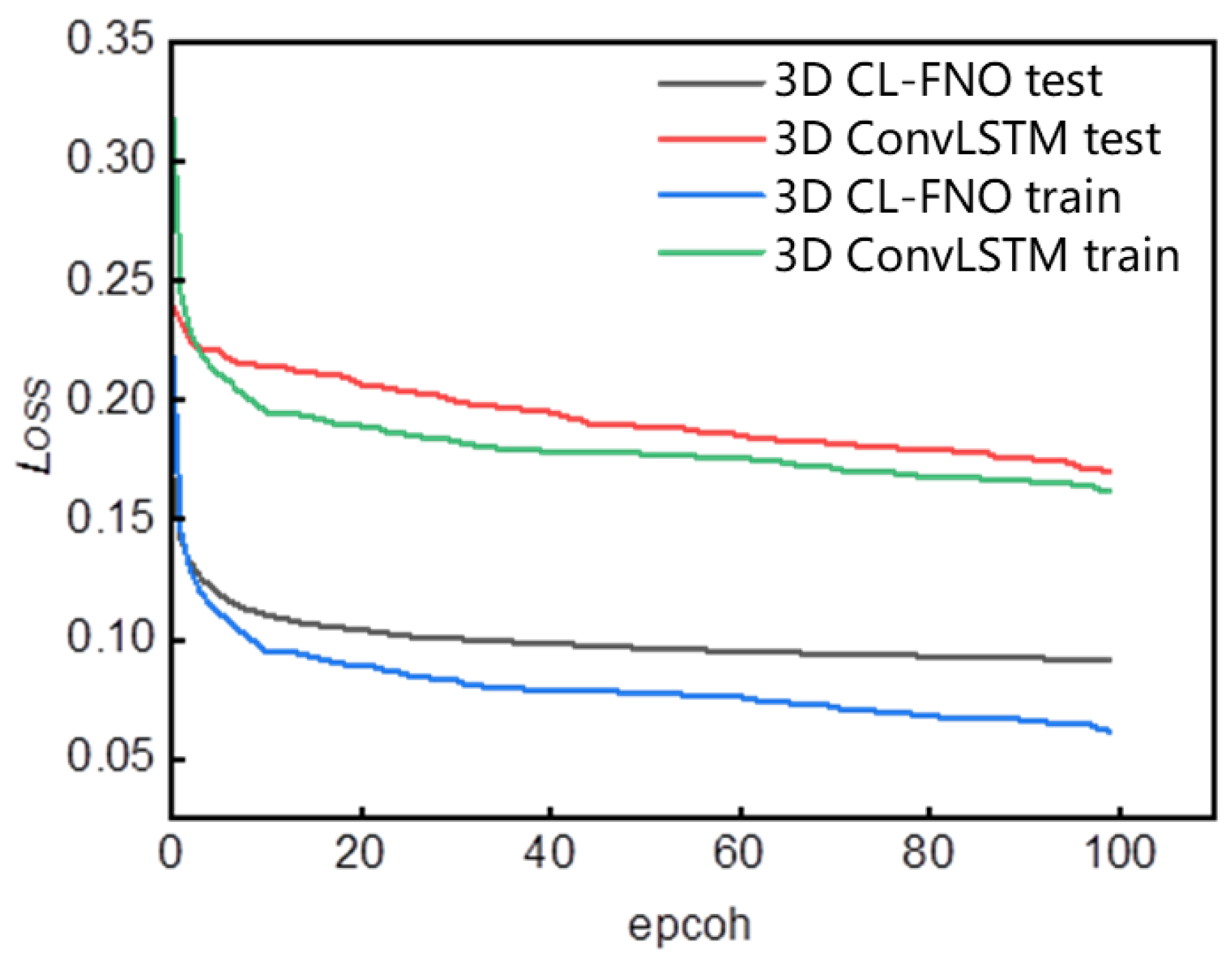
3.1. Synthetic Case
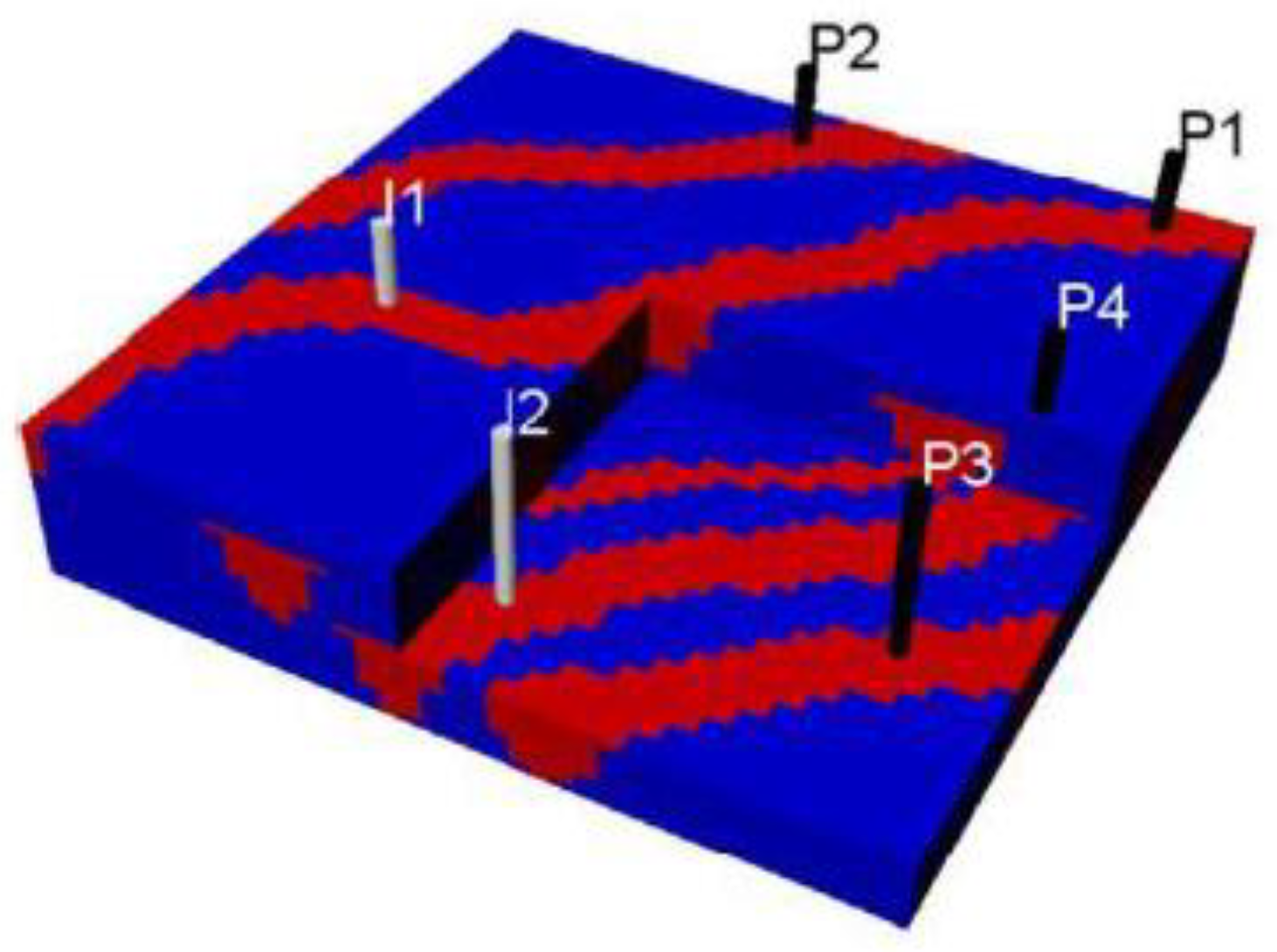
3.2. Actual Reservoir Case
4. Conclusions
- A novel CL-FNO is designed based on the U-shaped architecture, combining the physical constraints Fourier neural operator, the temporal processing convolutional long short-term memory, and the spatial 3D convolution block.
- A surrogate model is trained based on a synthetic numerical model and the CL-FNO is validated, exhibiting satisfactory long-term forecasting performance.
- Based on an actual reservoir, a practical surrogate model is trained and the CL-FNO is demonstrated to possess the potential for addressing practical engineering requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Lin, X.; Jiang, L.; Liu, Z. An oilfield production prediction method based on clustering and long short-term memory neural network. Pet. Sci. Bull. 2023, 2023, 62–72. [Google Scholar]
- Tompson, J.; Schlachter, K.; Sprechmann, P.; Perlin, K. Accelerating eulerian fluid simulation with convolutional networks. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Zha, W.; Li, D.; Shen, L.; Zhang, W.; Liu, X. Review of neural network-based methods for solving partial differential equations. Chin. J. Theor. Appl. Mech. 2022, 54, 543–556. [Google Scholar]
- Zhu, Y.; Zabaras, N. Bayesian deep convolutional encoder–decoder networks for surrogate modeling and uncertainty quantification. J. Comput. Phys. 2018, 366, 415–447. [Google Scholar] [CrossRef]
- Ma, T.; Xiang, G.; Shi, Y.; Gui, J.; Zhang, D. Horizontal in-situ stress prediction method based on the bidirectional long short-term memory neural network. Pet. Sci. Bull. 2022, 2022, 487–504. [Google Scholar]
- Tang, M.; Liu, Y.; Durlofsky, L.J. A deep-learning-based surrogate model for data assimilation in dynamic subsurface flow problems. J. Comput. Phys. 2020, 413, 109456. [Google Scholar] [CrossRef]
- Tang, M.; Liu, Y.; Durlofsky, L.J. Deep-learning-based surrogate flow modeling and geological parameterization for data assimilation in 3D subsurface flow. Comput. Methods Appl. Mech. Eng. 2021, 376, 113636. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier Neural Operator for Parametric Partial Differential Equations. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Wang, N.; Zhang, D.; Chang, H.; Li, H. Deep learning of subsurface flow via theory-guided neural network. J. Hydrol. 2020, 584, 124700. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Y.; Li, G.; Ma, X.; Cui, S.; Luo, Q.; Wang, J.; Yang, Y.; Yao, J. Prediction of Field Saturations Using a Fully Convolutional Network Surrogate. SPE J. 2021, 26, 1824–1836. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, Y.; Zhao, H.; Ma, X.; Gu, J.; Wang, J.; Yang, Y.; Yao, C.; Yao, J. Fourier Neural Operator for Solving Subsurface Oil/Water Two-Phase Flow Partial Differential Equation. SPE J. 2022, 27, 1815–1830. [Google Scholar] [CrossRef]
- Zhong, Z.; Sun, A.Y.; Yang, Q.; Ouyang, Q. A Deep Learning Approach to Anomaly Detection in Geological Carbon Sequestration Sites Using Pressure Measurements. J. Hydrol. 2019, 573, 885–894. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Zhang, K.; Zhang, L.; Liu, P.; Peng, W.; Zhang, H.; Yan, X.; Liu, C.; Yang, Y.; Sun, H.; et al. Towards efficient and accurate CO2 sequestration optimization: Integrating hierarchical spatiotemporal information into deep-learning-based surrogate models. Fuel 2024, 356, 129343. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, X.; Liu, B.; Gao, M. Solving Partial Differential Equations Using Deep Learning and Physical Constraints. Appl. Sci. 2020, 10, 5917. [Google Scholar] [CrossRef]
- Karumuri, S.; Tripathy, R.; Bilionis, I.; Panchal, J. Simulator-free solution of high-dimensional stochastic elliptic partial differential equations using deep neural networks. J. Comput. Phys. 2019, 404, 109120. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.-S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.; Wong, W.; Woo, W. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef]
- Bianchi, M.; Zheng, C. SGeMS: A Free and Versatile Tool for Three-Dimensional Geostatistical Applications. Groundwater 2009, 47, 8–12. [Google Scholar] [CrossRef]

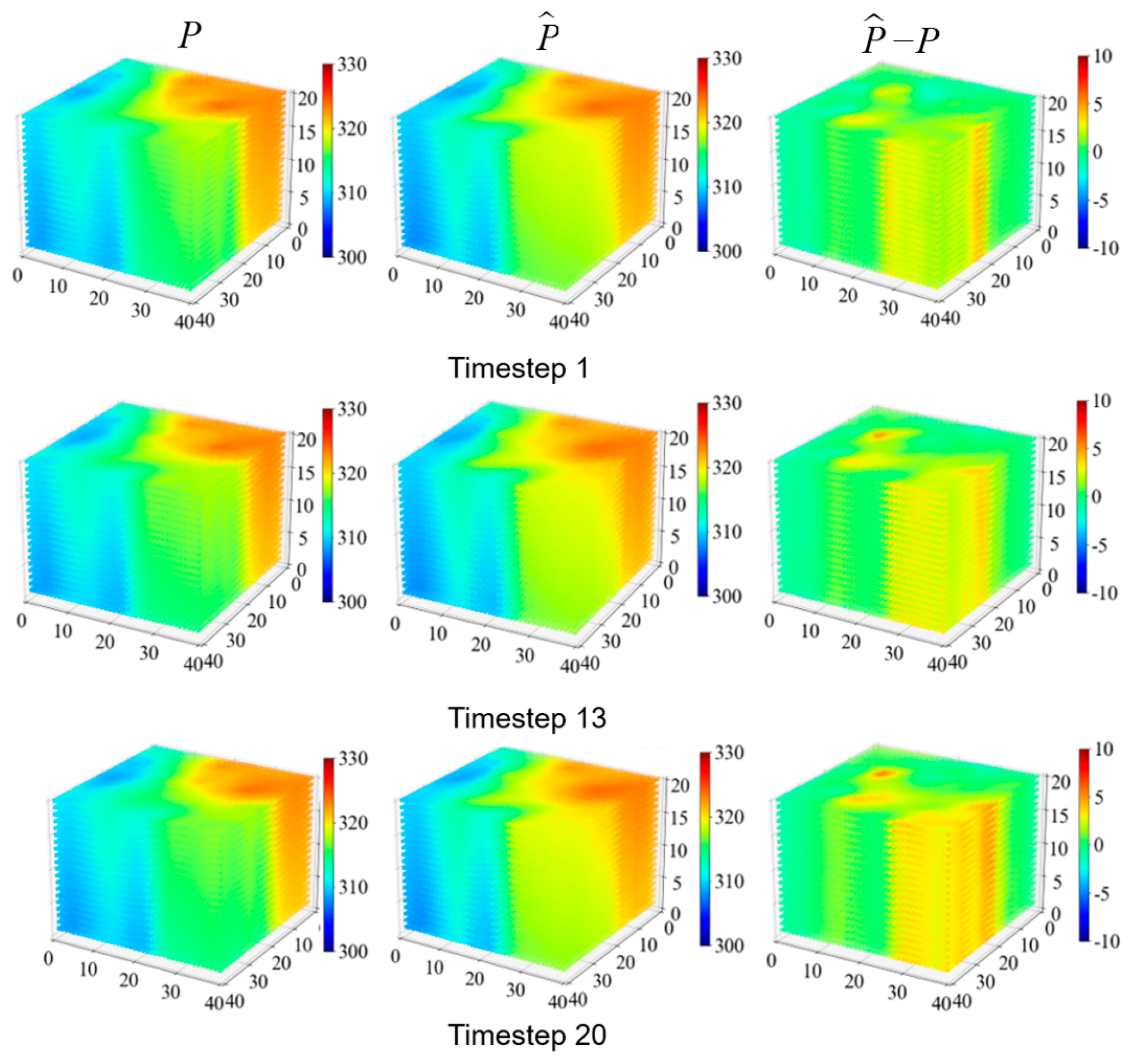
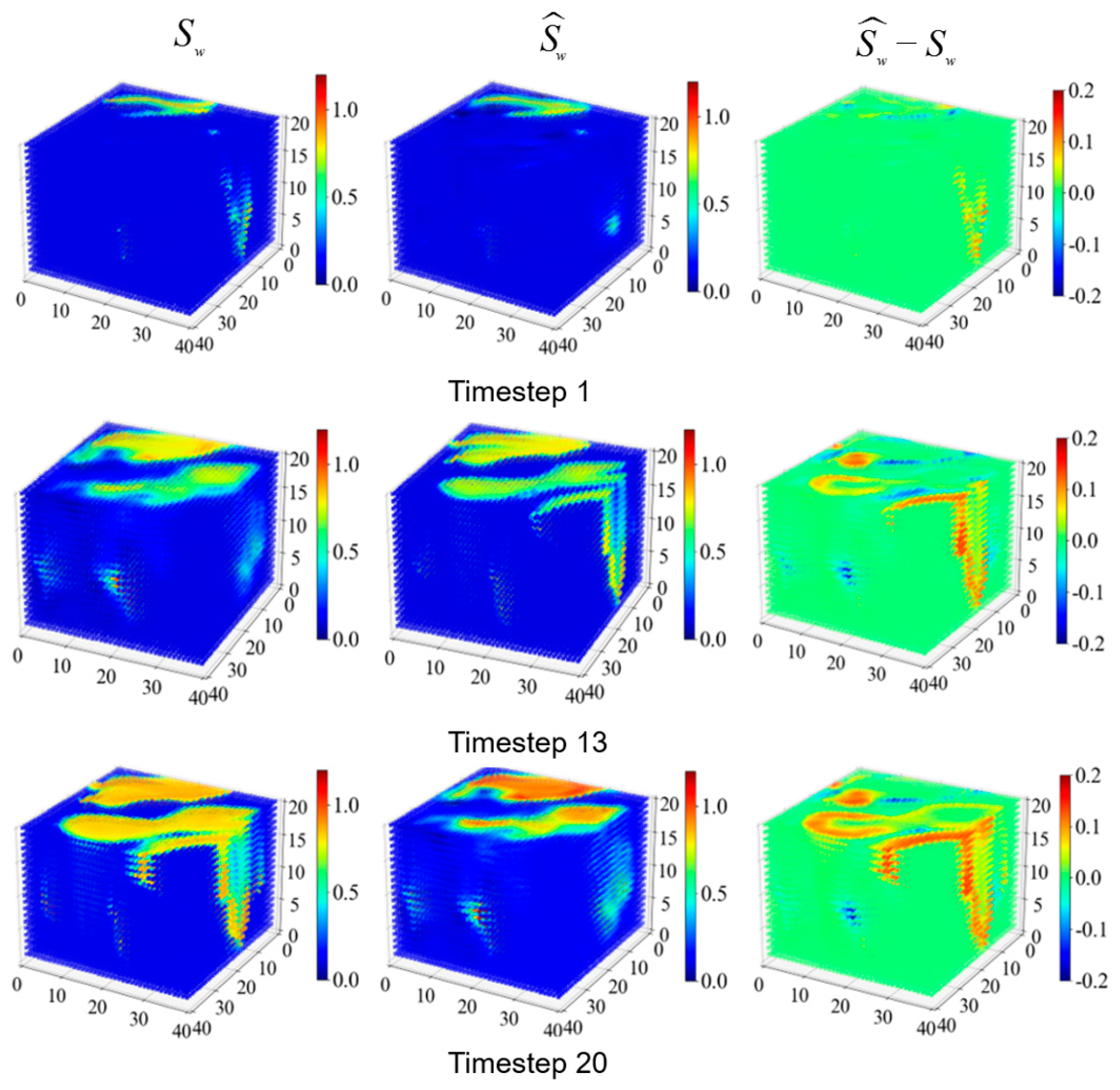
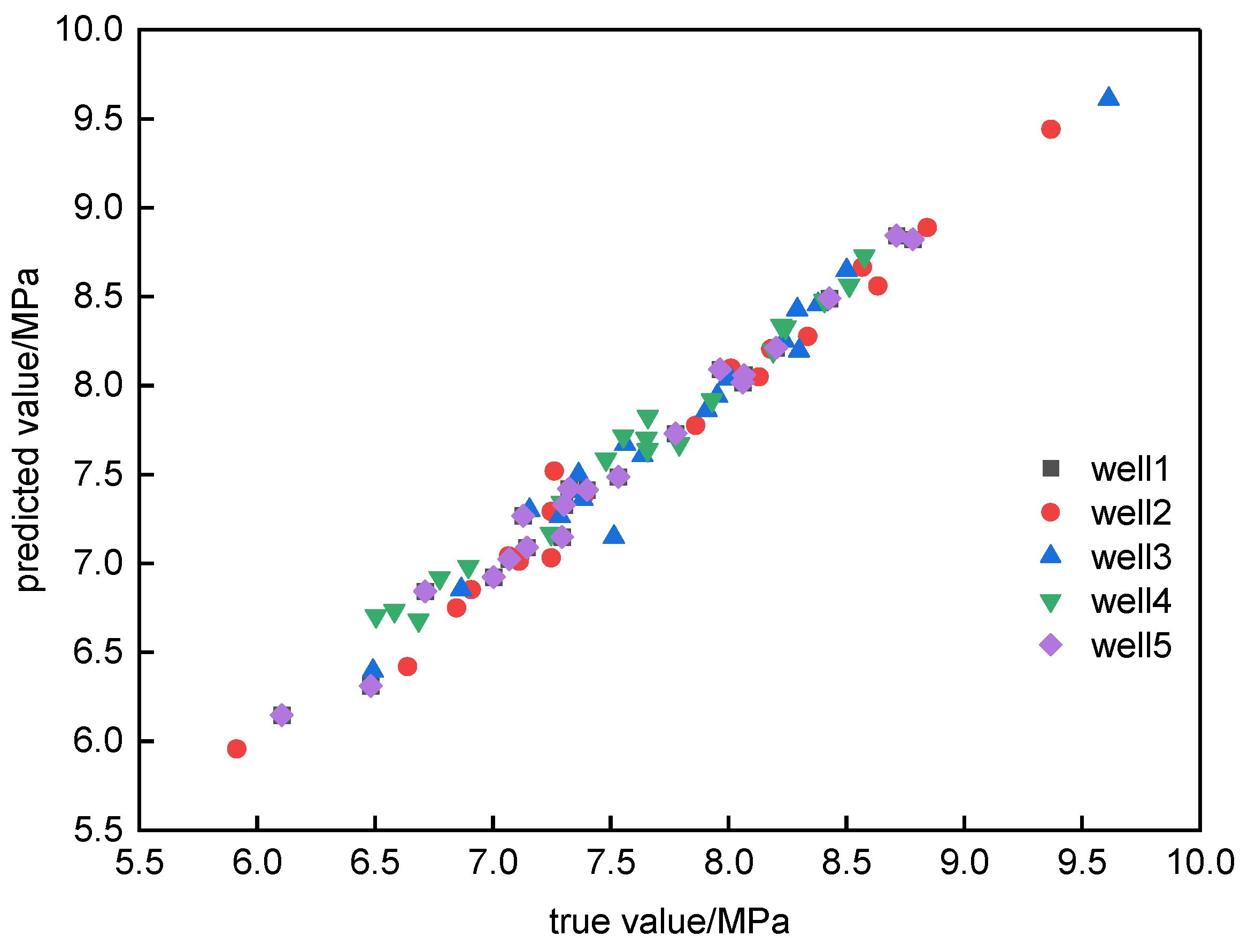
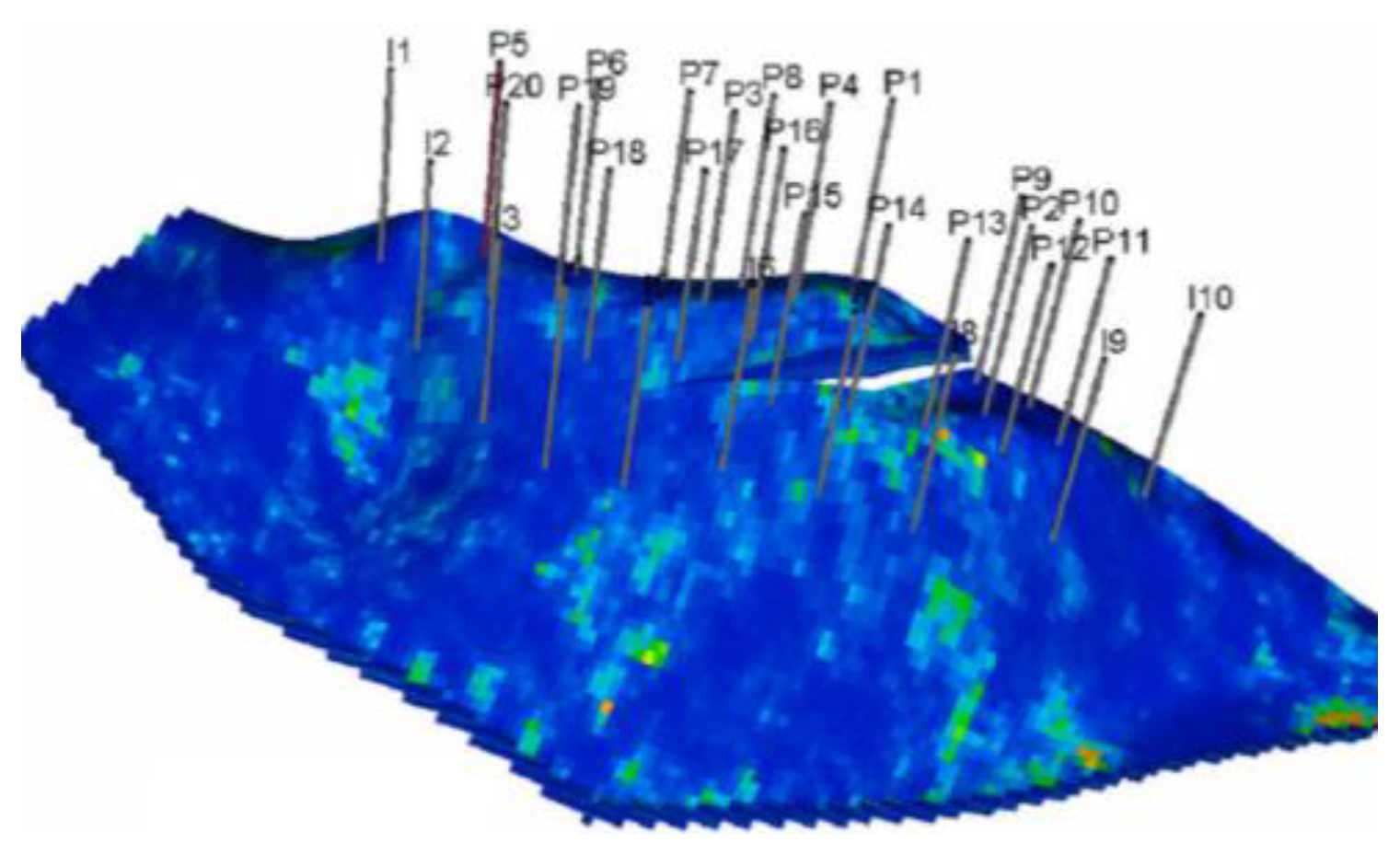

| Portion | Details | Data Size |
|---|---|---|
| Input data | - | 40 × 40 × 20 × n |
| Encoding layer 1 | 3D Conv and 3D Fourier/Sum/ReLU | 40 × 40 × 20 × 16 |
| Encoding layer 2 | 3D Conv and 3D Fourier/Sum/ReLU | 20 × 20 × 10 × 32 |
| Encoding layer 3 | 3D Conv and 3D Fourier/Sum/ReLU | 10 × 10 × 5 × 32 |
| Encoding layer 4 | 3D Conv and 3D Fourier/Sum/ReLU | 10 × 10 × 5 × 64 |
| Intermediate layer 1 | 3D Fourier × 4 | 10 × 10 × 5 × 64 |
| Intermediate layer 2 | ConvLSTM layer | 10 × 10 × 5 × 64 × 20 |
| Decoding layer 4 | Upsampling/Deconvolution/ReLU | 10 × 10 × 5 × 64 × 20 |
| Decoding layer 3 | Upsampling/Deconvolution/ReLU | 10 × 10 × 5 × 32 × 20 |
| Decoding layer 2 | Upsampling/Deconvolution/ReLU | 20 × 20 × 10 × 32 × 20 |
| Decoding layer 1 | Upsampling/Deconvolution/ReLU | 40 × 40 × 20 × 32 × 20 |
| Output data | - | 40 × 40 × 20 × 1 × 20 |
| Parameter | RMSE | /% |
|---|---|---|
| P | 0.0642 | 0.95 |
| Sw | 0.0651 | 5.21 |
| Portion | Details | Data Size |
|---|---|---|
| Input data | - | 138 × 49 ×9 × n |
| Encoding layer 1 | 3D Conv and 3D Fourier/Sum/ReLU | 138 × 49 ×9× 16 |
| Encoding layer 2 | 3D Conv and 3D Fourier/Sum/ReLU | 69 × 25 × 5 × 32 |
| Encoding layer 3 | 3D Conv and 3D Fourier/Sum/ReLU | 40 × 13 × 3 × 32 |
| Encoding layer 4 | 3D Conv and 3D Fourier/Sum/ReLU | 40 × 13 × 3 × 64 |
| Intermediate layer 1 | 3D Fourier × 4 | 40 × 13 × 3 × 64 |
| Intermediate layer 2 | ConvLSTM layer | 40 × 13 × 3 × 64 × 20 |
| Decoding layer 4 | Upsampling/Deconvolution/ReLU | 40 × 13 × 3 × 64 × 20 |
| Decoding layer 3 | Upsampling/Deconvolution/ReLU | 40 × 13 × 3 × 32 × 20 |
| Decoding layer 2 | Upsampling/Deconvolution/ReLU | 69 × 25 × 5 × 32 × 20 |
| Decoding layer 1 | Upsampling/Deconvolution/ReLU | 138 × 49 × 9 × 32 × 20 |
| Output data | - | 138 × 49 × 9 × 1 × 20 |
| Parameter | RMSE | /% |
|---|---|---|
| P | 0.0747 | 2.46 |
| Sw | 0.1151 | 7.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, G.; Zhang, K.; Wan, H.; Yao, W.; Zuo, Y.; Lin, J.; Liu, P.; Zhang, L.; Yang, Y.; Yao, J.; et al. Enhancing Oil–Water Flow Prediction in Heterogeneous Porous Media Using Machine Learning. Water 2024, 16, 1411. https://doi.org/10.3390/w16101411
Feng G, Zhang K, Wan H, Yao W, Zuo Y, Lin J, Liu P, Zhang L, Yang Y, Yao J, et al. Enhancing Oil–Water Flow Prediction in Heterogeneous Porous Media Using Machine Learning. Water. 2024; 16(10):1411. https://doi.org/10.3390/w16101411
Chicago/Turabian StyleFeng, Gaocheng, Kai Zhang, Huan Wan, Weiying Yao, Yuande Zuo, Jingqi Lin, Piyang Liu, Liming Zhang, Yongfei Yang, Jun Yao, and et al. 2024. "Enhancing Oil–Water Flow Prediction in Heterogeneous Porous Media Using Machine Learning" Water 16, no. 10: 1411. https://doi.org/10.3390/w16101411
APA StyleFeng, G., Zhang, K., Wan, H., Yao, W., Zuo, Y., Lin, J., Liu, P., Zhang, L., Yang, Y., Yao, J., Li, A., & Liu, C. (2024). Enhancing Oil–Water Flow Prediction in Heterogeneous Porous Media Using Machine Learning. Water, 16(10), 1411. https://doi.org/10.3390/w16101411









