Abstract
In order to study the stress–strain–permeability coefficient relationship of overlying strata in a fractured zone after coal mining, taking the Changcun coal mine in the Changzhi basin as an example, the permeability evolution law of coarse sandstone, fine sandstone, siltstone and mudstone during a stress–strain process was analyzed through a triaxial compression permeability test. The generalized model of the rock mass permeability evolution process under mining stress was summarized, and then a coupling model of the stress–water pressure–permeability coefficient of fractured rock was established based on the continuum model of rock mass. The results showed that the maximum permeability coefficient of different coal overburden types was quite different, and the peak strength of the rock mass preceded the maximum permeability coefficient during the rock mass failure process; the permeability coefficient first decreased and then increased, reaching its maximum value after the peak stress, which occurred during the strain-softening stage; the generalized model of rock mass permeability included the compaction stage, elasticity stage, stable fracture stage, unstable fracture stage, macroscopic failure stage and residual strength stage.
1. Introduction
The occurrence of coal resources is often adjacent to the underground aquifer, and coal mining has a significant impact on alterations in groundwater resources. For many years, due to the lack of scientific guidance, the coal mining sector in China has not taken effective measures to protect groundwater resources during coal mining, which has led to great damage to underground aquifers in many coal mining areas in China [1,2,3,4]. The continuous exploitation of coal mine resources has led to an increasingly severe loss of underground water [5,6,7] and resulted in the occurrence of various coal mine disasters in recent years as well [8,9,10].
In coal mining, the seepage of overlying strata is a crucial issue. As coal seams are exploited, alterations in the stress state of the surrounding layers lead to the fragmentation, cracking and deformation of the overburden. The impact zone of overlying strata mining can be classified based on its degree of destruction into a caving zone, a fracture zone and a bending zone [11], which is shown in Figure 1. The development of pores and cracks in the caving zone and fracture zone leads to drastic changes in water permeability [12,13]. During coal mining, the changes in the stress and strain of the rock result in an exponential increase in its permeability coefficient, directly affecting the groundwater flow and flow field of aquifers [14]. Therefore, scholars are paying more and more attention to the coupled effects of stress and seepage.
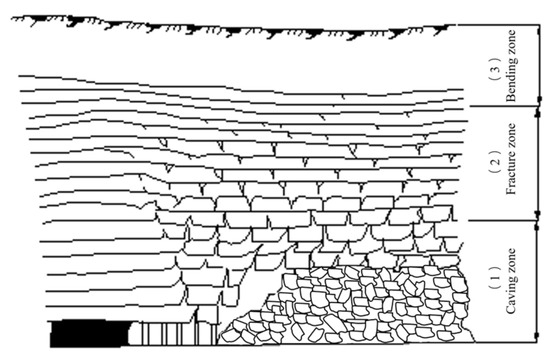
Figure 1.
Distribution of three zones in overlying strata.
K. Terzaghi first began to study the coupling of fluid–solid deformation, and based on much measured data, he put forward the concept of effective stress and established a consolidation model in one dimension [15]. Biot creatively put forward the three-dimensional consolidation theory, which laid the foundation for many scholars to study water–rock coupling in a later period [16,17,18]. Ma C. Y. et al. studied the physical simulation of nonlinear flow in a fractured anisotropic medium and revealed the variation mechanism of full tensor permeability with stress sensitivity in anisotropic medium through numerical calculation and physical experiments [19]. Ki-bokmin et al. investigated fractured rock mass permeability using the two-dimensional discrete element method, and based on the numerical simulation approach and results, the stress–permeability relationship equation of rock mass was put forward [20]. Based on Biot’s theory, Noorishad et al. extended the constitutive equation of porous elastic medium to that of damaged medium and put forward a fluid–solid coupling analysis model of fracture [21]. Zhao et al. proposed a permeability model for fractured rocks considering elastoplastic deformation. The model, based on elastoplastic contact analysis, described the evolution of permeability in fractured rocks as a process from elastic deformation to plastic deformation and then to fracturing [22]. Yu et al. conducted triaxial compression tests under varying seepage pressure and confining pressure conditions, leading to the development of a novel damage constitutive model that more accurately captures the stress–strain relationship [23]. Teng et al. developed a permeability correction model for muddy sandstone under coupling fluid mechanics conditions, revealing the correlation between the permeability of muddy sandstone and effective stress (including external stress and pore pressure) [24]. Zhang et al. conducted triaxial permeability tests to investigate the correlation between the permeability of weakly cemented sandstone and porosity, cementation structure and mineral composition and further advanced a model establishing the relationship between stress, damage and permeability for weakly cemented sandstone [25].
Taking the Changcun coal mine in Changzhi basin as an example, this paper examined the evolutionary pattern of overlying strata in a fracture zone under mining stress through a triaxial compression permeability test of rock mass permeability under mining stress. Then, based on the test results, a generalized model describing the evolutionary process of rock mass permeability under mining stress was constructed, and the six-stage characteristics of the rock mass permeability evolution process were summarized. Finally, based on a rock mass continuum model, a stress–water pressure–permeability coefficient coupling model of fractured rock was established with strain as the medium and stress and pore water pressure inside the rock mass as the permeability coefficient function.
2. Coal-Bearing Strata Characteristics in the Changzhi Basin
The main coal-bearing strata in the Changzhi basin are the Shanxi formation and the Taiyuan formation. The developed thickness of coal-bearing strata is 168.98 m, comprising 8–18 coal layers. The total thickness of the developed coal seams is about 11.53 m, with a coal-bearing coefficient of 6.82%.
The average thickness of the Shanxi formation is 54.20 m, and it consists of 3–5 coal-bearing layers, namely No. 1, No. 2 and No. 3 coal seams and some other coal seams, among which the No. 3 coal seam is the most important minable coal seam in the study area, with a thickness of 4.30–7.50 m and a coal-bearing coefficient of 12.13%. The average thickness of the Taiyuan formation is about 114.78 m. Among them, the developed No. 15-3 coal seam is relatively stable, most of which is minable in the area. The No. 15-1 coal seam is generally partially minable, while the No. 9 coal seam sporadically contains minable portions. The total thickness of the coal seam developed in the Taiyuan Formation is about 5.20 m, with a coal-bearing coefficient of 4.53%.
The No. 3 coal seam is in the middle and lower part of the Shanxi formation. According to the production status of most coal mines, the average thickness is about 6 m, and the structure is simple, and the lithology of the gangue is carbonaceous mudstone. The lithology of the coal seam roof mainly comprises mudstone, sandy mudstone and siltstone. In some areas, the roof of the coal seam is fine sandstone or coarse sandstone, and the lithology of floor mainly comprises mudstone, sandy mudstone and silty-fine sandstone. In some areas, it is medium-grained sandstone. This coal seam has a high degree of control and is a stable coal seam that can be mined in the whole area, and its roof is the study subject in this paper.
3. Materials and Methods
3.1. Samples
The samples for the test were collected from the overburden of No. 3 coal seam in Changcun coal mine from Changzhi basin, and they are siltstone, fine sandstone, coarse sandstone and mudstone. The basic physical and mechanical parameters of the rock are presented in Table 1. After the samples were retrieved, they were processed into Φ50 × 100 mm cylindrical test blocks and its upper and lower ends were ground flat, which can be seen in Figure 2. Then, they could be tested on the machine.

Table 1.
Basic physical and mechanical parameters of rock.

Figure 2.
Processed samples. (a) Fine sandstone; (b) siltstone; (c) mudstone; (d) coarse sandstone.
3.2. Test Equipment and Conditions
3.2.1. Choice of the Test Machine
The TAW-2000 rock servo testing machine, which is produced by Chaoyang Test Instrument Co., Ltd. (Changchun, China), was employed in this study, and it has three independent loading systems: axial loading system, confining pressure loading system and seepage loading system.
The main technical parameters are as follows:
- (1)
- Axial loading system:
Maximum test force: 2000 KN; effective force measuring range: 20–2000 KN; loading rate range of test force: 0.01–20 KN/s.
- (2)
- Confining pressure loading system:
Maximum confining pressure: 150 MPa; confining pressure loading rate range: 0.001–0.5 MPa/s; confining pressure resolution: 0.0003 MPa.
- (3)
- Seepage loading system:
Maximum seepage pressure: 50 MPa; the loading rate of seepage water pressure: 0.001–0.1 MPa/s; pressure sensor: 60 MPa liquid pressure sensor.
3.2.2. Choice of the Test Conditions
On the basis of the burial conditions of coal seams in the Changzhi basin and the spatial distribution of horizontal stress on rocks, the seepage pressure difference and confining pressure selected in this study are 1.5 MPa and 3.0 MPa, respectively.
3.3. Test Principle
The purpose of this test is to test the permeability coefficient and strain variation of rocks under different stress conditions. In order to simplify the conditions, the following assumptions are made during the test construction: (1) there are evenly distributed micro-fractures and pores in the rock mass; (2) the seepage process of water in the sample test is incompressible; (3) the movement of water in the sample follows Darcy’s law.
During the triaxial compression permeation process of rocks, the permeability coefficient of each test point in the rock sample was calculated based on the variation in water flow rate according to Darcy’s law. The formula to calculate the permeability coefficient K of the rock sample is presented below:
where Q represents the water flow through the sample (cm3/s); I represents the length of the selected sample (cm); Ap represents cross-sectional area (cm2); and H1 and H2 are the water head heights at two ends of the sample (cm).
3.4. Test Process
The process of the triaxial compression permeability test is shown below:
- (1)
- The rock sample was sealed with a heat-shrinkable rubber sleeve and installed on the base of the testing machine.
- (2)
- Axial load was applied to fix the rock sample, then confining pressure was applied to the triaxial chamber, and it was maintained at 3.0 MPa.
- (3)
- Seepage water pressure was applied to the upper end of the rock sample, creating a pressure difference with atmospheric pressure, and the pressure difference was maintained at 1.5 MPa once it is reached.
- (4)
- Axial load was applied at a loading rate of 0.05 MPa/s until the rock sample is broken, and each test was repeated three times. The stress diagram of the triaxial compression seepage process is shown in Figure 3.
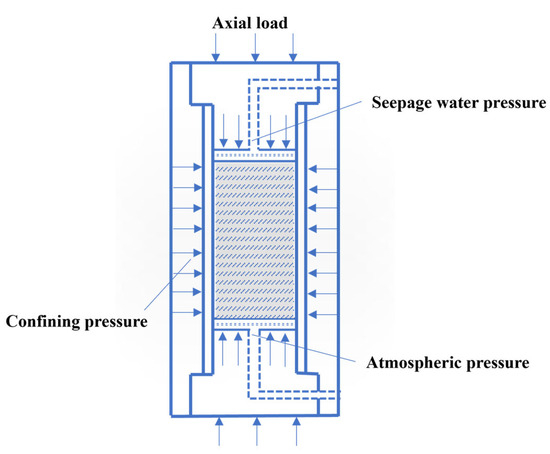 Figure 3. Schematic diagram of the triaxial compression seepage process.
Figure 3. Schematic diagram of the triaxial compression seepage process.
The data collector automatically recorded data such as axial stress, axial strain and water flow when gradually applying axial stress. This process allows for the acquisition of comprehensive data, enabling the plotting of stress–strain–permeability coefficient curves for different rock types.
4. Results and Discussion
4.1. Stress–Strain Permeability Test of Rock Samples
4.1.1. Test Results Presentation
Four groups of rock samples, including coarse sandstone, fine sandstone, siltstone and mudstone, were tested in this study. The results of the mechanical characteristics of different lithologies are presented in Table 2, and the stress–strain–permeability coefficient curves of different lithologies are given in Figure 4.

Table 2.
Results of mechanical characteristics for different lithologies under mining stress.
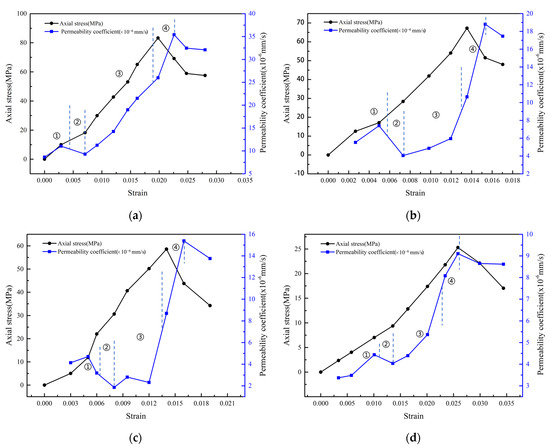
Figure 4.
Stress–strain–permeability coefficient curves of different lithologies: (a) coarse sandstone; (b) fine sandstone; (c) siltstone; (d) mudstone.
4.1.2. Analysis of Test Results
As is seen in Figure 4, the stress–strain curve and permeability coefficient–strain curve of rocks with different lithologies in coal seam overburden are generally similar but not the same. Further, from Table 2, it can be observed that coarse sandstone has the strongest permeability, while mudstone has the poorest permeability, which can be attributed to the size of the rock particle [26]. The typical order of the permeability coefficient from largest to smallest is generally as follows: coarse sandstone > fine sandstone > siltstone > mudstone. Moreover, the peak strength of rock was not synchronous with the maximum permeability coefficient of rock mass but ahead of it. This is because when the peak strength is attained, the formation of macro-cracks in rock is completed instantly, but the water seepage process takes time to complete, resulting in a certain lag in permeability change compared with stress change [27].
According to the comparative analysis of the curve in Figure 4 and the previous research [28,29], it can be concluded that the variation tendency of the stress–strain curve can directly reflect the process of rock change until it is broken, in which the permeability coefficient of coal seam overburden can be regarded as a volume strain function. This is because under normal circumstances, rock solid particles do not easily expand and contract. Under triaxial conditions, the expansion and contraction of rock is mainly that of pores and fissure spaces, and the volume strain of rock reflects the changes in pores and fissure spaces. Therefore, volume strain can be used to describe the permeability evolution of rocks, and rock mass basically goes through the following stages in the test process:
- (1)
- Compaction stage (➀): the original fissures and pores within the rock mass are compacted, exhibiting a tendency towards closure, causing a decrease in rock volume and a corresponding decrease in the permeability coefficient.
- (2)
- Elastic deformation stage (➁): the pores and fissures within the rock mass are further compacted, leading to a further reduction in rock volume and a continued decrease in the permeability coefficient.
- (3)
- Plastic deformation stage (➂): microscopic fissures within the rock mass begin to expand and extend, achieving partial connectivity. Additionally, under further stress, a significant number of new fissures are generated, leading to an increase in rock volume. The permeability coefficient increases with the increase in fissures and volume.
- (4)
- Strain sliding stage (➃): strain softening occurs during this stage, and when the applied stress continues to increase and reaches the peak strength condition of the rock, internal fractures start to form through the rock. During this process, the permeability performance of the rock continues to enhance as the fractures penetrate and extend within the rock until they start to be compressed and contract. At this point, the permeability coefficient reaches its peak value.
4.2. Generalized Model of Rock Stress–Strain Permeability
The change curve of the rock’s stress–strain–permeability characterizes the entire process from deformation to failure until the loss of the bearing capacity of the rock. Similarly, it also represents the variation in the permeability performance of the sample under different strain states. The reason why the permeability performance of rocks undergoes significant changes during deformation and failure under stress is that the internal fractures experience closure, extension, penetration and compaction under stress.
Combining previous research findings [30,31,32] with the present study in this paper, a generalized model of rock stress–strain permeability can be obtained, as shown in Figure 5. According to its morphology, the entire process can be segmented into 6 stages, namely OA (I): Compaction stage; AB (II): Elastic stage; BC (III): Stable fracture stage; CD (IV): Unstable fracture stage; DE (V): Macroscopic failure stage; EF (VI): Residual strength stage.
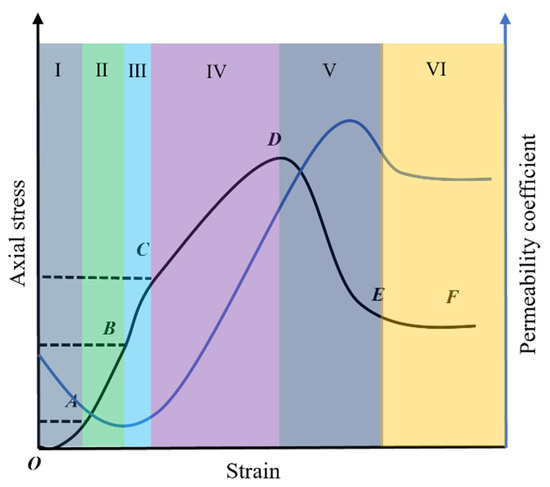
Figure 5.
Stress–strain–permeability coupling curve.
- (1)
- Compaction stage (I): at this stage, the stress–strain curve of the rock commonly shows an upward concave form. As the test progresses, the stress continuously increases, and at this point, the volume of internal fractures within the rock decreases under compression, resulting in nonlinear deformation, which is initially rapid and then slows down, during which the permeability performance of the rock weakens as the strain of the rock increases.
- (2)
- Elastic stage (II): during this stage, the stress–strain correlation of the rock is approximately linear, with a reduced slope. As the axial stress continues to increase, the internal fractures of the rock are further compressed, leading to densification and overall volume reduction. Consequently, the permeability performance continues to decrease. However, the rate of decrease in this stage is relatively smaller compared to the previous stage. Typically, at point B, the permeability of the rock reaches its lowest point.
- (3)
- Stable fracture stage (III): in this process, the stress–strain curve of the sample changes to a concave downward shape, and its physical significance shows that when the rock stress is higher than its elastic limit, the volume strain increases with the increase in the stress, and the rock volume changes from a compressed state to an expanded state. The rock begins to be damaged, and new fractures are generated in it. The density of fractures per unit volume was directly proportional to the stress, which led to better water circulation and enhanced rock permeability.
- (4)
- Unstable fracture stage (IV): the curve in this process continues the concave state of the previous stage. The physical significance of this stage is that fractures develop and extend rapidly under the continuous condition of applying axial stress, the strain of the sample increases sharply at the same time, and the rock volume expands at an accelerated rate. Then, there are tensile fracture surfaces and shear fracture surfaces in it. In this process, even if the axial stress is stopped, the cracks will spontaneously expand. When the axial stress continues to increase to its ultimate strength (also known as peak strength), the rock structure is destroyed.
- (5)
- Macroscopic failure stage (V): while the axial stress keeps increasing until it reaches the peak strength of the rock, internal fractures rapidly and continuously develop, extending and penetrating through. Subsequently, the effective stress decreases, and the rock begins to experience compression. Consequently, the permeability performance gradually decreases from its peak value. Rocks generally exhibit their strongest permeability during this stage.
- (6)
- Residual strength stage (VI): after the rock is damaged by compression, due to the previous volume expansion, the effective axial stress gradually decreases and eventually stabilizes. The fractured rock, once stabilized, still retains a certain level of bearing capacity. During this process, the permeability performance of the rock gradually decreases and eventually stabilizes as well.
4.3. Coupling Model of Stress–Water Pressure–Permeability Coefficient
In this study, in order to establish the correlation between permeability coefficient and stress in the rock mass, it is assumed that pores and fractures in the rock mass form a continuous network with a uniform distribution, and their actual mechanical and hydraulic properties are equivalent to those of the original rock. It can be inferred that the deformation, fragmentation and bending of the rock mass occur under the condition of stress change, which is in the form of strain, and the consequence is that the parameters such as pores, cracks and pore water pressure in the rock mass change, and so does the permeability coefficient. In other words, during the process of the strain of the rock mass, it is feasible to describe the stress–permeability coefficient with the pores as the medium, and the strain and porosity of the rock mass as the bridge.
Hubbert put forward a theory about the rock permeability coefficient and the rock particle size in the 1940s, and he thought that the rock permeability coefficient had the following relationship with the rock particle size [33]:
where k represents the permeability coefficient of rock; N represents a coefficient associated with the particle size, shape and the nature of interstitial materials between particles in the rock; d represents the average particle radius of the sample; ρ is the weight of water per unit volume; g represents the gravitational acceleration; and μ represents the dynamic viscosity coefficient of water in the flow.
It is hypothesized that the permeability coefficient of the rock follows the subsequent functional relationship with its porosity:
where σ represents the effective stress; p is the pore water pressure; K0 represents the permeability coefficient of the initial state of the rock; a represents a constant; φ′ is the porosity of the rock; φ0 represents the initial porosity of the rock; and φ′ − φ0 can be expressed by Δφ.
At the same time, porosity can be expressed by the following equation:
where VP0 is the pore volume of rock mass in initial state; V0 represents the total rock mass volume in the initial state; ΔV represents the numerical change in volume of the rock; and ΔVp represents the numerical change in pore volume.
In general, the compressibility of the rock particles itself is very small, which is negligible compared with the compressibility of pores and fractures. Therefore, in Equation (4), ΔV is approximately equal to ΔVp, and the following equation is obtained:
where represents the rock mass porosity in the initial state, and represents the volume strain.
Usually, the volume strain of rock is very small, meaning that , so the above equation can be written as follows:
and then Equation (7) is obtained:
In this way, the functional correlation between the change in porosity and volume strain of rock becomes a bridge between the stress and permeability coefficients.
According to the constitutive equation of solid phase in Biot’s theory [16,17,18], the following applies:
where εij represents the strain modulus; ν represents the poisson’s ratio of the rock; E represents the elastic modulus of the rock; δij represents the stress tensor; p represents the fluid pressure; M is the Biot’s modulus; and .
The Biot coefficient is as follows:
where B represents the bulk modulus, and Bs represents the bulk modulus of solid phase.
Inserting Equation (11) into Equation (3), the following equation is obtained:
For general rock materials, the relationship between bulk modulus and elastic modulus is as follows:
Inserting Equation (13) into Equation (12), the coupling model of the stress–water pressure–permeability coefficient of fractured rock is obtained by the following equation:
The model can concisely describe how the permeability coefficient of fractured rock varies with stress and water pressure. The model equation contains six parameters that can be easily determined: the initial permeability coefficient k0, a constant α, Poisson’s ratio v, elastic modulus E, stress σkk and water pressure p. Among them, α is a constant; k0, v and E can also be determined for specific rocks; σkk can be obtained through rock mechanics experiments or numerical simulation methods; p can be measured using laboratory pressure gauges. According to the calculation results, the hydraulic behavior of fractured rocks under different stress and water pressure can be further analyzed, which is helpful in understanding the permeability evolution law of rocks and has important application prospects in the fields of groundwater resources development, geological hazard prediction and geotechnical engineering.
5. Conclusions
The stress conditions of the surrounding rock mass undergo significant changes after coal mining, and the overburden undergoes deformation, destruction and movement, resulting in strong changes in the permeability of the rock mass around the coal seam, which is the fundamental reason for the change in groundwater in the overlying rock after coal mining. On the basis of fully understanding the main rock types of coal seam roof in the Changzhi mining area, the variation law of the permeability of coarse sandstone, fine sandstone, siltstone and mudstone in the stress–strain process that can represent the overburden in the fracture zone was systematically analyzed, and the relationship and mechanism between the permeability and stress and strain of the overburden in the fracture zone after coal mining were clarified.
The main results are shown below:
- (1)
- The maximum permeability coefficients of different coal overburden types are quite different, the permeability characteristics are intimately tied to the overburden particle size, and the stress–strain process is segmented into a compaction stage, elastic deformation stage, plastic deformation stage and strain-sliding stage, during which the permeability coefficient first decreases and then increases, reaching its maximum after the peak stress.
- (2)
- The generalized model of rock mass permeability included six stages: compaction stage, elasticity stage, stable fracture stage, unstable fracture stage, strain-softening stage and residual strength stage. The closure, generation, extension and interpenetration of pores and fractures in the rock are the fundamental reasons for the drastic changes in its permeability, and its peak strength precedes the peak value of the permeability coefficient in the process of rock mass failure.
- (3)
- Based on a rock mass continuum model, and with strain as the medium and stress and pore water pressure inside the rock mass as the permeability coefficient function, a stress–water pressure–permeability coefficient coupling model of fractured rock was established which can be expressed by the following equation: .
Author Contributions
Data curation, methodology, formal analysis, original draft preparation, P.Z.; methodology, review and editing, X.J.; resources, project administration, funding acquisition, supervision, data curation, methodology, review and editing, Y.L.; methodology, review and editing, M.X.; methodology, review and editing, B.Y.; methodology, review and editing, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Hebei (Grant No. D2020402013; Grant No. D2022402040).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lyv, Y.; Qiao, W.; Chen, W.; Cheng, X.; Liu, M.; Liu, Y. Quantifying the Impact of Coal Mining on Underground Water in Arid and Semi-Arid Area: A Case Study of the New Shanghai No. 1 Coal Mine, Ordos Basin, China. Water 2023, 15, 1765. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Lai, X.; Cao, S.; Yang, Y.; Yan, B.; Bai, L.; Tong, L.; He, W. Transport mechanism and control technology of heavy metal ions in gangue backfill materials in short-wall block backfill mining. Sci. Total Environ. 2023, 895, 165139. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Tian, R.; Xue, C.; Wu, J. Progress, opportunities, and key fields for groundwater quality research under the impacts of human activities in China with a special focus on western China. Environ. Sci. Pollut. Res. 2017, 24, 13224–13234. [Google Scholar] [CrossRef]
- Yang, Y.; Li, P.; Elumalai, V.; Ning, J.; Xu, F.; Mu, D. Groundwater quality assessment using EWQI with updated water quality classification criteria: A case study in and around Zhouzhi County, Guanzhong Basin (China). Expo. Health 2023, 15, 825–840. [Google Scholar] [CrossRef]
- Carmona, S.; Jaramillo, P. Anticipating futures through enactments of expertise: A case study of an environmental controversy in a coal mining region of Colombia. Extr. Ind. Soc. 2020, 7, 1086–1095. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, K.; Reniers, G.; You, G. Statistical analysis the characteristics of extraordinarily severe coal mine accidents (ESCMAs) in China from 1950 to 2018. Process Saf. Environ. Prot. 2020, 133, 332–340. [Google Scholar] [CrossRef]
- Guo, W.; Li, P.; Du, Q.; Zhou, Y.; Xu, D.; Zhang, Z. Hydrogeochemical processes regulating the groundwater geochemistry and human health risk of groundwater in the rural areas of the Wei River Basin, China. Expo. Health 2023, 16, 291–306. [Google Scholar] [CrossRef]
- Wang, F.; Tu, S.; Zhang, C.; Zhang, Y.; Bai, Q. Evolution mechanism of water-flowing zones and control technology for longwall mining in shallow coal seams beneath gully topography. Environ. Earth Sci. 2016, 75, 1309. [Google Scholar] [CrossRef]
- Zeng, Y.; Lian, H.; Du, X.; Tan, X.; Liu, D. An Analog Model Study on Water–Sand Mixture Inrush Mechanisms During the Mining of Shallow Coal Seams. Mine Water Environ. 2022, 41, 428–436. [Google Scholar] [CrossRef]
- Giam, X.; Olden, J.D.; Simberloff, D. Impact of coal mining on stream biodiversity in the US and its regulatory implications. Nat. Sustain. 2018, 1, 176–183. [Google Scholar] [CrossRef]
- Zhang, J.; He, M.; Shimada, H.; Wang, Y.; Hou, S.; Liu, B.; Yang, G.; Zhou, P.; Li, H.; Wu, X. Similar model study on the principle of balanced mining and overlying strata movement law in shallow and thin coal seam based on N00 mining method. Eng. Fail. Anal. 2023, 152, 107457. [Google Scholar] [CrossRef]
- Adhikary, D.P.; Guo, H. Modelling of longwall mining-induced strata permeability change. Rock Mech. Rock Eng. 2015, 48, 345–359. [Google Scholar] [CrossRef]
- Tammetta, P. Estimation of the change in hydraulic conductivity above mined longwall panels. Groundwater 2015, 53, 122–129. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Meng, S.; Wu, Q.; Mei, A.; Bu, W. Ecological water security impact of large coal base development and its protection. J. Hydrol. 2023, 619, 129319. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons, Inc.: New York, NY, USA, 1943; pp. i–xvii. [Google Scholar]
- Biot, M.A. The elastic coefficients of the theory of consolidation. J. Appl. Mech. 1957, 24, 594–601. [Google Scholar] [CrossRef]
- Biot, M.A. General solutions of equations of elasticity and consolidation for a porous material. J. Appl. Phys. 1956, 23, 91–96. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Ma, C.Y.; Liu, Y.T.; Wu, J.L. Simulated flow model of fractured anisotropic media: Permeability and fracture. Theor. Appl. Fract. Mech. 2013, 65, 28–33. [Google Scholar] [CrossRef]
- Min, K.-B.; Rutqvist, J.; Tsang, C.-F.; Jing, L. Stress-dependent permeability of fractured rock masses: A numerical study. Int. J. Rock Mech. Min. Sci. 2004, 41, 1191–1210. [Google Scholar] [CrossRef]
- Noorishad, J.; Ayatollahi, M.S.; Witherspoon, P.A. A finite-element method for coupled stress and fluid flow analysis in fractured rock masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1982, 19, 185–193. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, C.; Bi, J. Permeability model of fractured rock with consideration of elastic-plastic deformation. Energy Sci. Eng. 2020, 8, 441–451. [Google Scholar] [CrossRef]
- Yu, M.; Liu, B.; Chu, Z.; Sun, J.; Deng, T.; Wang, Q. Permeability, deformation characteristics, and damage constitutive model of shale under triaxial hydromechanical coupling. Bull. Eng. Geol. Environ. 2022, 81, 85. [Google Scholar] [CrossRef]
- Teng, T.; Li, Z.; Wang, Y.; Liu, K.; Jia, W. Experimental and Numerical Validation of an Effective Stress-Sensitive Permeability Model Under Hydromechanical Interactions. Transp. Porous Media 2024, 151, 449–467. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, G.; Zhang, D.; Li, W.; Luo, T.; Liang, S.; Fan, Z. A Model of Stress-Damage-Permeability Relationship of Weakly Cemented Rocks under Triaxial Compressive Conditions. Materials 2023, 16, 210. [Google Scholar] [CrossRef]
- Kozusníková, A.; Konecny, P. Influence of temperature on the permeability of rocks. Geotechnique 2011, 61, 1081–1085. [Google Scholar] [CrossRef]
- Zuo, J.; Jiang, G.; Su, H.; Chen, Y. Nonlinear model characterizing stress–strain relationship and permeability change of contact compression fracture at closing stage. J. Rock Mech. Geotech. Eng. 2016, 8, 896–903. [Google Scholar] [CrossRef]
- Yang, T. Study on Infiltrate Character and Coupling Analysis of Seepage and Stress in Rock Failure Process. Ph.D. Thesis, Northeastern University, Shenyang, China, 2001. (In Chinese). [Google Scholar]
- Zhao, Y.; Tang, J.; Wang, W.; Cheng, G.; Luo, S.; Fu, C. Study on failure behavior of fluid-solid coupling under conventional triaxial compression for Maokou limestone. J. Min. Saf. Eng. 2018, 35, 205–212. (In Chinese) [Google Scholar] [CrossRef]
- Qin, S.; Jiao, J.J.; Wang, S. A nonlinear dynamical model of landslide evolution. Geomorphology 2002, 43, 77–85. [Google Scholar] [CrossRef]
- Zhu, W.; David, C.; Wong, T.F. Network modeling of permeability evolution during cementation and hot isostatic pressing. J. Geophys. Res. Solid Earth 1995, 100, 15451–15464. [Google Scholar] [CrossRef]
- Oda, M. An equivalent continuum model for coupled stress and fluid flow analysis in jointed rock masses. Water Resour. Res. 1986, 22, 1845–1856. [Google Scholar] [CrossRef]
- Hubbert, M.K. The Theory of Ground-Water Motion. J. Geol. 1940, 48, 785–944. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).