Abstract
Snow and watershed models typically do not account for forest structure and shading; therefore, they display substantial uncertainty when attempting to account for forest change or when comparing hydrological response between forests with varying characteristics. This study collected snow water equivalent (SWE) measurements in a snow-dominated forest in Colorado, the United States, with variable canopy structure. The SWE measurements were integrated with 1 m Lidar derived canopy structure metrics and incoming solar radiation to create empirical SWE offset equations for four canopy structure groupings (forest gaps, south-facing forest edges, north-facing forest edges, and the interior forest) that varied in size compared to an open area. These simple equations indirectly integrate terrain shading and canopy shading and were able to estimate 40 to 70% of SWE variation in a heterogenous forested environment. The equations were then applied to a snow melt model with a 100 m grid size by applying the area-weighted average of SWE offsets from the four canopy structure groupings in each model cell. This tiled model configuration allowed for the model to better represent the subgrid heterogeneity of a forest environment that can be seen through an ensemble or range of potential outputs rather than a singular estimate.
1. Introduction
Forest type and structure are key determinants of water supply, quality, and timing of availability, and their importance is increasing as freshwater resources become scarcer [1,2]. In the western United States, approximately 65% of the water supply comes from forested regions, and the majority of snowmelt originates from mountain forests [2,3]. Within the southwest, approximately 70% of the total streamflow from the region’s primary water arteries, the Colorado River and Rio Grande, originates as snow [4,5,6,7]. Uncertainty in the hydrological response to land cover disturbance in mountain forests is increasing because of climate change, changing land management strategies, and a variety of natural disturbances such as wildfire and bark beetle infestations [8,9]. These forest disturbances change biophysical processes (e.g., interception and transpiration) and are important drivers of hydrological variation [10,11]. Already, forest disturbance has impacted many areas with seasonal snow. For example, more than 85% of the coniferous forests of the headwaters of the Rio Grande have been affected by the bark beetle [12,13]. Furthermore, in the headwater regions of the Rio Grande and Colorado river basins, burned areas are projected to increase by 300% to 700% with every 1 °C increase in the average global temperature [14,15], with researchers having a limited understanding of how this will affect downstream water resources [16]. Additionally, the snowpack across much of the western United States is declining as precipitation regimes shift from snow to mixed precipitation or rain-dominated regimes, with an average decline in April 1st snow water equivalent (SWE) of 15–30% [17].
Forest disturbance reduces canopy cover (forest density) and increases canopy gaps and edges (canopy structure), which impact the spatial and temporal patterns of snow accumulation and ablation [18]. During accumulation, the reduction in forest cover decreases interception, which is a primary driver of heterogeneous snow accumulation patterns in forests [19,20,21]. This can result in increased snow accumulation on the ground because less snow is intercepted and subsequently sublimated. The sublimation of intercepted snow can be as high as 60% of total annual snowfall, which is much higher than sublimation rates on the sub-canopy snow surface [16,22,23,24,25,26,27]. At the same time, changes in canopy density and structure affect snow ablation (snowpack sublimation, wind transport, and melt) by changing the snow energy balance [16]. During accumulation, a change in canopy can change the snow distribution patterns from wind, impacting sensible and latent heat on the snowpack, which is challenging to represent in snow models [25,28,29,30,31,32].
Reductions in canopy cover can increase shortwave radiation and decrease longwave radiation not just underneath but also beside canopy stands. Thus, changes in forest structure drive shifts in snow accumulation within forested areas, impacting the time and rate at which the snow melts, having substantial influences on hydrological partitioning (i.e., how much snow becomes streamflow and when).
Currently, there is a disconnect between modeling and observational studies of post-disturbance snow water equivalence (SWE) because most current land surface models are not able to accurately represent canopy shading, the impacts of wind, and the subsequent radiation attenuation that occurs adjacent to the canopy rather than just beneath the canopy. Observational studies have shown that there can be both increases and decreases in post-disturbance SWE [18,33,34,35,36]. Goeking et al. [8] synthesized 42 published studies that attempted to quantify the effects of canopy disturbance on snow water resources, and approximately half of the projects that directly measured snow from field campaigns displayed both increases and decreases in post-disturbance SWE. However, coarse-scale models struggle to show these subgrid or tiled differences due to a lack of forest structure representation at the grid scale. Not until coarse-scale models (defined here as a model coarser than the individual tree scale) can better simulate forest snow heterogeneity will we improve the accuracy of quantifying the impact of large-scale characterizations of forest disturbance on the water budget.
There has been a significant body of work showing that the geometric arrangement of canopy elements is a primary predictor of snowmelt due to their effects on the energy balance [37,38,39]. For example, canopy gaps can display highly disparate snow patterns, depending upon their size relative to the surrounding local tree height [40,41]. Moeser et al. [42] demonstrated that the shapes of canopy gaps and how canopy gaps changed shape after a disturbance were more important than knowing just the gap size. Canopy gaps are not the only structure class that display heterogenous snow patterns relative to an open area or forest of uniform density. Canopy edges, in particular, can enhance or attenuate ablation processes related to shifts in radiation and wind [30,43]. Canopy edges have some of the most heterogenous snow conditions anywhere in the forest and depend on the size of and their position relative to the forest gap that the edges sit on. Canopy density and height estimates (e.g., leaf area index [LAI] and canopy closure [CC]) are typically the only metrics used in snow melt models to describe the canopy [31,44,45,46]. Unless these metrics are explicitly represented at a very fine scale, or if further canopy structure parameters are integrated, models cannot accurately simulate how snowpack is affected by the surrounding forest [20,43,47].
Spatially distributed models that are relevant to better understanding water availability and water resource management need to be run across watershed or basin extents and, therefore, realistically need to be computed with model grid elements much coarser than the spatial scale of 1 m that we define as fine-scale within this paper [48,49]. Therefore, a substantial challenge of accurately modeling snowpack evolution in forested areas is successfully incorporating the subgrid influence of canopy structure and elements within coarse-scale snowmelt models. Recent studies have demonstrated novel coarse-scale model improvements in representing subgrid snow accumulation and snowmelt dynamics. For example, Mazzotti et al. [43] displayed a simple fix for complicated longwave radiation-based ablation energetics in a coarse-scale model that treated distant canopy elements equal to air temperature, while only near canopy elements were integrated in the coupled snow and energy balance. This basic distinction between local and non-local canopy elements greatly improved simulations, which were able to mimic snow patterns measured on ground at a scale coarser than that of an individual tree. Sun et al. [50] integrated shading in canopy gaps in a coarse-scale model and demonstrated that a changing gap size can affect SWE estimates by creating unique model partitions. Currier et al. [30,51] developed a watershed model that integrated subgrid tiles to represent general canopy edges and openings. They found that in some cases, during ablation, significant differences in snowpack and streamflow were seen between the tiled model and the non-tiled model. However, in these examples variations in the model, outputs could not be explained because more specific canopy structure elements were not analyzed.
In this study, we attempted to improve estimates of SWE under varying forest structure types by creating simple SWE offsets, or empirical equations, to better represent site-specific subgrid-modeled SWE heterogeneity, which is typically lacking in snow models. These SWE offsets for four generalized canopy structure groupings were applied to modeled SWE output by using the area-weighted average of each of the four canopy groupings within each modeled grid cell from a process-based snow model, SnowModel [52].
The SWE offsets for each generalized canopy grouping integrated two parameters. The first parameter, relative forest structure, was unique to each canopy grouping and developed to be a potential proxy for canopy shading. The second parameter, incoming shortwave radiation, was used to be a proxy for terrain and aspect-based shading. This study outlines the steps leading towards the objective of displaying a forest snow output range in the form of a multi-component ensemble output rather than a singular output to answer the following research questions (RQ):
(RQ1) How much snow variability in forested areas can be captured by using just incoming shortwave radiation and relative forest structure metrics?
(RQ2) Can simplified and localized SWE offsets be leveraged to better represent the true heterogeneity of snow in forest environments in a model platform?
2. Materials and Methods
To answer the above research questions, we performed the following:
- (1)
- Created high-resolution 1 m lidar-based representations of canopy structure and density.
- (2)
- Integrated this information relative to lidar-derived average local tree height and aspect to define relative forest structure metrics.
- (3)
- Analyzed and correlated relative forest structure metrics with local solar radiation data and manual snow measurements.
- (4)
- Generated empirical equations from these data to be used as offsets for modeled SWE from an open area for four generalized canopy groupings (that vary in size): forest gaps, south-facing forest edges, north-facing forest edges, and the interior forest. Taken individually, these canopy groupings represent unique accumulation and ablation zones. Taken as a whole, these canopy groups represent the total forest area captured with the lidar data.
- (5)
- Integrated these empirical equations with a tiled 100 m snow model output to create a multi-component ensemble SWE output range.
2.1. Field Area
The field area for this study is on U.S. Highway 550, 21 km south of the town of Silverton in the San Juan Mountains of southwest Colorado, USA. The site is predominantly flat and has a mean elevation of 3019 m and a typical climate for the Rocky Mountains of Colorado, with cold, snowy winters; dry spring and fall conditions; and monsoonal rain events during the summer months. The field area is located approximately 1.75 km due east of the Spud Mountain SNOTEL station (https://wcc.sc.egov.usda.gov/nwcc/site?sitenum=780) (accessed on 13 May 2023) and is approximately 200 m lower in elevation. The Spud Mountain SNOTEL station shows an average total annual precipitation of 1137 mm, with most precipitation falling as snow during the winter months, with high-intensity rain events from monsoonal storms in the summer. Average monthly SWE peaks in April, with an average value of 611.6 mm. Average monthly temperatures fluctuate between a low of −6 °C in January and an average monthly high of 12.3 °C in July. The ecology of the study site is emblematic of the mixed conifer forest that dominates the sub-alpine band of the Rocky Mountains, consisting of Engelmann spruce (Picea engelmannii), blue spruce (P. pungens), Dougla fir (Pseudotsuga menziesii var. glauca), and white fir (Abies concolor). The field area comprises 311 surveyed points in, on the perimeter of, and surrounding six flat forest openings (gaps) of varying sizes with minimal terrain shading (Figure 1).

Figure 1.
Panel (A) (upper left) is an aerial image of the field location that is 2 km in width. Panel (B) (upper right) is the 1 m resolution canopy height model derived from the lidar data that is 1 km in width. Panel (C) (lower right) is 1 m resolution canopy edginess without aspect (non-directional edginess) that is 400 m in width. Panel (D) (lower right) is the same aerial image as tile A but is 160 m in width, where shading from individual trees can be seen.
2.2. Snow Measurements
Snow measurements including snow depth (SD) and SWE were taken during 16 field campaigns in water year (WY, defined as the 12-month period from October 1 to September 30 of the following year) 2022 and WY 2023 to investigate the relationship between snow accumulation and snow melt patterns among forest gaps of various sizes, as well as forest edges of various sizes (edge of forest gaps) and the interior forest, or locations directly underneath the canopy with no influence of forest gaps or edges.
SD was collected using a graticulated snow probe at each of the surveyed field points for each campaign for a total of 4976 SD measurements. Three SWE measurements from a federal snow sampler were taken in each of the six forest openings for each campaign; this includes one SWE measurement in the middle of the respective forest gap, one on the south-facing edge of the gap, and one on the north-facing edge of the gap. SWE measurements were also taken at three locations within the interior forest (locations that are not a gap or an edge and fall directly underneath canopy) during each campaign, for a total of 288 SWE measurements. The snow densities from the SWE measurements were then used to convert the SD measurements to SWE based on the forest structure values at the specific point. For example, a SD measurement taken on a south-facing edge of a forest opening would be converted to SWE from a density measurement taken on the same south-facing edge. The snow density measurements display low variance within similar canopy groupings. These measurements are publicly available, and further details can be found within a supplemental data release [53].
2.3. Canopy Estimates
Canopy height, density, and structure metrics were derived for the San Juan Mountains of southwest Colorado from aerial point cloud data at a 1-meter (m) resolution over an area of 8459 km2. The aerial lidar data originated from the ‘CO_Southwest_NRCS_2018’ project prepared by Quantum Spatial for the U.S. Geological Survey (USGS) from a series of flyovers between 2018 and 2019 and had a minimum resolution of 2 ground returns/m2 [54]. No fires or forest disturbances have been noted between the lidar flights and sampling for this work. Canopy density metrics include canopy closure (CC) and the leaf area index (LAI). Canopy structure metrics include total gap area, mean distance to canopy, forest edginess with a southern aspect, and forest edginess with a northern aspect.
Canopy height was defined as the difference between the bare ground lidar returns and the canopy returns. The density metrics were estimated using lidar return ratio methods outlined in Fleck et al. [9] and Solberg et al. [55] and were validated by a series of hemispherical images taken in varying canopy densities within the field area. The canopy structure metrics were estimated and defined using methods outlined in Moeser et al. [42,56]. The programs used to derive these metrics can be found in Moeser [57]. Total gap area, forest edginess with a southern aspect, and edginess with a northern aspect were defined relative to the mean local canopy height. Total gap area was converted to relative gap area (Equation (1)), whereby if the diameter of a forest gap was 3 times the local mean canopy height (h), it would be given a value of 3 (or 3 h) in the following manner:
Forest edginess parameters were then defined in relation to the relative gap area with a threshold value of 3 h, where a value of 1 would sit in a relative gap area of ≥3 h.
The canopy metrics derived from lidar were used to partition or tile the 100 m grid cells of a snowmelt model into the four canopy structure groupings of varying size: (1) relative gap area, (2) edginess-south, (3) edginess-north and, (4) the interior forest. This is described in detail in the ‘SnowModel and Data Analysis Integration’ section below.
Each of these four tiles within a grid were defined or initialized from the forest edginess parameter. Forest edginess is based upon a metric that measures the distance to the nearest canopy elements, and a location can still have an edginess value, even if it is in the interior forest group area. As such, a threshold was defined, and the two edginess tiles were defined as any location that had an edginess value >0.1. The relative gap area tile was defined as any area that had an edginess value of 0. The interior forest was defined as any area that is not part of the forest edge or gap area partitions.
The percentage of each canopy structure grouping tile was quantified for each 100 m grid, whereby the four tiles sum to 100%. Mean canopy metric values within each of these tiles were then computed for each 100 m model grid cell. For example, for each 100 m model grid, mean LAI within the interior forest tile was computed based upon the spatial extent of the interior forest tile, and mean LAI within the edginess-south tile was based upon the spatial extent of the edginess-south tile, and so on. For each 100 m model grid cell, there is a percentage attached along with mean canopy metric values. The 1-meter metrics along with the 100 m tiled output are publicly available, and further details can be found within the supplemental data release [54].
2.4. Solar Radiation Data
Incoming shortwave radiation (SWR) data were collected from a radiometer at the Swamp Angel study plot at the Center for Snow and Avalanche Studies (CSAS) (snowstudies.org), approximately 21 km north of the site, in a small mixed-conifer forest opening with low terrain shading at a 3350 m elevation [58]. These data were converted into a cumulative daily measurement (in megajoules) from the start of each water year (WY) to the end of the season in June for WY 2022 and WY 2023 (1 October 2021 to June 2022; October 2022 to June 2023).
2.5. Data Analysis
A data-mining platform was developed to analyze the predictive capability of paring SWE in an open area with cumulative SWR to estimate SWE through time in the four canopy structure groupings derived from the lidar data: (1) relative gap area (gap area), (2) forest edginess with a southern aspect (edginess-south), (3) forest edginess with a northern aspect (edginess-north), and (4) the interior forest defined from canopy closure.
Measurements of the absolute difference (offset) between open-field SWE measurement and SWE measurements at the four canopy groupings were taken, where open-field measurements were taken in gap areas >3 h. Regression equations for each of the 4 canopy structure groupings were developed that used SWR and a unique canopy grouping as independent variables to represent the measured SWE offset.
The equation variables were left flexible where they were individually log-transformed, squared, and varied from a first- to a third-order polynomial with and without independent variable interactions, giving a large array of potential linear and nonlinear regression relationships. The best fit equation was selected for each of the four forest structure groups based upon the minimization of the R2 and root mean square error (RMSE) and least complicated regression if there was <5% change in the R2. For example, if Equation (1) showed an R2 of 0.65 and was a second-order polynomial with no log transforms, Equation (2) showed an R2 of 0.69 and was a second-order polynomial with a log transform, and Equation (3) showed an R2 of 0.65 and was a first-order polynomial with no transforms, then Equation (3) would be chosen.
The data were randomly split into a calibration (70%) and a validation (30%) dataset. The calibration dataset was used for the above regression mining. The best fit equations were then attached to the validation datasets. The data were blindly split in this manner, and the method was repeated 100 times (blind 100-fold cross validation).
The R, R2, RMSE, mean absolute error (MAE), p value, and percentage of independent variable influence on the equations were calculated for each run. The percentage of influence for each of the two independent variables was calculated for each equation. Finally, the spread of the statistics was calculated within the blind 100-fold cross validations.
2.6. SnowModel and Data Analysis Integration
SnowModel is a snow evolution modeling system for simulating the spatiotemporal distribution of snow [52]. We developed a SnowModel domain with a spatial resolution of 100 m that encompasses the field area for this study (Figure 1). A spatial resolution of 100 m was chosen, as it is a common choice in process-based snow modeling [16,59]. SnowModel simulations were run at a 3-hour timestep for WY 2022 and WY 2023 using the National Land Data Assimilation System-2 atmospheric forcing data [60]. A description of the collection of SnowModel submodels including the downscaling of input meteorology can be found in other recent SnowModel studies [16,59,61]. To ensure a reasonable representation of input meteorology for the SnowModel simulations, we utilized both the Spud Mountain SNOTEL and CSAS Swamp Angel study plot stations to perform a standard bias correction to the coarser 1/8 degree resolution, from October to April, for NLDAS-2 air temperature, precipitation, and incoming shortwave radiation for both simulation years.
We constructed two SnowModel configurations for comparison in this study. The first was the “standard”, non-tiled model configuration [52,61] using the parameters described in Sexstone et al., 2020a. The standard SnowModel configuration simulates snow evolution and wind redistribution in forested and non-forested environments based on land cover type, assuming uniform canopy conditions, and does not account for subgrid, tiled SWE heterogeneity. The second approach developed by this study is the “tiled” model configuration that accounts for subgrid SWE heterogeneity. The tiled SnowModel configuration utilized the same parameters as the standard approach but simulated snow for a uniform, open canopy land cover in each grid and then incorporated the four empirical equations developed by this study to estimate the forest snow subgrid heterogeneity.
As highlighted in the ‘Canopy Estimates’ subsection above, the 100 m model grid cells were partitioned into four tiles: (1) relative gap area, (2) edginess-south, (3) edginess-north, and (4) the interior forest, and they were defined from the forest edginess parameter. The empirical equations developed to represent differences in open-area SWE and the four model tiles were then applied to simulate SnowModel’s output.
Specifically, the tiled SnowModel approach included simulating SWE by using the parameters described in Liston and Elder [52] within each 100 m model grid for a non-forested or “open” land cover type. The open-canopy SWE simulation utilized the standard SnowModel equations based on the grassland land cover type. The model grid average canopy height (lidar derived) was used to set the vegetation snow-holding depth to provide a realistic representation of when and where blowing snow (wind) redistribution processes occur across the landscape. The empirical equations developed for each model tile were integrated with the SnowModel open-canopy simulations within and surrounding the field area to estimate SWE through time at the four canopy tiles within each model grid. This gave a four-component model grid ensemble output or range for each model grid. Finally, the average SWE per model grid was derived based upon the weighted average using the initial four-component model grid ensemble and the percentage of each of the four canopy groupings. See Figure 2 for a conceptual model of the tiled SnowModel integration process.
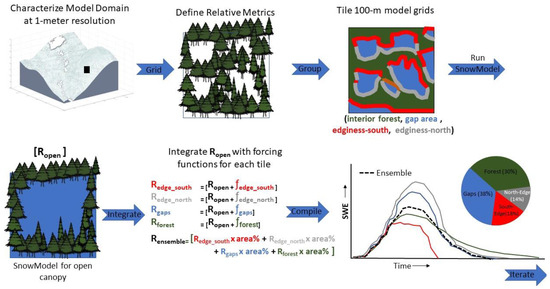
Figure 2.
Generalized schematic of tiled model workflow to integrate empirical functions with SnowModel. The four canopy structure groupings were derived from the lidar data: (1) relative gap area (gap area), (2) forest edginess with a southern aspect (edginess-south), (3) forest edginess with a northern aspect (edginess-north), and (4) the interior forest defined from canopy closure.
3. Results
3.1. Field Data
3.1.1. Snow Measurements
Snow depth and SWE at the field area was lower than at the Spud Mountain SNOTEL site for each of the two snow seasons. WY 2022 was a low snow year and peak SWE from the Spud Mountain SNOTEL was close to the 25% SWE quantile for the period of record (1986 to 2023). Peak SWE from the field measurements in WY 2022 was in March, and the melt-out date ranged between late April and mid-May depending upon the forest class. These measurements were juxtaposed with those taken in WY 2023. WY 2023 was a very high snow year, and peak SWE from the Spud Mountain SNOTEL was greater than the 95% SWE quantile for the period of record. Peak SWE from the field measurements in WY 2023 was in April, and the melt-out date ranged between late May and late June depending upon the forest class (Figure 3).
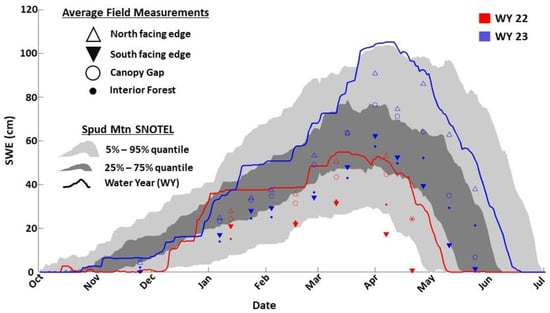
Figure 3.
Overview of field measurements for snow water equivalence (SWE) from water years 2022 (red) and 2023 (blue) compared to the local SNOTEL station 1.75 km away for the equivalent water years, as well as a range of SWE data from the entire collection period from 1986 to 2023. The mean of each forest class for each measurement campaign is shown. Solid lines represent SNOTEL data for each water year (WY), where a WY is October 1 through September 30 of the following year.
Despite large differences between water years, the SWE measurements displayed similar general trends through time when grouped by canopy class (Figure 3). For both water years, the SWE difference between the canopy groupings was the smallest at the start of accumulation and increased through time. Canopy gaps and north-facing edges displayed similar SWE values during accumulation. However, during ablation, north-facing edges displayed much higher SWE values. The north-facing edges of large gaps displayed the highest SWE values regardless of time and some of the lowest melt rates (minus some interior forest points) during ablation. The south-facing edges of large gaps displayed the lowest SWE values regardless of time. The south-facing edges displayed the highest melt rates and were the earliest to melt out. The interior forest points displayed some of the lowest SWE values during accumulation but also displayed the lowest melt rates during ablation. For more details, see the supplemental data release [53].
3.1.2. Canopy Measurements
Canopy metrics for the 311 measurement points were variable. The relative gap area ranged between 0.1 h and 5 h, edginess metrics were between 0 and 1, CC was between 0 and 0.95, and LAI was between 0 and 4.6. Seventy-seven measurement points were in the middle of canopy gaps that had a relative gap area ranging between 0.86 h and 5 h (mean: 3.0 h). One hundred and three measurement points were on a south-facing edge with edginess metrics ranging between 0.1 and 1 (mean: 0.55). One hundred and eleven measurement points were on a north-facing edge with edginess metrics ranging between 0.11 and 1 (mean 0.51). Twenty-four measurement points were in the interior forest where the canopy closure value ranged between 0.62 and 0.95 (mean: 0.78) and LAI ranged between 2.2 and 4.6 (mean: 3.16). These metrics are publicly available in a supplemental data release [54].
3.1.3. Solar Radiation Measurements
WY 2022 and WY 2023 displayed similar incoming shortwave energy dynamics in the early season between October and mid-December. After this, WY 2023 displayed much cloudier conditions and, therefore, reduced incoming solar radiation between mid-December and the beginning of April. For example, cumulative SWR reached ~1600 megajoules (mj) around the beginning of March in WY 2022 but did not reach that level until around the beginning of April in WY 2023. This can be directly seen in Figure 4, as well as indirectly in Figure 3, by the difference in snow accumulation at the SNOTEL site between water years.
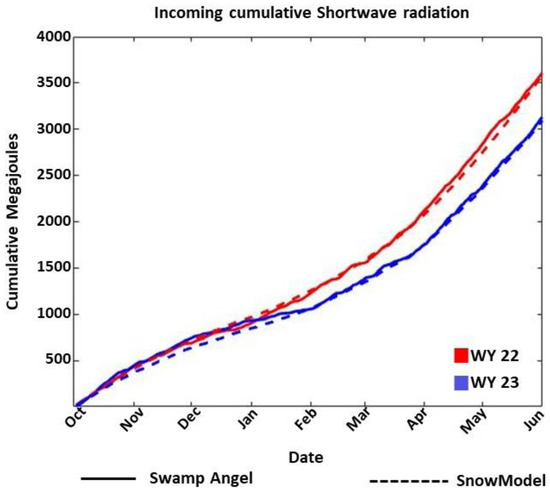
Figure 4.
Comparison of cumulative incoming shortwave radiation data between water years (WY, October 1 through September 30 of the following year) from the Swamp Angel radiometer and SnowModel estimations for the Coal Creek field area of southwest Colorado.
3.2. Data Analysis
All best fit equations presented below took the same polynomial form and displayed a nonlinear shape. Each equation has two independent variables. Cumulative SWR was one of these variables in each of the equations and was always squared. The second independent variable was a canopy parameter unique to each group. No independent variables were log-transformed in any of the equations. All equations estimated a SWE offset in cm SWE and are used as an additive to SnowModel’s output.
3.2.1. SWE in Forest Gaps
Cumulative SWR was used in tandem with relative gap area (Equation (2)) as independent variables to estimate the offset between SWE in an open area and SWE in forest gaps. In general, large relative gap areas in the early accumulation (low cumulative SWR) and late ablation (high cumulative SWR) display higher values (positive SWE offsets) than an open area, while large gaps displayed negative SWE offset values during the rest of the time (Figure 5). Large relative gaps are the only gap size that displayed positive offsets, albeit they were not large differences, and ranged up to ~3 cm (Figure 5). The magnitude of the offset depended on the relative gap size, where smaller gaps displayed lower snow holding capacity than larger gaps and, as such, presented larger negative offsets. The smaller relative gaps had negative offsets as low as 12 cm during times around peak SWE and the beginning to mid-ablation time periods. All gaps during peak SWE, regardless of size, displayed lower values than those in an open area (Figure 5).
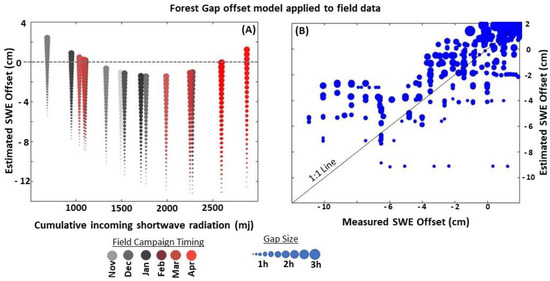
Figure 5.
The left-hand panel (A) displays the estimated snow water equivalence (SWE) offset for relative gap areas of varying sizes (y-axis) during each field campaign from WY 2022 to WY 2023 as they relate to cumulative annual shortwave radiation (SWR) on the x-axis. The right-hand panel (B) displays the estimated (Equation (2)) SWE offset for forest gaps vs. the measured SWE offset. The printed point size relates to the size of the relative gap in both tiles. On the left-hand pane, the color relates to the time at which the data were collected. Water year (WY) is defined as October 1 through September 30th of the following year.
The model from the calibration dataset was able to capture 70% of the measured field data variability, where the use of the relative gap area accounted for 32% of the total variability and SWR accounted for 21% of the total variability (RMSE: 4.18 cm, p value < 0.001). The validation data displayed similar statistics, and a less than 5% change was seen through the 100-fold cross validation step.
Offsetgaps = 2.07 × Gap − 0.013 × SWR + 9.24 × 10−4 × (Gap × SWR) + 2.73 × 10−6 × SWR2 + 1.8839
3.2.2. SWE on North-Facing Edges
The north-facing edginess parameter (EN) was used as the second independent variable. (Equation (3)). This equation displayed much larger SWE offsets than the forest gaps, particularly during the ablation period (Figure 6). Regardless of time of year or SWR regime, the largest north-facing edges displayed equivalent and or higher SWE values than an open area by up to ~35 cm. When cumulative SWR was low, most north-facing edges displayed low to moderately higher SWEs (~±10 cm) than the open area. However, during ablation season or during times with high cumulative SWR values, all north-facing edges (minus the smallest edges) displayed moderate to substantial increases in SWE offsets, ranging up to 35 cm, which highlights reduced melt rates relative to the open area. The smallest canopy edges displayed moderate to substantially lower SWE offsets relative to an open area during accumulation and into the peak SWE while displaying higher offsets during the ablation period.
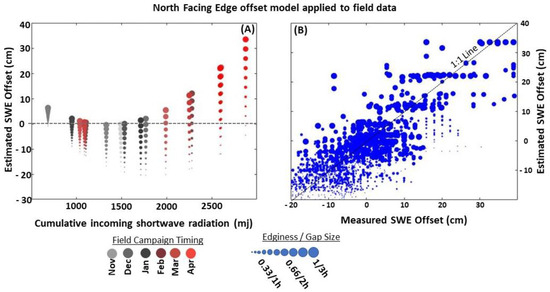
Figure 6.
The left-hand panel (A) displays the estimated snow water equivalence (SWE) offset for north-facing edges of varying sizes (y-axis) during each field campaign from WY 2022 to WY 23 as it relates to cumulative annual shortwave radiation (SWR) on the x-axis. The right-hand panel (B) displays the estimated (Equation (3)) SWE offset for north-facing edges vs. the measured SWE offset. The printed point size relates to the size of the edge in both tiles. On the left-hand panel, the color relates to the time at which the data were collected. Water year (WY) is defined as October 1 through September 30th of the following year.
The model from the calibration dataset was able to capture 56% of the measured field data variability, where the north-facing edges variable accounted for 30% of the total variability and SWR accounted for 22% of the total variability (RMSE: 8.4 cm, p value < 0.001). The validation data displayed similar statistics, and a less than 5% change was seen through the 100-fold cross validation step.
Offsetnorth-edge = −2.34 × EN − 0.054 × SWR + 0.014 × (EN × SWR) + 1.47 × 10−5 × SWR2 + 29.23
3.2.3. SWE on South-Facing Edges
The south-facing edginess parameter (ES) was used as the secondary independent variable in this equation (Equation (4)). The equation displayed a similar shape to the relative gap area and north-facing edges but also displayed several substantial inverse relationships (Figure 7).
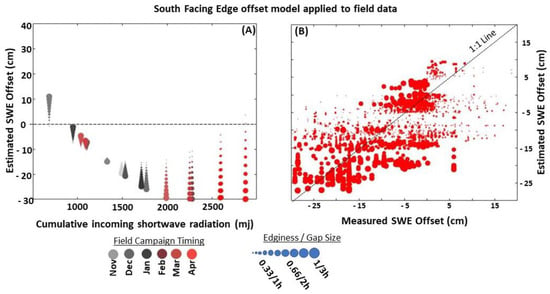
Figure 7.
The left-hand panel (A) displays the estimated snow water equivalence (SWE) offset for south-facing edges of varying sizes (y-axis) during each field campaign in southwest Colorado from WY 2022 to WY 2023 as it relates to cumulative annual shortwave radiation (SWR) on the x-axis. The right-hand panel (B) displays the estimated SWE offset for south-facing edges (Equation (4)) vs. the measured SWE offset. The printed point size relates to the size of the edge in both tiles. On the left-hand panel, the color relates to the time at which the data were collected. Water year (WY) is defined as October 1 through September 30th of the following year.
For example, north-facing edges and relative gap areas displayed a higher magnitude of negative SWE offsets as the gap or edge size reduced regardless of the time period or cumulative radiation. While south-facing edges also displayed this trend during early accumulation, this trend flipped during late accumulation when the larger edges displayed a higher magnitude of negative SWE offsets, and the smaller edges displayed less of a difference from the open areas (~0 cm offset). This tipping point can be seen on the left-hand panel of Figure 7 at approximately 1300 mj of SWR. At the beginning of accumulation, south-facing and north-facing edge equations were plotted similarly, and both displayed increases in SWE (up to 10 cm) relative to an open area if the edge was large and cumulative radiation was low. Large south-facing edges displayed the largest negative offsets (up to 30 cm) in SWE (of all canopy groups) relative to an open area attributed to increased and earlier melt with periods of prolonged mid-winter melt.
The use of this model with the calibration dataset allowed us to capture 42% of the measured field data variability, where use of south-facing edges accounted for approximately 10% of the total variability and SWR accounted for 25% of the total variability (RMSE: 9.1 cm, p value < 0.001). The validation data displayed similar statistics, and a less than 5% change was seen through the 100-fold cross validation step.
Offsetsouth-edge = 25.89 × ES − 0.047 × SWR − 0.02 × (ES × SWR) + 1.39 × 10−5 × SWR2 + 24.87
3.2.4. SWE in the Interior Forest
The best fit equation used CC as the second independent variable to represent the interior forest. CC was paired with squared cumulative SWR. Neither of these independent variables were log-transformed (Equation (5)). The equation shape was nonlinear and displayed a similar shape to those of the other canopy group models. Except for early accumulation and late ablation, most points, regardless of canopy closure values, displayed negative SWE offsets relative to an open area by up to 25 cm (Figure 8). Like the other groupings, there was a large range of offsets that depended upon the canopy variable and cumulative SWR. Only during the latest sampling event (ablation period) did all points, regardless of CC, have a positive offset relative to an open area. Points with the lowest CC values displayed minimal SWE reductions (~5 cm) during peak SWE.
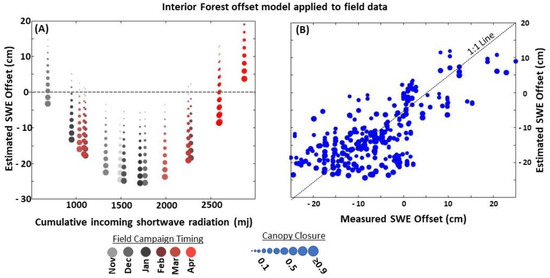
Figure 8.
The left-hand panel (A) displays the estimated snow water equivalence (SWE) offset for the interior forest of varying sizes defined by canopy closure (y-axis) during each field campaign from WY 2022 to WY 2023 as it relates to cumulative annual shortwave radiation (SWR) on the x-axis. The right-hand panel (B) displays the estimated (Equation (5)) SWE offset for the interior forest vs. the measured SWE offset. The printed point size relates to canopy closure in both panels. On the left-hand tile, the color relates to the time at which the data were collected. Water year (WY) is defined as October 1 through September 30th of the following year.
The use of the model with the calibration dataset was able to capture 53% of the measured field data variability, where CC accounted for 10% of total variability, and SWR accounted for 40% of the total variability (RMSE: 8.51 cm, p value <0.001). The validation data displayed similar statistics, and a less than 5% change was seen through the 100-fold cross validation step. Minimal changes in the descriptive statistics were seen when LAI was used in place of canopy closure.
Offsetforest = −16.69 × CC − 0.071 × SWR − 1.77 × 10−53 × (CC × SWR) + 2.13 × 10−5 × SWR2 + 53.11
3.3. SnowModel Calibration
The model’s results are publicly available, and further details can be found within a supplemental data release [62]. Observations of air temperature and precipitation collected by the Spud Mountain SNOTEL station were used to evaluate the meteorological forcing of SnowModel simulations during the months of October through April for each water year. Both simulated SnowModel precipitation and air temperature exhibited a low bias when compared to observations. Therefore, SNOTEL station observations were used to adjust the mean bias of the NLDAS-2 meteorological forcing data. This correction was necessary due to differences in scale between the NLDAS-2 and SnowModel grid and highlights challenges associated with NLDAS-2 forcing data to represent orographic precipitation and cloud cover patterns across steep elevation gradients in complex mountainous terrain [58]. Precipitation correction factors (multipliers) of 1.565 and 1.434 and air temperature adjustments (offsets) of 3.21 °C and 1.15 °C were implemented for the WY 2022 and WY 2023 simulations, respectively. Furthermore, observations of incoming shortwave radiation collected by the CSAS Swamp Angel station (Figure 4) were used to evaluate shortwave radiation inputs simulated using SnowModel. Simulated incoming shortwave radiation compared well to observations during WY 2022 but was biased high during WY 2023 due to the above average cloudy sky conditions. To adjust for this bias, we implemented the cloud fraction adjustment parameter [52] value of 0.98 and 1.8 for WY 2022 and WY 2023. Following these bias corrections, simulated SWE (for an open land cover) at the Spud Mountain SNOTEL station was reasonably well correlated with observations (R2 = 0.78 and 0.95 for WY 2022 and 2023, respectively) and exhibited a RMSE of 10 and 8 cm during WY 2022 and WY 2023, respectively, for all time periods when either the simulated SWE or observed SWE was greater than zero (Figure 9).
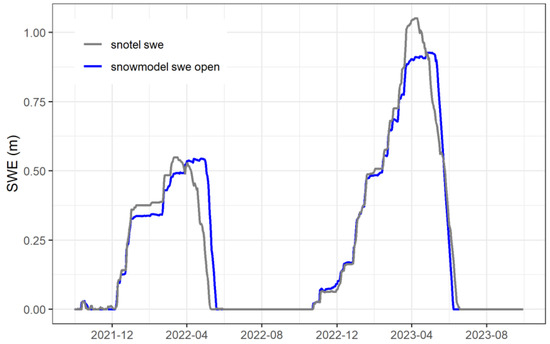
Figure 9.
Comparison between SnowModel estimates and SNOTEL measurements at the Spud Mountain site.
3.4. SnowModel Data Analysis Integration
A comparison between the “standard” and “tiled” SnowModel simulations for model grid cells highlights important differences in the results between the modeling approaches (Figure 10). In WY 2022, the lower SWE of the two snow years evaluated in this study, the tiled approach highlighted in Figure 10 demonstrates a range of peak SWE between 25 and 58 cm and melt-out dates ranging from 02 May to 20 May (16 days). The tiled simulation also shows substantial mid-winter ablation effects that are not highlighted in the standard SnowModel simulation approach (Figure 10). The tiled simulations highlight a comparable peak SWE value but later peak SWE timing when compared to the standard model for WY 2022. In WY 2023, the higher SWE of the two snow years with lower solar radiation input, the SWE ensemble for the tiled approach showed a range of peak SWE between 58 and 95 cm and melt-out dates ranging from 21 May to 09 June (19 days). The tiled simulation shows a higher peak SWE but a similar peak SWE time to the standard SnowModel simulation approach (Figure 10). When these two years are taken together, the results suggest that the standard SnowModel simulation does not represent mid-winter snowmelt ablation that is shown by the tiled approach and driven by radiation influences along forest edges. Furthermore, the standard SnowModel approach appears to estimate greater sublimation losses from forested areas than the tiled approach.
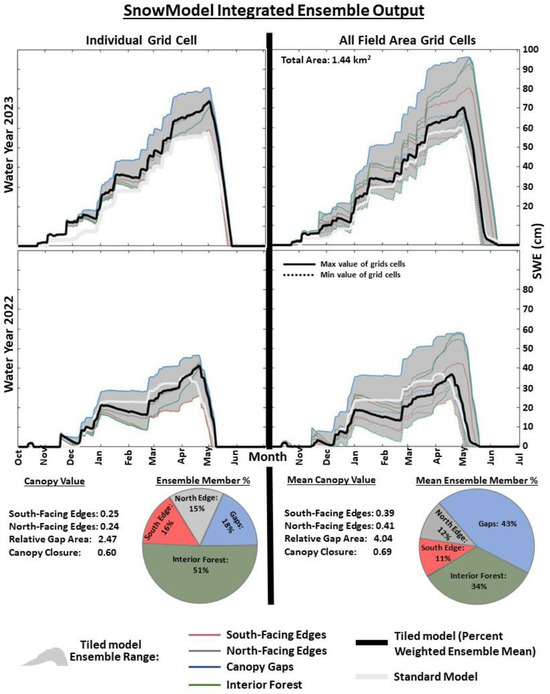
Figure 10.
SnowModel ensemble output with empirical canopy class models integrated. One grid cell in the middle of the field area is on the left. All field area grid cells are on the right. SWE = snow water equivalent. Water year = the period from 1 October to 30 September of the following year.
4. Discussion
Quantifying the interaction between canopy structure and SWE can be used to better understand the influence of canopy disturbance and forest structure, as well as how this may modulate snow storage and retention. This is needed to improve forecasting of water availability, as most models assume uniform canopy structure and do not capture the heterogeneity and true complexity of hydrological mechanisms [44,63,64]. Canopy affects site-specific physical processes that drive snow retention and melt in a manner hard to model at a variety of scales [29,46]. There is a growing body of work highlighting the interactions between the orientation of trees and the sub-canopy energy budget [29,35,56,65,66,67]. As highlighted in the introduction, many of these interactions have been modeled at a fine scale [50,51,68]. However, models that can be run over larger domains are generally too coarse (greater than the scale of individual trees, typically ≥100 m) to capture the subgrid heterogeneity of these processes, lack efficient input data to represent these fine scale processes over many areas, and/or do not have the computational resources needed to simulate these fine scale processes over large domains [69,70,71].
This work outlines the steps required to develop and integrate SWE offset equations with snowmelt models to improve the representation of sub-canopy snow in coarse models (≥100 m grid) using a tiled approach. The empirical SWE offset equations reduce the disagreement between model predictions and field observations of forest snow due to a lack of fidelity of forest representation (RQ2). They were developed to be as simple as possible, utilizing widely available lidar data, while still retaining as much variation in the measured dataset as possible. Each canopy class model integrated two independent parameters: a canopy metric to represent a general canopy structure group and cumulative SWR. Defining general structure groups such as the interior forest, canopy gaps, and canopy edges can better define a forest than canopy density alone. These groups can also be used to qualitatively assess general trends between structure classes and changing snow regimes (RQ1), as highlighted in Table 1.

Table 1.
Qualitative general trends of field data and canopy class models. Dark red arrows that point down represent reduced peak snow water equivalence (SWE) or an earlier melt-out date. Light blue arrows that point up represent increased peak SWE or a later melt-out date relative to an open area. Double arrows represent substantial differences.
Field data were collected in a structurally diverse forest comprising gaps, edges, and forest stands of varying sizes and densities during two water years. One year represented a warm, sunny, and very low snow year, and the other year represented a cold, cloudy, and very high snow year. SD and SWE were repeatedly measured in disparate canopy structure and density classes, producing a representative and extremely heterogenous dataset comprising more than 5000 measurements. Despite the substantial differences in water years, as well as the complicated energetics and mass balance of snow in a forest, we were able to resolve a significant portion of SWE variability in the field area by knowing just two parameters: the relative geometry of the forest structure and incoming shortwave radiation. The large range of the ensemble output from these empirical equations reflects a much more detailed picture of what is happening within the model grid cell. The empirical equations developed for the four canopy groups were able to resolve between 42 and 70% of the measured data variability, meaning that the major source of snow heterogeneity in this field area was from the canopy. This highlights the importance of improving canopy representation in model environments. Similarly, this represents a model platform that has improved subgrid heterogeneity representation by between 42 and 70% from the base version.
4.1. Relative Gap Area
The canopy classes with the lowest SWE heterogeneity relative to an open area were the canopy gaps. The offsets were primarily negative (Table 1) and ranged between +2 and −12 cm, representing differences up to 20% from the model output. This represents a lower holding capacity and a lower melt rate (up to ~25% lower than an open area and compared to prior work) [40,41,42]. Conversely, where the gaps were large, lower melt rates translated to a later melt-out date than in the open area. The magnitude of the offset was defined by the relative gap size, where smaller gaps displayed the largest magnitudes of offset, typically negative, while the larger gaps displayed smaller offsets. This structure class displayed the highest correlations and goodness of fit metrics, explaining 70 percent of the dataset’s variation. This aligns with prior research showing the influence of relative gap sizes on snow accumulation and ablation [38,43].
4.2. Canopy Edges
Forest edges have been shown in prior studies to significantly enhance or attenuate ablation processes [30,42,43]. The canopy edges displayed the highest SWE differences relative to an open area. In general, the two classes, including the north and south edges, were plotted inversely through the snow season, where north-facing edges held more snow than south-facing edges. However, early in the season, as snow first started accumulating, both edge classes displayed small gains in SWE relative to an open area, most likely due to the low solar zenith angle creating high canopy shading. More substantial differences between the open area and edges were found later in the accumulation and ablation season.
The north-facing edges displayed increased SWE offsets, demonstrating increasing SWE holding capacity relative to an open area, with offsets upwards of ~+30 cm of SWE or almost double the value from SnowModel by the end of the season. This highlights a reduction in melt rates through the season, a reduction in mid-winter melt events, and a later melt in general compared to the open area and other structure classes for north edges. This was the only structure class that showed (dependent upon size) both an increase in peak SWE and a later melt-out date relative to an open area. The relative size of the edge determined the magnitude of the offset. During peak SWE, large north-facing edges displayed higher SWEs (up to ~5 cm) than the open areas, while smaller north-facing edges showed reductions in their SWEs relative to the open areas. More than half of the dataset variation was captured with the empirical model.
South-facing edges displayed decreasing SWE holding capacity relative to an open area, and the offset ranged up to approximately −30 cm by the end of the season. Inverse to north-facing edges, these data display an increased melt rate and earlier melt-out date that were augmented from significant mid-winter melt events representing reductions of up to ~60% from SnowModel. During early accumulation, the relative size of the canopy edge displayed the same trend as north-facing edges, where small edges showed smaller and more negative offsets, while large edges had SWE values closer to those of the open area. However, this relationship flipped as mid-winter ablation events become more prevalent on the south-facing edges. After this tipping point, smaller edges had a lower offset magnitude than larger edges (which show the largest negative offsets). Despite these trends being clear in both the field data and empirical model, this canopy class displayed the lowest R2 and goodness of fit metrics.
4.3. Interior Forest
The measured and modeled differences between the interior forest and an open area were defined more by the mass balance than melt processes. The interior forest displayed a significantly lower holding capacity at most time periods, with peak SWE showing the largest negative offset of approximately −25 cm or a slightly greater than a 20% reduction relative to SnowModel. At the end of ablation, this canopy class could hold snow for longer due to less SWR leading to a lower melt rate, giving a potentially later melt-out date. Slightly more than half of the dataset variation was captured with the empirical model.
Interception is typically dominant during the snow accumulation season for areas with dense canopy [24], and land surface models are able to reasonably model snowpack in areas with homogenous canopy density such as the interior forest [38,72,73,74]. Overall, it was not our goal to try to improve upon physically based models by using an empirical one for the interior forest. Rather, we wanted to create a set of models, including one for dense canopy, to model all canopy structures given an estimate of an open area. Physically based modeling of open canopy and interior forest conditions could both be used with our empirical equations to develop a similar tiled model approach.
4.4. Model Parameters and Transferability
The offset equations are not run within SnowModel, but rather integrated after SnowModel runs. This is a significant advantage if this method was to integrate potential future changes in forest density and structure. Instead of having to rerun a model for a preset domain, new canopy structure values (and relative percentages) can be used in the empirical equations. This creates an environment where canopy changes can quickly be analyzed for a preset domain, rather than having to rerun a snow model for each canopy change scenario, improving the flexibility and run time of the model. Additionally, this method can be applied across other model applications that have methods of simulating SWE, increasing the flexibility and applicability of this approach.
The independent parameters used in the equations are proxies for potential canopy, terrain, and aspect-based shading. The canopy metrics for the gaps and edges were defined relative to a tree height to better understand the potential of the canopy to amplify or attenuate solar radiation through forest shading or lack thereof. Cumulative shortwave radiation is a proxy for terrain and aspect-based shading. For example, a location that is primarily shaded due to a mountain positioned south of the point or that sits on a north-facing slope will have lower SWR values than a point on a south-facing slope with no terrain blocking the sun.
Clearly, there are many simplifications within these empirical models as they do not account for the full range of mass and energy balance processes. However, at this field area, reasonable approximations of snow dynamics were estimated using just two components: relative canopy metrics and solar radiation. When paired with a physically based model of an open area at the field area, a multi-component ensemble output of SWE can produce a much richer and more accurate picture of sub-canopy snow than a singular estimate based on a large false assumption, as is prevalent in most coarse-scale models: canopy is uniform in all grid cells.
Relative canopy metrics had the greatest influence on model performance within the gap and north-facing edge classes. They were able to capture ~30% of the dataset’s variability, while SWR accounted for ~20%. This is contrasted by the south-facing edge class and the interior forest, where cumulative radiation had a greater influence on model performance and captured 25–40% of the dataset’s variability, while the south-facing edginess metric and canopy closure captured ~10%.
We initially hypothesized that these differences were because of the increasing influence of longwave radiation on snowmelt in the forest and the south-facing edges [37,38,39] compared to canopy gaps and the north-facing edges. However, if longwave radiation (from the same sensor array) or a composite of SWR and longwave radiation was used as an independent variable instead of cumulative SWR, there were significant reductions in goodness of fit that ranged from 5 to 15% lower R2 values.
It is possible that more SWE variation could be captured by these equations from an improved definition of relative gap area. Relative gap area can be thought of as a proxy of potential gap shading, as it includes the surrounding tree height. Canopy edges also integrate relative gap area. For example, if a south-facing edge has a maximum value of 1, we can assume that this point receives substantial incoming radiation and generates a considerable amount of heat (longwave radiation) against the south-facing canopy elements if it is not terrain shaded [39], which is reflected in the incoming SWR data. Equation (1) assumes that canopy gaps are spherical. However, in circumstances where this is not the case, the equation loses positive correlation to increasing potential radiation. For example, a south-facing edge that sits on a gap that is long in the east and west direction and narrow in the north and south direction can have a very large relative value despite having a significant amount of shading from the canopy elements on the north side. This method does not discriminate between directions and can, thus, give a reasonable approximation of relative size without a directional bias. However, since we are using these metrics as potential energy proxies, it is possible that if the relative gaps sizes were instead defined based upon width from the north–south axis, the goodness of fit statistics would be further improved compared to those based on the total area.
As the likelihood of canopy disturbances in snow-dominated forested watersheds from wildfire, wildfire mitigation, drought stress, and insect mortality [75,76,77,78] increases, an improved understanding of the effects of those disturbances is needed. Similarly, model platforms are needed that can quickly estimate forest change to improve water management in disturbed forests. This platform allows for the effects of changing canopy structure and density on snowpack to be quickly estimated due to the disconnect between the snow model and the subgrid empirical model routines that represent varying canopy structure groupings. The mean values and percentages of the canopy groupings originating from the lidar data can be manually changed (per grid cell or model domain) to represent potential changes in the forest landscape and will not necessitate a complete re-working of the model input data or running of the base SnowModel. This saves computational time and allows for the potential of a model interface to be built where the percentages of the four groupings can be changed by the end user to look at changes in snow through the landscape. However, one cannot indiscriminately change canopy structure or density values for a grid cell or domain without understanding the relationship of those changing values with the percentage of the grid cell or domain. For example, if one was to change south-facing edges from a mean value of 0.2 to 0.8, the total area of the south-facing edges within the grid cell or domain would also need to increase. However, it is unclear how the changing canopy values relate to changing canopy percentages. The relationship between changing canopy values and percentages needs to be explicitly defined before this is used in place of external datasets such as lidar.
This study focused on and displayed the importance of relative canopy metrics. However, the empirical equations developed for this study should be tested in other snow regimes to assess transferability to other regions. The empirically derived equations integrate site-specific interactions that may not be seen in other areas. For example, wind can be a dominant factor in snow redistribution. However, prevailing wind speed and direction may vary in other areas. While SnowModel integrates wind, the interplay between prevailing wind direction and speed is further complicated in forested areas and is a challenge to accurately represent in snow models. Similar empirical equations may be further optimized using varying dominant meteorological forcing data such as wind combined with canopy structure information across snow-dominated regions. This study presents a framework that can be built on for the better integration of forest snow representation into snow or land surface models that can be run across large areas.
5. Conclusions
Through the correlation of the high-resolution, lidar-based representation of canopy structure and density metrics, local incoming shortwave radiation, and manual snow measurements, we created empirical equations that estimate the offset of SWE for four generalized canopy structure groupings (forest gaps, south-facing forest edges, north-facing forest edges, and the interior forest) compared to an open area. Additionally, these SWE offsets were integrated with a snow model to create a multi-component ensemble SWE output range for a forested area in southwest Colorado. This research demonstrates that by using just two pieces of information, SWR and canopy structure metrics, we can estimate 40 to 70% of the variation in SWE in a heterogeneous forested environment. This is largely because SWR and the canopy structure metrics indirectly integrate terrain and canopy shading, respectively.
When these empirical equations are analyzed alone, they align with a significant body of prior research showing the importance of shading, forest gap sizes, and forest edges. Our analysis showed that of the four canopy structure groups, only large north-facing edges display substantial increases in SWE relative to an open area throughout the accumulation and ablation seasons. This is consistent with other studies such as Dickerson and Lange et al. [69], and indicates that if increasing water yields is of importance, mitigation efforts should focus on creating large north-facing edges relative to gap size and tree height. Our analysis also highlighted that large and small north-facing edges, as well as dense and sparse interior forest, had later melt-out dates compared to an open area. This is contrasted by south-facing edges of any size, as well as small gaps that have earlier melt out-dates and lower peak SWE, compared to an open area. This again indicates the value of basic empirical models for highlighting where in the forest landscape greater snow-holding capacity and retention are located (Table 1). At our field area, these results suggest that north-facing edges, particularly those that are large relative to gap size and tree height, have the greatest potential to influence the timing of water availability, delaying snowmelt to later in the season, when water demand is higher.
When these empirical equations are integrated into a snow model, snow heterogeneity can be represented at a scale finer than that of the model grid, improving the representation of snow heterogeneity in model environments that run at large and coarse scales (≥100 m). In general, the tiled model better represented snow accumulation, retention, and melt dynamics. This was partially due to the ensemble or range of potential outputs rather than a singular output being used to represent snow heterogeneity. These performance increases originated from improved representations of shading, or the lack thereof, on melt dynamics. For example, the tiled model more accurately depicted mid-season ablation events compared to the standard model because of the improved representation of forest edges, demonstrating the additional value of depicting seasonal drivers of snowpack dynamics.
This unique approach improves our ability to represent snow in changing forests. The offsets were applied to the snow model after the model was calibrated and run. This reduced computational time, and it presents a path forward to be integrated with other model platforms. It could reduce reliance on multiple datasets and model iterations to represent forest change. Instead, the modeler could represent generalized changes in forest structure by changing the percentages of the canopy groupings and values rather than needing multiple high-resolution datasets as direct inputs into the model. As we face shifts in both our forest structure and snowpack across the western United States, it is important that we develop effective and efficient tools, such as those presented in this work, that are capable of better representing complex interactions between forests and snow.
Author Contributions
Conceptualization, methodology, and analysis came from C.D.M. and G.S. Field data collection originated from C.D.M. and J.K. Writing, reviewing, and editing were performed by C.D.M., G.S. and J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Department of the Interior South Central Climate Adaptation Science Center, which is managed by the USGS National Climate Change and Wildlife Science Center (EN05ESH).
Data Availability Statement
Snow data are available from a supplemental data release found via this link: Moeser, D., Kurzweil, J., and Sexstone, G.A., 2023a. Snow Measurements in Specific Canopy Structure Regimes for the 2022–2023 Water Years, North of Coal Creek, San Juan Mountains, Colorado, USA: U.S. Geological Survey data release, https://doi.org/10.5066/P9E943GE (accessed on 13 May 2023). Canopy data are available from a supplemental data release found via this link: Moeser, C.D. and Sexstone, G.A., 2023. High Resolution Canopy Structure and Density Metrics for Southwest Colorado Derived from 2019 Aerial Lidar: U.S. Geological Survey data release, https://doi.org/10.5066/P9ESQIAV (accessed on 13 May 2023). SnowModel output data are available from a supplemental data release found via this link: Sexstone, G.A. and Moeser, C.D., 2024. SnowModel Simulations for the 2022–2023 Water Years, near Coal Creek, San Juan Mountains, Colorado, USA: U.S. Geological Survey data release, https://doi.org/10.5066/P13OM8Y3 (accessed on 13 May 2023).
Acknowledgments
The authors would like to acknowledge field support from the undergraduate students involved in the 2023 course ‘Collaborative Environmental Research’ at Fort Lewis College. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bates, B.C.; Kundzewicz, Z.W.; Wu, S.; Palutikof, J.P. (Eds.) Climate Change and Water; Technical Paper of the Intergovernmental Panel on Climate Change; IPCC Secretariat: Geneva, Switzerland, 2008; 210p. [Google Scholar]
- Furniss, M.; Staab, B.; Hazelhurst, S.; Clifton, C.; Roby, K.; Ilhadrt, B.; Edwards, P. Water, Climate Change, and Forests: Watershed Stewardship for a Changing Climate; General Technical Report PNW-GTR812; Pacific Northwest Research Station: Portland, OR, USA, 2010; 75p. [CrossRef]
- Li, D.; Wrzesien, M.L.; Durand, M.; Adam, J.; Lettenmaier, D.P. How much runoff originates as snow in the Western United States, and how will that change in the future? Geophys. Res. Lett. 2017, 44, 6163–6172. [Google Scholar] [CrossRef]
- Christensen, N.S.; Lettenmaier, D.P. A multi model ensemble approach to assessment of climate change impacts on the hydrology and water resources of the Colorado River Basin. Hydrol. Earth Syst. Sci. 2007, 11, 1417–1434. [Google Scholar] [CrossRef]
- Guido, B.Z. Mountain Snowpack in the West and Southwest. 2008. Available online: https://www.southwestclimatechange.org/impacts/water/snowpack (accessed on 5 September 2016).
- Rango, A. Snow: The real water supply for the Rio Grande basin. N. Mex. J. Sci. 2006, 44, 99–118. [Google Scholar]
- Talsma, C.J.; Bennett, K.E.; Vesselinov, V.V. Characterizing drought behavior in the Colorado River Basin using unsupervised machine learning. Earth Space Sci. 2022, 9, e2021EA002086. [Google Scholar] [CrossRef]
- Goeking, S.; Tarboton, D. Forests and water yield: A synthesis of recent disturbance effects on streamflow and snowpack in western coniferous forests. J. For. 2020, 118, 172–192. [Google Scholar] [CrossRef]
- Fleck, S.R.S.; Cater, M.; Schleppi, P.; Ukonmaanaho, L.; Greve, M.; Hertel, C.; Weis, W.; Rumpf, S. Manual on Methods and Criteria for Harmonized Sampling, Assessment, Monitoring and Analysis of the Effects of Air Pollution on Forests: Part XVII, Leaf Area Measurements; United Nations Economic Commission for Europe International Cooperative Programme on Assessment and Monitoring of Air Pollution Effects on Forests (ICP Forests): Hamburg, Germany, 2012. [Google Scholar]
- Giles-Hansen, K.; Li, Q.; Wei, X. The cumulative effects of forest disturbance and climate variability on streamflow in the Deadman River watershed. Forests 2019, 10, 196. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, N.; Harper, R.; Li, Q.; Liu, K.; Wei, X. A global review on hydrological responses to forest change across multiple spatial scales: Importance of scale, climate, forest type and hydrological regime. J. Hydrol. 2017, 546, 44–59. [Google Scholar] [CrossRef]
- United States Forest Service. Rio Grande National Forest. 2019. Available online: https://www.fs.usda.gov/riogrande (accessed on 27 July 2019).
- United States Forest Service. CP District-Wide Salvage Project Final Environmental Impact Statement Conejos and Rio Grande Counties, Colorado. Rio Grande National Forest. La Jara, Colorado. 2018. Available online: https://www.fs.usda.gov/nfs/11558/www/nepa/103623_FSPLT3_4292373.pdf (accessed on 28 July 2019).
- Gleason, K.E.; McConnell, J.R.; Arienzo, M.M.; Chellman, N.; Calvin, W.M. Four-fold increase in solar forcing on snow in western U.S. burned forests since 1999. Nat. Commun. 2019, 10, 2026. [Google Scholar] [CrossRef] [PubMed]
- National Research Council. Climate Stabilization Targets: Emissions, Concentrations, and Impacts over Decades to Millennia; The National Academies Press: Washington, DC, USA, 2011. [Google Scholar]
- Sexstone, G.A.; Clow, D.W.; Fassnacht, S.R.; Liston, G.E.; Hiemstra, C.A.; Knowles, J.F.; Penn, C.A. Snow Sublimation in Mountain Environments and its Sensitivity to Forest Disturbance and Climate Warming. Water Resour. Res. 2018, 54, 1191–1211. [Google Scholar] [CrossRef]
- Mote, P.W.; Li, S.; Lettenmaier, D.P.; Xiao, M.; Engel, R. Dramatic declines in snowpack in the western US. npj Clim. Atmos. Sci. 2018, 1, 2. [Google Scholar] [CrossRef]
- Stevens, J.T. Scale-dependent effects of post-fire canopy cover on snowpack depth in montane coniferous forests. Ecol. Appl. 2017, 27, 1888–1900. [Google Scholar] [CrossRef] [PubMed]
- Moeser, D.; Stähli, M.; Jonas, T. Improved snow interception modeling using canopy parameters derived from airborne LIDAR data. Water Resour. Res. 2015, 51, 5041–5051. [Google Scholar] [CrossRef]
- Moeser, D.; Mazzotti, G.; Helbig, N.; Jonas, T. Representing spatial variability of forest snow: Implementation of a new interception model. Water Resour. Res. 2016, 52, 1208–1226. [Google Scholar] [CrossRef]
- Roth, T.R.; Nolin, A.W. Characterizing maritime snow canopy interception in forested mountains. Water Resour. Res. 2019, 55, 4564–4581. [Google Scholar] [CrossRef]
- Essery, R.; Pomeroy, J. Soil-Vegetation-Atmosphere transfer schemes and large-scale hydrological models. In Proceedings of the International Association of Hydrological Science Conference, Maastricht, The Netherlands, 18–27 July 2001; pp. 343–347. [Google Scholar]
- Lundberg, A.; Halldin, S. Snow interception evaporation—Rates, processes, and measurement techniques. Theor. Appl. Climatol. 2001, 70, 117–133. [Google Scholar] [CrossRef]
- Montesi, J.; Elder, K.; Schmidt, R.A.; Davis, R.E. Sublimation of intercepted snow within a subalpine forest canopy at two elevations. J. Hydrometeorol. 2003, 5, 763–773. [Google Scholar] [CrossRef]
- Pomeroy, J.; Gray, D.M.; Shook, K.; Toth, B.; Essery, R.; Pietroniro, A.; Hedstrom, N. An evaluation of snow accumulation and ablation processes for land surface modeling. Hydrol. Process. 1998, 12, 2339–2367. [Google Scholar] [CrossRef]
- Pomeroy, J.; Parviainen, J.; Hedstrom, N.R.; Gray, D.M. Coupled modelling of forest snow interception and sublimation. Hydrol. Process. 1998, 12, 2317–2337. [Google Scholar] [CrossRef]
- Suzuki, K.N.; Yuichiro, O.; Takeshi, N. Effect of snow interception on the energy balance above deciduous and coniferous forests during a snowy winter. In Proceedings of the IUGG—Water Resource Systems, Sapporo, Japan, 30 June–11 July 2003. [Google Scholar]
- Broxton, P.D.; Harpold, A.A.; Biederman, J.A.; Troch, P.A.; Molotch, N.P.; Brooks, P.D. Quantifying the effects of vegetation structure on snow accumulation and ablation in mixed-conifer forests. Ecohydrology 2015, 8, 1073–1094. [Google Scholar] [CrossRef]
- Broxton, P.D.; van Leeuwen WJ, D.; Biederman, J.A. Improving snow water equivalent maps with machine learning of snow survey and lidar measurements. Water Resour. Res. 2019, 55, 3739–3757. [Google Scholar] [CrossRef]
- Currier, W.R.; Lundquist, J.D. Snow depth variability at the Forest edge in multiple climates in the Western United States. Water Resour. Res. 2018, 54, 8756–8773. [Google Scholar] [CrossRef]
- Essery, R.; Rutter, N.; Pomeroy, J.; Baxter, R.; Stähli, M.; Gustafsson, D.; Barr, A.; Bartlett, P.; Elder, K. SNOWMIP2 an evaluation of forest snow process simulations. Bull. Am. Meteorol. Soc. 2009, 90, 1120–1135. [Google Scholar] [CrossRef]
- Wei, X.; Liu, W.; Zhou, P. Quantifying the relative contributions of forest change and climatic variability to hydrology in large watersheds: A critical review of research methods. Water 2013, 5, 728–746. [Google Scholar] [CrossRef]
- Biederman, J.A.; Somor, A.J.; Harpold, A.A.; Gutmann, E.D.; Breshears, D.D.; Troch, P.A.; Gochis, D.; Scott, R.; Meddens, A.; Brooks, P. Recent tree die-off has little effect on streamflow in contrast to expected increases from historical studies. Water Resour. Res. 2015, 51, 9775–9789. [Google Scholar] [CrossRef]
- Hallema, D.W.; Sun, G.; Caldwell, P.V.; Norman, S.P.; Cohen, E.C.; Liu, Y.; Bladon, K.D.; McNulty, S.G. Burned forests impact water supplies. Nat. Commun. 2018, 9, 1307. [Google Scholar] [CrossRef] [PubMed]
- Harpold, A.A.; Biederman, J.A.; Condon, K.; Merino, M.; Korgaonkar, Y.; Nan, T.; Sloat, L.; Ross, M.; Brooks, P. Changes in snow accumulation and ablation following the Las Conchas Forest Fire, New Mexico, USA. Ecohydrology 2014, 7, 440–452. [Google Scholar] [CrossRef]
- Varhola, A.; Coops, N.C.; Weiler, M.; Moore, R.D. Forest canopy effects on snow accumulation and ablation: An integrative review of empirical results. J. Hydrol. 2010, 392, 219–233. [Google Scholar] [CrossRef]
- Essery, R.; Pomeroy, J.; Ellis, C.; Link, T. Modelling longwave radiation to snow beneath forest canopies using hemispherical photography or linear regression. Hydrol. Process. 2008, 22, 2788–2800. [Google Scholar] [CrossRef]
- Lundquist, J.D.; Dickerson-Lange, S.E.; Lutz, J.A.; Cristea, N.C. Lower forest density enhances snow retention in regions with warmer winters: A global framework developed from plot-scale observations and modeling. Water Resour. Res. 2013, 49, 6356–6370. [Google Scholar] [CrossRef]
- Webster, C.; Rutter, N.; Jonas, T. Improving representation of canopy temperatures for modeling subcanopy incoming longwave radiation to the snow surface. J. Geophys. Res. Atmos. 2017, 122, 9154–9172. [Google Scholar] [CrossRef]
- Lawler, R.R.; Link, T.E. Quantification of incoming all-wave radiation in discontinuous forest canopies with application to snowmelt prediction. Hydrol. Process. 2011, 25, 3322–3331. [Google Scholar] [CrossRef]
- Musselman, K.N.; Pomeroy, J.W.; Link, T.E. Variability in shortwave irradiance caused by forest gaps: Measurements, modelling, and implications for snow energetics. Agric. For. Meteorol. 2015, 207, 69–82. [Google Scholar] [CrossRef]
- Moeser, D.; Broxton, P.; Harpold, A. Estimating the effects of forest structure changes from wildfire on snow water resources under varying meteorological conditions. Water Resour. Res. 2020, 56, e2020WR027071. [Google Scholar] [CrossRef]
- Mazzotti, G.; Currier, W.R.; Deems, J.S.; Pflug, J.M.; Lundquist, J.D.; Jonas, T. Revisiting Snow Cover Variability and Canopy Structure within Forest Stands: Insights from Airborne Lidar Data. Water Resour. Res. 2019, 55, 6198–6216. [Google Scholar] [CrossRef]
- Kurzweil, J.R.; Metlen, K.; Abdi, R.; Strahan, R.; Hogue, T.S. Surface water runoff response to forest management: Low-intensity forest restoration does not increase surface water yields. For. Ecol. Manag. 2021, 496, 119387. [Google Scholar] [CrossRef]
- Smith, K.A.; Schneider, K.E.; Kinoshita, A.; Kurzweil, J.; Prucha, B.; Hogue, T.S. Water yield response to forest treatment patterns in a sierra nevada watershed. J. Hydrol. Reg. Stud. 2024, 53, 101762. [Google Scholar] [CrossRef]
- Varhola, A.; Coops, N.C. Estimation of watershed-level distributed forest structure metrics relevant to hydrologic modeling using lidar and Landsat. J. Hydrol. 2013, 487, 70–86. [Google Scholar] [CrossRef]
- Mazzotti, G.; Essery, R.; Moeser, D.; Jonas, T. Resolving small-scale forest snow patterns using an energy balance snow model with a 1-layer canopy. Water Resour. Res. 2020, 56, e2019WR026129. [Google Scholar] [CrossRef]
- Luce, C.H.; Tarboton, D.G.; Cooley, R.R. The influence of the spatial distribution of snow on basin-averaged snowmelt. Hydrol. Process. 1998, 12, 1671–1683. [Google Scholar] [CrossRef]
- Sexstone, G.A.; Driscoll, J.M.; Hay, L.E.; Hammond, J.C.; Barnhart, T.B. Runoff sensitivity to snow depletion curve representation within a continental scale hydrologic model. Hydrol. Process. 2020, 34, 2365–2380. [Google Scholar] [CrossRef]
- Sun, N.; Wigmosta, M.; Zhou, T.; Lundquist, J.; Dickerson-Lange, S.; Cristea, N. Evaluating the functionality and streamflow impacts of explicitly modelling forest–snow interactions and canopy gaps in a distributed hydrologic model. Hydrol. Process. 2018, 32, 2128–2140. [Google Scholar] [CrossRef]
- Currier, W.R.; Sun, N.; Wigmosta, M.; Cristea, N.; Lundquist, J.D. The impact of forest-controlled snow variability on late-season streamflow varies by climatic region and forest structure. Hydrol. Process. 2022, 36, e14614. [Google Scholar] [CrossRef]
- Liston, G.E.; Elder, K. A distributed snow-evolution modeling system (SnowModel). J. Hydrometeorol. 2006, 7, 1259–1276. [Google Scholar] [CrossRef]
- Moeser, D.; Kurzweil, J.; Sexstone, G.A. Snow Measurements in Specific Canopy Structure Regimes for the 2022–2023 Water Years, North of Coal Creek, San Juan Mountains, Colorado, USA; U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2023. [CrossRef]
- Moeser, C.D.; Sexstone, G.A. High Resolution Canopy Structure and Density Metrics for Southwest Colorado Derived from 2019 Aerial Lidar; U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2023. [CrossRef]
- Solberg, S.; Brunner, A.; Hanssen, K.H.; Lange, H.; Næsset, E.; Rautiainen, M.; Stenberg, P. Mapping LAI in a Norway spruce forest using airborne laser scanning. Remote Sens. Environ. 2009, 113, 2317–2327. [Google Scholar] [CrossRef]
- Moeser, D.; Morsdorf, F.; Jonas, T. Novel forest structure metrics from airborne LiDAR data for improved snow interception estimation. Agric. For. Meteorol. 2015, 208, 40–49. [Google Scholar] [CrossRef]
- Moeser, D.; Morsdorf, F.; Jonas, T. Lidar2CanopyMetrics, Version 1.1 [Lidar2CanopyMetrics]; Novel Forest Structure Metrics from Airborne LiDAR Data for Improved Snow Interception Estimation; Zenodo. 2020. Available online: https://zenodo.org/records/4088667 (accessed on 13 May 2023).
- Landry, C.C.; Buck, K.A.; Raleigh, M.S.; Clark, M.P. Mountain system monitoring at Senator Beck Basin, San Juan Mountains, Colorado: Anew integrative data source to develop and evaluate models of snow and hydrologic processes. Water Resour. Res. 2014, 50, 1773–1788. [Google Scholar] [CrossRef]
- Hammond, J.C.; Sexstone, G.A.; Putman, A.L.; Barnhart, T.B.; Rey, D.M.; Driscoll, J.M.; Liston, G.E.; Rasmussen, K.L.; McGrath, D.; Fassnacht, S.R.; et al. High Resolution SnowModel Simulations Reveal Future Elevation-Dependent Snow Loss and Earlier, Flashier Surface Water Input for the Upper Colorado River Basin. Earth’s Future 2023, 11, e2022EF003092. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; et al. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. Atmos. 2012, 117, D03109. [Google Scholar] [CrossRef]
- Liston, G.E. SnowModel (Version 2020_10_02). 2020. Available online: https://gliston.cira.colostate.edu/SnowModel/code/snowmodel_2020_10_02.zip (accessed on 13 May 2021).
- Sexstone, G.A.; Moeser, C.D. SnowModel Simulations for the 2022–2023 Water Years, near Coal Creek, San Juan Mountains, Colorado, USA; U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2024. [CrossRef]
- Saksa, P.C.; Conklin, M.H.; Battles, J.J.; Tague, C.L.; Bales, R.C. Forest thinning impacts on the water balance of Sierra Nevada mixed-conifer headwater basins. Water Resour. Res. 2017, 53, 5364–5381. [Google Scholar] [CrossRef]
- Tague, C.L.; Moritz, M.; Hanan, E. The changing water cycle: The eco-hydrologic impacts of forest density reduction in Mediterranean (seasonally dry) regions. Wiley Interdiscip. Rev. Water 2019, 6, e1350. [Google Scholar] [CrossRef]
- Dwivedi, R.; Biederman, J.A.; Broxton, P.D.; Lee, K.; van Leeuwen, W.J.D. Snowtography quantifies effects of forest cover on net water input to soil at sites with ephemeral or stable seasonal snowpack in Arizona, USA. Ecohydrology 2023, 16, e2494. [Google Scholar] [CrossRef]
- Harpold, A.A.; Guo, Q.; Molotch, N.; Brooks, P.; Bales, R.; Fernandez-Diaz, J.C.; Musselman, K.; Swetnam, T.; Kirchner, P.; Meadows, M.; et al. LiDAR-derived snowpack data sets from mixed conifer forests across the Western United States. Water Resour. Res. 2014, 50, 2749–2755. [Google Scholar] [CrossRef]
- Moeser, D.; Roubinek, J.; Schleppi, P.; Morsdorf, F.; Jonas, T. Canopy closure, LAI, and radiation transfer from airborne LiDAR synthetic images. Agric. For. Meteorol. 2014, 197, 158–168. [Google Scholar] [CrossRef]
- Mower, R.; Gutmann, E.D.; Lundquist, J.; Liston, G.E.; Rasmussen, S. Parallel SnowModel (v1.0): A parallel implementation of a Distributed Snow-Evolution Modeling System (SnowModel). EGUsphere 2023. preprint. [Google Scholar] [CrossRef]
- Dickerson-Lange, S.E.; Howe, E.R.; Patrick, K.; Gersonde, R.; Lundquist, J.D. Forest gap effects on snow storage in the transitional climate of the Eastern Cascade Range, Washington, United States. Front. Water 2023, 5, 1115264. [Google Scholar] [CrossRef]
- Helbig, N.; Moeser, D.; Teich, M.; Vincent, L.; Lejeune, Y.; Sicart, J.-E.; Monnet, J.-M. Snow processes in mountain forests: Interception modeling for coarse-scale applications. Hydrol. Earth Syst. Sci. Discuss. 2020, 24, 2545–2560. [Google Scholar] [CrossRef]
- Sun, N.; Yan, H.; Wigmosta, M.S.; Leung, L.R.; Skaggs, R.; Hou, Z. Regional Snow Parameters Estimation for Large-Domain Hydrological Applications in the Western United States. J. Geophys. Res. Atmos. 2019, 124, 5296–5313. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Storck, P.; Lettenmaier, D.P. Modeling snow accumulation and ablation processes in forested environments. Water Resour. Res. 2009, 45, W05429. [Google Scholar] [CrossRef]
- Gelfan, A.N.; Pomeroy, J.W.; Kuchment, L.S. Modeling forest cover influences on snow accumulation, sublimation, and melt. J. Hydrometeorol. 2004, 5, 785–803. [Google Scholar] [CrossRef]
- Strasser, U.; Warscher, M.; Liston, G.E. Modeling snow-canopy processes on an idealized mountain. J. Hydrometeorol. 2011, 12, 663–677. [Google Scholar] [CrossRef]
- Burke, M.; Driscoll, A.; Heft-Neal, S.; Xue, J.; Burney, J.; Wara, M. The changing risk and burden of wildfire in the United States. Proc. Natl. Acad. Sci. USA 2021, 118, e2011048118. [Google Scholar] [CrossRef] [PubMed]
- Essen, M.; McCaffrey, S.; Abrams, J.; Paveglio, T. Improving wildfire management outcomes: Shifting the paradigm of wildfire from simple to complex risk. J. Environ. Plan. Manag. 2023, 66, 909–927. [Google Scholar] [CrossRef]
- Knapp, E.E.; Bernal, A.A.; Kane, J.M.; Fettig, C.J.; North, M.P. Variable thinning and prescribed fire influence tree mortality and growth during and after a severe drought Eric. For. Ecol. Manag. 2020, 479, 118595. [Google Scholar] [CrossRef]
- Venturas, M.D.; Todd, H.N.; Trugman, A.T.; Anderegg, W.R.L. Understanding and predicting forest mortality in the western United States using long-term forest inventory data and modeled hydraulic damage. New Phytol. 2021, 230, 1896–1910. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).