Hazard Assessment of Debris Flow: A Case Study of the Huiyazi Debris Flow
Abstract
1. Introduction
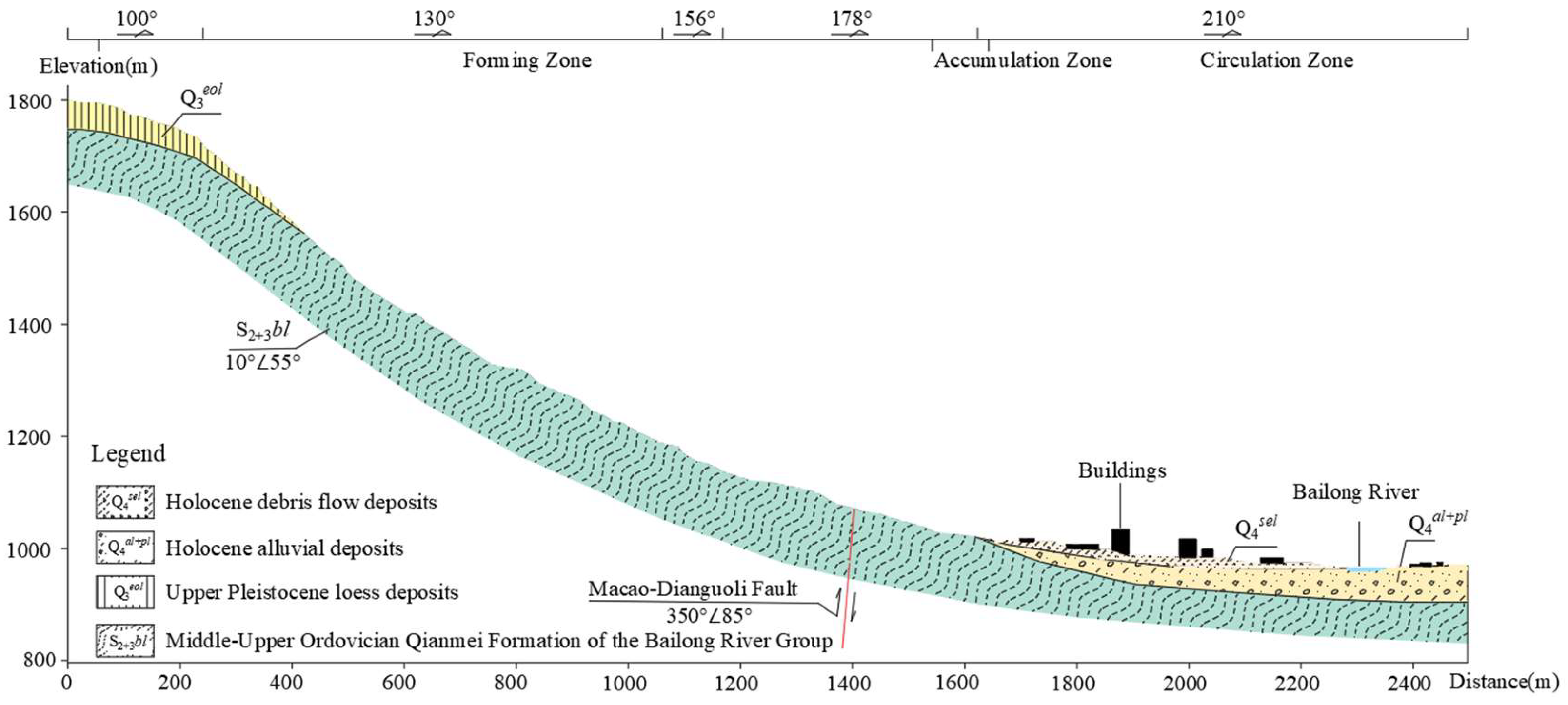
2. Study Area
3. Method and Data Preprocessing
3.1. Method
3.1.1. FLO-2D Model
- (1)
- Continuity equation:
- (2)
- Equations of motion:
- (3)
- Rheological equation:
3.1.2. Hazard Zoning Model
3.2. Data Preprocessing
3.2.1. Volumetric Sediment Concentration
3.2.2. Viscosity Coefficient
3.2.3. Manning’s Coefficient
3.2.4. Resistance Parameter for Laminar Flow
3.2.5. Simulation Time
3.2.6. Inflow Node and Peak Discharge
4. Hazard Assessment of Debris Flow
4.1. Simulation Results
4.2. Assessment of the Degree of Hazard
- (1)
- The high hazard areas account for 16.74% of the total area. Due to the uneven width and steep terrain of the mudslide ditch, the blockage of buildings, and the narrow width of the drainage channel, the high-hazard areas are mainly concentrated in the channels, factory buildings, and drainage channels. Damage to the factory buildings is particularly significant due to siltation phenomena. There is a high risk of damage in the event of future mudslides, and it is important to remove silt in a timely manner to prevent further siltation from damaging the factory buildings.
- (2)
- The medium hazard area accounts for 62% of the area, which occupies the largest area and is mainly located on both sides of the channels, buildings, and within the Bailong River, and although its hazard level is relatively low, the potential hazard of mudslides should not be ignored due to its wide range. Therefore, effective monitoring, early warning, and risk management measures need to be taken for the medium-hazard area in order to mitigate the potential damage caused by mudslides.
- (3)
- The low hazard area accounts for 21.26% of the area and is mainly located within the buildings and the Bailong River, which is less hazardous to the buildings. However, there is still a need for vigilance and ongoing monitoring and assessment to ensure safety.
5. Discussion
5.1. Comparison of DEM and DSM Simulation Results
5.2. Debris Flow Characteristics Analysis and Protective Measure Suggestions
6. Conclusions
- (1)
- Under different recurrence periods, the flow velocities of the debris flow after exiting the gully range from 0 to 6 m/s, with velocities near the factory buildings generally ranging from 0 to 1.5 m/s. The velocities in the drainage channels are relatively higher, typically around 0 to 4.5 m/s. But the flow velocities noticeably decrease after entering the Bailong River. After leaving the gully, the debris flow exhibits distinct diversion, primarily flowing towards the cement plant area. Limited flow is observed on the left and right sides, likely due to the obstruction of the mountainous terrain and narrow channels.
- (2)
- Under different recurrence periods, the depth of debris deposition in the factory area is generally less than 1.5 m. With an increase in debris flow volume, the depth of deposition gradually increases, with the maximum deposition depth typically occurring within the drainage channels. Upon flowing into the Bailong River, the debris flow does not cause deposition material to cross the river channel, posing a risk of diversion to downstream buildings. At this point, the Bailong River serves as a barrier intercepting sediment deposition at the foot of the slope.
- (3)
- According to Swiss and Austrian standards, combined with the intensity and probability of debris flow occurrences, the hazard of debris flows is classified into three levels: low, medium, and high. By categorizing the intensity of the Huiyazi debris flow and considering the frequency of occurrences under different recurrence periods, corresponding hazard zone maps were generated. High-hazard areas are mainly concentrated in the channels, factory buildings, and drainage channels, where enhanced protective measures are required. The medium hazard area is primarily distributed along both sides of the channels, buildings, and within the Bailong River, with a widespread distribution and significant potential hazard. The low hazard area is mainly located within buildings and the Bailong River, posing minimal hazard to buildings. Based on terrain and remote sensing images, the main threatened objects for all four recurrence periods are the cement factory and the houses below it, providing valuable insights for debris flow risk management and mitigation.
- (4)
- Debris flow channels typically lack vegetation or have sparse vegetation cover. Compared to traditional Digital Elevation Model (DEM), high-precision Digital Surface Model (DSM) ensure that the terrain of debris flow channels accurately reflects reality while also preserving digital model information of structures and other vulnerable elements. The simulation results indicate that employing high-precision DSM (Digital Surface Model) for debris flow hazard assessment demonstrates characteristics such as sediment deposition and diversion when encountering buildings in the deposition zone. The movement process and disaster features of debris flows closely resemble real conditions, resulting in more accurate evaluation outcomes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, C.; Zhu, J.; Li, W.L.; Liang, J.T. Rainfall-Triggered Debris Flows Following the Wenchuan Earthquake. Bull. Eng. Geol. Environ. 2009, 68, 187–194. [Google Scholar] [CrossRef]
- Ouyang, C.; Wang, Z.; An, H.; Liu, X.; Wang, D. An Example of a Hazard and Risk Assessment for Debris Flows—A Case Study of Niwan Gully, Wudu, China. Eng. Geol. 2019, 263, 105351. [Google Scholar] [CrossRef]
- Lee, S.H.-H.; Widjaja, B. Phase Concept for Mudflow Based on the Influence of Viscosity. Soils Found. 2013, 53, 77–90. [Google Scholar] [CrossRef]
- Wang, Z.F.; Zhang, X.S.; Zhang, X.Z.; Wu, M.T.; Wu, B. Hazard Assessment of Potential Debris Flow: A Case Study of Shaling Gully, Lingshou County, Hebei Province, China. Front. Earth Sci. 2023, 11, 1089510. [Google Scholar] [CrossRef]
- Dai, Z.; Wang, L.; Fu, X.; Huang, B.; Zhang, S.; Gao, X.; He, X. Degradation of Typical Reverse Sand-Mudstone Interbedded Bank Slope Based on Multi-Source Field Experiments. Int. J. Environ. Res. Public Health 2023, 20, 2591. [Google Scholar] [CrossRef] [PubMed]
- Dai, Z.; Yang, L.; Zhang, N.; Zhang, C.; Zhang, Z.; Wang, H. Deformation Characteristics and Reactivation Mechanism of an Old Landslide Induced by Combined Action of Excavation and Heavy Rainfall. Front. Earth Sci. 2023, 10, 1009855. [Google Scholar] [CrossRef]
- Zhang, A.; Dai, Z.; Qin, W.; Fu, X.; Gao, J.; Guo, L.; Liu, L.; Jiang, X.; Wang, H. Risk Assessment of the Xigou Debris Flow in the Three Gorges Reservoir Area. Front. Ecol. Evol. 2023, 11, 1264936. [Google Scholar] [CrossRef]
- Hürlimann, M.; Copons, R.; Altimir, J. Detailed Debris Flow Hazard Assessment in Andorra: A Multidisciplinary Approach. Geomorphology 2006, 78, 359–372. [Google Scholar] [CrossRef]
- Hungr, O.; McDougall, S.; Wise, M.; Cullen, M. Magnitude–Frequency Relationships of Debris Flows and Debris Avalanches in Relation to Slope Relief. Geomorphology 2008, 96, 355–365. [Google Scholar] [CrossRef]
- Yu, X.; Wei, J. Grey system analysis and its application in the forecast of mud-rock flow criticality of Beijing. Zhongzhongguo Dizhizaihai Yu Fangzhi Xuebao 2004, 1, 121–123. [Google Scholar]
- Feng, P.; Xiang, L.; Luo, L.; Lei, Q.; Cui, K.; Liang, M. Comparative Analysis of Debris Flow Risk Assessment Based on Disaster Entropy and Analytic Hierarchy Process: A Case Study of Diebu County, Gansu Province. Sci. Technol. Eng. 2023, 23, 12416–12426. [Google Scholar]
- Yu, Z.; Deng, Y.; Zhao, P. Evaluation on Fuzzy Mathematics Method for Analyzing Risk of Ridigou Debris Flow. Subgrade Eng. 2016, 1, 44–49. [Google Scholar]
- Gu, X.; Chen, H.; Liu, H. Method and application of debris flow hazard assessment based on SIGA-BP neural network. J. Chongqing Jiaotong Univ. 2010, 29, 98–102. [Google Scholar]
- Liu, T.; Sun, S.; Zhao, Z.; Zhang, X. Massflow model-based evaluation on effect of engineering treatment of debris flow in Lengzigou Gully. Water Resour. Hydropower Eng. 2020, 51, 195–201. [Google Scholar]
- Zhang, F.; Zhang, L.; Zhou, J.; Wang, S. Risk assessment of debris flow in Ruoru Village, Tibet Based on FLO-2D. J. Water Resour. Water Eng. 2019, 30, 95–102. [Google Scholar]
- Gong, K.; Yang, T.; Xia, C.; Yang, Y. Assessment on the hazard of debris flow based on FLO-2D: A case study of debris flow in Cutou Gully, Wenchuan, Sichuan. J. Water Resour. Water Eng. 2017, 28, 134–138. [Google Scholar]
- Wang, Z.; Chang, M.; Liu, P.; Xu, L. Hazard assessment of typical gully debris flow in Anning river:A case study at the Lengzi gully. Chin. J. Geol. Hazard Control. 2022, 33, 31–38. [Google Scholar]
- Quan Luna, B.; Blahut, J.; Van Westen, C.J.; Sterlacchini, S.; Van Asch, T.W.J.; Akbas, S.O. The Application of Numerical Debris Flow Modelling for the Generation of Physical Vulnerability Curves. Nat. Hazards Earth Syst. Sci. 2011, 11, 2047–2060. [Google Scholar] [CrossRef]
- Peng, S.-H.; Lu, S.-C. FLO-2D Simulation of Mudflow Caused by Large Landslide Due to Extremely Heavy Rainfall in Southeastern Taiwan during Typhoon Morakot. J. Mt. Sci. 2013, 10, 207–218. [Google Scholar] [CrossRef]
- Gentile, F.; Bisantino, T.; Trisorio Liuzzi, G. Debris-Flow Risk Analysis in South Gargano Watersheds (Southern-Italy). Nat. Hazards 2008, 44, 1–17. [Google Scholar] [CrossRef]
- Franco-Ramos, O.; Ballesteros-Cánovas, J.A.; Figueroa-García, J.E.; Vázquez-Selem, L.; Stoffel, M.; Caballero, L. Modelling the 2012 lahar in a sector of Jamapa Gorge (Pico de Orizaba Volcano, Mexico) using RAMMS and Tree-Ring evidence. Water 2020, 12, 333. [Google Scholar] [CrossRef]
- Hussin, H.Y.; Quan Luna, B.; Van Westen, C.J.; Christen, M.; Malet, J.P.; Van Asch, T.W. Parameterization of a numerical 2-D debris flow model with entrainment: A case study of the Faucon catchment, Southern French Alps. Nat. Hazards Earth Syst. Sci. 2012, 12, 3075–3090. [Google Scholar] [CrossRef]
- Horton, A.J.; Hales, T.C.; Ouyang, C.; Fan, X. Identifying post-earthquake debris flow hazard using Massflow. Eng. Geol. 2019, 258, 105134. [Google Scholar] [CrossRef]
- Choi, S.K.; Park, J.Y.; Lee, D.H.; Fan, X. Assessment of barrier location effect on debris flow based on smoothed particle hydrodynamics (SPH) simulation on 3D terrains. Landslides 2021, 18, 217–234. [Google Scholar] [CrossRef]
- An, H.; Ouyang, C.; Wang, F.; Xu, Q.; Wang, D.; Yang, W.; Fan, T. Comprehensive analysis and numerical simulation of a large debris flow in the Meilong catchment, China. Eng. Geol. 2022, 298, 106546. [Google Scholar] [CrossRef]
- Lin, J.Y.; Yang, M.D.; Lin, B.R.; Lin, P.S. Risk assessment of debris flows in Songhe Stream, Taiwan. Eng. Geol. 2011, 123, 100–112. [Google Scholar] [CrossRef]
- Notti, D.; Giordan, D.; Cina, A.; Manzino, A.; Maschio, P.; Bendea, L. Debris flow and rockslide analysis with advanced photogrammetry techniques based on high-resolution RPAS data. Ponte Formazza case study (NW Alps). Remote Sens. 2021, 13, 1797. [Google Scholar] [CrossRef]
- García, R.; Rodríguez, J.J.; O’Brien, J.S. Hazard Zone Delineation for Urbanized Alluvial Fans. In Critical Transitions in Water and Environmental Resources Management; American Society of Civil Engineers: Salt Lake City, UT, USA, 2004; pp. 1–10. [Google Scholar]
- Wang, Y.Y.; Zhan, Q.D.; Han, W. Stress-strain properties of viscous debris flow and determination of volocity parameter. Chin. J. Geol. Hazard Control 2003, 14, 9–13. [Google Scholar]
- Crosta, G.B. Failure and ¯ow Development of a Complex Slide: The 1993 Sesa Landslide. Eng. Geol. 2001, 59, 173–199. [Google Scholar] [CrossRef]
- O’Brien, J.S. FLO-2D User Manual; FLO-2D Software, Inc.: Nutrioso, AZ, USA, 2018. [Google Scholar]
- Zhang, H.W.; Liu, F.Z.; Wang, J.C. Hazard assessment of debris flows in Kongpo Gyamda, Tibet based on FLO-2D numerical simulation. J. Geomech. 2022, 28, 306–318. [Google Scholar]
- Chang, M.; Tang, C.; Van Asch, T.W.J.; Cai, F. Hazard assessment of debris flows in the Wenchuan earthquake-stricken area, South West China. Landslides 2017, 14, 1783–1792. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Gan, J. Numerical simulation of debris flow runout using Ramms: A case study of Luzhuang Gully in China. Comput. Model. Eng. Sci. 2019, 121, 981–1009. [Google Scholar]
- Han, M.; Hu, T.; Wang, Y.; Hong, M. Dynamics Character and River-Blocking Analysis of Narrow-Steep Channels Debris Flow in Wenchuan Earthquake Region—Illustrated with Case of Mozi Gully along Duwen Freeway. J. Eng. Geol. 2016, 24, 559–568. [Google Scholar]

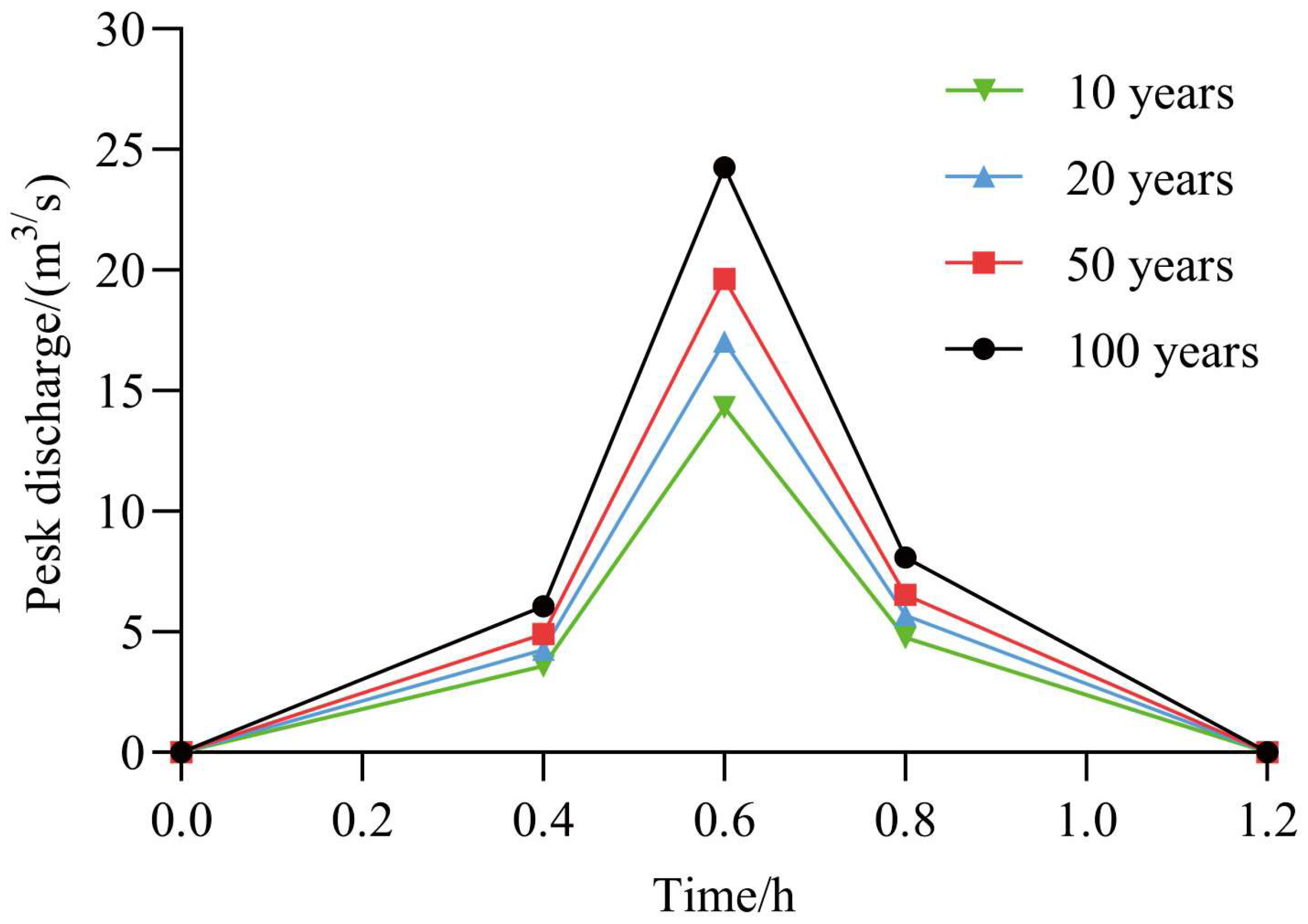



| Recurrence Periods/Years | Deposition Area (km2) | Deposition Volume (×104 m3) | Average Deposition Thickness (m) |
|---|---|---|---|
| 10 | 0.068 | 2.44 | 0.36 |
| 20 | 0.078 | 2.93 | 0.38 |
| 50 | 0.087 | 3.42 | 0.39 |
| 100 | 0.102 | 4.26 | 0.42 |
| Debris Flow Intensity | Maximum Depth H (m) | Relation | Maximum Depth H Multiplied by Maximum Velocity (V) (m2/s) |
|---|---|---|---|
| High | H ≥ 1 | OR | VH ≥ 1 |
| Medium | 0.5 ≤ H < 1 | AND | 0.5 ≤ VH ≤ 1 |
| Low | 0 ≤ H < 0.5 | AND | VH < 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Feng, Z.; Wang, L.; Tian, Y.; Chen, L. Hazard Assessment of Debris Flow: A Case Study of the Huiyazi Debris Flow. Water 2024, 16, 1349. https://doi.org/10.3390/w16101349
Guo Y, Feng Z, Wang L, Tian Y, Chen L. Hazard Assessment of Debris Flow: A Case Study of the Huiyazi Debris Flow. Water. 2024; 16(10):1349. https://doi.org/10.3390/w16101349
Chicago/Turabian StyleGuo, Yuntao, Zhen Feng, Lichao Wang, Yifan Tian, and Liang Chen. 2024. "Hazard Assessment of Debris Flow: A Case Study of the Huiyazi Debris Flow" Water 16, no. 10: 1349. https://doi.org/10.3390/w16101349
APA StyleGuo, Y., Feng, Z., Wang, L., Tian, Y., & Chen, L. (2024). Hazard Assessment of Debris Flow: A Case Study of the Huiyazi Debris Flow. Water, 16(10), 1349. https://doi.org/10.3390/w16101349






