Abstract
Cavitation happening inside an inclined V-shaped corner is a common and important phenomenon in practical engineering. In the present study, the lattice Boltzmann models coupling velocity and temperature fields are adopted to investigate this complex collapse process. Based on a series of simulations, the fields of density, pressure, velocity and temperature are obtained simultaneously. Overall, the simulation results agree with the experiments, and they prove that the coupled lattice Boltzmann models are effective to study cavitation bubble collapse. It was found that the maximum temperature of bubble collapse increases approximately linearly with the rise of the distance between the single bubble center and the corner. Meanwhile, the velocity of the micro-jet increases and the pressure peak at the corner decreases correspondingly. Moreover, the effect of angle of the V-shaped wall on the collapse process of bubbles is similar to the effect of distance between the single bubble center and the corner. Moreover, with the increase in bubble radius, the maximum temperature of bubble collapse increases proportionally, the starting and ending of the micro-jet are delayed and the pressure peak at the corner becomes larger and also is delayed. In the double bubble collapse, the effect of distance between two bubble centers on the collapse process of bubbles is discussed in detail. Based on the present study, appropriate measures can be proposed to prevent or utilize cavitation in practical engineering.
1. Introduction
The collapse of cavitation bubbles can cause high pressure and temperature, accompanied by strong shock wave and high-speed micro-jet. Therefore, the collapse of cavitation bubbles near a wall may cause serious damage to the surrounding walls. On the other hand, the collapse energy of cavitation bubbles can lead to some beneficial effects in some fields such as high-intensity ultrasound treatment [1], material surface cleaning [2] and ice breaking [3]. Therefore, the collapse mechanism of cavitation bubbles deserves further study.
In recent years, the collapse of cavitation bubbles has been studied experimentally. For example, high-speed photography and other techniques have been adopted to study the collapse process of single or multiple cavitation bubbles near flat walls [4,5,6] and uneven walls [7,8,9,10,11]. However, the above experiments only reveal the bubble morphology in the process of collapse, and it is difficult to obtain the fields of velocity, pressure and temperature by these experiments. Therefore, numerical simulation has gradually become another effective method to study cavitation because it can provide detailed flow and thermal fields. Furthermore, it can describe the evolution process of the cavitation bubble collapse under complex boundary conditions. For example, Fukaya et al. adopted a bubble flow model to simulate the bubble behavior in cavitating flow [12]. Han et al. adopted the boundary integral method to study the collapse of multiple cavitation bubbles near a rigid wall [13]. Li et al. studied the collapse process of cavitation bubbles near the conical rigid boundary by the finite volume method and the volume of fluid method [14]. Lyu et al. simulated the collapse behavior of a single cavitation bubble near a solid particle using the volume of fluid (VOF) method. Based on the simulation, the pressure field, velocity field and collapse time were studied [15]. Li et al. proposed an accurate three-dimensional boundary integral model for inertial cavitation bubble dynamics [16]. In this study, a density potential method and a weighted moving least-squares method were used to maintain a high level of mesh regularity. Duy et al. simulated the evolution of a cavitation bubble and its interactions with the gas–liquid interface by a fully compressible mixture model. This model was developed based on a general curvilinear grid [17]. Zhang et al. used OpenFOAM to simulate the collapse process of the cavitation bubble near a solid wall. It is found that the cavitation bubble near the wall collapsed in an axial symmetric heart shape [18]. Zhang et al. studied the bubble cavitation dynamics between a rigid wall and an elastic wall. In this study, the pressure of the satellite bubble was obtained, and the formation of the satellite bubble was explained [19]. Lu et al. simulated the collapse process of cavitation bubbles within a diesel droplet, including the phase change or not, using OpenFOAM with the volume of fluid method [20]. Zhang et al. simulated the collapses of both a single cavitation bubble and a cluster consisting of eight bubbles using direct numerical simulation (DNS) with volume of fluid [21]. Ye et al. simulated the collapse process of a near-wall bubble cluster using the direct numerical simulation with the VOF method where viscosity, compressibility and surface tension were taken into account [22]. However, these computational fluid dynamics (CFD) methods need to solve the Poisson equation for obtaining the pressure field, and most of them need interface capture [23]. Both of them will obviously increase the difficulty of simulation.
In recent years, the lattice Boltzmann method (LBM) has been developed to be a successful method of simulating multiphase flow. For example, the isothermal LBM pseudo-potential model [24,25,26] has been adopted to simulate the growth and collapse process of cavitation bubbles near an infinite or flat wall [27,28,29,30,31]. Up to now, there have been four main kinds of two-phase LBM, namely, the free energy model [32], the Shan–Chen model [33], the color-gradient model [34] and the mean-field model [35]. On the other hand, the collapse process near a non-flat wall also was studied via an LBM pseudo-potential model [36,37,38,39,40]. In order to investigate the thermal collapse process of cavitation bubbles, the double distribution function based on the LBM has been adopted. For example, Yang et al. studied the thermodynamic effect of cavitation bubble collapse using pseudo-potential and the thermal multiple-relaxation-time lattice Boltzmann method (MRT-LBM) [41]. Liu and Peng studied the collapse process of cavitation bubbles near straight walls and convex walls using the improved LBM with double distribution function [42]. Yuan et al. studied the effects of wall wettability on cavitation bubble collapse based on the simulation of the pseudo-potential lattice Boltzmann method including an appropriate external force term and wall contact angle boundary condition [43]. Moreover, the effect of wall wettability on the maximum pressure and micro-jet velocity also were discussed in this study. Here, the Shan–Chen single-component multiphase LBM was used to simulate the fluid field and the finite difference method was used to simulate the temperature field. He et al. applied the two-dimensional thermal pseudo-potential lattice Boltzmann model with double distribution function to study the inception and evolution processes of cavitation bubbles [44]. The inception process was reproduced using a high-temperature spot, while the growth and collapse processes were obtained by varying the boundary pressure. Additionally, interactions between two equal-sized/unequal-sized bubbles were studied [44]. Wang et al. used a tunable-surface-tension thermal lattice Boltzmann pseudo-potential model with large density ratio to investigate the effects of surface tension and initial input energy on cavitation properties [45].
Compared with traditional CFD, two-phase LBM has been developed quickly in recent years and has a few major advantages [46]. In the LBM, the Boltzmann equation is directly discretized, so its algorithm is simple and efficient. For complex geometries, various boundary condition can be easily implemented, e.g., the bounce-back scheme for the no-slip boundary condition. Moreover, the interface between two phases can be captured automatically. The fourth advantage is that the LBM is easy for parallel computation due to the locality of much of the computation. Finally, the pressure is often related to the density through the equation of state, then the pressure field can be computed directly once the density field is known. There is no need to solve the Poisson equation that will take significant computational time in traditional CFD. Up to now, there has been little research on simulating cavitation bubbles near non-flat walls by using a thermal LBM model although it is a common and important phenomenon in engineering applications. Therefore, the main objective of the present study is to investigate the thermal cavitation process of cavitation bubbles near non-flat walls.
In this paper, the complex collapse process of a single cavitation bubble and double cavitation bubbles inside an inclined V-shaped corner will be simulated by using the pseudo-potential and thermal MRT-LBM models. Based on the simulation, the fields of density, pressure, velocity and temperature can be obtained simultaneously. Moreover, the factors impacting the evolution of cavitation will be discussed in detail such as the distance between the cavitation bubble and corner point, radius of the cavitation bubble, angle of the V-shaped corner and center distance between double cavitation bubbles. The present study can be used to explain the mechanism and influencing factors of cavitation bubble collapse near complex boundaries. Based on the present study, appropriate measures can be proposed to prevent or utilize cavitation in engineering.
2. Numerical Methods
2.1. Pseudo-Potential MRT-LBM Model
Using the pseudo potential MRT-LBM [24,37,47,48,49], the mesoscopic governing equation can be expressed as follows:
where is the density distribution function, is the equilibrium distribution function, is discrete velocity in the direction, is the relaxation matrix, is the diagonal matrix, is the transformation matrix.
Multiplying on both sides of Equation (1) [49], the density field equation is shown as follows:
where and are density distribution function and equilibrium distribution function in moment space, respectively, , is a source term in the velocity space.
The transformation matrix M [50] can be given as follows:
Thus, the becomes
The diagonal matrix is written as:
is given by [37]:
in which is the total force including fluid–fluid interaction, solid–fluid interaction, as well as the volume force. The fluid–fluid interaction [51] is calculated using the following equation:
where is strength of the interaction, is the weight coefficient, is the interaction potential [52]:
where c = 1 is lattice speed, is lattice sound speed.
Moreover, the fluid–solid interaction [53] is calculated using the following expression:
where is the interaction between the solid and the fluid, is a switch function.
The pressure is obtained by Carnahan–Starling (C-S) EOS [54] as follows:
where is temperature, represents gas constant, , , is the critical temperature and the critical pressure.
The density is obtained by the following expression:
The fluid speed is obtained by the following equation:
Using the Chapman–Enskog analysis, the following Navier–Stokes equations can be derived:
where is the viscous stress tensor. Equations (13) and (14) are macroscopic governing equations.
2.2. Thermal MRT-LBM Model
The macroscopic temperature governing equation [55] can be expressed as follows:
where is the temperature, is the thermal diffusivity, is the thermal conductivity, is the specific heat, is the source term.
The temperature equation can be solved by a thermal MRT-LBM model [56],
where and are temperature distribution function and equilibrium distribution function in moment space, respectively, is the diagonal matrix, is the source term in the moment space.
The expression of is given by:
The diagonal matrix is written as:
is written as:
where , is adopted to remove the discrete effect of the source term [56].
The temperature can be obtained by the following:
It should be noted that the fluid density and velocity can affect the temperature and vice versa using the present coupled MRT-LBM models.
3. Collapse of a Single Cavitation Bubble inside an Inclined V-Shaped Corner
3.1. Numerical Model
The simulated geometry layout is shown in Figure 1. The half-way bounce-back scheme is adopted for the red side wall and the open boundary is used for the part without a wall. For the temperature field, an isothermal boundary is applied to these three sides. The domain has a 1001 × 909 lattice in total and the parameters for the diagonal matrix are , , .
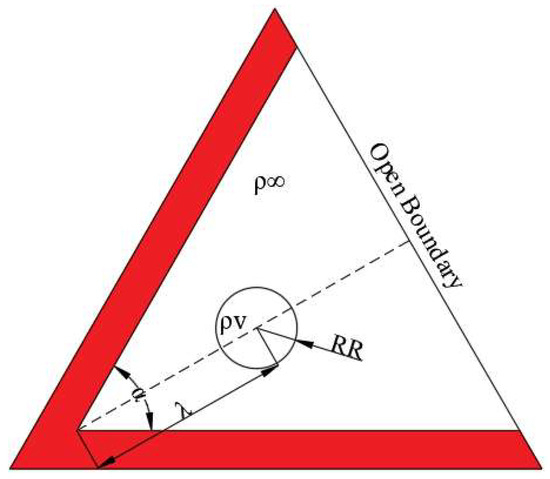
Figure 1.
Simulated geometry layout (RR—radius, λ—distance between cavitation bubble center and wall, α—wall angle, ρv—vapor pressure, ρ∞—ambient pressure).
The initialized density field can be given by
where is the liquid density, is the vapor density, , are the bubble center’s coordinates. RR is the bubble’s radius. W is the interface width and is set to be 5 in the present study.
The initialized temperature field is given as
where is the temperature outside of the bubble and is the temperature inside of the bubble.
In this simulation, the unit of length is lu, the unit of time is tu, the unit of mass is mu, the unit of pressure is mu·lu-1tu-2, the unit of velocity is lu·tu-1 and the unit of density is mu·lu-3. The used parameters are shown in Table 1.

Table 1.
Parameters used for a single bubble with different λ.
3.2. Collapse of Single Bubble inside an Inclined V-Shaped Corner with Different λ
In this section, the bubble collapse process inside an inclined V-shaped corner under different λ will be studied. Moreover, the influence of λ on the maximum collapse temperature, the micro-jet and pressure at the corner will also be discussed in detail.
In Figure 2, we compare the experimental results and the simulation results of bubble collapse in Case 2. It can be seen that the high internal pressure makes the bubble expand in a spherical way. When the open boundary pressure is transferred to the upper part of the bubble, the bubble is gradually compressed. As the compression becomes larger and larger, the bubble finally collapses. Overall, the simulation results agree with the experiments, which proves the applicability of the present numerical model.
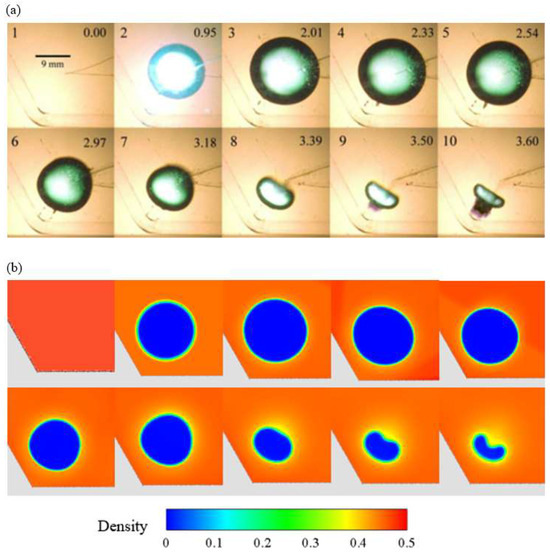
Figure 2.
Experimental results and simulation results in Case 2. (a) Experimental results [8], reproduced or adapted from adequate reference, with permission from publisher Elsevier (Amsterdam, Netherlands), 2020; (b) Simulated results.
Moreover, Figure 3 shows the temperature and velocity fields in Case 2 predicted by the present thermal lattice Boltzmann method. During the bubble expansion process, due to the volume expansion, the internal gas will become sparser so the temperature will be slightly lower. Similarly, in the process of bubble contraction, because the volume of the bubble becomes smaller, the internal temperature of the bubble increases gradually. At the last moment of bubble collapse, due to the rapid compression of the internal gas, high temperature is produced and the maximum collapse temperature can be found at this stage.
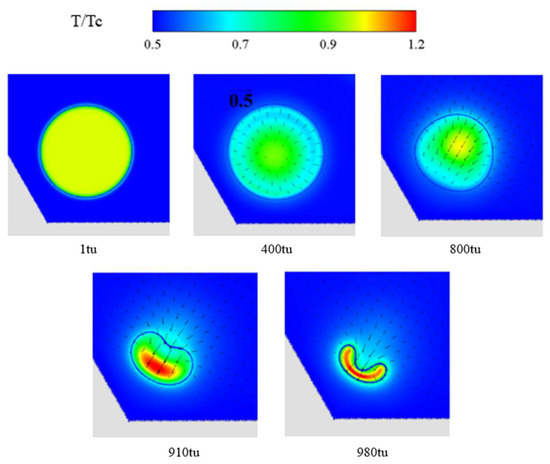
Figure 3.
Temperature field and velocity vector in Case 2.
In Figure 4, we show the experimental and simulated results of bubble collapse in Case 1. In this case, the distance between the wall and the bubble center is less than the radius of the bubble, so the bubble is limited by the corner when it expands. When the open boundary pressure is transferred to the upper part of the bubble, the top of the bubble shows compression and the bubble gradually collapses near the corner.
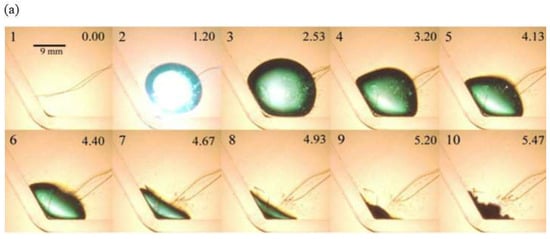
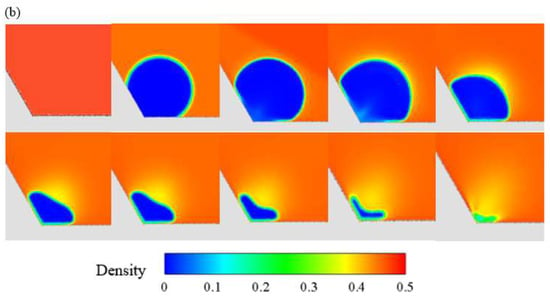
Figure 4.
Experimental results and simulation results in Case 1. (a) Experimental results [8], reproduced or adapted from adequate reference, with permission from publisher Elsevier (Amsterdam, The Netherlands), 2020; (b) simulation results.
Figure 5a presents the maximum collapse temperature of a single bubble with different λ. The maximum collapse temperature of Case 1 does not reach the initial bubble temperature due to the obstruction of the wall. It is obvious from Figure 5 that the maximum temperature of bubble collapse approximately increases linearly with the rise of the distance between the corner and the bubble center except for Case 1. Figure 5b describes the change in the micro-jet for a single bubble with different λ. In the present study, the velocity at the top of the cavitation bubble is taken as the micro-jet velocity to avoid the effect of virtual velocity in numerical simulation. The micro-jet velocity reaches the maximum in a period of time before bubble collapse and then decreases. In Case 1, it is not easy to identify the peak of micro-jet velocity because the bubble is close to the wall at the beginning and the micro-jet is restrained by the wall. Compared with various cases, it is clear that the velocity of the micro-jet increases and its peak is more advanced with the increase in the distance between the corner and the bubble center. That indicates that the bubble collapse time will advance with the increase in that distance and this is consistent with the conclusion based on the density field. Figure 5c displays the change in the corner pressure with different λ. For a period of time after bubble collapse, when the pressure wave is transmitted to the corner, the corner pressure reaches the peak. From the curve, as the distance between the corner and bubble center becomes smaller, the pressure peak at the corner becomes larger and the peak is also slightly delayed. This finding is also consistent with the conclusion in the study of micro-jet and density field, i.e., the larger the distance between the corner and bubble center, the earlier the bubble collapses. It should be noted that the corner pressure for Case 1 seems much larger than other cases. The possible reason is that the location of bubble collapse is closer than other cases.
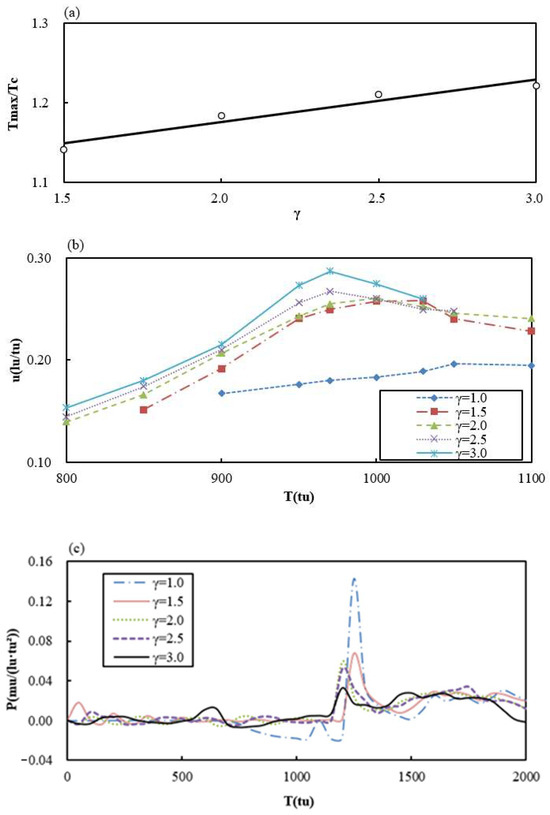
Figure 5.
The maximum collapse temperature (a), micro-jet (b), and corner pressure (c) of a single bubble under different λ.
3.3. Collapse of Single Bubble inside an Inclined V-Shaped Wall with Different α
In this section, the influence of α on the evolution of the micro-jet and the pressure at the corner will be investigated. Figure 6 displays the experimental and simulated results of bubble collapse in Case 6. In this case, compared with the case with an obtuse angle, the effect of the wall on the bubble is more significant. Thus, the bubble surface becomes flat along the wall earlier in the stage of expansion and, after that, the depression still appears at the top and finally gradually collapses.
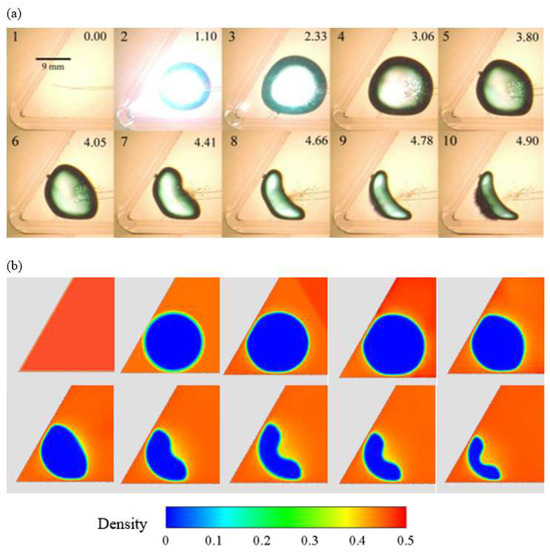
Figure 6.
Experimental results and simulation results in Case 6. (a) Experimental results [8], reproduced or adapted from adequate reference, with permission from publisher Elsevier (Amsterdam, Netherlands), 2020; (b) simulation results.
Figure 7a shows the evolution of a single bubble micro-jet with different α. It is clear that the peak of the bubble micro-jet will be more advanced and the peak will be larger with the increase in the angle. This is because the inhibition of the wall becomes smaller with the increase in the angle and the micro-jet velocity will be larger. Figure 7b displays that the pressure peak at the corner decreases and the pressure peak appears earlier with the increase in the angle.
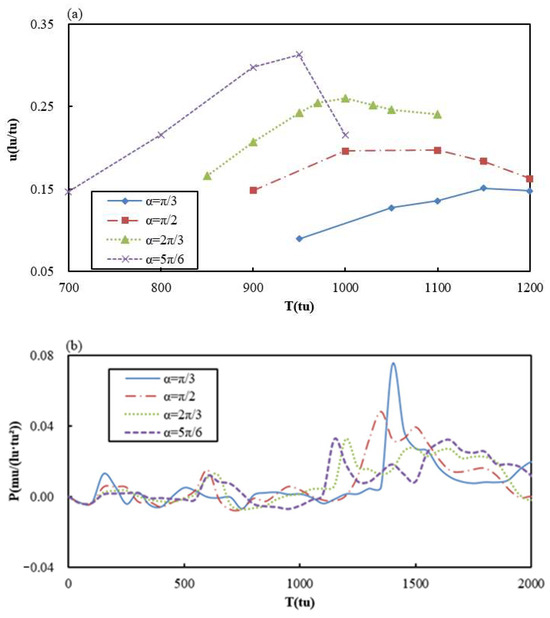
Figure 7.
The micro-jet (a) and corner pressure peak (b) of a single bubble under different α.
3.4. Collapse of Single Bubble inside an Inclined V-Shaped Wall with Different RR
In this section, influence of RR on the maximum collapse temperature, the micro-jet and the pressure at the corner will be studied. Figure 8a shows that the maximum collapse temperature increases proportionally with the increase in bubble radius. Figure 8b indicates that the time of micro-jet starting and ending becomes earlier with the decrease in bubble radius. Figure 8c shows that the peak of corner pressure increases and its appearing is delayed with the increase in single bubble radius.
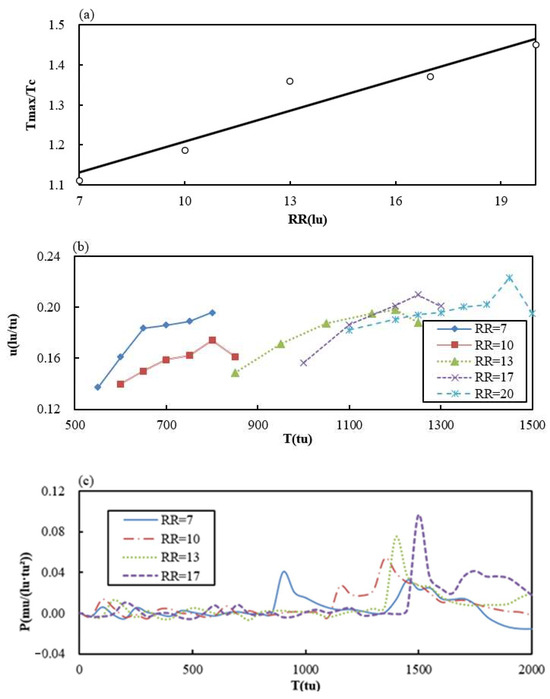
Figure 8.
The maximum collapse temperature (a), micro-jet (b) and corner pressure (c) of a single bubble under different RR.
4. Collapse of Double Cavitation Bubbles inside an Inclined V-Shaped Wall
In this section, the collapse of double cavitation bubbles inside an inclined V-shaped corner will be studied.
4.1. Computational Layout
The simulated geometry layout is shown in Figure 9.
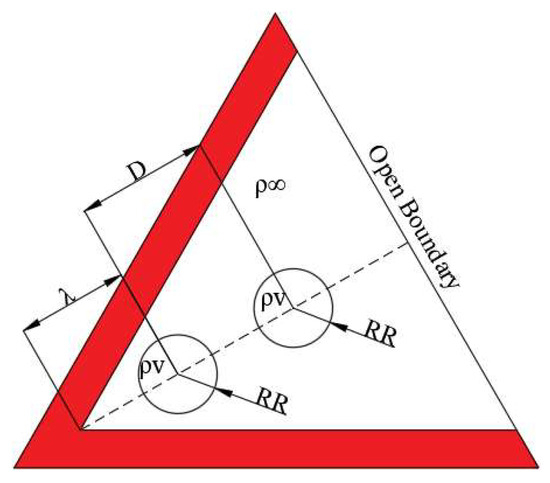
Figure 9.
Simulated layout (R—radius, λ—distance between wall and cavitation bubble center, D—center distance between two cavitation bubbles, ρv—vapor pressure, ρ∞—ambient pressure).
4.2. Numerical Simulation of Double Bubble Collapse inside an Inclined V-Shaped Wall
Here, the collapse process of double cavitation bubbles inside an inclined V-shaped wall will be simulated. Moreover, the influence of center distance between two cavitation bubbles (D) on the maximum collapse temperature, micro-jet and corner pressure will be discussed. The used parameters are shown in Table 2.

Table 2.
Parameters used for double bubbles with different D.
Figure 10 shows the collapse process of two cavitation bubbles inside an inclined V-shaped corner in Case 14. Both cavitation bubbles expand with different degrees at first. Because the lower bubble is closer to the wall, the inhibition effect of the wall is stronger, so its expansion is less obvious than that of the upper bubble. After that, the two bubbles begin to contract under the influence of pressure and the upper bubble contracts more obviously. After the collapse of the upper cavitation bubble, the lower cavitation bubble also begins to be depressed and gradually collapses.
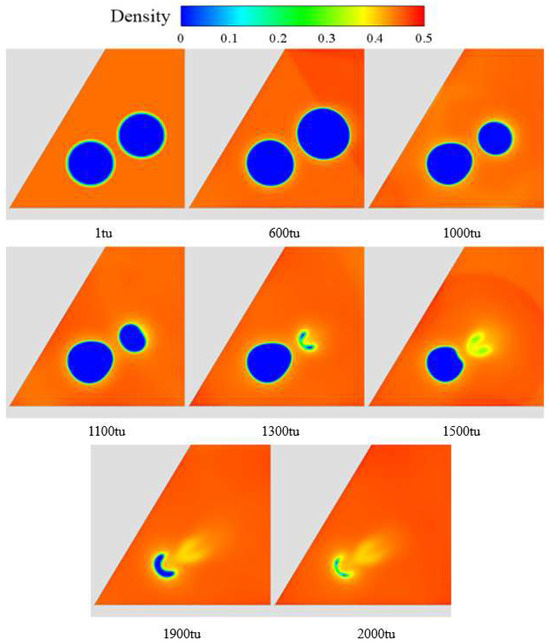
Figure 10.
Density field of double cavitation bubble collapse in Case 14.
Figure 11 shows the temperature and velocity fields in Case 14. The temperature change behavior of each cavitation bubble is similar to that for the single bubble collapse.
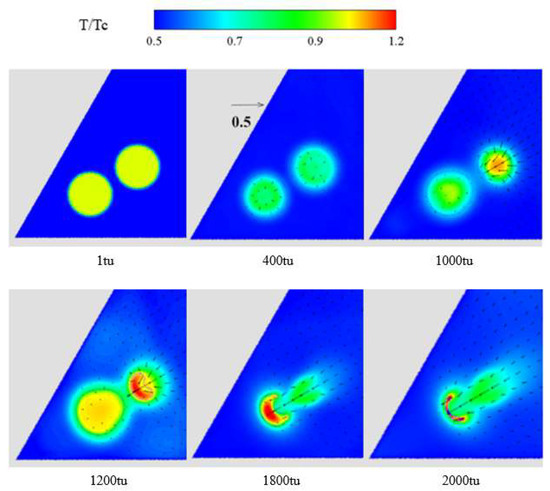
Figure 11.
Temperature field and velocity vector of double cavitation bubble collapse in Case 14.
Figure 12 shows the evolution of double bubble micro-jet, the maximum collapse temperature and corner pressure with different D. It is clear that the micro-jet velocity of the lower cavitation bubble is smaller than that of the upper cavitation bubble from formation to collapse. By comparing various cases, it can be concluded that the micro-jet velocity peak of the upper bubble is higher and the time of the micro-jet appearing and ending is earlier with the increase in D. Moreover, the maximum temperature of the upper bubble is higher than that of the lower bubble in all cases. Additionally, the maximum collapse temperature of each bubble increases with the increase in D. Compared with the case of a single bubble, the corner pressure fluctuation before the collapse of the lower bubble in double bubble cases is much smaller. This is because the pressure wave produced by the collapse of the upper bubble will be blocked by the lower cavitation bubble and the lower bubble plays a role of protecting the corner before its collapse. By comparing the simulated cases, we found that the corner pressure peak increases with the increase in D. And in Case 17, the corner pressure reaches 0.1549 mu/(lu·tu2), which is when the distance between the corner and the lower bubble is 4RR, which is further than the cases with a single bubble. Thus, it indicates that the pressure wave superposition of double bubbles has great influence on the corner.
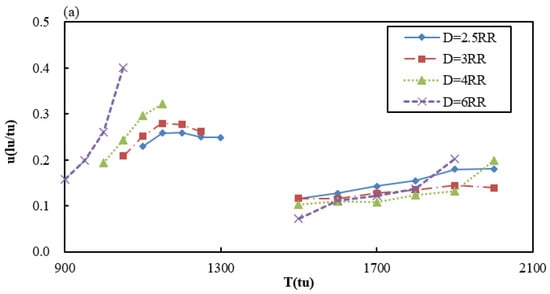
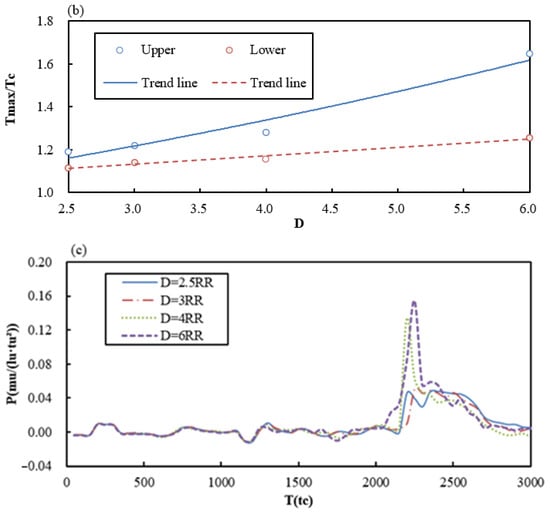
Figure 12.
The micro-jet, the maximum collapse temperature and corner pressure of double bubbles under different D.
5. Conclusions
In the present study, the collapse processes of a single and double cavitation bubbles inside an inclined V-shaped corner are simulated by using the pseudo-potential and thermal MRT-LBM models with double distribution function. In our simulation, the density and pressure fields, micro-jet and temperature field have been obtained simultaneously. Moreover, the influence factors of the evolution of cavitation bubble collapse have been studied in detail such as the distance between the corner and cavitation bubble, the angle of the V-shaped corner, the radius of the cavitation bubble and the distance between two cavitation bubbles. Overall, 13 cases of a single cavitation bubble and 4 cases of double bubbles have been simulated. Based on these simulated results, the following conclusions can be drawn:
- The simulated density fields during the collapse process of a single cavitation bubble are compared with the experimental results and the agreement is acceptable. It is proved that the present pseudo-potential and thermal MRT-LBM models with double distribution function are reasonable to study the cavitation bubble collapse.
- The temperature field evolution during cavitation bubble collapse is similar. Firstly, the temperature inside the cavitation bubble gradually decreases in the process of bubble expansion. Then, the temperature will gradually increase in the contraction stage. When the bubble collapses, the temperature reaches the maximum. This law is also applicable to the double bubble collapse.
- It is found that the micro-jet velocity reaches the maximum in a period of time before bubble collapse and then decreases. With the rise of the distance between the single bubble center and the corner, the maximum temperature of bubble collapse increases approximately linearly, the velocity of micro-jet increases and its peak is more advanced and the pressure peak at the corner decreases. As the V-shaped angle increases, the velocity peak of micro-jet is larger and appears earlier, and the pressure peak at the corner is smaller and more advanced. With the increase in bubble radius, the maximum temperature of bubble collapse increases with an approximately linear relationship, the starting and ending of the micro-jet are delayed and the pressure peak at the corner is larger and also is delayed.
- In the double bubble simulation, the micro-jet velocity of the lower cavitation bubble is smaller than that of the upper one from formation to collapse. The maximum temperature of the upper bubble is higher than that of the lower one in all cases. Compared with the cases of a single bubble, the fluctuation of the pressure at the corner is much smaller before the collapse of the lower bubble in double bubble cases. With the increase in distance between two bubble centers, the maximum collapse temperature of each bubble increases, the velocity peak of the micro-jet of the upper bubble is higher, the time of the micro-jet appearing and ending is earlier and the corner pressure peak also increases.
Author Contributions
Conceptualization, Y.P. and Y.L. (Yu Li); methodology, J.O.; software, J.O.; validation, Y.L. (Yang Liu); formal analysis, Y.P.; investigation, Y.L.(Yu Li); resources, Y.L. (Yang Liu); data curation, Y.L. (Yang Liu); writing—original draft preparation, Y.L. (Yu Li); writing—review and editing, Y.P. and J.O.; visualization, Y.P.; supervision, Y.P.; project administration, Y.P.; funding acquisition, Y.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant Number: 51979184) and the APC was funded by the National Natural Science Foundation of China.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Suo, D.J.; Jin, Z.Y.; Jiang, X.N.; Dayton, P.A.; Jing, Y. Microbubble mediated dual-frequency high intensity focused ultrasound thrombolysis: An In vitro study. Appl. Phys. Lett. 2017, 110, 023703. [Google Scholar] [CrossRef]
- Rivas, D.F.; Verhaagen, B. Preface to the Special Issue: Cleaning with bubbles. Ultrason. Sonochem. 2016, 29, 517–518. [Google Scholar] [CrossRef] [PubMed]
- Cui, P.; Zhang, A.M.; Wang, S.P.; Khoo, B.C. Ice breaking by a collapsing bubble. J. Fluid Mech. 2018, 841, 287–309. [Google Scholar] [CrossRef]
- Xu, W.L.; Bai, L.X.; Zhang, F.X. Interaction of a Cavitation Bubble and an Air Bubble with a rigid boundary. J. Hydrodyn. 2010, 22, 503–512. [Google Scholar] [CrossRef]
- Muller, M.; Hujer, J.; Kotek, M.; Zima, P. Identification of collapse patterns of cavitation bubbles close to a solid wall. EPJ Web Conf. 2013, 45, 01120. [Google Scholar] [CrossRef]
- Li, X.F.; Duan, Y.X.; Zhang, Y.N.; Tang, N.N. Retardant Effects of Collapsing Dynamics of a Laser-Induced Cavitation Bubble Near a Solid Wall. Symmetry 2019, 11, 1051. [Google Scholar] [CrossRef]
- Brujan, E.A.; Noda, T.; Ishigami, A.; Ogasawara, T.; Takahira, H. Dynamics of laser-induced cavitation bubbles near two perpendicular rigid walls. Fluid Mech. 2018, 841, 28–49. [Google Scholar] [CrossRef]
- Cui, J.; Chen, Z.P.; Wang, Q.; Zhou, T.R.; Corbett, C. Experimental studies of bubble dynamics inside a corner. Ultrason. Sonochem. 2020, 64, 104951. [Google Scholar] [CrossRef]
- Tomita, Y.; Robinson, P.B.; Tong, R.P.; Blake, J.R. Growth and collapse of cavitation bubbles near a curved rigid boundary. J. Fluid Mech. 2002, 466, 259–283. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Qiu, X.; Zhang, X.Q.; Tang, N.N. Collapsing dynamics of a laser-induced cavitation bubble near the edge of a rigid wall. Ultrason. Sonochem. 2020, 67, 105157. [Google Scholar] [CrossRef]
- Kim, D.; Kim, D. Underwater bubble collapse on a ridge-patterned structure. Phys. Fluids 2020, 32, 053312. [Google Scholar] [CrossRef]
- Fukaya, M.; Tamura, Y.; Matsumoto, Y. Prediction of Cavitation Intensity and Erosion Area in Centrifugal Pump by Using Cavitating Flow Simulation with Bubble Flow Model. J. Fluid Sci. Technol. 2010, 5, 305–316. [Google Scholar] [CrossRef]
- Han, R.; Tao, L.B.; Zhang, A.M.; Li, S. A three-dimensional modeling for coalescence of multiple cavitation bubbles near a rigid wall. Phys. Fluids 2019, 31, 062107. [Google Scholar] [CrossRef]
- Li, B.B.; Jia, W.; Zhang, H.C.; Lu, J. Investigation on the collapse behavior of a cavitation bubble near a conical rigid boundary. Shock Waves 2014, 24, 317–324. [Google Scholar] [CrossRef]
- Lyu, F.X.; Zhang, X.T.; Yuan, H.X.; Han, S.Y.; Tang, M. Research on the collapse characteristics of single cavitation bubble near solid particle by the VOF method. Heliyon 2023, 9, e21855. [Google Scholar] [CrossRef]
- Li, S.; Zhang, A.M.; Han, R. 3D model for inertial cavitation bubble dynamics in binary immiscible fluids. J. Comput. Phys. 2023, 494, 112508. [Google Scholar] [CrossRef]
- Duy, T.N.; Nguyen, V.T.; Phan, T.H.; Nguyen, Q.T.; Park, S.H.; Park, W.G. Numerical study of bubble dynamics near a solid wall with a gas-entrapping hole. Ocean. Eng. 2023, 285, 115344. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Du, Y.X.; Liu, J.Q.; Sun, Y.R.; Yao, Z.F.; Zhong, Q. Experimental and numerical investigations of the collapse of a laser-induced cavitation bubble near a solid wall. J. Hydrodyn. 2022, 34, 189–199. [Google Scholar] [CrossRef]
- Zhang, C.; Yin, Z.Q.; Tu, C.X.; Huang, Z.M.; Chen, T.H.; Bao, F.B.; Lu, J.L.; Ge, X.F. Dynamic behavior of the cavitation bubbles collapsing between a rigid wall and an elastic wall. AIP Adv. 2021, 11, 065025. [Google Scholar] [CrossRef]
- Lü, M.; Ning, Z.; Sun, C.H.; Ning, Z. Numerical simulation of cavitation bubble collapse within a droplet. Comput. Fluids. 2017, 152, 157–163. [Google Scholar]
- Zhang, J.; Zhang, L.X.; Deng, J. Numerical Study of the Collapse of Multiple Bubbles and the Energy Conversion during Bubble Collapse. Water 2019, 11, 247. [Google Scholar] [CrossRef]
- Ye, J.C.; Zhang, J.; Huang, T.Y. Direct Numerical Simulation of Bubble Cluster Collapse: Shape Evolution and Energy Transfer Mechanisms. Processes 2023, 11, 2191. [Google Scholar] [CrossRef]
- Popinet, S.; Zaleski, S. Bubble collapse near a solid boundary a numerical study of the influence of viscosity. J. Fluid Mech. 2002, 464, 137–163. [Google Scholar] [CrossRef]
- Shan, X.W.; Chen, H.D. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef] [PubMed]
- d’Humières, D. Generalized Lattice-Boltzmann Equations. In AIAA Rarefied Gas Dynamics: Theory and Applications; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1994. [Google Scholar]
- Li, Q.; Luo, K.H.; Li, X.J. Lattice Boltzmann modeling of multiphase flows at large density ratio with an improved pseudopotential model. Phys. Rev. E 2013, 87, 053301. [Google Scholar] [CrossRef] [PubMed]
- Sukop, M.C.; Or, D. Lattice Boltzmann method for homogeneous and heterogeneous cavitation. Phys. Rev. E 2005, 71, 046703. [Google Scholar] [CrossRef]
- Mishra, S.K.; Deymier, P.A.; Muralidharan, K.; Frantziskonis, G.; Pannala, S.; Simunovic, S. Modeling the coupling of reaction kinetics and hydrodynamics in a collapsing cavity. Ultrason. Sonochem. 2010, 17, 258–265. [Google Scholar] [CrossRef]
- Ezzatneshan, E.; Vaseghnia, H. Simulation of collapsing cavitation bubbles in various liquids by lattice Boltzmann model coupled with the Redlich-Kwong-Soave equation of state. Phys. Rev. E 2020, 102, 053309. [Google Scholar] [CrossRef]
- Mao, Y.F.; Peng, Y.; Zhang, J.M. Study of Cavitation Bubble near a wall by the modified Lattice Boltzmann Mothod. Water 2018, 10, 1439. [Google Scholar] [CrossRef]
- Peng, C.; Tian, S.C.; Li, G.S.; Sukop, M.C. Simulation of laser-produced single cavitation bubbles with hybrid thermal Lattice Boltzmann method. Int. J. Heat Mass Transf. 2020, 149, 119136. [Google Scholar] [CrossRef]
- Swift, M.R.; Orlandini, E.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Physical Rev. E 1996, 54, 5041–5052. [Google Scholar] [CrossRef] [PubMed]
- Shan, X.W. Pressure tensor calculation in a class of nonideal gas lattice Boltzmann models. Physical Rev. E 2008, 77, 066702. [Google Scholar] [CrossRef] [PubMed]
- Gunstensen, A.K.; Rothman, D.H.; Zaleski, S.; Zanetti, G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320. [Google Scholar] [CrossRef] [PubMed]
- Zheng, R.Y.; Liu, H.H.; Sun, J.J.; Ba, Y. Droplet hysteresis investigation on non-wetting striped textured surfaces: A lattice Boltzmann study. Physica A 2014, 411, 53–62. [Google Scholar] [CrossRef]
- Shi, D.Y.; Wang, Z.K.; Zhang, A.M. Study on coupling characteristics between bubble and complex walls at the same scale. Acta Phys. Sin. 2014, 63, 174701. [Google Scholar]
- Ahmad, S.; Eze, C.; Liu, H.Q.; Zhao, J.Y. Lattice Boltzmann study of bubble dynamics and heat transfer on a hybrid rough surface with a cavity-pillar structure. Int. Commun. Heat Mass Transf. 2020, 119, 104896. [Google Scholar] [CrossRef]
- Dong, B.; Zhang, Y.J.; Zhou, X.; Chen, C.; Li, W.Z. Numerical simulation of bubble dynamics in subcooled boiling along inclined structured surface. J. Thermophys. Heat Transf. 2021, 35, 16–27. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, Y. Study on the Collapse Process of Cavitation Bubbles Near the Concave Wall by Lattice Boltzmann Method Pseudo-Potential Model. Energies 2020, 13, 4398. [Google Scholar] [CrossRef]
- Xue, H.H.; Shan, F.; Guo, X.S.; Tu, J.; Zhang, D. Cavitation bubble collapse near a curved wall by the Multiple-Relaxation-Time Shan-Chen Lattice Boltzmann Model. Chin. Phys. Lett. 2017, 34, 084301. [Google Scholar] [CrossRef]
- Yang, Y.; Shan, M.L.; Kan, X.F.; Shangguan, Y.Q.; Han, Q.B. Thermodynamic of collapsing cavitation bubble investigated by pseudopotential and thermal MRT-LBM. Ultrason. Sonochem. 2020, 62, 104873. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, Y. Study on the collapse process of cavitation bubbles including heat transfer by Lattice Boltzmann Method. J. Mar. Sci. Eng. 2021, 9, 219. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, J.B.; Zhou, J.Y.; Tan, J.W.; Wang, Z.B.; Gan, W.D. Study of wall wettability effects on cavitation bubble collapse using lattice Boltzmann method. AIP Adv. 2021, 11, 065011. [Google Scholar] [CrossRef]
- He, X.L.; Song, X.; Peng, H.N.; Yuan, H. A lattice Boltzmann study of the thermodynamics of an interaction between two cavitation bubbles. In Discrete and Continuous Dynamical Systems—S; AIMS: Pasadena, CA, USA, 2023. [Google Scholar] [CrossRef]
- Wang, Y.R.; Peng, H.N.; He, X.L.; Zhang, J.M. Cavitation bubbles with a tunable-surface-tension thermal lattice Boltzmann model. Phys. Fluids 2022, 34, 102008. [Google Scholar] [CrossRef]
- Huang, H.B.; Sukop, M.C.; Lu, X.Y. Multiphase Lattice Boltzmann Methods: Theory and Application; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mukherjee, S.; Abraham, J. A pressure-evolution-based multi-relaxation-time high-density-ratio two-phase lattice-Boltzmann model. Comput. Fluids 2007, 36, 1149–1158. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; He, Y.L.; Tang, G.H.; Tao, W.Q. Improved axisymmetric lattice Boltzmann scheme. Phys. Rev. E 2010, 81, 056707. [Google Scholar] [CrossRef] [PubMed]
- Mohamad, A.A. Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes; Springer: London, UK, 2017. [Google Scholar]
- Chen, S.Y.; Doolen, G.D. lattice Boltzmann method for fluid flows. Ann. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Sbragaglia, M.; Benzi, R.; Biferale, L.; Succi, S.; Sugiyama, K.; Toschi, F. Generalized lattice Boltzmann method with multirange pseudopotential. Phys. Rev. E 2007, 75, 026702. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Kang, Q.J.; Chen, Q. Contact angles in the pseudopotential lattice Boltzmann modeling of wetting. Phys. Rev. E 2014, 90, 053301. [Google Scholar] [CrossRef]
- Yuan, P.; Schaefer, L. Equations of state in a lattice Boltzmann model. Phys. Fluids 2006, 18, 042101. [Google Scholar] [CrossRef]
- Guo, Z.L.; Shi, B.C.; Zheng, C.G. A coupled lattice BGK model for the Boussinesq equations. Int. J. Numer. Methods 2002, 39, 325–342. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, P.; Yan, H.J. Improved thermal lattice Boltzmann model for simulation of liquid-vapor phase change. Phys. Rev. E 2017, 96, 063303. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).