Influence of 3D Fracture Geometry on Water Flow and Solute Transport in Dual-Conduit Fracture
Abstract
:1. Introduction
2. Theoretical Background
3. Numerical Models’ Setup
4. Results and Discussion
4.1. Water Flow Test
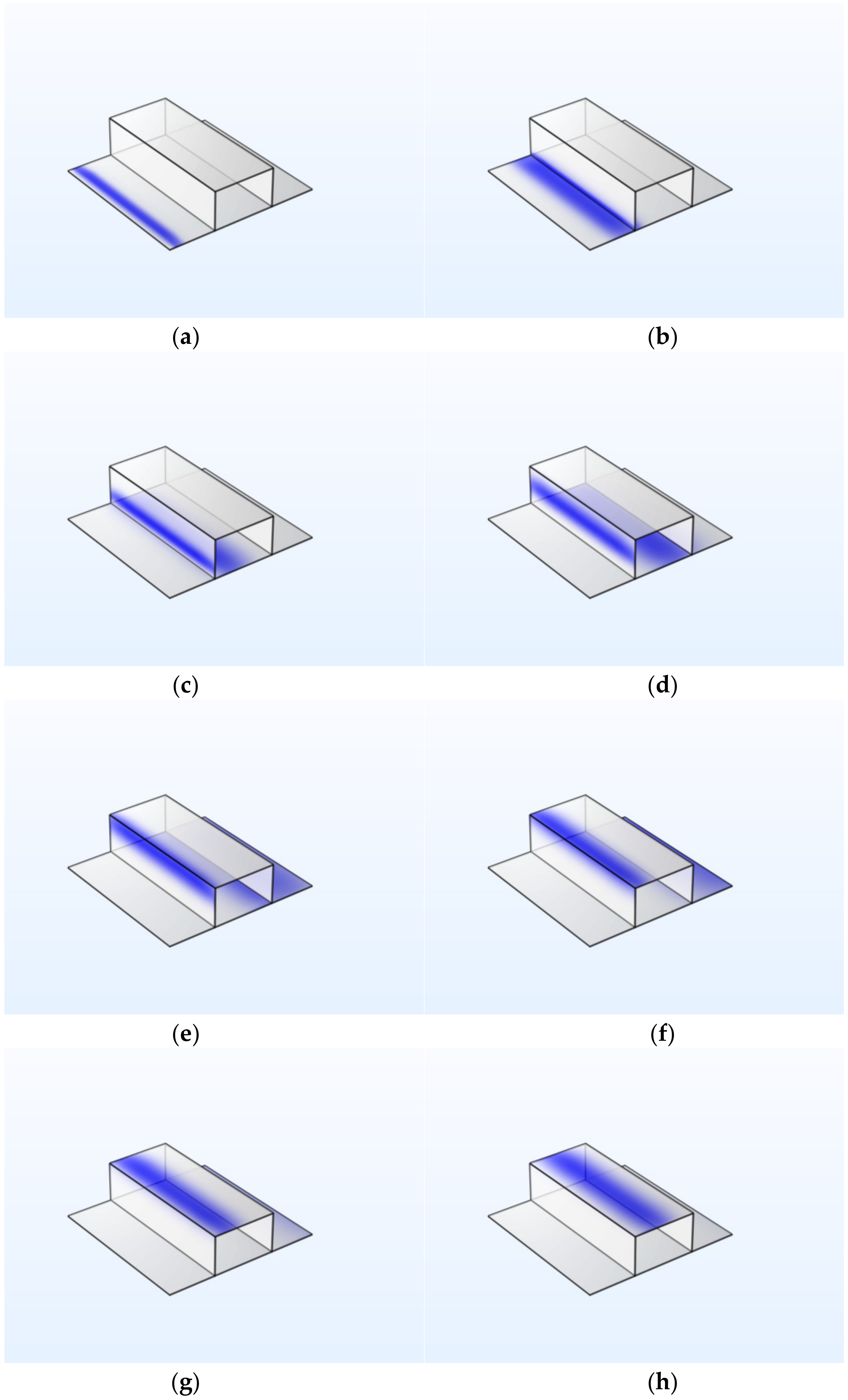
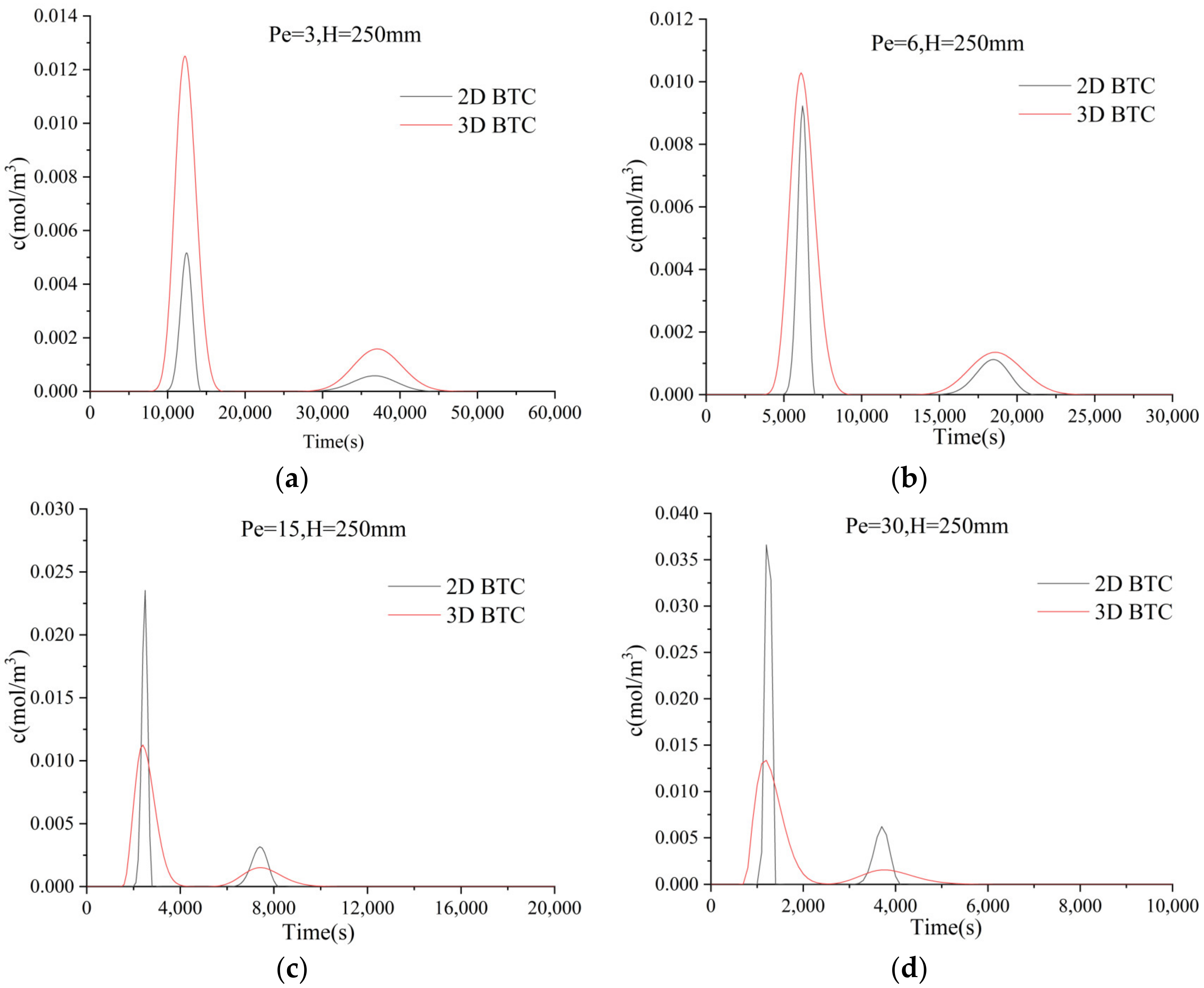
4.2. Solute Concentration Distribution
4.3. Discussion
5. Conclusions
- Based on the numerical results, the Forchheimer equations can more accurately describe the nonlinear fracture flow characteristics in DCFs. The further apart the branch fractures are from each other, the more the coefficient A representing the cohesive force increases while the coefficient B representing the inertial force decreases in 2D fractures, and the coefficients A and B are essentially constant in 3D fractures.
- Relative to the 2D fracture, the 3D DCFs cause a more pronounced non-Darcy phenomenon. Additionally, the Rec of 2D fractures can be approximately 40% less than that of 3D fractures. With an increasing flow rate, the friction coefficient in the bypass is nonlinearly related to the flow rate at exponential conditions, demonstrating the diversion fractures as the main scene of the non-Darcy phenomenon.
- The BTC in each graph shows a double-peak phenomenon with significant differences in propagation times in the main and diversion fractures due to the variation in flow rates. Dual-peaked BTCs can be reproduced by the WSADE model. Furthermore, the further apart the branch fractures are from each other, the larger the Pe number, when the values of parameter D1 of WSADE decrease and parameter D2 and the ratio of w1/w2 increase. Moreover, in the same geometry and flow conditions, the BTC of the 2D fracture is steeper than that of the 3D fracture, and this phenomenon becomes more obvious with increases in Pe.
- Both the complete mixing model and the streamlined routing model affect the transport of fractured solutes, and the streamlined routing mode plays a major role in the solute transfer. With increasing flow rates, the effect of the complete mixing mode is weakened in the solute transport. From a statistics point of view, the streamlined routing mode is more obvious in 3D than that in 2D.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Ma, G.; Wang, H. Heat Extraction Mechanism in a Geothermal Reservoir with Rough-Walled Fracture Networks. Int. J. Heat Mass Transf. 2018, 126, 1083–1093. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, G.; Wang, H. The Simulation of Thermo-Hydro-Chemical Coupled Heat Extraction Process in Fractured Geothermal Reservoir. Appl. Therm. Eng. 2018, 143, 859–870. [Google Scholar] [CrossRef]
- Ma, G.; Chen, Y.; Jin, Y.; Wang, H. Modelling Temperature-Influenced Acidizing Process in Fractured Carbonate Rocks. Int. J. Rock Mech. Min. 2018, 105, 73–84. [Google Scholar] [CrossRef]
- Fan, L.F.; Wu, Z.J.; Wan, Z.; Gao, J.W. Experimental Investigation of Thermal Effects on Dynamic Behavior of Granite. Appl. Therm. Eng. 2017, 125, 94–103. [Google Scholar] [CrossRef]
- Dai, F.; Wei, M.D.; Xu, N.W.; Ma, Y.; Yang, D.S. Numerical Assessment of the Progressive Rock Fracture Mechanism of Cracked Chevron Notched Brazilian Disc Specimens. Rock Mech. Rock Eng. 2014, 48, 463–479. [Google Scholar] [CrossRef]
- Johnson, J.; Brown, S.; Stockman, H. Fluid Flow and Mixing in Rough-Walled Fracture Intersections. J. Geophys. Res.-Sol. Earth 2006, 111, 2169–9313. [Google Scholar] [CrossRef]
- Tsang, C.-F.; Neretnieks, I.; Tsang, Y. Hydrologic Issues Associated with Nuclear Waste Repositories. Water Resour. Res. 2015, 51, 6923–6972. [Google Scholar] [CrossRef]
- Sayed, M.; Chang, F.; Cairns, A.J. Low-Viscosity Single Phase Acid System for Acid Fracturing in Deep Carbonate Reservoirs. MRS Commun. 2021, 11, 796–803. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Darlington, W. Nonlinear Single-Phase Flow in Real Rock Joints. Water Resour. Res. 2007, 43, W09502. [Google Scholar] [CrossRef]
- Huang, H.; Babadagli, T.; Li, H.A.; Develi, K.; Wei, G. Effect of Injection Parameters on Proppant Transport in Rough Vertical Fractures: An Experimental Analysis on Visual Models. J. Pet. Sci. Eng. 2019, 180, 380–395. [Google Scholar] [CrossRef]
- Zhong, Z.; Ding, J.; Hu, Y. Size Effect on the Hydraulic Behavior of Fluid Flow through Rough-Walled Fractures: A Case of Radial Flow. Hydrogeol. J. 2021, 30, 97–109. [Google Scholar] [CrossRef]
- Luo, S.; Zhao, Z.; Peng, H.; Pu, H. The Role of Fracture Surface Roughness in Macroscopic Fluid Flow and Heat Transfer in Fractured Rocks. Int. J. Rock. Mech. Min. Sci. 2016, 87, 29–38. [Google Scholar] [CrossRef]
- Fan, L.F.; Wang, H.D.; Wu, Z.J.; Zhao, S.H. Effects of Angle Patterns at Fracture Intersections on Fluid Flow Nonlinearity and Outlet Flow Rate Distribution at High Reynolds Numbers. Int. J. Rock. Mech. Min. Sci. 2019, 124, 104136. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Modeling of Flow and Mixing in 3D Rough-Walled Rock Fracture Intersections. Adv. Water Resour. 2017, 107, 1–9. [Google Scholar] [CrossRef]
- Wang, C.; Majdalani, S.; Guinot, V.; Jourde, H. Solute Transport in Dual Conduit Structure: Effects of Aperture and Flow Rate. J. Hydrol. 2022, 613, 128315. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Majdalani, S.; Guinot, V.; Jourde, H. Influence of Dual Conduit Structure on Solute Transport in Karst Tracer Tests: An Experimental Laboratory Study. J. Hydrol. 2020, 590, 125255. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Y. Experimental Study and Characteristic Finite Element Simulation of Solute Transport in a Cross-Fracture. Geosci. Front. 2016, 7, 963–967. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing Flow and Transport in Fractured Geological Media: A Review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Xing, K.; Qian, J.; Zhao, W.; Ma, H.; Ma, L. Experimental and Numerical Study for the Inertial Dependence of Non-Darcy Coefficient in Rough Single Fractures. J. Hydrol. 2021, 603, 127148. [Google Scholar] [CrossRef]
- Liu, X.; Chen, D.; Li, M.; Li, Y.; Yang, X. Characteristics of Fluid Flow and Solute Transport in Multicrossed Rough Rock Fractures Based on Three-Dimensional Simulation. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 072095. [Google Scholar] [CrossRef]
- Pot, V.; Genty, A. Dispersion Dependence on Retardation in a Real Fracture Geometry Using Lattice-Gas Cellular Automaton. Adv. Water Resour. 2007, 30, 273–283. [Google Scholar] [CrossRef]
- Benson, D.A.; Meerschaert, M.M. A Simple and Efficient Random Walk Solution of Multi-Rate Mobile/Immobile Mass Transport Equations. Adv. Water Resour. 2009, 32, 532–539. [Google Scholar] [CrossRef]
- Berkowitz, B.; Scher, H. Exploring the Nature of Non-Fickian Transport in Laboratory Experiments. Adv. Water Resour. 2009, 32, 750–755. [Google Scholar] [CrossRef]
- Majdalani, S.; Guinot, V.; Delenne, C.; Gebran, H. Modelling Solute Dispersion in Periodic Heterogeneous Porous Media: Model Benchmarking against Intermediate Scale Experiments. J. Hydrol. 2018, 561, 427–443. [Google Scholar] [CrossRef]
- Zhao, X.; Chang, Y.; Wu, J.; Peng, F. Laboratory Investigation and Simulation of Breakthrough Curves in Karst Conduits with Pools. Hydrogeol. J. 2017, 25, 2235–2250. [Google Scholar] [CrossRef]
- Field, M.S.; Leij, F.J. Solute Transport in Solution Conduits Exhibiting Multi-Peaked Breakthrough Curves. J. Hydrol. 2012, 440–441, 26–35. [Google Scholar] [CrossRef]
- Goldscheider, N.; Meiman, J.; Pronk, M.; Smart, C. Tracer Tests in Karst Hydrogeology and Speleology. Int. J. Speleol. 2008, 37, 27–40. [Google Scholar] [CrossRef]
- Sedahmed, M.; Coelho, V.; Warda, H.A. An Improved Multicomponent Pseudopotential Lattice Boltzmann Method for Immiscible Fluid Displacement in Porous Media. Phys. Fluids 2022, 34, 023102. [Google Scholar] [CrossRef]
- Sedahmed, M.; Rodrigo, C.V.; Nuno, A.M.; Wahba, E.M.; Warda, H.A. Study of Fluid Displacement in Three-Dimensional Porous Media with an Improved Multicomponent Pseudopotential Lattice Boltzmann Method. Phys. Fluids 2022, 34, 103303. [Google Scholar] [CrossRef]
- Secchi, E.; Marbach, S.; Niguès, A.; Stein, D.; Siria, A.; Bocquet, L. Massive Radius-Dependent Flow Slippage in Carbon Nanotubes. Nature 2016, 537, 210–213. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, J.; Li, X.; Xu, J.; Dong, X. Wettability Effect on Nanoconfined Water Flow. Proc. Natl. Acad. Sci. USA 2017, 114, 3358–3363. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Yang, Z.; He, Y.; Wang, X. An Overview on Nonlinear Porous Flow in Low Permeability Porous Media. Theor. Appl. Mech. Lett. 2013, 3, 022001. [Google Scholar] [CrossRef]
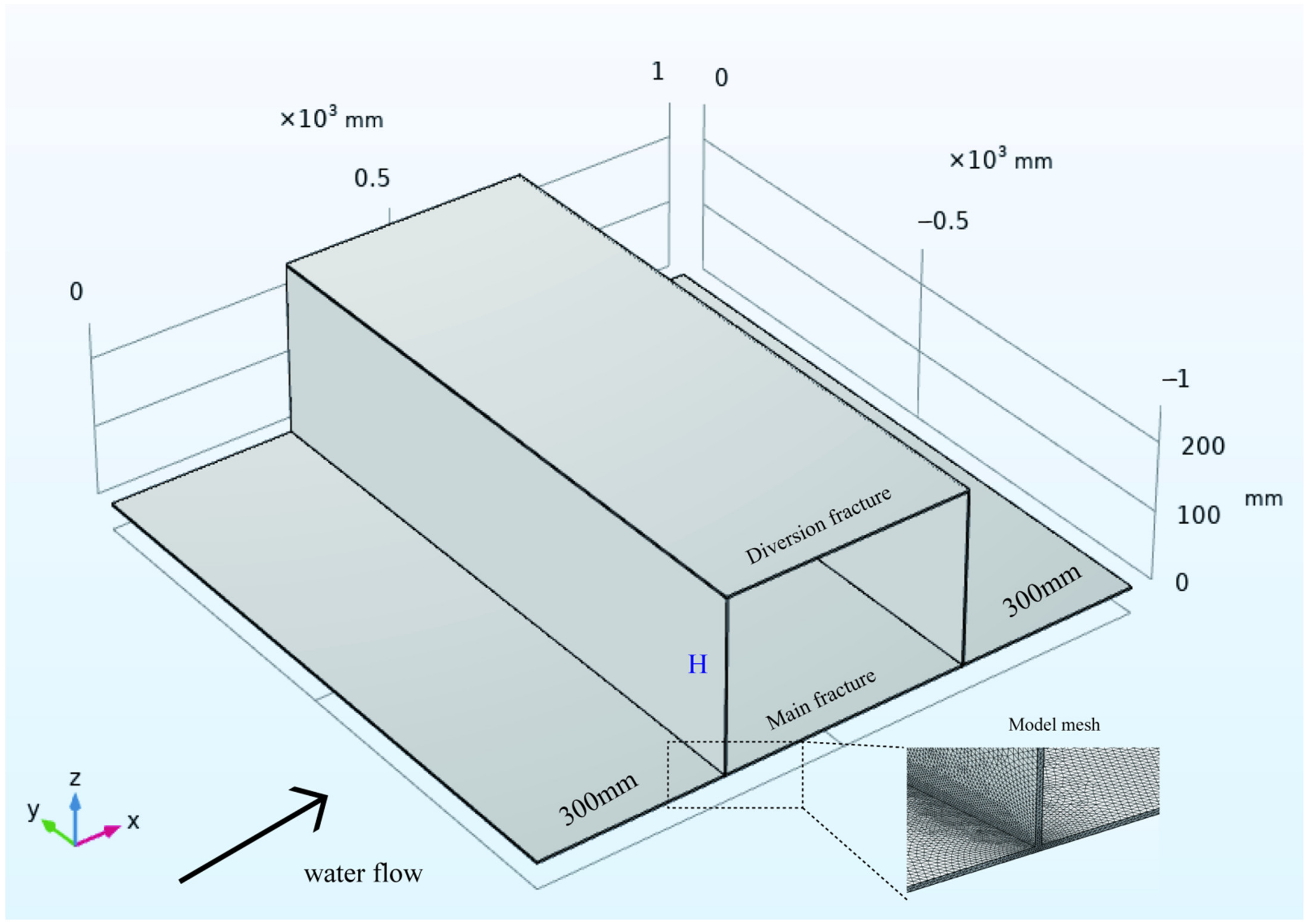
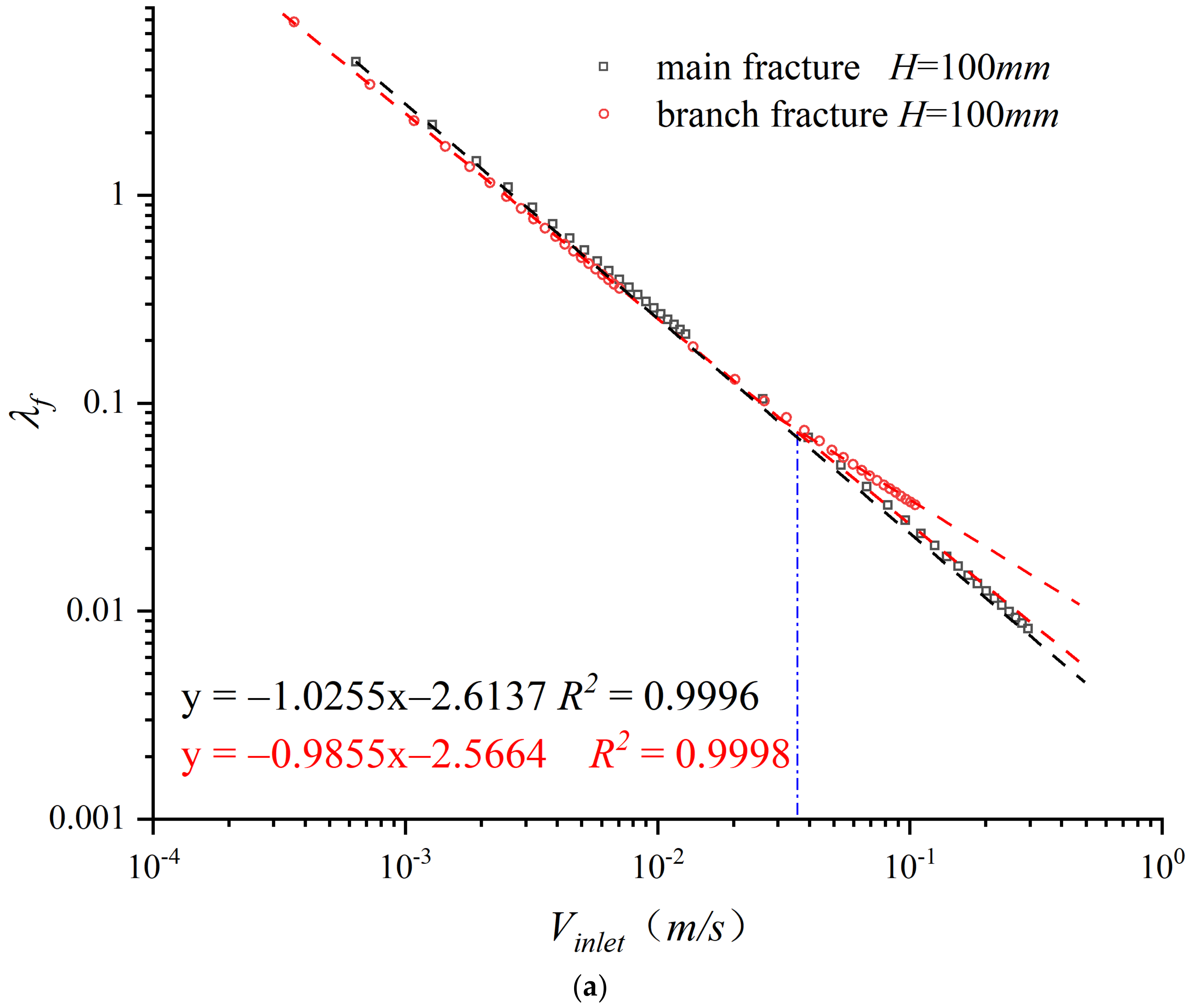
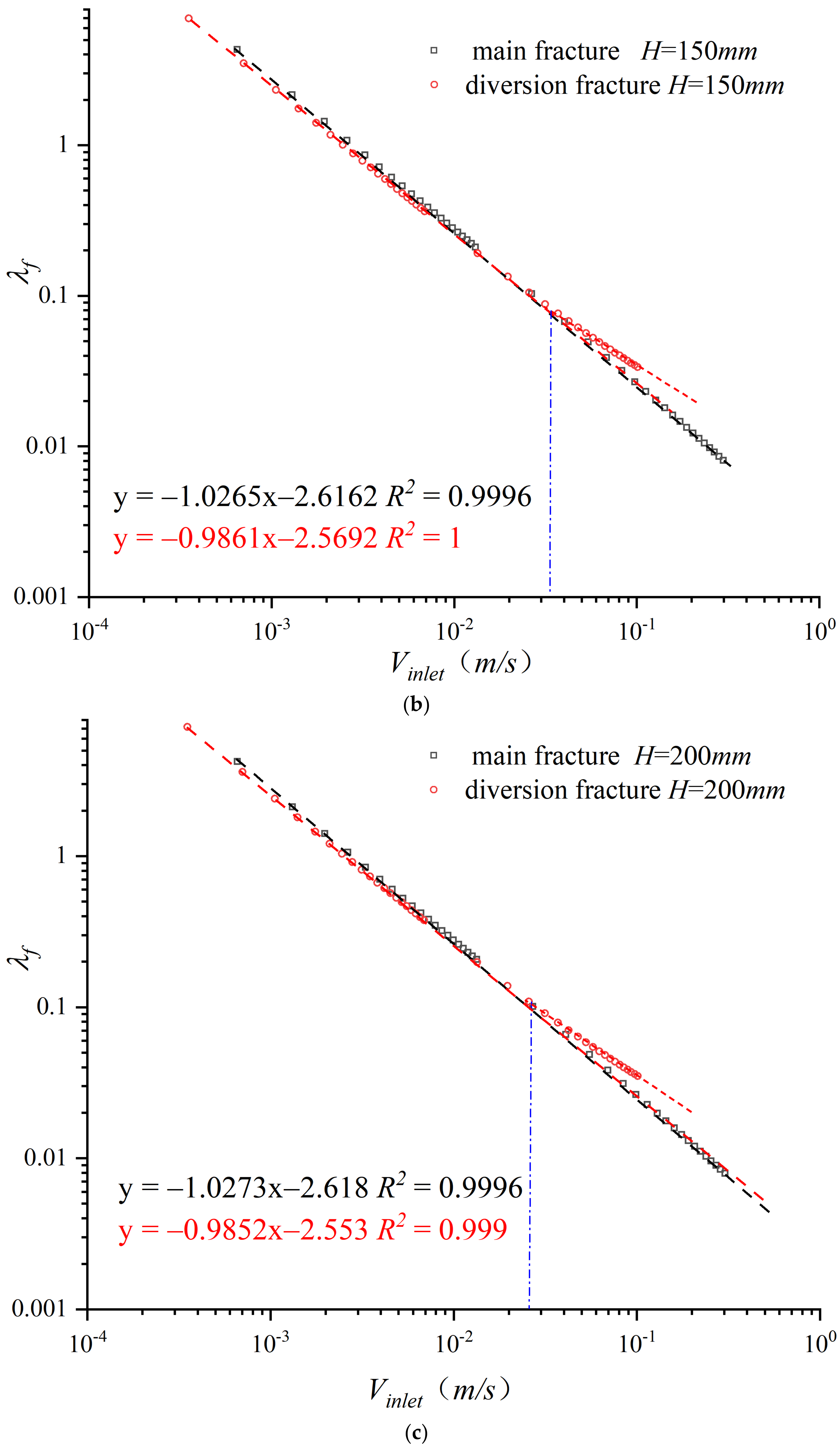
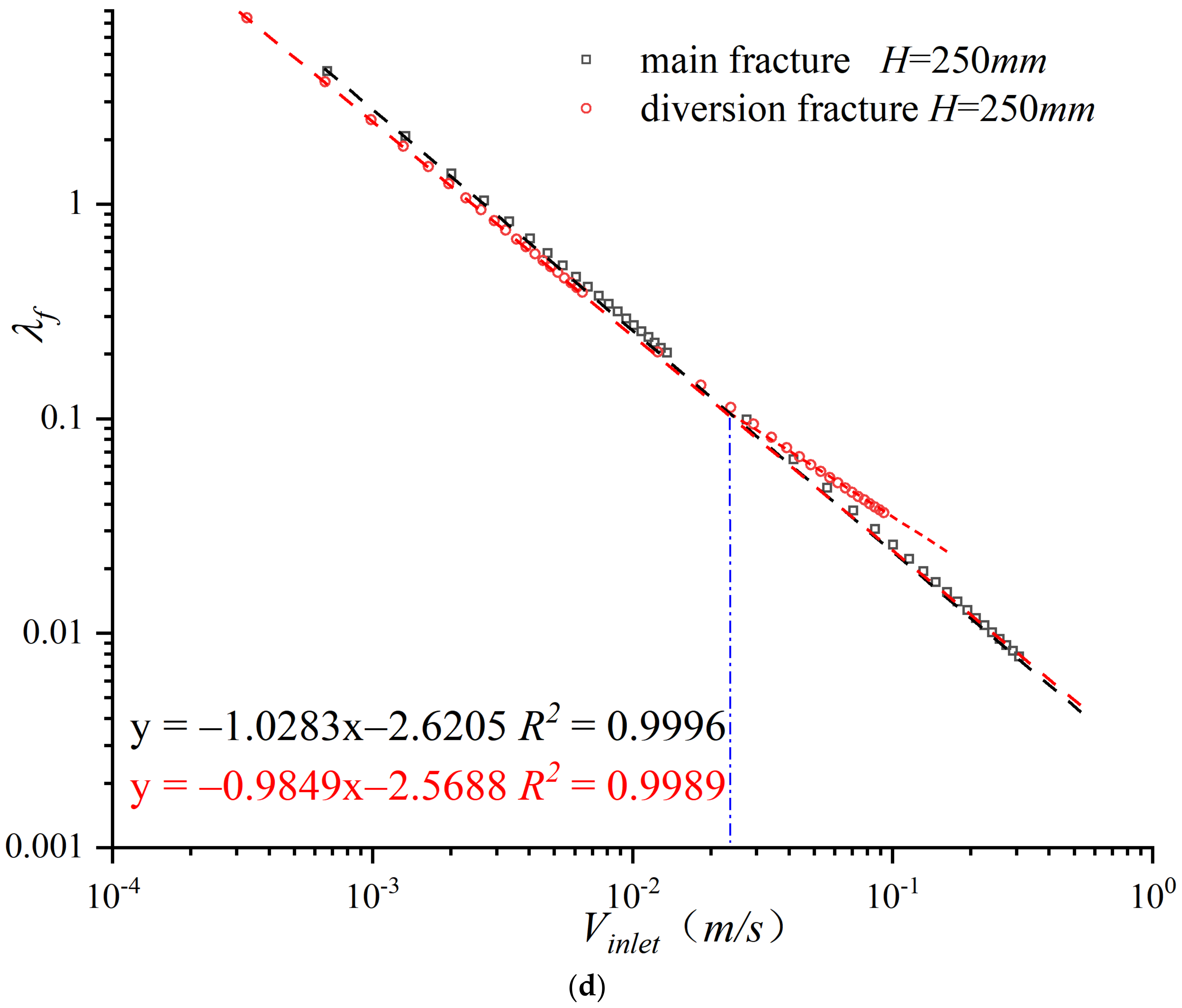
| Fracture | H (mm) | A (105) | B (107) | Rec | R2 | Q1/Q2 |
|---|---|---|---|---|---|---|
| 2D | 100 | 3.75 | 7.63 | 54.61 | 0.998 | 1.60 |
| 150 | 3.82 | 7.88 | 53.86 | 0.997 | 1.88 | |
| 200 | 3.88 | 7.25 | 59.46 | 0.996 | 2.14 | |
| 250 | 3.93 | 6.94 | 62.92 | 0.999 | 2.41 | |
| 3D | 100 | 3.92 | 11.6 | 37.55 | 0.999 | 1.63 |
| 150 | 3.88 | 11.7 | 36.85 | 0.999 | 1.89 | |
| 200 | 3.88 | 11.7 | 36.85 | 0.998 | 2.17 | |
| 250 | 3.92 | 11.6 | 37.55 | 0.999 | 2.43 |
| Pe | H (mm) | v1 (m/s) | v2 (m/s) | D1 (m2/s) | D2 (m2/s) | w1/w2 |
|---|---|---|---|---|---|---|
| 3 | 250 | 8.06 × 10−5 | 2.72 × 10−5 | 0.0121 | 0.0688 | 2.39 |
| 200 | 7.79 × 10−5 | 3.21 × 10−5 | 0.0132 | 0.0656 | 2.06 | |
| 150 | 7.65 × 10−5 | 3.82 × 10−5 | 0.0197 | 0.0621 | 1.79 | |
| 100 | 7.53 × 10−5 | 4.61 × 10−5 | 0.0191 | 0.0598 | 1.52 | |
| 6 | 250 | 1.67 × 10−4 | 5.45 × 10−5 | 0.0083 | 0.13 | 2.44 |
| 200 | 1.59 × 10−4 | 6.37 × 10−5 | 0.0096 | 0.138 | 2.12 | |
| 150 | 1.48 × 10−4 | 7.58 × 10−5 | 0.0111 | 0.149 | 1.84 | |
| 100 | 1.40 × 10−4 | 9.98 × 10−5 | 0.0122 | 0.162 | 1.55 | |
| 15 | 250 | 4.21 × 10−4 | 1.35 × 10−4 | 0.0065 | 0.233 | 2.73 |
| 200 | 4.02 × 10−4 | 1.58 × 10−4 | 0.0074 | 0.174 | 2.22 | |
| 150 | 3.88 × 10−4 | 1.89 × 10−4 | 0.0083 | 0.141 | 1.9 | |
| 100 | 3.76 × 10−4 | 2.27 × 10−4 | 0.0102 | 0.143 | 1.53 | |
| 30 | 250 | 7.75 × 10−4 | 2.70 × 10−4 | 0.0041 | 0.272 | 2.84 |
| 200 | 7.65 × 10−4 | 3.13 × 10−4 | 0.0083 | 0.162 | 2.30 | |
| 150 | 7.59 × 10−4 | 3.7 × 10−4 | 0.0076 | 0.129 | 1.93 | |
| 100 | 7.51 × 10−4 | 4.55 × 10−4 | 0.012 | 0.097 | 1.52 |
| Pe | H (mm) | v1 (m/s) | v2 (m/s) | D1 (m2/s) | D2 (m2/s) | w1/w2 |
|---|---|---|---|---|---|---|
| 3 | 250 | 7.75 × 10−5 | 2.7 × 10−5 | 0.142 | 0.113 | 3.50 |
| 200 | 7.65 × 10−5 | 3.16 × 10−5 | 0.144 | 0.107 | 3.22 | |
| 150 | 7.59 × 10−5 | 3.75 × 10−5 | 0.149 | 0.113 | 2.92 | |
| 100 | 7.51 × 10−5 | 4.05 × 10−5 | 0.156 | 0.111 | 2.67 | |
| 6 | 250 | 1.64 × 10−4 | 5.37 × 10−5 | 0.117 | 0.132 | 3.57 |
| 200 | 1.61 × 10−4 | 6.32 × 10−5 | 0.118 | 0.134 | 3.35 | |
| 150 | 1.53 × 10−4 | 7.47 × 10−5 | 0.124 | 0.138 | 3.08 | |
| 100 | 1.45 × 10−4 | 9.02 × 10−5 | 0.135 | 0.162 | 2.82 | |
| 15 | 250 | 4.28 × 10−4 | 1.35 × 10−4 | 0.097 | 0.164 | 3.93 |
| 200 | 4.16 × 10−4 | 1.56 × 10−4 | 0.153 | 0.152 | 3.64 | |
| 150 | 4.01 × 10−4 | 1.85 × 10−4 | 0.178 | 0.164 | 3.39 | |
| 100 | 3.89 × 10−4 | 2.39 × 10−4 | 0.213 | 0.143 | 3.06 | |
| 30 | 250 | 8.78 × 10−4 | 2.7 × 10−4 | 0.0334 | 0.224 | 4.59 |
| 200 | 8.69 × 10−4 | 3.13 × 10−4 | 0.0184 | 0.232 | 4.14 | |
| 150 | 8.62 × 10−4 | 3.7 × 10−4 | 0.0100 | 0.221 | 3.69 | |
| 100 | 8.54 × 10−4 | 4.54 × 10−4 | 0.0056 | 0.191 | 3.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Chen, L.; Shi, Y. Influence of 3D Fracture Geometry on Water Flow and Solute Transport in Dual-Conduit Fracture. Water 2023, 15, 1754. https://doi.org/10.3390/w15091754
Li Y, Chen L, Shi Y. Influence of 3D Fracture Geometry on Water Flow and Solute Transport in Dual-Conduit Fracture. Water. 2023; 15(9):1754. https://doi.org/10.3390/w15091754
Chicago/Turabian StyleLi, Yubo, Linjie Chen, and Yonghong Shi. 2023. "Influence of 3D Fracture Geometry on Water Flow and Solute Transport in Dual-Conduit Fracture" Water 15, no. 9: 1754. https://doi.org/10.3390/w15091754




