Riverbed Morphologies Induced by Local Scour Processes at Single Spur Dike and Spur Dikes in Cascade
Abstract
:1. Introduction
2. Empirical Equations from Literature
3. Experiments
3.1. Experimental Setup
3.2. Scale Effects
3.3. Experimental Observations
4. Data Analysis and Results
4.1. Uncertainty and Statistical Analysis
4.2. Comparison of the Experimental Data to Literature Formulas for Scour at the Equilibrium Stage
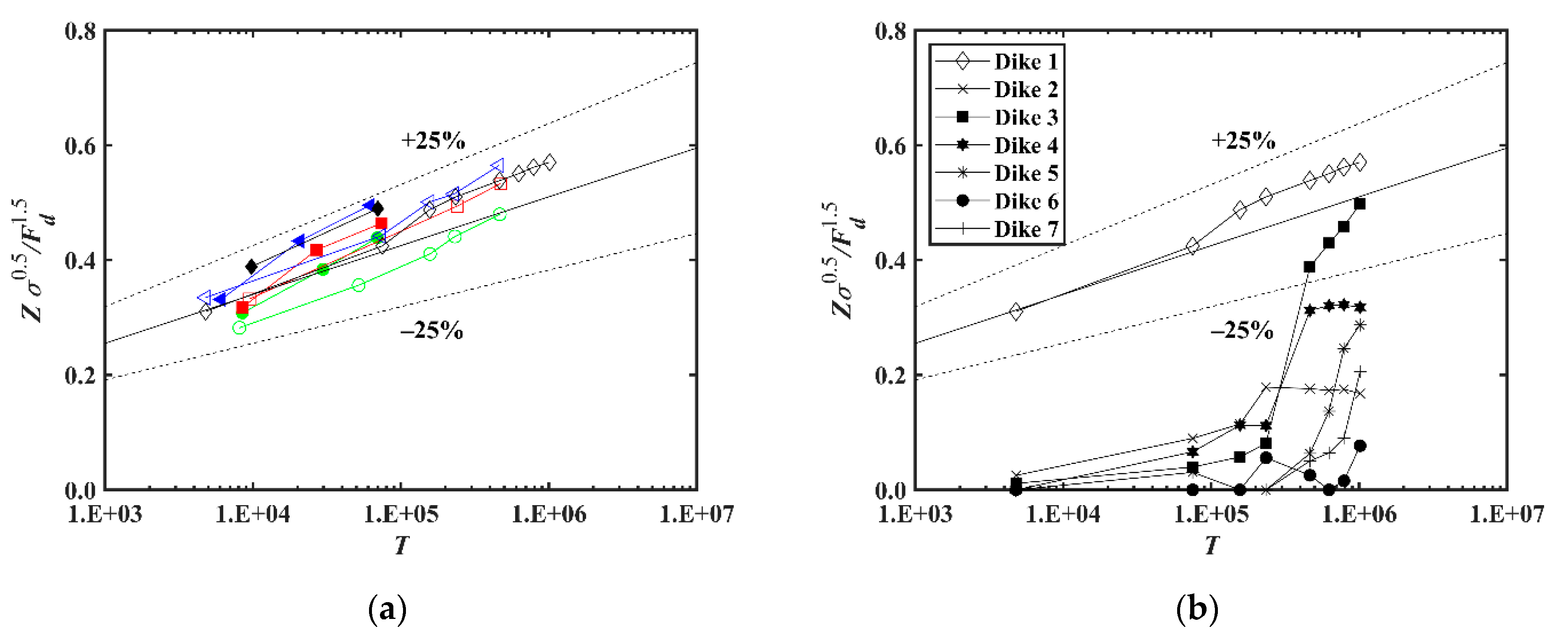
4.3. Temporal Evolution of Scour Depth
5. Discussion
6. Conclusions
- -
- Some limitations of the formulas for the equilibrium scour depth at the first spur dike reported in the literature were emphasised. Underestimations (i.e., the ratio between the actual and predicted values) up to 160% and overestimation (i.e., the ratio between the predicted and actual values) up to 200% at the earlier scour stages were found.
- -
- The temporal evolution of scour depth at the first spur dike was satisfactorily predicted with a coefficient of correlation (CC), mean absolute error (MAE), and mean square error (MSE) of 0.91, 0.085, and 0.0097, respectively.
- -
- Similar scour hole geometries around the first spur dike were observed in all runs, with the maximum scour depth (at the end of each run) remaining almost unchanged, but strictly increasing as the number of spur dikes increased.
- -
- The scour depths on the second spur dike, although slightly increasing over time, were significantly lower than those at the first spur dike. Therefore, this experimental study confirmed some literature findings that also found that the scouring range at the second spur dike is largely covered by the deposition of sediment flowing from the first spur dike for a spacing of 3b.
- -
- For the third, fourth, and fifth spur dikes, the scour processes were delayed and started at a dimensionless time T greater than approximately 103. However, the scour rates increased to a high degree, with scour depths tending to match the observed values at the first spur dike. In the case of the first spur dike, as in the case of the other spur dikes around which the local scour process was quite advanced, the position of the maximum scour depth migrated from the spur dike head to the channel wall.
- -
- The scour depths at the fifth, sixth, and seventh spur dikes were found to be approximately zero; therefore, only these elements could be considered effectively protected from the upstream ones.
- -
- Three distinct mounds of decreasing size, moving downstream, and interlaced by eroded areas were observed for a single spur dike. The primary and secondary mounds reached the bank, requiring protection, and extended transversally to the channel axis. As the number of spur dikes increased, the aggradation areas, although of a more modest size, tended to be confined between adjacent dikes, leaving the central region of the channel less disturbed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barkdoll, B.D.; Ettema, R.; Melville, B.W. Countermeasures to Protect Bridge Abutments from Scour; NCHRP Report 587; Transportation Research Board: Washington, DC, USA, 2007; pp. 38–41. [Google Scholar]
- Copeland, R.R. Bank Protection Techniques Using Spur Dikes; Miscellaneous Paper HL-83-1; National Information Service: Springfield, VA, USA, 1983; pp. 7–12. [Google Scholar]
- Inglis, C.C. The Behaviour and Control of Rivers and Canals; Yeravda Prison Press: Poona, India, 1941; pp. 327–348. [Google Scholar]
- Garde, R.J.; Subramanya, K.; Nambudripad, K.D. Study of scour around spur-dikes. J. Hydraul. Div. ASCE 1961, 87, 23–37. [Google Scholar] [CrossRef]
- Garde, R.J.; Subramanya, K.; Nambudripad, K.D. Scour around obstructions. Irrig. Power 1961, 18, 651–660. [Google Scholar]
- Cunha, L.V. Time evolution of local scour. In Proceedings of the 12th IAHR Congress, Fort Collins, CO, USA, 11–14 September 1967. [Google Scholar]
- Gill, M.A. Erosion of sand beds around spur dikes. J. Hydraul. Div. ASCE 1972, 98, 1587–1602. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Ranga Raju, K.G. Scour around spur dikes and bridge abutments. J. Hydraul. Res. 2001, 39, 367–374. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Alonso, C.V.; Shields, F.D., Jr. Local scour associated with angled spur dikes. J. Hydraul. Eng. ASCE 2002, 128, 1087–1093. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Further results to time-dependent local scour at bridge elements. J. Hydraul. Eng. ASCE 2005, 131, 97–105. [Google Scholar] [CrossRef]
- Pandey, M.; Ahmad, Z.; Sharma, P.K. Estimation of maximum scour depth near a spur dike. Can. J. Civ. Eng. 2016, 43, 270–278. [Google Scholar] [CrossRef]
- Pandey, M.; Valyrakis, M.; Qi, M.; Sharma, A. Experimental assessment and prediction of temporal scour depth around a spur dike. Int. J. Sediment Res. 2021, 36, 17–28. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal evolution of clear-water pier and abutment scour. J. Hydraul. Eng. ASCE 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Gu, Z.; Cao, X.; Jiao, Y.; Lu, W.-Z. Appropriate CFD models for simulating flow around spur dike group along urban riverways. Water Reour. Manage. 2016, 30, 4559–4570. [Google Scholar] [CrossRef]
- Ning, J.; Li, G.; Li, S. Numerical simulation of the influence of spur dikes spacing on local scour and flow. Appl. Sci. 2019, 9, 2306. [Google Scholar] [CrossRef]
- Han, X.; Lin, P.; Parker, G. Influence of layout angles on river flow and local scour in grouped spur dikes field. J. Hydrol. 2022, 614, 128502. [Google Scholar] [CrossRef]
- Gu, Z.; Cao, X.; Cao, M.; Lu, W. Integrative study on flow characteristics and impact of non-submerged double spur dikes on the river systems. Int. J. Environ. Res. Public Health 2023, 20, 4262. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M. Experiments on design and behavior of spur dikes. In Proceedings of the 5th IAHR Congress, Minneapolis, MN, USA, 1–4 September 1953. [Google Scholar]
- Dey, S.; Barbhuiya, A.K. Time variation of scour at abutments. J. Hydraul. Eng. ASCE 2005, 131, 11–23. [Google Scholar] [CrossRef]
- Gisonni, C.; Hager, W.H. Spur failure in river engineering. J. Hydraul. Eng. ASCE 2008, 134, 135–145. [Google Scholar] [CrossRef]
- Oliveto, G.; Marino, M.C. Temporal scour evolution at non-uniform bridge piers. Water Manag. 2017, 170, 254–261. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V. Scour in long contractions. J. Hydraul. Eng. ASCE 2005, 131, 1036–1049. [Google Scholar] [CrossRef]
- Graf, W.H.; Altinakar, M.S. Fluvial Hydraulics-Flow and Transport Processes in Channels of Simple Geometry; John Wiley & Sons Inc: Chichester, UK, 1998; pp. 10–12. [Google Scholar]
- Chiew, Y.M.; Melville, B.W. Local scour around bridge piers. J. Hydraul. Res. 1987, 25, 15–26. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hager, W.H.; Oliveto, G. Generalized approach for clear-water scour at bridge foundation elements. J. Hydraul. Eng. ASCE 2007, 133, 1229–1240. [Google Scholar] [CrossRef]






| Run | No. of Dikes | Q (m3/s) | h0 (m) | Fd (-) | Fdi (-) | t (hrs) | Re·105 (-) |
|---|---|---|---|---|---|---|---|
| CII-1 | 1 | 0.075 | 0.226 | 2.000 | 3.565 | 25 | 1.812 |
| CII-3 | 3 | 0.075 | 0.225 | 2.007 | 3.564 | 26 | 1.814 |
| CII-5 | 5 | 0.075 | 0.236 | 1.916 | 3.582 | 26 | 1.788 |
| CII-7 | 7 | 0.075 | 0.234 | 1.932 | 3.569 | 25 | 1.793 |
| CI-1 | 1 | 0.042 | 0.150 | 1.688 | 3.391 | 144 | 1.134 |
| CI-3 | 3 | 0.042 | 0.162 | 1.563 | 3.425 | 150 | 1.113 |
| CI-5 | 5 | 0.042 | 0.158 | 1.602 | 3.414 | 145 | 1.120 |
| CI-7 | 7 | 0.042 | 0.157 | 1.613 | 3.411 | 318 | 1.122 |
| Instruments | No. of Dikes |
|---|---|
| Point gauge | ±1 mm |
| Shoe gauge | ±2 mm |
| Low-speed probe | ±1.5% true velocity |
| Orifice plate | ±5% |
| Percentage of Change | X | ΔX | ΔY | AS | RS | RE |
|---|---|---|---|---|---|---|
| +10% increase | Fd | 0.158 | 0.120 | 0.759 | 1.332 | 0.133 |
| log(T) | 0.567 | 0.078 | 0.138 | 0.909 | 0.091 | |
| −10% increase | Fd | 0.158 | −0.114 | −0.723 | −1.712 | −0.171 |
| log(T) | 0.567 | −0.078 | −0.138 | −1.111 | −0.111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aung, H.; Onorati, B.; Oliveto, G.; Yu, G. Riverbed Morphologies Induced by Local Scour Processes at Single Spur Dike and Spur Dikes in Cascade. Water 2023, 15, 1746. https://doi.org/10.3390/w15091746
Aung H, Onorati B, Oliveto G, Yu G. Riverbed Morphologies Induced by Local Scour Processes at Single Spur Dike and Spur Dikes in Cascade. Water. 2023; 15(9):1746. https://doi.org/10.3390/w15091746
Chicago/Turabian StyleAung, HtayHtay, Beniamino Onorati, Giuseppe Oliveto, and Guoliang Yu. 2023. "Riverbed Morphologies Induced by Local Scour Processes at Single Spur Dike and Spur Dikes in Cascade" Water 15, no. 9: 1746. https://doi.org/10.3390/w15091746







