Probability-Based Rule Curves for Multi-Purpose Reservoir System in the Seine River Basin, France
Abstract
:1. Introduction
2. Materials and Methods
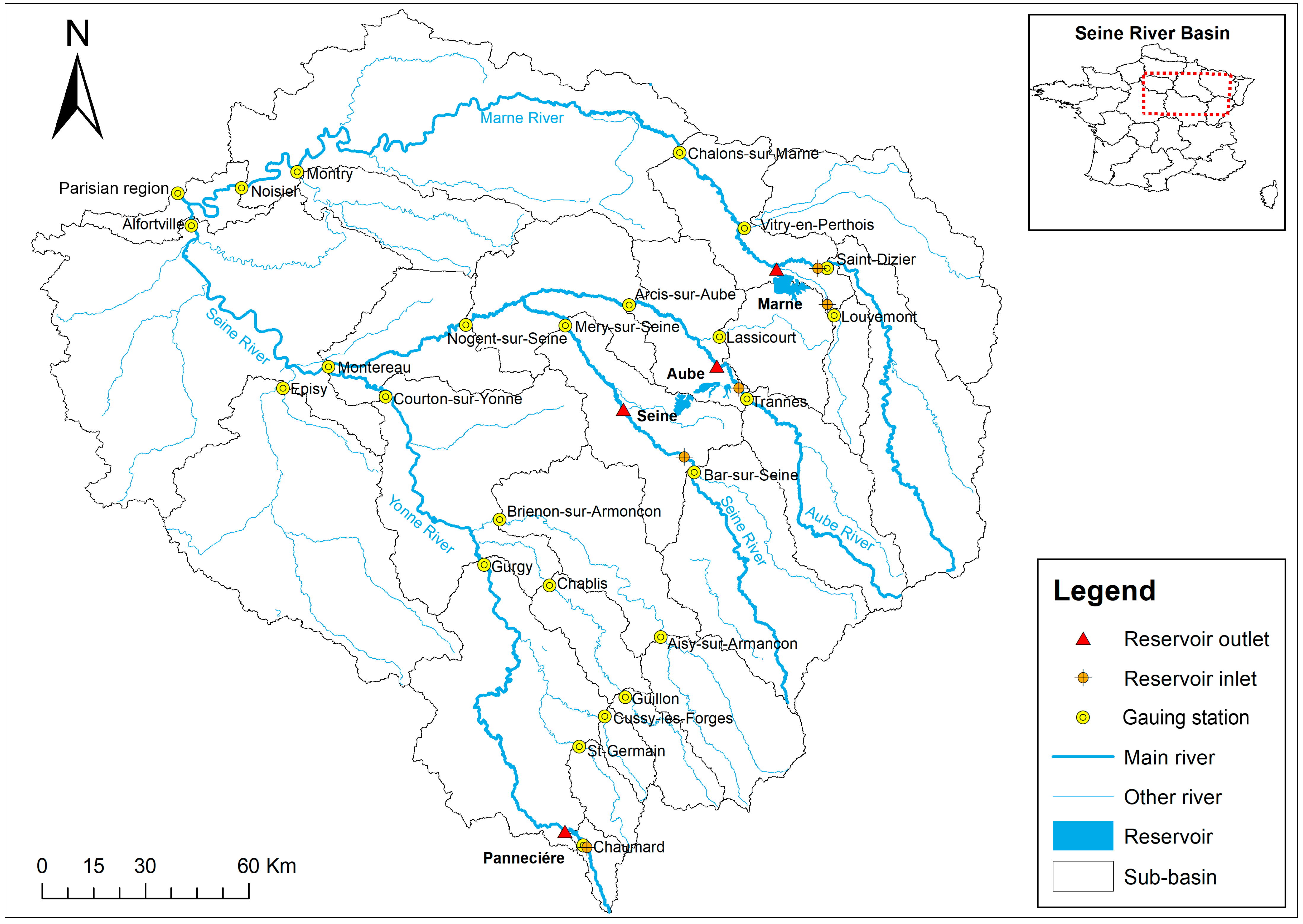
2.1. Introducing the Case Study: Seine River Basin, France
2.2. Data Sources
2.3. Objective Function
2.4. Application of Dynamic Programming for Optimization of Reservoir Operation
2.5. Joint Operation of Multiple Reservoir System
2.6. Identification of Optimal Rule Curves
3. Results
3.1. Efficient Water Allocation under Reservoir Joint Operation
3.2. Annual Optimal Rule Curves
3.2.1. The Proposed URC for Flood Control
3.2.2. The Proposed LRC for Low-Flow Support Objective
3.3. Web-Based Application for Optimization of Multiple Reservoir Operation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adeloye, A.J.; Dau, Q.V. Hedging as an adaptive measure for climate change induced water shortage at the Pong reservoir in the Indus Basin Beas River, India. Sci. Total Environ. 2019, 687, 554–566. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, T.; Cai, X.; Zhou, Y.; Wang, X. Improved dynamic programming for parallel reservoir system operation optimization. Adv. Water Resour. 2019, 131, 103373. [Google Scholar] [CrossRef]
- Oliveira, R.; Loucks, D.P. Operating rules for multireservoir systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- McMahon, T.A.; Adeloye, A. Water Resources Yield; Water Resources Publications: Littleton, CO, USA, 2005. [Google Scholar]
- Yeh, W.W.-G. Reservoir management and operations models: A state-of-the-art review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Cuvelier, T.; Archambeau, P.; Dewals, B.; Louveaux, Q. Comparison between robust and stochastic optimisation for long-term reservoir management under uncertainty. Water Resour. Manag. 2018, 32, 1599–1614. [Google Scholar] [CrossRef]
- Loucks, D.P.; Stedinger, J.R.; Haith, D.A. Water Resource Systems Planning and Analysis; Prentice-Hall: Hoboken, NJ, USA, 1981. [Google Scholar]
- Maass, A.; Hufschmidt, M.M.; Dorfman, R.; Thomas, H.A., Jr.; Marglin, S.A.; Fair, G.M. Design of Water-Resource Systems; Harvard University Press: Cambridge, MA, USA, 1962. [Google Scholar]
- Ghimire, B.N.S.; Reddy, M.J. Optimal reservoir operation for hydropower production using particle swarm optimization and sustainability analysis of hydropower. ISH J. Hydraul. Eng. 2013, 19, 196–210. [Google Scholar] [CrossRef]
- Neelakantan, T.R.; Sasireka, K. Hydropower reservoir operation using standard operating and standard hedging policies. Int. J. Eng. Technol. 2013, 5, 1191–1196. [Google Scholar]
- Stedinger, J.R. The performance of LDR models for preliminary design and reservoir operation. Water Resour. Res. 1984, 20, 215–224. [Google Scholar] [CrossRef]
- Neelakantan, T.R.; Pundarikanthan, N.V. Hedging rule optimisation for water supply reservoirs system. Water Resour. Manag. 1999, 13, 409–426. [Google Scholar] [CrossRef]
- Rittima, A. Hedging policy for reservoir system operation: A case study of mun bon and lam chae reservoirs. Kasetsart J. Nat. Sci. 2009, 43, 833–842. [Google Scholar]
- Bertoni, F. Advancing joint design and operation of water resources systems under uncertainty. In Special Topics in Information Technology. SpringerBriefs in Applied Sciences and Technology; Geraci, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Uysal, G.; Schwanenberg, D.; Alvarado-Montero, R.; Şensoy, A. Short term optimal operation of water supply reservoir under flood control stress using model predictive control. Water Resour. Manag. 2018, 32, 583–597. [Google Scholar] [CrossRef]
- Antonik, P.; Massar, S.; Duport, F. Advanced Reservoir Computers: Analogue Autonomous Systems and Real Time Control. In Photonic Reservoir Computing: Optical Recurrent Neural Networks; Brunner, D., Soriano, M., Van der Sande, G., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; pp. 205–258. [Google Scholar] [CrossRef]
- Amini, S.; Mohaghegh, S. Application of machine learning and artificial intelligence in proxy modeling for fluid flow in porous media. Fluids 2019, 4, 126. [Google Scholar] [CrossRef]
- Faber, B.A.; Harou, J.J. Multi-objective optimization of reservoir systems using HEC-ResPRM. Restoring Our Nat Habitat. In Proceedings of the 2007 World Environmental and Water Resources Congress, Tampa, FL, USA, 15–19 May 2007; pp. 1–14. [Google Scholar]
- Leta, M.K.; Demissie, T.A.; Tränckner, J. Optimal operation of Nashe hydropower reservoir under land use land cover change in Blue Nile River Basin. Water 2022, 14, 1606. [Google Scholar] [CrossRef]
- Eschenbach, E.A.; Magee, T.; Zagona, E.; Goranflo, M.; Shane, R. Goal programming decision support system for multiobjective operation of reservoir systems. J. Water Resour. Plan. Manag. 2001, 127, 108–120. [Google Scholar] [CrossRef]
- Zagona, E.A.; Fulp, T.J.; Shane, R.; Magee, T.; Goranflo, H.M. Riverware: A generalized tool for complex reservoir system modeling. J. Am. Water Resour. Assoc. 2001, 37, 913–929. [Google Scholar] [CrossRef]
- Labadie, J.W. MODSIM: Decision support system for integrated river basin management. In International Congress on Environmental Modelling and Software; Brigham Young University: Provo, UT, USA, 2006; p. 242. [Google Scholar]
- Schwanenberg, D.; Fan, F.M.; Naumann, S.; Kuwajima, J.I.; Montero, R.A.; Reis, A.d.R. Short-term reservoir optimization for flood mitigation under meteorological and hydrological forecast uncertainty. Water Resour. Manag. 2015, 29, 1635–1651. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Cohon, J.L.; ReVelle, C.S. Gains from joint operation of multiple reservoir systems. Water Resour. Res. 1977, 13, 239–245. [Google Scholar] [CrossRef]
- Clark, E.J. New York control curves. J. Am. Water Work. Assoc. 1950, 42, 823–827. [Google Scholar]
- Bower, T.B.; Hufschmidt, M.M.; Reedy, W.W. Operating procedures: Their role in the design of water-resource systems by simulation analyses. In Design of Water Resources Systems; Maass, A., Hufschmidt, M.M., Dorfman, R., Thomas, H.A., Marglin, S.A., Fair, G.M., Eds.; Havard University Press: Cambridge, MA, USA, 1962; pp. 443–458. [Google Scholar]
- Edirisinghe, N.C.P.; Patterson, E.I.; Saadouli, N. Capacity planning model for a multipurpose water reservoir with target-priority operation. Ann. Oper. Res. 2000, 100, 273–303. [Google Scholar] [CrossRef]
- Young, G.K. Finding reservoir operating rules. J. Hydraul. Div. 1967, 93, 297–322. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November 1995–1 December 1995. [Google Scholar]
- Ma, Y.; Zhong, P.; Xu, B.; Zhu, F.; Lu, Q.; Han, W. Spark-based parallel dynamic programming and particle swarm optimization via cloud computing for a large-scale reservoir system. J. Hydrol. 2021, 598, 126444. [Google Scholar] [CrossRef]
- Chen, H.; Wang, W.; Chen, X.; Qiu, L. Multi-objective reservoir operation using particle swarm optimization with adaptive random inertia weights. Water Sci. Eng. 2020, 13, 136–144. [Google Scholar] [CrossRef]
- Dahmani, S.; Yebdri, D. Hybrid algorithm of particle swarm optimization and grey wolf optimizer for reservoir operation management. Water Resour. Manag. 2020, 34, 4545–4560. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in natural and artificial Systems: An introductory analysis with applications to biology, control and artificial Intelligence. In Complex Adaptive Systems; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Ren, M.; Zhang, Q.; Yang, Y.; Wang, G.; Xu, W.; Zhao, L. Research and application of reservoir flood control optimal operation based on improved genetic algorithm. Water 2022, 14, 1272. [Google Scholar] [CrossRef]
- Anand, J.; Gosain, A.K.; Khosa, R. Optimisation of multipurpose reservoir operation by coupling Soil and Water Assessment Tool (SWAT) and Genetic Algorithm for optimal operating policy (case study: Ganga River Basin). Sustainability 2018, 10, 1660. [Google Scholar] [CrossRef]
- Mathur, Y.; Nikam, S. Optimal reservoir operation policies using genetic algorithm. Int. J. Eng. Technol. 2009, 1, 184–187. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
- Shaw, A.R.; Sawyer, H.S.; LeBoeuf, E.J.; McDonald, M.P.; Hadjerioua, B. Hydropower optimization using artificial neural network surrogate models of a high-fidelity hydrodynamics and water quality model. Water Resour. Res. 2017, 53, 9444–9461. [Google Scholar] [CrossRef]
- Shaikh, S.A. Application of artificial neural network for optimal operation of a multi-purpose multi-reservoir system, I: Initial solution and selection of input variables. Sustain. Water Resour. Manag. 2020, 6, 60. [Google Scholar] [CrossRef]
- Zhao, T.; Cai, X.; Lei, X.; Wang, H. Improved dynamic programming for reservoir operation optimization with a concave objective function. J. Water Resour. Plan. Manag. 2012, 138, 590–596. [Google Scholar] [CrossRef]
- Chaleeraktrakoon, C.; Kangrang, A. Dynamic programming with the principle of progressive optimality for searching rule curves. Can. J. Civ. Eng. 2007, 34, 170–176. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Ouyang, S.; Ding, X.; Chen, L. Improved decomposition–coordination and discrete differential dynamic programming for optimization of large-scale hydropower system. Energy Convers. Manag. 2014, 84, 363–373. [Google Scholar] [CrossRef]
- Azevedo, A.T.; Oliveira, A.R.L.; Soares, S. Interior point method for long-term generation scheduling of large-scale hydrothermal systems. Ann. Oper. Res. 2009, 169, 55–80. [Google Scholar] [CrossRef]
- Kumar, D.N.; Baliarsingh, F. Folded dynamic programming for optimal operation of multireservoir System. Water Resour. Manag. 2003, 17, 337–353. [Google Scholar] [CrossRef]
- Curie, F.; Ducharne, A.; Bendjoudi, H.; Billen, G. Spatialization of denitrification by river corridors in regional-scale watersheds: Case study of the Seine river basin. Phys. Chem. Earth Parts A/B/C 2011, 36, 530–538. [Google Scholar] [CrossRef]
- Dorchies, D.; Thirel, G.; Jay-Allemand, M.; Chauveau, M.; Dehay, F.; Bourgin, P.-Y.; Thépot, R. Climate change impacts on multi-objective reservoir management: Case study on the Seine River basin, France. Int. J. River Basin Manag. 2014, 12, 265–283. [Google Scholar] [CrossRef]
- Bellman, R.E.; Dreyfus, S.E. Applied Dynamic Programming. Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Larson, R.E.; Keckler, W.G. Applications of dynamic programming to the control of water resource systems. Automatica 1969, 5, 15–26. [Google Scholar] [CrossRef]
- Meylan, P.; Favre, A.C.; Musy, A. Predictive Hydrology: A Frequency Analysis Approach; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Giuliani, M.; Herman, J.D.; Quinn, J.D. Kirsch-Nowak Streamflow Generator. Available online: https://github.com/julianneq/Kirsch-Nowak_Streamflow_Generator (accessed on 21 November 2022).
- Bader, J.-C.; Dorchies, D. Calcul des Limites de Volumes d’eau à Respecter Dans des Réservoirs Implantés en Parallèle sur un Réseau Hydrographique, Pour Permettre la Meilleure Satisfaction Future d’un Objectif Commun de Gestion à L’aval (Soutien D’étiage ou Laminage de Crue): Logiciel VGEST—Application au Cas du Bassin de la Seine (Amélioration et Extension de la Méthode Précédemment Développée Dans le Cadre du Programme Climaware). AP: Autres Productions. IRD. 2016, Montpellier. Available online: https://www.documentation.ird.fr/hor/fdi:010070461 (accessed on 12 August 2022).

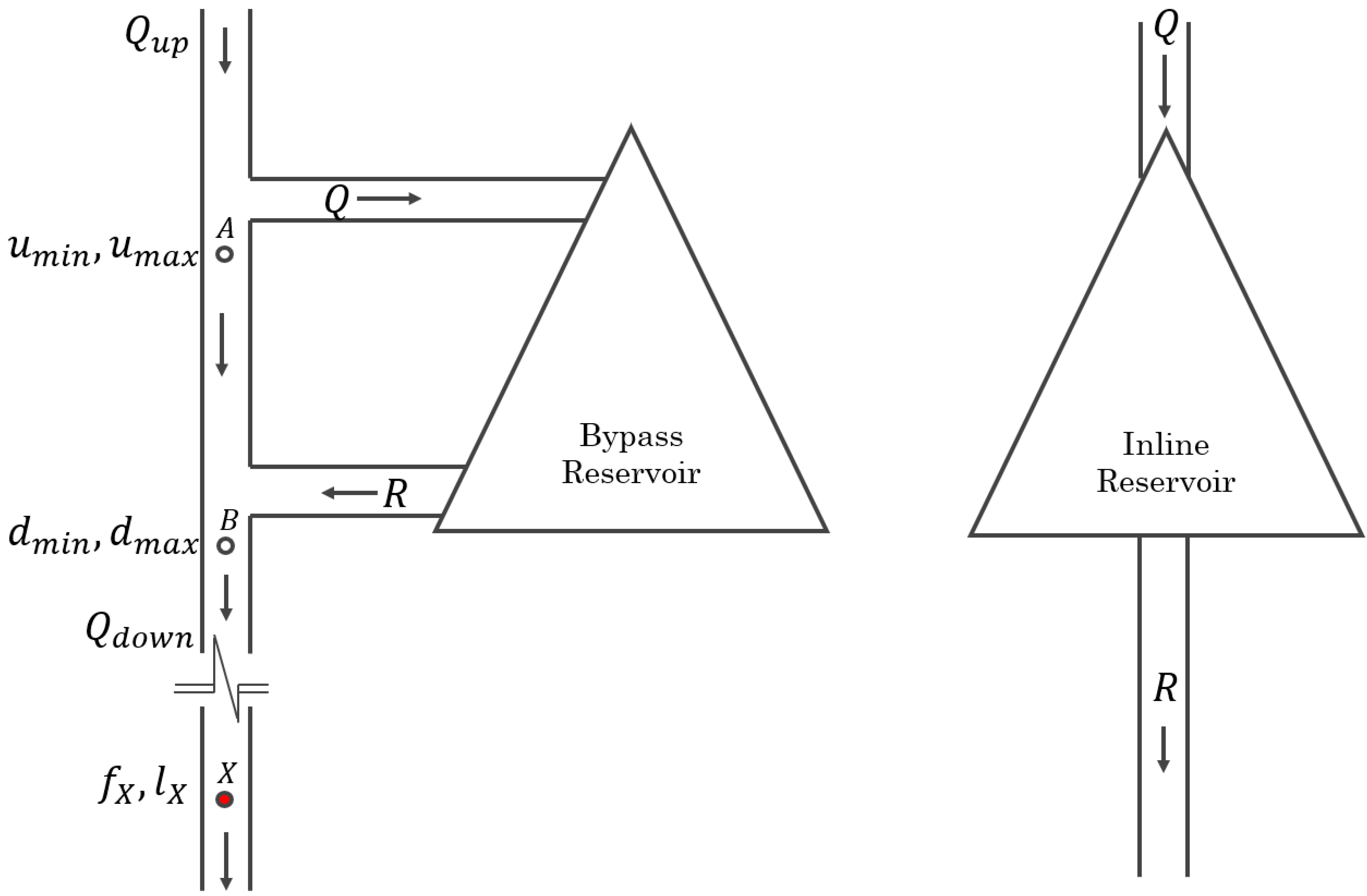



| Elements | Pannecière | Seine | Aube | Marne |
|---|---|---|---|---|
| Type of reservoir | Inline | Bypass | Bypass | Bypass |
| Water surface area (km2) | 5.2 | 23.2 | 23.2 | 28 |
| Catchment area (km2) | 220 | 2380 | 1650 | 2900 |
| Maximum dam height (m) | 49.0 | 25.0 | 22.5 | 20.0 |
| Crest length (m) | 352 | 5700 | 3500 | 20,300 |
| Gross storage capacity (MCM) | 82.5 | 219.5 | 183.5 | 364.5 |
| Live storage capacity (MCM) | 74.0 | 212.9 | 181.2 | 354.5 |
| Dead storage capacity (MCM) | 8.5 | 6.6 | 2.3 | 10.0 |
| Monitoring Station | River | Impact | Low Flow Thresholds (m3/s) | High Flow Thresholds (m3/s) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Vigilance | Alert | Reinforced Alert | Crisis | Vigilance | Regular | Exceptional | |||
| Arcis-sur-Aube | Aube | A | 6.3 | 5 | 4 | 3.5 | 110 | 260 | 400 |
| Mery-sur-Seine | Seine | S | 7.3 | 5 | 4 | 3.5 | 140 | 170 | 400 |
| Nogent-sur-Seine | Seine | A + S | 25 | 20 | 17 | 16 | 180 | 280 | 420 |
| Gurgy | Yonne | P | 14 | 12.5 | 11 | 9.2 | 220 | 340 | 400 |
| Courlon-sur-Yonne | Yonne | P | 23 | 16 | 13 | 11 | 550 | 700 | 900 |
| Alfortvile | Seine | A + S + P | 64 | 48 | 41 | 36 | 850 | 1200 | 1400 |
| Chalons-sur-Marne | Marne | M | 12 | 11 | 9 | 8 | 330 | 520 | 700 |
| Noisiel | Marne | M | 32 | 23 | 20 | 17 | 350 | 500 | 650 |
| Paris | Seine | A + S + P + M | 81 | 60 | 51 | 45 | 950 | 1600 | 2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dau, Q.V.; Kangrang, A.; Kuntiyawichai, K. Probability-Based Rule Curves for Multi-Purpose Reservoir System in the Seine River Basin, France. Water 2023, 15, 1732. https://doi.org/10.3390/w15091732
Dau QV, Kangrang A, Kuntiyawichai K. Probability-Based Rule Curves for Multi-Purpose Reservoir System in the Seine River Basin, France. Water. 2023; 15(9):1732. https://doi.org/10.3390/w15091732
Chicago/Turabian StyleDau, Quan Van, Anongrit Kangrang, and Kittiwet Kuntiyawichai. 2023. "Probability-Based Rule Curves for Multi-Purpose Reservoir System in the Seine River Basin, France" Water 15, no. 9: 1732. https://doi.org/10.3390/w15091732








