A Screening Procedure for Identifying Drought Hot-Spots in a Changing Climate
Abstract
1. Introduction
2. Study Area
3. Data
3.1. Observational Data
3.2. Climate Model Data
3.3. Preliminary Data Elaborations
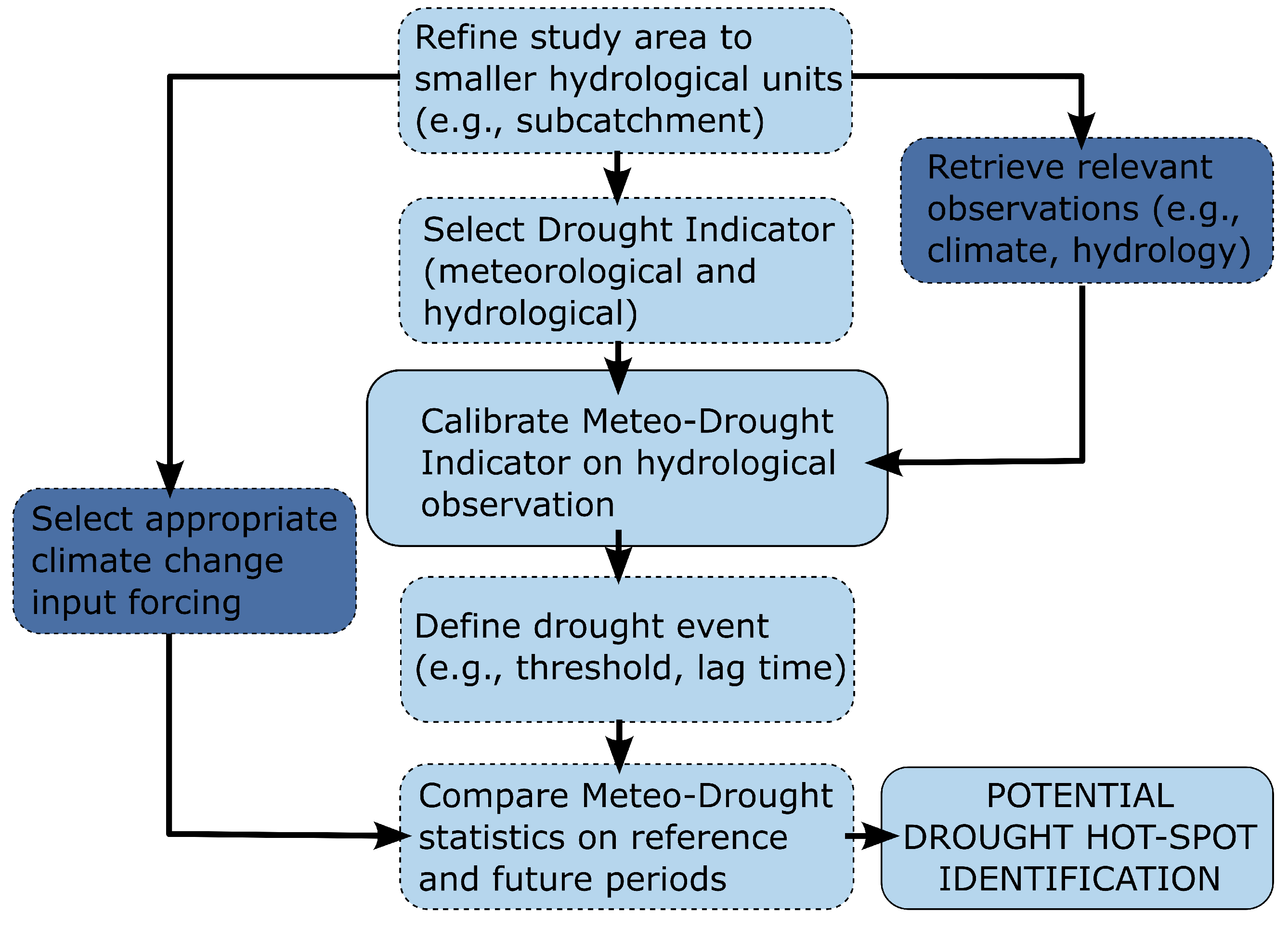
4. Methodology
4.1. Meteorological Drought Index
4.2. Hydrological Drought Index
4.3. Characteristic Timescale
4.4. Identification and Definition of Drought Events
4.5. Identification of Future Drought Hot-Spots
5. Results
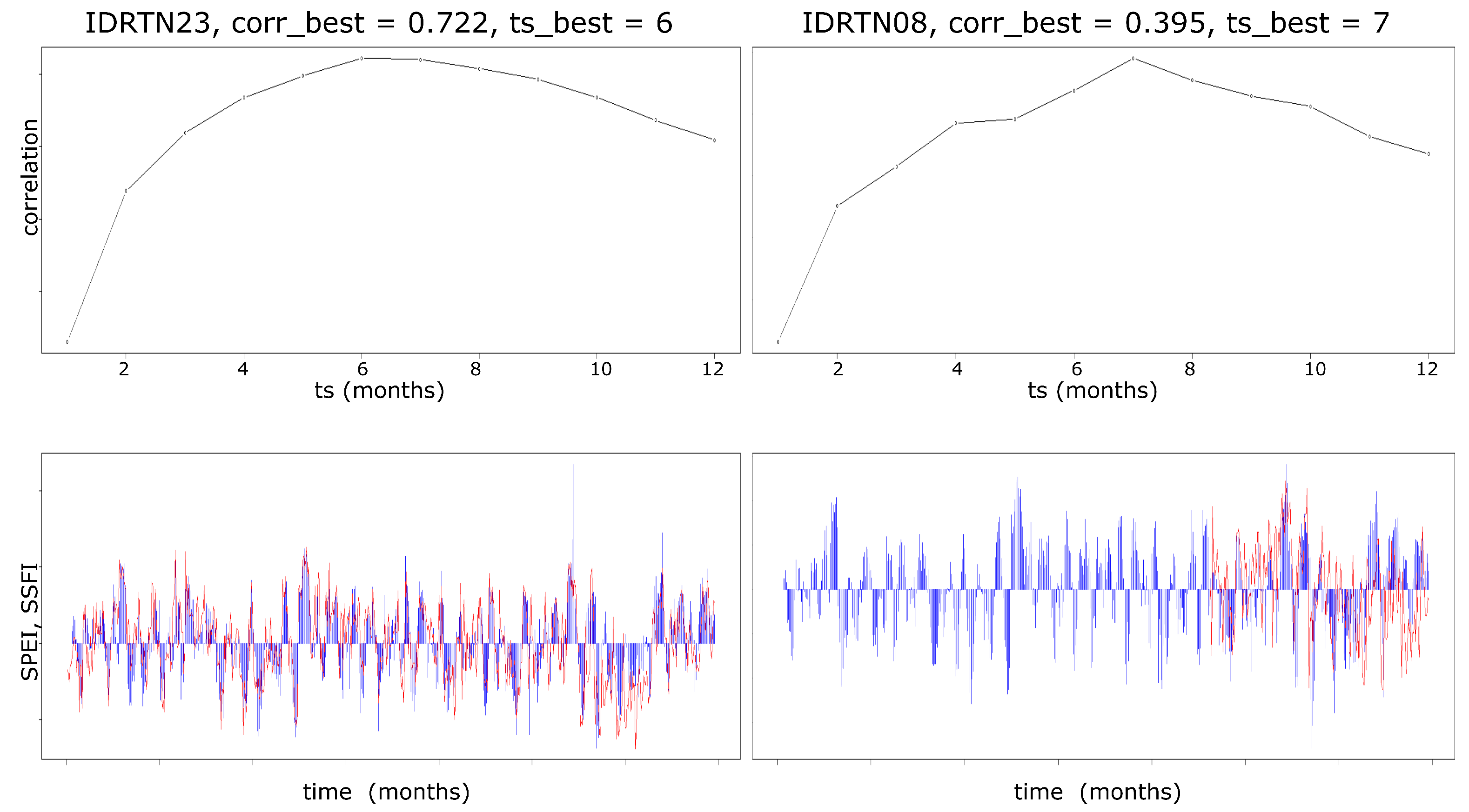
5.1. Characteristic Timescale for Each Catchment
5.2. Drought Hot-Spots
6. Discussion
6.1. Characteristic Timescales
6.2. Drought Hot-Spots
6.3. Strengths and Limitations of the Methodology
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mastrotheodoros, T.; Pappas, C.; Molnar, P.; Burlando, P.; Manoli, G.; Parajka, J.; Rigon, R.; Széles, B.; Bottazzi, M.; Hadjidoukas, P.; et al. More green and less blue water in the Alps during warmer summers. Nat. Clim. Chang. 2020, 10, 155–161. [Google Scholar] [CrossRef]
- Agency, E.E.; Collins, R.; Thyssen, N.; Kristensen, P. Water Resources across Europe: Confronting Water Scarcity and Drought; Publications Office: Luxembourg, 2009. [Google Scholar] [CrossRef]
- Lutz, S.R.; Mallucci, S.; Diamantini, E.; Majone, B.; Bellin, A.; Merz, R. Hydroclimatic and water quality trends across three Mediterranean river basins. Sci. Total Environ. 2016, 571, 1392–1406. [Google Scholar] [CrossRef]
- Diamantini, E.; Lutz, S.R.; Mallucci, S.; Majone, B.; Merz, R.; Bellin, A. Driver detection of water quality trends in three large European river basins. Sci. Total Environ. 2018, 612, 49–62. [Google Scholar] [CrossRef]
- Smajgl, A.; Ward, J.; Pluschke, L. The water–food–energy Nexus—Realising a new paradigm. J. Hydrol. 2016, 533, 533–540. [Google Scholar] [CrossRef]
- Anghileri, D.; Botter, M.; Castelletti, A.; Weigt, H.; Burlando, P. A Comparative Assessment of the Impact of Climate Change and Energy Policies on Alpine Hydropower. Water Resour. Res. 2018, 54, 9144–9161. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhai, X.; Zhao, T. Annual shifts of flow regime alteration: New insights from the Chaishitan Reservoir in China. Sci. Rep. 2018, 8, 1414. [Google Scholar] [CrossRef] [PubMed]
- Rajczak, J.; Pall, P.; Schär, C. Projections of extreme precipitation events in regional climate simulations for Europe and the Alpine Region. J. Geophys. Res. Atmos. 2013, 118, 3610–3626. [Google Scholar] [CrossRef]
- Auer, I.; Böhm, R.; Jurkovic, A.; Lipa, W.; Orlik, A.; Potzmann, R.; Schöner, W.; Ungersböck, M.; Matulla, C.; Briffa, K.; et al. HISTALP—Historical instrumental climatological surface time series of the Greater Alpine Region. Int. J. Climatol. 2007, 27, 17–46. [Google Scholar] [CrossRef]
- Gobiet, A.; Kotlarski, S.; Beniston, M.; Heinrich, G.; Rajczak, J.; Stoffel, M. 21st century climate change in the European Alps—A review. Sci. Total Environ. 2014, 493, 1138–1151. [Google Scholar] [CrossRef]
- Pepin, N.C.; Lundquist, J.D. Temperature trends at high elevations: Patterns across the globe. Geophys. Res. Lett. 2008, 35, L14701. [Google Scholar] [CrossRef]
- Scherrer, S.C.; Ceppi, P.; Croci-Maspoli, M.; Appenzeller, C. Snow-albedo feedback and Swiss spring temperature trends. Theor. Appl. Climatol. 2012, 110, 509–516. [Google Scholar] [CrossRef]
- Notarnicola, C. Overall negative trends for snow cover extent and duration in global mountain regions over 1982–2020. Sci. Rep. 2022, 12, 13731. [Google Scholar] [CrossRef] [PubMed]
- Baronetti, A.; Dubreuil, V.; Provenzale, A.; Simona, F. Future droughts in northern Italy: High-resolution projections using EURO-CORDEX and MED-CORDEX ensembles. Clim. Chang. 2022, 172, 22. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Stahl, K.; Di Baldassarre, G.; Clark, J.; Rangecroft, S.; Wanders, N.; Gleeson, T.; Van Dijk, A.I.J.M.; Tallaksen, L.M.; Hannaford, J.; et al. Drought in a human-modified world: Reframing drought definitions, understanding, and analysis approaches. Hydrol. Earth Syst. Sci. 2016, 20, 3631–3650. [Google Scholar] [CrossRef]
- Destouni, G.; Jaramillo, F.; Prieto, C. Hydroclimatic shifts driven by human water use for food and energy production. Nat. Clim. Chang. 2013, 3, 213–217. [Google Scholar] [CrossRef]
- Bieber, N.; Ker, J.H.; Wang, X.; Triantafyllidis, C.; van Dam, K.H.; Koppelaar, R.H.; Shah, N. Sustainable planning of the energy-water-food nexus using decision making tools. Energy Policy 2018, 113, 584–607. [Google Scholar] [CrossRef]
- Vittoz, P.; Cherix, D.; Gonseth, Y.; Lubini, V.; Maggini, R.; Zbinden, N.; Zumbach, S. Climate change impacts on biodiversity in Switzerland: A review. J. Nat. Conserv. 2013, 21, 154–162. [Google Scholar] [CrossRef]
- Pütz, M.; Gallati, D.; Kytzia, S.; Elsasser, H.; Lardelli, C.; Teich, M.; Waltert, F.; Rixen, C. Winter Tourism, Climate Change, and Snowmaking in the Swiss Alps: Tourists’ Attitudes and Regional Economic Impacts. Mt. Res. Dev. 2011, 31, 357–362. [Google Scholar] [CrossRef]
- Gaudard, L.; Gilli, M.; Romerio, F. Climate Change Impacts on Hydropower Management. Water Resour. Manag. 2013, 27, 5143–5156. [Google Scholar] [CrossRef]
- Majone, B.; Villa, F.; Deidda, R.; Bellin, A. Impact of climate change and water use policies on hydropower potential in the south-eastern Alpine region. Sci. Total Environ. 2016, 543, 965–980, Special Issue on Climate Change, Water and Security in the Mediterranean. [Google Scholar] [CrossRef] [PubMed]
- Wagner, T.; Themeßl, M.; Schuppel, A.; Gobiet, A.; Stigler, H.; Birk, S. Impacts of climate change on stream flow and hydro power generation in the Alpine region. Environ. Earth Sci. 2016, 76, 4. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; Lorenzo-Lacruz, J.; Camarero, J.J.; López-Moreno, J.I.; Azorin-Molina, C.; Revuelto, J.; Morán-Tejeda, E.; Sanchez-Lorenzo, A. Performance of Drought Indices for Ecological, Agricultural, and Hydrological Applications. Earth Interact. 2012, 16, 1–27. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Heim, R.R.J. A Review of Twentieth-Century Drought Indices Used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1166. [Google Scholar] [CrossRef]
- Haslinger, K.; Blöschl, G. Space-Time Patterns of Meteorological Drought Events in the European Greater Alpine Region Over the Past 210 Years. Water Resour. Res. 2017, 53, 9807–9823. [Google Scholar] [CrossRef]
- Haslinger, K.; Schöner, W.; Anders, I. Future drought probabilities in the Greater Alpine Region based on COSMO-CLM experiments-Spatial patterns and driving forces. Meteorol. Z. 2015, 25, 137–148. [Google Scholar] [CrossRef]
- Burke, E.J.; Brown, S.J. Evaluating Uncertainties in the Projection of Future Drought. J. Hydrometeorol. 2008, 9, 292–299. [Google Scholar] [CrossRef]
- Heinrich, G.; Gobiet, A. The future of dry and wet spells in Europe: A comprehensive study based on the ENSEMBLES regional climate models. Int. J. Climatol. 2012, 32, 1951–1970. [Google Scholar] [CrossRef]
- Bowell, A.; Salakpi, E.; Guigma, K.; Mumina, J.; Mwangi, J.; Rowhani, P. Validating commonly used drought indicators in Kenya. Environ. Res. Lett. 2021, 16, 084066. [Google Scholar] [CrossRef]
- Stephan, R.; Erfurt, M.; Terzi, S.; Žun, M.; Kristan, B.; Haslinger, K.; Stahl, K. An inventory of Alpine drought impact reports to explore past droughts in a mountain region. Nat. Hazards Earth Syst. Sci. 2021, 21, 2485–2501. [Google Scholar] [CrossRef]
- Formetta, G.; Marra, F.; Dallan, E.; Zaramella, M.; Borga, M. Differential orographic impact on sub-hourly, hourly, and daily extreme precipitation. Adv. Water Resour. 2022, 159, 104085. [Google Scholar] [CrossRef]
- Kay, A.; Davies, H.; Lane, R.; Rudd, A.; Bell, V. Grid-based simulation of river flows in Northern Ireland: Model performance and future flow changes. J. Hydrol. Reg. Stud. 2021, 38, 100967. [Google Scholar] [CrossRef]
- Collet, L.; Harrigan, S.; Prudhomme, C.; Formetta, G.; Beevers, L. Future hot-spots for hydro-hazards in Great Britain: A probabilistic assessment. Hydrol. Earth Syst. Sci. 2018, 22, 5387–5401. [Google Scholar] [CrossRef]
- Visser-Quinn, A.; Beevers, L.; Collet, L.; Formetta, G.; Smith, K.; Wanders, N.; Thober, S.; Pan, M.; Kumar, R. Spatio-temporal analysis of compound hydro-hazard extremes across the UK. Adv. Water Resour. 2019, 130, 77–90. [Google Scholar] [CrossRef]
- Chaves, M.; Maroco, J.; Pereira, J. Understanding plant responses to drought—From genes to the whole plant. Funct. Plant Biol. 2003, 30, 239–264. [Google Scholar] [CrossRef]
- Lorenzo-Lacruz, J.; Vicente-Serrano, S.; López-Moreno, J.; Morán-Tejeda, E.; Zabalza, J. Recent trends in Iberian streamflows (1945–2005). J. Hydrol. 2012, 414-415, 463–475. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J.R. The Relationship of Drought Frequency and Duration to Time Scales; American Meteorological Society: Boston, MA, USA, 1993. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Haslinger, K.; Holawe, F.; Blöschl, G. Spatial characteristics of precipitation shortfalls in the Greater Alpine Region—A data-based analysis from observations. Theor. Appl. Climatol. 2019, 136, 717–731. [Google Scholar] [CrossRef]
- Jabbi, F.F.; Li, Y.; Zhang, T.; Bin, W.; Hassan, W.; Songcai, Y. Impacts of Temperature Trends and SPEI on Yields of Major Cereal Crops in the Gambia. Sustainability 2021, 13, 12480. [Google Scholar] [CrossRef]
- Lee, S.H.; Yoo, S.H.; Choi, J.Y.; Bae, S. Assessment of the Impact of Climate Change on Drought Characteristics in the Hwanghae Plain, North Korea Using Time Series SPI and SPEI: 1981–2100. Water 2017, 9, 579. [Google Scholar] [CrossRef]
- Spinoni, J.; Vogt, J.V.; Naumann, G.; Barbosa, P.; Dosio, A. Will drought events become more frequent and severe in Europe? Int. J. Climatol. 2018, 38, 1718–1736. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; López-Moreno, J.; Beguería, S.; Lorenzo-Lacruz, J.; Sanchez-Lorenzo, A.; García-Ruiz, J.M.; Azorin-Molina, C.; Morán-Tejeda, E.; Revuelto, J.; Trigo, R.; et al. Evidence of Increasing Drought Severity Caused by Temperature Rise in Southern Europe. Environ. Res. Lett. 2014, 9, 044001. [Google Scholar] [CrossRef]
- Lorenzo-Lacruz, J.; Vicente-Serrano, S.; Gonzalez-Hidalgo, J.; López-Moreno, J.; Cortesi, N. Hydrological drought response to meteorological drought in the Iberian Peninsula. Clim. Res. 2013, 58, 117–131. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Yao, H.; Gao, L.; Chen, Y.; Liu, M. Non-linear relationship of hydrological drought responding to meteorological drought and impact of a large reservoir. J. Hydrol. 2017, 551, 495–507. [Google Scholar] [CrossRef]
- Bayer Altin, T.; Altin, B.N. Response of hydrological drought to meteorological drought in the eastern Mediterranean Basin of Turkey. J. Arid. Land 2021, 13, 470–486. [Google Scholar] [CrossRef]
- Laiti, L.; Mallucci, S.; Piccolroaz, S.; Bellin, A.; Zardi, D.; Fiori, A.; Nikulin, G.; Majone, B. Testing the Hydrological Coherence of High-Resolution Gridded Precipitation and Temperature Data Sets. Water Resour. Res. 2018, 54, 1999–2016. [Google Scholar] [CrossRef]
- Mallucci, S.; Majone, B.; Bellin, A. Detection and attribution of hydrological changes in a large Alpine river basin. J. Hydrol. 2019, 575, 1214–1229. [Google Scholar] [CrossRef]
- Larsen, S.; Majone, B.; Zulian, P.; Stella, E.; Bellin, A.; Bruno, M.C.; Zolezzi, G. Combining Hydrologic Simulations and Stream-network Models to Reveal Flow-ecology Relationships in a Large Alpine Catchment. Water Resour. Res. 2021, 57, e2020WR028496. [Google Scholar] [CrossRef]
- Galletti, A.; Avesani, D.; Bellin, A.; Majone, B. Detailed simulation of storage hydropower systems in large Alpine watersheds. J. Hydrol. 2021, 603, 127125. [Google Scholar] [CrossRef]
- Avesani, D.; Galletti, A.; Piccolroaz, S.; Bellin, A.; Majone, B. A dual-layer MPI continuous large-scale hydrological model including Human Systems. Environ. Model. Softw. 2021, 139, 105003. [Google Scholar] [CrossRef]
- Avesani, D.; Zanfei, A.; Di Marco, N.; Galletti, A.; Ravazzolo, F.; Righetti, M.; Majone, B. Short-term hydropower optimization driven by innovative time-adapting econometric model. Appl. Energy 2022, 310, 118510. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resource Evaluation; Oxford University Press: Oxford, UK, 1997; Volume 42, Chapter 8; pp. 388–390. [Google Scholar]
- Hargreaves, G.; Samani, Z. Estimating Potential Evapotranspiration. J. Irrig. Drain. Div. ASCE 1982, 108, 225–230. [Google Scholar] [CrossRef]
- Giorgi, F.; Jones, C.; Asrar, G.R. Addressing climate information needs at the regional level: The CORDEX framework. World Meteorol. Organ. (WMO) Bull. 2009, 58, 175. [Google Scholar]
- Vrzel, J.; Ludwig, R.; Gampe, D.; Ogrinc, N. Hydrological system behaviour of an alluvial aquifer under climate change. Sci. Total Environ. 2019, 649, 1179–1188. [Google Scholar] [CrossRef]
- Majone, B.; Avesani, D.; Zulian, P.; Fiori, A.; Bellin, A. Analysis of high streamflow extremes in climate change studies: How do we calibrate hydrological models? Hydrol. Earth Syst. Sci. 2022, 26, 3863–3883. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate Distributions for Climatological Drought Indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Modarres, R. Streamflow drought time series forecasting. Stoch. Environ. Res. Risk Assess. 2007, 21, 223–233. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; López-Moreno, J.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Accurate Computation of a Streamflow Drought Index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1987, 100, 441–471. [Google Scholar] [CrossRef] [PubMed]
- Barker, L.J.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardised indicators. Hydrol. Earth Syst. Sci. 2016, 20, 2483–2505. [Google Scholar] [CrossRef]
- Nayak, A.; Biswal, B.; Sudheer, K. Drought hotspot maps and regional drought characteristics curves: Development of a novel framework and its application to an Indian River basin undergoing climatic changes. Sci. Total Environ. 2022, 807, 151083. [Google Scholar] [CrossRef]
- Dobriyal, P.; Badola, R.; Tuboi, C.; Hussain, S.A. A review of methods for monitoring streamflow for sustainable water resource management. Appl. Water Sci. 2017, 7, 2617–2628. [Google Scholar] [CrossRef]
- Eder, G.; Fuchs, M.; Nachtnebel, H.; Loibl, W. Semi-Distributed Modeling of the Monthly Water Balance in an Alpine Catchment. Hydrol. Process. 2005, 19, 2339–2360. [Google Scholar] [CrossRef]
- Brauchli, T.; Trujillo, E.; Huwald, H.; Lehning, M. Influence of Slope-Scale Snowmelt on Catchment Response Simulated With the Alpine3D Model. Water Resour. Res. 2017, 53, 10723–10739. [Google Scholar] [CrossRef]
- Soulsby, C.; Tetzlaff, D.; Rodgers, P.; Dunn, S.; Waldron, S. Runoff processes, stream water residence times and controlling landscape characteristics in a mesoscale catchment: An initial evaluation. J. Hydrol. 2006, 325, 197–221. [Google Scholar] [CrossRef]
- López-Moreno, J.; Vicente-Serrano, S.; Zabalza, J.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Hydrological response to climate variability at different time scales: A study in the Ebro basin. J. Hydrol. 2013, 477, 175–188. [Google Scholar] [CrossRef]
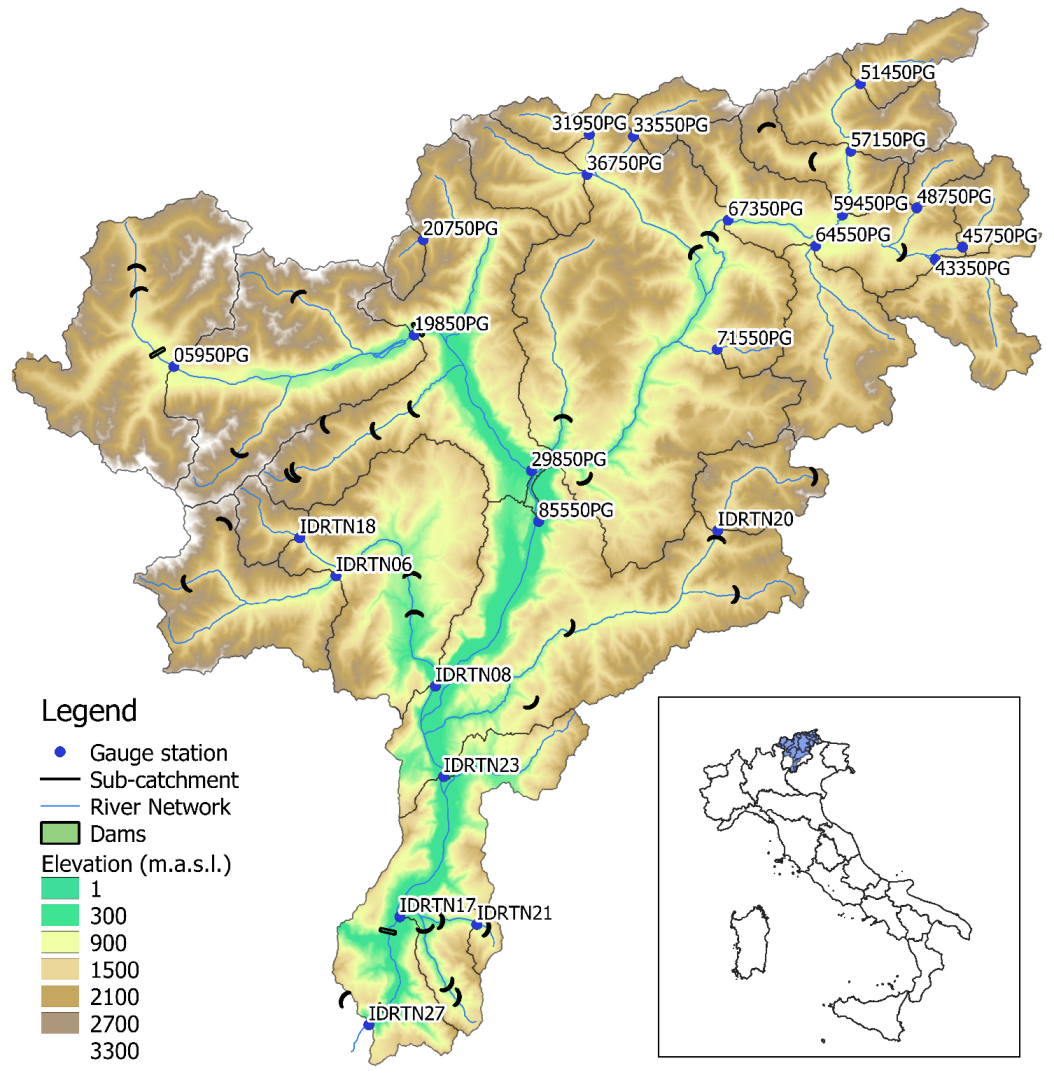





| Station | Area [km2] | VTOT [Mm3] | QAVG [m3/s] | QMON cov. [%] | RC [Days] |
|---|---|---|---|---|---|
| 05950PG | 831.74 | 122.00 | 12.31 | 49.43 | 114.71 |
| 19850PG | 1645.86 | 184.71 | 32.61 | 94.83 | 65.56 |
| 20750PG | 47.76 | 0.00 | 3.56 | 35.34 | 0.00 |
| 29850PG | 2726.27 | 241.74 | 54.88 | 95.69 | 50.98 |
| 31950PG | 73.85 | 0.00 | 3.03 | 98.28 | 0.00 |
| 33550PG | 107.98 | 0.00 | 4.06 | 41.38 | 0.00 |
| 36750PG | 207.77 | 0.00 | 7.56 | 48.28 | 0.00 |
| 43350PG | 265.73 | 0.00 | 5.36 | 52.73 | 0.00 |
| 45750PG | 118.13 | 0.00 | 2.48 | 56.32 | 0.00 |
| 48750PG | 70.42 | 0.00 | 1.98 | 48.28 | 0.00 |
| 51450PG | 155.57 | 0.00 | 6.08 | 46.55 | 0.00 |
| 57150PG | 418.87 | 0.00 | 14.60 | 51.72 | 0.00 |
| 59450PG | 607.93 | 15.34 | 20.85 | 56.90 | 8.52 |
| 64550PG | 392.62 | 0.00 | 8.09 | 76.44 | 0.00 |
| 67350PG | 1921.53 | 20.14 | 44.74 | 94.68 | 5.21 |
| 71550PG | 44.78 | 0.00 | 0.92 | 35.78 | 0.00 |
| 85550PG | 6920.82 | 265.68 | 147.18 | 93.10 | 20.89 |
| IDRTN06 | 467.15 | 28.91 | 10.96 | 32.90 | 30.53 |
| IDRTN08 | 1354.35 | 201.54 | 35.34 | 33.76 | 66.01 |
| IDRTN18 | 93.65 | 0.00 | 3.31 | 37.50 | 0.00 |
| IDRTN20 | 205.76 | 16.00 | 6.07 | 85.20 | 30.51 |
| IDRTN23 | 9793.21 | 531.26 | 198.72 | 100.00 | 30.94 |
| IDRTN21 | 29.63 | 0.17 | 0.27 | 33.19 | 7.29 |
| IDRTN17 | 174.29 | 12.39 | 4.48 | 33.62 | 32.01 |
| IDRTN27 | 10,650.81 | 543.65 | 107.36 | 32.90 | 58.61 |
| RCM | GCM | Acronym |
|---|---|---|
| CLMcom-CCLM4-8-17 | EC-EARTH-r1 | CLMcom |
| KNMI-RACMO22E | EC-EARTH-r12 | KNMI |
| SMHI-RCA4 | HadGEM2-ES | SMHI |
| Precipitation | ADIGE | CLM | KNMI | SMHI | ||||
|---|---|---|---|---|---|---|---|---|
| Q25 | IQR | Q25 | IQR | Q25 | IQR | Q25 | IQR | |
| January | 19.31 | 32.45 | 15.81 | 26.11 | 10.08 | 27.92 | 11.94 | 29.42 |
| February | 12.89 | 30.72 | 17.37 | 28.57 | 15.85 | 34.18 | 10.63 | 25.39 |
| March | 30.16 | 30.69 | 30.57 | 27.69 | 24.54 | 37.99 | 29.58 | 31.50 |
| April | 44.31 | 42.16 | 57.62 | 33.70 | 44.41 | 60.74 | 42.13 | 39.52 |
| May | 67.67 | 52.68 | 57.81 | 45.48 | 68.86 | 38.15 | 54.78 | 48.70 |
| June | 86.52 | 43.82 | 82.82 | 78.71 | 96.35 | 38.23 | 70.62 | 51.30 |
| July | 99.55 | 25.81 | 87.00 | 67.40 | 99.31 | 43.92 | 79.70 | 58.33 |
| August | 84.64 | 56.33 | 86.88 | 60.07 | 94.00 | 46.24 | 63.56 | 63.48 |
| September | 56.54 | 58.65 | 68.14 | 51.01 | 64.16 | 32.40 | 50.23 | 50.38 |
| October | 41.68 | 86.39 | 51.63 | 46.70 | 54.20 | 65.42 | 38.47 | 92.05 |
| November | 28.93 | 92.25 | 62.06 | 60.84 | 48.68 | 76.91 | 50.54 | 46.49 |
| December | 34.00 | 36.31 | 24.27 | 53.62 | 19.78 | 54.20 | 29.24 | 23.28 |
| 49.02 | 48.33 | 46.36 | 46.65 | |||||
| 0.9608 | 0.9657 | 0.9657 | ||||||
| Temperature | ADIGE | CLM | KNMI | SMHI | ||||
|---|---|---|---|---|---|---|---|---|
| Q25 | IQR | Q25 | IQR | Q25 | IQR | Q25 | IQR | |
| January | −4.86 | 2.87 | −5.18 | 1.54 | −5.34 | 1.99 | −5.73 | 2.60 |
| February | −4.60 | 3.69 | −4.27 | 2.22 | −4.53 | 2.33 | −4.87 | 2.98 |
| March | −0.99 | 3.21 | −1.67 | 2.60 | −1.35 | 2.25 | −0.50 | 1.60 |
| April | 3.20 | 1.39 | 2.78 | 1.91 | 3.37 | 1.35 | 2.74 | 2.04 |
| May | 8.37 | 1.70 | 7.93 | 2.80 | 8.14 | 3.00 | 8.71 | 2.25 |
| June | 11.65 | 1.56 | 11.96 | 1.85 | 12.05 | 2.59 | 12.41 | 2.94 |
| July | 13.68 | 1.99 | 14.66 | 2.19 | 13.83 | 2.79 | 13.52 | 2.71 |
| August | 13.79 | 1.52 | 12.63 | 2.39 | 12.60 | 2.47 | 13.28 | 2.10 |
| September | 9.55 | 2.24 | 8.90 | 1.59 | 8.65 | 2.14 | 8.99 | 1.84 |
| October | 5.78 | 2.12 | 4.13 | 2.03 | 5.06 | 1.32 | 4.32 | 2.21 |
| November | 0.12 | 1.94 | −1.33 | 2.62 | −1.73 | 2.35 | −0.57 | 1.81 |
| December | −3.62 | 2.07 | −5.89 | 2.74 | −4.44 | 1.27 | −4.15 | 0.99 |
| 2.19 | 2.21 | 2.16 | 2.17 | |||||
| 0.9959 | 0.9964 | 0.9956 | ||||||
| Station ID | corrbest | tsbest |
|---|---|---|
| 05950PG | 0.416 | 9 |
| 19850PG | 0.513 | 9 |
| 20750PG | 0.564 | 9 |
| 29850PG | 0.655 | 7 |
| 36750PG | 0.565 | 7 |
| 31950PG | 0.696 | 10 |
| 33550PG | 0.509 | 10 |
| 51450PG | 0.409 | 10 |
| 57150PG | 0.481 | 9 |
| 59450PG | 0.581 | 7 |
| 48750PG | 0.623 | 7 |
| 45750PG | 0.579 | 6 |
| 43350PG | 0.519 | 6 |
| 64550PG | 0.578 | 8 |
| 67350PG | 0.678 | 7 |
| 71550PG | 0.584 | 7 |
| 85550PG | 0.660 | 7 |
| IDRTN06 | 0.544 | 9 |
| IDRTN08 | 0.395 | 7 |
| IDRTN18 | 0.609 | 7 |
| IDRTN20 | 0.559 | 7 |
| IDRTN23 | 0.722 | 6 |
| IDRTN21 | 0.432 | 6 |
| IDRTN17 | 0.692 | 3 |
| IDRTN27 | 0.533 | 4 |
| Station ID | CLMcom | KNMI | SMHI | Average |
|---|---|---|---|---|
| 05950PG | 1 | 14 | 2 | 6 |
| 19850PG | 7 | 18 | 6 | 10 |
| 20750PG | 13 | 17 | 12 | 14 |
| 29850PG | 11 | 18 | 8 | 12 |
| 31950PG | 17 | 11 | 6 | 12 |
| 33550PG | 10 | 18 | 1 | 10 |
| 36750PG | 16 | 17 | 7 | 13 |
| 43350PG | 14 | 17 | 1 | 11 |
| 45750PG | 11 | 14 | 2 | 9 |
| 48750PG | 14 | 15 | −4 | 8 |
| 51450PG | 6 | 20 | 4 | 10 |
| 57150PG | 8 | 21 | 4 | 11 |
| 59450PG | 11 | 17 | 0 | 9 |
| 64550PG | 21 | 16 | 4 | 14 |
| 67350PG | 16 | 18 | 1 | 11 |
| 71550PG | 20 | 10 | 2 | 11 |
| 85550PG | 16 | 17 | 5 | 13 |
| IDRTN06 | 10 | 27 | 9 | 15 |
| IDRTN08 | 17 | 23 | 7 | 15 |
| IDRTN17 | 10 | 9 | 5 | 8 |
| IDRTN18 | 10 | 23 | 2 | 12 |
| IDRTN20 | 20 | 19 | 4 | 14 |
| IDRTN21 | 18 | 17 | 8 | 14 |
| IDRTN23 | 18 | 15 | 5 | 13 |
| IDRTN27 | 13 | 15 | −5 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galletti, A.; Formetta, G.; Majone, B. A Screening Procedure for Identifying Drought Hot-Spots in a Changing Climate. Water 2023, 15, 1731. https://doi.org/10.3390/w15091731
Galletti A, Formetta G, Majone B. A Screening Procedure for Identifying Drought Hot-Spots in a Changing Climate. Water. 2023; 15(9):1731. https://doi.org/10.3390/w15091731
Chicago/Turabian StyleGalletti, Andrea, Giuseppe Formetta, and Bruno Majone. 2023. "A Screening Procedure for Identifying Drought Hot-Spots in a Changing Climate" Water 15, no. 9: 1731. https://doi.org/10.3390/w15091731
APA StyleGalletti, A., Formetta, G., & Majone, B. (2023). A Screening Procedure for Identifying Drought Hot-Spots in a Changing Climate. Water, 15(9), 1731. https://doi.org/10.3390/w15091731









