Effects of Spatial Data Acquisition on Determination of a Gravel-Bed River Geomorphology
Abstract
:1. Introduction
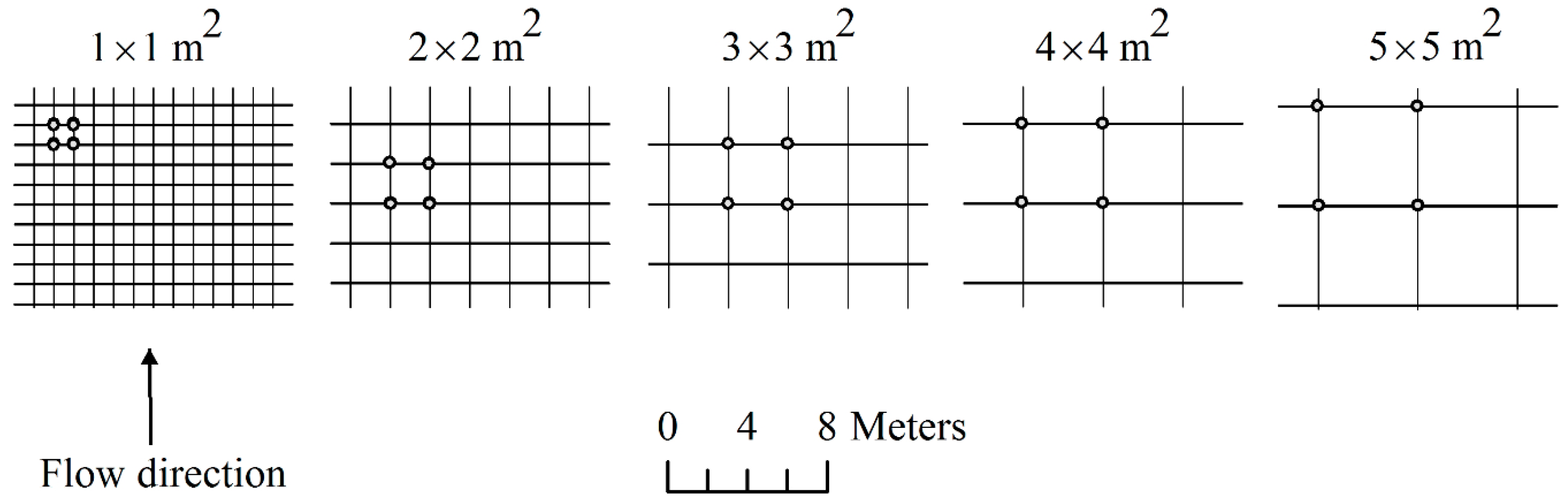
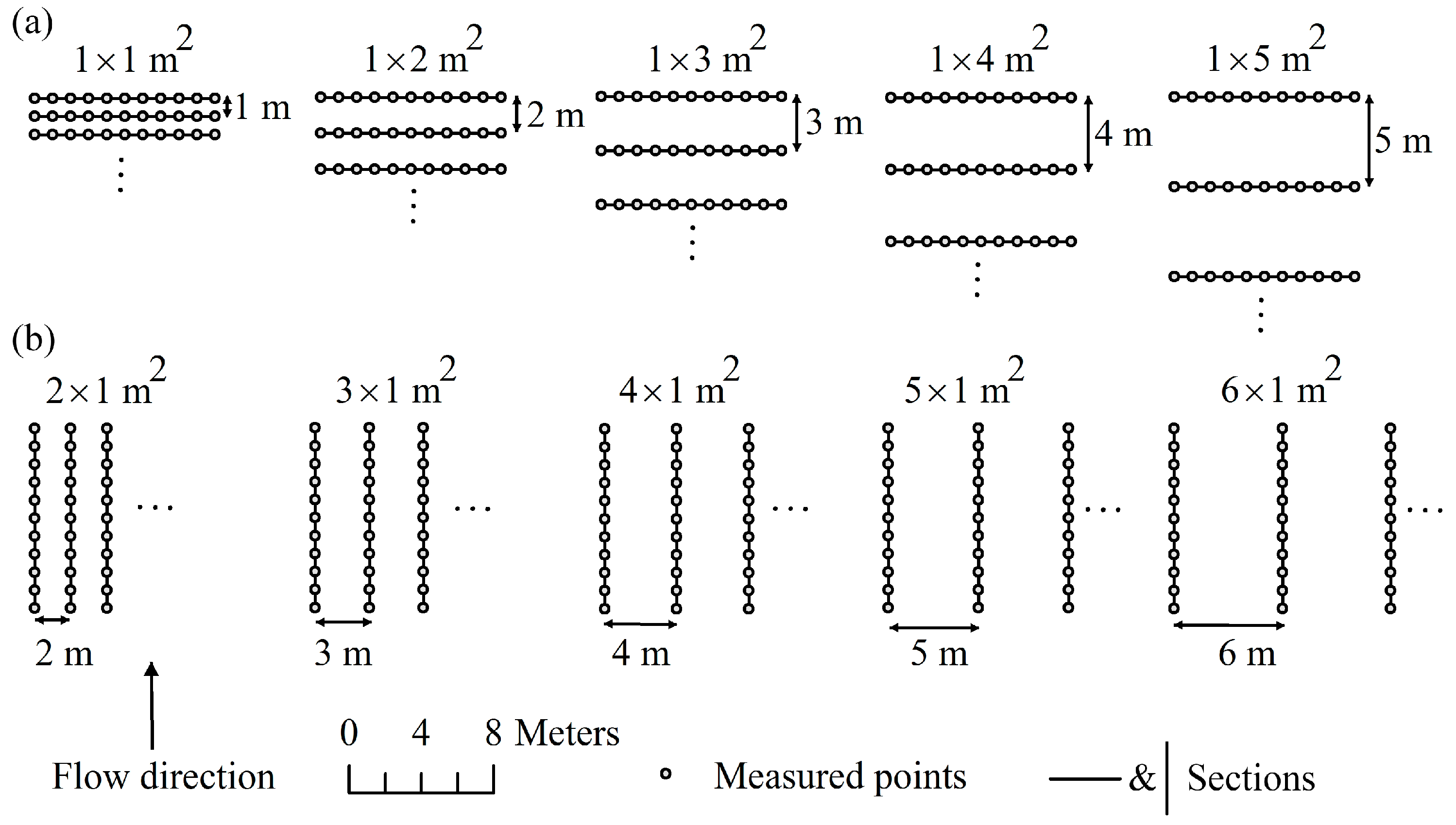
2. Materials and Methods
3. Results
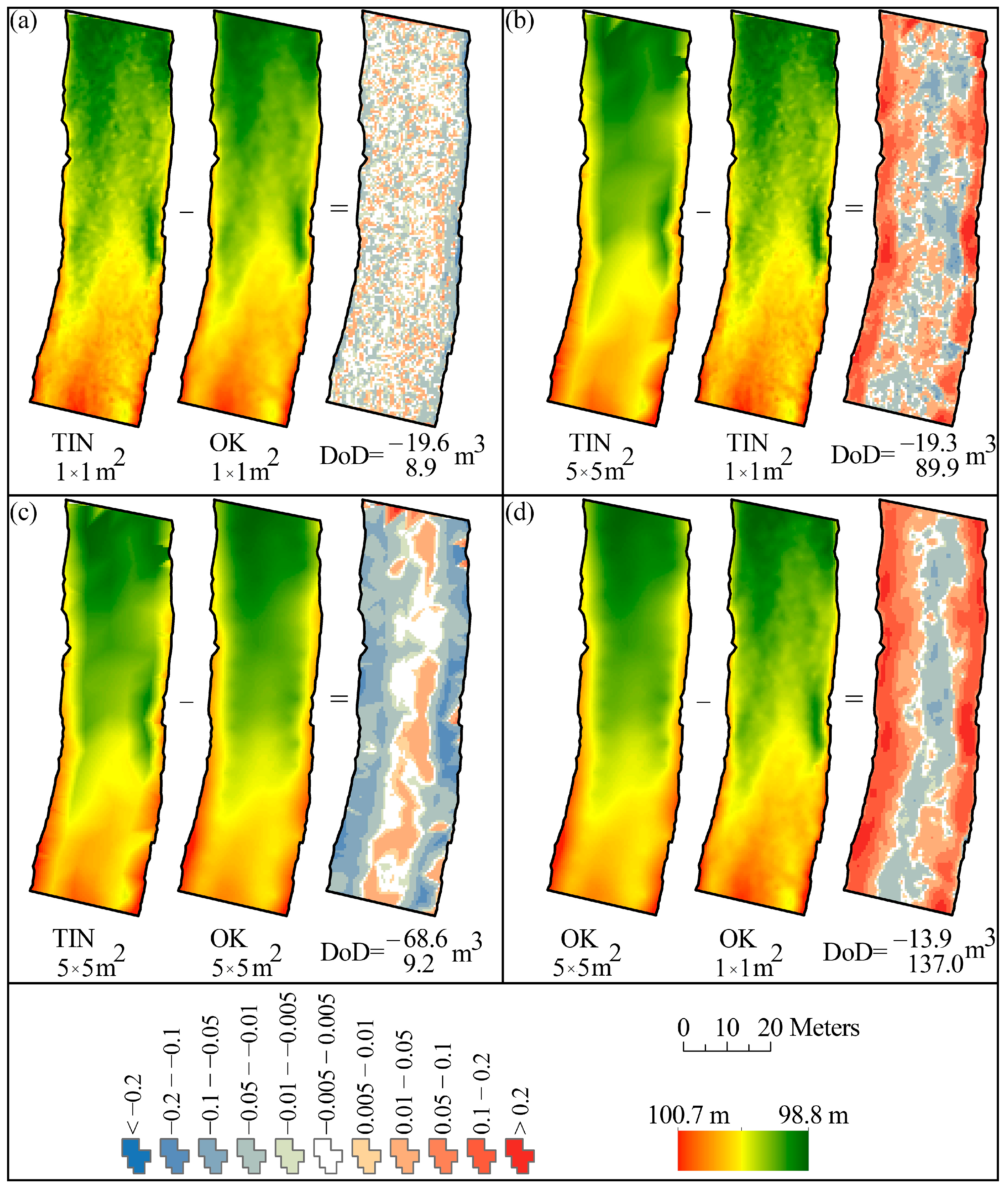
3.1. Different Interpolation Methods
3.2. Regular Grid Methods
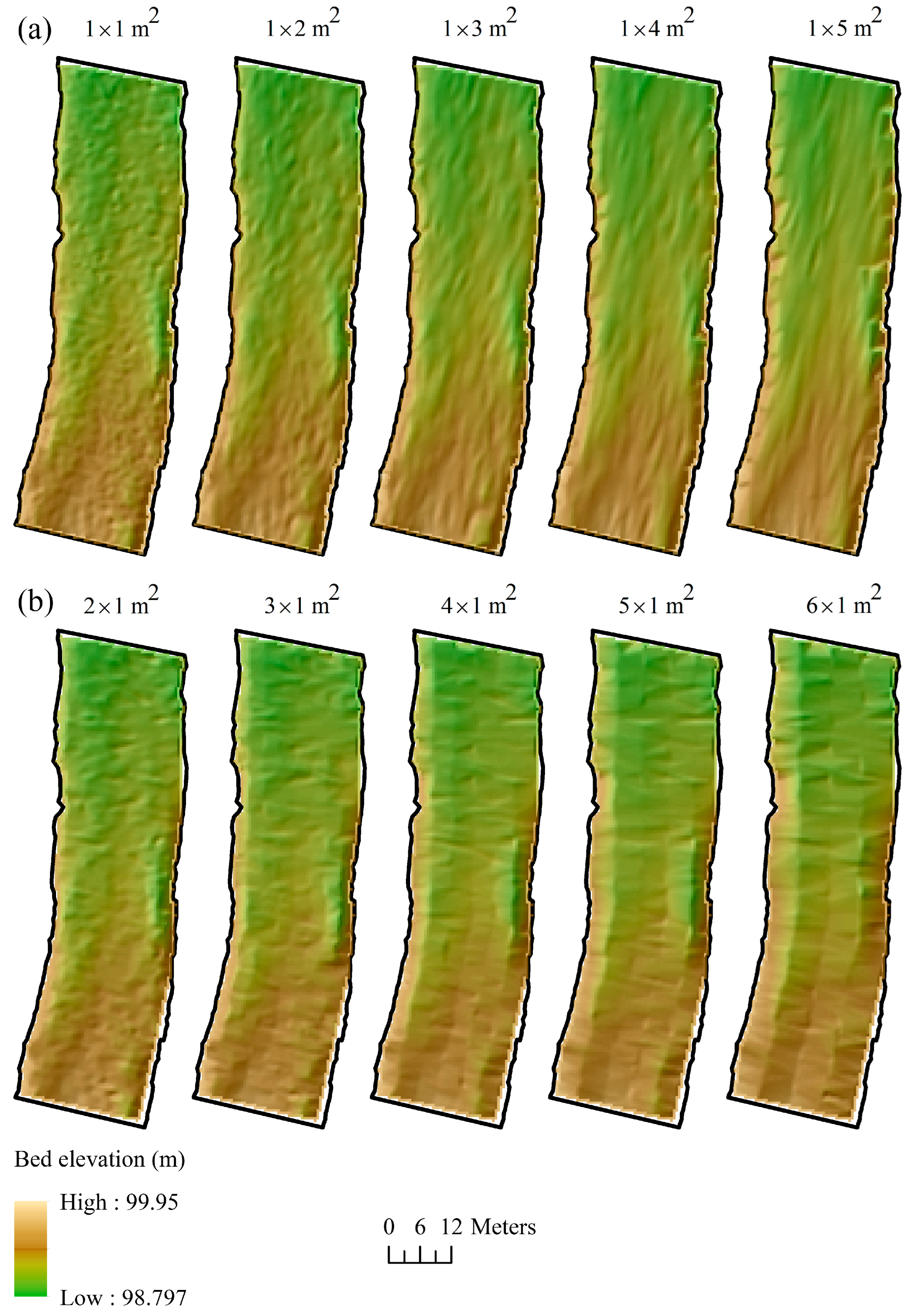
3.3. Cross and Longitudinal Section Methods
3.4. Zigzag Methods
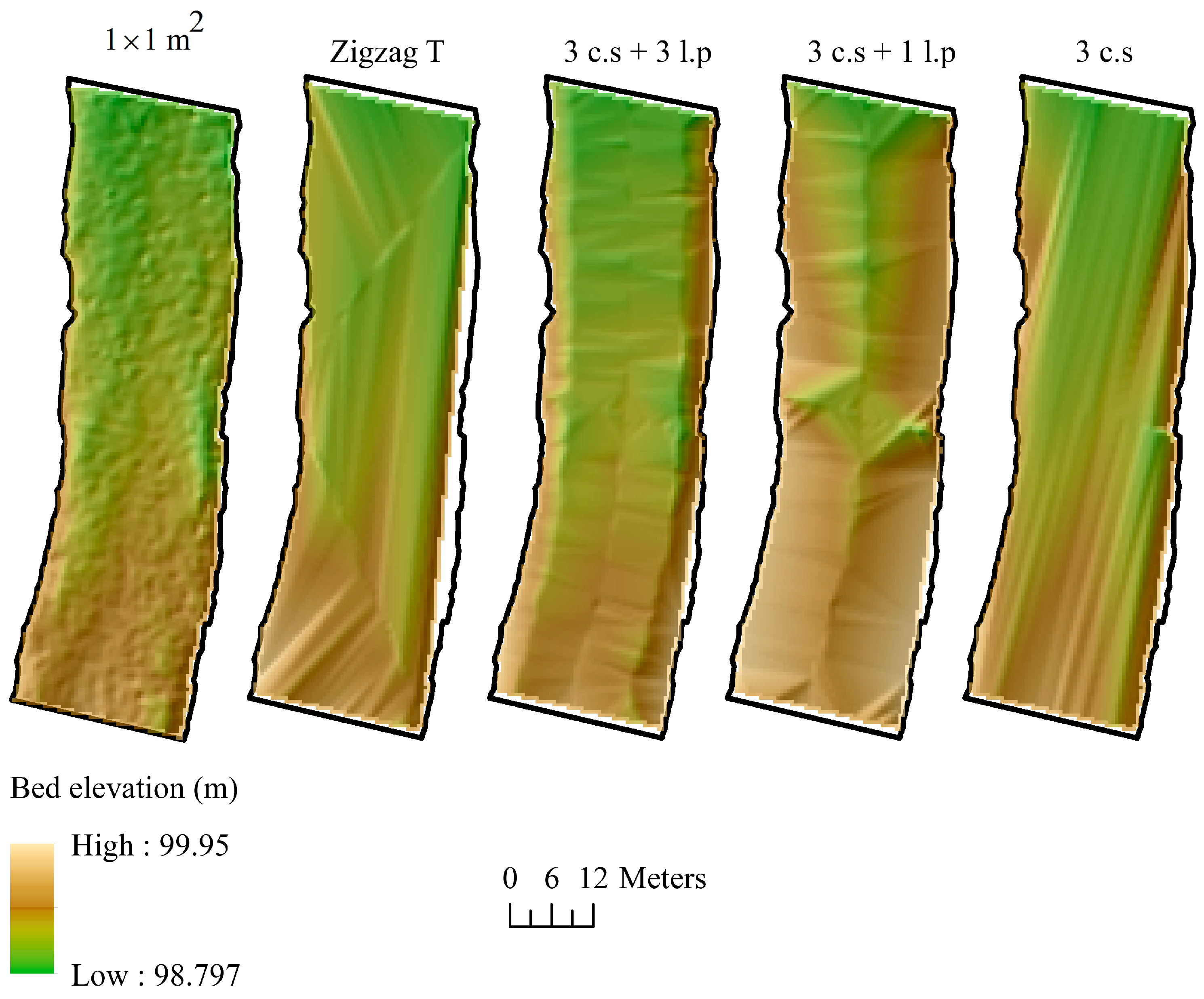
3.5. Large-Scale Methods
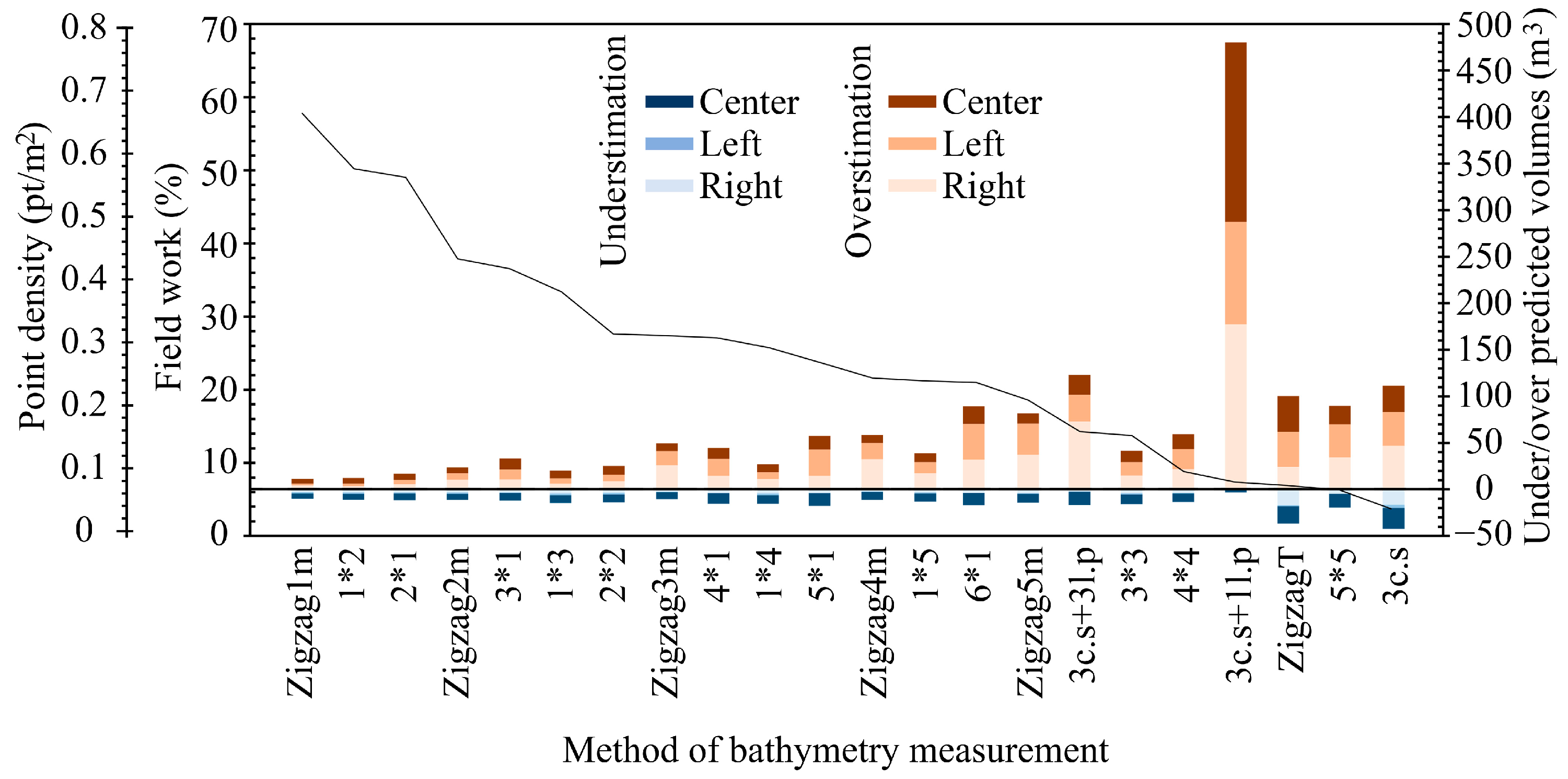
3.6. Measurement Errors and Durations of Each Method
4. Discussion
4.1. Interpolation Methods
4.2. Measurement Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schäppi, B.; Perona, P.; Schneider, P.; Burlando, P. Integrating river cross section measurements with digital terrain models for improved flow modelling applications. Comput. Geosci. 2010, 36, 707–716. [Google Scholar] [CrossRef]
- Jaballah, M.; Camenen, B.; Paquier, A.; Jodeau, M. An optimized use of limited ground based topographic data for river applications. Int. J. Sediment Res. 2019, 34, 216–225. [Google Scholar] [CrossRef]
- Milan, D.J.; Hetherington, D.; Heritage, G.L. Application of a 3D laser scanner in the assessment of a proglacial fluvial sediment budget. Earth Surf. Process. Landf. 2007, 32, 1657–1674. [Google Scholar] [CrossRef]
- Rumsby, B.T.; Brasington, J.; Langham, J.A.; McLelland, S.J.; Middeton, R.; Rollinson, G. Monitoring and modelling particle and reach-scale morphological change in gravel-bed rivers: Applications and challenges. Geomorphology 2008, 93, 40–54. [Google Scholar] [CrossRef]
- Wang, J.; Shi, B.; Yuan, Q.; Zhao, E.; Bai, T.; Yang, S. Hydro-geomorphological regime of the lower Yellow river and delta in response to the water-sediment regulation scheme: Process, mechanism and implication. Catena 2022, 219, 106646. [Google Scholar] [CrossRef]
- Kummu, M.; Varis, O. Sediment-related impacts due to upstream reservoir trapping, the Lower Mekong River. Geomorphology 2007, 85, 275–293. [Google Scholar] [CrossRef]
- Bengora, D.; Khiari, L.; Gallichand, J.; Dechemi, N.; Gumiere, S. Optimizing the dataset size of a topo-bathymetric survey for Hammam Debagh Dam, Algeria. Int. J. Sediment Res. 2018, 33, 518–524. [Google Scholar] [CrossRef]
- Nikora, V.; Roy, A.G. Secondary flows in rivers: Theoretical framework, recent advances, and current challenges. In Gravel-Bed Rivers: Processes, Tools, Environments; Wiley: Chichester, UK, 2012; pp. 3–22. [Google Scholar]
- Charles, J.A. The engineering behavior of fill materials and its influence on the performance of embankment dams. Dams Reserv. 2009, 19, 21–33. [Google Scholar] [CrossRef]
- Brasington, J.; Langham, J.; Rumsby, B. Methodological sensitivity of morphometric estimates of coarse fluvial sediment transport. Geomorphology 2003, 53, 299–316. [Google Scholar] [CrossRef]
- Legleiter, C.J. Remote measurement of river morphology via fusion of LiDAR topography and spectrally based bathymetry. Earth Surf. Process. Landf. 2012, 37, 499–518. [Google Scholar] [CrossRef]
- Woodget, A.S.; Carbonneau, P.E.; Visser, F.; Maddock, I.P. Quantifying submerged fluvial topography using hyper spatial resolution UAS imagery and structure from motion photogrammetry. Earth Surf. Process. Landf. 2015, 40, 47–64. [Google Scholar] [CrossRef]
- Heritage, G.L.; Milan, D.J.; Large, A.R.G.; Fuller, I.C. Influence of survey strategy and interpolation model on DEM quality. Geomorphology 2009, 112, 334–344. [Google Scholar] [CrossRef]
- Carley, J.; Pasternack, G.B.; Wyrick, J.R.; Barker, J.R.; Bratovich, P.M.; Massa, D.A.; Reedy, G.D.; Johnson, T.R. Significant decadal channel change 58-67 years post-dam accounting for uncertainty in topographic change detection between contour maps and point cloud models. Geomorphology 2012, 179, 71–88. [Google Scholar] [CrossRef]
- Fuller, I.C.; Large, A.R.G.; Milan, D.J. Quantifying development and sediment transfer following chute cutoff in a wandering gravel-bed river. Geomorphology 2003, 54, 307–323. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kyriakidis, P.C. Spatial prediction of river channel topography by kriging. Earth Surf. Process. Landf. 2008, 33, 841–867. [Google Scholar] [CrossRef]
- Wheaton, J.M.; Brasington, J.; Darby, S.E.; Sear, D.A. Accounting for uncertainty in DEMs from repeat topographic surveys: Improved sediment budgets. Earth Surf. Process. Landf. 2010, 35, 136–156. [Google Scholar] [CrossRef]
- Banjavcic, S.D.; Schmidt, A.R. Spatial uncertainty in depth averaged velocity determined from stationary, transect, and longitudinal ADCP measurements. J. Hydraul. Eng. 2018, 144, 04018070. [Google Scholar] [CrossRef]
- Martirosyan, A.V.; Ilyushin, Y.V.; Afanaseva, O.V. Development of a distributed mathematical model and control system for reducing pollution risk in mineral water aquifer systems. Water 2022, 14, 151. [Google Scholar] [CrossRef]
- Ilyushin, Y.V.; Asadulagi, M.-A.M. Development of a Distributed Control System for the Hydrodynamic Processes of Aquifers, Taking into Account Stochastic Disturbing Factors. Water 2023, 15, 770. [Google Scholar] [CrossRef]
- Rennie, C.D.; Church, M. Mapping spatial distribution and uncertainty of water and sediment flux in a large gravel bed river reach using an acoustic Doppler current profiler. J. Geophys. Res. 2010, 115, F03035. [Google Scholar] [CrossRef]
- Milan, D.J. Terrestrial laser-scan derived topographic and roughness data for hydraulic modelling of gravel-bed rivers. In Laser Scanning for the Environmental Sciences; Heritage, G.L., Large, A.R.G., Eds.; Wiley-Blackwell: Chichester, UK, 2009; pp. 133–146. [Google Scholar]
- Fuller, I.C.; Large, A.R.G.; Heritage, G.L.; Milan, D.J.; Charlton, M.E. Derivation of reach-scale sediment transfers in the River Coquet, Northumberland, UK. In Fluvial Sedimentology VII, IAS Special Publication; Blum, M., Marriott, S., Leclair, S., Eds.; Wiley-Blackwell: Chichester, UK, 2005; Volume 35, pp. 61–74. [Google Scholar]
- Maleika, W.; Palczynski, M.; Frejlichowski, D. Interpolation methods and the accuracy of bathymetric seabed models based on multibeam echosounder data. In Intelligent Information and Database Systems; Pan, J.S., Chen, S.M., Nguyen, N.T., Eds.; ACIIDS 2012, Lecture Notes in Computer Science 7198; Springer: Berlin/Heidelberg, Germany, 2012; pp. 466–475. [Google Scholar]
- Hera, Á.; López-Pamo, E.; Santofimia, E.; Gallego, G.; Morales, R.; Durán–Valsero, J.J.; Murillo-Díaz, J.M. A case study of geometric modelling via 3-d point interpolation for the bathymetry of the Rabasa lakes (Alicante, Spain). In Mathematics of Planet Earth; Pardo-Igúzquiza, E., Guardïola-Albert, C., Heredia, J., Moreno-Merino, L., Duran, J., Vargas-Guzman, J., Eds.; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 503–506. [Google Scholar]
- Bechler, A.; Romary, T.; Jeannée, N.; Desnoyers, Y. Geostatistical sampling optimization of contaminated facilities. Stoch. Environ. Res. Risk Assess. J. 2013, 27, 1967–1974. [Google Scholar] [CrossRef]
- Wang, J.; Yang, R.; Bai, Z. Spatial variability and sampling optimization of soil organic carbon and total nitrogen for minesoils of the Loess Plateau using geostatistics. Ecol. Eng. 2015, 82, 159–164. [Google Scholar] [CrossRef]
- Erdogan, S.A. comparison of interpolation methods for producing digital elevation models at the field scale. Earth Surf. Process. Landf. 2009, 34, 366–376. [Google Scholar] [CrossRef]
- Lane, S.N. The use of digital terrain modelling in the understanding of dynamic river systems. In Landform Monitoring, Modelling and Analysis; Lane, S.N., Richards, K.S., Chandler, J.H., Eds.; John Wiley and Son Ltd.: Chichester, UK, 1998; pp. 311–342. [Google Scholar]
- Gaeuman, D.; Jacobson, R.B. Aquatic Habitat Mapping with an Acoustic Doppler Current Profiler: Considerations for Data Quality; U.S. Geological Survey Open File Report; USGS: Reston, VA, USA, 2005; p. 1163. [Google Scholar]
- Dinehart, R.L.; Burau, J.R. Averaged indicators of secondary flow in repeated acoustic Doppler current profiler crossings of bends. Water Resour. Res. 2005, 41, W09405. [Google Scholar] [CrossRef]
- Parsons, D.R.; Best, J.L.; Lane, S.N.; Orfeo, O.; Hardy, R.J.; Kostaschuk, R. Form roughness and the absence of secondary flow in a large confluence-diffluence, Rio Parana, Argentina. Earth Surf. Process. Landf. 2007, 32, 155–162. [Google Scholar] [CrossRef]
- Jackson, P.R. Mississippi River ADCP Data; USGS: Reston, VA, USA, 2017. [Google Scholar]
- Williams, R.D.; Brasington, J.; Hicks, M.; Measures, R.; Rennie, C.D.; Vericat, D. Hydraulic validation of two-dimensional simulations of braided river flow with spatially continuous ADCP data. Water Resour. Res. 2013, 49, 5183–5205. [Google Scholar] [CrossRef]
- Flener, C.; Wang, Y.; Laamanen, L.; Kasvi, E.; Vesakoski, J.M.; Alho, P. Empirical modeling of spatial 3D flow characteristics using a remote-controlled ADCP system: Monitoring a spring flood. Water 2015, 7, 217–247. [Google Scholar] [CrossRef]
- Krüger, R.; Karrasch, P.; Bernard, L. Evaluating Spatial Data Acquisition and Interpolation Strategies for River Bathymetries. In Geospatial Technologies for All; Mansourian, A., Pilesjö, P., Harrie, L., van Lammeren, R., Eds.; AGILE 2018, Lecture Notes in Geoinformation and Cartography; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Aggett, G.R.; Wilson, J.P. Creating and coupling a high-resolution DTM with a 1-D hydraulic model in a GIS for scenario-based assessment of avulsion hazard in a gravel bed river. Geomorphology 2009, 113, 21–34. [Google Scholar] [CrossRef]
- Andes, L.C.; Cox, A.L. Rectilinear inverse distance weighting methodology for bathymetric cross-section interpolation along the Mississippi River. J. Hydrol. Eng. 2017, 22, 04017014. [Google Scholar] [CrossRef]
- Jamieson, E.C.; Rennie, C.D.; Jacobson, R.B.; Townsend, R.D. 3-D flow and scour near a submerged wing dike: ADCP measurements on the Missouri River. Water Resour. Res. 2011, 47, W07544. [Google Scholar] [CrossRef]
- Puente, C.E.; Bras, R.L. Disjunctive kriging, universal kriging, or no kriging: Small sample results with simulated fields. Math. Geol. 1986, 18, 287–305. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Fuller, I.C.; Hutchinson, E. Sediment flux in a small gravel-bed stream: Response to channel remediation works. N. Z. Geogr. 2007, 63, 169–180. [Google Scholar] [CrossRef]
- Chaplot, V.; Darboux, F.; Bourennane, H.; Leguedois, S.; Silvera, N.; Phachomphon, K. Accuracy of interpolation techniques for the derivation of digital elevation models in relation to landform types and data density. Geomorphology 2006, 77, 126–141. [Google Scholar] [CrossRef]
- Yue, T.; Du, Z.; Song, D.; Gong, Y. A new method of surface modelling and its application to DEM construction. Geomorphology 2007, 91, 161–172. [Google Scholar] [CrossRef]
- Glenn, J.; Tonina, D.; Morehead, M.; Fiedler, F.; Benjankar, R. Effect of transect location, transect spacing and interpolation methods on river bathymetry accuracy. Earth Surf. Process. Landf. 2016, 41, 1185–1198. [Google Scholar] [CrossRef]










| L 1 (m) | W 2 (m) | h 3 (m) | U 4 (m/s) | Q 5 (m3/s) | d50 6 (mm) |
|---|---|---|---|---|---|
| 90 | 24 | 0.3 | 0.8 | 5 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maddahi, M.; Rahimpour, M. Effects of Spatial Data Acquisition on Determination of a Gravel-Bed River Geomorphology. Water 2023, 15, 1719. https://doi.org/10.3390/w15091719
Maddahi M, Rahimpour M. Effects of Spatial Data Acquisition on Determination of a Gravel-Bed River Geomorphology. Water. 2023; 15(9):1719. https://doi.org/10.3390/w15091719
Chicago/Turabian StyleMaddahi, Mohammadreza, and Majid Rahimpour. 2023. "Effects of Spatial Data Acquisition on Determination of a Gravel-Bed River Geomorphology" Water 15, no. 9: 1719. https://doi.org/10.3390/w15091719







