Numerical Investigation of the Stress on a Cylinder Exerted by a Stratified Current Flowing on Uneven Ground
Abstract
:1. Introduction
2. Numerical Models
2.1. Governing Equations
2.2. Scalar Transport Equation
2.3. Turbulence Model
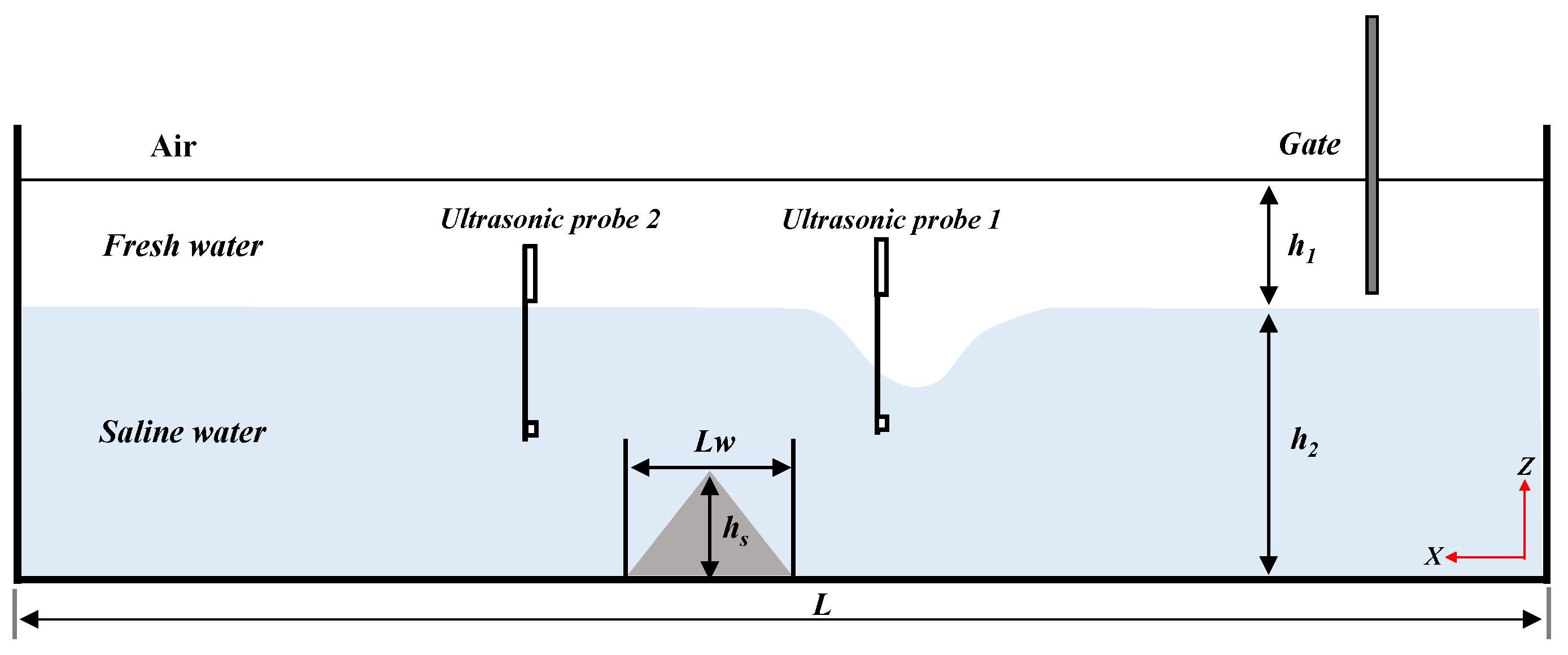
2.4. Establishment of a Numerical Tank
2.5. Numerical Model Verification
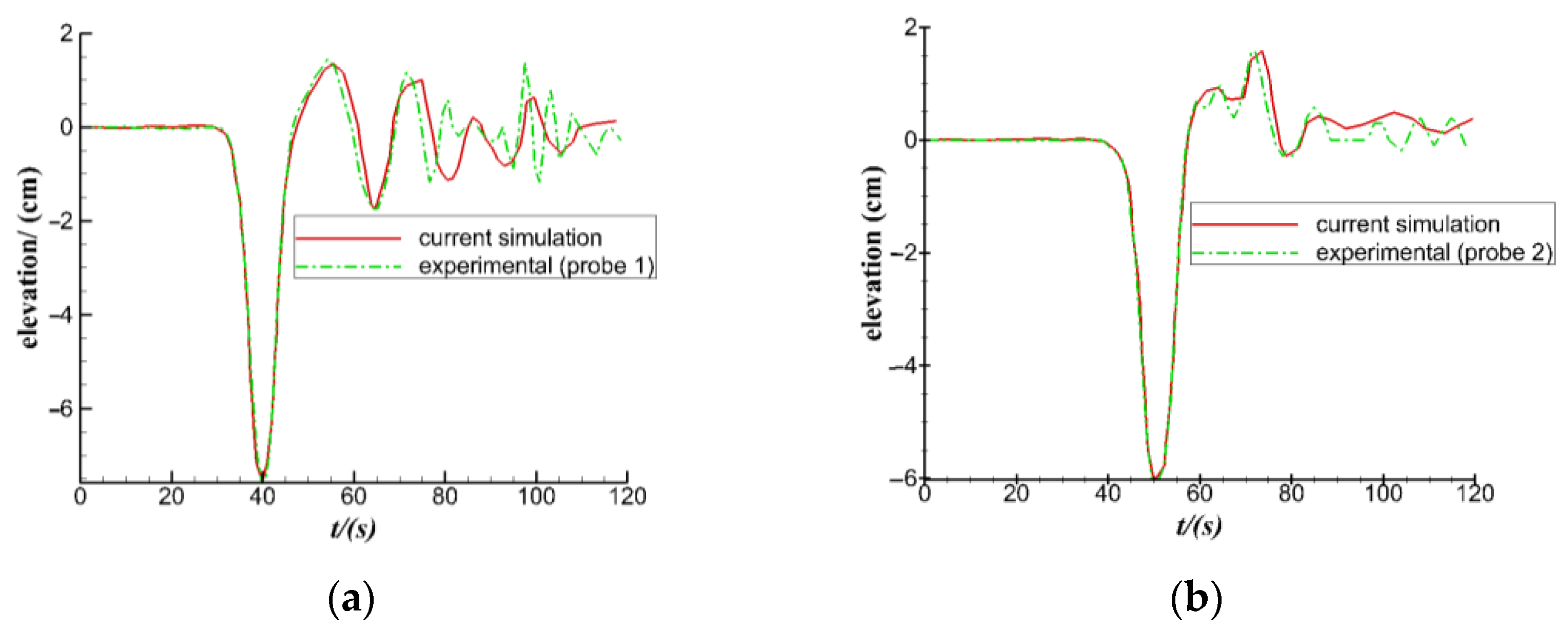
2.5.1. Verification by Physical Model Test
2.5.2. Grid Independence Test
3. Result and Analysis
3.1. Coupled Influence of Terrain and IWs on the Forces on the Cylinder
3.2. Comparison of the Vertical Distribution of the Force on the Cylinder in Different Cases
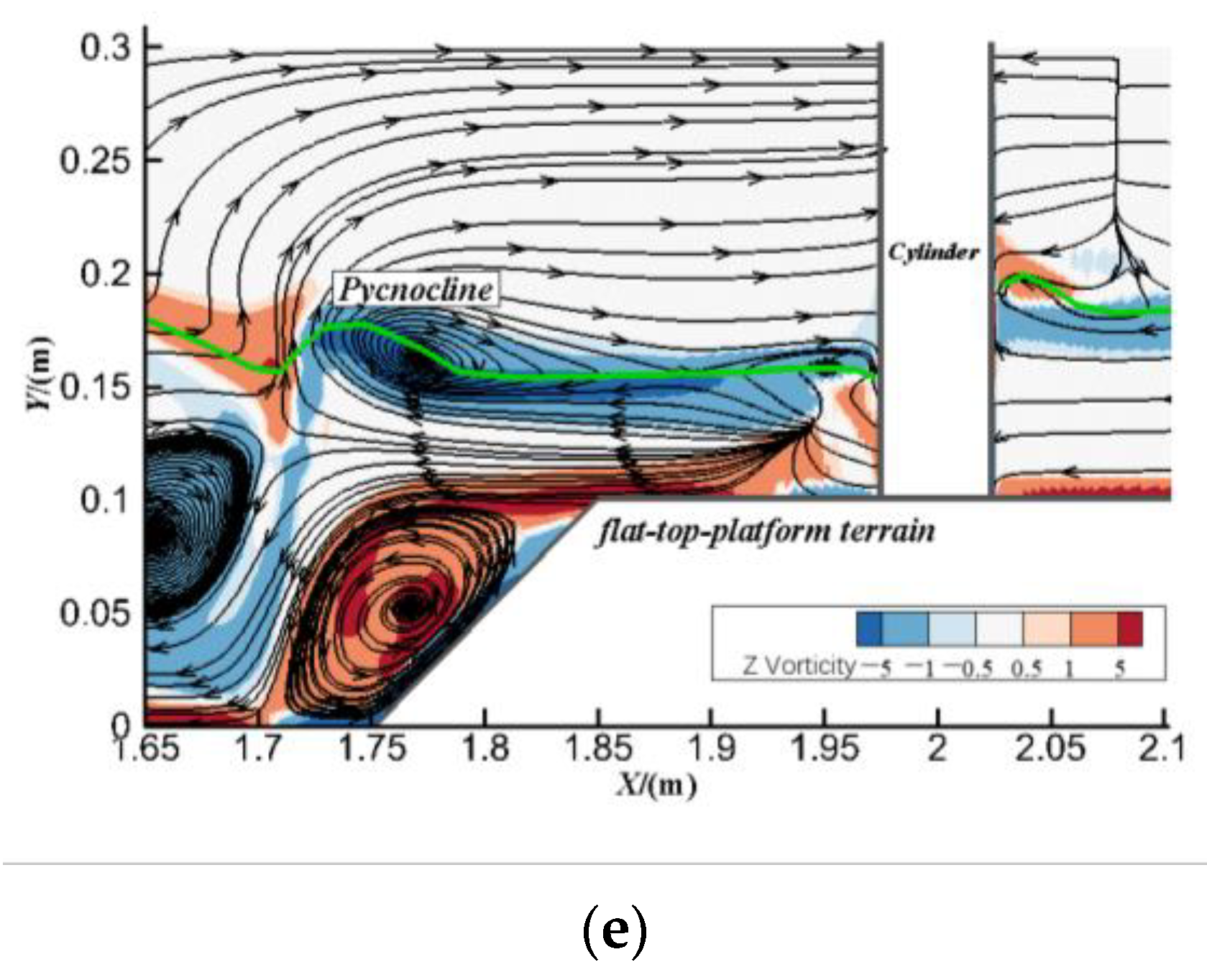
3.3. Variation in the Flow Field around the Cylinder under Different Cases
3.4. Influence of the Amplitudes on the IWs Forces and the Flow Field over the Terrain
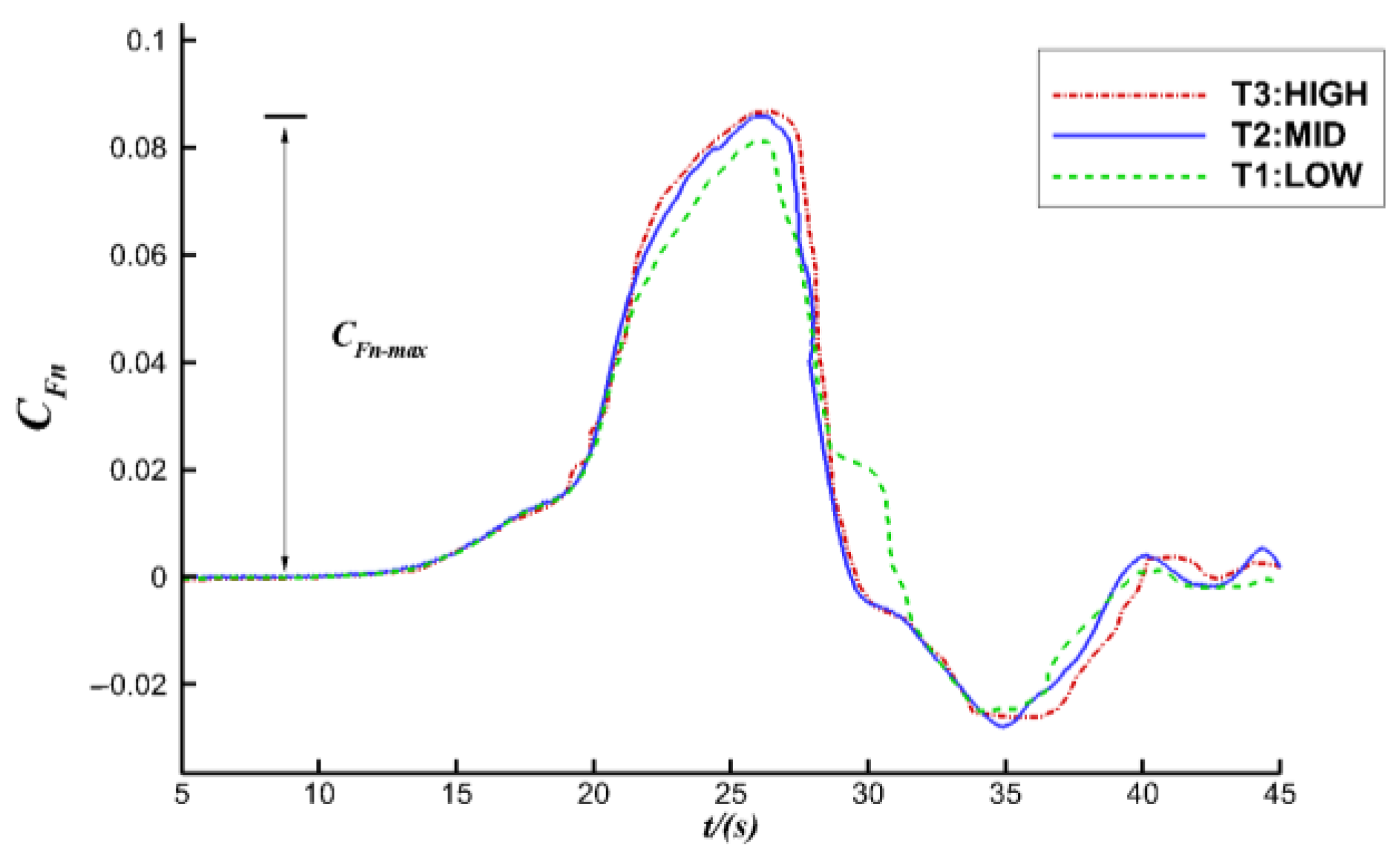
3.4.1. Influence on the IWs Forces
3.4.2. Influence on the Flow Field
4. Conclusions
- (1)
- The topographic factors of the terrain significantly affect the IW forces on the cylinder. There is a strong distinction between the SC case and the three terrain cases: in the SC case, the maximum resultant forces on the cylinder are positive, and the maximum resultant forces are negative in the terrain cases.
- (2)
- Compared with the SC case, the shallow-water effect caused by the IW-terrain coupled environment enhances the strength of the flow field around the cylinder, so that the lower parts of the cylinder are subjected to larger forces in the reverse wave direction.
- (3)
- Compared with the SC case, when the IWs propagate over the terrain, the interactions between the IWs and the terrain make the flow field around the cylinder more complex and changeable. As a result, the complex hydrodynamic environment compels the cylinder to experience larger forces.
- (4)
- A percentage parameter RFn-max is applied in this research to specify the differences of CFn-max between the SC case and the terrain case. RFn-max decreases as the IW amplitude increases when the amplitude is relatively small, but it sharply increases when amplitude is large enough. It is can be explained by the shallow-water effect. When IWs with large amplitude propagate to the bottom terrain, the interaction between the IW and the terrain is intensified and the shallow-water effect occurs, which strengthens the flow field strength near the terrain in the lower layer.
- (5)
- With the increase of IW amplitude, the interaction between the IW and the terrain is enhanced. Vortices can be found on the bank slope in all the cases, but the size of the vortices is obviously different when amplitude changes. The vortex size increases with the amplitude, and more than one vortex appears when the amplitude is large enough.
- (6)
- With the increase of the IW amplitude, the IW pattern is more strongly disturbed by the terrain. IW propagating over the bank slope is partially reflected, causing a “blockage” near the terrain and a “elevation” in the reverse wave propagation direction. Therefore, the intensification of the interaction strength between the IWs and the terrain could not only cause greater horizontal forces on the lower parts of the cylinder, but also make the flow field around the terrain more complex.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mei, Y.; Wang, J.; Huang, S.; Mu, H.; Chen, X. Experimental investigation on the optical remote sensing images of internal solitary waves with a smooth surface. Acta Oceanol. Sin. 2019, 38, 124–131. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.-F.; Wang, Z.; You, Y.-X. A numerical and experimental study of internal solitary wave loads on semi-submersible platforms. Ocean Eng. 2018, 150, 298–308. [Google Scholar] [CrossRef]
- Xu, W.; Lin, Z.Y.; You, Y.X.; Yu, R. Numerical Simulations for the Load Characteristics of Internal Solitary Waves on a Vertical Cylinder. J. Ship 2017, 21, 1071–1085. [Google Scholar]
- Colosi, J.A.; Kumar, N.; Suanda, S.H.; Freismuth, T.M.; MacMahan, J.H. Statistics of Internal Tide Bores and Internal Solitary Waves Observed on the Inner Continental Shelf off Point Sal, California. J. Phys. Oceanogr. 2018, 48, 123–143. [Google Scholar] [CrossRef]
- Moum, J.N.; Farmer, D.M.; Smyth, W.D.; Armi, L.; Vagle, S. Structure and Generation of Turbulence at Interfaces Strained by Internal Solitary Waves Propagating Shoreward over the Continental Shelf. J. Phys. Oceanogr. 2003, 33, 2093–2112. [Google Scholar] [CrossRef]
- Timothy, W. Internal Solitons on the Pycnocline: Generation, Propagation, and Shoaling and Breaking over a Slope. J. Fluid Mech. 1985, 159, 19–53. [Google Scholar]
- Chen, M.; Chen, K.; You, Y.X. Experimental investigation of internal solitary wave forces on a semi-submersible. Ocean Eng. 2017, 141, 205–214. [Google Scholar] [CrossRef]
- Jia, T.; Liang, J.J.; Li, X.-M.; Sha, J. SAR Observation and Numerical Simulation of Internal Solitary Wave Refraction and Reconnection Behind the Dongsha Atoll. J. Geophys. Res. Oceans 2018, 123, 74–89. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, Q.; Xiong, X.; Yuan, Y.; Xie, H.; Guo, Y.; Yu, L.; Yun, S. Dynamic and Statistical Features of Internal Solitary Waves on the Continental Slope in the Northern South China Sea Derived From Mooring Observations. J. Geophys. Res. Oceans 2019, 124, 4078–4097. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Michallet, H.; Barthelemy, E. Experimental study of large interfacial solitary waves. Fluid Mech. 1998, 366, 159–177. [Google Scholar] [CrossRef]
- Camassa, R.; Choi, W.; Michallet, H.; Rusås, P.-O.; Sveen, J.K. On the realm of validity of strongly nonlinear asymptotic approximations for internal waves. J. Fluid Mech. 2006, 549, 1–23. [Google Scholar] [CrossRef]
- Li, X.; Ren, B.; Wang, G.Y.; Wang, Y.X. Numerical simulation of hydrodynamic characteristics on an arx crown wall using volumn of fluid method based on BFC. J. Hydrodyn. 2001, 23, 767–776. [Google Scholar] [CrossRef]
- Chen, Y.X. Flow simulation of car air conditioner duct based on simple algorithm. Mech. Eng. 2008, 11, 111–112. [Google Scholar]
- Cao, Y.; Ye, Y.T.; Liang, L.L.; Zhao, H.; Jiang, Y.; Wang, H.; Wang, J. Uncertainty analysis of two-dimensional hydrodynamic model parameters and boundary conditions. J. Hydroelectr. Eng. 2018, 37, 47–61. (In Chinese) [Google Scholar]
- Forgia, G.L.; Sciortino, G. Free-surface effects induced by internal solitons forced by shearing currents. Phys. Fluids 2021, 33, 072102. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, L.L.; Avital, E.J.; Tang, H.W.; Williams, J.J.R. Numerical Simulation of Shoaling Broad-Crested Internal Solitary Waves. J. Hydraul. Eng. 2017, 143, 04017006. [Google Scholar] [CrossRef]
- Chen, C.-Y. Amplitude decay and energy dissipation due to the interaction of internal solitary waves with a triangular obstacle in a two-layer fluid system: The blockage parameter. J. Mar. Sci. Technol. 2009, 14, 499–512. [Google Scholar] [CrossRef]
- Chen, C.Y.; Hsu, J.R.C.; Chen, C.W.; Chen, H.H.; Kuo, C.F. Generation of internal solitary wave by gravity collapse. J. Mar. Sci. Technol. 2007, 15, 1–7. [Google Scholar] [CrossRef]
- Talipova, T.; Terletska, K.; Maderich, V.; Brovchenko, I.; Jung, K.T.; Pelinovsky, E.; Grimshaw, R. Internal solitary wave transformation over a bottom step: Loss of energy. Phys. Fluids 2013, 25, 032110. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Hsu, J.R.C.; Chen, M.H. An investigation on internal solitary waves in a two-layer fluid:Propagation and reflection from steep slopes. Ocean. Eng. 2007, 34, 171–184. [Google Scholar] [CrossRef]
- Cheng, M.-H.; Hsu, J.R.-C.; Chen, C.-Y. Laboratory experiments on waveform inversion of an internal solitary wave over a slope-shelf. Environ. Fluid Mech. 2011, 11, 353–384. [Google Scholar] [CrossRef]
- Shroyer, E.L.; Moum, J.N.; Nash, J. Observations of Polarity Reversal in Shoaling Nonlinear Internal Waves. J. Phys. Oceanogr. 2009, 39, 691–701. [Google Scholar] [CrossRef]
- Sutherland, B.R.; Barrett, K.J.; Ivey, G.N. Shoaling internal solitary waves. J. Geophys. Res. Ocean. 2013, 118, 4111–4124. [Google Scholar] [CrossRef]
- Wei, G.; Du, H.; Xu, X.; Zhang, Y.; Qu, Z.; Hu, T.; You, Y. Experimental investigation of the generation of large-amplitude internal solitary wave and its interaction with a submerged slender body. Sci. China Phys. Mech. Astron. 2014, 57, 301–310. [Google Scholar] [CrossRef]
- Zou, P.; Bricker, J.D.; Uijttewaal, W. The impacts of internal solitary waves on a submerged floating tunnel. Ocean Eng. 2021, 238, 109762. [Google Scholar] [CrossRef]

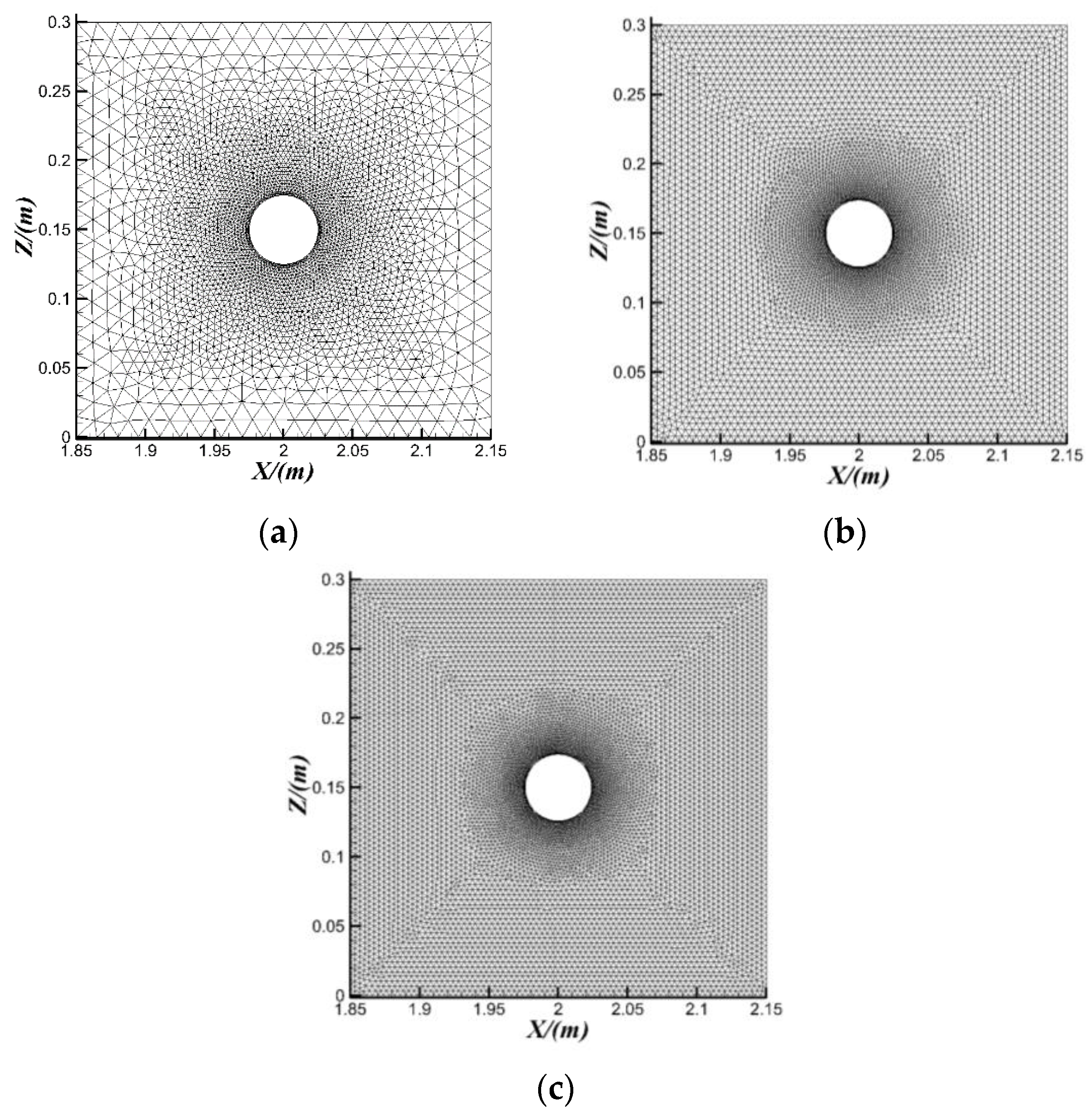
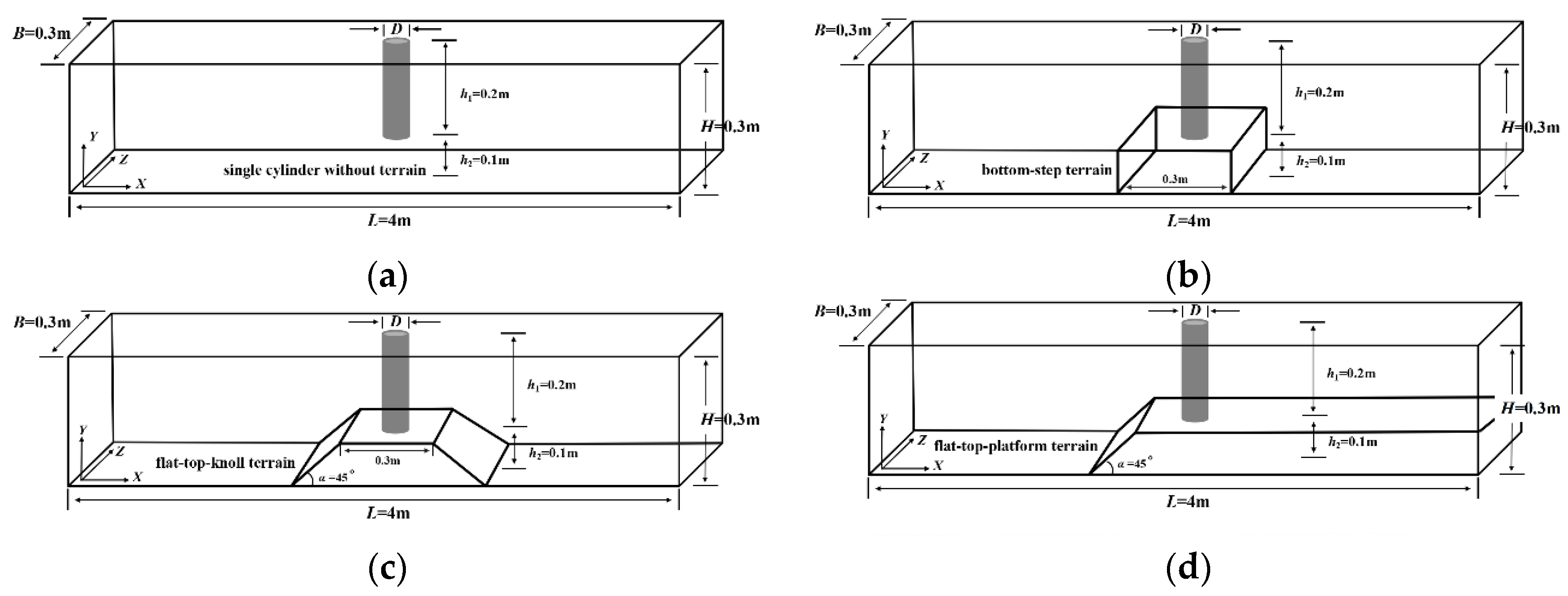

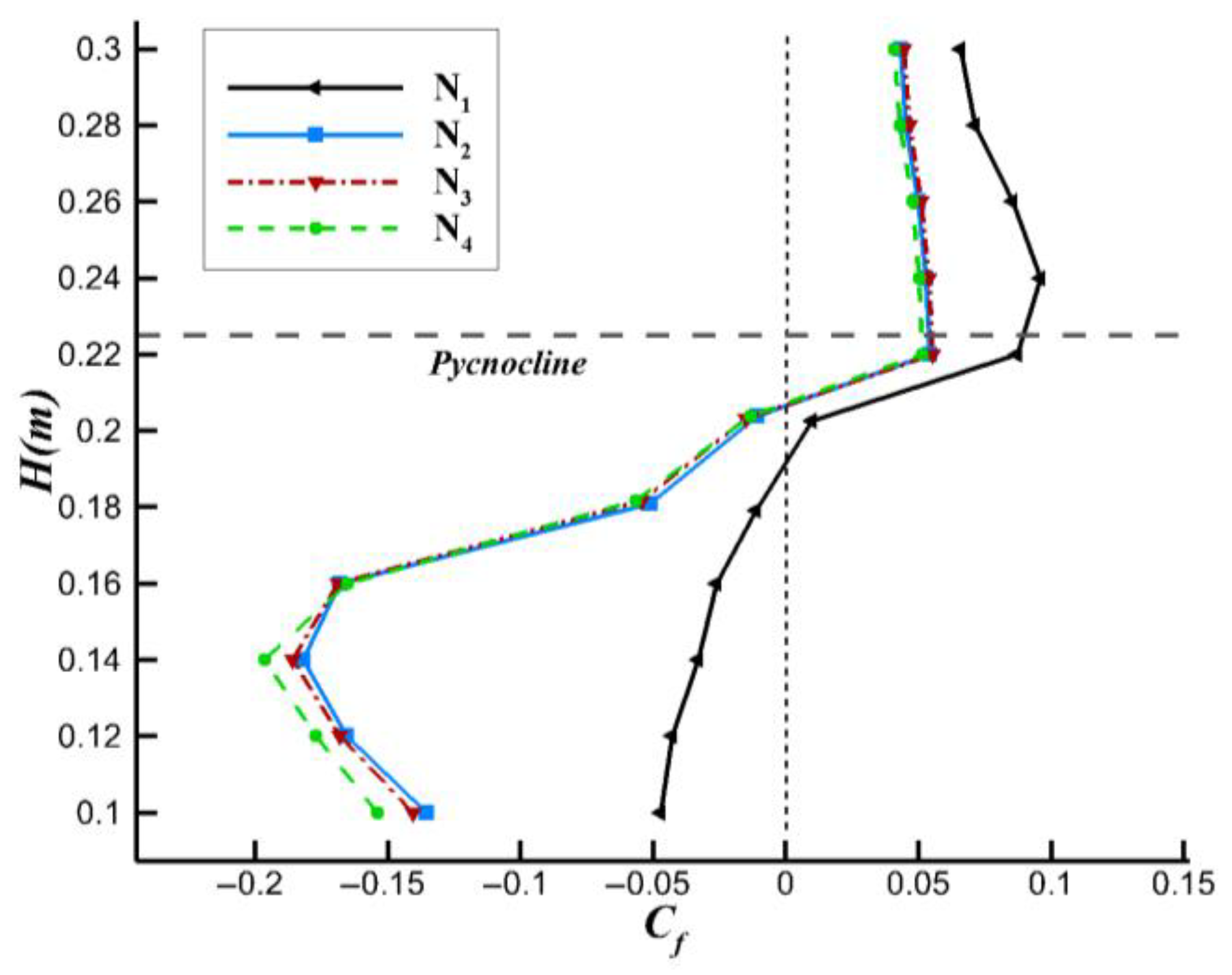
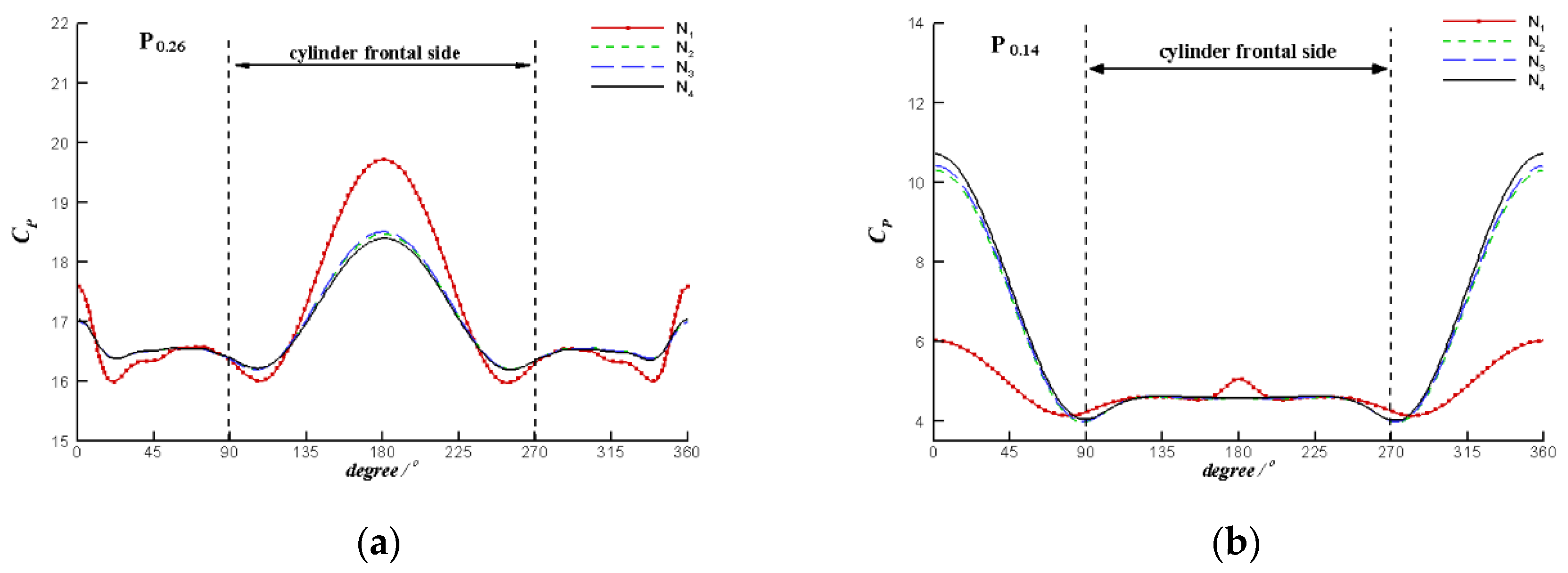
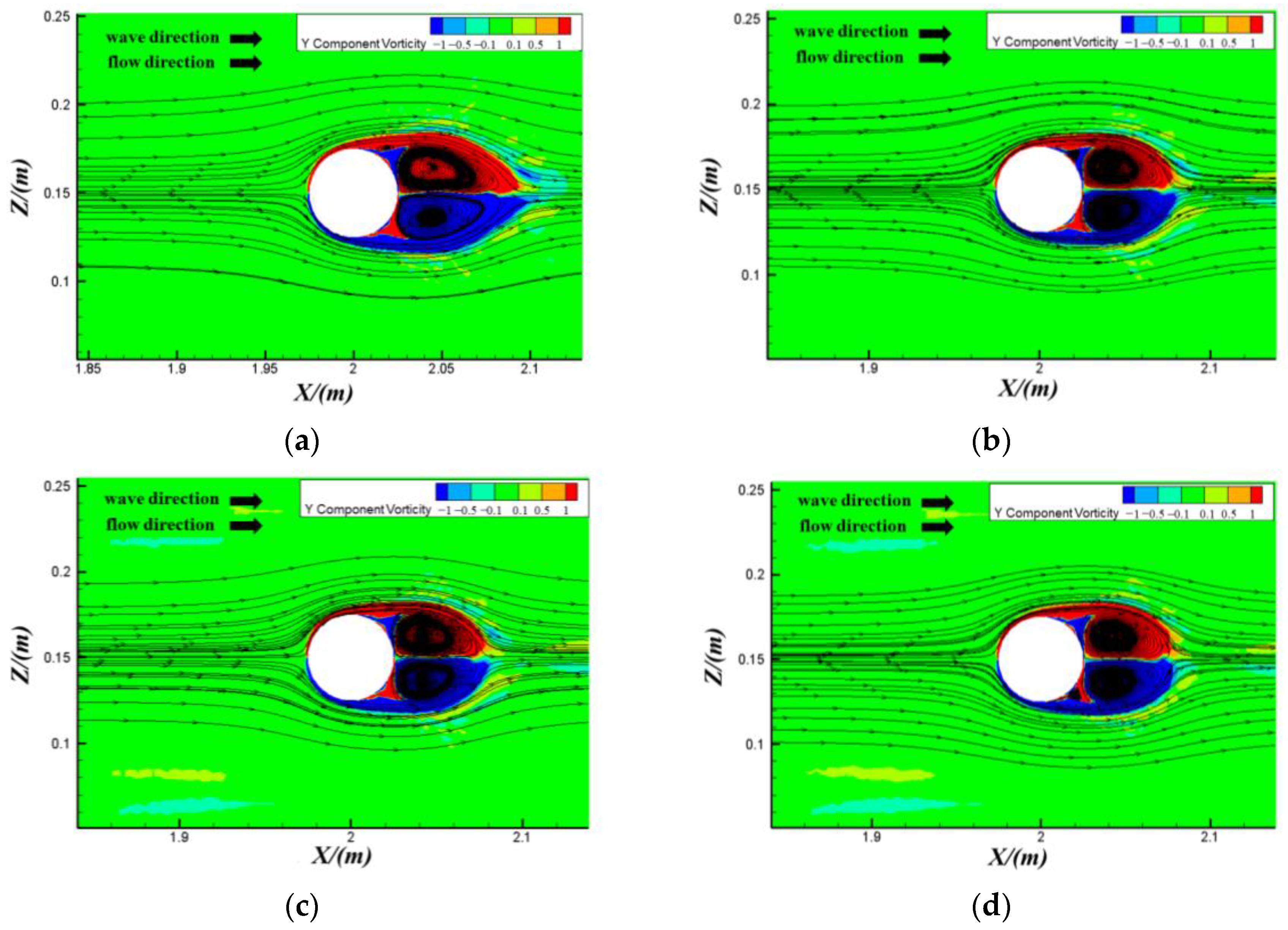
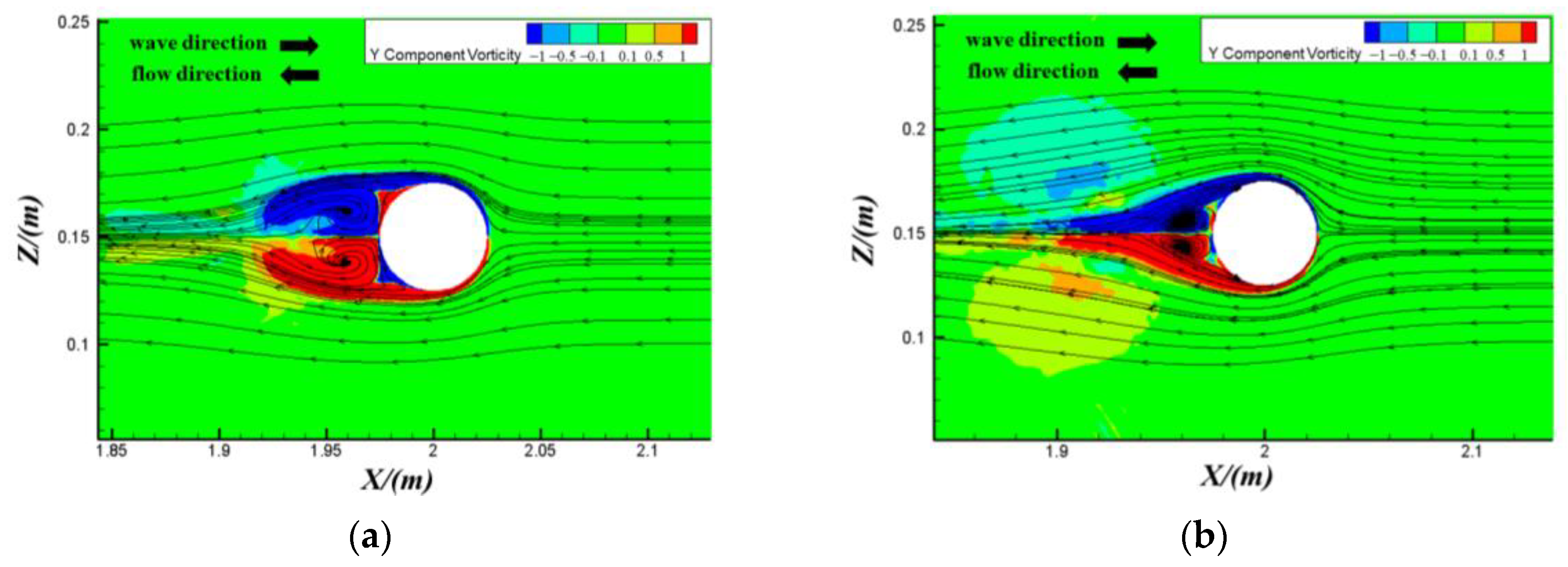
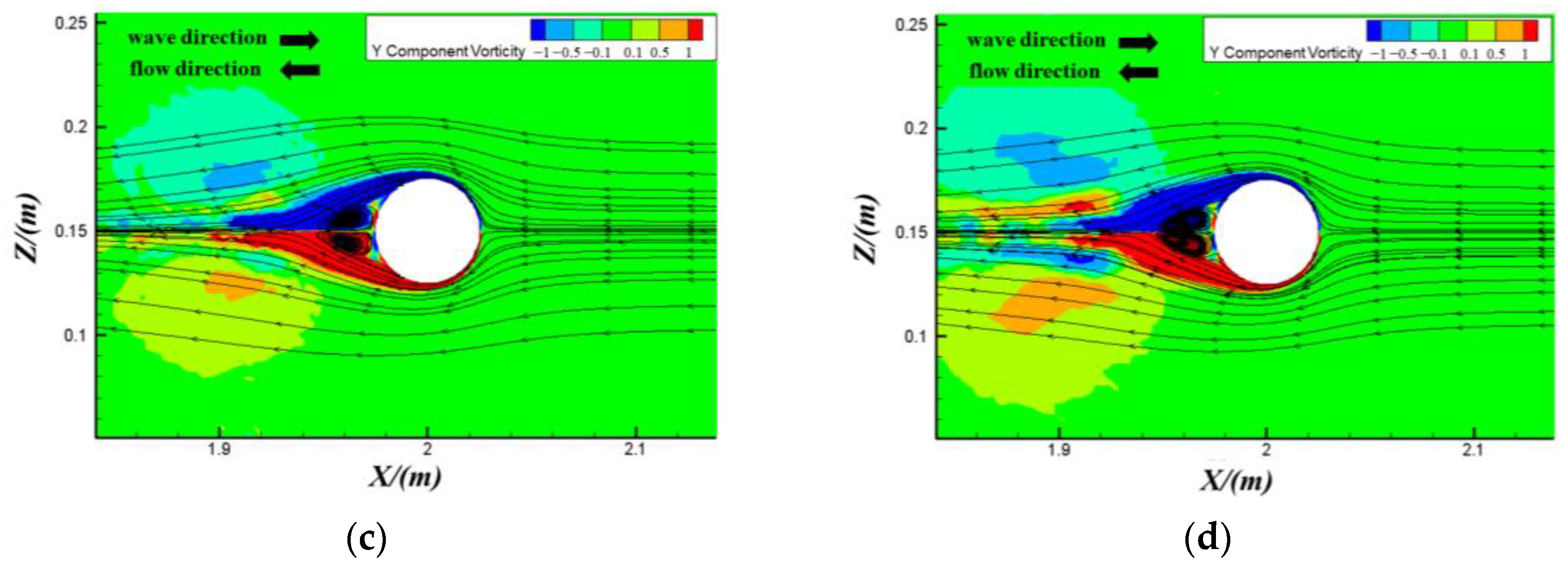

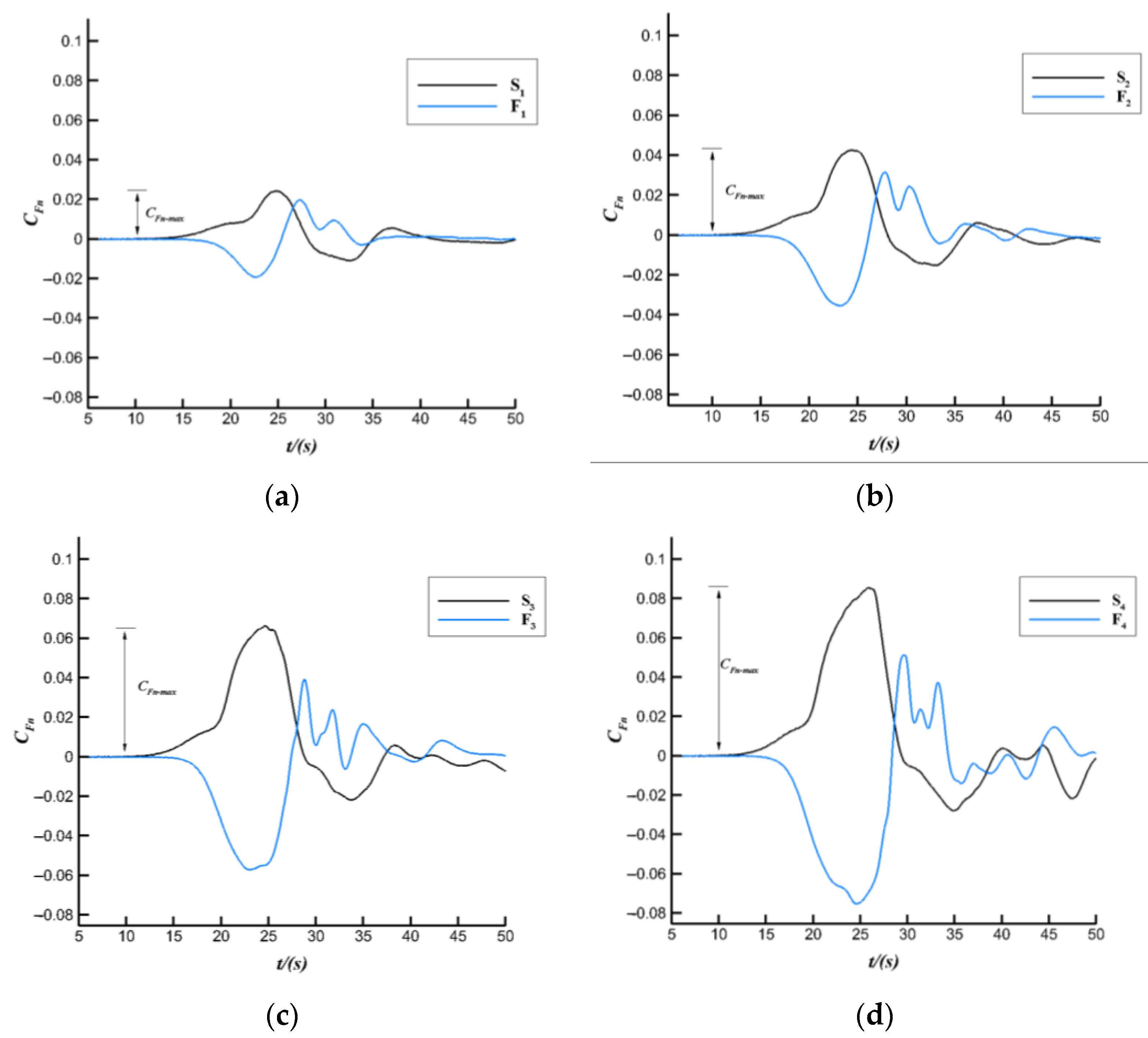



| No. | Case | ∆t (s) | CFn-max | Elements Number |
|---|---|---|---|---|
| 1 | T1 (low density) | 0.02 | 0.0810 | 525,454 |
| 2 | T2 (moderate density) | 0.01 | 0.0857 | 2,384,640 |
| 3 | T3 (high density) | 0.006 | 0.0862 | 3,318,278 |
| No. | Case | h1/h2 | η0/H | CFn-max |
|---|---|---|---|---|
| 1 | Single cylinder (N1) | 0.33 | 0.0575 | 0.0857 |
| 2 | Bottom-step terrain (N2) | 0.33 | 0.0575 | −0.0683 |
| 3 | Flat-top-knoll terrain (N3) | 0.33 | 0.0575 | −0.0692 |
| 4 | Flat-top-knoll terrain (N4) | 0.33 | 0.0575 | −0.0753 |
| No. | Case | h1/h2 | η0/H | CFn-max | RFn-max |
|---|---|---|---|---|---|
| 1 | S1 | 0.33 | 0.0275 | 0.0245 | 17.6% |
| 2 | F1 | 0.33 | 0.0275 | 0.0202 | |
| 3 | S2 | 0.33 | 0.0384 | 0.0428 | 17.5% |
| 4 | F2 | 0.33 | 0.0384 | −0.0353 | |
| 5 | S3 | 0.33 | 0.0494 | 0.0664 | 13.9% |
| 6 | F3 | 0.33 | 0.0494 | −0.0572 | |
| 7 | S4 | 0.33 | 0.0575 | 0.0857 | 12.1% |
| 8 | F4 | 0.33 | 0.0575 | −0.0753 | |
| 9 | S5 | 0.33 | 0.0674 | 0.132 | 34.5% |
| 10 | F5 | 0.33 | 0.0674 | −0.0864 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, M.; Wang, L.; Shi, S.; Zhang, C.; Wu, X.; Wang, H.; Xiong, X.; Wang, C. Numerical Investigation of the Stress on a Cylinder Exerted by a Stratified Current Flowing on Uneven Ground. Water 2023, 15, 1598. https://doi.org/10.3390/w15081598
Wang Y, Xu M, Wang L, Shi S, Zhang C, Wu X, Wang H, Xiong X, Wang C. Numerical Investigation of the Stress on a Cylinder Exerted by a Stratified Current Flowing on Uneven Ground. Water. 2023; 15(8):1598. https://doi.org/10.3390/w15081598
Chicago/Turabian StyleWang, Yin, Ming Xu, Lingling Wang, Sha Shi, Chenhui Zhang, Xiaobin Wu, Hua Wang, Xiahui Xiong, and Chunling Wang. 2023. "Numerical Investigation of the Stress on a Cylinder Exerted by a Stratified Current Flowing on Uneven Ground" Water 15, no. 8: 1598. https://doi.org/10.3390/w15081598





