Trend Analysis of Streamflows in Relation to Precipitation: A Case Study in Central Italy
Abstract
1. Introduction
1.1. State of the Art
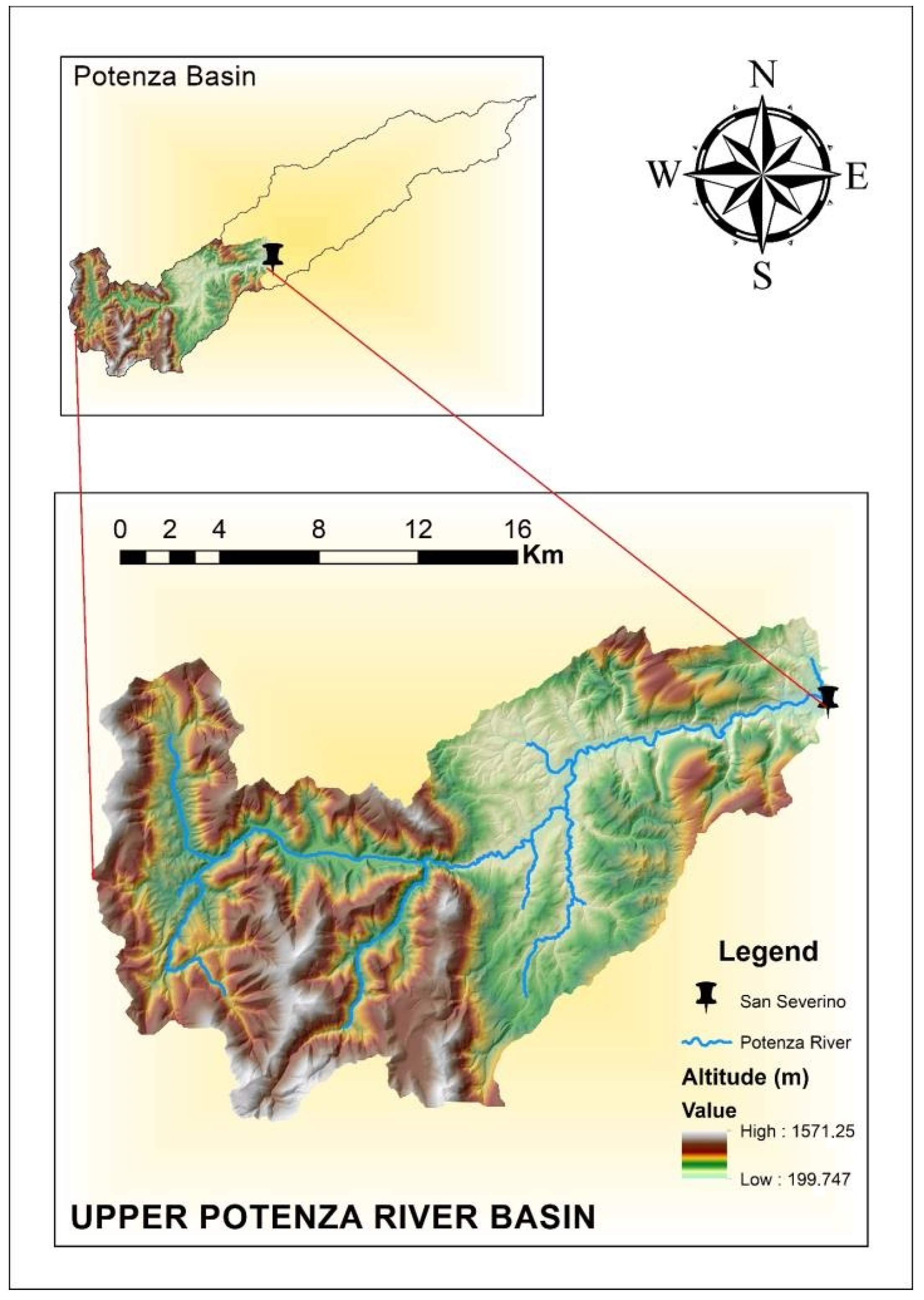
1.2. Study Area
2. Materials and Methods
3. Results
3.1. Verification of Land Use Change
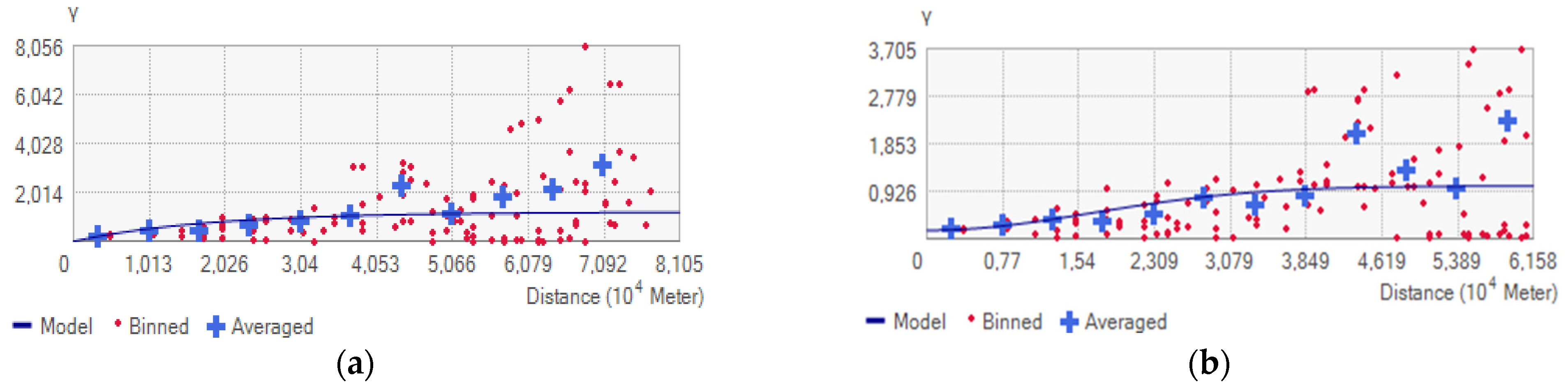
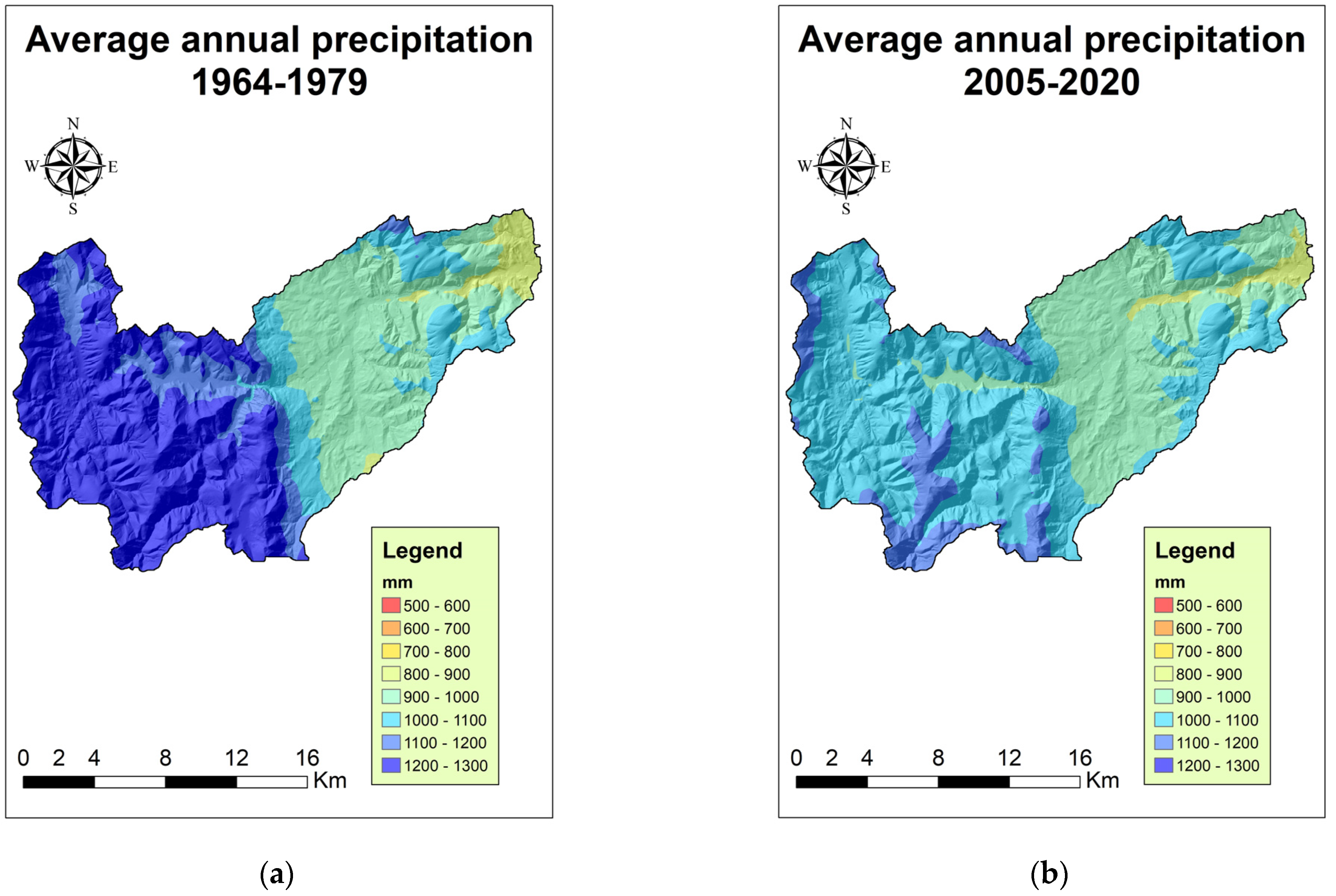
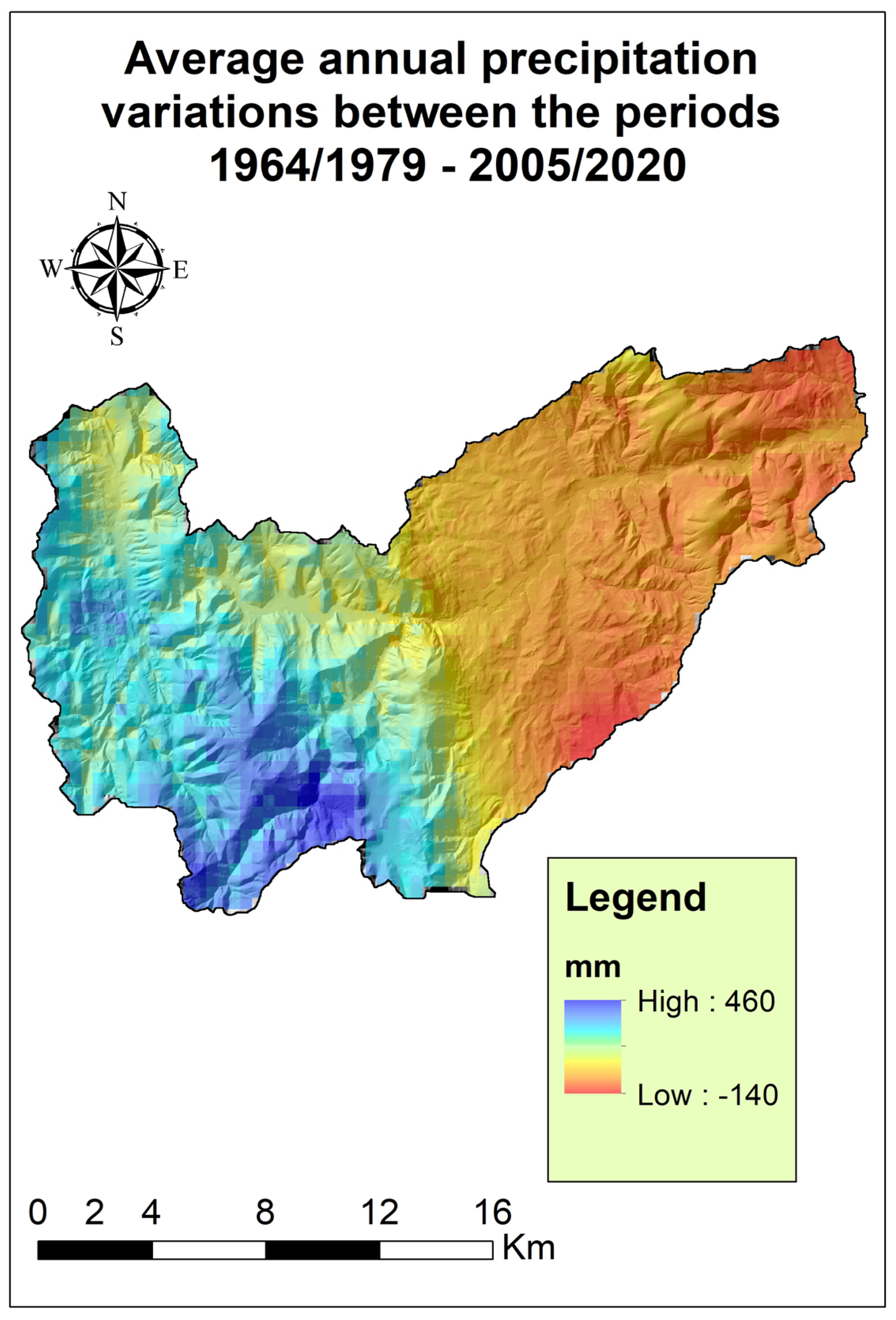
3.2. Interpolation of Precipitation
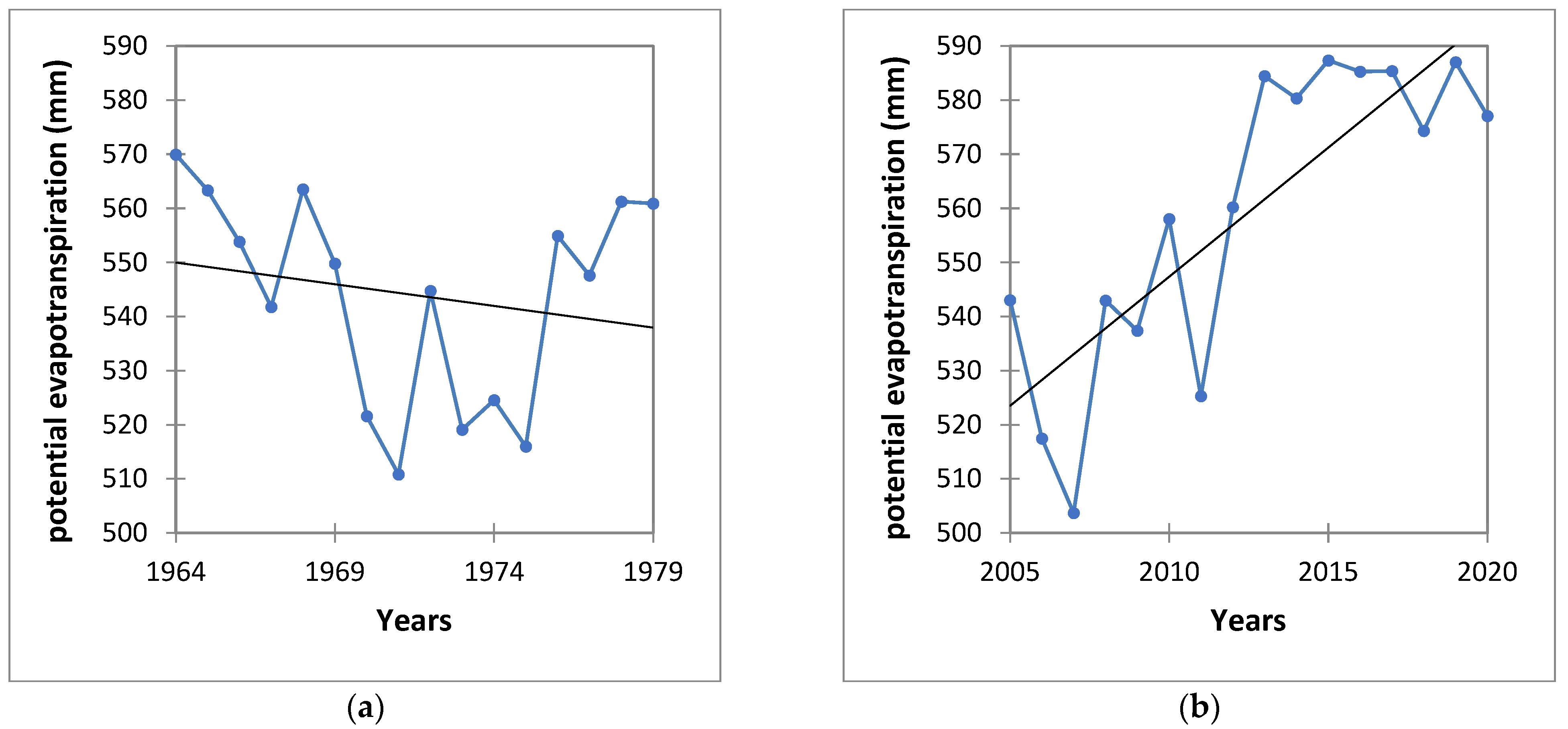
3.3. Evapotranspiration
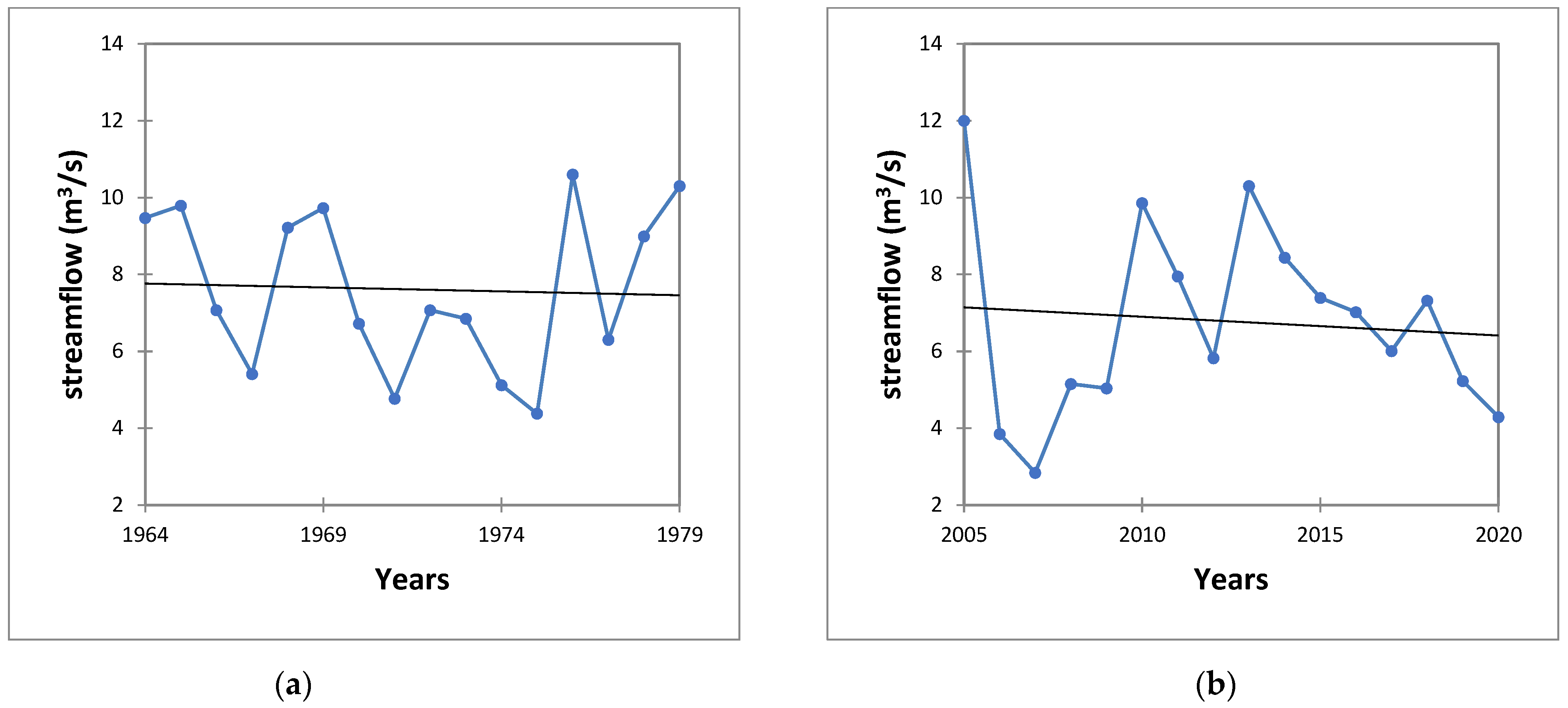
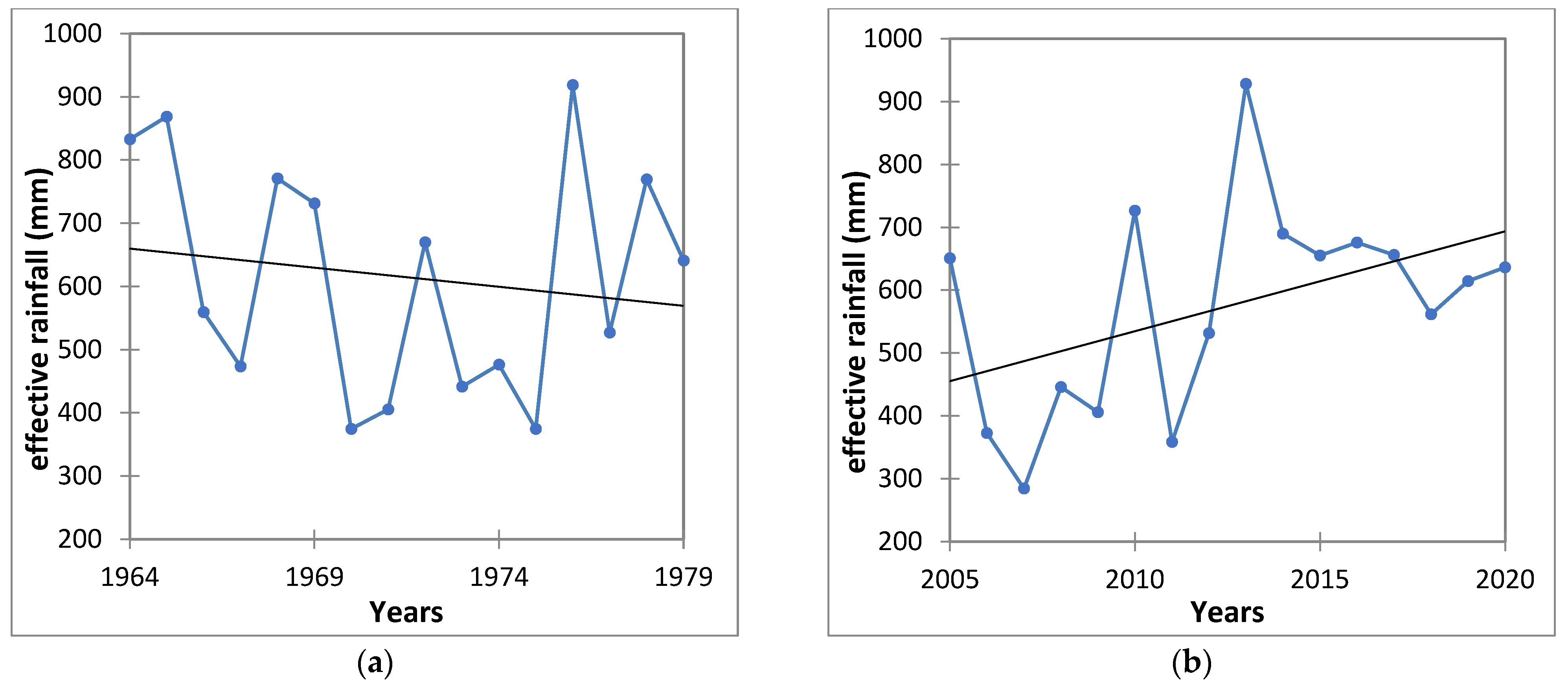
3.4. Streamflow Trend and Effective Rainfall Trend
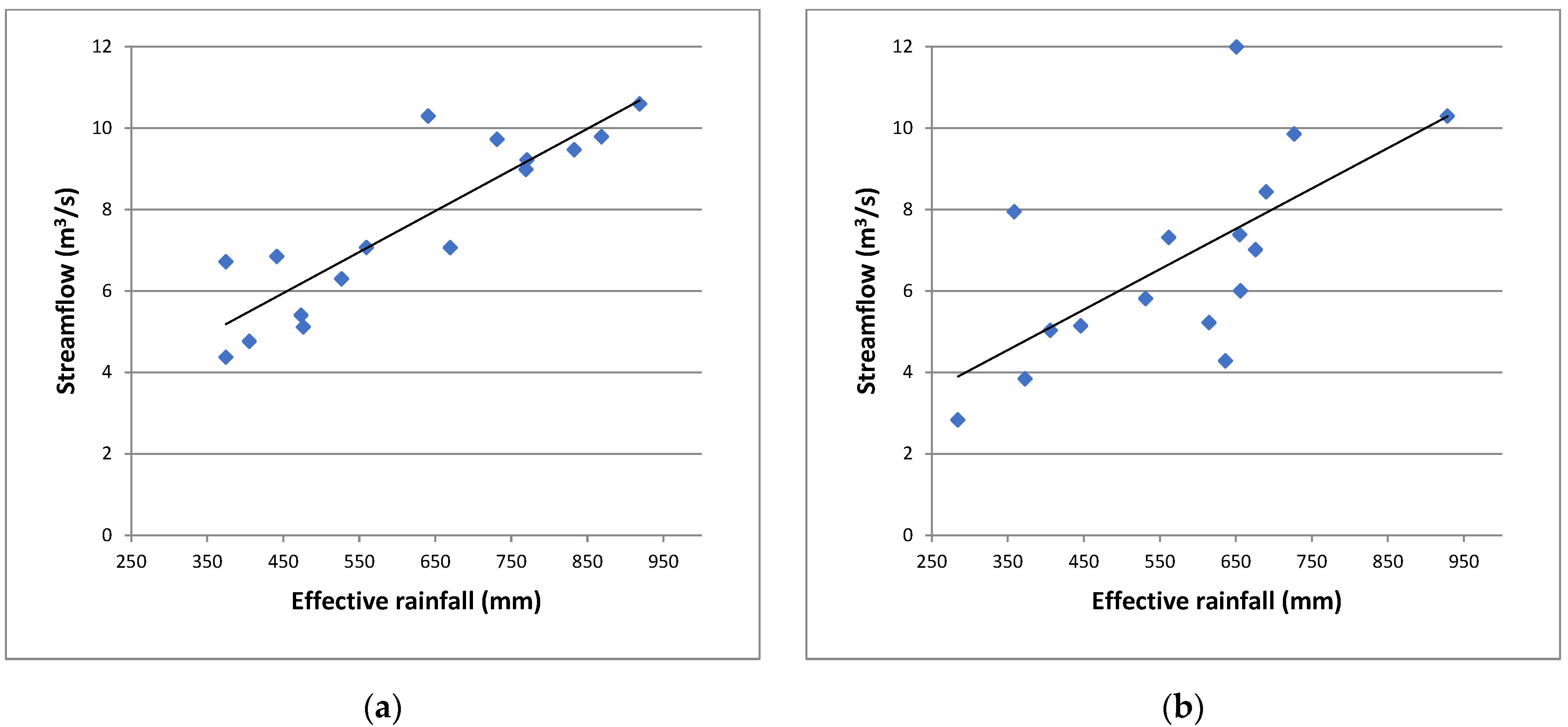
3.5. Analysis of the Relationship between Streamflow and Effective Precipitation and Averages of the Analysed Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Döll, P.; Fiedler, K.; Zhang, J. Global-scale analysis of river flow alterations due to water withdrawals and reservoirs. Hydrol. Earth Syst. Sci. 2009, 13, 2413–2432. [Google Scholar] [CrossRef]
- Mengistu, D.; Bewket, W.; Dosio, A.; Panitz, H.J. Climate change impacts on water resources in the upper blue nile (Abay) river basin, ethiopia. J. Hydrol. 2021, 592, 125614. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, G.; Yin, X. Hydrological responses to climate change in Nenjiang river basin, northeastern China. Water Res. Manag. 2011, 25, 677–689. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Le risque d’inondation et les perspectives de changement climatique mondial et régional. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Tao, H.; Gemmer, M.; Bai, Y.; Su, B.; Mao, W. Trends of streamflow in the Tarim River Basin during the past 50 years: Human impact or climate change? J. Hydrol. 2011, 400, 1–9. [Google Scholar] [CrossRef]
- Binder, L.C.W. Climate Change and Watershed Planning in Washington State 1. J. Am. Water Res. Assoc. 2006, 42, 915–926. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Chiew, F.H.; McMahon, T.A. Global ENSO-streamflow teleconnection, streamflow forecasting and interannual variability. Hydrol. Sci. J. 2002, 47, 505–522. [Google Scholar] [CrossRef]
- Dai, A.; Qian, T.; Trenberth, K.E.; Milliman, J.D. Changes in continental freshwater discharge from 1948 to 2004. J. Clim. 2009, 22, 2773–2792. [Google Scholar] [CrossRef]
- Fu, G.; Barber, M.E.; Chen, S. Hydro-climatic variability and trends in Washington State for the last 50 years. Hydrol. Process. 2010, 24, 866–878. [Google Scholar] [CrossRef]
- Nohara, D.; Kitoh, A.; Hosaka, M.; Oki, T. Impact of climate change on river discharge projected by multimodel ensemble. J. Hydrometeorol. 2006, 7, 1076–1089. [Google Scholar] [CrossRef]
- Vogl, A.L.; Lopes, V.L. Impacts of water resources development on flow regimes in the Brazos River. Environ. Monit. Assess. 2009, 157, 331–345. [Google Scholar] [CrossRef] [PubMed]
- Hannah, D.M.; Demuth, S.; van Lanen, H.A.; Looser, U.; Prudhomme, C.; Rees, G.; Stahl, K.; Tallaksen, L.M. Large-scale river flow archives: Importance, current status and future needs. Hydrol. Process. 2011, 25, 1191–1200. [Google Scholar] [CrossRef]
- Marsh, T.J. Capitalising on river flow data to meet changing national needs—A UK perspective. Flow Meas. Instrum. 2002, 13, 291–298. [Google Scholar] [CrossRef]
- Stahl, K.; Hisdal, H.; Hannaford, J.; Tallaksen, L.M.; van Lanen, H.A.J.; Sauquet, E.; Demuth, S.; Fendekova, M.; Jódar, J. Streamflow trends in Europe: Evidence from a dataset of near-natural catchments. Hydrol. Earth Syst. Sci. 2010, 14, 2367–2382. [Google Scholar] [CrossRef]
- Rojas, R.; Feyen, L.; Bianchi, A.; Dosio, A. Assessment of future flood hazard in Europe using a large ensemble of bias-corrected regional climate simulations. J. Geophys. Res. Atmos. 2012, 117, D17109. [Google Scholar]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef]
- Blöschl, G.; Gaál, L.; Hall, J.; Kiss, A.; Komma, J.; Nester, T.; Parajka, J.; Perdigão, R.A.P.; Plavcová, L.; Rogger, M.; et al. Increasing river floods: Fiction or reality? Wiley Interdiscip. Rev. Water 2015, 2, 329–344. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Burt, P. Climate and territorial suitability for the Vineyards developed using GIS techniques. In Proceeding of the Conference of the Arabian Journal of Geosciences; Springer: Cham, Switzerland, 2018; pp. 11–13. [Google Scholar]
- Reidsma, P.; Ewert, F.; Lansink, A.O.; Leemans, R. Adaptation to climate change and climate variability in European agriculture: The importance of farm level responses. Eur. J. Agron. 2010, 32, 91–102. [Google Scholar] [CrossRef]
- Gentilucci, M.; Moustafa, A.A.; Abdel-Gawad, F.K.; Mansour, S.R.; Coppola, M.R.; Caserta, L.; Inglese, S.; Pambianchi, G.; Guerriero, G. Advances in Egyptian mediterranean coast climate change monitoring. Water 2021, 13, 1870. [Google Scholar] [CrossRef]
- Gentilucci, M.; Parisi, C.; Coppola, M.R.; Majdoubi, F.Z.; Madonna, A.; Guerriero, G. Influence of mediterranean sea temperature increase on Gaeta Gulf (Tyrrhenian Sea) biodiversity. Proc. Zool. Soc. 2021, 74, 91–103. [Google Scholar] [CrossRef]
- Antonetti, G.; Gentilucci, M.; Aringoli, D.; Pambianchi, G. Analysis of landslide Susceptibility and Tree Felling Due to an Extreme Event at Mid-Latitudes: Case Study of Storm Vaia, Italy. Land 2022, 11, 1808. [Google Scholar] [CrossRef]
- Bračko, T.; Žlender, B.; Jelušič, P. Implementation of Climate Change Effects on Slope Stability Analysis. Appl. Sci. 2022, 12, 8171. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Materazzi, M.; Pambianchi, G. Effects of Climate Change on Vegetation in the Province of Macerata (Central Italy). In Advanced Studies in Efficient Environmental Design and City Planning; Springer: Cham, Switzerland, 2021; pp. 463–474. [Google Scholar]
- Theurillat, J.P.; Guisan, A. Potential impact of climate change on vegetation in the European Alps: A review. Clim. Chang. 2001, 50, 77–109. [Google Scholar] [CrossRef]
- Fagerberg, J.; Laestadius, S.; Martin, B.R. The triple challenge for Europe: The economy, climate change, and governance. Challenge 2016, 59, 178–204. [Google Scholar] [CrossRef]
- Gentilucci, M.; D’Aprile, F. Variations in trends of temperature and its influence on tree growth in the Tuscan Apennines. Arab. J. Geosci. 2021, 14, 1418. [Google Scholar] [CrossRef]
- Lionello, P.; Scarascia, L. The relation between climate change in the Mediterranean region and global warming. Reg. Environ. Chang. 2018, 18, 1481–1493. [Google Scholar] [CrossRef]
- Gorguner, M.; Kavvas, M.L. Modeling impacts of future climate change on reservoir storages and irrigation water demands in a Mediterranean basin. Sci. Total Environ. 2020, 748, 141246. [Google Scholar] [CrossRef]
- Javadian, M.; Behrangi, A.; Smith, W.K.; Isher, J.B. Global trends in evapotranspiration dominated by increases across large cropland regions. Remote Sens. 2020, 12, 1221. [Google Scholar] [CrossRef]
- Yue, T.X.; Zhao, N.; Ramsey, R.D.; Wang, C.L.; Fan, Z.M.; Chen, C.F.; Lu, Y.M.; Li, B.L. Climate change trend in China, with improved accuracy. Clim. Chang. 2013, 120, 137–151. [Google Scholar] [CrossRef]
- Bhutiyani, M.R.; Kale, V.S.; Pawar, N.J. Climate change and the precipitation variations in the northwestern Himalaya: 1866–2006. Int. J. Climatol. 2010, 30, 535–548. [Google Scholar] [CrossRef]
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef] [PubMed]
- Grazzini, F.; Craig, G.C.; Keil, C.; Antolini, G.; Pavan, V. Extreme precipitation events over northern Italy. Part I: A systematic classification with machine-learning techniques. Q. J. R. Meteorol. Soc. 2020, 146, 69–85. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; D’Aprile, F.; Zardi, D. Analysis of extreme precipitation indices in the Marche region (central Italy), combined with the assessment of energy implications and hydrogeological risk. Energy Rep. 2020, 6, 804–810. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A. Nonstationary precipitation intensity-duration-frequency curves for infrastructure design in a changing climate. Sci. Rep. 2014, 4, 7093. [Google Scholar] [CrossRef]
- Olmstead, S.M. Climate change adaptation and water resource management: A review of the literature. Energy Econ. 2014, 46, 500–509. [Google Scholar] [CrossRef]
- Brandolini, P.; Cevasco, A.; Firpo, M.; Robbiano, A.; Sacchini, A. Geo-hydrological risk management for civil protection purposes in the urban area of Genoa (Liguria, NW Italy). Nat. Hazards Earth Syst. Sci. 2012, 12, 943–959. [Google Scholar] [CrossRef]
- Aguilar, E.; Auer, I.; Brunet, M.; Peterson, T.C.; Wieringa, J. Guidance on Metadata and Homogenization; WMOv (World Meteorological Organization): Geneva, Switzerland, 2003. [Google Scholar]
- Gentilucci, M.; Catorci, A.; Panichella, T.; Moscatelli, S.; Hamed, Y.; Missaoui, R.; Pambianchi, G. Analysis of Snow Cover in the Sibillini Mountains in Central Italy. Climate 2023, 11, 72. [Google Scholar] [CrossRef]
- Goovaerts, P. Ordinary Cokriging Revisited. Math. Geol. 1998, 30, 21–42. [Google Scholar] [CrossRef]
- Turc, L. Calcul du bilan de l’eau évaluation en fonction des précipitations et des températures. IAHS Publ. 1954, 37, 88–200. [Google Scholar]
- Gentilucci, M.; Barbieri, M.; Burt, P.; D’Aprile, F. Preliminary data validation and reconstruction of temperature and precipitation in Central Italy. Geosciences 2018, 8, 202. [Google Scholar] [CrossRef]
- Novotny, E.V.; Stefan, H.G. Stream flow in Minnesota: Indicator of climate change. J. Hydrol. 2007, 334, 319–333. [Google Scholar] [CrossRef]
- Esvandzibaie, F.; Farajzadeh, M.; Ghavidel, Y. Analysis of temporal and spatial changes of precipitation and flow rate in arid regions with a statistical approach (case study: Central Plateau catchment area of Iran). Int. J. Environ. Sci. Technol. 2022, 19, 6803–6824. [Google Scholar] [CrossRef]
- Ortega, J.A.; Razola, L.; Garzón, G. Recent human impacts and change in dynamics and morphology of ephemeral rivers. Nat. Hazards Earth Syst. Sci. 2014, 14, 713–730. [Google Scholar] [CrossRef]
- Usowicz, B.; Lipiec, J.; Łukowski, M.; Słomiński, J. Improvement of spatial interpolation of precipitation distribution using cokriging incorporating rain-gauge and satellite (SMOS) soil moisture data. Remote Sens. 2021, 13, 1039. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments. Hydrol. Process. 2017, 31, 2143–2161. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Annual actual evapotranspiration estimation via GIS models of three empirical methods employing remotely sensed data for the peloponnese, Greece, and comparison with annual MODIS ET and pan evaporation measurements. ISPRS Int. J. Geo-Inf. 2021, 10, 522. [Google Scholar] [CrossRef]
- Zhang, Q.; Singh, V.P.; Sun, P.; Chen, X.; Zhang, Z.; Li, J. Precipitation and streamflow changes in China: Changing patterns, causes and implications. J. Hydrol. 2011, 410, 204–216. [Google Scholar] [CrossRef]
- Han, H.; Hou, J.; Huang, M.; Li, Z.; Xu, K.; Zhang, D.; Xu, K.; Zhang, D.; Bai, G.; Wang, C. Impact of soil and water conservation measures and precipitation on streamflow in the middle and lower reaches of the Hulu River Basin, China. Catena 2020, 195, 104792. [Google Scholar] [CrossRef]
- Santos, R.M.B.; Fernandes, L.S.; Moura, J.P.; Pereira, M.G.; Pacheco, F.A.L. The impact of climate change, human interference, scale and modeling uncertainties on the estimation of aquifer properties and river flow components. J. Hydrol. 2014, 519, 1297–1314. [Google Scholar] [CrossRef]
- Schnorbus, M.; Werner, A.; Bennett, K. Impacts of climate change in three hydrologic regimes in British Columbia, Canada. Hydrol. Process. 2014, 28, 1170–1189. [Google Scholar] [CrossRef]
- Ceppi, A.; Gambini, E.; Lombardi, G.; Ravazzani, G.; Mancini, M. (SOL40: Forty Years of Simulations under Climate and Land Use Change. Water 2022, 14, 837. [Google Scholar] [CrossRef]



| Month | MSE | RMSSE | RMSE | ASE |
|---|---|---|---|---|
| January | −0.034 | 0.94 | 20.86 | 23.35 |
| February | −0.012 | 0.95 | 23.35 | 26.43 |
| March | −0.031 | 0.94 | 23.79 | 26.60 |
| April | −0.022 | 0.95 | 24.86 | 27.36 |
| May | −0.029 | 0.94 | 26.18 | 29.45 |
| June | −0.045 | 0.98 | 19.92 | 20.53 |
| July | −0.028 | 0.95 | 22.16 | 23.96 |
| August | −0.030 | 0.96 | 18.53 | 19.28 |
| September | −0.071 | 0.94 | 27.73 | 29.60 |
| October | −0.024 | 0.87 | 24.66 | 28.71 |
| November | −0.078 | 1.01 | 24.80 | 24.37 |
| December | −0.028 | 0.92 | 27.17 | 30.95 |
| Month | MSE | RMSSE | RMSE | ASE |
|---|---|---|---|---|
| January | −0.012 | 0.89 | 20.06 | 23.26 |
| February | −0.051 | 0.93 | 26.21 | 29.45 |
| March | −0.061 | 0.97 | 35.18 | 41.35 |
| April | −0.054 | 0.94 | 30.27 | 35.16 |
| May | −0.042 | 0.90 | 25.07 | 29.46 |
| June | −0.029 | 1.02 | 31.03 | 34.77 |
| July | −0.006 | 1.09 | 30.12 | 29.84 |
| August | 0.003 | 0.94 | 23.11 | 24.86 |
| September | −0.071 | 1.02 | 35.61 | 34.81 |
| October | −0.021 | 0.99 | 29.76 | 33.30 |
| November | −0.045 | 0.96 | 29.23 | 33.93 |
| December | −0.054 | 1.00 | 35.62 | 38.21 |
| Month | Prec. 1964–1979 | Prec. 2005–2020 |
|---|---|---|
| January | 82.6 | 75.5 |
| February | 93.5 | 76.6 |
| March | 95.1 | 115.7 |
| April | 103.9 | 83.5 |
| May | 82.6 | 82.9 |
| June | 88.9 | 79.9 |
| July | 72.9 | 49.1 |
| August | 117.7 | 72.5 |
| September | 111.8 | 89.5 |
| October | 92.7 | 90.2 |
| November | 107.4 | 112.5 |
| December | 104.0 | 95.2 |
| Annual | 1158.6 | 1133.9 |
| Period | Kendall’s Tau | p-Value | Sen’s Slope (m3/Year) |
|---|---|---|---|
| 1964–1979 | −0.092 | 0.620 | −0.051 |
| 2005–2020 | −0.050 | 0.825 | −0.078 |
| Period | Kendall’s Tau | p-Value | Sen’s Slope (m3/Year) |
|---|---|---|---|
| 1964–1979 | −0.050 | −0.822 | −1.807 |
| 2005–2020 | −0.067 | 0.753 | −2.395 |
| Period | P | T | ETp | ER | Q |
|---|---|---|---|---|---|
| 1964–1979 | 1159 | 12.2 | 544 | 615 | 7.6 |
| 2005–2020 | 1134 | 13.2 | 559 | 575 | 6.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gentilucci, M.; Djouohou, S.I.; Barbieri, M.; Hamed, Y.; Pambianchi, G. Trend Analysis of Streamflows in Relation to Precipitation: A Case Study in Central Italy. Water 2023, 15, 1586. https://doi.org/10.3390/w15081586
Gentilucci M, Djouohou SI, Barbieri M, Hamed Y, Pambianchi G. Trend Analysis of Streamflows in Relation to Precipitation: A Case Study in Central Italy. Water. 2023; 15(8):1586. https://doi.org/10.3390/w15081586
Chicago/Turabian StyleGentilucci, Matteo, Sophie Ingrid Djouohou, Maurizio Barbieri, Younes Hamed, and Gilberto Pambianchi. 2023. "Trend Analysis of Streamflows in Relation to Precipitation: A Case Study in Central Italy" Water 15, no. 8: 1586. https://doi.org/10.3390/w15081586
APA StyleGentilucci, M., Djouohou, S. I., Barbieri, M., Hamed, Y., & Pambianchi, G. (2023). Trend Analysis of Streamflows in Relation to Precipitation: A Case Study in Central Italy. Water, 15(8), 1586. https://doi.org/10.3390/w15081586










