An Event-Based Stochastic Parametric Rainfall Simulator (ESPRS) for Urban Stormwater Simulation and Performance in a Sponge City
Abstract
:1. Introduction
2. Study Area and Data
3. Methodology
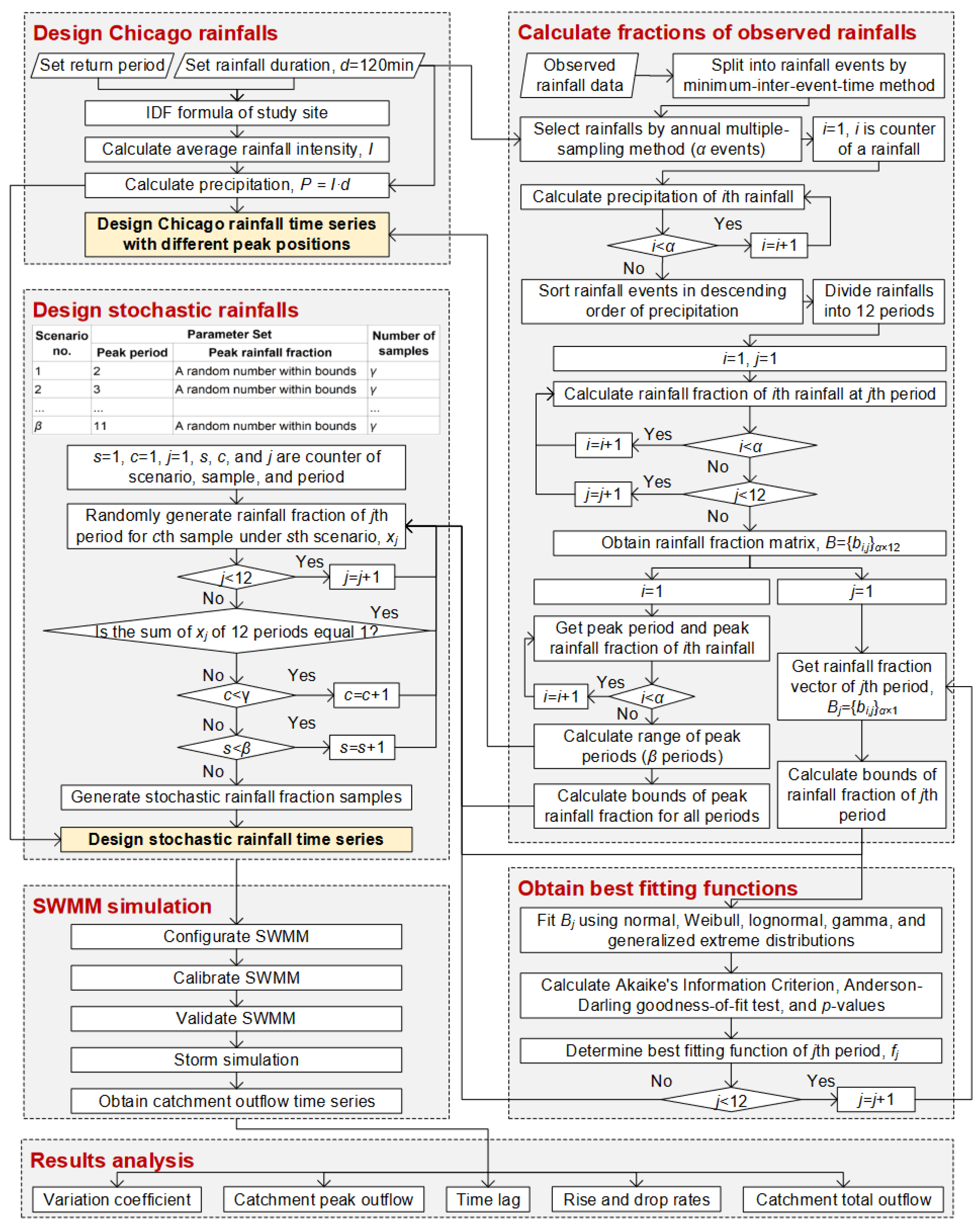
3.1. Event-Based Stochastic Parametric Rainfall Simulator (ESPRS)
3.1.1. Rainfall Fractions (RFs)
3.1.2. Probability Distribution Functions (PDFs)
3.1.3. Goodness-of-Fit Statistics
3.1.4. Stochastic Rainfall Fraction Series
3.1.5. Stochastic and Chicago Rainfall Time Series
3.2. Storm Water Management Model (SWMM)
3.3. Performance Evaluation
4. Results and Discussion
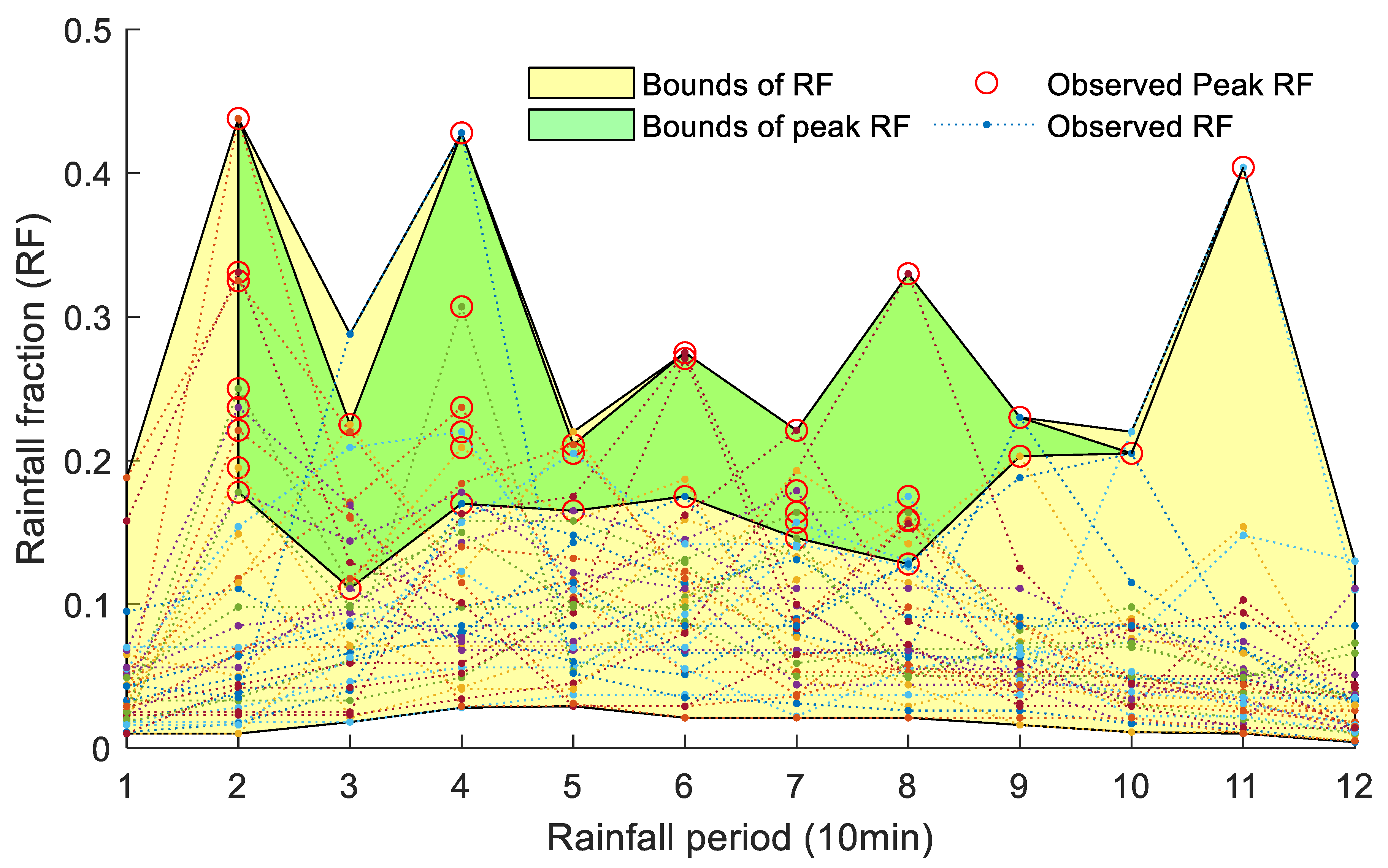
4.1. Stochastic Rainfall Fractions
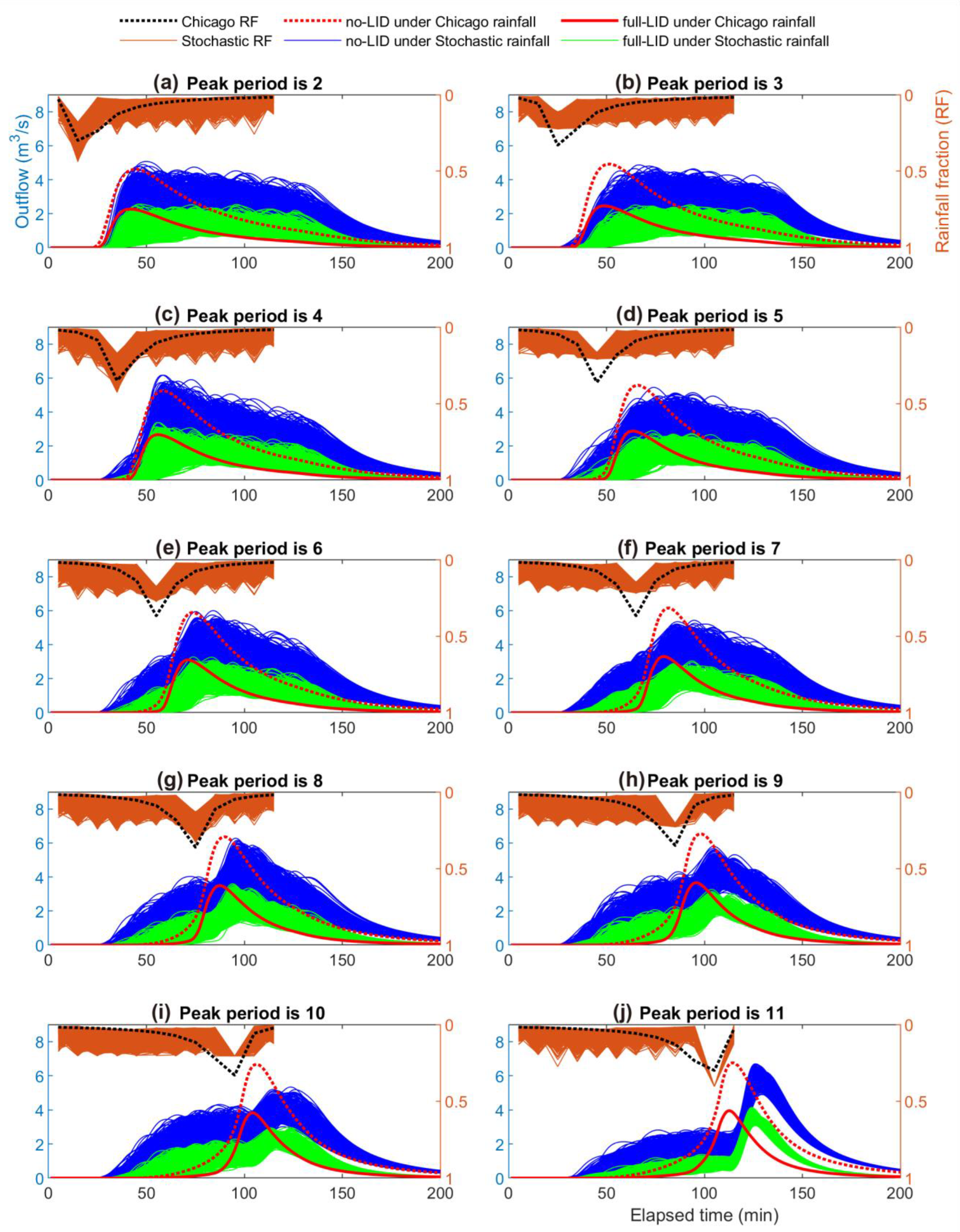
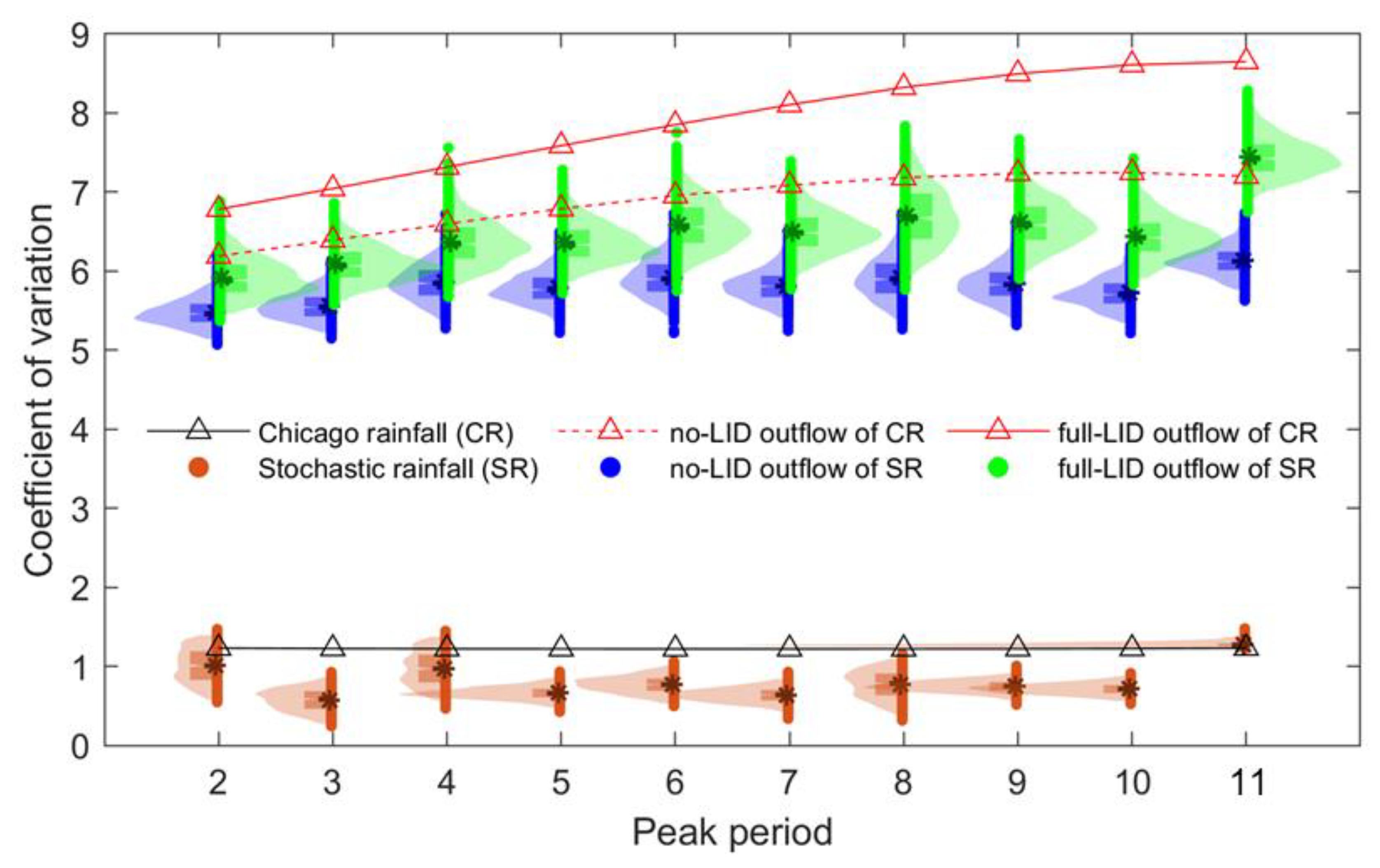
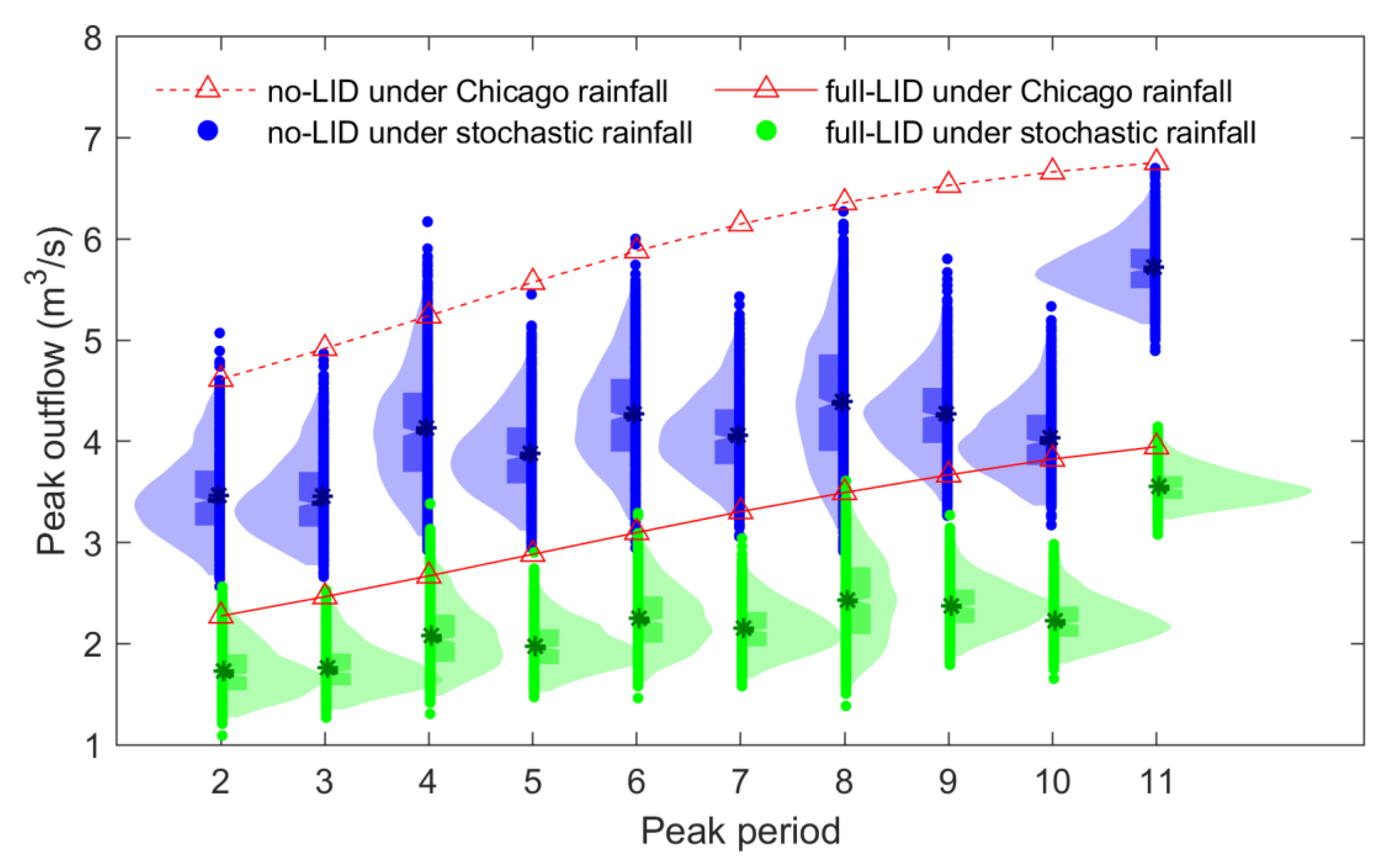
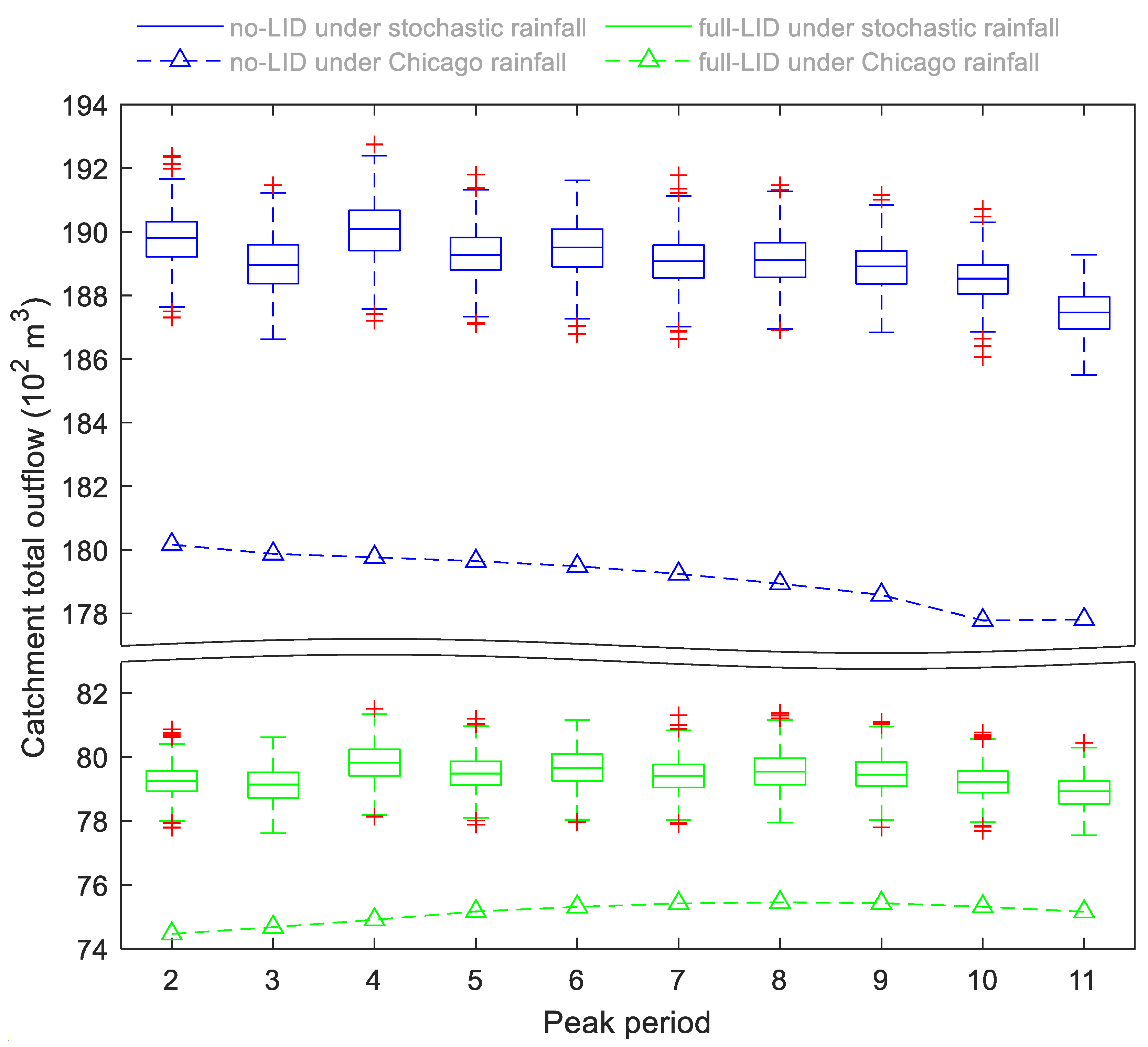
4.2. Catchment Outflow
4.3. Low-Impact Development Facilities
5. Conclusions
- The ESPRS outperformed the Chicago method in predicting extreme precipitation events for urban stormwater simulation and control. Fixed rain patterns can hardly represent the actual temporal structures of precipitation events, especially the extreme ones, leading to uncertainties. Using an ESPRS has strong potential for revealing the influence of temporal rainfall characteristics on hydrological responses.
- The rainfall peak period, rainfall peak fraction, and cumulative rainfall depth at the peak period are control factors for an ESPRS.
- Rear-type precipitation events with high peak fractions present the most negative pattern for outflow control by LIDs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.Y.; Li, Y.B.; Huang, Q.; Xia, J.; Li, J.K. Surrogate-based multiobjective optimization to rapidly size low impact development practices for outflow capture. J. Hydrol. 2023, 616, 128848. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Xu, K.; Dong, N.P.; Wang, H. Optimally integrating multi-source products for improving long series precipitation precision by using machine learning methods. J. Hydrol. 2022, 609, 127707. [Google Scholar] [CrossRef]
- Cristiano, E.; ten Veldhuis, M.C.; van De Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Ten Veldhuis, M.-C.; Zhou, Z.; Yang, L.; Liu, S.; Smith, J. The role of storm scale, position and movement in controlling urban flood response. Hydrol. Earth Syst. Sci. 2018, 22, 417–436. [Google Scholar] [CrossRef]
- Zhou, Z.; Smith, J.A.; Wright, D.B.; Baeck, M.L.; Yang, L.; Liu, S. Storm Catalog-Based Analysis of Rainfall Heterogeneity and Frequency in a Complex Terrain. Water Resour. Res. 2019, 55, 1871–1889. [Google Scholar] [CrossRef]
- Wright, D.B.; Yu, G.; England, J.F. Six decades of rainfall and flood frequency analysis using stochastic storm transposition: Review, progress, and prospects. J. Hydrol. 2020, 585, 124816. [Google Scholar] [CrossRef]
- Bruni, G.; Reinoso, R.; van de Giesen, N.C.; Clemens, F.H.L.R.; ten Veldhuis, J.A.E. On the sensitivity of urban hydrodynamic modelling to rainfall spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2015, 19, 691–709. [Google Scholar] [CrossRef]
- Cristiano, E.; ten Veldhuis, M.-c.; Wright, D.B.; Smith, J.A.; van de Giesen, N. The Influence of Rainfall and Catchment Critical Scales on Urban Hydrological Response Sensitivity. Water Resour. Res. 2019, 55, 3375–3390. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.P.; Gires, A.; Pina, R.D.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J.; et al. Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modelling outputs: A multi-catchment investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Paschalis, A.; Fatichi, S.; Molnar, P.; Rimkus, S.; Burlando, P. On the effects of small scale space-time variability of rainfall on basin flood response. J. Hydrol. 2014, 514, 313–327. [Google Scholar] [CrossRef]
- Nerini, D.; Besic, N.; Sideris, I.; Germann, U.; Foresti, L. A non-stationary stochastic ensemble generator for radar rainfall fields based on the short-space Fourier transform. Hydrol. Earth Syst. Sci. 2017, 21, 2777–2797. [Google Scholar] [CrossRef]
- Akil, N.; Artigue, G.; Savary, M.; Johannet, A.; Vinches, M. Uncertainty Estimation in Hydrogeological Forecasting with Neural Networks: Impact of Spatial Distribution of Rainfalls and Random Initialization of the Model. Water 2021, 13, 1690. [Google Scholar] [CrossRef]
- Wang, Y.T.; Xie, J.K.; You, Y.F.; Wang, Y.J.; Xu, Y.P.; Guo, Y.X. A new multi-site multi-variable stochastic model with inter-site and inter-variable correlations, low frequency attributes and stochasticity: A case study in the lower Yellow River basin. J. Hydrol. 2021, 599, 126365. [Google Scholar] [CrossRef]
- Yan, J.; Li, F.; Bárdossy, A.; Tao, T. Conditional simulation of spatial rainfall fields using random mixing: A study that implements full control over the stochastic process. Hydrol. Earth Syst. Sci. 2021, 25, 3819–3835. [Google Scholar] [CrossRef]
- Gao, C.; Guan, X.J.; Booij, M.J.; Meng, Y.; Xu, Y.P. A new framework for a multi-site stochastic daily rainfall model: Coupling a univariate Markov chain model with a multi-site rainfall event model. J. Hydrol. 2021, 598, 126478. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Serinaldi, F. Random Fields Simplified: Preserving Marginal Distributions, Correlations, and Intermittency, With Applications From Rainfall to Humidity. Water Resour. Res. 2020, 56, e2019WR026331. [Google Scholar] [CrossRef]
- Peleg, N.; Blumensaat, F.; Molnar, P.; Fatichi, S.; Burlando, P. Partitioning the impacts of spatial and climatological rainfall variability in urban drainage modeling. Hydrol. Earth Syst. Sci. 2017, 21, 1559–1572. [Google Scholar] [CrossRef]
- Zhu, Z.; Wright, D.B.; Yu, G. The Impact of Rainfall Space-Time Structure in Flood Frequency Analysis. Water Resour. Res. 2018, 54, 8983–8998. [Google Scholar] [CrossRef]
- Hettiarachchi, S.; Wasko, C.; Sharma, A. Increase in flood risk resulting from climate change in a developed urban watershed—The role of storm temporal patterns. Hydrol. Earth Syst. Sci. 2018, 22, 2041–2056. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Li, J.; Huang, Q.; Xia, J.; Li, J.K.; Liu, D.F.; Tan, Q.T. Performance assessment of sponge city infrastructure on stormwater outflows using isochrone and SWMM models. J. Hydrol. 2021, 597, 126151. [Google Scholar] [CrossRef]
- Nguyen, N.S.; Liu, J.; Raghavan, S.V.; Liong, S.-Y. Deriving high spatiotemporal rainfall information over Singapore through dynamic-stochastic modelling using ‘HiDRUS’. Stoch. Environ. Res. Risk Assess. 2020, 35, 1453–1462. [Google Scholar] [CrossRef]
- Pons, V.; Benestad, R.; Sivertsen, E.; Muthanna, T.M.; Bertrand-Krajewski, J.L. Forecasting green roof detention performance by temporal downscaling of precipitation time-series projections. Hydrol. Earth Syst. Sci. 2022, 26, 2855–2874. [Google Scholar] [CrossRef]
- Müller, H.; Haberlandt, U. Temporal rainfall disaggregation using a multiplicative cascade model for spatial application in urban hydrology. J. Hydrol. 2018, 556, 847–864. [Google Scholar] [CrossRef]
- Gao, C.; Booij, M.J.; Xu, Y.P. Development and hydrometeorological evaluation of a new stochastic daily rainfall model: Coupling Markov chain with rainfall event model. J. Hydrol. 2020, 589, 125337. [Google Scholar] [CrossRef]
- Yang, L.; Zhong, P.-a.; Zhu, F.; Ma, Y.; Wang, H.; Li, J.; Xu, C. A comparison of the reproducibility of regional precipitation properties simulated respectively by weather generators and stochastic simulation methods. Stoch. Environ. Res. Risk Assess. 2021, 36, 495–509. [Google Scholar] [CrossRef]
- Kim, D.; Onof, C. A stochastic rainfall model that can reproduce important rainfall properties across the timescales from several minutes to a decade. J. Hydrol. 2020, 589, 125150. [Google Scholar] [CrossRef]
- Mosthaf, T.; Bárdossy, A. Regionalizing nonparametric models of precipitation amounts on different temporal scales. Hydrol. Earth Syst. Sci. 2017, 21, 2463–2481. [Google Scholar] [CrossRef]
- Balbastre-Soldevila, R.; García-Bartual, R.; Andrés-Doménech, I. Estimation of the G2P Design Storm from a Rainfall Convectivity Index. Water 2021, 13, 1943. [Google Scholar] [CrossRef]
- Shmilovitz, Y.; Marra, F.; Wei, H.; Argaman, E.; Nearing, M.; Goodrich, D.; Assouline, S.; Morin, E. Frequency analysis of storm-scale soil erosion and characterization of extreme erosive events by linking the DWEPP model and a stochastic rainfall generator. Sci. Total Environ. 2021, 787, 147609. [Google Scholar] [CrossRef]
- Pavlides, A.; Agou, V.D.; Hristopulos, D.T. Non-parametric kernel-based estimation and simulation of precipitation amount. J. Hydrol. 2022, 612, 127988. [Google Scholar] [CrossRef]
- Zhang, H.; Loáiciga, H.A.; Ren, F.; Du, Q.; Ha, D. Semi-empirical prediction method for monthly precipitation prediction based on environmental factors and comparison with stochastic and machine learning models. Hydrol. Sci. J. 2020, 65, 1928–1942. [Google Scholar] [CrossRef]
- Wang, C.; Hou, J.; Miller, D.; Brown, I.; Jiang, Y. Flood risk management in sponge cities: The role of integrated simulation and 3D visualization. Int. J. Disaster Risk Reduct. 2019, 39, 101139. [Google Scholar] [CrossRef]
- Hou, J.; Mao, H.; Li, J.; Sun, S. Spatial simulation of the ecological processes of stormwater for sponge cities. J. Environ. Manag. 2019, 232, 574–583. [Google Scholar] [CrossRef] [PubMed]
- Fengxi Sponge City (China). Available online: http://ecohydrology-ihp.org/demosites/view/1220 (accessed on 4 March 2023).
- Storm Water Management Model (SWMM). Available online: www.epa.gov/water-research/storm-water-management-model-swmm (accessed on 4 March 2023).
- Fengxi Management Committee. Available online: http://fxxc.xixianxinqu.gov.cn (accessed on 4 March 2023).
- Hou, J.; Guo, K.; Liu, F. Report on Storm Pattern Design and Storm Intensity Formula in Xixian New Area; Xi’an University of Technology: Xi’an, China, 2018. [Google Scholar]
- Pirone, D.; Cimorelli, L.; Del Giudice, G.; Pianese, D. Short-term rainfall forecasting using cumulative precipitation fields from station data: A probabilistic machine learning approach. J. Hydrol. 2023, 617, 128949. [Google Scholar] [CrossRef]
- Papalexiou, S.M. Rainfall Generation Revisited: Introducing CoSMoS-2s and Advancing Copula-Based Intermittent Time Series Modeling. Water Resour. Res. 2022, 58, e2021WR031641. [Google Scholar] [CrossRef]
- Gao, C.; Xu, Y.P.; Zhu, Q.; Bai, Z.X.; Liu, L. Stochastic generation of daily rainfall events: A single-site rainfall model with Copula-based joint simulation of rainfall characteristics and classification and simulation of rainfall patterns. J. Hydrol. 2018, 564, 41–58. [Google Scholar] [CrossRef]
- MATLAB. Available online: https://www.mathworks.com/products/matlab.html (accessed on 4 March 2023).
- Riaño-Briceño, G.; Barreiro-Gomez, J.; Ramirez-Jaime, A.; Quijano, N.; Ocampo-Martinez, C. MatSWMM—An open-source toolbox for designing real-time control of urban drainage systems. Environ. Modell. Softw. 2016, 83, 143–154. [Google Scholar] [CrossRef]


| Distribution Function | AIC 1 | p-Value 1 | |
|---|---|---|---|
| Normal | −151.09 | 3.08 | 0.005 |
| Weibull | −191.93 | 1.16 | 0.010 |
| Generalized extreme value | −247.46 | 0.93 | 0.017 |
| Gamma | −198.76 | 0.82 | 0.040 |
| Lognormal | −233.94 | 0.31 | 0.549 |
| Period | Best Fitting Form | Formula | Bounds of Rainfall Fraction (x) |
|---|---|---|---|
| 1 | Lognormal | 0.01–0.19 | |
| 2 | Lognormal | 0.01–0.44 | |
| 3 | Gamma | 0.02–0.29 | |
| 4 | Lognormal | 0.03–0.43 | |
| 5 | Gamma | 0.03–0.22 | |
| 6 | Generalized extreme value | 0.02–0.28 | |
| 7 | Gamma | 0.02–0.22 | |
| 8 | Lognormal | 0.02–0.33 | |
| 9 | Generalized extreme value | 0.02–0.23 | |
| 10 | Lognormal | 0.01–0.22 | |
| 11 | Lognormal | 0.01–0.40 | |
| 12 | Lognormal | 0.00–0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Xu, X.; Liu, D. An Event-Based Stochastic Parametric Rainfall Simulator (ESPRS) for Urban Stormwater Simulation and Performance in a Sponge City. Water 2023, 15, 1561. https://doi.org/10.3390/w15081561
Yang Y, Xu X, Liu D. An Event-Based Stochastic Parametric Rainfall Simulator (ESPRS) for Urban Stormwater Simulation and Performance in a Sponge City. Water. 2023; 15(8):1561. https://doi.org/10.3390/w15081561
Chicago/Turabian StyleYang, Yuanyuan, Xiaoyan Xu, and Dengfeng Liu. 2023. "An Event-Based Stochastic Parametric Rainfall Simulator (ESPRS) for Urban Stormwater Simulation and Performance in a Sponge City" Water 15, no. 8: 1561. https://doi.org/10.3390/w15081561






