A Comparative Analysis of Multiple Machine Learning Methods for Flood Routing in the Yangtze River
Abstract
:1. Introduction
2. Materials and Methods
2.1. Comparative ML Models
2.1.1. Support Vector Regression
2.1.2. Gaussian Process Regression
2.1.3. Random Forest Regression
2.1.4. Multilayer Perceptron
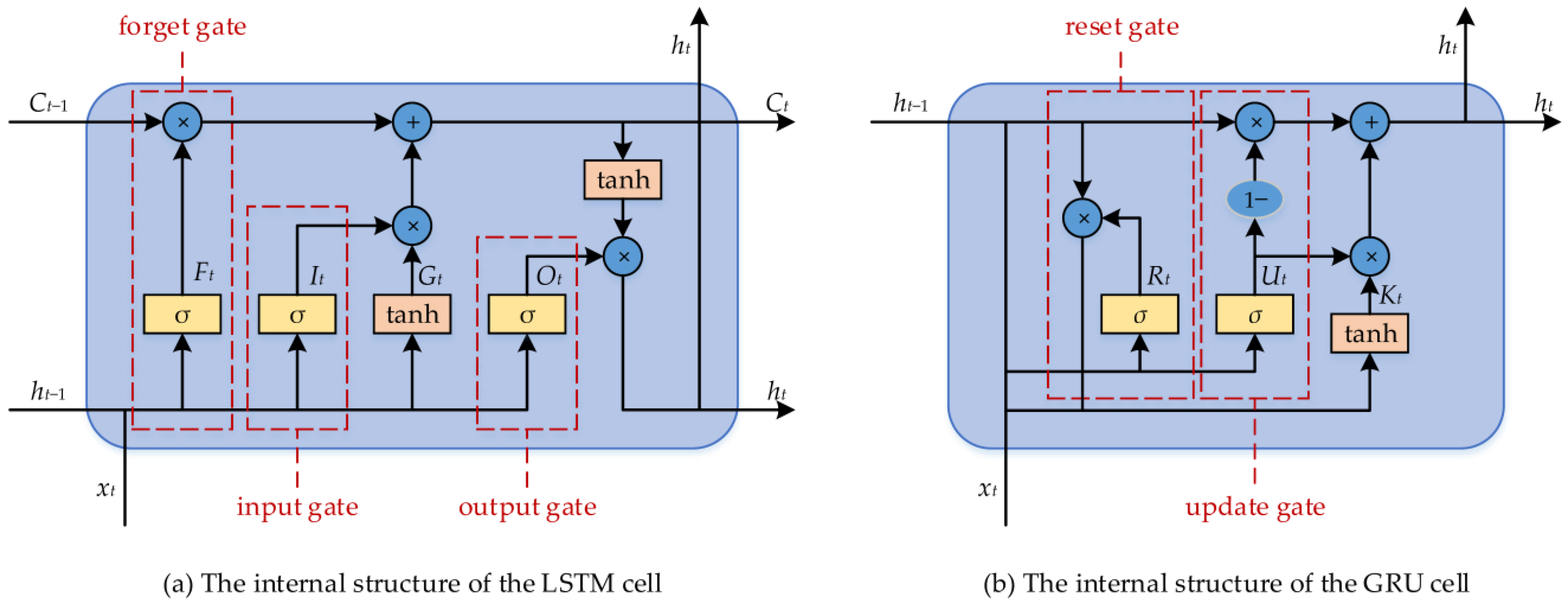
2.1.5. Long Short-Term Memory
2.1.6. Gated Recurrent Unit
2.2. Experimental Methods
2.2.1. Data Normalization
2.2.2. Efficiency Criteria
2.2.3. Taylor Diagram
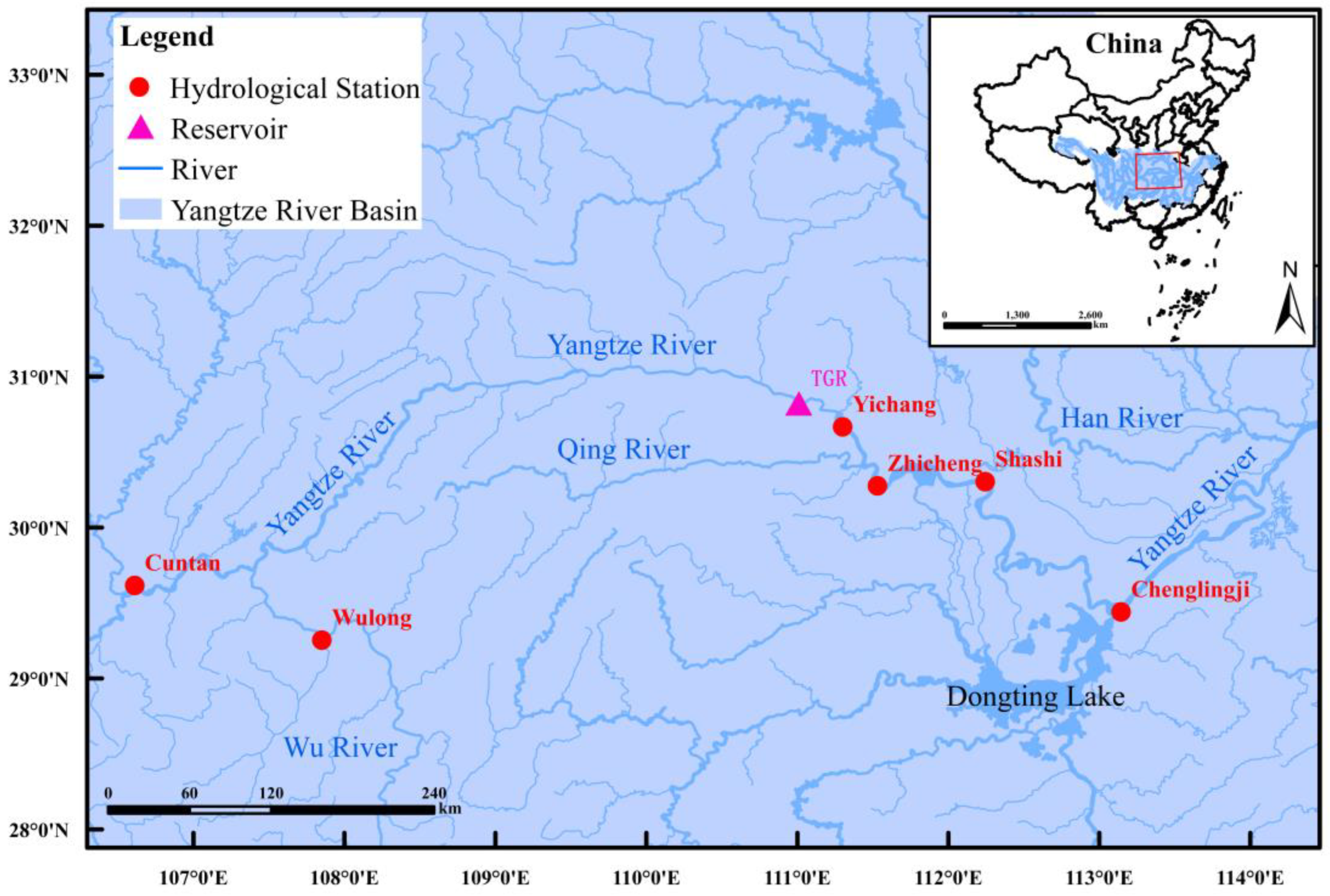
3. Case Study
4. Results and Discussion
4.1. Experimental Conditions
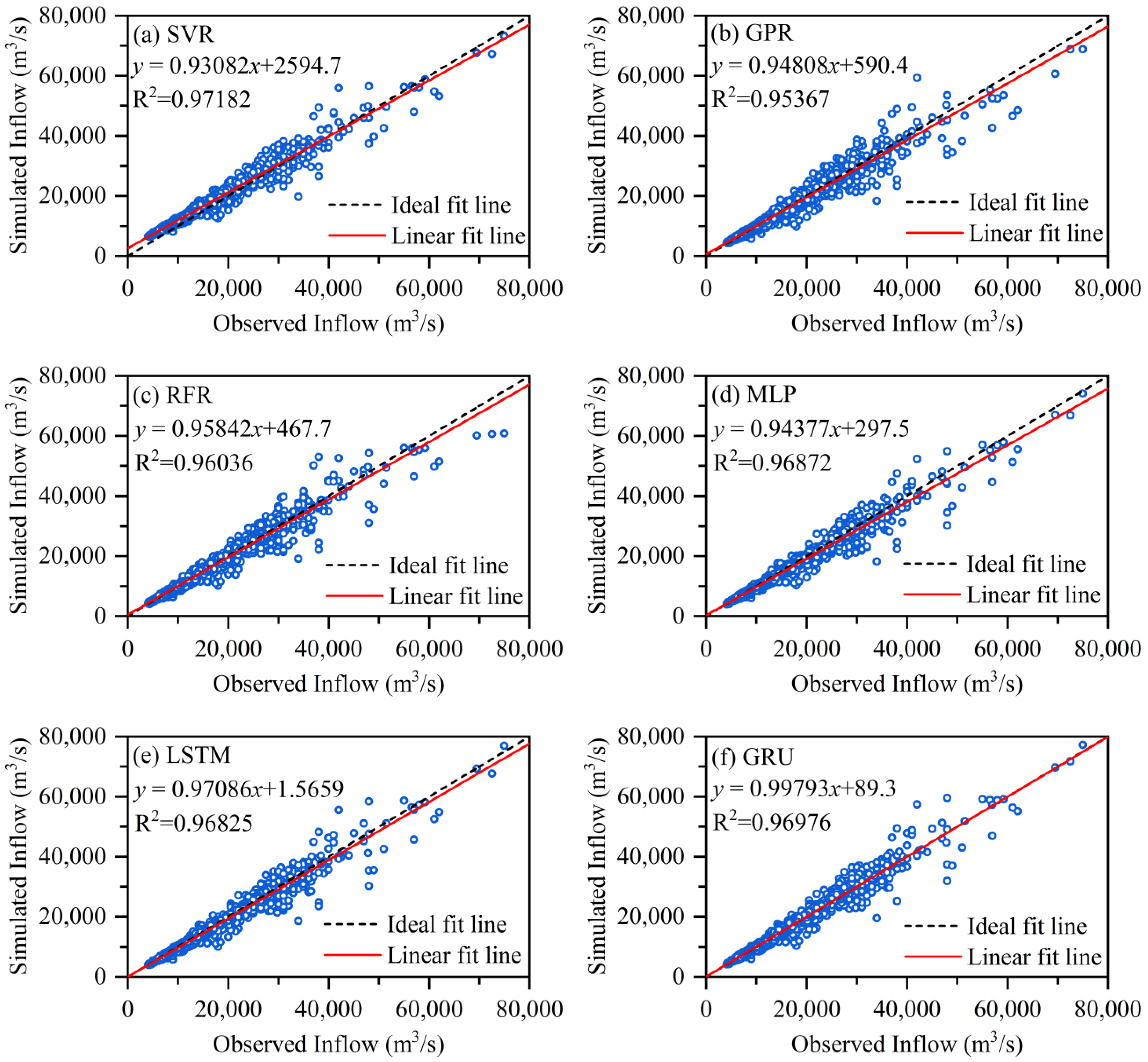
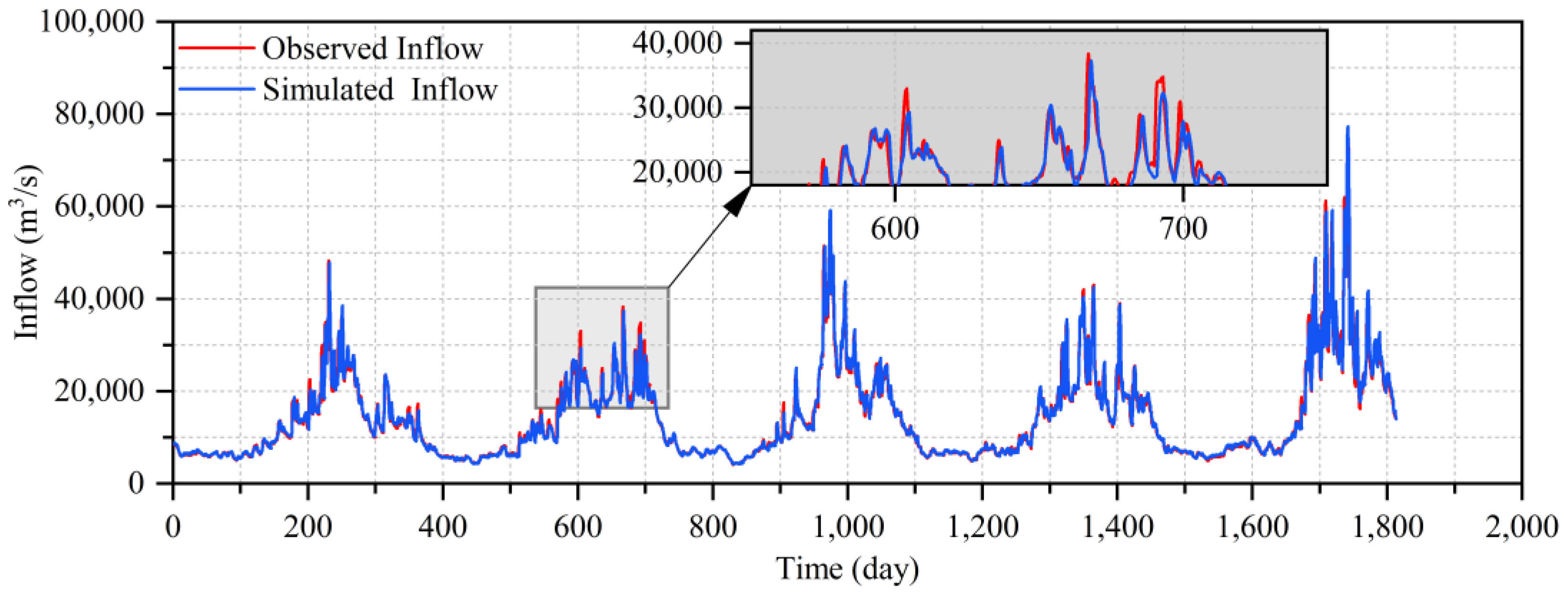
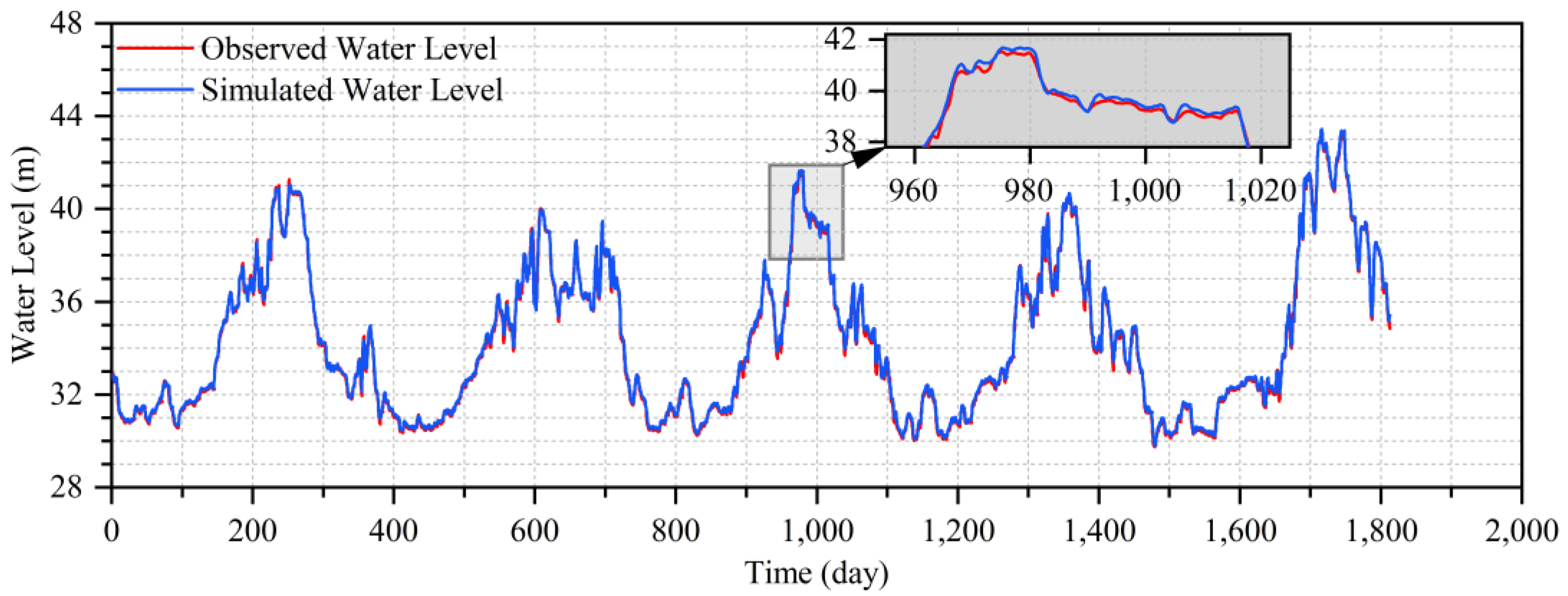
4.2. The Inflow Hydrograph Prediction of the TGR
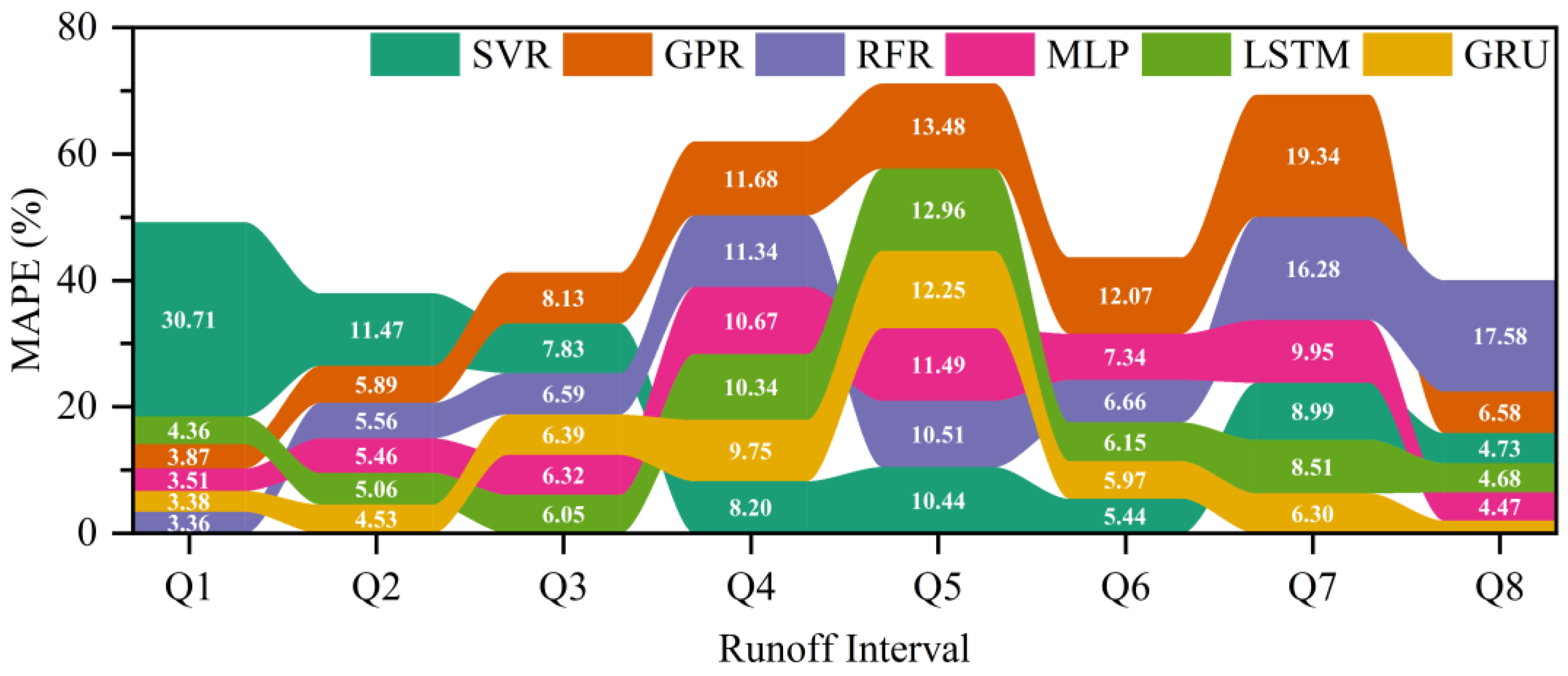
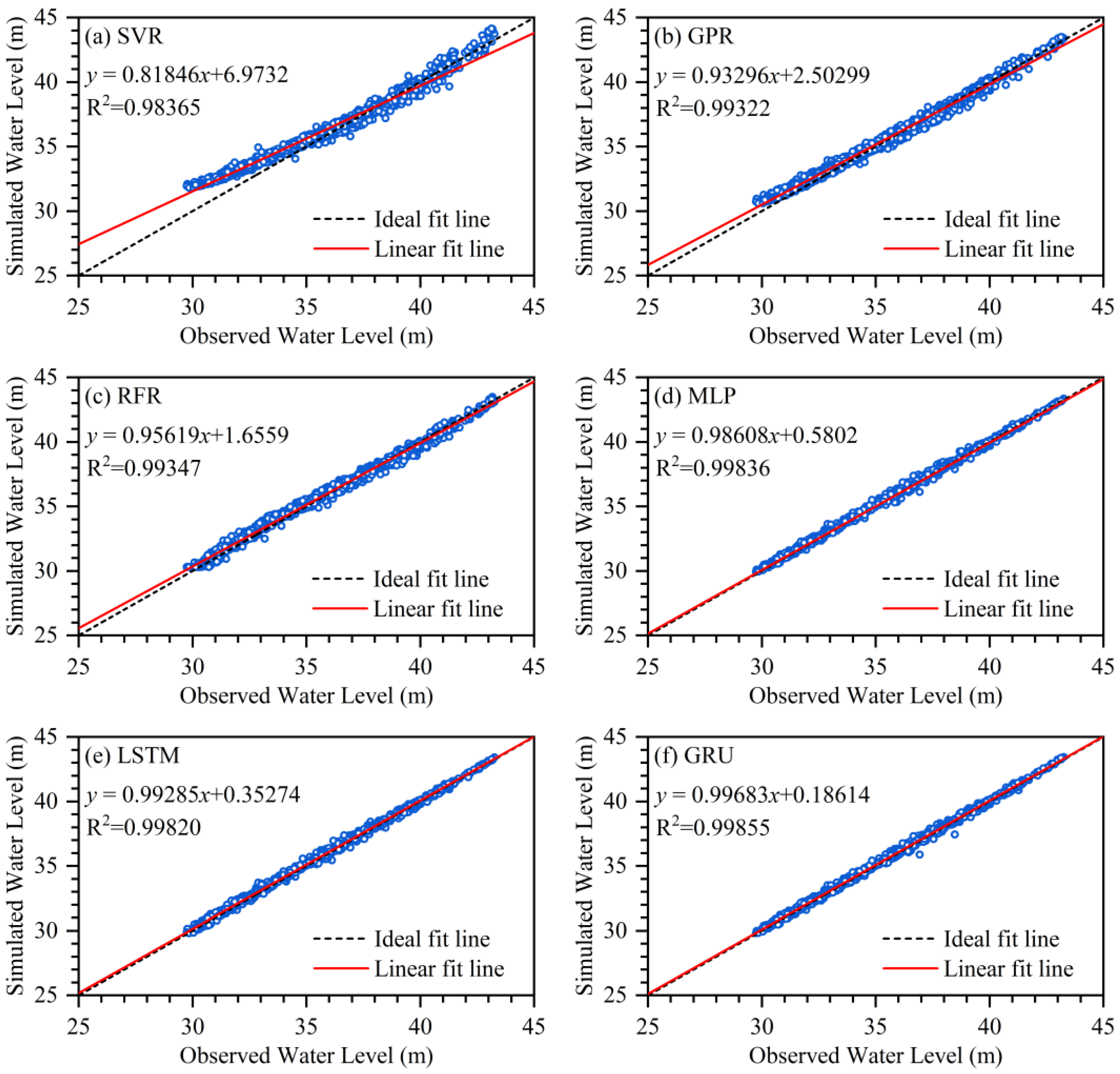
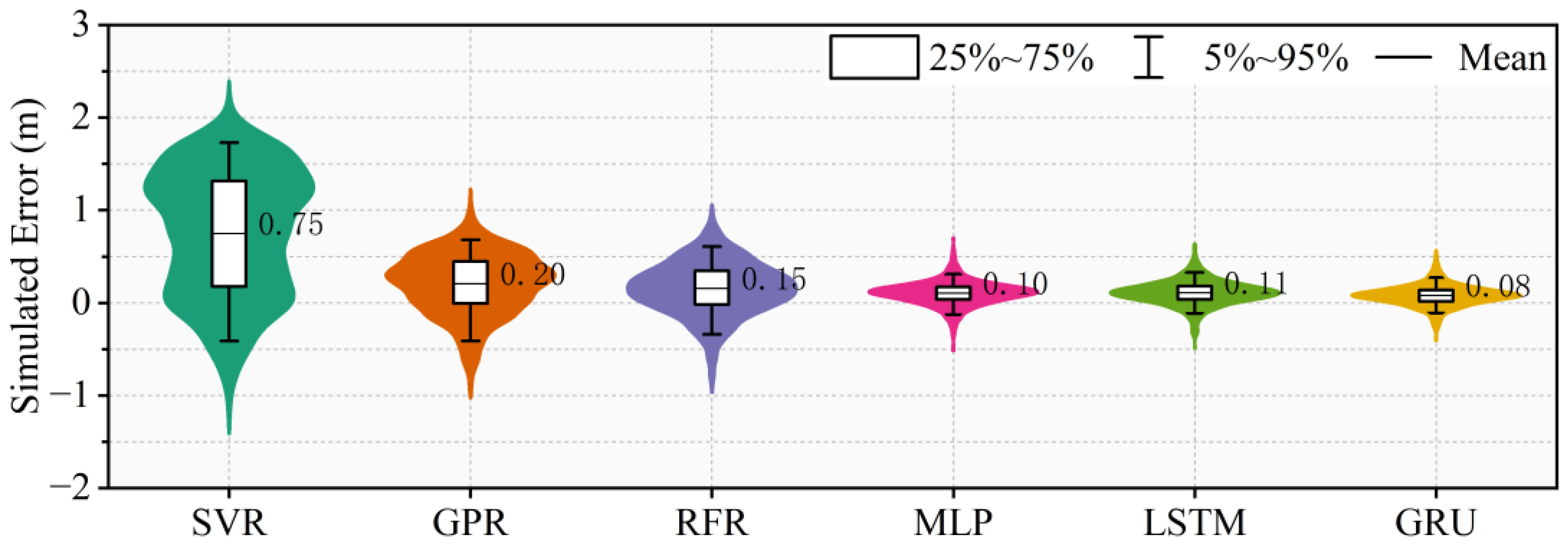
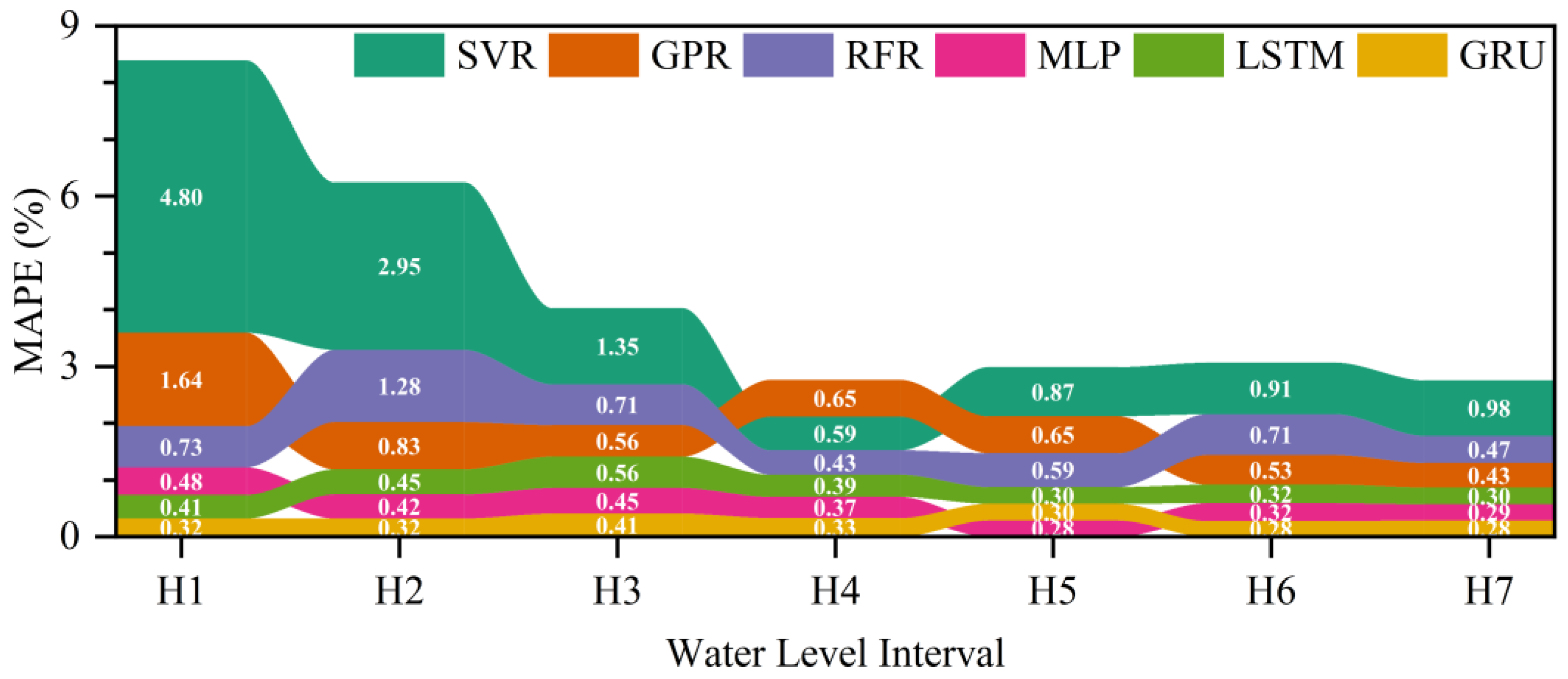
4.3. The Water Level Hydrograph Prediction of Shashi Station
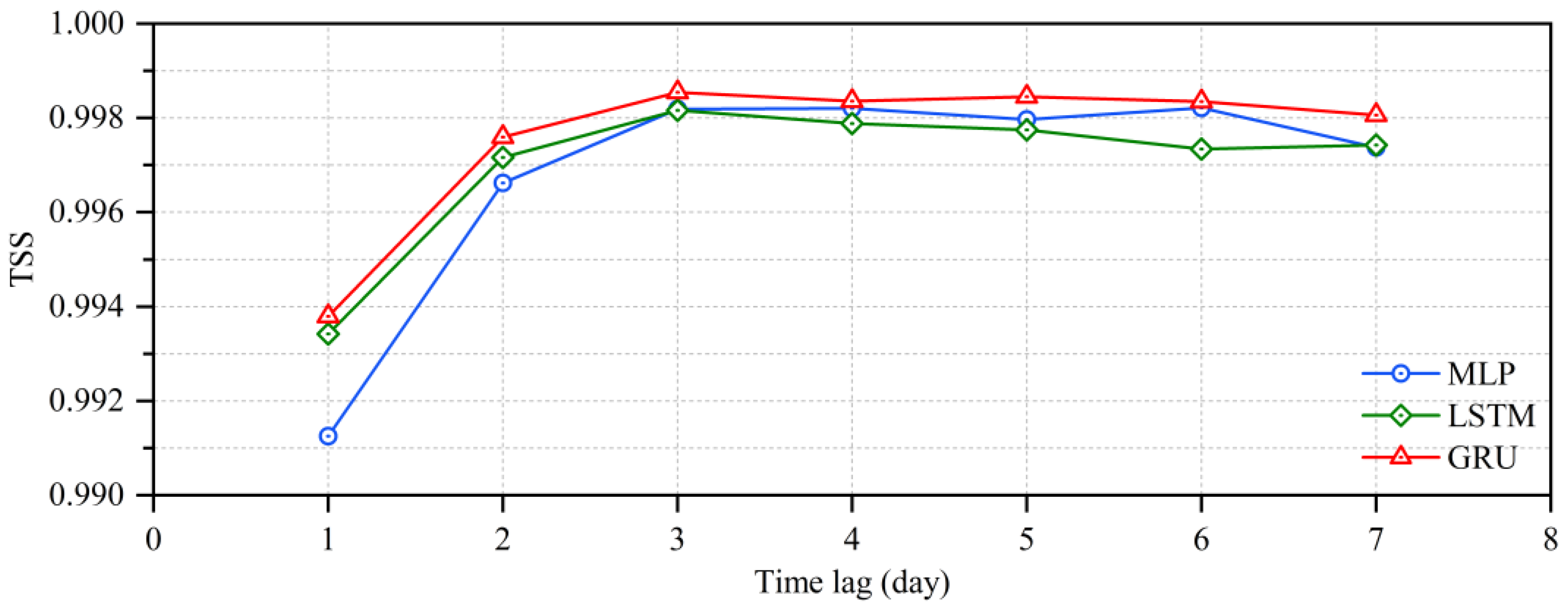
4.4. Performance Comparison among Three Deep Learning Models with Different Time Lags for Flood Routing
5. Conclusions
- (1)
- The ML models were verified as effective and efficient in obtaining accurate flood hydrographs in river flood routing with fewer data (e.g., only flows and water levels that are daily measured). Therefore, the ML models could be widely used for flood routing in complex natural rivers. However, it is important to note that not all ML models were equally effective in flood routing, as some may overfit during the training phase.
- (2)
- The deep learning models, including the MLP, LSTM and GRU models, were more efficient than the SVR, GPR and RFR models. The GRU model, in particular, outperformed the others in almost all efficiency criteria, including MAPE, RMSE, NSE, TSS and KGE. The reductions in MAPE and RMSE were significant, with at least 7.66% and 3.80% for the first case study and 19.51% and 11.76% for the second case study during the testing period.
- (3)
- The model that had higher accuracy may necessitate a longer training time, but the GRU exhibited a faster training rate than the LSTM. Although the training times of the LSTM and GRU were longer than those of the other models, the GRU’s training times were, respectively, 32.19% and 26.14% shorter than those of the LSTM for the two case studies due to its simpler structure and more effortless convergence.
- (4)
- The time lag in flood routing determined the number of input variables of the models, which in turn may have affected the accuracy of flood routing. As a result, the accuracy of flood routing gradually increased and then slightly decreased as the time lag increased for the MLP, LSTM and GRU models. Interestingly, the GRU model performed better than the MLP and LSTM models for different time lags.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akbari, R.; Hessami-Kermani, M.R.; Shojaee, S. Flood Routing: Improving Outflow Using a New Non-linear Muskingum Model with Four Variable Parameters Coupled with PSO-GA Algorithm. Water Resour. Manag. 2020, 34, 3291–3316. [Google Scholar] [CrossRef]
- Kang, L.; Zhou, L.; Zhang, S. Parameter Estimation of Two Improved Nonlinear Muskingum Models Considering the Lateral Flow Using a Hybrid Algorithm. Water Resour. Manag. 2017, 31, 4449–4467. [Google Scholar] [CrossRef]
- Zhang, S.; Kang, L.; Zhou, L.; Guo, X. A new modified nonlinear Muskingum model and its parameter estimation using the adaptive genetic algorithm. Hydrol. Res. 2017, 48, 17–27. [Google Scholar] [CrossRef]
- Yuan, X.; Wu, X.; Tian, H.; Yuan, Y.; Adnan, R.M. Parameter Identification of Nonlinear Muskingum Model with Backtracking Search Algorithm. Water Resour. Manag. 2016, 30, 2767–2783. [Google Scholar] [CrossRef]
- Kim, D.H.; Georgakakos, A.P. Hydrologic routing using nonlinear cascaded reservoirs. Water Resour. Res. 2014, 50, 7000–7019. [Google Scholar] [CrossRef]
- Jeng, R.I.; Coon, G.C. True Form of Instantaneous Unit Hydrograph of Linear Reservoirs. J. Irrig. Drain. Eng. 2003, 129, 11–17. [Google Scholar] [CrossRef]
- Dhote, P.R.; Thakur, P.K.; Domeneghetti, A.; Chouksey, A.; Garg, V.; Aggarwal, S.P.; Chauhan, P. The use of SARAL/AltiKa altimeter measurements for multi-site hydrodynamic model validation and rating curves estimation: An application to Brahmaputra River. Adv. Space Res. 2021, 68, 691–702. [Google Scholar] [CrossRef]
- Singh, R.K.; Kumar Villuri, V.G.; Pasupuleti, S.; Nune, R. Hydrodynamic modeling for identifying flood vulnerability zones in lower Damodar river of eastern India. Ain Shams Eng. J. 2020, 11, 1035–1046. [Google Scholar] [CrossRef]
- Chatterjee, C.; Förster, S.; Bronstert, A. Comparison of hydrodynamic models of different complexities to model floods with emergency storage areas. Hydrol. Process. 2008, 22, 4695–4709. [Google Scholar] [CrossRef]
- Cho, M.; Kim, C.; Jung, K.; Jung, H. Water Level Prediction Model Applying a Long Short-Term Memory (LSTM)-Gated Recurrent Unit (GRU) Method for Flood Prediction. Water 2022, 14, 2221. [Google Scholar] [CrossRef]
- Jeong, J.; Park, E. Comparative applications of data-driven models representing water table fluctuations. J. Hydrol. 2019, 572, 261–273. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Singh, V.P. Univariate streamflow forecasting using commonly used data-driven models: Literature review and case study. Hydrol. Sci. J. 2018, 63, 1091–1111. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Feng, B.F.; Min, Y.W.; Cheng, C.T.; Zhou, J.Z. Comparison of Multiple Linear Regression, Artificial Neural Network, Extreme Learning Machine, and Support Vector Machine in Deriving Operation Rule of Hydropower Reservoir. Water 2019, 11, 17. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Xiao, H.; Fang, H. Component-based Reconstruction Prediction of Runoff at Multi-time Scales in the Source Area of the Yellow River Based on the ARMA Model. Water Resour. Manag. 2022, 36, 433–448. [Google Scholar] [CrossRef]
- Yan, B.; Mu, R.; Guo, J.; Liu, Y.; Tang, J.; Wang, H. Flood risk analysis of reservoirs based on full-series ARIMA model under climate change. J. Hydrol. 2022, 610, 127979. [Google Scholar] [CrossRef]
- Lian, Y.; Luo, J.; Xue, W.; Zuo, G.; Zhang, S. Cause-driven Streamflow Forecasting Framework Based on Linear Correlation Reconstruction and Long Short-term Memory. Water Resour. Manag. 2022, 36, 1661–1678. [Google Scholar] [CrossRef]
- Ebrahimi, E.; Shourian, M. River Flow Prediction Using Dynamic Method for Selecting and Prioritizing K-Nearest Neighbors Based on Data Features. J. Hydrol. Eng. 2020, 25, 04020010. [Google Scholar] [CrossRef]
- Dehghani, R.; Babaali, H.; Zeydalinejad, N. Evaluation of statistical models and modern hybrid artificial intelligence in the simulation of precipitation runoff process. Sustain. Water Resour. Manag. 2022, 8, 154. [Google Scholar] [CrossRef]
- Rahbar, A.; Mirarabi, A.; Nakhaei, M.; Talkhabi, M.; Jamali, M. A Comparative Analysis of Data-Driven Models (SVR, ANFIS, and ANNs) for Daily Karst Spring Discharge Prediction. Water Resour. Manag. 2022, 36, 589–609. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, X.; Xu, Z.; Ye, L. Seasonal streamflow forecasts using mixture-kernel GPR and advanced methods of input variable selection. Hydrol. Res. 2019, 50, 200–214. [Google Scholar] [CrossRef]
- Desai, S.; Ouarda, T.B.M.J. Regional hydrological frequency analysis at ungauged sites with random forest regression. J. Hydrol. 2021, 594, 125861. [Google Scholar] [CrossRef]
- Wang, W.; Jin, J.; Li, Y. Prediction of Inflow at Three Gorges Dam in Yangtze River with Wavelet Network Model. Water Resour. Manag. 2009, 23, 2791–2803. [Google Scholar] [CrossRef]
- Lee, W.J.; Lee, E.H. Runoff Prediction Based on the Discharge of Pump Stations in an Urban Stream Using a Modified Multi-Layer Perceptron Combined with Meta-Heuristic Optimization. Water 2022, 14, 99. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Groundwater level forecasting with artificial neural networks: A comparison of long short-term memory (LSTM), convolutional neural networks (CNNs), and non-linear autoregressive networks with exogenous input (NARX). Hydrol. Earth Syst. Sci. 2021, 25, 1671–1687. [Google Scholar] [CrossRef]
- Peng, A.; Zhang, X.; Xu, W.; Tian, Y. Effects of Training Data on the Learning Performance of LSTM Network for Runoff Simulation. Water Resour. Manag. 2022, 36, 2381–2394. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Yue, Q.; Zheng, Y.; Yao, X.; Yu, J. Impact of Input Filtering and Architecture Selection Strategies on GRU Runoff Forecasting: A Case Study in the Wei River Basin, Shaanxi, China. Water 2020, 12, 3532. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Li, R.; Suo, X.; Lu, E. Medium and Long-term Precipitation Prediction Using Wavelet Decomposition-prediction-reconstruction Model. Water Resour. Manag. 2022, 36, 971–987. [Google Scholar] [CrossRef]
- He, R.; Zhang, L.; Chew, A.W.Z. Modeling and predicting rainfall time series using seasonal-trend decomposition and machine learning. Knowl. Based Syst. 2022, 251, 109125. [Google Scholar] [CrossRef]
- Shabbir, M.; Chand, S.; Iqbal, F. A Novel Hybrid Method for River Discharge Prediction. Water Resour. Manag. 2022, 36, 253–272. [Google Scholar] [CrossRef]
- He, X.; Luo, J.; Zuo, G.; Xie, J. Daily Runoff Forecasting Using a Hybrid Model Based on Variational Mode Decomposition and Deep Neural Networks. Water Resour. Manag. 2019, 33, 1571–1590. [Google Scholar] [CrossRef]
- Ghasempour, R.; Azamathulla, H.M.; Roushangar, K. EEMD and VMD based hybrid GPR models for river streamflow point and interval predictions. Water Supply 2021, 21, 3960–3975. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, B.; He, S.; Wu, X.; Zhao, D. A new precipitation forecast method based on CEEMD-WTD-GRU. Water Supply 2022, 22, 4120–4132. [Google Scholar] [CrossRef]
- Li, B.-J.; Sun, G.-L.; Liu, Y.; Wang, W.-C.; Huang, X.-D. Monthly Runoff Forecasting Using Variational Mode Decomposition Coupled with Gray Wolf Optimizer-Based Long Short-term Memory Neural Networks. Water Resour. Manag. 2022, 36, 2095–2115. [Google Scholar] [CrossRef]
- Ye, S.; Wang, C.; Wang, Y.; Lei, X.; Wang, X.; Yang, G. Real-time model predictive control study of run-of-river hydropower plants with data-driven and physics-based coupled model. J. Hydrol. 2023, 617, 128942. [Google Scholar] [CrossRef]
- Adnan, R.M.; Kisi, O.; Mostafa, R.R.; Ahmed, A.N.; El-Shafie, A. The potential of a novel support vector machine trained with modified mayfly optimization algorithm for streamflow prediction. Hydrol. Sci. J. 2022, 67, 161–174. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Kisi, O.; Yaseen, Z.M.; Shahid, S.; Zounemat-Kermani, M. Improving streamflow prediction using a new hybrid ELM model combined with hybrid particle swarm optimization and grey wolf optimization. Knowl. Based Syst. 2021, 230, 107379. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Trajkovic, S.; Zounemat-Kermani, M.; Li, B.; Kisi, O. Daily streamflow prediction using optimally pruned extreme learning machine. J. Hydrol. 2019, 577, 123981. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Muhammad Adnan, R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. Predicting flood susceptibility using LSTM neural networks. J. Hydrol. 2021, 594, 125734. [Google Scholar] [CrossRef]
- Lian, Y.; Luo, J.; Wang, J.; Zuo, G.; Wei, N. Climate-driven Model Based on Long Short-Term Memory and Bayesian Optimization for Multi-day-ahead Daily Streamflow Forecasting. Water Resour. Manag. 2022, 36, 21–37. [Google Scholar] [CrossRef]
- Kilinc, H.C.; Haznedar, B. A Hybrid Model for Streamflow Forecasting in the Basin of Euphrates. Water 2022, 14, 80. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Mostafa, R.R.; Chen, Z.; Parmar, K.S.; Kisi, O.; Zounemat-Kermani, M. Water Temperature Prediction Using Improved Deep Learning Methods through Reptile Search Algorithm and Weighted Mean of Vectors Optimizer. J. Mar. Sci. Eng. 2023, 11, 259. [Google Scholar] [CrossRef]
- Zhang, F.; Kang, Y.; Cheng, X.; Chen, P.; Song, S. A Hybrid Model Integrating Elman Neural Network with Variational Mode Decomposition and Box–Cox Transformation for Monthly Runoff Time Series Prediction. Water Resour. Manag. 2022, 36, 3673–3697. [Google Scholar] [CrossRef]
- Alizadeh, B.; Bafti, A.G.; Kamangir, H.; Zhang, Y.; Wright, D.B.; Franz, K.J. A novel attention-based LSTM cell post-processor coupled with bayesian optimization for streamflow prediction. J. Hydrol. 2021, 601, 126526. [Google Scholar] [CrossRef]
- Noor, F.; Haq, S.; Rakib, M.; Ahmed, T.; Jamal, Z.; Siam, Z.S.; Hasan, R.T.; Adnan, M.S.G.; Dewan, A.; Rahman, R.M. Water Level Forecasting Using Spatiotemporal Attention-Based Long Short-Term Memory Network. Water 2022, 14, 612. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Wang, G.; Tan, Q. Actual evapotranspiration estimation over the Tuojiang River Basin based on a hybrid CNN-RF model. J. Hydrol. 2022, 610, 127788. [Google Scholar] [CrossRef]
- Zhou, S.; Song, C.; Zhang, J.; Chang, W.; Hou, W.; Yang, L. A Hybrid Prediction Framework for Water Quality with Integrated W-ARIMA-GRU and LightGBM Methods. Water 2022, 14, 1322. [Google Scholar] [CrossRef]
- Xu, W.; Chen, J.; Zhang, X.J. Scale Effects of the Monthly Streamflow Prediction Using a State-of-the-art Deep Learning Model. Water Resour. Manag. 2022, 36, 3609–3625. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, P.; Cheng, L.; Chen, G.; Zhou, Y.; Zhang, X.; Xu, W. Determining dynamic water level control boundaries for a multi-reservoir system during flood seasons with considering channel storage. J. Flood Risk Manag. 2020, 13, e12586. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Yang, Z.-L.; Wang, J.; Lin, P.; Liang, J.; Li, Z.; Gu, Z. Improving flood simulation capability of the WRF-Hydro-RAPID model using a multi-source precipitation merging method. J. Hydrol. 2021, 592, 125814. [Google Scholar] [CrossRef]
- Ping, F.; Jia-chun, L.; Qing-quan, L. Flood routing models in confluent and dividing channels. Appl. Math. Mech. 2004, 25, 1333–1343. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Z.; Liu, K.; Cheng, L.; Bai, Y.; Jin, G. Optimizing flood diversion siting and its control strategy of detention basins: A case study of the Yangtze River, China. J. Hydrol. 2021, 597, 126201. [Google Scholar] [CrossRef]
- Chiang, S.; Chang, C.-H.; Chen, W.-B. Comparison of Rainfall-Runoff Simulation between Support Vector Regression and HEC-HMS for a Rural Watershed in Taiwan. Water 2022, 14, 191. [Google Scholar] [CrossRef]
- Roushangar, K.; Chamani, M.; Ghasempour, R.; Azamathulla, H.M.; Alizadeh, F. A comparative study of wavelet and empirical mode decomposition-based GPR models for river discharge relationship modeling at consecutive hydrometric stations. Water Supply 2021, 21, 3080–3098. [Google Scholar] [CrossRef]
- Kumar, M.; Elbeltagi, A.; Pande, C.B.; Ahmed, A.N.; Chow, M.F.; Pham, Q.B.; Kumari, A.; Kumar, D. Applications of Data-driven Models for Daily Discharge Estimation Based on Different Input Combinations. Water Resour. Manag. 2022, 36, 2201–2221. [Google Scholar] [CrossRef]
- Rezaie-Balf, M.; Nowbandegani, S.F.; Samadi, S.Z.; Fallah, H.; Alaghmand, S. An Ensemble Decomposition-Based Artificial Intelligence Approach for Daily Streamflow Prediction. Water 2019, 11, 709. [Google Scholar] [CrossRef] [Green Version]
- Acharya, U.; Daigh, A.L.M.; Oduor, P.G. Machine Learning for Predicting Field Soil Moisture Using Soil, Crop, and Nearby Weather Station Data in the Red River Valley of the North. Soil Syst. 2021, 5, 57. [Google Scholar] [CrossRef]
- Khosravi, K.; Golkarian, A.; Tiefenbacher, J.P. Using Optimized Deep Learning to Predict Daily Streamflow: A Comparison to Common Machine Learning Algorithms. Water Resour. Manag. 2022, 36, 699–716. [Google Scholar] [CrossRef]
- Xie, J.; Liu, X.; Tian, W.; Wang, K.; Bai, P.; Liu, C. Estimating Gridded Monthly Baseflow From 1981 to 2020 for the Contiguous US Using Long Short-Term Memory (LSTM) Networks. Water Resour. Res. 2022, 58, e2021WR031663. [Google Scholar] [CrossRef]
- Li, Z.; Kang, L.; Zhou, L.; Zhu, M. Deep Learning Framework with Time Series Analysis Methods for Runoff Prediction. Water 2021, 13, 575. [Google Scholar] [CrossRef]
- Nevo, S.; Morin, E.; Gerzi Rosenthal, A.; Metzger, A.; Barshai, C.; Weitzner, D.; Voloshin, D.; Kratzert, F.; Elidan, G.; Dror, G.; et al. Flood forecasting with machine learning models in an operational framework. Hydrol. Earth Syst. Sci. 2022, 26, 4013–4032. [Google Scholar] [CrossRef]
- Anderson, S.; Radić, V. Evaluation and interpretation of convolutional long short-term memory networks for regional hydrological modelling. Hydrol. Earth Syst. Sci. 2022, 26, 795–825. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Y. Suspended sediment concentration forecast based on CEEMDAN-GRU model. Water Supply 2020, 20, 1787–1798. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Bai, T.; Wei, J.; Yang, W.W.; Huang, Q. Multi-Objective Parameter Estimation of Improved Muskingum Model by Wolf Pack Algorithm and Its Application in Upper Hanjiang River, China. Water 2018, 10, 14. [Google Scholar] [CrossRef] [Green Version]
- Dazzi, S.; Vacondio, R.; Mignosa, P. Flood Stage Forecasting Using Machine-Learning Methods: A Case Study on the Parma River (Italy). Water 2021, 13, 1612. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, L. A novel dynamic predictive method of water inrush from coal floor based on gated recurrent unit model. Nat. Hazards 2021, 105, 2027–2043. [Google Scholar] [CrossRef]
- Wang, J.; Cui, Q.; Sun, X. A novel framework for carbon price prediction using comprehensive feature screening, bidirectional gate recurrent unit and Gaussian process regression. J. Clean. Prod. 2021, 314, 128024. [Google Scholar] [CrossRef]
- Park, K.; Jung, Y.; Seong, Y.; Lee, S. Development of Deep Learning Models to Improve the Accuracy of Water Levels Time Series Prediction through Multivariate Hydrological Data. Water 2022, 14, 469. [Google Scholar] [CrossRef]


| Dataset | Model | MAPE (%) | RMSE (m3/s) | NSE | R | TSS | KGE | Time (s) |
|---|---|---|---|---|---|---|---|---|
| Training | LMM | 6.25 | 1834 | 0.9681 | 0.9858 | 0.9701 | 0.9370 | 7.969 |
| SVR | 27.19 | 2348 | 0.9478 | 0.9898 | 0.9757 | 0.8506 | 0.057 | |
| GPR | 6.28 | 1698 | 0.9727 | 0.9864 | 0.9721 | 0.9662 | 6.159 | |
| RFR | 4.72 | 1171 | 0.9870 | 0.9935 | 0.9869 | 0.9852 | 8.992 | |
| MLP | 5.12 | 1438 | 0.9804 | 0.9915 | 0.9811 | 0.9462 | 2.370 | |
| LSTM | 5.58 | 1404 | 0.9813 | 0.9911 | 0.9820 | 0.9694 | 13.841 | |
| GRU | 5.17 | 1401 | 0.9814 | 0.9909 | 0.9819 | 0.9837 | 9.386 | |
| Testing | LMM | 6.48 | 2262 | 0.9429 | 0.9733 | 0.9463 | 0.9361 | \ |
| SVR | 19.96 | 2301 | 0.9410 | 0.9858 | 0.9687 | 0.8720 | \ | |
| GPR | 5.65 | 2044 | 0.9534 | 0.9766 | 0.9531 | 0.9612 | \ | |
| RFR | 5.01 | 1889 | 0.9602 | 0.9800 | 0.9601 | 0.9691 | \ | |
| MLP | 4.96 | 1763 | 0.9653 | 0.9842 | 0.9672 | 0.9436 | \ | |
| LSTM | 5.21 | 1736 | 0.9664 | 0.9840 | 0.9682 | 0.9643 | \ | |
| GRU | 4.58 | 1670 | 0.9689 | 0.9848 | 0.9697 | 0.9793 | \ |
| Dataset | Model | MAPE (%) | RMSE (m) | NSE | R | TSS | KGE | Time (s) |
|---|---|---|---|---|---|---|---|---|
| Training | SVR | 1.65 | 0.67 | 0.9601 | 0.9908 | 0.9659 | 0.8796 | 0.014 |
| GPR | 0.57 | 0.28 | 0.9932 | 0.9966 | 0.9932 | 0.9882 | 5.291 | |
| RFR | 0.30 | 0.15 | 0.9979 | 0.9989 | 0.9979 | 0.9975 | 3.723 | |
| MLP | 0.22 | 0.14 | 0.9983 | 0.9992 | 0.9984 | 0.9968 | 3.845 | |
| LSTM | 0.23 | 0.15 | 0.9981 | 0.9991 | 0.9982 | 0.9985 | 11.912 | |
| GRU | 0.24 | 0.14 | 0.9983 | 0.9993 | 0.9986 | 0.9943 | 8.798 | |
| Testing | SVR | 2.64 | 1.02 | 0.9037 | 0.9918 | 0.9483 | 0.8237 | \ |
| GPR | 0.99 | 0.39 | 0.9857 | 0.9966 | 0.9889 | 0.9358 | \ | |
| RFR | 0.78 | 0.33 | 0.9899 | 0.9967 | 0.9918 | 0.9589 | \ | |
| MLP | 0.41 | 0.17 | 0.9972 | 0.9992 | 0.9984 | 0.9869 | \ | |
| LSTM | 0.42 | 0.18 | 0.9971 | 0.9991 | 0.9944 | 0.9937 | \ | |
| GRU | 0.33 | 0.15 | 0.9980 | 0.9993 | 0.9985 | 0.9966 | \ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Kang, L. A Comparative Analysis of Multiple Machine Learning Methods for Flood Routing in the Yangtze River. Water 2023, 15, 1556. https://doi.org/10.3390/w15081556
Zhou L, Kang L. A Comparative Analysis of Multiple Machine Learning Methods for Flood Routing in the Yangtze River. Water. 2023; 15(8):1556. https://doi.org/10.3390/w15081556
Chicago/Turabian StyleZhou, Liwei, and Ling Kang. 2023. "A Comparative Analysis of Multiple Machine Learning Methods for Flood Routing in the Yangtze River" Water 15, no. 8: 1556. https://doi.org/10.3390/w15081556





