The Impacts of Climate Change on the Hydrological Process and Water Quality in the Three Gorges Reservoir Area, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Methods of Analysis
2.2.1. Mann–Kendall Test
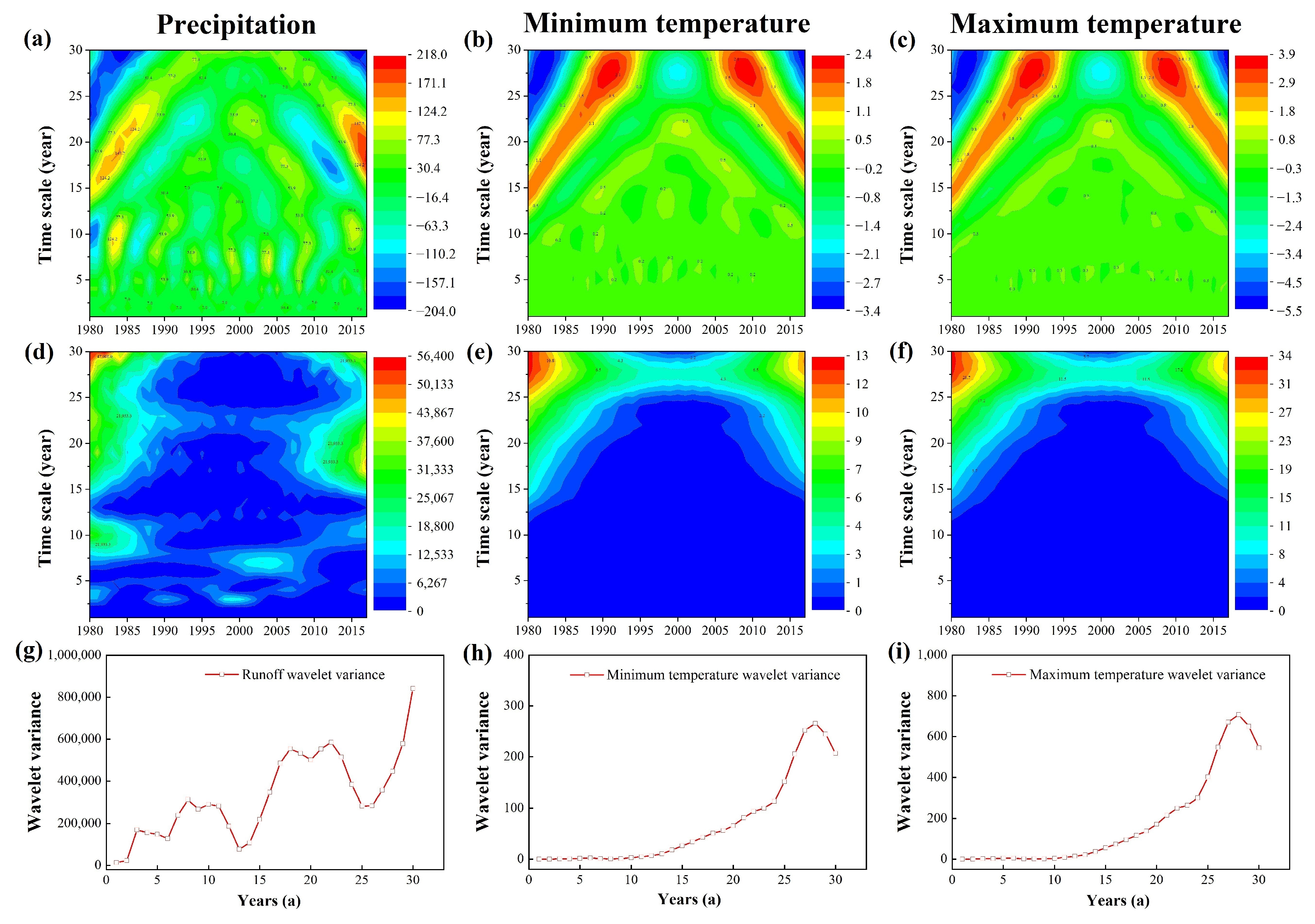
2.2.2. Wavelet Analysis
2.2.3. Moving Average Analysis
2.2.4. Anomaly Analysis
2.2.5. Spatial Interpolation
2.3. Hydrological Model
2.3.1. Data Source
2.3.2. Model Setup
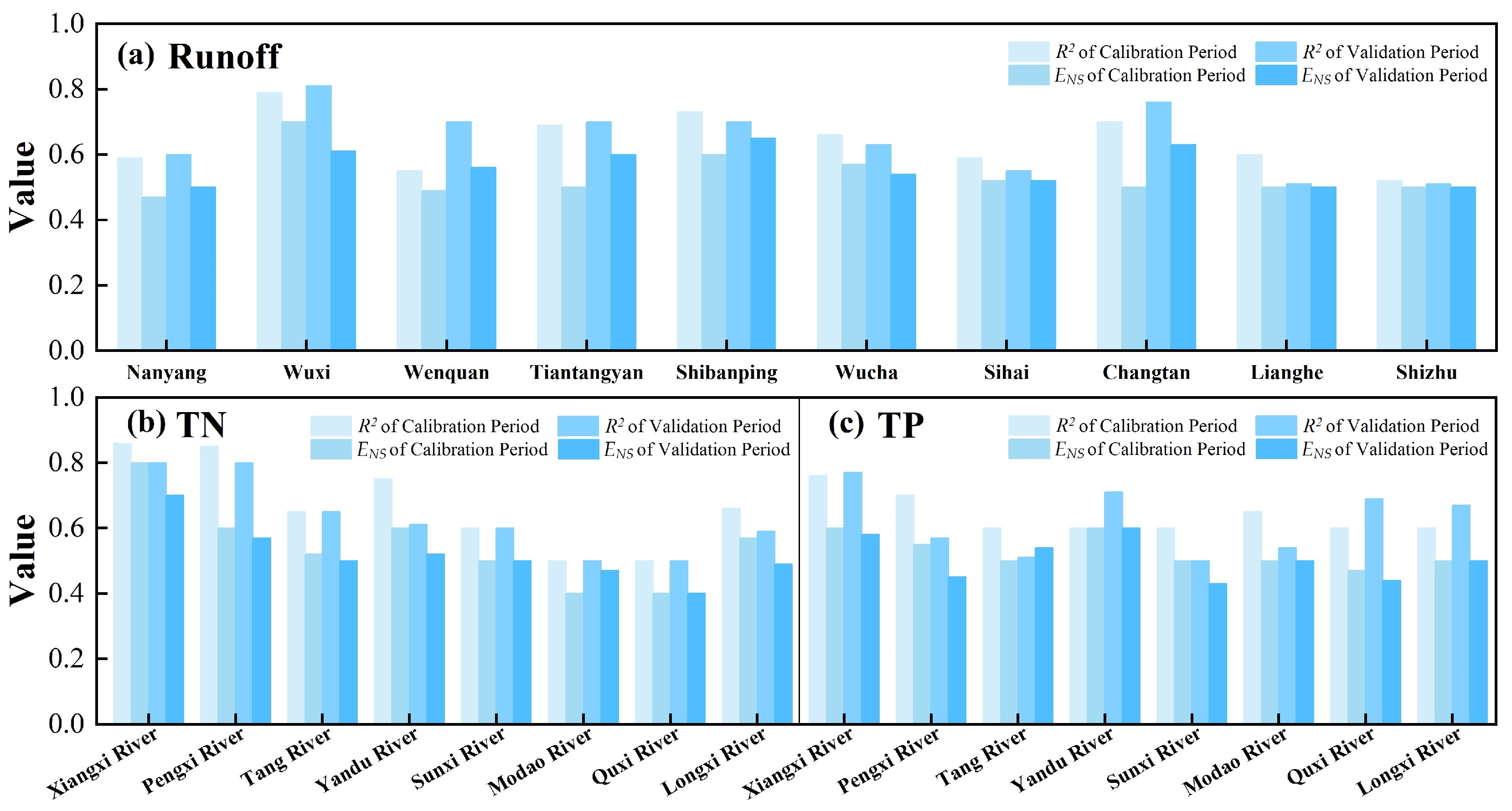
2.3.3. Model Calibration and Validation
2.4. Correlation Analysis
3. Results and Discussion
3.1. Calibration and Validation Results
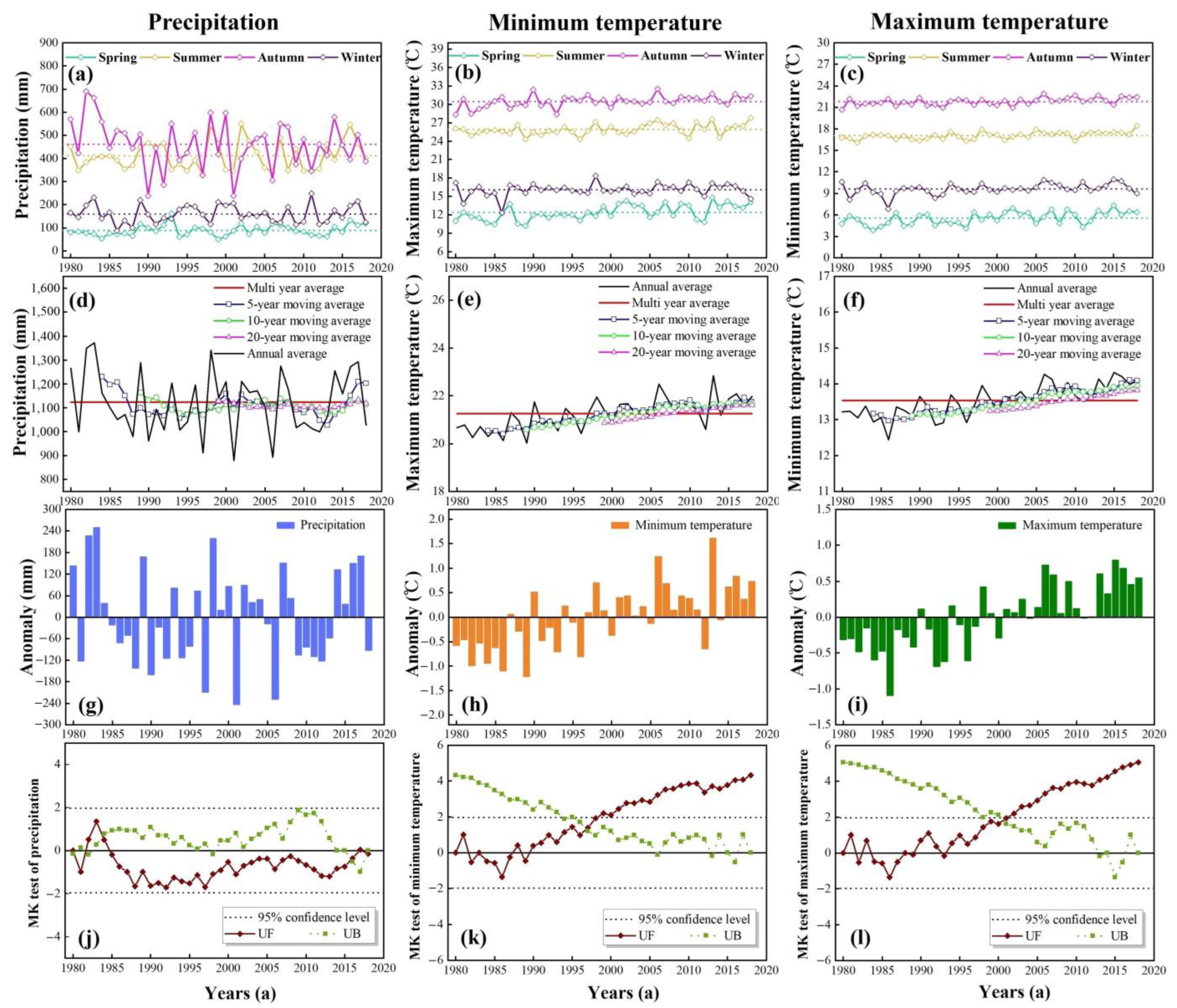
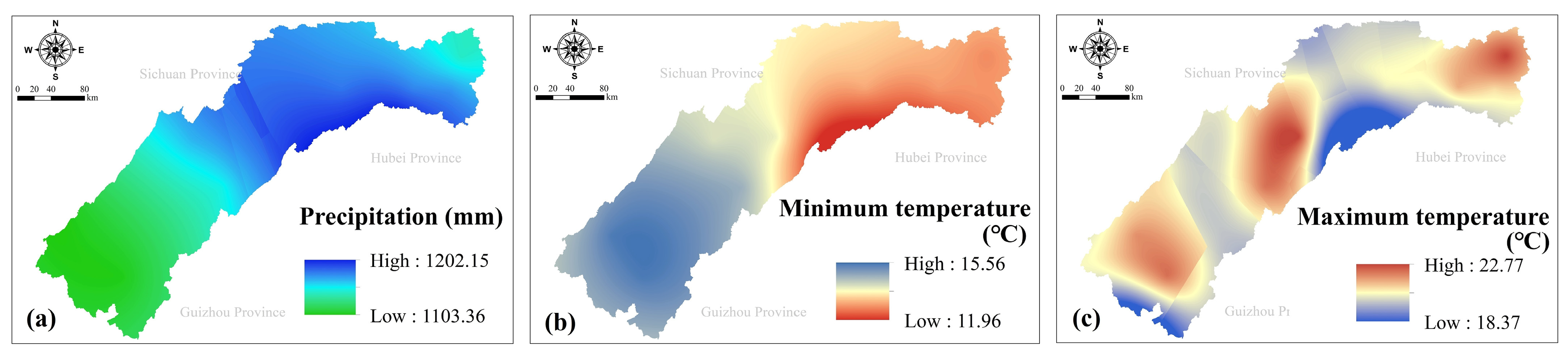
3.2. Spatial and Temporal Distribution of Climate Change
3.2.1. Temporal Distribution
3.2.2. Spatial Distribution
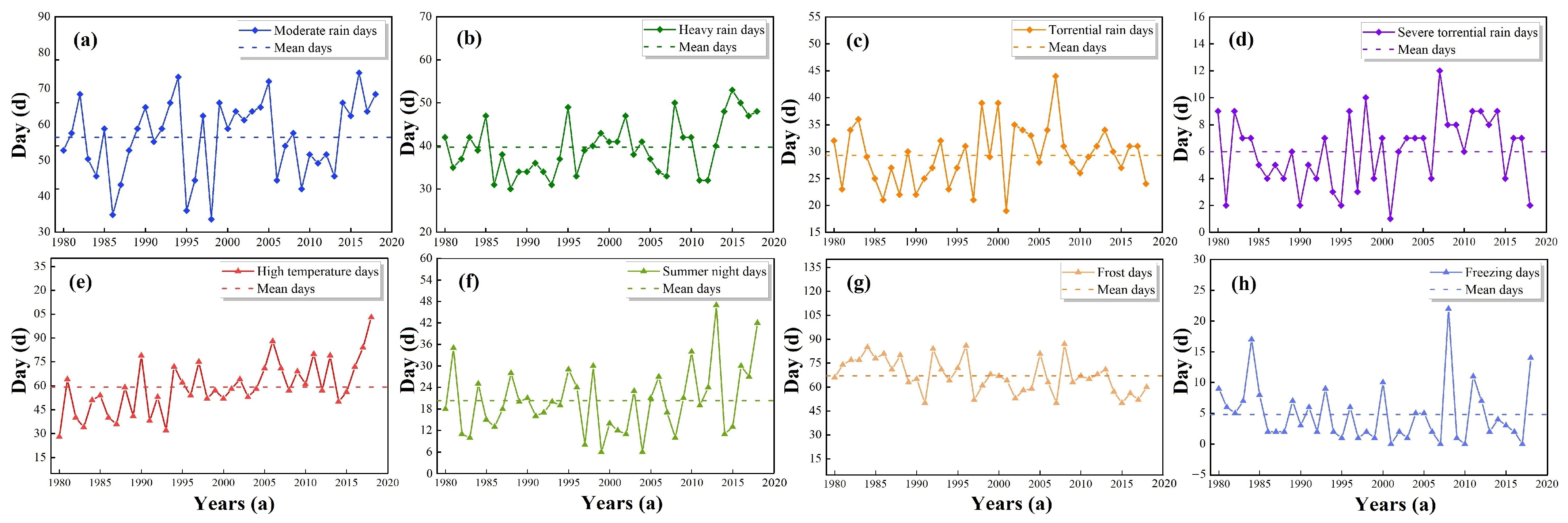
3.2.3. Extreme Weather
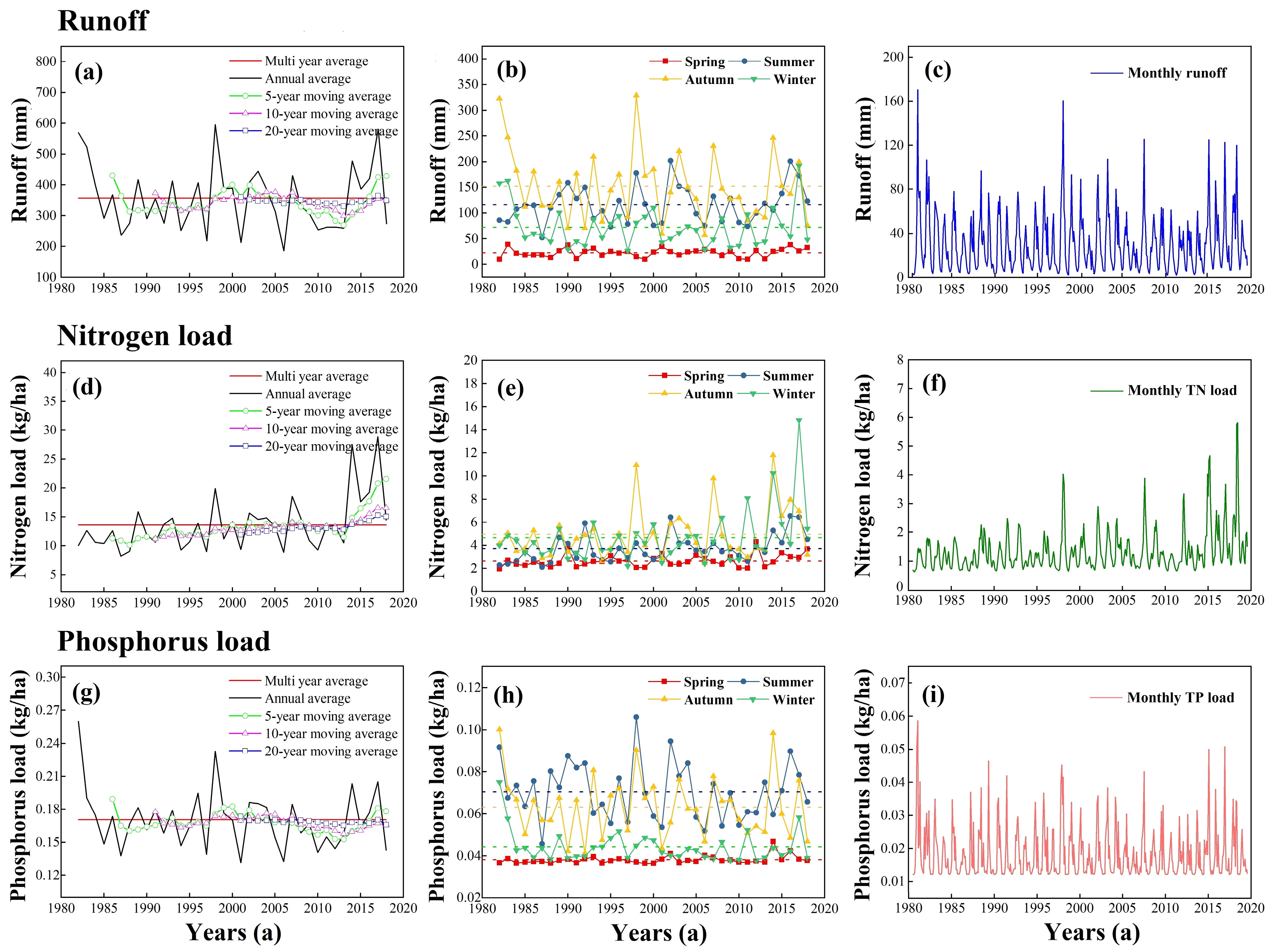
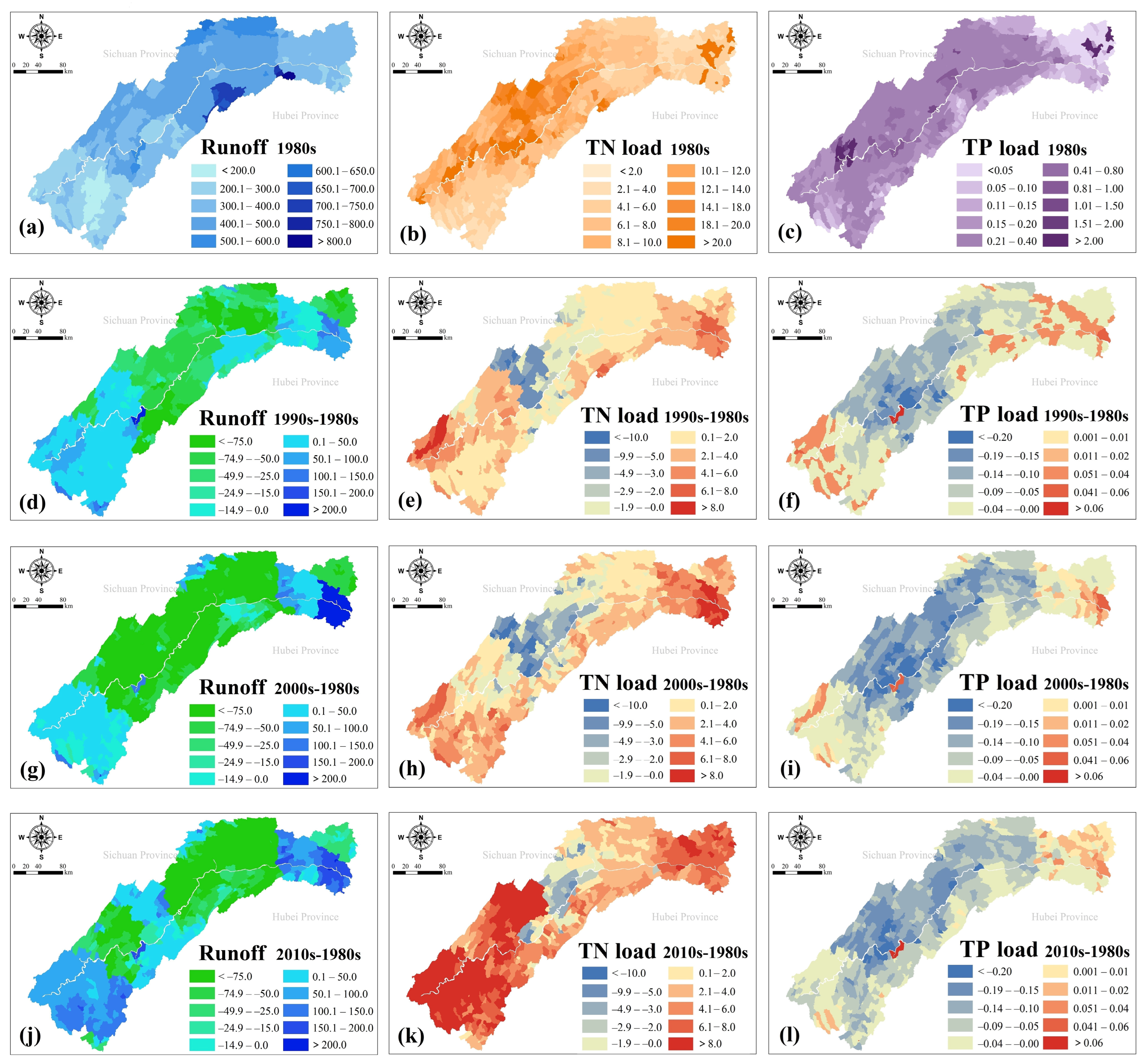
3.3. Spatial and Temporal Distribution of Runoff, TN and TP Loads
3.3.1. Temporal Distribution
3.3.2. Spatial Distribution
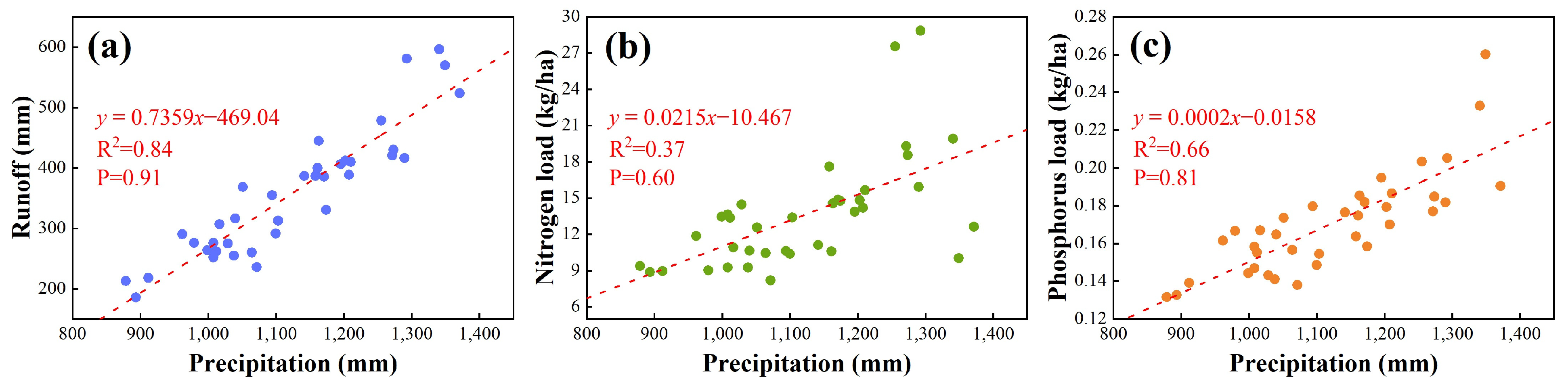
3.4. Response Relation
3.4.1. Climate Change Impact
3.4.2. Extreme Weather Impact
4. Conclusions
- The inter-annual variation in precipitation fluctuated greatly during the study period, and there was no abrupt change point. The temperature showed an increasing trend; the increasing rates of the maximum and minimum temperature were 0.38 °C/10a and 0.29 °C/10a, respectively. The precipitation presented a spatial distribution trend of less-more-less from west to east, while high temperatures mainly appeared in the urban area. Extreme precipitation events and extremely hot weather have increased during the past decades.
- The average annual value of runoff, TN, and TP loads showed a decreasing trend followed by an increasing trend and fluctuated violently within the short period. The runoff decreased significantly at the head and middle reservoir region, while it also showed an increasing trend at the tail reservoir area. Except for a few areas of the middle region, TN in most areas showed an increasing trend while TP decreased.
- Climate change and extreme precipitation events have had a significant impact on the runoff and TP load, while the impact on the TN load has increased significantly over the past 20 years. With climate change, variability in the water cycle has intensified, which may bring floods and greater pollution in the water environment. It is necessary for the national government and various departments to conduct more comprehensive assessments of climate change and its influence to support integrated water resources management.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Li, S.Y.; Dong, R.Z.; Jiang, C.S.; Ni, M.F. Influences of land use metrics at multi-spatial scales on seasonal water quality: A case study of river systems in the Three Gorges Reservoir Area, China. J. Clean Prod. 2018, 206, 76–85. [Google Scholar] [CrossRef]
- Ye, X.C.; Zhang, Q.; Liu, J.; Li, X.H.; Xu, C.Y. Distinguishing the relative impacts of climate change and human activities on variation of streamflow in the Poyang Lake catchment, China. J. Hydrol. 2013, 494, 83–95. [Google Scholar] [CrossRef]
- Sinha, E.; Michalak, A.M. Precipitation Dominates Interannual Variability of Riverine Nitrogen Loading across the Continental United States. Environ. Sci. Technol. 2016, 50, 12874–12884. [Google Scholar] [CrossRef] [PubMed]
- Elsner, M.M.; Cuo, L.; Voisin, N.; Deems, J.S.; Hamlet, A.F.; Vano, J.A.; Mickelson, K.E.B.; Lee, S.Y.; Lettenmaier, D.P. Implications of 21st century climate change for the hydrology of Washington State. Clim. Chang. 2010, 102, 225–260. [Google Scholar] [CrossRef] [Green Version]
- Steinman, B.A.; Abbott, M.B. Isotopic and hydrologic responses of small, closed lakes to climate variability: Hydroclimate reconstructions from lake sediment oxygen isotope records and mass balance models. Geochim. Cosmochim. Acta 2013, 105, 342–359. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef]
- Marhaento, H.; Booij, M.J.; Hoekstra, A.Y. Hydrological response to future land-use change and climate change in a tropical catchment. Hydrolog. Sci. J. 2018, 63, 1368–1385. [Google Scholar] [CrossRef] [Green Version]
- Archer, D.R.; Fowler, H.J. Spatial and temporal variations in precipitation in the Upper Indus Basin, global teleconnections, and hydrological implications. Hydrol. Earth Syst. Sc. 2004, 8, 47–61. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, S.; Bhatta, B.; Shrestha, M.; Shrestha, P.K. Integrated assessment of the climate and land use change impact on hydrology and water quality in the Songkhram River Basin, Thailand. Sci. Total Environ. 2018, 653, 1610–1622. [Google Scholar] [CrossRef]
- Wang, X.; He, K.; Dong, Z. Effects of climate change and human activities on runoff in the Beichuan River Basin in the northeastern Tibetan Plateau, China. Catena 2019, 176, 81–93. [Google Scholar] [CrossRef]
- Shahid, M.; Rahman, K.U. Identifying the Annual and Seasonal Trends of Hydrological and Climatic Variables in the Indus Basin Pakistan. J. Atmos. Sci. 2020, 57, 191–205. [Google Scholar] [CrossRef]
- Hang, Y.F.; Guan, D.X.; Jin, C.J.; Wang, A.Z.; Wu, J.B.; Yuan, F.H. Analysis of impacts of climate variability and human activity on streamflow for a river basin in northeast China. J. Hydrol. 2011, 410, 239–247. [Google Scholar] [CrossRef]
- Chen, X.M.; Xu, G.H.; Zhang, W.S.; Peng, H.; Xia, H.; Zhang, X.; Ke, Q.; Wan, J. Spatial Variation Pattern Analysis of Hydrologic Processes and Water Quality in Three Gorges Reservoir Area. Water 2020, 11, 2608. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Xu, Y.; Chen, Y.; Xu, C.Y.; Gao, Y.; Du, J. Hydrological Response to Urbanization at Different Spatio-Temporal Scales Simulated by Coupling of CLUE-S and the SWAT Model in the Yangtze River Delta Region. J. Hydrol. 2013, 485, 113–125. [Google Scholar] [CrossRef]
- Qian, S.S.; Kennen, J.G.; May, J.; Freeman, M.C.; Cuffney, T.F. Evaluating the impact of watershed development and climate change on stream ecosystems: A Bayesian network modeling approach. Water Res. 2021, 205, 117685. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, W.; Zhao, Y.; Peng, H.; Shi, Y. Modelling water quality and quantity with the influence of inter-basin water diversion projects and cascade reservoirs in the Middle-lower Hanjiang River. J. Hydrol. 2016, 541, 1348–1362. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.C.; Kalcic, M.; Muenich, R.L.; Yang, Y.C.E.; Scavia, D. Evaluating the impact of climate change on fluvial flood risk in a mixed-use watershed. Environ. Modell. Softw. 2019, 122, 104031. [Google Scholar] [CrossRef]
- Worku, G.; Teferi, E.; Bantider, A.; Dile, Y.T. Modelling hydrological processes under climate change scenarios in the Jemma sub-basin of upper Blue Nile Basin, Ethiopia. Clim. Risk Manag. 2021, 31, 100272. [Google Scholar] [CrossRef]
- Debele, B.; Srinivasan, R.; Parlange, J.Y. Coupling upland watershed and downstream waterbody hydrodynamic and water quality models (SWAT and CE-QUALW2) for better water resources management in complex river basins. Environ. Model Assess. 2008, 13, 135–153. [Google Scholar] [CrossRef]
- Wang, R.Y.; Yuan, Y.P.; Yen, H.; Grieneisen, M.; Arnold, J.; Wang, D.; Wang, C.Z.; Zhang, M.H. A review of pesticide fate and transport simulation at watershed level using SWAT: Current status and research concerns. Sci. Total Environ. 2019, 669, 512–526. [Google Scholar] [CrossRef]
- Yuan, Z.; Yan, D.H.; Yang, Z.Y.; Xu, J.J.; Huo, J.J.; Zhou, Y.L.; Zhang, C. Attribution assessment and projection of natural runoff change in the Yellow River Basin of China. Mitig. Adapt. Strat. Gl. 2018, 23, 27–49. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, G.; Wang, Y.; Engel, B.A.; Peng, H.; Zhang, W.; Cheng, M.; Dai, M. Modelling hydrology and water quality processes in the Pengxi River basin of the Three Gorges Reservoir using the soil and water assessment tool. Agric. Water Manag. 2017, 182, 24–38. [Google Scholar] [CrossRef]
- Gao, H.; He, X.; Ye, B.; Pu, J. Modeling the runoff and glacier mass balance in a small watershed on the Central Tibetan Plateau, China, from 1955 to 2008. Hydrol. Process. 2012, 26, 1593–1603. [Google Scholar] [CrossRef]
- Gu, H.H.; Yu, Z.B.; Wang, G.L.; Wang, J.G.; Ju, Q.; Yang, C.G.; Fan, C.H. Impact of climate change on hydrological extremes in the Yangtze River Basin, China. Stoch. Env. Res. Risk A. 2015, 29, 693–707. [Google Scholar] [CrossRef]
- Duan, W.L.; He, B.; Chen, Y.N.; Zou, S.; Wang, Y.; Nover, D.; Chen, W.; Yang, G.S. Identification of long-term trends and seasonality in high-frequency water quality data from the Yangtze River basin, China. PLoS ONE 2017, 13, e0188889. [Google Scholar] [CrossRef]
- Xia, J.; Chen, J. A new era of flood control strategies from the perspective of managing the 2020 Yangtze River flood. Sci. China Earth Sci. 2021, 64, 1–9. [Google Scholar] [CrossRef]
- Sheng, L.; Liu, D.Y.; Wang, B.H.; Yu, S.H.; Zuo, Y.W. Temporal variations characteristic of precipitation in the Three Gorges Reservoir area from 1961 to 2016. J. Water Clim. Chang. 2022, 13, 1765–1775. [Google Scholar] [CrossRef]
- Di, M.X.; Wang, J. Microplastics in surface waters and sediments of the Three Gorges Reservoir, China. Sci. Total Environ. 2018, 616, 1620–1627. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, M.L.; Chen, J.; Zhong, P.A.; Wu, X.F.; Wu, S.Q. Multiscale attribution analysis for assessing effects of changing environment on runoff: Case study of the Upstream Yangtze River in China. J. Water Clim. Chang. 2021, 12, 627–646. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, Y.J.; Ye, B.S.; Liu, F.J.; Wang, J.; Wang, J. Contributions of climate and human activities to changes in runoff of the Yellow and Yangtze rivers from 1950 to 2008. Sci. China Earth Sci. 2013, 56, 1398–1412. [Google Scholar] [CrossRef]
- Pandey, B.K.; Tiwari, H.; Khare, D. Trend analysis using discrete wavelet transform (DWT) for long-term precipitation (1851–2006) over India. Hydrolog. Sci. J. 2017, 62, 2187–2208. [Google Scholar] [CrossRef]
- Malede, D.A.; Alamirew, T.; Andualem, T.G. Integrated and Individual Impacts of Land Use Land Cover and Climate Changes on Hydrological Flows over Birr River Watershed, Abbay Basin, Ethiopia. Water 2023, 18, 116. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.B.; Zhao, L.; Gong, D.Z.; Zhang, K.D. Spatio-temporal variation of reference evapotranspiration during 1954–2013 in Southwest China. Quatern. Int. 2017, 441, 129–139. [Google Scholar] [CrossRef]
- Zhang, L.; Karthikeyan, R.; Bai, Z.; Wang, J. Spatial and temporal variability of temperature, precipitation, and streamflow in upper Sang-kan basin, China. Hydrol. Process. 2017, 31, 279–295. [Google Scholar] [CrossRef]
- Chueh, Y.Y.; Fan, C.H.; Huang, Y.Z. Copper concentration simulation in a river by SWAT-WASP integration and its application to assessing the impacts of climate change and various remediation strategies. J. Environ. Manag. 2021, 279, 111613. [Google Scholar] [CrossRef]
- Qiao, P.W.; Lei, M.; Yang, S.C.; Yang, J.; Zhou, X.Y.; Dong, N.; Guo, G.H. Development of a model to simulate soil heavy metals lateral migration quantity based on SWAT in Huanjiang watershed, China. J. Environ. Sci. 2019, 77, 115–129. [Google Scholar] [CrossRef]
- Kudo, R.; Yoshida, T.; Masumoto, T. Uncertainty analysis of impacts of climate change on snow processes: Case study of interactions of GCM uncertainty and an impact model. J. Hydrol. 2017, 548, 196–207. [Google Scholar] [CrossRef]
- Zhao, Q.D.; Ding, Y.J.; Wang, J.; Gao, H.K.; Zhang, S.Q.; Zhao, C.C.; Xu, J.L.; Han, H.D.; ShangGuan, D.H. Projecting climate change impacts on hydrological processes on the Tibetan Plateau with model calibration against the glacier inventory data and observed streamflow. J. Hydrol. 2019, 573, 60–81. [Google Scholar] [CrossRef]
- George, J.; Athira, P. Long-term changes in climatic variables over the Bharathapuzha river basin, Kerala, India. Theor. Appl. Climatol. 2020, 142, 269–286. [Google Scholar] [CrossRef]
- Trang, N.T.T.; Shrestha, S.; Shrestha, M.; Datta, A.; Kawasaki, A. Evaluating the impacts of climate and land-use change on the hydrology and nutrient yield in a transboundary river basin: A case study in the 3S River Basin (Sekong, Sesan, and Srepok). Sci. Total Environ. 2017, 576, 586–598. [Google Scholar] [CrossRef]
- Wang, Y.T.; Liu, J.; Li, R.; Suo, X.Y.; Lu, E.H. Precipitation forecast of the Wujiang River Basin based on artificial bee colony algorithm and backpropagation neural network. Alex. Eng. J. 2020, 59, 1473–1483. [Google Scholar] [CrossRef]
- Zhang, L.; Podlasly, C.; Ren, Y.; Feger, K.H.; Wang, Y.; Schwärzel, K. Separating the Effects of Changes in Land Management and Climatic Conditions on Long-Term Streamflow Trends Analyzed for a Small Catchment in the Loess Plateau Region, NW China. Hydrol. Process. 2014, 28, 1284–1293. [Google Scholar] [CrossRef]
- Lopes, T.R.; Zolin, C.A.; Mingoti, R.; Vendrusculo, L.G.; Almeida, F.T.; Souza, A.P.; Oliveira, R.F.; Paulino, J.; Uliana, E.M. Hydrological Regime, Water Availability and Land Use/Land Cover Change Impact on the Water Balance in a Large Agriculture Basin in the Southern Brazilian Amazon. J. South Am. Earth Sci. 2021, 108, 103224. [Google Scholar] [CrossRef]
- Vaezi, A.R.; Zarrinabadi, E.; Auerswald, K. Interaction of land use, slope gradient and rain sequence on runoff and soil loss from weakly aggregated semi-arid soils. Soil Tillage Res. 2017, 172, 22–31. [Google Scholar] [CrossRef]
- Jin, H.; Ju, Q.; Yu, Z.; Hao, J.; Gu, H.; Gu, H.; Li, W. Simulation of snowmelt runoff and sensitivity analysis in the Nyang River Basin, southeastern Qinghai-Tibetan Plateau, China. Nat. Hazards 2019, 99, 931–950. [Google Scholar] [CrossRef]
- Tamm, O.; Saaremae, E.; Rahkema, K.; Jaagus, J.; Tamm, T. The intensification of short-duration rainfall extremes due to climate change-Need for a frequent update of intensity-duration-frequency curves. Clim. Serv. 2023, 30, 100349. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W.; Engel, B.A.; Peng, H.; Theller, L.; Shi, Y.; Hu, S. A fast mobile early warning system for water quality emergency risk in ungauged river basins. Environ. Model Softw. 2015, 73, 76–89. [Google Scholar] [CrossRef]
- Liu, Y.G.; Xu, Y.X.; Zhao, Y.Q.; Long, Y. Using SWAT Model to assess the impacts of land use and climate changes on flood in the upper Weihe River, China. Water 2022, 14, 2098. [Google Scholar] [CrossRef]
- Newcombe, G.; Chorus, I.; Falconer, I.; Lin, T.F. Cyanobacteria: Impacts of climate change on occurrence, toxicity and water quality management. Water Res. 2012, 46, 1347–1348. [Google Scholar] [CrossRef]
- Ding, Y.H.; Wang, Z.Y.; Sun, Y. Inter-decadal variation of the summer precipitation in East China and its association with decreasing Asian summer monsoon. Part I: Observation evidences. Int. J. Climatol. 2007, 28, 1139–1161. [Google Scholar] [CrossRef]
- Gebremicael, T.G.; Mohamed, Y.A.; Zaag, P.V.; Hagos, E.Y. Temporal and Spatial Changes of Rainfall and Streamflow in the Upper Tekeze-Atbara River Basin, Ethiopia. Hydrol. Earth Syst. Sci. 2016, 21, 2127–2142. [Google Scholar] [CrossRef] [Green Version]
- Salmivaara, A.; Leinonen, A.; Palviainen, M.; Korhonen, N.; Launiainen, S.; Tuomenvirta, H.; Ukonmaanaho, L.; Finer, L.; Lauren, A. Exploring the Role of Weather and Forest Management on Nutrient Export in Boreal Forested Catchments Using Spatially Distributed Model. Forests 2023, 14, 89. [Google Scholar] [CrossRef]
- Tao, H.; Gemmer, M.; Bai, Y.G.; Su, B.D.; Mao, W.Y. Trends of streamflow in the Tarim River Basin during the past 50 years: Human impact or climate change. J. Hydrol. 2011, 400, 1–9. [Google Scholar] [CrossRef]
- Mu, X.M.; Zhang, L.; McVicar, T.R.; Chille, B.S.; Gao, P. Analysis of the impact of conservation measures on stream flow regime in catchments of the Loess Plateau, China. Hydrol. Process. 2007, 21, 2124–2134. [Google Scholar] [CrossRef]
- Lisboa, M.S.; Schneider, R.L.; Sullivan, P.J.; Walter, M.T. Drought and post-drought rain effect on stream phosphorus and other nutrient losses in the Northeastern USA. J. Hydrol. Reg. Stud. 2020, 28, 100672. [Google Scholar] [CrossRef]
- Siam, M.S.; Eltahir, E.A.B. Climate change enhances interannual variability of the Nile River flow. Nat. Clim. Chang. 2017, 7, 350. [Google Scholar] [CrossRef]
- Uhl, A.; Hahn, H.J.; Jager, A.; Luftensteiner, T.; Siemensmeyer, T.; Doll, P.; Noack, M.; Schwenk, K.; Berkhoff, S.; Weiler, M.; et al. Making waves: Pulling the plug-Climate change effects will turn gaining into losing streams with detrimental effects on groundwater quality. Water Res. 2022, 220, 118649. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Shi, X.; Zeng, C.; Wang, L.; Xiao, X.; Wang, G.; Chen, Y.; Zhang, H.; Lu, X.; Immerzeel, W. Recent stepwise sediment flux increases with climate change in the Tuotuo River in the central Tibetan Plateau. Sci. Bull. 2020, 65, 410–418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duan, W.L.; He, B.; Nover, D.; Yang, G.S.; Chen, W.; Meng, H.F.; Zou, S.; Liu, C.M. Water Quality Assessment and Pollution Source Identification of the Eastern Poyang Lake Basin Using Multivariate Statistical Methods. Sustainability 2016, 8, 133. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.Y.; He, R.M.; Ye, J.Y.; Tan, M.L.; Ji, X.Y.; Tan, L.; Wang, G.Q. Integrating an hourly weather generator with an hourly rainfall SWAT model for climate change impact assessment in the Ru River Basin, China. Atmos. Res. 2020, 244, 105062. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, J.; Yang, Q.; Baartman, J.E.M.; Gai, L.; Yang, X.; Li, S.Q.; Yu, J.; Ritsema, C.J.; Geissen, V. An improved method for calculating slope length (λ) and the LS parameters of the Revised Universal Soil Loss Equation for large watersheds. Geoderma 2017, 308, 36–45. [Google Scholar] [CrossRef]
- Chang, C.; Sun, D.; Feng, P.; Zhang, M.; Ge, N. Impacts of Nonpoint Source Pollution on Water Quality in the Yuqiao Reservoir. Environ. Eng. Sci. 2017, 34, 418–432. [Google Scholar] [CrossRef]
- Takele, A.; Lakew, H.B.; Kabite, G. Does the Recent Afforestation Program in Ethiopia Influenced Vegetation Cover and Hydrology? A Case Study in the Upper Awash Basin, Ethiopia. Heliyon 2022, 8, e09589. [Google Scholar] [CrossRef] [PubMed]
- Babaei, H.; Nazari-Sharabian, M.; Karakouzian, M.; Ahmad, S. Identification of Critical Source Areas (CSAs) and Evaluation of Best Management Practices (BMPs) in Controlling Eutrophication in the Dez River Basin. Environments 2019, 6, 20. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.M.; Kang, S.Z.; Zhang, L.; Tong, L.; Su, X.L. Analysis of impacts of climate variability and human activity on streamflow for a river basin in arid region of northwest China. J. Hydrol. 2008, 352, 239–249. [Google Scholar] [CrossRef]
- Zeman-Kuhnert, S.; Thiel, V.; Heim, C. Effects of Weather Extremes on the Nutrient Dynamics of a Shallow Eutrophic Lake as Observed during a Three-Year Monitoring Study. Water 2022, 14, 2032. [Google Scholar] [CrossRef]
- Gao, X.J.; Chen, N.W.; Yu, D.; Wu, Y.Q.; Huang, B.Q. Hydrological controls on nitrogen (ammonium versus nitrate) fluxes from river to coast in a subtropical region: Observation and modeling. J. Environ. Manag. 2018, 213, 382–391. [Google Scholar] [CrossRef]
| Parameter | Parameter Definition | Sensitivity Value | Level | Rank | |
|---|---|---|---|---|---|
| Runoff | CN2 | Moisture condition II curve number | 2.99 | IV | 1 |
| CH_K2 | Effective hydraulic conductivity | 2.67 | IV | 2 | |
| SOL_AWC | Soil available moisture content | 2.28 | IV | 3 | |
| ALPHA_BF | Baseflow alpha factor | 1.97 | III | 4 | |
| ESCO | Soil evaporation compensation factor | 1.91 | III | 5 | |
| GW_DELAY | Groundwater delay | 1.85 | III | 6 | |
| GWQMN | Threshold depth of water in the shallow aquifer required for return flow to occur | 0.97 | III | 7 | |
| REVAPMN | Threshold depth of water in the shallow aquifer for evaporation to occur | 0.81 | III | 8 | |
| CH_N2 | Manning’s value for main channel | 0.60 | III | 9 | |
| SOL_BD | Soil moisture bulk density | 0.30 | III | 10 | |
| TN | RCN | Concentration of nitrogen in rainfall | 3.31 | IV | 1 |
| SOL_ORGN | Initial organic N concentration in the soil layer | 1.58 | IV | 2 | |
| SDNCO | Denitrification threshold water content | 0.87 | III | 3 | |
| BC1 | Rate constant for biological oxidation of NH3 | 0.82 | III | 4 | |
| BC2 | Rate constant for biological oxidation of NO2 to NO3 | 0.28 | III | 5 | |
| TP | FILTERW | Width of the edge of field filter strip | 2.71 | IV | 1 |
| SOL_ORGP | initial humic organic phosphorus in soil layer | 2.13 | IV | 2 | |
| PHOSKD | Phosphorus soil partitioning coefficient | 1.08 | IV | 3 | |
| BC4 | Phosphorus soil partitioning coefficient | 0.88 | III | 4 | |
| PSP | Phosphorus sorption coefficient | 0.76 | III | 5 |
| Indicator | Runoff | TN | TP | |
|---|---|---|---|---|
| P100 | Severe torrential rain days | 0.54 | 0.44 | 0.55 |
| P50 | Torrential rain days | 0.57 | 0.40 | 0.52 |
| P25 | Heavy rain days | 0.19 | 0.35 | 0.03 |
| P10 | Moderate rain days | 0.07 | 0.22 | 0.02 |
| FD | Frost days | −0.13 | −0.40 | −0.05 |
| SND | Summer night days | −0.17 | −0.01 | −0.16 |
| HTD | High temperature days | −0.37 | 0.08 | −0.37 |
| FRD | Freezing days | 0.01 | −0.02 | −0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, W.; Peng, H.; Zhou, F.; Jiang, A.; Chen, X.; Wang, H. The Impacts of Climate Change on the Hydrological Process and Water Quality in the Three Gorges Reservoir Area, China. Water 2023, 15, 1542. https://doi.org/10.3390/w15081542
Sun Y, Zhang W, Peng H, Zhou F, Jiang A, Chen X, Wang H. The Impacts of Climate Change on the Hydrological Process and Water Quality in the Three Gorges Reservoir Area, China. Water. 2023; 15(8):1542. https://doi.org/10.3390/w15081542
Chicago/Turabian StyleSun, Yidian, Wanshun Zhang, Hong Peng, Feng Zhou, Anna Jiang, Xiaomin Chen, and Hao Wang. 2023. "The Impacts of Climate Change on the Hydrological Process and Water Quality in the Three Gorges Reservoir Area, China" Water 15, no. 8: 1542. https://doi.org/10.3390/w15081542






