Linear and Non-Linear Modelling of Bromate Formation during Ozonation of Surface Water in Drinking Water Production
Abstract
:1. Introduction
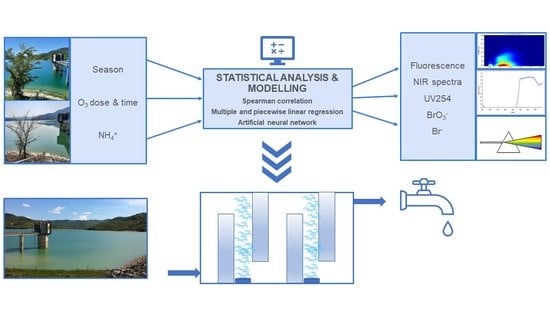
2. Materials and Methods
2.1. Water Samples
2.2. Ozonation Experiment
2.3. Analytical Determination
2.3.1. Conventional Analytical Methods
2.3.2. Fluorescence
2.3.3. NIR Spectroscopy
2.4. Data Analysis and Modelling
2.4.1. Descriptive Statistics
2.4.2. Principal Component Analysis (PCA) of NIR Spectra
2.4.3. Multiple Linear Regression (MLR), Piecewise Linear Regression (PLR) and Artificial Neural Network (ANN) Modelling
3. Results and Discussion
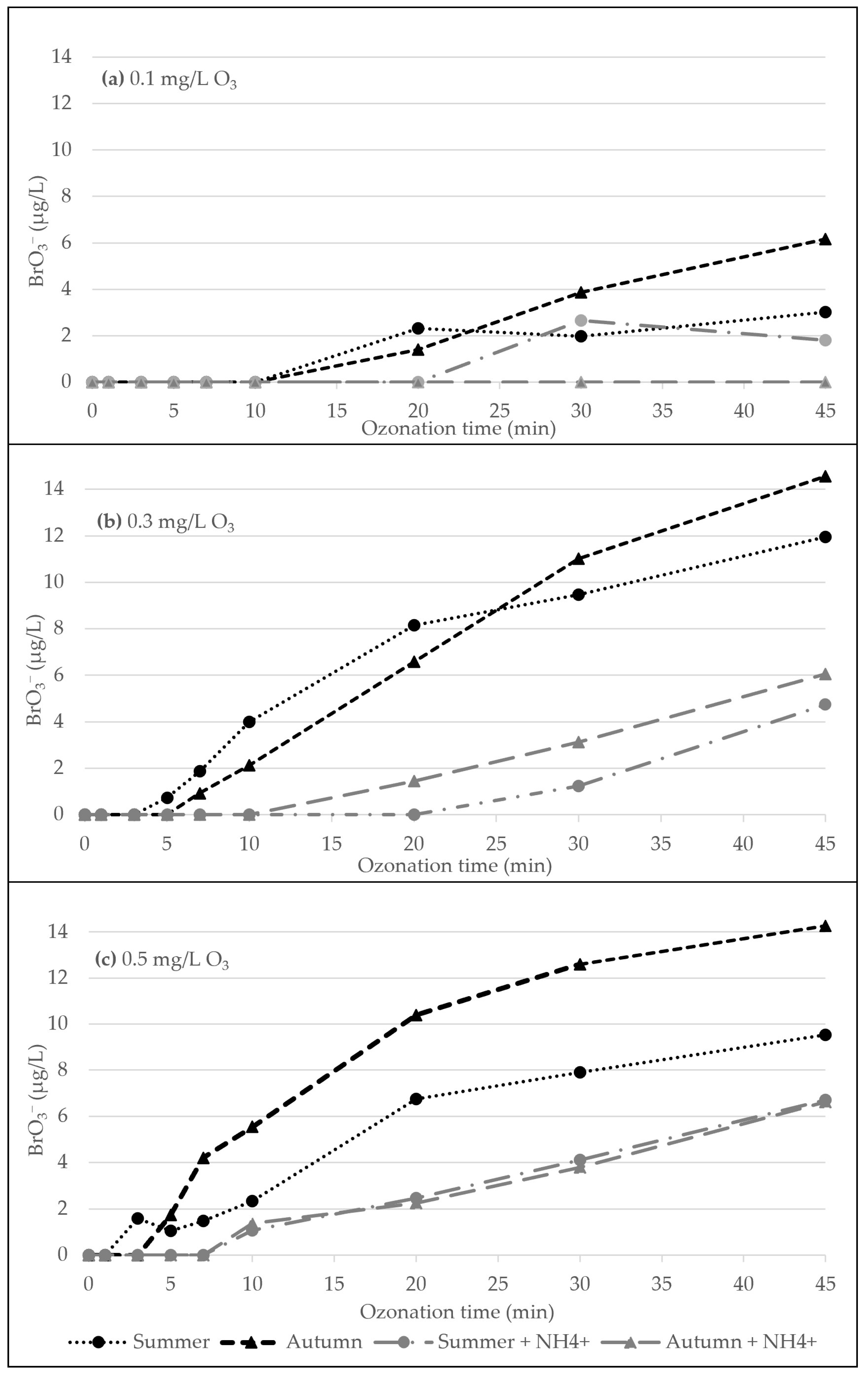
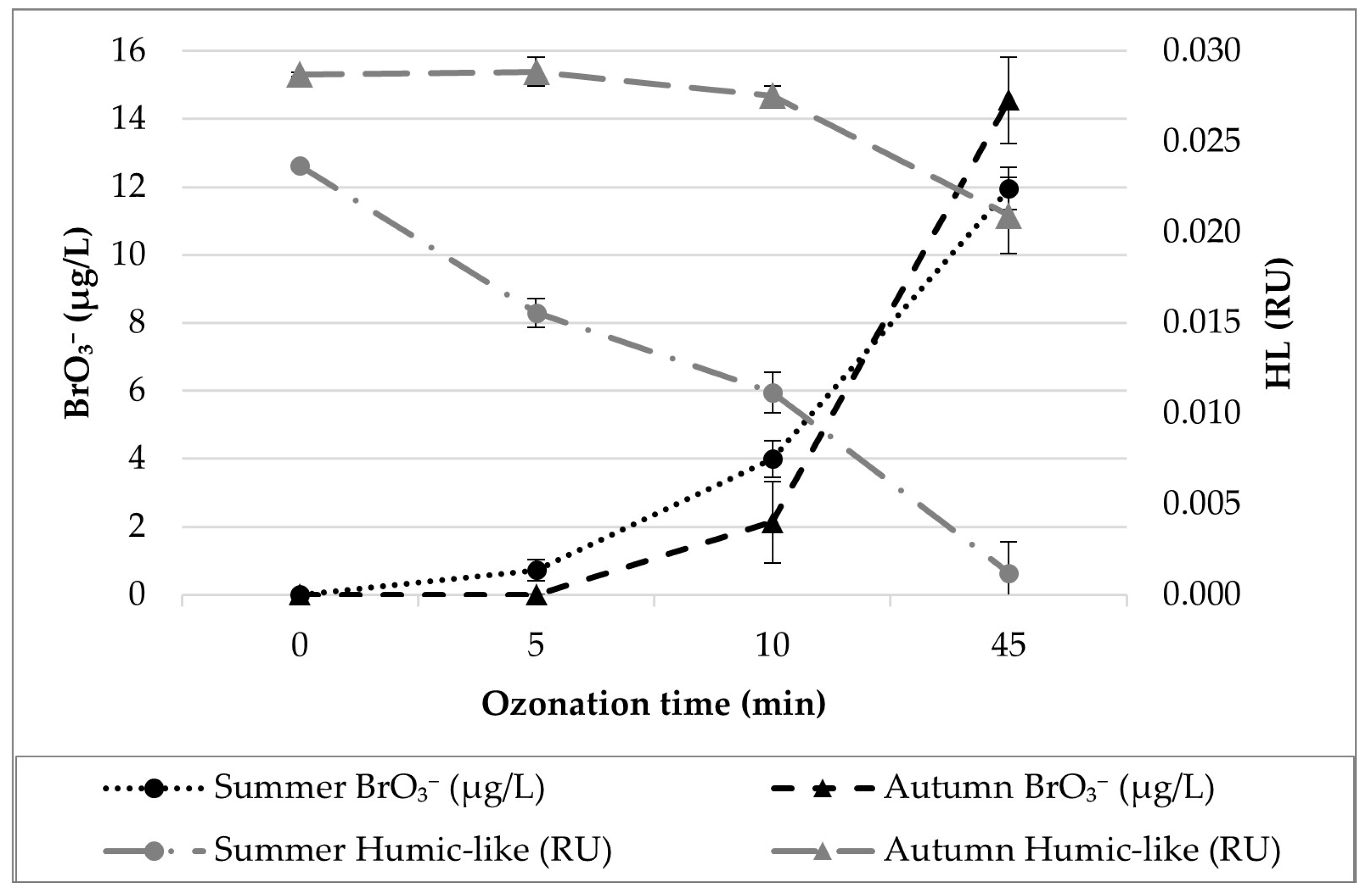
3.1. Ozonation Experiment
3.2. Data Analysis and Modelling
3.2.1. Spearman’s Correlation Matrix
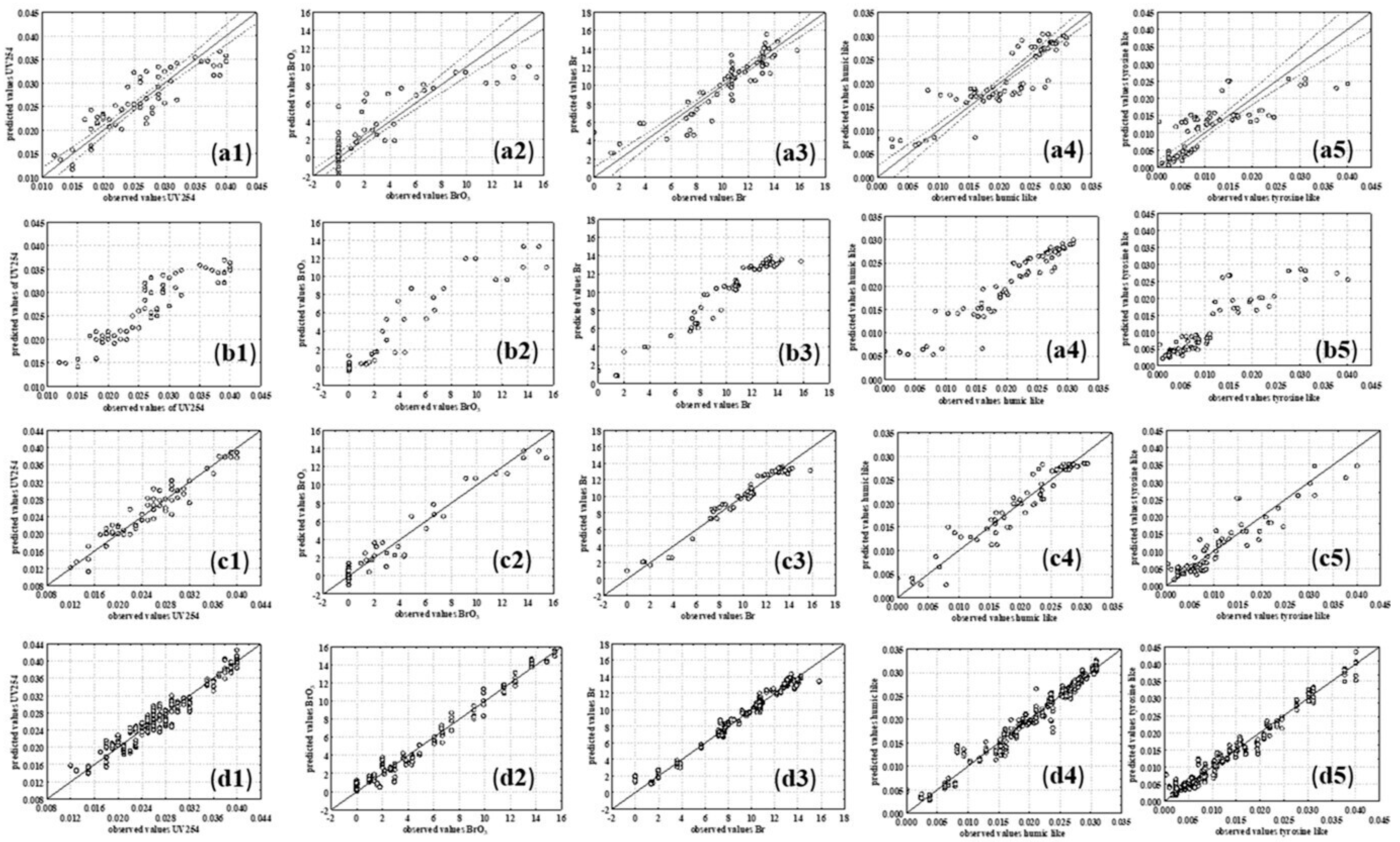
3.2.2. Multiple Linear Regression and Piecewise Linear Regression Models
3.2.3. Near-Infrared (NIR) Spectroscopy and Principal Component Analysis (PCA)
3.2.4. ANN Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UNESCO. Groundwater 1. Making the Invisible Visible. 2022. Available online: https://reliefweb.int/report/world/united-nations-world-water-development-report-2022-groundwater-making-invisible-visible?gclid=EAIaIQobChMI3cC79Lmh_gIVmAcGAB2QVgh1EAAYASAAEgLLIfD_BwE (accessed on 2 May 2022).
- Hou, P.; Chang, F.; Duan, L.; Zhang, Y.; Zhang, H. Seasonal Variation and Spatial Heterogeneity of Water Quality Parameters in Lake Chenghai in Southwestern China. Water 2022, 14, 1640. [Google Scholar] [CrossRef]
- Liang, L.; Singer, P.C. Factors Influencing the Formation and Relative Distribution of Haloacetic Acids and Trihalomethanes in Drinking Water. Environ. Sci. Technol. 2003, 37, 2920–2928. [Google Scholar] [CrossRef] [PubMed]
- Wada, Y.; Flörke, M.; Hanasaki, N.; Eisner, S.; Fischer, G.; Tramberend, S.; Satoh, Y.; van Vliet, M.T.H.; Yillia, P.; Ringler, C.; et al. Modeling global water use for the 21st century: The Water Futures and Solutions (WFaS) initiative and its approaches. Geosci. Model Dev. 2016, 9, 175–222. [Google Scholar] [CrossRef] [Green Version]
- Siddiqui, M.S.; Amy, G.L.; Rice, R.G. Bromate ion formation: A critical review. J. Am. Water Work. Assoc. 1995, 87, 58–70. [Google Scholar] [CrossRef]
- Tyrovola, K.; Diamadopoulos, E. Bromate formation during ozonation of groundwater in coastal areas in Greece. Desalination 2005, 176, 201–209. [Google Scholar] [CrossRef]
- Milosevic, N.; Thomsen, N.; Juhler, R.; Albrechtsen, H.-J.; Bjerg, P. Identification of discharge zones and quantification of contaminant mass discharges into a local stream from a landfill in a heterogeneous geologic setting. J. Hydrol. 2012, 446–447, 13–23. [Google Scholar] [CrossRef]
- De Angelo, A.B.; George, M.H.; Kilburn, S.R.; Moore, T.M.; Wolf, D.C. Carcinogenicity of Potassium Bromate Administered in the Drinking Water to Male B6C3F1 Mice and F344/N Rats. Toxicol. Pathol. 1998, 26, 587–594. [Google Scholar] [CrossRef] [Green Version]
- WHO. Bromate in Drinking Water: Background Document for Development of WHO Guidelines for Drinking-Water Quality; WHO: Geneva, Switzerland, 2005. [Google Scholar]
- Song, R.; Donohoe, C.; Minear, R.; Westerhoff, P.; Ozekin, K.; Amy, G. Empirical modeling of bromate formation during ozonation of bromide-containing waters. Water Res. 1996, 30, 1161–1168. [Google Scholar] [CrossRef]
- Gillogly, T. Bromate Formation and Control during Ozonation of Low Bromide Waters; AWWA Research Foundation and American Water Works Association: Denver, CO, USA, 2001. [Google Scholar]
- Wang, Y.; Man, T.; Zhang, R.; Yan, X.; Wang, S.; Zhang, M.; Wang, P.; Ren, L.; Yu, J.; Li, C. Effects of organic matter, ammonia, bromide, and hydrogen peroxide on bromate formation during water ozonation. Chemosphere 2021, 285, 131352. [Google Scholar] [CrossRef]
- Uyak, V.; Ozdemir, K.; Toroz, I. Multiple linear regression modeling of disinfection by-products formation in Istanbul drinking water reservoirs. Sci. Total. Environ. 2007, 378, 269–280. [Google Scholar] [CrossRef]
- Mandel, P. Modelling Ozonation Processes for Disinfection By-Product Control in Potable Water Treatment: From Laboratory to Industrial Units. 2011. Available online: https://tel.archives-ouvertes.fr/tel-00564767 (accessed on 28 May 2020).
- Gregov, M.; Jukić, A.; Ćurko, J.; Matošić, M.; Gajšak, F.; Crnek, V.; Ujević Bošnjak, M. Bromide occurrence in Croatian groundwater and application of literature models for bromate formation. Environ. Monit. Assess. 2022, 194, 544. [Google Scholar] [CrossRef] [PubMed]
- Von Gunten, U. Ozonation of drinking water: Part II. Disinfection and by-product formation in presence of bromide, iodide or chlorine. Water Res. 2003, 37, 1469–1487. [Google Scholar] [CrossRef]
- Jarvis, P.; Parsons, S.A.; Smith, R. Modeling Bromate Formation During Ozonation. Ozone Sci. Eng. 2007, 29, 429–442. [Google Scholar] [CrossRef] [Green Version]
- Legube, B.; Parinet, B.; Gelinet, K.; Berne, F.; Croue, J.-P. Modeling of bromate formation by ozonation of surface waters in drinking water treatment. Water Res. 2004, 38, 2185–2195. [Google Scholar] [CrossRef] [PubMed]
- Adamowski, J.; Chan, H.F.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48, 3–4. [Google Scholar] [CrossRef]
- Valinger, D. Development of Near Infrared Spectroscopy Models for Quantitative Prediction of the Content of Bioactive Compounds in Olive Leaves. Chem. Biochem. Eng. Q. 2018, 32, 535–543. [Google Scholar] [CrossRef]
- Shi, W.; Zhuang, W.-E.; Hur, J.; Yang, L. Monitoring dissolved organic matter in wastewater and drinking water treatments using spectroscopic analysis and ultra-high resolution mass spectrometry. Water Res. 2021, 188, 116406. [Google Scholar] [CrossRef] [PubMed]
- Balbino, S.; Vincek, D.; Trtanj, I.; Egređija, D.; Gajdoš- Kljusurić, J.; Kraljić, K.; Obranović, M.; Škevin, D. Assessment of Pumpkin Seed Oil Adulteration Supported by Multivariate Analysis: Comparison of GC-MS, Colourimetry and NIR Spectroscopy Data. Foods 2022, 11, 835. [Google Scholar] [CrossRef]
- Gajdoš Kljusurić, J.; Boban, A.; Mucalo, A.; Budić-Leto, I. Novel Application of NIR Spectroscopy for Non-Destructive Determination of ‘Maraština’ Wine Parameters. Foods 2022, 11, 1172. [Google Scholar] [CrossRef]
- Matilainen, A.; Gjessing, E.T.; Lahtinen, T.; Hed, L.; Bhatnagar, A.; Sillanpää, M. An overview of the methods used in the characterisation of natural organic matter (NOM) in relation to drinking water treatment. Chemosphere 2011, 83, 1431–1442. [Google Scholar] [CrossRef]
- Bicanic, D.; Streza, M.; Dóka, O.; Valinger, D.; Luterotti, S.; Ajtony, Z.S.; Kurtanjek, Z.; Dadarlat, D. Non-destructive Measurement of Total Carotenoid Content in Processed Tomato Products: Infrared Lock-In Thermography, Near-Infrared Spectroscopy/Chemometrics, and Condensed Phase Laser-Based Photoacoustics—Pilot Study. Int. J. Thermophys. 2015, 36, 2380–2388. [Google Scholar] [CrossRef]
- Brereton, R.G. Graphical introduction to principal components analysis. J. Chemom. 2022, 36, e3404. [Google Scholar] [CrossRef]
- Xu, M.; Wu, C.; Zhou, Y. Advancements in the Fenton Process for Wastewater Treatment. In Advanced Oxidation Processes; IntechOpen Limited: London, UK, 2020; pp. 61–77. [Google Scholar] [CrossRef]
- Wang, X.; Tong, Y.; Chang, Q.; Lu, J.; Ma, T.; Zhou, F.; Li, J. Source identification and characteristics of dissolved organic matter and disinfection by-product formation potential using EEM-PARAFAC in the Manas River, China. RSC Adv. 2021, 11, 28476–28487. [Google Scholar] [CrossRef]
- Buffle, M.-O.; Galli, S.; von Gunten, U. Enhanced Bromate Control during Ozonation: The Chlorine-Ammonia Process. Environ. Sci. Technol. 2004, 38, 5187–5195. [Google Scholar] [CrossRef]
- Song, R.; Westerhoff, P.; Minear, R.; Amy, G. Bromate minimization during ozonation. J. Am. Water Work. Assoc. 1997, 89, 69–78. [Google Scholar] [CrossRef]
- Siddiqui, M.S.; Amy, G.L. Factors Affecting DBP Formation During Ozone-Bromide Reactions. J. Am. Water Work. Assoc. 1993, 85, 63–72. [Google Scholar] [CrossRef]
- Aitkenhead-Peterson, J.A.; McDowell, W.H.; Neff, J.C. Sources, Production, and Regulation of Allochthonous Dissolved Organic Matter Inputs to Surface Waters. In Aquatic Ecosystems; Elsevier: San Diego, CA, USA, 2003; pp. 25–70. [Google Scholar] [CrossRef]
- Elovitz, M.S.; von Gunten, U.; Kaiser, H.-P. Hydroxyl Radical/Ozone Ratios During Ozonation Processes. II. The Effect of Temperature, pH, Alkalinity, and DOM Properties. Ozone Sci. Eng. 2000, 22, 123–150. [Google Scholar] [CrossRef]
- Li, W.-T.; Cao, M.-J.; Young, T.; Ruffino, B.; Dodd, M.; Li, A.-M.; Korshin, G. Application of UV absorbance and fluorescence indicators to assess the formation of biodegradable dissolved organic carbon and bromate during ozonation. Water Res. 2017, 111, 154–162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ryan, S.E.; Porth, L.S. A Tutorial on the Piecewise Regression Approach Applied to Bedload Transport Data. 2007. Available online: https://www.fs.usda.gov/rm/pubs/rmrs_gtr189.pdf (accessed on 13 July 2022).
- Pilkington, J.L.; Preston, C.; Gomes, R.L. Comparison of response surface methodology (RSM) and artificial neural networks (ANN) towards efficient extraction of artemisinin from Artemisia annua. Ind. Crops. Prod. 2014, 58, 15–24. [Google Scholar] [CrossRef]
- Kim, S.Y.; Ćurko, J.; Gajdoš Kljusurić, J.; Matošić, M.; Crnek, V.; López-Vázquez, C.M.; Garcia, H.A.; Brdjanović, D.; Valinger, D. Use of near-infrared spectroscopy on predicting wastewater constituents to facilitate the operation of a membrane bioreactor. Chemosphere 2021, 272, 129899. [Google Scholar] [CrossRef]
- Liu, F.; He, Y.; Wang, L.; Sun, G. Detection of Organic Acids and pH of Fruit Vinegars Using Near-Infrared Spectroscopy and Multivariate Calibration. Food Bioprocess Technol. 2011, 4, 1331–1340. [Google Scholar] [CrossRef]
- Urbano-Cuadrado, M.; Luque de Castro, M.D.; Pérez-Juan, P.M.; García-Olmo, J.; Gómez-Nieto, M.A. Near infrared reflectance spectroscopy and multivariate analysis in enology: Determination or screening of fifteen parameters in different types of wines. Anal. Chim. Acta 2004, 527, 81–88. [Google Scholar] [CrossRef]
- Jurinjak Tušek, A.; Benković, M.; Malešić, E.; Marić, L.; Jurina, T.; Gajdoš Kljusurić, J.; Valinger, D. Rapid quantification of dissolved solids and bioactives in dried root vegetable extracts using near infrared spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 261, 120074. [Google Scholar] [CrossRef]
- Valinger, D.; Jurina, T.; Šain, A.; Matešić, N.; Panić, M.; Benković, M.; Gajdoš Kljusurić, J.; Jurinjak Tušek, A. Development of ANN models based on combined UV-vis-NIR spectra for rapid quantification of physical and chemical properties of industrial hemp extracts. Phytochem. Anal. 2021, 32, 326–338. [Google Scholar] [CrossRef]
- WHO, Climate-Resilient Water Safety Plans: Managing Health Risks Associated with Climate Variability and Change. 2017. Available online: http://apps.who.int/iris/bitstream/handle/10665/258722/9789241512794-eng.pdf?sequence=1 (accessed on 11 May 2022).
- Razavi, S. Deep learning, explained: Fundamentals, explainability, and bridgeability to process-based modelling. Environ. Model. Softw. 2021, 144, 105159. [Google Scholar] [CrossRef]
- Bakas, I.; Kontoleon, K.J. Performance Evaluation of Artificial Neural Networks (ANN) Predicting Heat Transfer through Masonry Walls Exposed to Fire. Appl. Sci. 2021, 11, 11435. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, J.Y.; Lee, M.H.; Lee, M.Y.; Kim, Y.W.; Hyung, J.S.; Kim, K.B.; Cha, Y.K.; Koo, J.Y. Development of a short-term water quality prediction model for urban rivers using real-time water quality data. Water Supply 2022, 22, 4082–4097. [Google Scholar] [CrossRef]
- El-Sari, B.; Biegler, M.; Rethmeier, M. Investigation of the Extrapolation Capability of an Artificial Neural Network Algorithm in Combination with Process Signals in Resistance Spot Welding of Advanced High-Strength Steels. Metals 2021, 11, 1874. [Google Scholar] [CrossRef]
- Kyono, T.; Otsuka, Y.; Fukumoto, Y.; Owaki, S.; Nakamura, M. Computational-Complexity Comparison of Artificial Neural Network and Volterra Series Transfer Function for Optical Nonlinearity Compensation with Time- and Frequency-Domain Dispersion Equalization. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Gregov, M.; Jurinjak Tušek, A.; Valinger, D.; Benković, M.; Jurina, T.; Surać, L.; Kurajica, L.; Matošić, M.; Gajdoš Kljusurić, J.; Ujević Bošnjak, M.; et al. Data for paper Linear and Non-linear Modelling of Bromate Formation During Ozonation of Surface Water in Drinking Water Production. Zenodo 2023. [Google Scholar] [CrossRef]
| Season | UV254 (cm−1) | BrO3− (µg/L) | Br− (µg/L) | Humic-Like (RU) | Tyrosine-Like (RU) |
|---|---|---|---|---|---|
| Summer | 0.039 ± 0.001 | 0 | 10.77 ± 0.08 | 0.0237 ± 0.0030 | 0.0084 ± 0.0026 |
| Autumn | 0.027 ± 0.002 | 0 | 13.20 ± 0.14 | 0.0287 ± 0.0024 | 0.0026 ± 0.0009 |
| Parameter | Season | Ozone Dose (mg/L) | Ozonation Time (min) | NH4+ (mg/L) | UV254 (cm−1) | BrO3− (µg/L) | Br− (µg/L) | HL (RU) | TL (RU) |
|---|---|---|---|---|---|---|---|---|---|
| Season | - | 0.036 | −0.006 | 0.011 | 0.603* | 0.021 | −0.518 * | −0.654 * | 0.672 * |
| Ozone dose (mg/L) | 0.036 | - | 0.033 | −0.038 | −0.213 | 0.265* | −0.203 | −0.002 | 0.075 |
| Ozonation time (min) | −0.006 | 0.033 | - | −0.024 | −0.650* | 0.784 * | −0.650 * | −0.583 * | 0.523 * |
| NH4+ (mg/L) | 0.011 | −0.038 | −0.024 | - | 0.113 | −0.254 * | 0.158 | −0.118 | −0.183 |
| UV254 (cm−1) | 0.603 * | −0.213 | −0.650 * | 0.113 | - | −0.586 * | 0.185 | −0.002 | 0.026 |
| BrO3− (µg/L) | 0.021 | 0.265 * | 0.784 * | −0.254 * | −0.586* | - | −0.760 * | −0.498 * | 0.499 * |
| Br− (µg/L) | −0.518 * | −0.203 | −0.650 * | 0.158 | 0.185 | −0.760 * | - | 0.766 * | −0.770 * |
| HL (RU) | −0.654 * | −0.002 | −0.583 * | −0.118 | −0.002 | −0.498 * | 0.766 * | - | −0.676 * |
| TL (RU) | 0.672 * | 0.075 | 0.523 * | −0.183 | 0.026 | 0.499 * | −0.770 * | −0.676 * | - |
| Model Output | b0 | b1 (Season) | b2 (Ozone Dose) | b3 (Ozonation Time) | b4 (NH4+) | Break Point | R2 | R2adj | SEE | F-Value | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MLR | UV254 | 0.019 ± 0.002 | 0.009 ± 0.001 | −0.010 ± 0.003 | −2.430 × 10−4 ± 2.500 × 10−5 | 0.002 ± 0.002 | 0.7722 | 0.7579 | 0.0036 | 54.227 | |
| BrO3− | −0.529 ± 1.033 | −0.610 ± 0.546 | 5.961 ± 1.709 | 0.181 ± 0.015 | −4.976 ± 1.432 | 0.7262 | 0.7091 | 2.2642 | 42.434 | ||
| Br− | 16.840 ± 0.739 | −2.284 ± 0.390 | −4.896 ± 1.222 | −0.160 ± 0.011 | 3.808 ± 1.025 | 0.8170 | 0.8056 | 1.6196 | 71.442 | ||
| HL | 0.040 ± 0.002 | −0.009 ± 0.001 | −0.002 ± 0.003 | −2.670 × 10−3 ± 2.500 × 10−4 | −0.003 ± 0.002 | 0.7857 | 0.7723 | 0.0037 | 58.668 | ||
| TL | −0.009 ± 0.003 | 0.011 ± 0.001 | 0.003 ± 0.004 | 2.630 × 10−3 ± 3.800 × 10−5 | −0.005 ± 0.004 | 0.6398 | 0.6173 | 0.0056 | 28.429 | ||
| PLR | UV254 | 0.019 ± 0.001 0.025 ± 0.011 | 0.005 ± 0.001 0.006 ± 0.002 | −0.004 ± 0.001 −0.011 ± 0.004 | −1.680 × 10−4 ± 1.248 × 10−5 −2.180 × 10−4 ± 1.113 × 10−5 | 3.160 × 10−4 ± 1.111 × 10−5 0.001 ± 0.001 | 0.026 | 0.9187 | 0.9136 | 1.7277 × 10−5 | 118.437 |
| BrO3− | −0.492 ± 0.025 −1.437 ± 0.078 | 0.186 ± 0.044 −1.370 ± 0.069 | 1.037 ± 0.128 11.681 ± 0.887 | 0.038 ± 0.012 0.226 ± 0.056 | −0.589 ± 0.023 −14.181 ± 0.785 | 2.466 | 0.9524 | 0.9494 | 3.5157 × 10−5 | 110.241 | |
| Br− | 16.519 ± 0.987 16.229 ± 0.547 | −0.526 ± 0.011 −2.604 ± 0.147 | −13.039 ± 0.567 −0.906 ± 0.025 | −0.180 ± 0.004 −0.065 ± 0.007 | 10.907 ± 0.147 0.960 ± 0.221 | 10.009 | 0.9753 | 0.9737 | 1.2528 × 10−5 | 105.138 | |
| HL | 0.043 ± 0.001 0.031 ± 0.003 | −0.013 ± 0.004 −0.004 ± 0.001 | −0.003 ± 0.001 0.005 ± 0.001 | −2.340 × 10−4 ± 1.870 × 10−5 −1.530 × 10−4 ± 3.125 × 10−5 | 0.001 ± 0.001 −0.005 ± 0.002 | 0.020 | 0.9507 | 0.9476 | 2.1110 × 10−6 | 110.641 | |
| TL | 6.250 × 10−4 ± 2.011 × 10−5 −0.007 ± 0.001 | 0.004 ± 0.002 0.011 ± 0.007 | −0.002 ± 0.001 0.006 ± 0.003 | 8.900 × 10−5 ± 2.155 × 10−6 2.260 × 10−4 ± 1.118 × 10−5 | −0.004 ± 0.001 0.001 ± 0.001 | 0.011 | 0.8923 | 0.8855 | 1.1199 × 10−7 | 75.402 |
| ANN Structure | Training perf./ Training Error | Test perf./ Test Error | Validation perf./ Validation Error | Hidden Activation | Output Activation | |
|---|---|---|---|---|---|---|
| ANN models without NIR data as the model input | MLP 4-5-5 | 0.9401 0.0179 | 0.9386 0.0191 | 0.9328 0.0175 | Tanh | Identity |
| MLP 4-9-5 | 0.9646 0.0106 | 0.9630 0.0113 | 0.9530 0.0124 | Tanh | Tanh | |
| MLP 4-6-5 | 0.9447 0.0176 | 0.9445 0.0179 | 0.9318 0.0184 | Exponential | Exponential | |
| MLP 4-8-5 | 0.9685 0.0097 | 0.9681 0.0099 | 0.9581 0.0110 | Exponential | Logistic | |
| MLP 4-6-5 | 0.9321 0.0194 | 0.9225 0.0221 | 0.9185 0.0164 | Logistic | Tanh | |
| ANN models including NIR data as the model input | MLP 14-14-5 | 0.9899 0.0031 | 0.9811 0.0062 | 0.9717 0.0071 | Logistic | Tanh |
| MLP 14-14-5 | 0.9916 0.0025 | 0.9826 0.0059 | 0.9732 0.0067 | Tanh | Logistic | |
| MLP 14-13-5 | 0.9814 0.0057 | 0.9726 0.0097 | 0.9616 0.0114 | Exponential | Exponential | |
| MLP 14-8-5 | 0.9838 0.0050 | 0.9789 0.0070 | 0.9737 0.0068 | Logistic | Exponential | |
| MLP 14-11-5 | 0.9878 0.0037 | 0.9806 0.0064 | 0.9755 0.0065 | Logistic | Logistic | |
| MLP 14-14-5 | 0.9899 0.0032 | 0.9811 0.0063 | 0.9717 0.0071 | Logistic | Tanh |
| Model Output | Training | Test | Validation | |
|---|---|---|---|---|
| ANN models without NIR data as the model input | UV254 | 0.9712 | 0.9620 | 0.9431 |
| BrO3− | 0.9760 | 0.9811 | 0.9623 | |
| Br− | 0.9824 | 0.9903 | 0.9774 | |
| HL | 0.9622 | 0.9713 | 0.9365 | |
| TL | 0.9311 | 0.9104 | 0.9459 | |
| ANN models including NIR data as the model input | UV254 | 0.9789 | 0.9657 | 0.9559 |
| BrO3− | 0.9898 | 0.9921 | 0.9876 | |
| Br− | 0.9851 | 0.9916 | 0.9795 | |
| HL | 0.9848 | 0.9735 | 0.9688 | |
| TL | 0.9803 | 0.9716 | 0.9766 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gregov, M.; Jurinjak Tušek, A.; Valinger, D.; Benković, M.; Jurina, T.; Surać, L.; Kurajica, L.; Matošić, M.; Gajdoš Kljusurić, J.; Ujević Bošnjak, M.; et al. Linear and Non-Linear Modelling of Bromate Formation during Ozonation of Surface Water in Drinking Water Production. Water 2023, 15, 1516. https://doi.org/10.3390/w15081516
Gregov M, Jurinjak Tušek A, Valinger D, Benković M, Jurina T, Surać L, Kurajica L, Matošić M, Gajdoš Kljusurić J, Ujević Bošnjak M, et al. Linear and Non-Linear Modelling of Bromate Formation during Ozonation of Surface Water in Drinking Water Production. Water. 2023; 15(8):1516. https://doi.org/10.3390/w15081516
Chicago/Turabian StyleGregov, Marija, Ana Jurinjak Tušek, Davor Valinger, Maja Benković, Tamara Jurina, Lucija Surać, Livia Kurajica, Marin Matošić, Jasenka Gajdoš Kljusurić, Magdalena Ujević Bošnjak, and et al. 2023. "Linear and Non-Linear Modelling of Bromate Formation during Ozonation of Surface Water in Drinking Water Production" Water 15, no. 8: 1516. https://doi.org/10.3390/w15081516